Abstract
Classical black holes contain a singularity at their core. This has prompted various researchers to propose a multitude of modified spacetimes that mimic the physically observable characteristics of classical black holes as best as possible, but that crucially do not contain singularities at their cores. Due to recent advances in near-horizon astronomy, the ability to observationally distinguish between a classical black hole and a potential black hole mimicker is becoming increasingly feasible. Herein, we calculate some physically observable quantities for a recently proposed regular black hole with an asymptotically Minkowski core—the radius of the photon sphere and the extremal stable timelike circular orbit (ESCO). The manner in which the photon sphere and ESCO relate to the presence (or absence) of horizons is much more complex than for the Schwarzschild black hole. We find situations in which photon spheres can approach arbitrarily close to (near extremal) horizons, situations in which some photon spheres become stable, and situations in which the locations of both photon spheres and ESCOs become multi-valued, with both ISCOs (innermost stable circular orbits) and OSCOs (outermost stable circular orbits). This provides an extremely rich phenomenology of potential astrophysical interest.
1. Introduction
Karl Schwarzschild first derived the spacetime metric for the region exterior to a static, spherically symmetric source in 1916 [1]; only some 50 years later was it properly understood that this spacetime could be extrapolated inwards to describe a black hole. Without any loss of generality, any static spherically symmetric spacetime can be described by a metric of the form
For the standard Schwarzschild metric, one sets and . Over the past century, a vast host of black hole spacetimes, qualitatively distinct from that of Schwarzschild, have been investigated by multiple researchers [2,3,4,5,6,7,8,9,10,11,12,13,14].
Furthermore, the field has now grown to not only include classical black holes, but also quantum-modified black holes [15,16,17,18], regular black holes [19,20,21,22,23], and various other exotic spherically symmetric spacetimes that are fundamentally different from black holes but mimic many of their observable phenomena (e.g., traversable wormholes [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], gravastars [40,41,42,43,44,45,46], ultracompact objects [47,48], etc. [49,50,51]; see [52] for an in-depth discussion). Herein, we investigate a specific model spacetime representing a regular black hole. That is, a spacetime that has a well-defined horizon structure, but the curvature invariants are everywhere finite.
Investigating black hole mimickers is becoming increasingly relevant due to recent advances in both observational and gravitational wave astronomy. Projects such as the Event Horizon Telescope [53,54,55,56,57,58], LIGO [59,60], and the planned LISA [61] are and will be continuously probing closer to the horizons of compact massive objects (CMOs), and so there is hope that such projects will eventually be able to distinguish between the near-horizon physics of classical black holes and possible astrophysical mimickers [52]. Herein, we focus on photon rings, ISCOs and OSCOs. Modifications to photon rings would potentially affect the images gathered by the EHT. Modifications to ISCOs would potentially affect both accretion disks and the final inspiral and plunge events detected by LIGO. In contrast, OSCOs (outermost stable circular orbits) do not exist for Schwarzschild or Kerr black holes—so any evidence for the existence of an OSCO would be of immediate astrophysical interest.
The model spacetime investigated in this work is a specific regular black hole with an asymptotically Minkowski core, as discussed in [62,63]. This is an example of a metric with an exponential mass suppression, and is described by the line element
A rather different (extremal) version of this model spacetime, based on nonlinear electrodynamics, was previously discussed by Culetu [64], with follow-up on some aspects of the non-extremal case in [65,66,67] (see also [68,69]).
Most regular black holes have a core that is asymptotically de Sitter (with constant positive curvature) [19,20,21,22]. However, the regular black hole described by the metric (2) has an asymptotically Minkowski core (in the sense that the stress-energy tensor asymptotes to zero). Such models have some attractive features compared to the more common de Sitter core regular black holes: the stress–energy tensor vanishes at the core, greatly simplifying the physics in this region; and many messy algebraic expressions are replaced by simpler expressions involving the exponential and Lambert W functions, whilst still allowing for explicit closed form expressions for quantities of physical interest [62]. Additionally, the results obtained in this work reproduce the standard results for the Schwarzschild metric by letting the parameter . Thus, the value of the parameter a determines the extent of the “deviation” from the Schwarzschild spacetime.
If , then the spacetime described by the metric (2) has two horizons located at
Here, and are the real-valued branches of Lambert W function. We could also write
Perturbatively, for small a, we have
nicely reproducing Schwarzschild in the limit. For the inner horizon, since ,
implies , whence we have a strict upper bound given by the simple analytic expression:
Certainly, as we would expect to recover Schwarzschild; however, the form of is not analytic. This bound can also be viewed as the first term in an asymptotic expansion [70] based on (as )
This leads to
More specifically (as or ),
If , then the two horizons merge at and one has an extremal black hole. If , then there are no horizons, and one is dealing with a regular horizonless extended but compact object (the energy density peaks at ).
This object could either be extended all the way down to , or alternatively be truncated at some finite value of r, to be used as the exterior geometry for some static and spherically symmetric mass source that is not a black hole. This is potentially useful as a model for planets, stars, etc. Consequently, we also incorporate aspects of the analysis for as and when required to generate astrophysical observables in the case when Equation (2) is modeling a compact object other than a black hole.
2. Geodesics and the Effective Potential
Continuing the analysis of [62], we now calculate the location of the photon sphere and extremal stable circular orbit (ESCO) for the regular black hole with line element given by equation (2). Photon spheres (or more precisely the closely related black hole silhouettes) have been recently observed for the massive objects M87 and Sgr A* [53,54,55,56,57,58]. As such, they are, along with the closely related ESCOs, practical and useful quantities to calculate for black hole mimickers.
We begin by considering the affinely parameterized tangent vector to the worldline of a massive or massless particle in our spacetime (2):
where , with corresponding to a massive (timelike) particle and 0 corresponding to a massless (null) particle. (The case would correspond to tachyonic particles following spacelike geodesics, a situation of no known physical applicability.) Since we are working with a spherically symmetric spacetime, we can set without any loss of generality and reduce Equation (11) to
Due to the presence of time-translation and angular Killing vectors, we can now define the conserved quantities
corresponding to the energy and angular momentum of the particle, respectively. Thus, Equation (12) implies
This defines an “effective potential” for geodesic orbits
with the circular orbits corresponding to extrema of this potential.
3. Photon Spheres
We subdivide the discussion into two topics: First the existence of circular photon orbits (photon spheres) and then the stability of circular photon orbits. The discussion is considerably more complex than for the Schwarzschild spacetime, where there is only one circular photon orbit, at , and that circular photon orbit is unstable. Once the extra parameter a is nonzero, and in particular sufficiently large, the set of photon orbits exhibits more diversity.
3.1. Existence of Photon Spheres
For null trajectories, we have
Thus, for circular photon orbits,
To be explicit about this, the location of a circular photon orbit, , is given implicitly by the equation
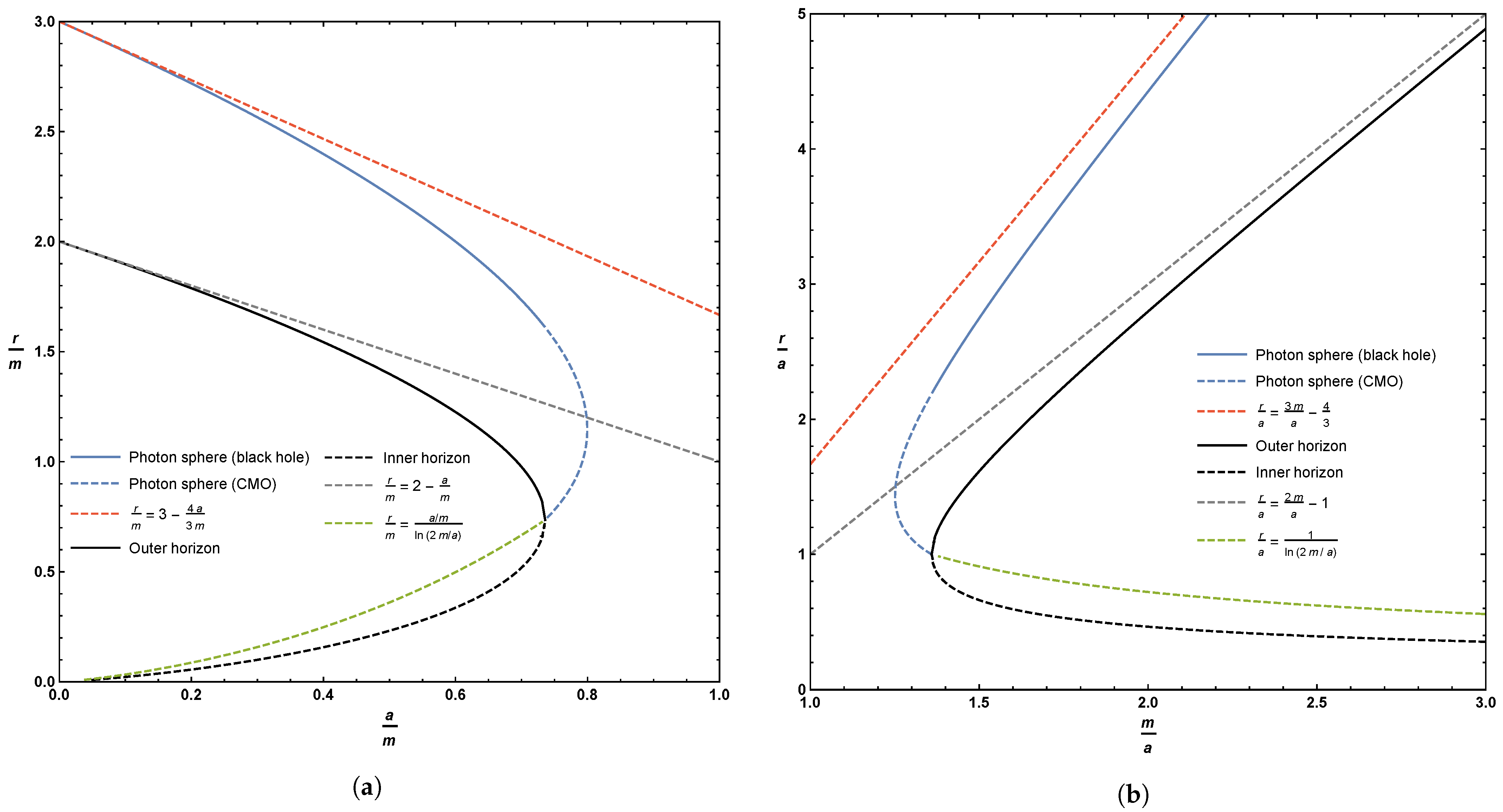
where a and m are fixed by the geometry of the spacetime. 1 The curve described by the loci of these circular photon orbits is plotted in two distinct ways in Figure 1.
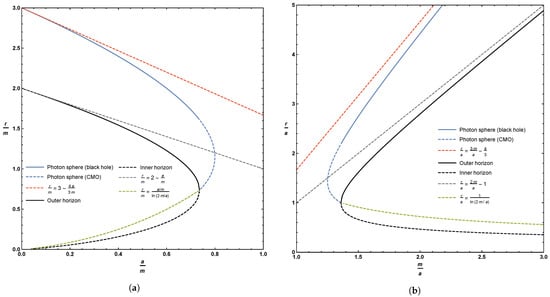
Figure 1.
Location of the photon sphere, inner horizon, and outer horizon. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m. The dashed blue line represents the extension of the photon sphere to horizonless compact massive objects (CMOs), whilst the dashed red line is the asymptotic solution for small values of the parameter a (Equation (21)). The dashed grey line is the asymptotic solution to the outer horizon for small values of a (Equation (5)). The dashed green line is the simple analytic bound and asymptotic estimate for the location of the inner horizon (Equations (7) and (10)).
For clarity, defining and , we can re-write the condition for circular photon orbits as
In Figure 1, we also plot the locations of both inner and outer horizons.
The inner and outer horizons merge at , i.e., at . For , i.e., for , one is dealing with a horizonless compact object and we see that there is a region where there are two circular photon orbits. Note that the curve described by the loci of circular photon orbits terminates once one hits a horizon, i.e., at . Sub-horizon curves of constant r are spacelike (tachyonic), and cannot be lightlike, so they are explicitly excluded. That is, photon spheres can only exist in the region .
Can we be more explicit about the key qualitative and quantitative features of this plot? Specifically, let us now analyze stability versus instability and find the exact location of the various turning points.
3.2. Stability versus Instability for Circular Photon Orbits
To check the stability of these circular photon orbits, we now need to investigate
3.2.1. Perturbative Analysis (small a)
We note that determining from Equation (18) is not analytically feasible, but can certainly be estimated perturbatively for small a. We have
Thus, for small values of a, we recover the standard result for the location of the photon sphere in Schwarzschild spacetime.
Estimating by now substituting the approximate location of the photon sphere as we find
This quantity is manifestly negative for small a. That is, (within the limits of the current small-a approximation), photons are in an unstable orbit at the small-a photon sphere.
3.2.2. Non-Perturbative Analysis
However, if we rephrase the problem, then we can make some much more explicit exact statements that are no longer perturbative in small a: Whereas determining is analytically infeasible, it should be noted that in contrast both and are easily determined analytically:
Consequently, at the peak we can write
Using properties of the Lambert W function, we quickly see that this is negative for , implying instability of the circular photon orbits in this region, (and stability outside this region).
That is, on the curve of circular photon orbits, at the point
This will certainly be negative for , implying instability of the circular photon orbits in this region, (and stability outside this region).
That is, on the curve of circular photon orbits, at the point
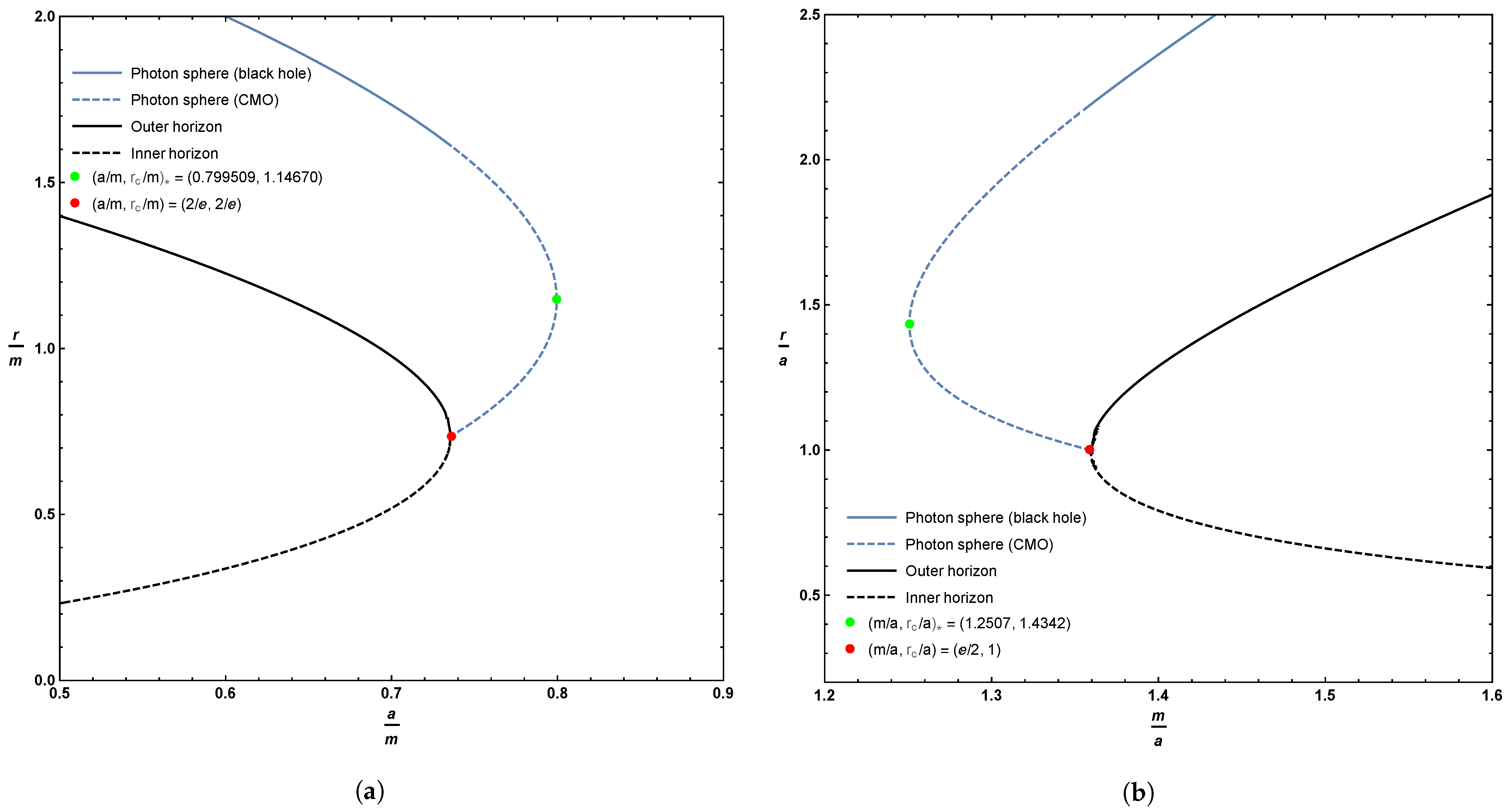
Consequently, on the curve of circular photon orbits, we have existence and stability in the region and existence and instability in the region . Precisely at the point , the photon sphere exhibits neutral stability.
3.3. Turning Points
To evaluate the exact location of the turning points on the curve described by the loci of circular photon orbits, recall that using and we can write this curve as
This allows us to calculate
which has a zero located at , where we have already seen that .
At this point, z takes on its maximum value
Consequently, no photon sphere can exist if
or equivalently
Note that this happens when
which is where, as shown above, .
As can be seen, originally in Figure 1, and now in more detail in the zoomed-in plot in Figure 2, for horizonless compact massive objects, there is a region where there are two possible locations for the photon sphere for fixed values of m and a. Furthermore, when this happens, it is the upper branch that corresponds to an unstable photon orbit, while the lower branch is a stable photon orbit.
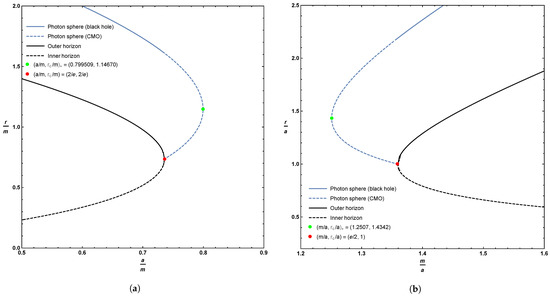
Figure 2.
Zoomed in plots of the location of the photon sphere, inner horizon, and outer horizon, focusing on the extremal and merger regions. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m. The dashed blue line represents the extension of the photon sphere to horizonless compact massive objects (CMOs). Whenever the location of the photon sphere is double-valued, the upper branch corresponds to an unstable photon orbit while the lower branch corresponds to a stable photon orbit.
4. Timelike Circular Orbits
Let us first check the existence, and then the stability, of timelike circular orbits. Even in Schwarzschild spacetime () this is not entirely trivial: Timelike circular orbits exist for all ; they are unstable for , exhibit neutral stability at , and are stable for . Once the parameter a is non-zero the situation is much more complex.
4.1. Existence of Circular Timelike Orbits
For timelike trajectories, the effective potential is given by
and so the locations of the circular orbits can be found from
That is, all timelike circular orbits (there will be infinitely many of them) must satisfy
This is not analytically solvable for , however we can solve for the required angular momentum of these circular orbits:
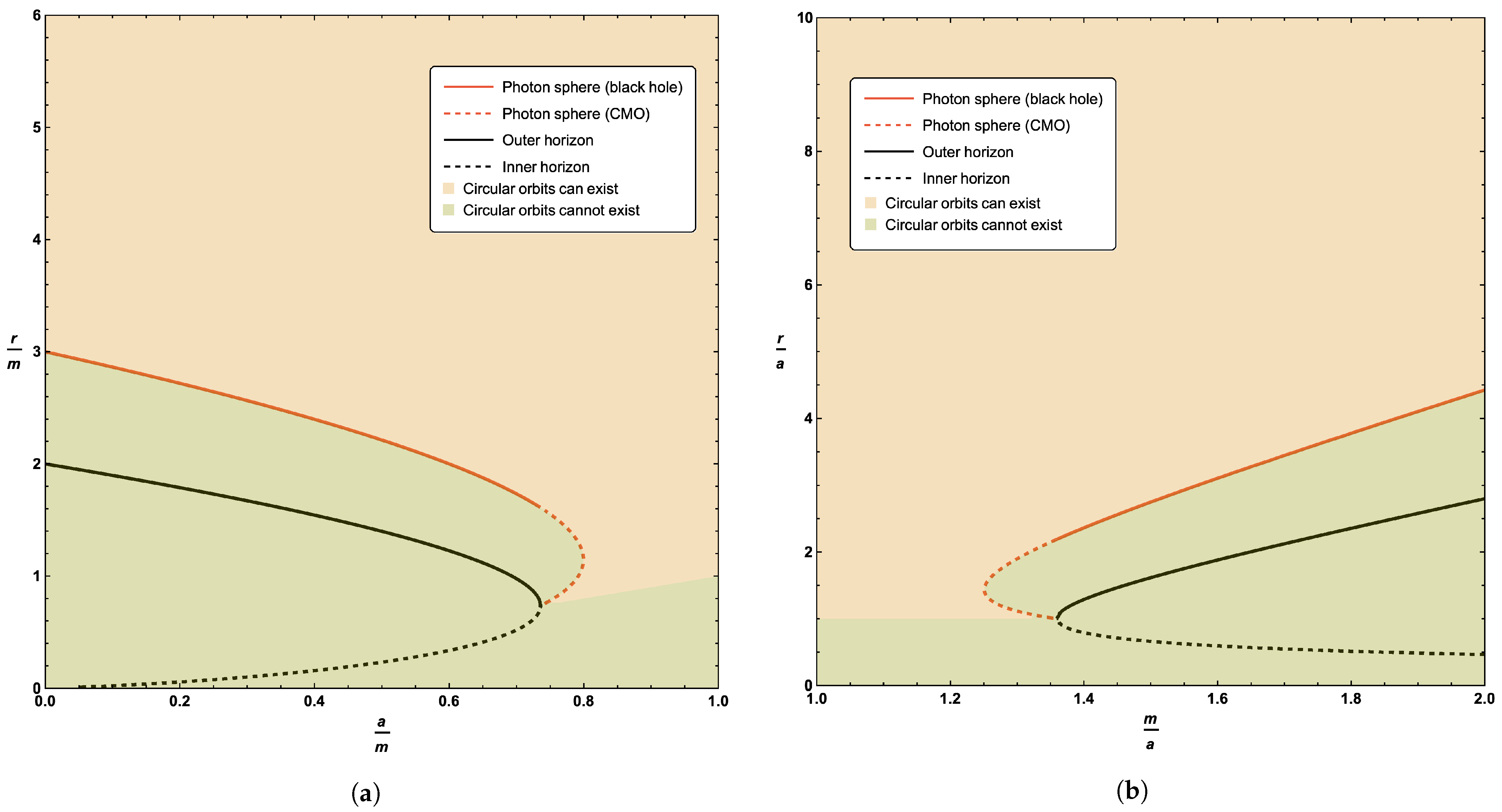
Physically, we must demand , so the boundaries for the existence region of circular orbits (whether stable or unstable) are given by
The first of these conditions, , comes from the fact that in this spacetime gravity is effectively repulsive for . Remember that , and that the pseudo-force due to gravity depends on . Specifically,
and this changes sign at . Thus, for , gravity attracts you to the center, but for gravity repels you from the center.
If gravity repels you, there is no way to counter-balance it with a centrifugal pseudo-force, and so there is simply no way to get a circular orbit, regardless of whether it is stable or unstable. Precisely at , there are stable “orbits” where the test particle just sits there, with zero angular momentum, no sideways motion required. Since by construction , this constraint is relevant only for horizonless CMOs.
The second of these conditions is exactly the location of the photon orbits considered in the previous sub-section. (Physically, what is going on is this: At large distances, it is easy to put a massive particle into a circular orbit with . As one moves inwards and approaches the photon orbit, the massive particle must move more and more rapidly, and the angular momentum per unit mass must diverge when a particle with nonzero invariant mass tries to orbit at the photon orbit.)
Thus, the existence region (rather than just its boundary) for timelike circular orbits is (see Figure 3):
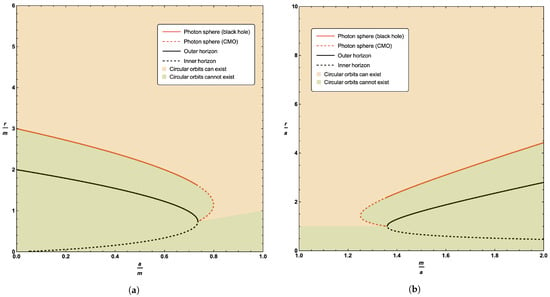
Figure 3.
Locations of the existence region for timelike circular orbits in terms of the circular null geodesics, outer horizon, and inner horizon. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m.
4.2. Stability versus Instability for Circular Timelike Orbits
Now, consider the general expression
and substitute the known value of for circular orbits (see (38)). Then,
Note that at the photon orbit (where the denominator has a zero).
To locate the boundary of the region of stable circular orbits, the ESCO (extremal stable circular orbit), we now need to set , leading to the equation
We note that locating this boundary is equivalent to extremizing . To see this, consider the quantity and differentiate:
This implies
Thence,
However, it is easily checked that is non-zero outside the photon sphere (that is, in the existence region for circular timelike geodesics). Thence,
Defining and , the curve describing the boundary of the region of stable timelike circular orbits can be rewritten as
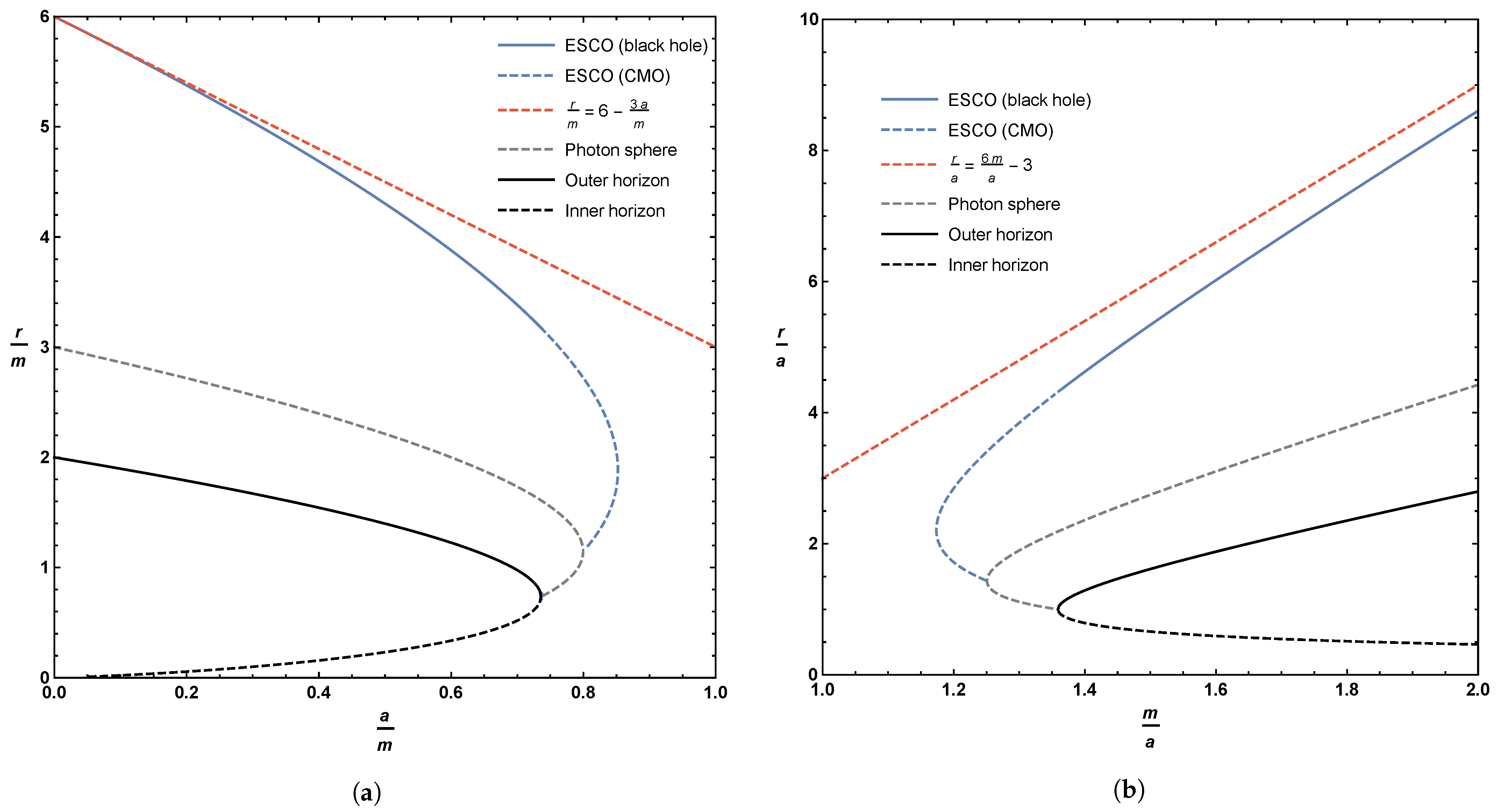
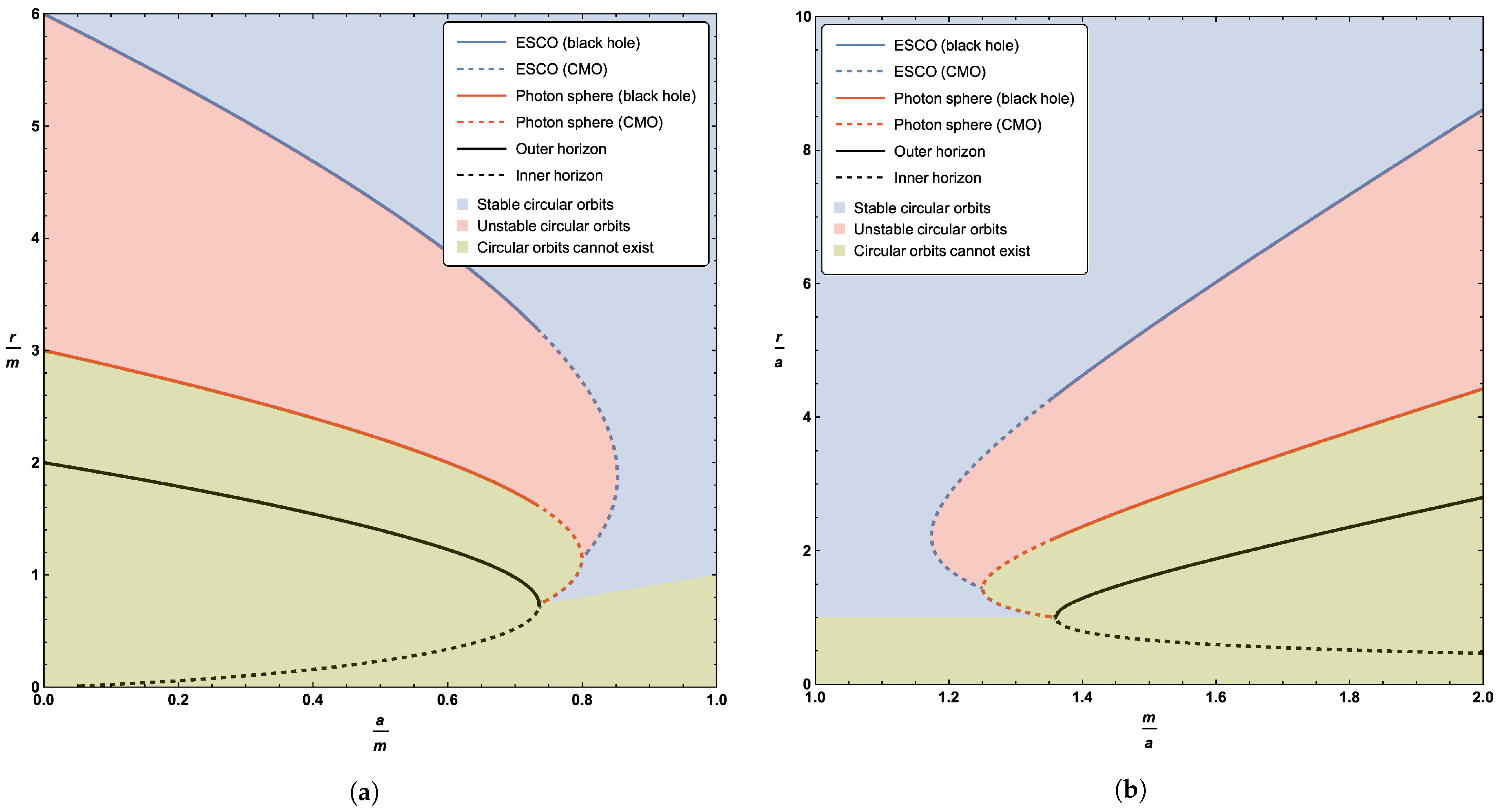
Plots of the boundary implied by Equation (44), or equivalently (49), can be seen in Figure 4. As for the photon sphere, we have the interesting result that the extension of the ESCO to horizonless compact massive objects results in up to two possible ESCO locations for fixed values of a and m. Perhaps unexpectedly, the curve of ESCOs does not terminate at the horizon—it terminates once it hits the curve of circular photon orbits at a very special point. Let us now turn to the detailed analysis of both the qualitative behavior and the various turning points presented in Figure 4 and Figure 5. Note that where the ESCO is single-valued, it is an ISCO (innermost stable circular orbit). Where the ESCO is double-valued, the upper branch is an ISCO and the lower branch is an OSCO (outermost stable circular orbit) [71].
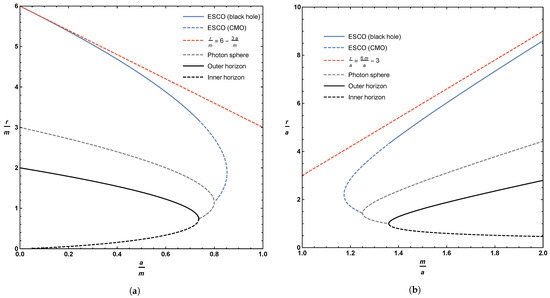
Figure 4.
Locations of the ESCO, photon sphere, outer horizon, and inner horizon. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m. The dashed blue line represents the extension of the ESCO to CMOs. The dashed red curves in (a,b) are the asymptotic location of the ISCO for small values of a (approaching the Schwarzschild solution).
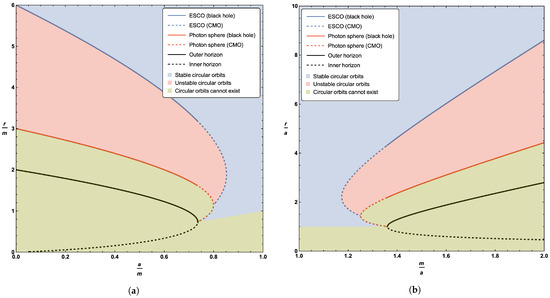
Figure 5.
Locations of the ESCO, photon sphere, outer horizon, and inner horizon. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m. The dashed blue line represents the extension of the ESCO to CMOs. The dashed red line represents the extension of the photon sphere to CMOs. The blue region denotes stable timelike circular orbits, while the red region denotes unstable timelike circular orbits, and the green region denotes the non-existence of timelike circular orbits. Where the ESCO is single-valued, it is an ISCO. Where the ESCO is double-valued, the upper branch is an ISCO and the lower branch is an OSCO (outermost stable circular orbit).
4.2.1. Perturbative Analysis (Small a)
Let us first investigate the existence region perturbatively for small a. We have
Note that this approximation diverges at the Schwarzschild photon sphere . Thus, for small a the boundary for the region of existence of timelike circular orbits is still .
Now, we investigate the stability region perturbatively for small a. Rearranging Equation (44), we see
Thence,
which sensibly reproduces the Schwarzschild ISCO to lowest order in a, and explains the asymptote in Figure 4b.
Furthermore, for small a, substituting into and expanding
Demanding that this quantity be zero self-consistently yields .
4.2.2. Non-Perturbative Analysis
We show above that, defining and , the curve describing the boundary of the region of stable timelike circular orbits can be rewritten as
Thence,
Let us look for the turning points of . The derivative is
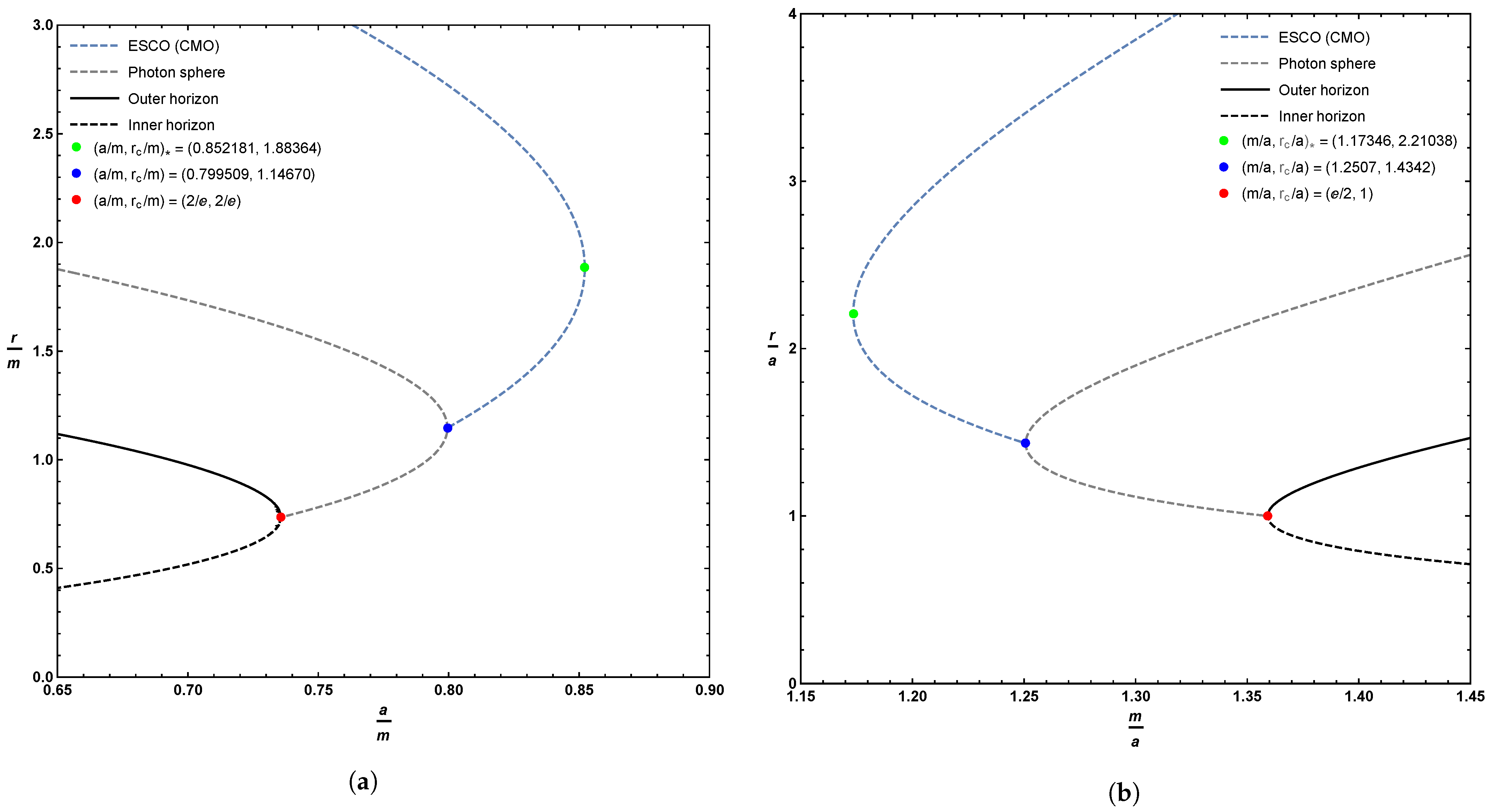
There is one obvious local extrema at , corresponding to . Physically, this corresponds to the point where inner and outer horizon merge and become extremal—but from inspection of Figure 4, the descriptive plots of Figure 5, and the zoomed-in plots of Figure 6, we see that the curve of ESCOs hits the photon orbit (and becomes unphysical) before getting to this point. In terms of the variables used when plotting Figure 4, Figure 5 and Figure 6, this unphysical (from the point of view of ESCOs) point corresponds to
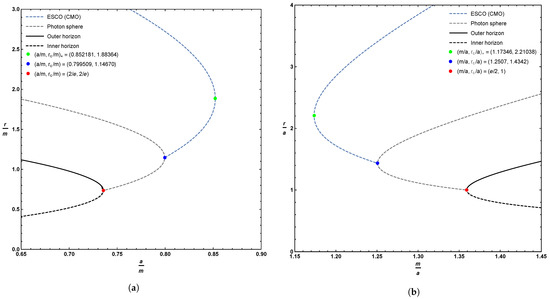
Figure 6.
Zoomed in plot of the locations of the ESCO, outer horizon, and inner horizon for various values of the parameters a and m, focusing on the turning points. Sub-figure (a) plots these quantities as a function of the parameter a; sub-figure (b) plots these quantities as a function of the parameter m. The dashed blue line represents the extension of the ESCO to CMOs. Where the ESCO is single-valued, it is an ISCO. Where the ESCO is double-valued, the upper branch is an ISCO and the lower branch is an OSCO.
The other local extrema is located at the only physical root of the quartic polynomial
While this can be solved analytically, the results are too messy to be enlightening and so we resort to numerics. Two roots are complex, one is negative, and the only physical root is , corresponding to . Physically, this implies that the ESCO curve should exhibit a non-trivial local extremum—and from inspection of Figure 4 we see that the curve of ESCOs does indeed have a local extremum at this point. In terms of the variables used when plotting Figure 4, this extremal point corresponds to
and
4.3. Intersection of ESCO and Photon Sphere
We can rewrite the curve for the loci of the photon spheres (19) as
Similarly, for the loci of ESCOs, we rewrite (55) as
These curves cross at
That is, at
with explicit roots at
The physically relevant root is , which is where we determine above that the photon sphere became stable and at the point where the curve of photon spheres maximizes the value of .
4.4. Explicit Result for the Angular Momentum
We can rewrite the curve for the angular momentum (38) as
Similarly, for the loci of ESCOs, we can rewrite (55) as
We then substitute this into back into :
This has a pole at , and is then positive and finite for all . (Of course, the point on the ESCO curve is exactly where the ESCO curve hits the photon curve, so we would expect the angular momentum to go to infinity there.) Asymptotically, for large r (large ), we have and , so as expected from the large-distance Newtonian limit.
4.5. Summary
Overall, we see that the boundary of the stability region for timelike circular orbits is rather complicated. In terms of the variable :
- For , we have an ESCO.This ESCO then subdivides as follows:
- -
- For , we have an ISCO.
- -
- For , we have an OSCO.
- For , the stability region is bounded by a stable photon orbit.
- The line bounds the stability and existence region for timelike circular orbits from below.
This is considerably more complicated than might reasonably have been expected.
5. Conclusions
In this work, we investigate astrophysically observable quantities of a specific novel regular black hole model based on an asymptotically Minkowski core [62,63]: Specifically, we investigate the photon sphere and ESCO. The spacetime under consideration is an example of a black hole mimicker. For the regular black hole model, both the photon sphere and the ESCO exist and are located outside of the outer horizon, and thus (at least in theory) could be astrophysically observable. The analysis of the photon sphere and ESCO is extended to horizonless compact massive objects, leading to the surprising results that, for fixed values of m and a, up to two possible photon sphere and up to two possible ESCO locations exist in our model spacetime; and that the very existence of the photon sphere and ESCO depends explicitly on the ratio . Somewhat unexpectedly, due to the effectively repulsive nature of gravity in the region near the core, we find some situations in which the photon orbits are stable and some situations where the ESCOs are OSCOs rather than ISCOs. There is a rich phenomenology here that is significantly more complex than for the Schwarzschild spacetime.
Author Contributions
Conceptualization, T.B., A.S. and M.V.; methodology, T.B., A.S. and M.V.; software, T.B., A.S. and M.V.; validation, T.B., A.S. and M.V.; formal analysis, T.B., A.S. and M.V.; resources, M.V.; writing—original draft preparation, T.B., A.S. and M.V.; writing—review and editing, T.B., A.S. and M.V.; visualization, T.B., A.S. and M.V.; supervision, M.V.; project administration, M.V.; and funding acquisition, M.V. All authors have read and agreed to the published version of the manuscript.
Funding
TB was supported by a Victoria University of Wellington MSc scholarship and was also indirectly supported by the Marsden Fund, via a grant administered by the Royal Society of New Zealand. AS acknowledges financial support via a PhD Doctoral Scholarship provided by Victoria University of Wellington. AS is also indirectly supported by the Marsden fund, via a grant administered by the Royal Society of New Zealand. MV was directly supported by the Marsden Fund, via a grant administered by the Royal Society of New Zealand.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ESCO | Extremal stable circular orbit |
| ISCO | Innermost stable circular orbit |
| OSCO | Outermost stable circular orbit |
| CMO | Compact massive object |
References
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsberichte Der KÖniglich Preuss. Akad. Der Wiss. 1916, 7, 189. [Google Scholar]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Der Phys. 1916, 50, 106. [Google Scholar] [CrossRef]
- Weyl, H. Zur Gravitationstheorie. Ann. Der Phys. 1917, 54, 117. [Google Scholar] [CrossRef]
- Nordström, G. On the Energy of the Gravitational Field in Einstein’s Theory. Verhandl. Koninkl. Ned. Akad. Wetenschap. Afdel. Natuurk. 1918, 24, 1201. [Google Scholar]
- Kerr, R. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237. [Google Scholar] [CrossRef]
- Newmann, E.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Kerr, R.; Schild, A. Republication of: A new class of vacuum solutions of the Einstein field equations. Gen. Rel. Grav. 2009, 41, 2485. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A brief introduction. arXiv 2007, arXiv:0706.0622. [Google Scholar]
- Wiltshire, D.L.; Visser, M.; Scott, S.M. The Kerr Spacetime: Rotating Black Holes in General Relativity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Baines, J.; Berry, T.; Simpson, A.; Visser, M. Unit-lapse versions of the Kerr spacetime. arXiv 2008, arXiv:2008.03817. [Google Scholar]
- Baines, J.; Berry, T.; Simpson, A.; Visser, M. Painleve-Gullstrand form of the Lense-Thirring spacetime. arXiv 2006, arXiv:2006.14258. [Google Scholar]
- Vaidya, P.C. The External Field of a Radiating Star in General Relativity. Curr. Sci. (India) 1943, 12, 183. [Google Scholar] [CrossRef]
- Vaidya, P.C. The external field of a radiating star. Proc. Indian Acad. Sci. 1951, 33, 264. [Google Scholar] [CrossRef]
- Vaidya, P.C. Nonstatic solutions of Einstein’s field equations for spheres of fluids radiating energy. Phys. Rev. 1951, 83, 10. [Google Scholar] [CrossRef]
- Calmet, X. Quantum Aspects of Black Holes; Springer Int. Pub.: Heidelberg, Germany, 2015. [Google Scholar]
- Calmet, X.; El-Menoufi, B.K. Quantum corrections to Schwarzschild black hole. Eur. Phys. J. C 2017, 77, 243. [Google Scholar] [CrossRef]
- Kazakov, D.I.; Solodukhin, S.N. On quantum deformation of the Schwarzschild solution. Nucl. Phys. B 1994, 429, 153. [Google Scholar] [CrossRef]
- Ali, A.F.; Khalil, M.M. Black hole with quantum potential. Nucl. Phys. B 2016, 909, 173. [Google Scholar] [CrossRef]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, Tbilisi, Georgia, USSR, 9–13 September 1968. [Google Scholar]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Frolov, V.P. Information loss problem and a ‘black hole’ model with a closed apparent horizon. J. High Energy Phys. 2014, 2014, 49. [Google Scholar] [CrossRef]
- Ansoldi, S. Spherical black holes with regular center: A review of existing models including a recent realization with Gaussian sources. arXiv 2008, arXiv:0802.0330. [Google Scholar]
- Carballo-Rubio, R.; di Filippo, F.; Liberati, S.; Pacilio, C.; Visser, M. On the viability of regular black holes. J. High Energy Phys. 2018, 2018, 20. [Google Scholar] [CrossRef]
- Morris, M.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching General Relativity. Am. J. Phys. 1988, 56, 395. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition? Phys. Rev. Lett. 1988, 61, 1446. [Google Scholar] [CrossRef] [PubMed]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; Springer: New York, NY, USA, 1995. [Google Scholar]
- Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 1989, 39, 3182. [Google Scholar] [CrossRef] [PubMed]
- Visser, M. Traversable wormholes from surgically modified Schwarzschild space-times. Nucl. Phys. B 1989, 328, 203–212. [Google Scholar] [CrossRef]
- Visser, M. Wormholes, Baby Universes and Causality. Phys. Rev. D 1990, 41, 1116. [Google Scholar] [CrossRef]
- Visser, M.; Kar, S.; Dadhich, N. Traversable wormholes with arbitrarily small energy condition violations. Phys. Rev. Lett. 2003, 90, 201102. [Google Scholar] [CrossRef]
- Visser, M. From wormhole to time machine: Comments on Hawking’s chronology protection conjecture. Phys. Rev. D 1993, 47, 554–565. [Google Scholar] [CrossRef]
- Kar, S.; Dadhich, N.; Visser, M. Quantifying energy condition violations in traversable wormholes. Pramana 2004, 63, 859–864. [Google Scholar] [CrossRef]
- Poisson, E.; Visser, M. Thin shell wormholes: Linearization stability. Phys. Rev. D 1995, 52, 7318–7321. [Google Scholar] [CrossRef]
- Cramer, J.G.; Forward, R.L.; Morris, M.S.; Visser, M.; Benford, G.; Landis, G.A. Natural wormholes as gravitational lenses. Phys. Rev. D 1995, 51, 3117–3120. [Google Scholar] [CrossRef]
- Dadhich, N.; Kar, S.; Mukherji, S.; Visser, M. R=0 space-times and selfdual Lorentzian wormholes. Phys. Rev. D 2002, 65, 064004. [Google Scholar] [CrossRef]
- Boonserm, P.; Ngampitipan, T.; Simpson, A.; Visser, A. The exponential metric represents a traversable wormhole. Phys. Rev. D 2018, 98, 084048. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. JCAP 2019, 1902, 42. [Google Scholar] [CrossRef]
- Simpson, A.; Martín-Moruno, P.; Visser, M. Vaidya spacetimes, black-bounces, and traversable wormholes. Class. Quant. Grav. 2019, 36, 145007. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Simpson, A.; Visser, M. Dynamic thin-shell black-bounce traversable wormholes. Phys. Rev. D 2020, 101, 124035. [Google Scholar] [CrossRef]
- Mazur, P.O.; Mottola, E. Gravitational vacuum condensate stars. Proc. Natl. Acad. Sci. USA 2004, 101, 9545. [Google Scholar] [CrossRef]
- Mazur, P.O.; Mottola, E. Gravitational Condensate Stars: An Alternative to Black Holes. arXiv 2001, arXiv:0109035. [Google Scholar]
- Visser, M.; Wiltshire, D. Stable gravastars: An alternative to black holes? Class. Quant. Grav. 2004, 21, 1135. [Google Scholar] [CrossRef]
- Cattoën, C.; Faber, T.; Visser, M. Gravastars must have anisotropic pressures. Class. Quant. Grav. 2005, 22, 4189–4202. [Google Scholar] [CrossRef]
- Lobo, F.S.N. Stable dark energy stars. Class. Quant. Grav. 2006, 23, 1525. [Google Scholar] [CrossRef]
- Martín-Moruno, P.; Montelongo-García, N.; Lobo, F.S.N.; Visser, M. Generic thin-shell gravastars. JCAP 2012, 3, 34. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Martín-Moruno, P.; Montelongo-García, N.; Visser, M. Novel stability approach of thin-shell gravastars. arXiv 2015, arXiv:1512.07659. [Google Scholar]
- Cunha, P.V.; Berti, E.; Herdeiro, C.A.R. Light-Ring Stability for Ultracompact Objects. Phys. Rev. Lett. 2017, 119, 251102. [Google Scholar] [CrossRef] [PubMed]
- Cunha, P.V.; Herdeiro, C.A.R. Stationary black holes and light rings. Phys. Rev. Lett. 2020, 124, 181101. [Google Scholar] [CrossRef] [PubMed]
- Carballo-Rubio, R.; di Filippo, F.; Liberati, S.; Visser, M. Opening the Pandora’s box at the core of black holes. Class. Quant. Grav. 2020, 37, 145005. [Google Scholar] [CrossRef]
- Visser, M.; Barceló, C.; Liberati, S.; Sonego, S. Small, dark, and heavy: But is it a black hole? PoS BHGRS 2008, 17. [Google Scholar] [CrossRef]
- Visser, M. Physical observability of horizons. Phys. Rev. D 2014, 90, 127502. [Google Scholar] [CrossRef]
- Carballo-Rubio, R.; di Filippo, F.; Liberati, S.; Visser, M. Phenomenological aspects of black holes beyond general relativity. Phys. Rev. D 2018, 98, 124009. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJL 2019, 875, L1. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. ApJL 2019, 875, L2. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. ApJL 2019, 875, L3. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. ApJL 2019, 875, L4. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. ApJL 2019, 875, L5. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. ApJL 2019, 875, L6. [Google Scholar] [CrossRef]
- Collection of Detection Papers from LIGO. Publications from the LIGO Scientific Collaboration and Virgo Collaboration. Available online: https://www.ligo.caltech.edu/page/detection-companion-papers (accessed on 20 December 2020).
- Current Gravitational Wave Observations. Available online: wikipedia.org/List_of_gravitational_wave_observations (accessed on 20 December 2020).
- Barausse, E.; Berti, E.; Hertog, T.; Hughes, S.A.; Jetzer, P.; Pani, P.; Sotiriou, T.P.; Tamanini, N.; Witek, H.; Yagi, K.; et al. Prospects for Fundamental Physics with LISA. Gen. Rel. Grav. 2020, 52, 8. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. Regular black holes with asymptotically Minkowski cores. Universe 2020, 6, 8. [Google Scholar] [CrossRef]
- Berry, T.; Lobo, F.S.; Simpson, A.; Visser, M. Simpson and M. Visser, Thin-shell traversable wormhole crafted from a regular black hole with asymptotically Minkowski core. Phys. Rev. D 2020, 102, 064054. [Google Scholar] [CrossRef]
- Culetu, H. On a regular modified Schwarzschild spacetime. arXiv 2013, arXiv:1305.5964. [Google Scholar]
- Culetu, H. On a regular charged black hole with a nonlinear electric source. Int. J. Theor. Phys. 2015, 54, 2855. [Google Scholar] [CrossRef]
- Culetu, H. Nonsingular black hole with a nonlinear electric source. Int. J. Mod. Phys. D 2015, 24, 1542001. [Google Scholar] [CrossRef]
- Culetu, H. Screening an extremal black hole with a thin shell of exotic matter. Phys. Dark Univ. 2016, 14, 1. [Google Scholar] [CrossRef][Green Version]
- Junior, E.L.B.; Rodrigues, M.E.; Houndjo, M.J.S. Regular black holes in f(T) Gravity through a nonlinear electrodynamics source. JCAP 2015, 1510, 60. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Junior, E.L.B.; Marques, G.T.; Zanchin, V.T. Regular black holes in f(R) gravity coupled to nonlinear electrodynamics. Phys. Rev. D 2016, 94, 024062. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Boonserm, P.; Ngampitipan, T.; Simpson, A.; Visser, M. Innermost and outermost stable circular orbits in the presence of a positive cosmological constant. Phys. Rev. D 2020, 101, 24050. [Google Scholar] [CrossRef]
| 1. | As , we have , as expected for Schwarzschild spacetime. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).