Abstract
We construct higher-dimensional and exact black holes in Einstein-Maxwell-scalar theory. The strategy we adopted is to extend the known, static and spherically symmetric black holes in the Einstein-Maxwell dilaton gravity and Einstein-Maxwell-scalar theory. Then we investigate the black hole thermodynamics. Concretely, the generalized Smarr formula and the first law of thermodynamics are derived.
1. Introduction
According to the Lovelock [1,2] and the Ostrogradsky instability [3] theorems, it is uniquely the Einstein gravity that consists of metric and its derivatives and with the equations of motion no more than second order. Therefore, to extend the Einstein gravity, the easiest way is to couple it with a scalar field. On the other hand, string theory is generally considered to be the most promising approach to unify quantum theory and gravity in higher dimensions. The low energy limit of string theory does lead to the Einstein gravity coupled non-minimally to a scalar dilaton field [4]. The dilaton field, coupled in a nontrivial way to other fields such as gauge fields has aroused many interests and many black hole solutions are found [5,6,7,8].
These solutions are all asymptotically flat. It has been proved [9,10] that in the presence of one or two Liouville-type potential which is considered to be a generalization of the cosmological constant, neither asymptotically flat nor (anti)-de Sitter solutions exist. However, by combining three Liouville-type dilaton potential, one successfully constructs a higher-dimensional asymptotically (anti)-de Sitter solutions [11]. Then the topological anti-de Sitter black branes with higher dimensions in Einstein-Maxwell dilaton theory were constructed and their properties were investigated [12]. With the same dilaton potential in [11], Sheykhi [13] finds the metric for the n-dimensional charged slowly rotating dilaton black hole in the background of asymptotically (anti)-de Sitter spacetime.
On the other hand, a remarkable phenomenon of spontaneous scalarization of charged black holes is recently discovered [14,15] and vast studies on the scalarization of black holes in various Einstein-Maxwell-scalar (EMS) models (see [16] and references therein) are carried out. Most of these studies are based on numerical calculations. In view of this point, we will construct exact charged black hole solutions in EMS theory. Our strategy is to extend the known, static and spherically symmetric black holes in the Einstein-Maxwell dilaton gravity to EMS theory. Actually, using this method, we have constructed the four-dimensional black holes in EMS in [17]. Thus, the purpose of this paper is to extend it from four dimensions to higher dimensions.
The paper is organized as follows. In Section 2, we derive the equations of motion for the fields and present the metric. In Section 3, we introduce the generalized Smarr formula for this solution and verify the validity of the first law of black hole thermodynamics. In Section 4, we investigate the thermodynamic stability problem and the phase transitions by using heat capacity and Gibbs free energy. In Section 5 we summarize our results.
2. Action and the Equations Motion
We start from the action of Einstein-Maxwell-scalar theory
where R is the Ricci scalar curvature, comes from the Maxwell field, is the coupling function between scalar field and Maxwell field. is the scalar potential.
Varying the action with respect to the metric, Maxwell and the scalar field, respectively, yields
We choose the most general form of the metric for static black hole as follows
where x denotes the radial variable. Then the Maxwell Equation (3) can be integrated to give
where q is the constant of integration and it has the dimension of . Then the equations of motion (2) to (4) reduce to three independent equations
There are five functions U, f, , V and K in these equations. However, we have only three equations. Therefore, the system of equations is not closed. In general, one usually presumes and then solve for . For example, Reference [11] assumes
Here is the dilaton potential in higher dimensions. It combines three Liouville-type potential which is considered to be a generalization of the cosmological constant. We have mentioned in the introduction that it has been proved [9,10,11] that only by combining more than two such potential, can the asymptotically (anti)-de Sitter solution exists.
Then Reference [11] gives the solution as follows
Here are two integration constants which are related to the black hole mass and electric charge. is the cosmological constant and is the coupling constant. is given by [11]
In contrast to the above example, here we shall presume in advance and then solve for . To find the desirable expressions for U and f, we observe Equation (12) and find that the term is proportional to .
On the other hand, the four-dimensional black hole solution in EMS theory is [17]
Equation (18) is the expression of in four dimensions. is the extension of dilaton coupling . We [17] have shown that with this extension, the well-known Reissner-Nordstrom-de Sitter solution can be included when .
Therefore, motivated by Equations (12) and (15), we presume a new solution
with
where is a constant. If we take the limit of , we shall find Equation (19) reduces to the metric describing (anti)-de Sitter metric. Therefore, the metric is asymptotically (anti)-de Sitter. Compared with metric (12), this metric includes a new term of which is related the charge squared. With the introduction of this new term, the higher-dimensional Reissner-Nordstrom-de Sitter black holes can be reduced provided that and . In fact, the metric is the higher-dimensional extension of the metric found in [17]
When , we find U and f reduce to the four-dimensional metric describing charged (Anti)-de-Sitter black holes. Therefore, given the Einstein-Maxwell-scalar theory (the extension of dilaton coupling Equation (27) and the dilaton potential Equation (11)), the metric Equation (19) is unique. Now a new term of is inserted in the expression of U. Since q has the dimension of , is dimensionless. Given the expressions of , the expressions of are then worked out from the equations of motion. To this end, we transform the equations of motion from coordinates to coordinates via the following coordinates transformation
Then the equations of motion Equations (7)–(9) turn out to be
Substituting Equation (20) into above equations of motion, we obtain
and
with V the exact form of Equation (11). When , K restores to Equation (17). Up to this point, the n-dimensional and exact black hole solution is constructed in EMS theory.
In the next, we calculate the electric charge and mass of the black hole. The electric charge is
The definition of variable is given by Equation (22). means . In other words, we take the limit at spatial infinity. The quasilocal mass of the dilaton (anti)de Sitter black hole can be calculated by using the subtraction method of Brown and York (BY) [18,19]. This is an extension of ADM definition of the mass. For asymptotically flat or asymptotically AdS spacetimes, the ADM mass at infinity coincides with the conserved mass in Brown York method. Therefore, following the procedures of [20], we choose the method of Brown and York in this paper. The definition of conserved mass is given by
where is the boundary surface of the spacetime, a timelike Killing vector field on , the determinant of the metric of the boundary , the extrinsic curvature of the background metric and the timelike unit normal vector to the boundary . In the context of counterterm method and following the procedure of [20], we get, after a detailed calculation,
which is the same as [20].
3. Thermodynamics
In this section, we explore the black hole thermodynamics. Concretely, we shall construct the generalized Smarr formula and the first law of thermodynamics. To this end, we start from the calculation of Hawking temperature which is defined as follows:
where is a Killing vector field which is null on the horizon. Since we are dealing with a static metric and we can choose . Then one can write the expression of temperature for black holes
with the metric
The coordinate system used here is singular on the black hole horizon. However, the divergence of coordinate system on the black hole horizon does not mean the thermodynamic quantities are divergent. This is because the thermodynamic quantities, for example, the mass, the temperature, the entropy and so on, evaluated below are all defined and observed by the observers in spatial infinity. Of course, for the observers resting on the horizon, these thermodynamic quantities are all divergent. The technique we adopt in the paper is very traditional in the literature. For example, the Schwarzschild coordinate system used in the Schwarzschild metric is singular on the black hole horizon. However, the corresponding thermodynamic quantities are all regular although they are evaluated in Schwarzschild coordinate system. As for the definition of the temperature, it is divergent on the horizon at first glance. However, it is not the case. Actually, since , we conclude that there is no singularity in the temperature.
After substituting the equation of event horizon , we get the formula for temperature
where and represents the radius of black hole event horizon.
The entropy of black holes generally satisfies the area law which states that the entropy is a quarter of the area of black hole event horizon [21,22,23]. This nearly universal law applies to almost all kinds of black holes, including Einstein-Maxwell-scalar black holes [24,25,26]. Therefore, we have the entropy
The electrical potential is defined by
where is defined by
When , reduces to that in [20].
We define the thermal pressure P
Given the equation of event horizon, can be expressed as the functions of . However, we do not bother to give it here because it is too lengthy.
The conjugate thermal volume is
Then we find that the generalized Smarr formula
is indeed satisfied. It is apparent the formula is related to dimension of spacetime.
Choosing a, b, as independent variables and making the differentiation M, S, Q, P with respect to a, b, , we obtain
After straightforward but complicated calculations, the first law of thermodynamics is indeed satisfied. In contrast to the Smarr formula, the first law is not related to the dimension of spacetime.
4. Heat Capacity and Stability in Canonical Assemble
The local stability of a thermodynamic system in canonical ensemble depends on the sign of the heat capacity. If the sign is positive, the system is thermodynamically stable. On the contrary, if the sign is negative, the system would go under phase transition and then acquires stable state. This phase transition could happen whenever heat capacity meets a root or has a divergency.
In Figure 1a,b, we plot the black hole temperature T and the heat capacity with respect to the black hole event horizon . We consider the parameters as follows for different . The negative means we are considering black hole in anti-Sitter universe. Figure 1a shows that when , there are two phases of black holes, the so-called small black holes and large black holes, respectively. On the other hand, if , there would be three phases of black holes, the so-called small, middle and large black holes, respectively. The case with positive has generally two event horizons, namely the inner horizon and the outer event horizon while the negative has only one outer event horizon. Figure 1b shows some points of divergence. According to the viewpoint of Davies [27], the divergence of heat capacity means the second-order phase transition. Comparing it with Figure 1a, we see, for negative , the heat capacity of small black hole is negative while the one of large black hole is positive. We conclude that the small black holes with one event horizon is thermodynamically unstable while the large black holes with one event horizon are stable. For positive , the heat capacity of middle black hole is negative while the heat capacity of both small and large black holes is positive. Thus, we conclude that the middle black hole with two horizons is unstable while the small and large black holes with two horizons are stable.
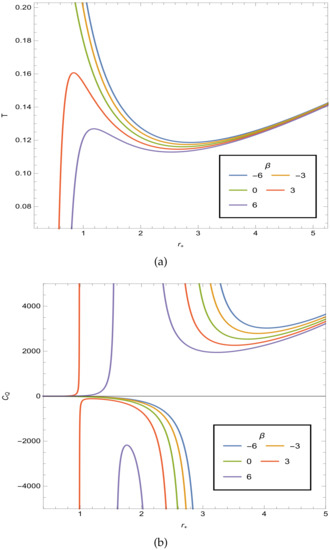
Figure 1.
(a)The black hole temperature with respect to event horizon . (b) The black hole heat capacity with respect to the event horizon . The parameters are , , , .
We can also identify these phase transitions through the diagram of Gibbs energy with respect to black hole temperature. In Figure 2, we plot the relations with running . It shows that when , the black holes make phases transition from small black holes to large black holes with the increasing of Hawking temperature. As is known, the specific heat is . Therefore, the thermodynamically stable and unstable phases have the concave downward and upward curves, respectively. Then we conclude that the large black holes are thermodynamically stable while the small black holes are unstable. Figure 2 also shows that when , the system makes phase transitions from small black hole to middle black hole, and finally to large black holes with the increasing of Hawking temperature. In this case, both the phase large and small black holes are thermodynamically stable while the middle black holes are unstable.
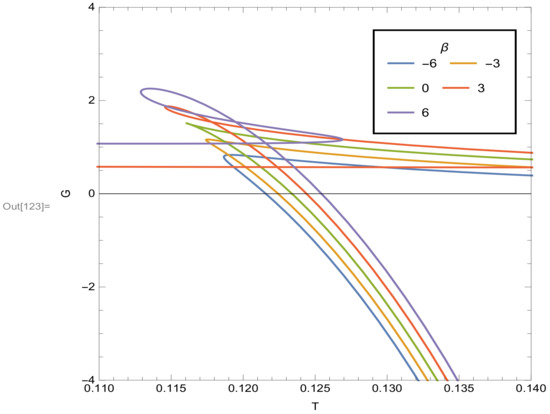
Figure 2.
The black hole Gibbs free energy with respect to temperature. The parameters are , , , .
5. Conclusions and Discussion
In Section 2, starting from the n-dimensional black hole solution in Einstein dilaton gravity and inspired by the four-dimensional black hole solution in Einstein-Maxwell-scalar theory, and the metric is (19), we construct n-dimensional black hole in Einstein-Maxwell-scalar theory. A new coupling function (27) between the scalar field and the Maxwell invariant is present. However, the scalar potential (11) remains the form in Einstein-Maxwell dilaton gravity.
The black hole is described by physical mass (31), electric charge (29), cosmological constant and two dimensionless coupling constants and . However, in essence, the solution has three hairs, namely the mass M, electric charge Q and cosmological constant . There are not any new hairs. Therefore, the solution is not inconsistent with the no-hair theorem.
Then in Section 3, we explore the corresponding thermodynamics. The fundamental thermodynamic functions, namely the enthalpy (31), the temperature (35), the entropy (36) and the thermal volume (40) are derived. Then the generalized Smarr formula (41) which contains the dimension of spacetime is found. By straightforward but complicated calculations, the first law of thermodynamics (42) is satisfied.
Finally, in Section 4, we also study the thermodynamic stability problem and the phase transitions in anti-de Sitter universe. We find, for negative , there is generally one event horizon. In this case, According to the figure of black hole temperature with respect to event horizon , we find there are two phases of black holes, namely the small black hole phase and large black hole phase, respectively. The small black hole is thermodynamically unstable while the large black hole is stable. With the increasing of Hawking temperature, the system makes phase transitions from small black hole phase to large black hole phase. For positive , there are generally two horizons, namely the inner horizon and outer event horizon. In this case, there are three phases corresponding to small, middle and large black holes, respectively (See Figure 1a). The middle black hole is thermodynamically unstable while both the small and large black holes are stable (See Figure 1b). With the increasing of Hawking temperature, the system makes phase transitions from small black hole to middle black hole, and finally to large black holes (See Figure 2).
Author Contributions
J.Q.: Conceptualization, validation, writing—original draft preparation, writing—review and editing. C.G.: Conceptualization, validation, supervision, project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the Strategic Priority Research Program “Multi-wavelength Gravitational Wave Universe” of the CAS, Grant No. XDB23040100 and the NSFC under grants 11633004, 11773031.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Lovelock, D. The four-dimensionality of space and the Einstein tensor. J. Math. Phys. 1972, 13, 874–876. [Google Scholar] [CrossRef]
- Woodard, R.P. The theorem of Ostrogradsky. arXiv 2015, arXiv:1506.02210. [Google Scholar]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory: Volume 2, Loop Amplitudes, Anomalies and Phenomenology; Cambridge University Press: Cambridge, UK, 1987; Volume 2. [Google Scholar]
- Gibbons, G.W.; Maeda, K.i. Black holes and membranes in higher-dimensional theories with dilaton fields. Nucl. Phys. B 1988, 298, 741–775. [Google Scholar] [CrossRef]
- Garfinkle, D.; Horowitz, G.T.; Strominger, A. Charged black holes in string theory. Phys. Rev. D 1991, 43, 3140. [Google Scholar] [CrossRef]
- Brill, D.; Horowitz, G.T. Negative energy in string theory. Phys. Lett. B 1991, 262, 437–443. [Google Scholar] [CrossRef]
- Gregory, R.; Harvey, J.A. Black holes with a massive dilaton. Phys. Rev. D 1993, 47, 2411. [Google Scholar] [CrossRef]
- Poletti, S.J.; Wiltshire, D.L. Global properties of static spherically symmetric charged dilaton spacetimes with a Liouville potential. Phys. Rev. D 1994, 50, 7260. [Google Scholar] [CrossRef]
- Poletti, S.J.; Twamley, J.; Wiltshire, D.L. Charged dilaton black holes with a cosmological constant. Phys. Rev. D 1995, 51, 5720. [Google Scholar] [CrossRef]
- Gao, C.J.; Zhang, S.N. Higher-dimensional dilaton black holes with cosmological constant. Phys. Lett. B 2005, 605, 185–189. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A.; Dehghani, M.H. Thermodynamics of higher dimensional topological charged AdS black branes in dilaton gravity. Eur. Phys. J. C 2010, 70, 703–712. [Google Scholar] [CrossRef]
- Sheykhi, A.; Allahverdizadeh, M. Higher dimensional charged rotating dilaton black holes. Gen. Relativ. Gravit. 2010, 42, 367–379. [Google Scholar] [CrossRef]
- Herdeiro, C.A.; Radu, E.; Sanchis-Gual, N.; Font, J.A. Spontaneous scalarization of charged black holes. Phys. Rev. Lett. 2018, 121, 101102. [Google Scholar] [CrossRef]
- Fernandes, P.G.; Herdeiro, C.A.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Spontaneous scalarisation of charged black holes: Coupling dependence and dynamical features. Class. Quantum Gravity 2019, 36, 134002. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.; Kunz, J.; Pombo, A.M.; Radu, E. Einstein-Maxwell-scalar black holes: The hot, the cold and the bald. Phys. Lett. B 2020, 806, 135493. [Google Scholar] [CrossRef]
- Yu, S.; Qiu, J.; Gao, C. Constructing black holes in Einstein-Maxwell-scalar theory. arXiv 2020, arXiv:2005.14476. [Google Scholar]
- Brown, J.D.; York, J.W., Jr. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407. [Google Scholar] [CrossRef]
- Brown, J.D.; Creighton, J.; Mann, R.B. Temperature, energy, and heat capacity of asymptotically anti-de Sitter black holes. Phys. Rev. D 1994, 50, 6394. [Google Scholar] [CrossRef]
- Sheykhi, A.; Dehghani, M.; Hendi, S. Thermodynamic instability of charged dilaton black holes in AdS spaces. Phys. Rev. D 2010, 81, 084040. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Hawking, S. Nature (London) 248, 30; Hawking, SW (1975). Commun. Math. Phys 1974, 43, 199. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738. [Google Scholar] [CrossRef]
- Hunter, C. Action of instantons with a nut charge. Phys. Rev. D 1998, 59, 024009. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hunter, C.; Page, D.N. NUT charge, anti-de Sitter space, and entropy. Phys. Rev. D 1999, 59, 044033. [Google Scholar] [CrossRef]
- Mann, R.B. Misner string entropy. Phys. Rev. D 1999, 60, 104047. [Google Scholar] [CrossRef]
- Davies, P.C. The thermodynamic theory of black holes. Proc. R. Soc. Lond. A 1977, 353, 499–521. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).