Spinors in Cylindrically Symmetric Space–Time

Abstract

We studied the behavior of nonlinear spinor field within the scope of a static cylindrically symmetric space–time. It is found that the energy-momentum tensor (EMT) of the spinor field in this case possesses nontrivial non-diagonal components. The presence of non-diagonal components of the EMT imposes three-way restrictions either on the space–time geometry or on the components of the spinor field or on both. It should be noted that the analogical situation occurs in cosmology when the nonlinear spinor field is exploited as a source of gravitational field given by the Bianchi type-I cosmological model.

1. Introduction

In recent years spinor field has been used in cosmology by many authors [1,2,3,4,5,6]. The ability of spinor field to simulate different kinds of source fields such as perfect fluid, dark energy etc. [7,8] allows one to study the evolution of the Universe at different stages and consider the spinor field as an alternative model of dark energy.

To our knowledge, except for the Friedmann–Robertson–Walker (FRW) model given in Cartesian coordinates, in all other space–times spinor field possesses nontrivial non-diagonal components of the energy-momentum tensor. This very fact imposes severe restrictions on the geometry of space–time and/or on the components of the spinor field [9]. As far as static spherically symmetric space–time is concerned, the presence of non-diagonal components of EMT imposes restrictions on the spinor field only [10].

Introduction of the spinor field in a classical theory such as general relativity and cosmology gives rise to several questions due to its quantum origin. Many specialists think that even if one uses the spinor field in general relativity, he should treat it as Grassmann variables. This is partially right, though we think that spinors can be treated as classical complex projective coordinates in the spirit of Dirac-Sommerfeld-Brioski [11,12,13] as well. In this approach they describe the condensation of “quark-antiquarks” and are ordinary classical fields [14].

Note that spinor fields were introduced into the Einstein system exploiting both quantum and classical interpretations. A Fermi field coupled to a homogeneous and isotropic gravitational field was considered in [15], while the spinor was treated as a Grassmann variable in [16]. Dolan has studied the Chiral Fermions and the torsion arising from it within the scope of FRW geometries in the early Universe [17]. In doing so he argued that a quantum matter can be used as a source for the classical field while the quantum aspects of the field itself can be ignored.

As it was mentioned earlier, recently spinor field is being used in astrophysics. Most of these works were done within the scope of static spherically symmetric space–time [10,14,18]. Since a number of astrophysical objects are given by cylindrically symmetric space–time [19] in this report we plan to consider the spinor field within this model. String-like configurations of nonlinear spinor field in a static cylindrically symmetric space–time was obtained in [20]. An interacting system of nonlinear spinor and scalar fields in a static cylindrically symmetric space–time filled with barotropic gas was considered in [21]. Unfortunately, the authors did not take into account influence of the spinor field that occurs due to the presence of non-diagonal components of EMT. In this paper I plan to address those problems overlooked there and see if spinor field can be exploited to construct different types of configurations seen in astrophysics.

2. Basic Equations

The action we choose in the form

$$\begin{array}{c}\hfill \mathcal{S}=\int \sqrt{-g}\left[\frac{R}{2\kappa }+L_{\mathrm{sp}}\right]d\mathsf{\Omega }.\end{array}$$

(1)

where $\kappa =8\pi G$ is Einstein’s gravitational constant, R is the scalar curvature and $L_{\mathrm{sp}}$ is the spinor field Lagrangian given by [2]

$$\begin{array}{c}\hfill L_{\mathrm{sp}}=\frac{ı}{2}\left[\overline{\psi }{\gamma }^{\mu }{\nabla }_{\mu }\psi -{\nabla }_{\mu }\overline{\psi }{\gamma }^{\mu }\psi \right]-m\overline{\psi }\psi -\lambda F\left(K\right).\end{array}$$

(2)

To maintain the Lorentz invariance of the spinor field equations the self-interaction (nonlinear term) $F\left(K\right)$ is constructed as some arbitrary functions of invariants generated from the real bilinear forms. On account of Fierz equality in (2) we set $K=K(I,J)=b_{1}I+b_{2}J.$ Setting $(b_1=1,b_2=0),(b_1=0,b_2=1),(b_1=1,b_2=1),(b_1=1,b_2=-1)$ for K we obtain one of the following expressions $\{I,J,I+J,I-J\}$. Here $I=S^2$ and $J=P^2$ are the invariants of bilinear spinor forms with $S=\overline{\psi }\psi$ and $P=ı\overline{\psi }{\overline{\gamma }}^5\psi$ being the scalar and pseudo-scalar, respectively. In (2) $\lambda$ is the self-coupling constant.

The covariant derivatives of spinor field takes the form [2]

$$\begin{array}{c}\hfill {\nabla }_{\mu }\psi ={\partial }_{\mu }\psi -{\mathsf{\Omega }}_{\mu }\psi ,{\nabla }_{\mu }\overline{\psi }={\partial }_{\mu }\overline{\psi }+\overline{\psi }{\mathsf{\Omega }}_{\mu },\end{array}$$

(3)

where ${\mathsf{\Omega }}_{\mu }$ is the spinor affine connection which can be defined as [2]

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_{\mu }& =& \frac{1}{8}\left[{\partial }_{\mu }{\gamma }_{\alpha },{\gamma }^{\alpha }\right]-\frac{1}{8}{\mathsf{\Gamma }}_{\mu \alpha }^{\beta }\left[{\gamma }_{\beta },{\gamma }^{\alpha }\right].\hfill \end{array}$$

(4)

Here $\left[a,b\right]=ab-ba$ and ${\mathsf{\Gamma }}_{\mu \alpha }^{\beta }$ is the Christoffel symbol. In (4) the Dirac matrices in curve space–time $\gamma$ are connected to the flat space–time Dirac matrices $\overline{\gamma }$ in the following way

$$\begin{array}{c}\hfill {\gamma }_{\beta }=e_{\beta }^{\left(b\right)}{\overline{\gamma }}_b,{\gamma }^{\alpha }=e_{\left(a\right)}^{\alpha }{\overline{\gamma }}^a,\end{array}$$

where $e_{\left(a\right)}^{\alpha }$ and $e_{\beta }^{\left(b\right)}$ are the tetrad vectors such that

$$\begin{array}{c}\hfill e_{\left(a\right)}^{\alpha }{e}_{\beta }^{\left(a\right)}={\delta }_{\beta }^{\alpha },e_{\left(a\right)}^{\alpha }{e}_{\alpha }^{\left(b\right)}={\delta }_a^b.\end{array}$$

The $\gamma$ matrices obey the following anti-commutation rules

$$\begin{array}{c}\hfill {\gamma }_{\mu }{\gamma }_{\nu }+{\gamma }_{\nu }{\gamma }_{\mu }=2g_{\mu \nu },{\gamma }^{\mu }{\gamma }^{\nu }+{\gamma }^{\nu }{\gamma }^{\mu }=2g^{\mu \nu }.\end{array}$$

Let us consider the cylindrically symmetric space–time given by

$$d{s}^2=e^{2\gamma }d{t}^2-e^{2\alpha }d{u}^2-e^{2\beta }d{\varphi }^2-e^{2\mu }d{z}^2,$$

(5)

where $\gamma ,\alpha ,\beta$ and $\mu$ are the functions of the radial coordinate u only.

The tetrad we will choose in the form

$$\begin{array}{cc}\hfill e_0^{\left(0\right)}& =e^{\gamma },e_1^{\left(1\right)}=e^{\alpha },e_2^{\left(2\right)}=e^{\beta },e_3^{\left(3\right)}=e^{\mu },\hfill \\ \hfill e_{\left(0\right)}^0& =e^{-\gamma },e_{\left(1\right)}^1=e^{-\alpha },e_{\left(2\right)}^2=e^{-\beta },e_{\left(3\right)}^3=e^{-\mu }.\hfill \end{array}$$

From ${\gamma }^{\eta }=e_{\left(a\right)}^{\eta }{\overline{\gamma }}^a$ we find

$$\begin{array}{cc}\hfill {\gamma }^0& =e^{-\gamma }{\overline{\gamma }}^0,{\gamma }^1=e^{-\alpha }{\overline{\gamma }}^1,{\gamma }^2=e^{-\beta }{\overline{\gamma }}^2,{\gamma }^3=e^{-\mu }{\overline{\gamma }}^3,\hfill \\ \hfill {\gamma }_0& =e^{\gamma }{\overline{\gamma }}_0,{\gamma }_1=e^{\alpha }{\overline{\gamma }}_1,{\gamma }_2=e^{\beta }{\overline{\gamma }}_2,{\gamma }_3=e^{\mu }{\overline{\gamma }}_3,\hfill \end{array}$$

with

$$\begin{array}{c}\hfill {\gamma }_0={\gamma }^0,{\gamma }_1=-{\gamma }^1,{\gamma }_2=-{\gamma }^2,{\gamma }_3=-{\gamma }^3.\end{array}$$

The nontrivial Christoffel symbols corresponding to the metric (5) are

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{01}^0& ={\gamma }^{\prime },{\mathsf{\Gamma }}_{11}^1={\alpha }^{\prime },{\mathsf{\Gamma }}_{21}^2={\beta }^{\prime },{\mathsf{\Gamma }}_{31}^3={\mu }^{\prime },\hfill \\ \hfill {\mathsf{\Gamma }}_{00}^1& =e^{2(\gamma -\alpha )}{\gamma }^{\prime },{\mathsf{\Gamma }}_{22}^1=-e^{2(\beta -\alpha )}{\beta }^{\prime },{\mathsf{\Gamma }}_{33}^1=-e^{2(\mu -\alpha )}{\mu }^{\prime }.\hfill \end{array}$$

Then from the definition (4) we find the following spinor affine connections ${\mathsf{\Omega }}_{\mu }$:

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_0& =-\frac{1}{2}{e}^{\gamma -\alpha }{\gamma }^{\prime }{\overline{\gamma }}^0{\overline{\gamma }}^1,{\mathsf{\Omega }}_1=0,{\mathsf{\Omega }}_2=\frac{1}{2}{e}^{\beta -\alpha }{\beta }^{\prime }{\overline{\gamma }}^2{\overline{\gamma }}^1,{\mathsf{\Omega }}_3=\frac{1}{2}{e}^{\mu -\alpha }{\mu }^{\prime }{\overline{\gamma }}^3{\overline{\gamma }}^1.\hfill \end{array}$$

(6)

The spinor field equations corresponding to the spinor field Lagrangian (2) are [2]

$$\begin{array}{cc}\hfill ı{\gamma }^{\mu }{\nabla }_{\mu }\psi -m\psi -\mathcal{D}\psi -ı\mathcal{G}{\overline{\gamma }}^5\psi & =0,\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill ı{\nabla }_{\mu }\overline{\psi }{\gamma }^{\mu }+m\overline{\psi }+\mathcal{D}\overline{\psi }+ı\mathcal{G}\overline{\psi }{\overline{\gamma }}^5& =0,\hfill \end{array}$$

(7b)

where we denote $\mathcal{D}=2\lambda F_K{b}_{1}S,\mathcal{G}=2\lambda F_K{b}_{2}P.$ On account of (7) from (2) one finds that $L_{\mathrm{sp}}=\lambda \left(2K{F}_K-F\right).$

Let the spinor field be a function of u only, then in view of (6) the spinor field equations can be written as

$$\begin{array}{cc}\hfill {\psi }^{\prime }+\frac{1}{2}{\tau }^{\prime }\psi -ıe^{\alpha }\left(m+\mathcal{D}\right){\overline{\gamma }}^1\psi -e^{\alpha }\mathcal{G}{\overline{\gamma }}^5{\overline{\gamma }}^1\psi & =0,\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill {\overline{\psi }}^{\prime }+\frac{1}{2}{\tau }^{\prime }\overline{\psi }+ıe^{\alpha }\left(m+\mathcal{D}\right)\overline{\psi }{\overline{\gamma }}^1-e^{\alpha }\mathcal{G}\overline{\psi }{\overline{\gamma }}^5{\overline{\gamma }}^1& =0,\hfill \end{array}$$

(8b)

where prime denotes differentiation with respect to u. In (8) we also define

$$\tau =\left(\gamma +\beta +\mu \right).$$

(9)

The energy-momentum tensor of the spinor field is defined as [2,22,23]

$$\begin{array}{cc}\hfill T_{\mu }^{\rho }& =\frac{ı}{4}{g}^{\rho \nu }\left(\overline{\psi }{\gamma }_{\mu }{\nabla }_{\nu }\psi +\overline{\psi }{\gamma }_{\nu }{\nabla }_{\mu }\psi -{\nabla }_{\mu }\overline{\psi }{\gamma }_{\nu }\psi -{\nabla }_{\nu }\overline{\psi }{\gamma }_{\mu }\psi \right)-{\delta }_{\mu }^{\rho }{L}_{\mathrm{sp}}\hfill \\ \hfill & =\frac{ı}{4}{g}^{\rho \nu }\left(\overline{\psi }{\gamma }_{\mu }{\partial }_{\nu }\psi +\overline{\psi }{\gamma }_{\nu }{\partial }_{\mu }\psi -{\partial }_{\mu }\overline{\psi }{\gamma }_{\nu }\psi -{\partial }_{\nu }\overline{\psi }{\gamma }_{\mu }\psi \right)\hfill \\ \hfill & -\frac{ı}{4}{g}^{\rho \nu }\overline{\psi }\left({\gamma }_{\mu }{\mathsf{\Omega }}_{\nu }+{\mathsf{\Omega }}_{\nu }{\gamma }_{\mu }+{\gamma }_{\nu }{\mathsf{\Omega }}_{\mu }+{\mathsf{\Omega }}_{\mu }{\gamma }_{\nu }\right)\psi -{\delta }_{\mu }^{\rho }{L}_{\mathrm{sp}}.\hfill \end{array}$$

(10)

From (10) one finds the non-trivial components of the energy-momentum tensor of the the spinor field

$$\begin{array}{cc}\hfill T_1^1& =mS+\lambda F,\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill T_0^0& =T_2^2=T_3^3=-\lambda \left(2K{F}_K-F\right),\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill T_2^0& =-\frac{ı}{4}{e}^{\beta -\alpha -\gamma }\left({\gamma }^{\prime }-{\beta }^{\prime }\right)A^3,\hfill \end{array}$$

(11c)

$$\begin{array}{cc}\hfill T_3^0& =-\frac{ı}{4}{e}^{\mu -\alpha -\gamma }\left({\gamma }^{\prime }-{\mu }^{\prime }\right)A^2,\hfill \end{array}$$

(11d)

$$\begin{array}{cc}\hfill T_3^2& =-\frac{ı}{4}{e}^{\mu -\beta -\alpha }\left({\beta }^{\prime }-{\mu }^{\prime }\right)A^0,\hfill \end{array}$$

(11e)

with $A^{\eta }=\overline{\psi }{\overline{\gamma }}^5{\overline{\gamma }}^{\eta }\psi$ being the pseudovector. It can be noticed that $T_0^0+T_1^1=mS+2\lambda \left(F-K{F}_K\right)$ and $T_0^0-T_1^1=-\left(mS+2K{F}_K\right)$ might be positive or negative under certain conditions.

From (8) we find the following system of equations for the bilinear spinor forms:

$$\begin{array}{cc}\hfill S^{\prime }+{\tau }^{\prime }S-2e^{\alpha }\mathcal{G}{A}^1& =0,\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill P^{\prime }+{\tau }^{\prime }P+2e^{\alpha }\left(m+\mathcal{D}\right)A^1& =0,\hfill \end{array}$$

(12b)

$$\begin{array}{cc}\hfill {A^1}^{\prime }+{\tau }^{\prime }{A}^1+2e^{\alpha }\left(m+\mathcal{D}\right)P-2e^{\alpha }\mathcal{G}S& =0.\hfill \end{array}$$

(12c)

Equation (12) yields the following relation

$$S^2+P^2-{\left(A^1\right)}^2=C_0{e}^{-2\tau },C_0=\mathrm{Const}.$$

(13)

In case of $K=I$, i.e., $\mathcal{G}=0$ from (12a) we find

$$S=C_s{e}^{-\tau }\Rightarrow K=C_s^2{e}^{-2\tau }.$$

(14)

If $K=J$, then in case of a massless spinor field from (12b) we find

$$P=C_p{e}^{-\tau }\Rightarrow K=C_p^2{e}^{-2\tau }.$$

(15)

Let us consider the case when $K=I+J$. In this case $b_1=b_2=1$. Then on account of expression for $\mathcal{D}$ and $\mathcal{G}$ from (12a,b) for the massless spinor field we find

$$\begin{array}{cc}\hfill S^{\prime }+{\tau }^{\prime }S-4e^{\alpha }\lambda F_K{A}^{1}P& =0,\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill P^{\prime }+{\tau }^{\prime }P+4e^{\alpha }\lambda F_K{A}^{1}S& =0,\hfill \end{array}$$

(16b)

which yields

$$K=I+J=S^2+P^2=C_1^2{e}^{-2\tau }.$$

(17)

Finally in case when $K=I-J$, i.e., $b_1=-b_2=1$ from (12a,b) for the massless spinor field we obtain

$$\begin{array}{cc}\hfill S^{\prime }+{\tau }^{\prime }S+4e^{\alpha }\lambda F_K{A}^{1}P& =0,\hfill \end{array}$$

(18a)

$$\begin{array}{cc}\hfill P^{\prime }+{\tau }^{\prime }P+4e^{\alpha }\lambda F_K{A}^{1}S& =0,\hfill \end{array}$$

(18b)

which leads to

$$K=I-J=S^2-P^2=C_2^2{e}^{-2\tau }.$$

(19)

The Einstein tensor corresponding to the metric (5) possesses only diagonal components. So let us first consider the diagonal equations of Einstein system

$$\begin{array}{cc}\hfill e^{-2\alpha }\left[{\gamma }^{\prime }{\beta }^{\prime }+{\beta }^{\prime }{\mu }^{\prime }+{\mu }^{\prime }{\gamma }^{\prime }\right]& =mS+\lambda F,\hfill \end{array}$$

(20a)

$$\begin{array}{cc}\hfill e^{-2\alpha }\left[{\gamma }^{″}+{\mu }^{″}+{\gamma }^{\prime 2}+{\mu }^{\prime 2}+{\gamma }^{\prime }{\mu }^{\prime }-{\alpha }^{\prime }{\gamma }^{\prime }-{\alpha }^{\prime }{\mu }^{\prime }\right]& =\lambda \left(F-2K{F}_K\right),\hfill \end{array}$$

(20b)

$$\begin{array}{cc}\hfill e^{-2\alpha }\left[{\gamma }^{″}+{\beta }^{″}+{\gamma }^{\prime 2}+{\beta }^{\prime 2}+{\gamma }^{\prime }{\beta }^{\prime }-{\alpha }^{\prime }{\gamma }^{\prime }-{\alpha }^{\prime }{\beta }^{\prime }\right]& =\lambda \left(F-2K{F}_K\right),\hfill \end{array}$$

(20c)

$$\begin{array}{cc}\hfill e^{-2\alpha }\left[{\beta }^{″}+{\mu }^{″}+{\beta }^{\prime 2}+{\mu }^{\prime 2}+{\beta }^{\prime }{\mu }^{\prime }-{\alpha }^{\prime }{\beta }^{\prime }-{\alpha }^{\prime }{\mu }^{\prime }\right]& =\lambda \left(F-2K{F}_K\right).\hfill \end{array}$$

(20d)

Subtraction of (20d) from (20b) yields

$${\gamma }^{″}-{\beta }^{″}+\left({\gamma }^{\prime }-{\beta }^{\prime }\right)\left({\tau }^{\prime }-{\alpha }^{\prime }\right)=0,$$

(21)

with the solution

$${\beta }^{\prime }={\gamma }^{\prime }-C_1{e}^{\left(\alpha -\tau \right)},$$

(22)

Analogically, subtracting (20d) from (20c) one finds

$${\mu }^{\prime }={\gamma }^{\prime }-C_2{e}^{\left(\alpha -\tau \right)},$$

(23)

In view of (9), (22) and (23) one finds

$${\gamma }^{\prime }=\frac{1}{3}\left[{\tau }^{\prime }+\left(C_1+C_2\right)e^{\left(\alpha -\tau \right)}\right].$$

(24)

Thus, $\gamma$, $\beta$ and $\mu$ can be found in terms of $\alpha$ and $\tau$. Let us find the equation for $\tau$. Summation of (20b–d) and 3 times (20a) gives

$$\begin{array}{c}\hfill e^{-2\alpha }\left[{\tau }^{″}+{\tau }^{\prime 2}-{\alpha }^{\prime }{\tau }^{\prime }\right]=\frac{3\kappa }{2}\left[mS+2\lambda \left(F-K{F}_K\right)\right].\end{array}$$

(25)

Recall that for non-diagonal components of the EMT of the spinor field we have non-trivial expressions, whereas the non-diagonal components of the Einstein tensor in this case are trivial. Equating these expressions to zero from (11c–e) we obtain the following constrains

$$\begin{array}{cc}\hfill \left({\gamma }^{\prime }-{\beta }^{\prime }\right)A^3& =0,\hfill \end{array}$$

(26a)

$$\begin{array}{cc}\hfill \left({\gamma }^{\prime }-{\mu }^{\prime }\right)A^2& =0,\hfill \end{array}$$

(26b)

$$\begin{array}{cc}\hfill \left({\beta }^{\prime }-{\mu }^{\prime }\right)A^0& =0.\hfill \end{array}$$

(26c)

The foregoing expressions give rise to three possibilities:

$$\begin{array}{cc}\hfill A^3& =A^2=A^0=0\mathrm{and}{\gamma }^{\prime }\ne {\beta }^{\prime }\ne {\mu }^{\prime }\Rightarrow C_1\ne C_2\ne 0\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill A^2& =A^0=0\mathrm{and}{\gamma }^{\prime }-{\beta }^{\prime }=0\Rightarrow C_1=0,\hfill \end{array}$$

(27b)

$$\begin{array}{cc}\hfill A^3,& A^2,A^0\mathrm{are}\mathrm{nontrivial}\mathrm{and}{\gamma }^{\prime }={\beta }^{\prime }={\mu }^{\prime }\Rightarrow C_1=C_2=0.\hfill \end{array}$$

(27c)

It should be noted that in a Bianchi type-I space–time there occur similar possibilities [16]. In that case under the assumption (27a) the spinor field becomes massless and linear [16]. In a static cylindrically symmetric space–time that is not necessarily the case.

Unfortunately, right now we cannot exactly solve the equation for defining either $\tau$ or $\alpha$. So we have to assume some coordinate conditions. There might be a few. In what follows, we consider the case with $K=I$, as in this case it is possible to consider massive spinor. Further we set $S=K_0{e}^{-\tau }$ and $K=K_0^2{e}^{-2\tau }.$

Case 1: Let us first consider the harmonic radial coordinate u such that the following relation holds for the metric functions [24]:

$$\alpha =\gamma +\beta +\mu .$$

(28)

In view of (9) Equation (25) takes the form

$$\begin{array}{c}\hfill {\tau }^{″}=\frac{3\kappa }{2}{e}^{2\alpha }\left[mS+2\lambda \left(F-K{F}_K\right)\right].\end{array}$$

(29)

Let us consider the case when F is a power law function of K, i.e., $F=K^{n+1}$. Inserting $S=K_0{e}^{-\tau }$ and $K=K_0^2{e}^{-2\tau }$ into (25) on account of $\alpha =\tau$ we find

$$\begin{array}{c}\hfill {\tau }^{″}=\frac{3\kappa }{2}m{K}_0{e}^{\tau }-3\kappa \lambda n{K}_0^{2(n+1)}{e}^{-2n\tau },\end{array}$$

(30)

with the first integral

$${\tau }^{\prime }=\sqrt{3\kappa m{K}_0{e}^{\tau }+3\kappa \lambda K_0^{2(n+1)}{e}^{-2n\tau }+C_3},C_3=\mathrm{const}.$$

(31)

So the solution can be given in quadrature

$$\int \frac{d\tau }{\sqrt{3\kappa m{K}_0{e}^{\tau }+3\kappa \lambda K_0^{2(n+1)}{e}^{-2n\tau }+C_3}}=u+u_0,u_0=\mathrm{const}.$$

(32)

Let us consider some simple cases those allow exact solution.

Fisrt we study the Heisenberg–Ivanenko type nonlinearity when $F\left(K\right)=K$. It can be obtained by setting $n=0$ in (31). In this case (31) takes the form

$${\tau }^{\prime }=\sqrt{3\kappa m{K}_0{e}^{\tau }+C_4},C_4=C_3+3\kappa \lambda K_0^2,$$

(33)

which finally gives

$$e^{\tau }=e^{\alpha }=\frac{C_4}{2\kappa m{K}_0{sinh}^2\left(-\sqrt{C_4}u/2+C_5\right)},C_5=\mathrm{const}.$$

(34)

For a general power law type nonlinearity we study the massless spinor field. Setting $m=0$ in (31) we have

$${\tau }^{\prime }=\sqrt{3\kappa K_0^{2(n+1)}{e}^{-2n\tau }+C_3},$$

(35)

with the solution

$$e^{\tau }=e^{\alpha }={\left[\sqrt{\frac{3\kappa K_0^{2(n+1)}}{C_3}}sinh\left(n\sqrt{C_3}u+C_6\right)\right]}^{1/n},C_6=\mathrm{const}.$$

(36)

For a more general solution to the Einstein equations with massive and nonlinear spinor field as source we rewrite it in the form of Cauchy:

$$\begin{array}{cc}\hfill {\tau }^{\prime }& =\eta ,\hfill \end{array}$$

(37a)

$$\begin{array}{cc}\hfill {\eta }^{\prime }& =\frac{3\kappa }{2}{e}^{2\tau }\left[mS+2\left(F-K{F}_K\right)\right],\hfill \end{array}$$

(37b)

$$\begin{array}{cc}\hfill {\gamma }^{\prime }& =\frac{1}{3}\left[\eta +\left(C_1+C_2\right)\right],\hfill \end{array}$$

(37c)

$$\begin{array}{cc}\hfill {\beta }^{\prime }& =\frac{1}{3}\left(\eta -2C_1+C_2\right),\hfill \end{array}$$

(37d)

$$\begin{array}{cc}\hfill {\mu }^{\prime }& =\frac{1}{3}\left(\eta +C_1-2C_2\right).\hfill \end{array}$$

(37e)

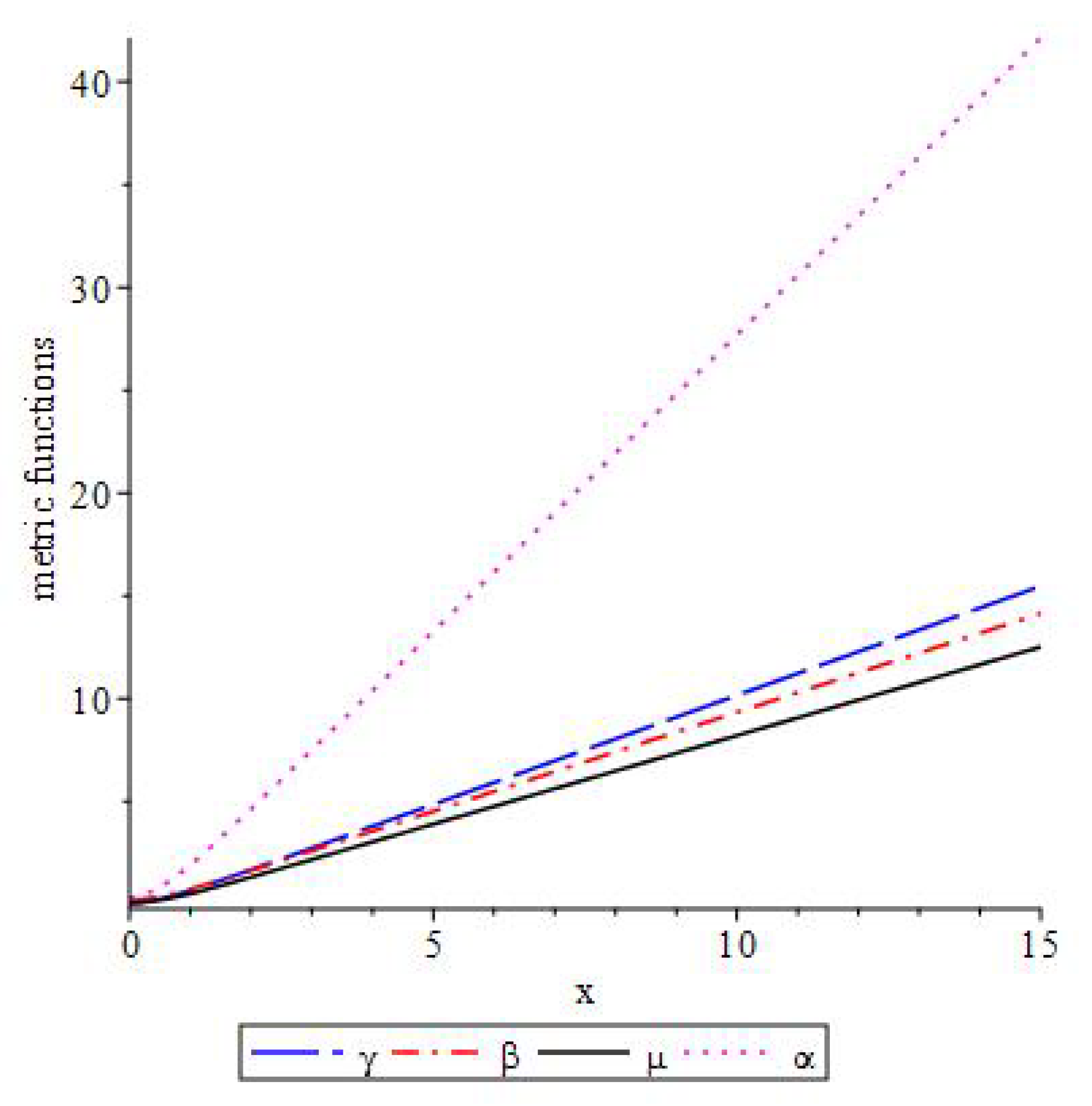
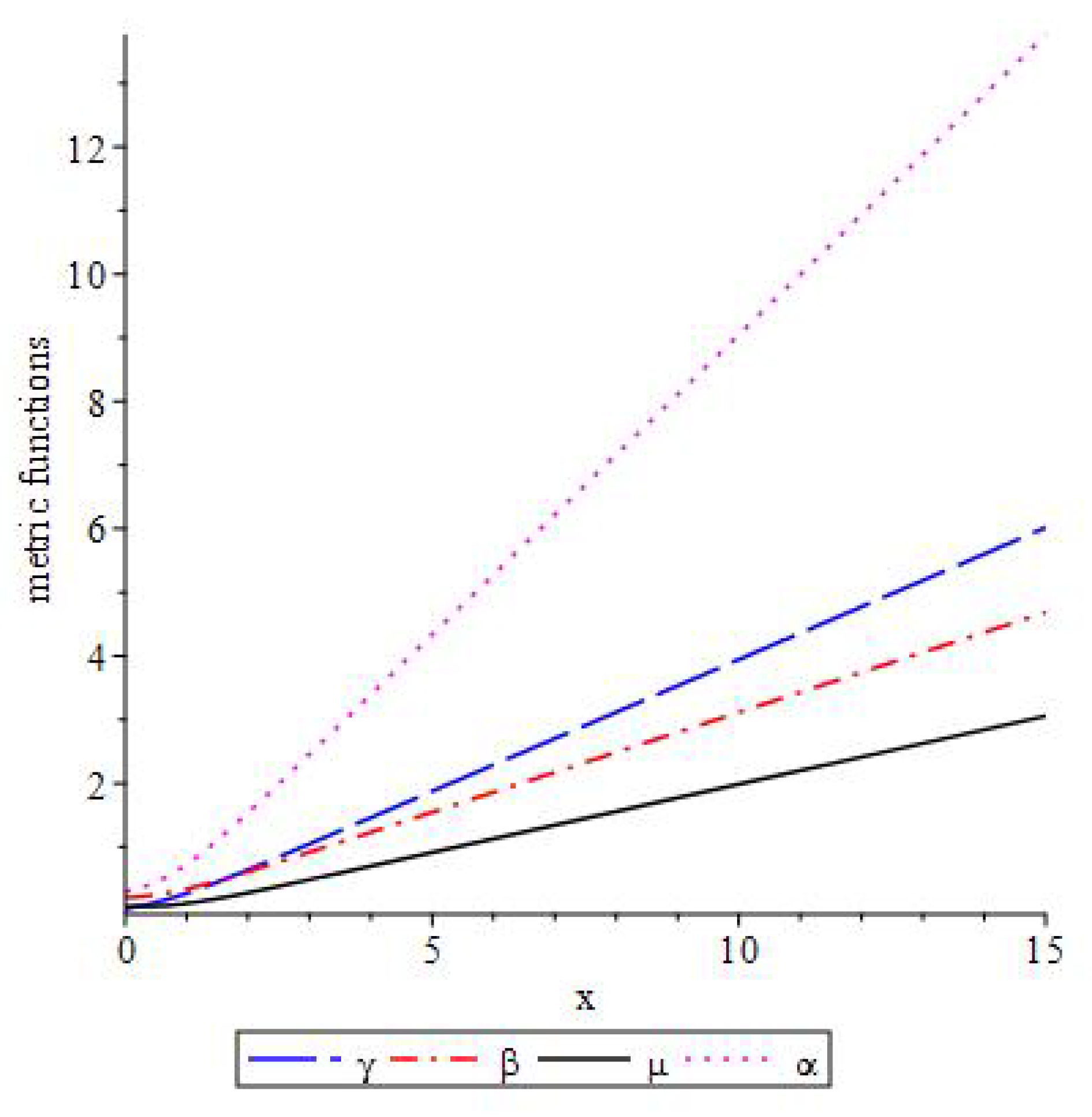
This system can be solved numerically. In Figure 1 and Figure 2, we have plotted the metric functions $\gamma \left(u\right),\alpha \left(u\right),\beta \left(u\right),\mu \left(u\right)$ for different types of nonlinearities, namely, $n=0$ (Heisenberg–Ivanenko case) and $n=4$. For simplisity, we set the following values for other parameters $C_1=1$, $C_2=2$ and $m=1$. The initial values were taken to be $\tau \left(0\right)=0.3$, $\gamma \left(0\right)=0.03$, $\beta \left(0\right)=0.2$, $\mu \left(0\right)=0.07$ and $\nu \left(0\right)=0.2$. As we see from the graphics, with the increase of the value of n the difference between the metric functions increases.

Figure 1. Plot of metric functions for Heisenberg–Ivanenko type nonlinearity for harmonic radial coordinate.

Figure 2. Plot of metric functions for a massive nonlinear spinor field with power on nonlinearity $n=4$ for harmonic radial coordinate.

Case 2: Let us consider the quasiblogal coordinate $\alpha =-\gamma$ [25]. In this case for $\tau$ we have

$$\begin{array}{c}\hfill {\tau }^{″}+{\tau }^{\prime 2}+{\gamma }^{\prime }{\tau }^{\prime }=\frac{3\kappa }{2}{e}^{-2\gamma }\left[mS+2\left(F-K{F}_K\right)\right],\end{array}$$

(38)

whereas inserting (22) and (23) into (20a) for $\gamma$ we find

$$\begin{array}{c}\hfill 3{\gamma }^{\prime 2}-2\left(C_1+C_2\right)e^{-\left(\gamma +\tau \right)}{\gamma }^{\prime }+C_1{C}_2{e}^{-2\left(\gamma +\tau \right)}=e^{-2\gamma }\left(mS+\lambda F\right).\end{array}$$

(39)

Let us rewrite (38) and (39) in the Cauchy form

$$\begin{array}{cc}\hfill {\tau }^{\prime }& =\eta ,\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill {\eta }^{\prime }& =-{\eta }^2-\frac{\eta }{3}\left(C_1+C_2\right)e^{-\left(\gamma +\tau \right)}\mp \frac{D}{6}\eta +\frac{3\kappa }{2}{e}^{-2\gamma }\left[mS+2\left(F-K{F}_K\right)\right],\hfill \end{array}$$

(40b)

$$\begin{array}{cc}\hfill {\gamma }^{\prime }& =\frac{1}{3}\left(C_1+C_2\right)e^{-\left(\gamma +\tau \right)}\pm \frac{D}{6},\hfill \end{array}$$

(40c)

$$\begin{array}{cc}\hfill {\beta }^{\prime }& =\frac{1}{3}\left(-2C_1+C_2\right)e^{-\left(\gamma +\tau \right)}\pm \frac{D}{6},\hfill \end{array}$$

(40d)

$$\begin{array}{cc}\hfill {\mu }^{\prime }& =\frac{1}{3}\left(C_1-2C_2\right)e^{-\left(\gamma +\tau \right)}\pm \frac{D}{6},\hfill \end{array}$$

(40e)

where $D=2\sqrt{{\left(C_1+C_2\right)}^2{e}^{-2\left(\gamma +\tau \right)}-3\left(C_1{C}_2{e}^{-2\left(\gamma +\tau \right)}-e^{-2\gamma }\left(mS+\lambda F\right)\right)}.$ As one sees, the above-going system is valid if and only if $D\ge 0$. The Equation (40c) is found from (39), which is a quadratic equation with respect to ${\gamma }^{\prime }$.

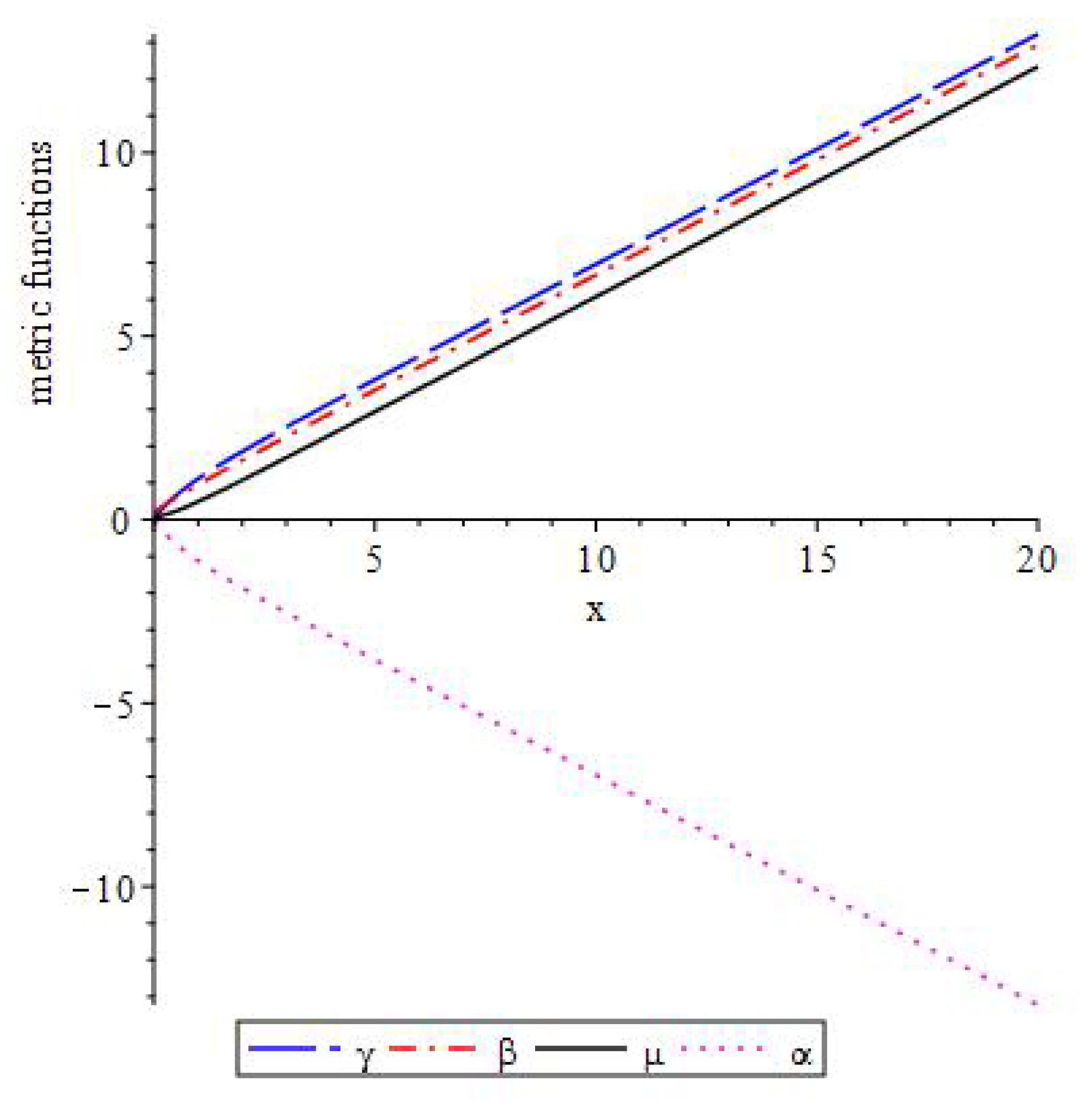
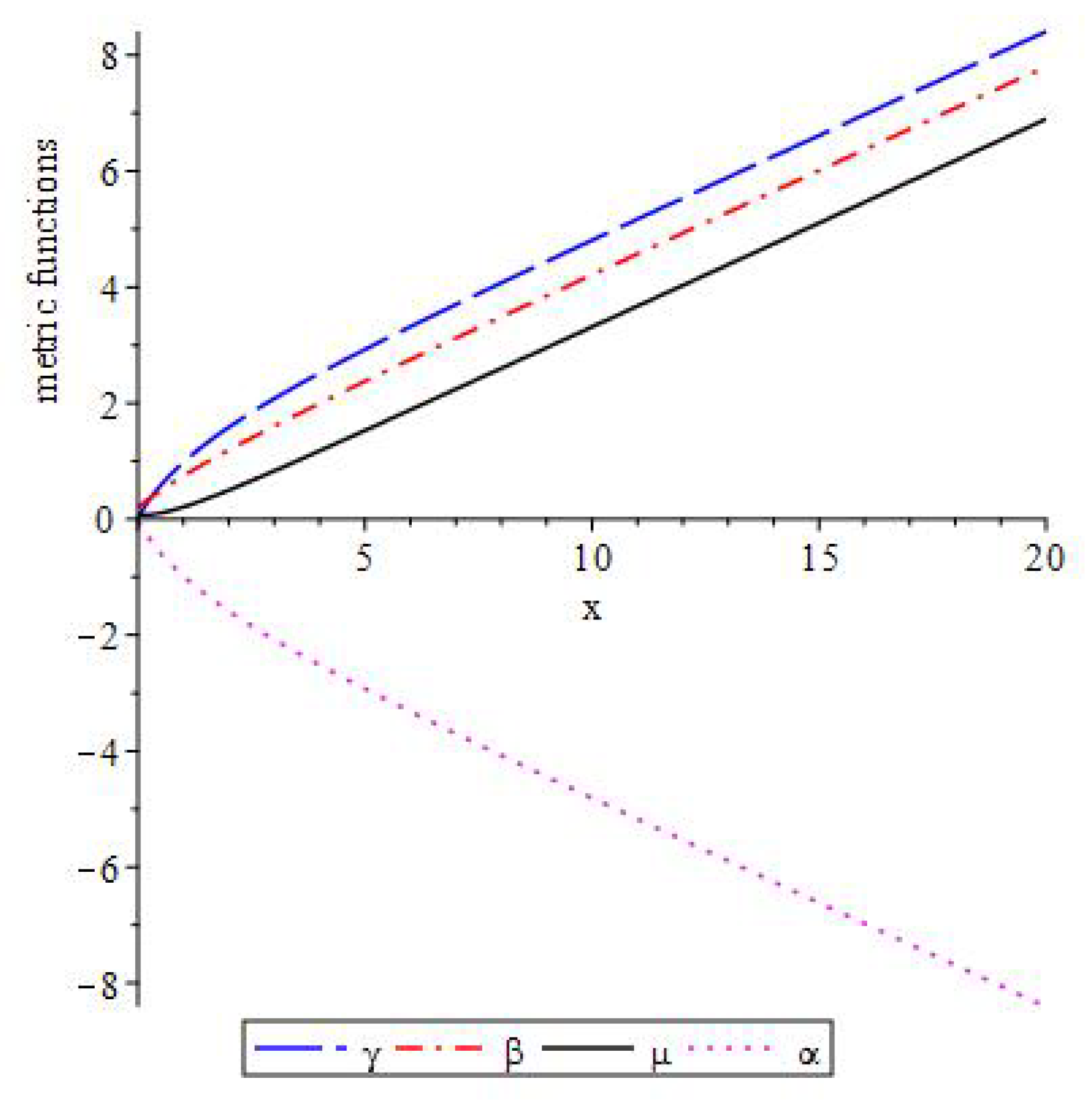
In the Figure 3 and Figure 4, we have plotted the metric functions for the same values as in previous cases, i.e., we set $C_1=1$, $C_2=2$ and $m=1$ and the initial values were taken to be $\tau \left(0\right)=0.3$, $\gamma \left(0\right)=0.03$, $\beta \left(0\right)=0.2$, $\mu \left(0\right)=0.07$ and $\nu \left(0\right)=0.2$. Here we have consider the cases with $n=0$ and $n=4$. Moreover, like the previous cases we see with the increase of n the difference between the metric functions increases.

Figure 3. Plot of metric functions for Heisenberg–Ivanenko typenonlinearity with $n=0$ for quasiglobal coordinate.

Figure 4. Plot of metric functions for a nonlinear spinor field with power on nonlinearity $n=4$ with nonzero mass.

3. Conclusions

We studied a system of nonlinear spinor field minimally coupled to a static cylindrically symmetric space–time. It is found that the energy-momentum tensor (EMT) of the spinor field has nontrivial non-diagonal components. The presence of non-diagonal components of the EMT imposes three-way restrictions on the space–time geometry and/or on the components of the spinor field. It should be noted that such situation occurs in Bianchi type-I cosmological model as well, but while in BI model under a specific type of restriction the spinor field becomes massless and linear, this is not the case in this model. Moreover, while in a static spherically symmetric space–time the presence of non-trivial non-diagonal components of EMT of the spinor field has no effect on the space–time geometry, in static cylindrically symmetric space–time it influences both the space–time geometry and the components of the spinor field. In the present model we have $T_0^0=T_2^2$ which in our view may play crucial role in the formation of configurations like wormhole. It should be noted that the expressions $(T_0^0+T_1^1)$ and $(T_0^0-T_1^1)$ can be both positive and negative, depending on the type of nonlinearity. In our view this fact may provide some very interesting results which we plan to study in our upcoming papers.