Abstract
Constraints on the Yukawa-type corrections to Newton’s gravitational law and on the coupling constant of axionlike particles to nucleons obtained from different laboratory experiments are reviewed and compared. The constraints on non-Newtonian gravity under discussion cover the wide interaction range from nanometers to millimeters and follow from the experiments on neutron scattering, measuring the Casimir force and Cavendish-type experiments. The constraints on the axion-to-nucleon coupling constant following from the magnetometer measurements, Cavendish-type experiments, Casimir physics, and experiments with beams of molecular hydrogen are considered, which refer to the region of axion masses from to 200 eV. Particular attention is given to the recent constraints obtained from measuring the Casimir force at nanometer separation distance between the test bodies. Several proposed experiments focussed on constraining the non-Newtonian gravity, axionlike particles and other hypothetical weakly interacting particles, such as chameleons and symmetrons, are discussed.
1. Introduction
In recent years, more and more experiments have been devoted to a search for some uncharged weakly interacting elementary particles, which are not accessible for the accelerator techniques used in high energy physics. Many particles of this kind were predicted in different extensions of the Standard Model, supergravity and supersymmetry [,], and their discovery would have a profound effect on several branches of physics and change our picture of the world. Thus, an exchange of light scalars (for instance, dilatons []) between atoms of neighboring macrobodies results in the Yukawa-type correction to the Newtonian gravitational law and opens up a new area to the experimenter: the search for non-Newtonian gravity []. The predicted light pseudoscalar particles called axions [,] not only provide a plausible explanation for the problem of strong violation and large electric dipole moment of a neutron in QCD, but suggest themselves as possible constituents of dark matter [].
The Yukawa-type interaction at short separations between the test masses has long been searched for as the so-called fifth force in the gravitational experiments of Eötvos and Cavendish-type []. According to the results of [,], both the Yukawa- and power-type corrections to Newtonian gravity can be recorded also in experiments on measuring the van der Waals and Casimir forces caused by the zero-point and thermal fluctuations of the electromagnetic field. The development of extradimensional theories, which anticipate the compactification scale at energies of the order of 1 TeV [,], made one more prediction of the Yukawa-type corrections to Newton’s law at short separations [,] and stimulated their search.
An exchange of one pseudoscalar particle between two fermions results in the spin-dependent interaction potential [,], which turns into zero after an averaging over the volumes of two unpolarized macroscopic bodies. Because of this, the process of one-axion exchange does not lead to any fifth force. An effective potential due to a simultaneous exchange of two axions is more complicated and depends on the details of an axion-to-fermion interaction. If this interaction is described by the pseudoscalar Lagrangian, the spin-independent effective potential leading to some fifth force between two macroscopic bodies is obtained [,]. If, however, an axion-to-fermion interaction is described by the pseudovector Lagrangian, as it holds for QCD axions which are the pseudo-Nambu-Goldstone bosons, the character of an effective potential due to the exchange of two axions remains a mystery [].
The constraints on the constant of Yukawa-type interaction are usually obtained as functions of the interaction range , where M is a mass of the exchange scalar particle (here and below we put ). For non-Newtonian gravity originating from extra dimensions has the meaning of the compactification scale. Depending on the interaction range, the strongest constraints on follow from different experiments. Over a long period of time, experiments on measuring the Casimir force were used for obtaining the strongest constraints on over the wide interaction range below a few micrometers []. For larger up to a few centimeters, the strongest constraints on were found from checking the inverse square law of Newtonian gravity (the Cavendish-type experiments [,,]) and for even greater from tests of the equivalence principle (the Eötvos-type experiments [,]). At the moment, the strongest constraints on in the interaction range below approximately 10 nm follow from the experiments on neutron scattering [,,]. The Casimir force measurements (and their modification where the Casimir force is nullified []) allow obtaining the strongest constraints on within the interaction range from approximately nm to m. For larger the gravitational experiments preserve their leading role in constraining the Yukawa-type corrections to Newtonian gravity.
Constraining the parameters of axions and axionlike particles is the subject of extensive studies. There are many types of axions in the literature grouped in the models of hadronic (QCD) axions [,] and Grand Unified Theory (GUT) axions [,], which in turn are divided into many submodels. Axionlike particles can interact with photons, electrons, and nucleons, and each interaction channel is used in the laboratory experiments and astrophysical observations dedicated to the axion quest (see reviews [,,,,]). Our interest here is focussed on the interaction of axions with nucleons. The constraints on the strength of an axion-to-nucleon interaction constant are usually obtained as functions of the nucleon mass . In fact the strongest constraints on follow from astrophysical arguments on stellar cooling accounted for by the axion emission []. It has been known, however, that the theory of dense nuclear matter suffers from significant uncertainties, which make the obtained constraints not fully reliable []. At the moment, the strongest laboratory constraints on in the range of of eV follow from the magnetometer measurements [] and for heavier axions from the Cavendish-type [,] and Casimir-less [,] experiments. For eV the strongest laboratory limits on were obtained from the experiment with beams of molecular hydrogen [,] and for eV from the experiment on nuclear magnetic resonance [] (see also review [] of the laboratory constraints on both the axionlike particles and Yukawa-type interactions with a focus on neutron experiments).
In this article, we review constraints on the Yukawa-type interaction and interaction of axions with nucleons obtained during the last few years from measurements of the Casimir force. These constraints are compared with the strongest limits following from the gravitational and some other laboratory experiments in the same interaction ranges. We also discuss several proposals focussed on further strengthening the constraints on both non-Newtonian gravity and axionlike particles.
The article structure is the following: In Section 2, we consider constraints on the strength of Yukawa-type correction to Newtonian gravity obtained from different measurements of the Casimir force and Casimir-less experiments. In Section 3, the same is done with respect to the constant of axion-to-nucleon interaction. Section 4 presents the constraints on both non-Newtonian gravity and axionlike particles obtained recently from measuring the Casimir force at the nanometer separation range. These constraints are compared with those outlined in Section 2 and Section 3 and with the most strong results following from some other laboratory experiments. In Section 5, several proposed experiments are discussed allowing further strengthening of the obtained constraints. Section 6 contains our discussion. Finally, in Section 7 the reader will find the conclusions.
2. The Yukawa-Type Correction to Newtonian Gravity and Constraints on It from the Casimir Effect
The Yukawa-type correction to the Newtonian gravitational potential between two particles with masses and situated at the points and is conventionally written in the form []
where , is the dimensionless interaction constant of the Yukawa interaction, and G is the Newtonian gravitational constant. As mentioned in Section 1, the interaction range has a meaning of either the Compton wavelength of an exchange scalar particle of mass M, , or the compactification scale of extra spatial dimensions.
For two test bodies and at the closest separation a the Yukawa interaction energy is obtained by interacting (1) over their volumes
where and are the respective mass densities. The Yukawa-type force acting between the two bodies can be calculated as the negative derivative of (2)
It should be noted that although the Yukawa-type force is often called a “correction” to Newtonian gravity, at short separations below a micrometer such an experimentally allowed “correction” may exceed the gravitational force by many orders of magnitude. For this reason, when obtaining the constraints, it is customary to omit the contribution of the genuinely Newtonian gravitation. This does not make any impact on the obtained results.
We begin with constraints found at the shortest interaction range from measuring the lateral Casimir force acting between the sinusoidally corrugated surfaces. It is common knowledge that the Casimir force between two parallel plates or between a plate and a sphere acts in a perpendicular direction to the surfaces. However, for surfaces covered with the sinusoidal corrugations of a common period but having some nonzero phase shift (see Figure 1) the Casimir free energy depends not only on a and on temperature T, but also on . This leads to initiation of the lateral Casimir force
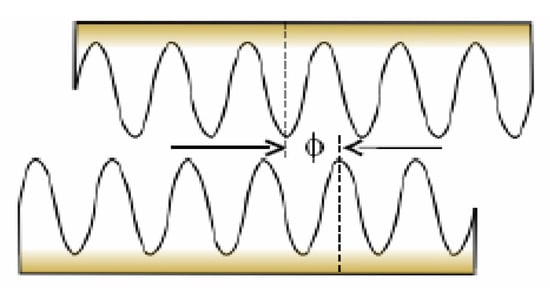
Figure 1.
The schematic of two sinusoidally corrugated plates having the phase shift between corrugations.
The sinusoidally corrugated surfaces are subjected to both the normal Casimir force acting perpendicular to the surface and the lateral Casimir force acting in a tangential direction. Due to the presence of corrugations, the closest separation between the two surfaces is smaller in this case than for the smooth bodies. Because of this, by measuring both the lateral and normal forces between corrugated surfaces it becomes possible to constrain hypothetical interactions within the shortest interaction range. Here, we discuss the constraints obtained from experiments on measuring both the lateral and normal Casimir forces starting from the lateral one. The constraints found from measurements of the normal Casimir force acting between the smooth surfaces are also considered.
The lateral Casimir force (4) was first predicted theoretically in [] and observed experimentally in [,]. In [,] it was measured more precisely in the configuration of a corrugated sphere in front of a corrugated plate with increased amplitudes at room temperature.
The schematic of the experimental setup is shown in Figure 2 []. A sinusoidally corrugated grating was vertically mounted on the piezoelectric tube. A smooth sphere was placed at the end of the cantilever of an atomic force microscope. A mica sheet was attached to the bottom of this sphere. The second sphere was attached to the bottom free end of the mica sheet. Then, the sinusoidal corrugations were imprinted on the second sphere from the grating as a template using a special procedure []. This ensures a parallelism of the corrugation axes on both test bodies. The interacting surfaces were covered with an Au layer.
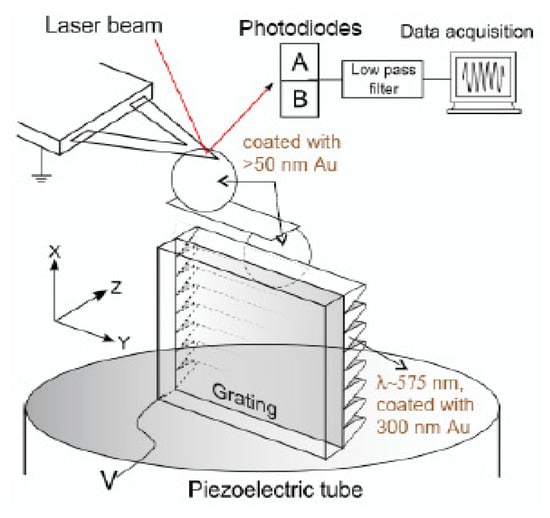
Figure 2.
Schematic diagram of the experimental setup using an atomic force microscope for measuring the lateral Casimir force between corrugated surfaces (see the text for further discussion).
The lateral Casimir force was measured at different values of the phase shift at different separations from 120 to 190 nm, and the total experimental errors have been determined at the 95% confidence level. The lateral Casimir force between the sinusoidally corrugated surfaces was also calculated using the generalization of the Lifshitz theory based on the Rayleigh scattering approach, and good agreement with the measurement data in the limits of the errors was observed. This means that the lateral force of Yukawa-type, which also should arise due to the presence of corrugations, satisfies the inequality
The hypothetical force in the experimental configuration of Figure 2 was calculated in [] using (1) and (2), where a dependence on arises for the corrugated plates, and subsequent negative differentiation with respect to similar to (4). This gave the possibility to determine the value of and which satisfy (5). The obtained results are shown in Figure 3 by line 1, where here and below the region of the plane above the line is excluded and the region below it is allowed by the experimental results. The constraints of the line 1 are stronger by up to a factor of than the previously known constraints obtained at a high confidence level [] (although the strength of constraints obtained in [] from the measurement data of [] is slightly stronger, their confidence level remains indefinite [,]).
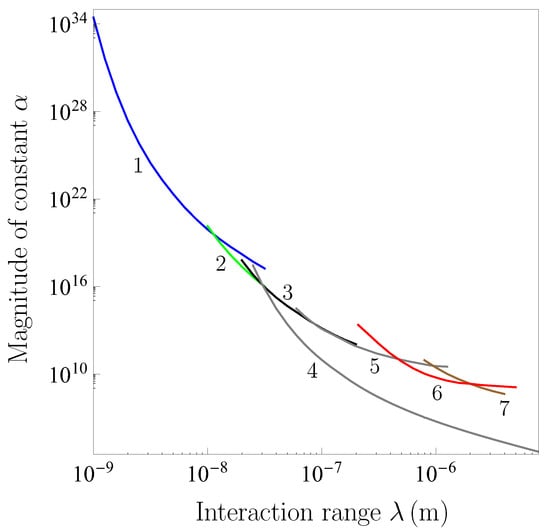
Figure 3.
The constraints on Yukawa-type correction to Newton’s gravitational law following from measuring the lateral and normal Casimir forces between corrugated surfaces (lines 1 and 2, respectively), the effective Casimir pressure (line 3), from the second and first Casimir-less experiments (lines 4 and 5, respectively), from sensing the difference of lateral forces (line 6), and from the torsion-pendulum experiment (line 7) are shown as functions of the interaction range. The regions above each line are excluded and below each line are allowed.
At larger interaction range nm the stronger constraints on the strength of Yukawa interaction follow from measurements of the normal Casimir force between sinusoidally corrugated surfaces of a sphere and a plate at different orientation angles of corrugations [,]. The schematic of the experimental setup is shown in Figure 4 []. In this case, unlike Figure 2, a sinusoidally corrugated grating was mounted on the piezoelectric tube laterally. An initially smooth sphere was attached to the end of the cantilever of an atomic force microscope. The sinusoidal corrugations on it were imprinted from the grating as a template. Both interacting surfaces were coated with an Au layer.
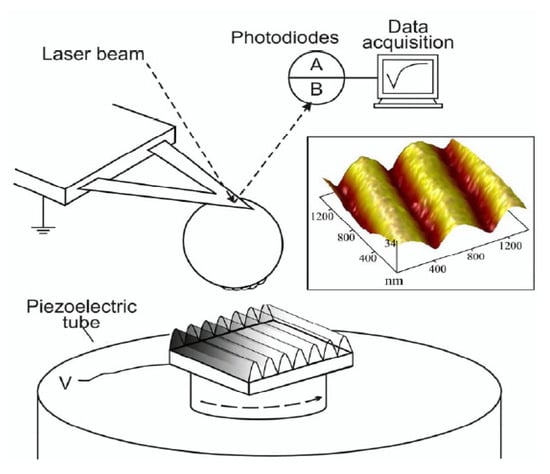
Figure 4.
Schematic diagram of the experimental setup using an atomic force microscope for measuring the normal Casimir force between corrugated surfaces (see the text for further discussion).
The normal Casimir force was measured at different separations from 127 to 200 nm for different angles between the axes of corrugations from 0 to at K. The total experimental errors have been determined at the 67% confidence level. However, we have recalculated them to the 95% confidence level in order to obtain constraints consistent with other results discussed here. In the limits of these errors, the measurement data were found in good agreement with the theoretical Casimir force calculated at K using the method of derivative expansion [,]. Thus, the Yukawa force perpendicular to the surface should satisfy the inequality
The Yukawa force in the configuration of Figure 4 was calculated in []. The resulting constraints on and are shown by line 2 in Figure 3. They were considered as the strongest ones up to 17.2 nm [].
At nm the stronger constraints have been obtained from measuring the effective Casimir pressure between two parallel plates by means of a micromechanical torsional oscillator [,]. The schematic diagram of this measurement is shown in Figure 5 []. The oscillator consisted of an Au-coated plate suspended at two opposite points on the midplane. Under the plate there were two electrically contacted electrodes used to measure the capacitance and to induce oscillation in the plate at the resonant frequency of the oscillator. Above the plate there was an Au-coated sphere of radius R attached to the side of an Au-coated optical fiber. The separation between the plate and the sphere was determined as
where the meanings of , , , , and b are clear from Figure 5. In the dynamic regime used in this experiment, an immediately measured quantity was a shift of the resonant frequency of the oscillator under an impact of the Casimir force acting between a sphere and a plate. The solution for the equation of motion of this oscillator allows recalculation of the frequency shift into the gradient of the Casimir force . Using the proximity force approximation [], which is valid in this case up to a fraction of a percent [,], one obtains the effective Casimir pressure between two parallel plates
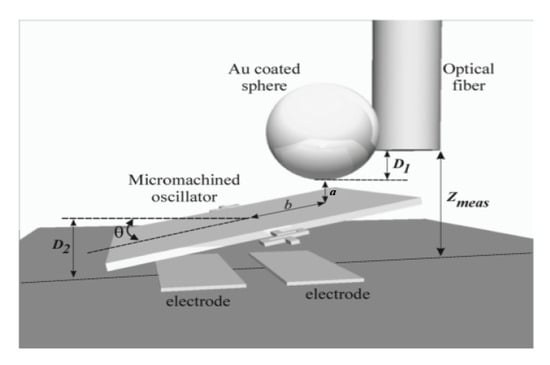
Figure 5.
Schematic diagram of the experimental setup using a micromechanical oscillator for determination of the effective Casimir pressure between two parallel plates (see the text for further discussion).
The effective Casimir pressure (8) was measured within the separation range from 162 to 746 nm at K, and the total experimental errors were determined at the 95% confidence level. A very good agreement was found between the measurement data and theoretical predictions of the Lifshitz theory using the optical data for the complex index of refraction of Au extrapolated down to zero frequency by the dissipationless plasma model [,]. An alternative extrapolation using the dissipative Drude model was excluded by the data. A discussion of both extrapolations can be found in [,,]. Later an exclusion of the Drude extrapolation was conclusively confirmed by the experiment [] where the theoretical predictions from two alternative extrapolations differ by up to a factor of 1000. We emphasize that a difference between predictions of the excluded and confirmed versions of the Lifshitz theory cannot be modeled by the Yukawa force []. This means that the effective Yukawa pressure between two parallel plates should satisfy the inequality
The Yukawa-type pressure between two parallel Au-coated plates was calculated in [,] and used for constraining the values of and in accordance with (9). The obtained constraints are shown by line 3 in Figure 3. For some time these constraints were considered as the strongest ones up to nm.
At larger the strong constraints on were obtained from the so-called Casimir-less experiment where an impact of the Casimir force was nullified []. This experiment was performed using the micromechanical oscillator shown in Figure 5. The plate of this oscillator was, however, composite. It consisted of two halves coated by Au and Ge films with a common Au overlayer. The oscillator was moved back and forth below the sphere, so that only a difference of forces from two halves of the plate has been measured. In doing so a common Au overlayer was sufficiently thick to make the Casimir forces from two halves of the plate equal. As to the Yukawa-type forces between the sphere and the plate halves coated with Au and Ge films, they were predicted to be different. The sensitivities of this setup to the differential force determined at the 95% confidence level were of the order of 1 fN at separations varying from 150 to 500 nm. This means that the difference of Yukawa forces from the Au and Ge films should satisfy the inequality
Both these Yukawa forces were calculated and used for constraining of and in []. The constraints following from (10) are shown by line 5 in Figure 3 (line 4 is discussed at the end of this section). They were the best ones within the range of from 89 to 465 nm.
At larger stronger constraints were obtained by sensing the difference of lateral forces between an Au sphere attached to the end of soft cantilever and a density modulation source mass []. To make a cantilever sensitive to the lateral force, it was placed normal to the source-mass surface. The obtained results are shown by line 6 in Figure 3. At m they are replaced by the stronger ones found from the measurement of the Casimir force between the Au-coated surfaces of a plate and a spherical lens of centimeter-size radius by means of the torsion pendulum []. These constraints are shown by line 7 in Figure 3. They extend from m to m. For larger the strongest constraints on the Yukawa-type interaction follow from the gravitational experiments (see Section 4).
In the end of this section, we present the results of the second Casimir-less experiment [], which improved the results of the first one [] significantly and resulted in stronger constraints over a wider interaction range than those ones obtained from several experiments listed above. As compared to the first Casimir-less experiment, the experimental setup for measuring the difference of forces was considerably upgraded. A differential force was measured between an Au-coated sphere and either Au or Si sectors of the rotating disc coated with an Au overlayer of sufficient thickness. In this way, the difference of Casimir forces between the sphere and the two neighboring sectors was again nullified, and the measurement result was determined by only the difference of Yukawa forces between the same sphere and either Au or Si sectors. Furthermore, the force sensitivity of the setup was improved, so that the minimum detectable force varied from 0.1 to 0.2 fN when separation distance increased from 200 to 1000 nm.
The constraints on the Yukawa-type interaction have been again derived from inequality (10) where the lower index Ge should be replaced with Si. The obtained results [] are shown by line 4 in Figure 3. It is seen that they extend the previously known constraints over a wide interaction range and strengthen them by up to a factor of . The constraints of line 4 are the strongest ones in the interaction region from nm to m. Thus, for nm they improve the constraints following from measurements of the Casimir pressure and all other constraints obtained from measuring the Casimir force at larger .
A summary of the strongest constraints on the Yukawa-type interaction over the interaction range from 1 nm to 1 mm obtained from measurements of the Casimir force and other laboratory experiments is presented in Section 4.
3. Constraints on the Coupling of Axions to Nucleons from the Casimir Effect
As was mentioned in Section 1, the effective potential due to an exchange of one axion between two nucleons depends on their spins and . An explicit form of this potential is given by [,,]
Here, we assume that the dimensionless coupling constants of an axion to a proton and a neutron are approximately equal . The nucleon mass is notated m, the axion mass is , and is the unit vector. Equation (11) is valid for both the QCD and GUT axions.
The effective potential (11) averages to zero after an integration over the volumes of two macrobodies. Because of this, the process of one-axion exchange does not lead to any additional force which could be searched for in the Casimir experiments (an experiment on measuring the Casimir force between two polarized test bodies has been proposed [] but is not realized yet). If, however, the axion-to-nucleon interaction is described by the pseudoscalar Lagrangian characteristic for GUT axions, a simultaneous exchange by two axions results in the spin-independent effective potential [,,]
where is the modified Bessel function of the second kind. This result, which is valid under the condition , resembles the Yukawa-type potential (1). As to the pseudovector Lagrangian, which can be also used to describe the interaction of axions to nucleons, it is characteristic for the QCD axion models. For this Lagrangian, the form of effective potential describing the two-axion exchange remains unknown []. The results presented below in this section are based on the use of (12) and, thus, are applicable to the GUT axions and axionlike particles.
Similar to the case of Yukawa-type forces, the interaction energy of two test bodies and due to an exchange of two GUT axions between their protons and neutrons is given by
where and are the numbers of nucleons per unit volume of the first and second test bodies, respectively. Then, the additional force arising due to two-axion exchange is given by
Different experiments on measuring the Casimir force were used to constrain the axion-to-nucleon interaction in the same way as described in Section 2 for the interaction of Yukawa type. We begin with the second Casimir-less experiment [] (see Section 2). Its results were used for constraining axions in []. For this purpose, the difference of additional forces arising in the experimental configuration due to two-axion exchange was found using (13) and (14). Taking into account that no force was registered up to the sensitivities varying from 0.1 to 0.2 fN, this difference should satisfy the inequality
The constraints on an axion-to-nucleon interaction are usually displayed graphically as depending on the axion mass . Similar to the Yukawa-type interaction, the region of the plane above the line is excluded by the results of the respective experiment and below the line is allowed. By line 1 in Figure 6 we show the constraints on the axion mass and interaction constant following from the Casimir-less experiment. Below they are compared with similar constraints following from several other experiments.
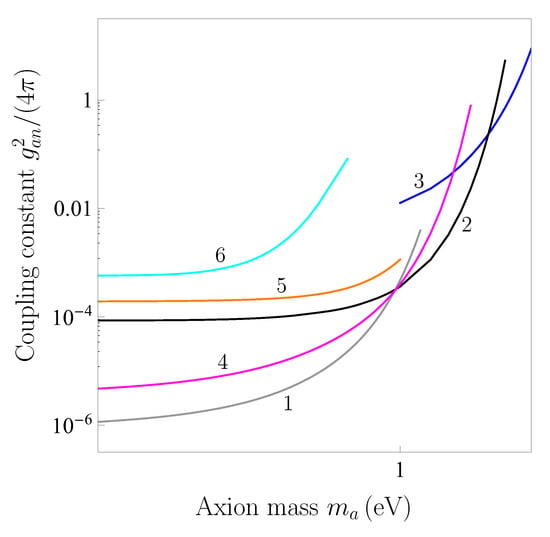
Figure 6.
The constraints on the coupling constant of axion to nucleon following from the Casimir-less experiment, experiments on measuring the Casimir pressure and lateral Casimir force (lines 1, 2, and 3, respectively) and from experiments on measuring the difference of Casimir forces, gradient of the Casimir force and Casimir-Polder force (lines 4, 5, and 6, respectively) are shown as functions of the axion mass. The regions above each line are excluded and below each line are allowed.
Next, we consider an experiment on measuring the effective Casimir pressure by means of a micromechanical oscillator shown schematically in Figure 5 [,]. This experiment was used for constraining the parameters of axions in []. For this purpose, an additional pressure was calculated arising in the experimental configuration due to the two-axion exchange. The constraints were obtained from the inequality
where the meaning of is explained in Section 2. These constraints are shown by line 2 in Figure 6. As is seen in Figure 6, the constraints on an axion following from measuring the Casimir pressure become stronger than those found from the Casimir-less experiment for axion masses eV.
For axion masses eV the stronger constraints on follow from measurements of the lateral Casimir force between corrugated surfaces (see Figure 2 for a schematic of the experimental setup and [,] for a description of the measurement procedure). To obtain these constraints, the additional force was calculated in []. Then the constraints were obtained from the inequality
where is the total experimental error in measuring the lateral Casimir force (see Section 2 for details). These constraints are shown by line 3 in Figure 6.
In addition to the constraints shown by lines 1–3, which are the strongest ones over the respective regions of axion masses, in Figure 3 we also present the constraints obtained from three more Casimir experiments. Although these experiments lead to somewhat weaker constraints, they are useful by providing a qualitatively similar picture based on the independent measurement data.
The line 4 in Figure 6 was obtained in [] from the measure of agreement between experiment and theory in measuring the difference in Casimir forces between a Ni-coated sphere and either Au or Ni sectors of a rotating disc coated with a thin Au overlayer []. As opposed to the Casimir-less experiments [,], the Au overlayer was sufficiently thin in this case and did not make equal the Casimir forces when a sphere was spaced above Au and Ni sectors. It is seen that line 4 is sandwiched between lines 1 and 2 discussed above. Thus, the constraints following from measuring the difference in Casimir forces are in agreement with those obtained from the Casimir-less experiment and experiment on measuring the Casimir pressure.
Line 5 in Figure 6 was obtained in [] from the dynamic experiment measuring the gradient of the Casimir force between an Au-coated sphere and an Au-coated plate performed by means of the dynamic force microscope []. Finally, line 6 in Figure 6 follows [] from the experiment on measuring the Casimir-Polder force between Rb ultracold atoms belonging to the Bose–Einstein condensate and a silica glass plate []. As is seen in Figure 6, lines 5 and 6 indicate the weaker constraints on the coupling constant of axions to nucleons than those shown by line 2 following from measuring the effective Casimir pressure.
In the next section the constraints of Figure 6 are compared with some other constraints obtained from the laboratory experiments unrelated to measurements of the Casimir force.
4. Constraints from Measuring the Casimir Force in Nanometer Separation Range and Other Laboratory Experiments
Here, we consider the constraints on the Yukawa-type hypothetical interaction and on the coupling constant of axions to nucleons obtained recently [] from measuring the Casimir force between an Au-coated sphere and a silicon carbide (SiC) plate at K in N atmosphere []. This experiment has the advantage that the surfaces of both interacting bodies are very smooth. This allowed to measure the Casimir force by means of an atomic force microscope over the separation region from 10 to 200 nm. The experimental results for the Casimir force were compared with theoretical predictions of the Lifshitz theory. For this purpose, the optical properties of the SiC plate have been determined by means of ellipsometers [], as well as the optical properties of Au coating on the sphere which were characterized earlier []. Both the experimental and theoretical errors were determined at the 67% confidence level. In [] the total measure of agreement between experiment and theory was found at the 95% confidence level. Within these errors no additional force was registered originating either from the non-Newtonian gravity or from the axion-to-nucleon interaction.
We begin with the Yukawa-type interaction (1). From (1)–(3) one obtains the following expression for the Yukawa force between an Au-coated sphere and a plate []:
where and are the densities of Au and SiC, respectively, d is the thickness of an Au coating on the sphere, and the function is given by
In the derivation of (18) it was taken into account that the sphere core material (borosilicate glass) gives only a minor contribution to the Yukawa force, which does not influence the obtained results.
The constraints on the Yukawa-type correction to Newtonian gravity have been found from the inequality
They are shown by the line labeled “new” in Figure 7. In the same figure, we reproduce from Figure 3 the lines 1, 2, 3, and 4 obtained from measuring the lateral and normal Casimir forces between corrugated surfaces, the Casimir pressure, and from the second Casimir-less experiment, respectively. As is seen in Figure 7, the new constraints are stronger than those of line 1 within the interaction range from 1 to 3.7 nm. The largest strengthening by the factor of is reached at nm.
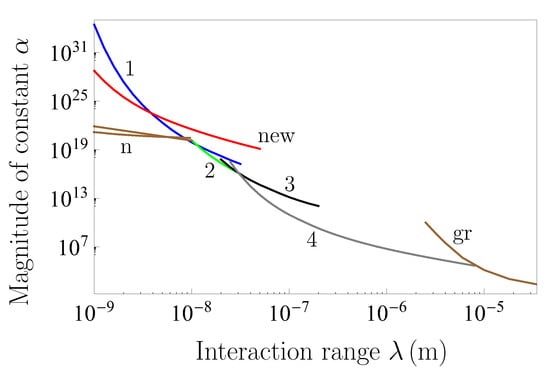
Figure 7.
The constraints on Yukawa-type correction to Newton’s gravitational law following from recent measuring the Casimir force at nanometer separations (line labeled “new”), from experiments on neutron scattering (lines labeled “n”), and from the Cavendish-type experiment (line labeled “gr”) are shown as functions of the interaction range. The lines 1–4, which also indicate the strongest constraints within the respective interaction ranges, are reproduced from Figure 3. The regions above each line are excluded and below each line are allowed.
Now we compare the constraints on the Yukawa interactions obtained from the Casimir effect and from some other laboratory experiments. The strongest constraints on in the nanometer interaction range have been found from the experiments on neutron scattering [,]. They are indicated in Figure 7 by the two lines labeled “n”. As is seen in Figure 7, the neutron scattering results in the strongest constraints on up to nm.
Over a wide interaction range from nm to m the strongest constraints on follow at the moment from the Casimir physics. In doing so, measurements of the lateral and normal Casimir forces between corrugated surfaces lead to the most strong results only within the very narrow ranges from 10 to 11.6 nm and from 11.6 to 17.2 nm, respectively (lines 1 and 2 in Figure 7). The measurement of the Casimir pressure results in the strongest constraints in the range from nm to nm (see line 3 in Figure 7). Finally, the second Casimir-less experiment leads to the most strong constraints in the wide range from nm to m (line 4 in Figure 7).
For larger the strongest constraints on the Yukawa-type corrections to Newtonian gravitational law are currently obtained from the gravitational experiments. Specifically, within the interaction range from m to cm the strongest constraints follow from the Cavendish-type experiments [,,]. Thus, in the range from 8 to m they were obtained in [], in the range from m to 4 mm in [], and for larger up to 1 cm in []. The initial part of the line representing these constraints in the region from 8 to m is labeled “gr” in Figure 7. Recently the constraints of [] were strengthened by up to a factor of 3 in the region of from 40 to m by means of the improved Cavendish-type experiment [].
Now we deal with the constraints on an axion that follow [] from measuring the Casimir force in the nanometer separation region []. An expression for the additional force acting between an Au-coated sphere and a SiC plate due to two-axion exchange is obtained from (13) and (14) []
where the function is defined as
and are the numbers of nucleons per unit volume of Au and SiC [].
The constraints on the coupling constant of axions to nucleons were obtained from the inequality
which is similar to (20) used to constrain the Yukawa-type interactions from the results of the same experiment. These constraints are shown by line “new” in Figure 8. In this figure the solid lines 1, 2, and 3 following from the second Casimir-less experiment, measurements of the Casimir pressure, and the lateral Casimir force between corrugated surfaces, respectively, are reproduced from Figure 6. As is seen in Figure 8, the new constraints are stronger than those found from measuring the lateral Casimir force for axion masses eV.
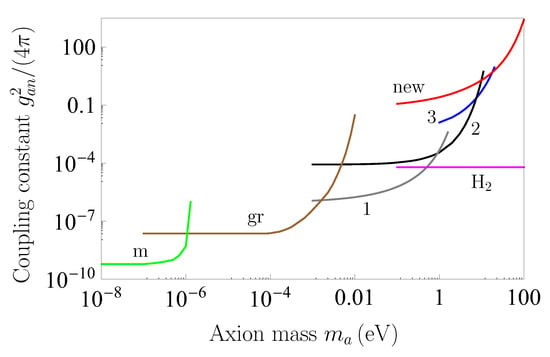
Figure 8.
The constraints on the coupling constant of axion to nucleon following from recent measuring the Casimir force at nanometer separations (line labeled “new”), from the magnetometer measurements (line labeled “m”), from the Cavendish-type experiment (line labeled “gr”), and from the experiment using beams of molecular hydrogen (line labeled “H”) are shown as functions of the axion mass. The lines 1–3, where line 1 indicates the strongest constraints within some range of axion masses, are reproduced from Figure 6. The regions above each line are excluded and below each line are allowed.
We are coming now to a comparison of the above constraints on an axion-to-nucleon coupling constant obtained from the Casimir effect with those following from some other laboratory experiments. Strong constraints on the coupling constant of axions to neutrons over the wide range of axion masses from eV to eV were obtained from the magnetometer measurements employing spin-polarized K and He atoms []. These constraints in the range of from eV to eV are shown by the line labeled “m” in Figure 8. We note that the constraints found by means of a magnetometer are derived from the one-axion exchange between two neutrons, which is described by the effective potential (11). Because of this they are equally applicable to both the QCD and GUT axions.
Within the wide range of from eV to 1.7 meV the strongest constraints on the axion-to-nucleon coupling constant valid for the GUT axions follow from the gravitational experiments of Cavendish type []. These constraints derived in [] are shown by the line labeled “gr” in Figure 8. For meV the strongest constraints on are given by line 1 reproduced from Figure 6 which was obtained from the Casimir-less experiment.
In the case of axions, this experiment leads to competitive constraints up to eV. For eV the constraints following from the Casimir physics (lines 1–3 and “new” in Figure 8) become much weaker than the constraints obtained from experiments on measuring the forces between protons in the beam of molecular hydrogen [,]. These constraints are shown by a line labeled “H” in Figure 8. For axions with eV the constraints of line “H” were further strengthened by comparing with theory the experimental results on the nuclear magnetic resonance for nucleons in deuterated molecular hydrogen [].
5. Proposed Experiments
In this section we consider several experiments suggested in the literature, which allow further strengthening the constraints on non-Newtonian gravity and axionlike particles but are not performed yet.
All the experiments on measuring the Casimir interaction considered above have been planned and performed for the purposes that were not directly connected with the investigation of hypothetical interactions. The obtained constraints can be considered as some by-product. In [] the parameters of these experiments were optimized in order so that the stronger constraints could be obtained on both the Yukawa-type interaction and the interaction due to two-axion exchange. It was shown [] that the prospective constraints are up to an order of magnitude stronger than those ones already obtained and outlined above.
All precise measurements of the Casimir interaction performed during the last few years employed the sphere-plate geometry and the separation distances below a micrometer. For this reason much attention was attracted to the proposed CANNEX (Casimir And Non-Newtonian force EXperiment) test designed to measure the Casimir force between two parallel plates spaced at separations up to a few micrometers [,]. In [] the parameters of this experiment were optimized for obtaining the strongest constraints on both the non-Newtonian gravity and axionlike particles. Here, we illustrate the potentialities of the proposed setup.
In Figure 9, the constraints on the Yukawa interaction constant , which could be obtained from the CANNEX test, are shown by the line labeled “proposed”. For comparison purposes, lines 4–7 and “gr” following from experiments discussed in Section 2 and Section 4 are reproduced from Figure 7. As is seen in Figure 9, the proposed line provides an order of magnitude stronger constraints on than those given by line 4 following from the Casimir-less experiment. It is seen also that the proposed constraints encroach on the province where the Cavendish-type experiments presently lead to the strongest constraints shown by the line labeled “gr”.
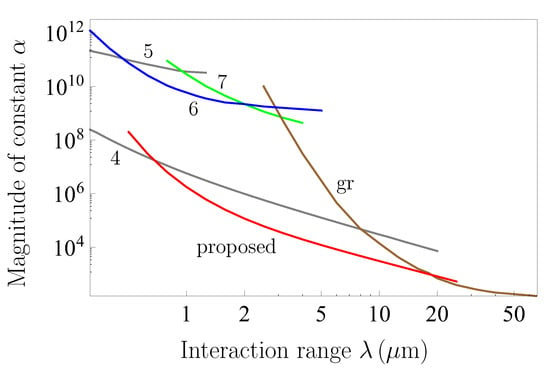
Figure 9.
The constraints on Yukawa-type correction to Newton’s gravitational law, which can be obtained from the proposed CANNEX test are shown by the line “proposed” as a function of the interaction range. For comparison purposes, the lines 4–7 and the line labeled “gr” are reproduced from Figure 3 and Figure 7, respectively. The regions above each line are excluded and below each line are allowed.
A similar state of affairs holds for the additional interaction between two parallel plates due to two-axion exchange. The constraints on , which could be obtained from the CANNEX test, are shown by the line labeled “proposed” in Figure 10. For comparison purposes, lines 1, 2, and labeled “gr” are reproduced from Figure 8. From Figure 10 it is seen that the proposed line suggests stronger constraints than those indicated by line 1 following from the Casimir-less experiment. Some additional potentialities are also suggested by the CANNEX setup in out of thermal equilibrium conditions [].
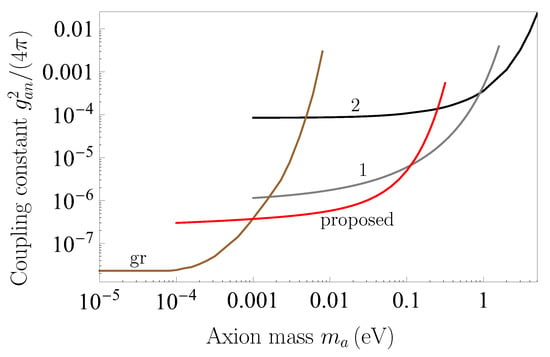
Figure 10.
The constraints on the coupling constant of axion to nucleon, which can be obtained from the proposed CANNEX test, are shown by the line “proposed” as a function of the axion mass. For comparison purposes, the lines 1, 2 and “gr” are reproduced from Figure 6 and Figure 8, respectively. The regions above each line are excluded and below each line are allowed.
There are several more proposed laboratory experiments aiming to strengthen the constraints on non-Newtonian gravity and interaction of axionlike particles to nucleons in the ranges of parameters considered above. Thus, it was suggested to measure the Casimir–Polder force between an Rb atom and a movable Si plate separated with a metallic shield in the form of an Au film []. It is expected that the experiment of this kind will help to obtain the stronger constraints on non-Newtonian gravity in the interaction range of m []. The respective strengthening of the constraints on is also expected.
According to [], the weakly bound molecules can be used as sensitive sensors for the non-Newtonian gravity. Calculations show that the precision spectroscopy of these systems will allow to strengthen constraints on the interaction of the Yukawa type obtained from the experiments on neutron scattering (lines labeled “n” in Figure 7) at least by the two orders of magnitude. Note that a few constraints obtained from atomic spectroscopy in the range of extremely small are discussed in [].
One more proposed detection of non-Newtonian gravity at short range exploits the levitated sensors []. It is based on the effect of normal mode splitting in the optomechanical cavity and aims at the detection of large extra dimensions proposed in [,] and the resulting Yukawa-type corrections to Newtonian gravity [,].
In addition to the Yukawa-type interaction and forces arising due to two-axion exchange between two nucleons, some other types of the fifth force are predicted, which are suppressed in the regions with high density of matter. These forces are connected with such hypothetical scalar particles of variable mass as chameleons and symmetrons. It was already pointed out [,,,] that experiments on measuring the Casimir force at large separations can be used for a search of chameleons as possible candidates for the constituents of dark energy. Recently the Casimir experiment was proposed [], which should be capable to place stronger constraints on symmetrons.
6. Discussion
In this article, we have reviewed the present state of the art in constraining the Yukawa-type corrections to Newton’s law of gravitation and the axion-to-nucleon interaction from laboratory experiments. In was shown that measurements of the Casimir force and Casimir-less experiments lead to strong constraints on the Yukawa interaction constant and on the coupling constant of axions to nucleons over the wide ranges of and , respectively. The very recent results were presented on constraining both and from the experiment on measuring the Casimir force between an Au-coated sphere and a SiC plate performed at short separations down to 10 nm. These constraints are much stronger than those found previously from measuring the lateral Casimir force between corrugated surfaces.
It should be noted, however, that within the interaction range of below 10 nm and above m the strongest constraints on the Yukawa-type interaction follow not from the Casimir experiments, but from the laboratory experiments of some other kind. Thus, for nm the most strong constraints on were obtained from experiments on neutron scattering whereas for m from the Cavendish-type experiments. In a similar way, for axion masses below 1.7 meV the strongest laboratory constraints on the coupling constant of axions to nucleons follow not from the Casimir physics, but from the magnetometer measurements and experiments of the Cavendish type. At eV the strongest constraints on were obtained from measuring the forces between protons in the beam of molecular hydrogen.
Thus, the future trends in this field of research are connected with different experimental approaches to constraining the Yukawa-type forces and the interaction of axions with nucleons.
7. Conclusions
To conclude, recent advances in experimental techniques have made possible performing more precise laboratory experiments in different branches of physics. The results of these experiments and the measure of their agreement with theory were used for obtaining stringent laboratory constraints on the strength of Yukawa-type interactions and the coupling constant of axions to nucleons. In this article, we summarized the strongest constraints of this kind following from the diversified experiments, each of which was used for obtaining the best result in some specific range of parameters. One may hope that by improving the characteristics of these experiments and by implementing some of the recent proposals discussed above it will be possible to obtain even stronger constraints on the non-Newtonian gravity, axionlike particles and on some other related objects, such as chameleons and symmetrons.
Author Contributions
Investigation, V.M.M. and G.L.K.; writing, V.M.M. and G.L.K. All authors have read and agreed to the published version of the manuscript.
Funding
V.M.M. was partially funded by the Russian Foundation for Basic Research grant No. 19-02-00453 A.
Acknowledgments
The authors were partially supported by the Peter the Great Saint Petersburg Polytechnic University in the framework of the Program “5–100–2020”. V.M.M. was partially supported by the Russian Government Program of Competitive Growth of Kazan Federal University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, J.E. Light pseudoscalars, particle physics and cosmology. Phys. Rep. 1987, 150, 1–177. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Giudice, G.F. Macroscopic forces from supersymmetry. Phys. Lett. B 1996, 379, 105–114. [Google Scholar] [CrossRef]
- Fujii, Y. The theoretical background of the fifth force. Int. J. Mod. Phys. A 1991, 6, 3505–3557. [Google Scholar] [CrossRef]
- Fischbach, E.; Talmadge, C.L. The Search for Non-Newtonian Gravity; Springer: New York, NY, USA, 1999. [Google Scholar]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–283. [Google Scholar] [CrossRef]
- Kawasaki, M.; Nakayama, K. Axions: Theory and Cosmological Role. Annu. Rev. Nucl. Part. Sci. 2013, 63, 69–95. [Google Scholar] [CrossRef]
- Kuzmin, V.A.; Tkachev, I.I.; Shaposhnikov, M.E. Restrictions imposed on light scalar particles by measurements of van der Waals forces. JETP Lett. 1982, 36, 59–62. [Google Scholar]
- Mostepanenko, V.M.; Sokolov, I.Y. The Casimir effect leads to new restrictions on long-range force constants. Phys. Lett. A 1987, 125, 405–408. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. New dimensions at a millimeter to a fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. Phenomenology, astrophysics, and cosmology of theories with millimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Floratos, E.G.; Leontaris, G.K. Low scale unification, Newton’s law and extra dimensions. Phys. Lett. B 1999, 465, 95–100. [Google Scholar] [CrossRef]
- Kehagias, A.; Sfetsos, K. Deviations from 1/r2 Newton law due to extra dimensions. Phys. Lett. B 2000, 472, 39–44. [Google Scholar] [CrossRef]
- Ferrer, F.; Nowakowski, M. Higg- and Goldstone-boson-mediated long range forces. Phys. Rev. D 1999, 59, 075009. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Fischbach, E.; Krause, D.E.; Newman, R.D. Constraining the couplings of massive pseudoscalars using gravity and optical experiments. Phys. Rev. D 2003, 68, 062002. [Google Scholar] [CrossRef]
- Aldaihan, S.; Krause, D.E.; Long, J.C.; Snow, W.M. Calculations of the dominant long-range, spin-independent contributions to the interaction energy between two nonrelativistic Dirac fermions from double-boson exchange of spin-0 and spin-1 bosons with spin-dependent couplings. Phys. Rev. D 2017, 95, 096005. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Smullin, S.J.; Geraci, A.A.; Weld, D.M.; Chiaverini, J.; Holmes, S.; Kapitulnik, A. Constraints on Yukawa-type deviations from Newtonian gravity at 20 microns. Phys. Rev. D 2005, 72, 122001. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef]
- Hoskins, J.K.; Newman, R.D.; Spero, R.; Schultz, J. Experimental tests of the gravitational inverse-square law for mass separations from 2 to 105 cm. Phys. Rev. D 1985, 32, 3084–3095. [Google Scholar] [CrossRef]
- Smith, G.L.; Hoyle, C.D.; Gundlach, J.H.; Adelberger, E.G.; Heckel, B.R.; Swanson, H.E. Short-range tests of the equivalence principle. Phys. Rev. D 2000, 61, 022001. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.-J.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the equivalence principle using a rotating torsion balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V. Neutron scattering and extra short range interactions. Phys. Rev. D 2008, 77, 034020. [Google Scholar] [CrossRef]
- Kamiya, Y.; Itagami, K.; Tani, M.; Kim, G.N.; Komamiya, S. Constraints on New Gravitylike Forces in the Nanometer Range. Phys. Rev. Lett. 2015, 114, 161101. [Google Scholar] [CrossRef] [PubMed]
- Haddock, C.C.; Oi, N.; Hirota, K.; Ino, T.; Kitaguchi, M.; Matsumoto, S.; Mishima, K.; Shima, T.; Shimizu, H.M.; Snow, W.M.; et al. Search for deviations from the inverse square law of gravity at nm range using a pulsed neutron beam. Phys. Rev. D 2018, 97, 062002. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30–8000 Nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Kim, J.E. Weak-Interaction Singlet and Strong CP Invariance. Phys. Rev. Lett. 1979, 43, 103–107. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainstein, A.I.; Zakharov, V.I. Can confinement ensure natural CP invariance of strong interactions? Nucl. Phys. B 1980, 166, 493–506. [Google Scholar] [CrossRef]
- Zhitnitskii, A.P. On the possible suppression of axion-hadron interactions. Sov. J. Nucl. Phys. 1980, 31, 260–263. [Google Scholar]
- Dine, M.; Fischler, F.; Srednicki, M. A simple solution to the strong CP problem with a harmless axion. Phys. Lett. B 1981, 104, 199–202. [Google Scholar] [CrossRef]
- Rosenberg, L.J.; van Bibber, K.A. Searches for invisible axions. Phys. Rep. 2000, 325, 1–39. [Google Scholar] [CrossRef]
- Raffelt, G.G. Axions—Motivation, limits and searches. J. Phys. A Math. Theor. 2007, 40, 6607–6620. [Google Scholar] [CrossRef]
- Ivastorza, I.G.; Redondo, J. New experimental approaches in the search for axion-like particles. Progr. Part. Nucl. Phys. 2018, 102, 89–159. [Google Scholar] [CrossRef]
- Raffelt, G. Limits on a CP-violating scalar axion-nucleon interaction. Phys. Rev. D 2012, 86, 015001. [Google Scholar] [CrossRef]
- Vasilakis, G.; Brown, J.M.; Kornak, T.R.; Romalis, M.V. Limits on New Long Range Nuclear Spin-Dependent Forces Set with a K-3He Comagnetometer. Phys. Rev. Lett. 2009, 103, 261801. [Google Scholar] [CrossRef] [PubMed]
- Adelberger, E.G.; Heckel, B.R.; Hoedl, S.; Hoyle, C.D.; Kapner, D.J.; Upadhye, A. Particle-Physics Implications of a Recent Test of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 2007, 98, 131104. [Google Scholar] [CrossRef] [PubMed]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Improved constraints on the coupling constants of axion-like particles to nucleons from recent Casimir-less experiment. Eur. Phys. J. C 2015, 75, 164. [Google Scholar] [CrossRef]
- Ramsey, N.F. The tensor force between two protons at long range. Phys. A 1979, 96, 285–289. [Google Scholar] [CrossRef]
- Ledbetter, M.P.; Romalis, M.V.; Jackson Kimball, D.F. Constraints on Short-Range Spin-Dependent Interactions from Scalar Spin-Spin Coupling in Deuterated Molecular Hydrogen. Phys. Rev. Lett. 2013, 110, 040402. [Google Scholar] [CrossRef]
- Antoniadis, I.; Baessler, S.; Bücher, M.; Fedorov, V.V.; Hoedl, S.; Lambrecht, A.; Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V.; Reynaud, S.; et al. Short-range fundamental forces. Compt. Rend. 2011, 12, 755–778. [Google Scholar] [CrossRef]
- Kardar, M.; Golestanian, R. The “friction” of vacuum, and other fluctuation-induced forces. Rev. Mod. Phys. 1999, 71, 1233–1245. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Demonstration of the Lateral Casimir Force. Phys. Rev. Lett. 2002, 88, 101801. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Experimental and theoretical investigation of the lateral Casimir force between corrugated surfaces. Phys. Rev. A 2002, 66, 032113. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the asymmetric lateral Casimir force between corrugated surfaces in the nonadditive regime. Phys. Rev. B 2009, 80, 121402. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Lateral Casimir force between sinusoidally corrugated surfaces: Asymmetric profiles, deviations from the proximity force approximation, and comparison with exact theory. Phys. Rev. B 2010, 81, 115417. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Advance and prospects in constraining the Yukawa-type corrections to Newtonian gravity from the Casimir effect. Phys. Rev. D 2010, 81, 055003. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Novello, M. Constraints on non-Newtonian gravity from the Casimir force measurements between two crossed cylinders. Phys. Rev. D 2001, 63, 115003. [Google Scholar] [CrossRef]
- Ederth, T. Template-stripped gold surfaces with 0.4-nm rms roughness suitable for force measurements: Application to the Casimir force in the 20–100-nm range. Phys. Rev. A 2000, 62, 062104. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Demonstration of Angle-Dependent Casimir Force between Corrugations. Phys. Rev. Lett. 2013, 110, 250403. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Experimental and theoretical investigation of the angular dependence of the Casimir force between sinusoidally corrugated surfaces. Phys. Rev. B 2014, 89, 235436. [Google Scholar] [CrossRef]
- Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Proximity force approximation for the Casimir energy as a derivative expansion. Phys. Rev. D 2011, 84, 105031. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Kardar, M. Material dependence of Casimir forces: Gradient expansion beyond proximity. Appl. Phys. Lett. 2012, 100, 074110. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Constraints on corrections to Newtonian gravity from two recent measurements of the Casimir interaction between metallic surfaces. Phys. Rev. D 2013, 87, 125031. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Progress in constraining axion and non-Newtonian gravity from the Casimir effect. Int. J. Mod. Phys. A 2016, 31, 1641020. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Bimonte, G. Going beyond PFA: A precise formula for the sphere-plate Casimir force. Europhys. Lett. 2017, 118, 20002. [Google Scholar] [CrossRef]
- Hartmann, M.; Ingold, G.-L.; Maia Neto, P.A. Plasma versus Drude Modeling of the Casimir Force: Beyond the Proximity Force Approximation. Phys. Rev. Lett. 2017, 119, 043901. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Bezerra, V.B.; Decca, R.S.; Geyer, B.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Romero, C. Present status of controversies regarding the thermal Casimir force. J. Phys. Math. Gen. 2006, 39, 6589–6600. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Bezerra, V.B.; Klimchitskaya, G.L.; Romero, C. New constraints on the Yukawa-type interactions from the Casimir effect. Int. J. Mod. Phys. A 2012, 27, 1260015. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Chan, H.B.; Fischbach, E.; Krause, D.E.; Jamell, C.R. Constraining New Forces in the Casimir Regime Using the Isoelectronic Technique. Phys. Rev. Lett. 2005, 94, 240401. [Google Scholar] [CrossRef]
- Wang, J.; Guan, S.; Chen, K.; Wu, W.; Tian, Z.; Luo, P.; Jin, A.; Yang, S.; Shao, C.; Luo, J. Test of non-Newtonian gravitational forces at micrometer range with two-dimensional force mapping. Phys. Rev. D 2016, 94, 122005. [Google Scholar] [CrossRef]
- Masuda, M.; Sasaki, M. Limits on Nonstandard Forces in the Submicrometer Range. Phys. Rev. Lett. 2009, 102, 171101. [Google Scholar] [CrossRef] [PubMed]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; Benjamin: New York, NY, USA, 1969; Volume 1. [Google Scholar]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion coupling constants from measuring the Casimir interaction between polarized test bodies. Phys. Rev. D 2016, 94, 035011. [Google Scholar] [CrossRef]
- Drell, S.D.; Huang, K. Many-Body Forces and Nuclear Saturation. Phys. Rev. 1953, 91, 1527–1542. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion-nucleon coupling constants from measurements of effective Casimir pressure by means of micromachined oscillator. Eur. Phys. J. C 2014, 74, 2859. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on axion-nucleon coupling constants from measuring the Casimir force between corrugated surfaces. Phys. Rev. D 2014, 90, 055013. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Constraints on axionlike particles and non-Newtonian gravity from measuring the difference of Casimir forces. Phys. Rev. D 2017, 95, 123013. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Stronger constraints on an axion from measuring the Casimir interaction by means of a dynamic atomic force microscope. Phys. Rev. D 2014, 89, 075002. [Google Scholar] [CrossRef]
- Chang, C.C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on the parameters of an axion from measurements of the thermal Casimir-Polder force. Phys. Rev. D 2014, 89, 035010. [Google Scholar] [CrossRef]
- Obrecht, J.M.; Wild, R.J.; Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Cornell, E.A. Measurement of the Temperature Dependence of the Casimir-Polder Force. Phys. Rev. Lett. 2007, 98, 063201. [Google Scholar] [CrossRef] [PubMed]
- Klimchitskaya, G.L.; Kuusk, P.; Mostepanenko, V.M. Constraints on non-Newtonian gravity and axionlike particles from measuring the Casimir force in nanometer separation range. Phys. Rev. D 2020, 101, 056013. [Google Scholar] [CrossRef]
- Sedighi, M.; Svetovoy, V.B.; Palasantzas, G. Casimir force measurements from silicon carbide surfaces. Phys. Rev. B 2016, 93, 085434. [Google Scholar] [CrossRef]
- Sedighi, M.; Svetovoy, V.B.; Broer, W.H.; Palasantzas, G. Casimir forces from conductive silicon carbide surfaces. Phys. Rev. B 2014, 89, 195440. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; van Zwol, P.J.; Palasantzas, G.; De Hosson, J.T.M. Optical properties of gold films and the Casimir force. Phys. Rev. B 2008, 77, 035439. [Google Scholar] [CrossRef]
- Tan, W.-H.; Du, A.-B.; Dong, W.-C.; Yang, S.-Q.; Shao, C.-G.; Guan, S.-G.; Wang, Q.-L.; Zhan, B.-F.; Luo, P.-S.; Tu, L.-C.; et al. Improvement for Testing the Gravitational Inverse-Square Law at the Submillimeter Range. Phys. Rev. Lett. 2020, 124, 051301. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. Recent breakthrough and outlook in constraining the non-Newtonian gravity and axion-like particles from Casimir physics. Eur. Phys. J. C 2017, 77, 315. [Google Scholar] [CrossRef]
- Almasi, A.; Brax, P.; Iannuzzi, D.; Sedmik, R.I.P. Force sensor for chameleon and Casimir force experiments with parallel-plate configuration. Phys. Rev. D 2015, 91, 102002. [Google Scholar] [CrossRef]
- Sedmik, R.; Brax, P. Status Report and first Light from Cannex: Casimir Force Measurements between flat parallel Plates. J. Phys. Conf. Ser. 2018, 1138, 012014. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P.; Abele, H. Prospects for Searching Thermal Effects, Non-Newtonian Gravity and Axion-Like Particles: CANNEX Test of the Quantum Vacuum. Symmetry 2019, 11, 407. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P. Casimir pressure between metallic plates out of thermal equilibrium: Proposed test for the relaxation properties of free electrons. Phys. Rev. A 2019, 100, 022511. [Google Scholar] [CrossRef]
- Bennett, R.; O’Dell, D.H.J. Revealing short-range non-Newtonian gravity through Casimir-Polder shielding. New J. Phys. 2019, 21, 033032. [Google Scholar] [CrossRef]
- Borkowski, M.; Buchachenko, A.A.; Ciuryło, R.; Julienne, P.S.; Yamada, H.; Kikuchi, Y.; Takasu, Y.; Takahashi, Y. Weakly bound molecules as sensors of new gravitylike forces. Sci. Rep. 2019, 9, 14807. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Jackson Kimball, D.F.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, K.-D. Detecting large extra dimensions with optomechanical levitated sensors. Eur. Phys. J. C 2019, 79, 18. [Google Scholar] [CrossRef]
- Sedmik, R.I.P. Casimir and non-Newtonian force experiment (CANNEX): Review, status, and outlook. Int. J. Mod. Phys. A 2020, 35, 2040008. [Google Scholar] [CrossRef]
- Elder, B.; Vardanyan, V.; Arkami, Y.; Brax, P.; Davis, A.-C.; Decca, R.S. Classical symmetron force in Casimir experiments. Phys. Rev. D 2020, 101, 064065. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).