Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars
Abstract
1. Introduction
1.1. EoS Constraints from M–R Measurements before GW170817
1.2. New Constraints on M–R Relations in the Era of Multi-Messenger Astronomy
1.3. Goals of the Present Work
2. Quark-Hadron Hybrid Equation of State
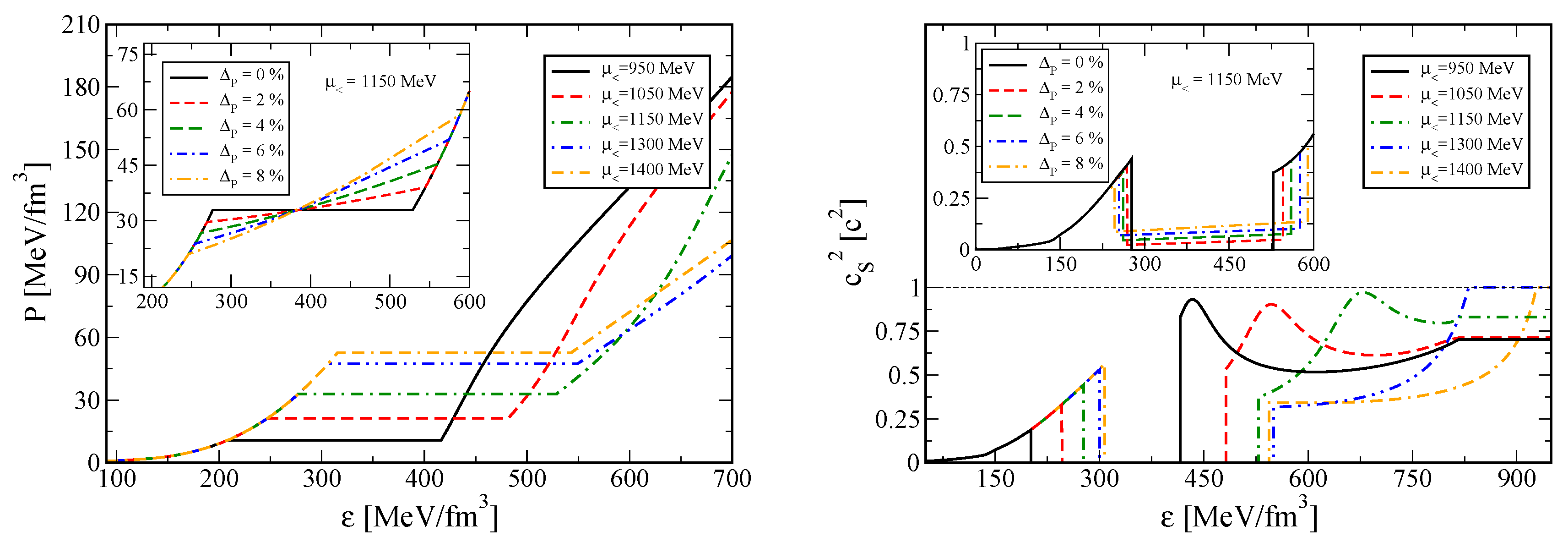
2.1. Quark Matter Model
2.2. Mixed Phase Construction
2.3. Constant Speed of Sound Extrapolation
3. Compact Star Configurations
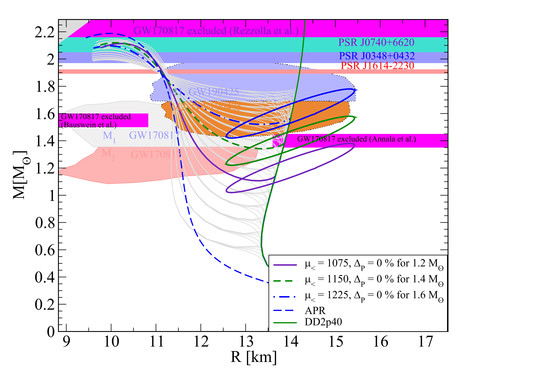
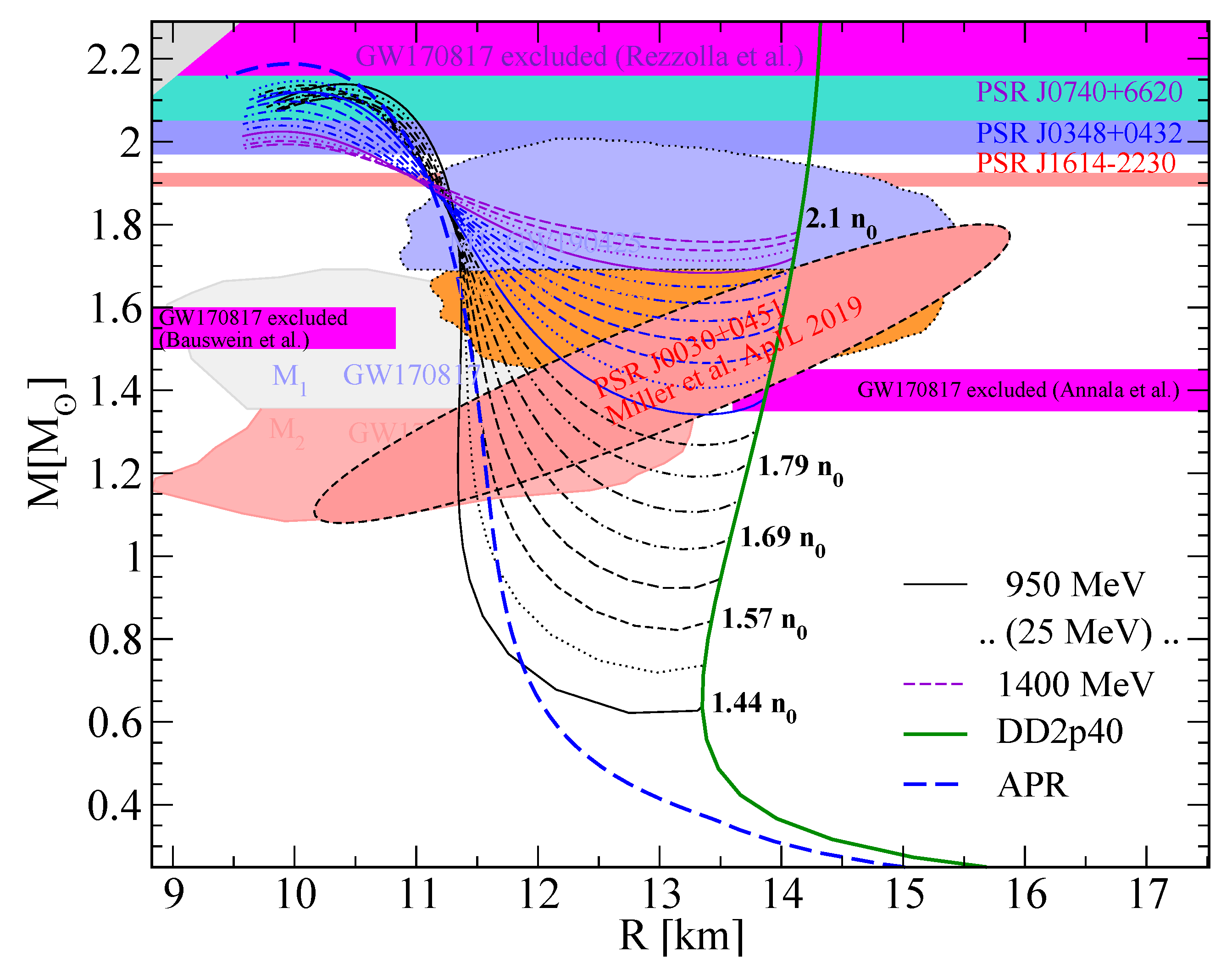
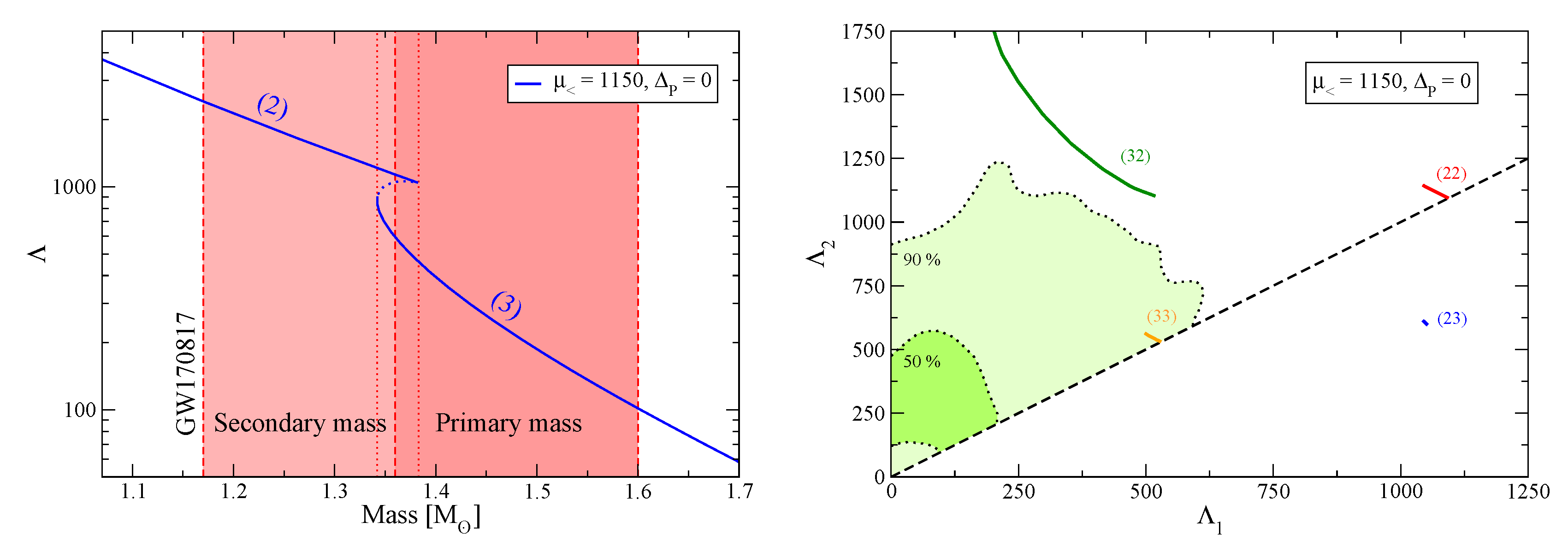
3.1. Mass and Radius
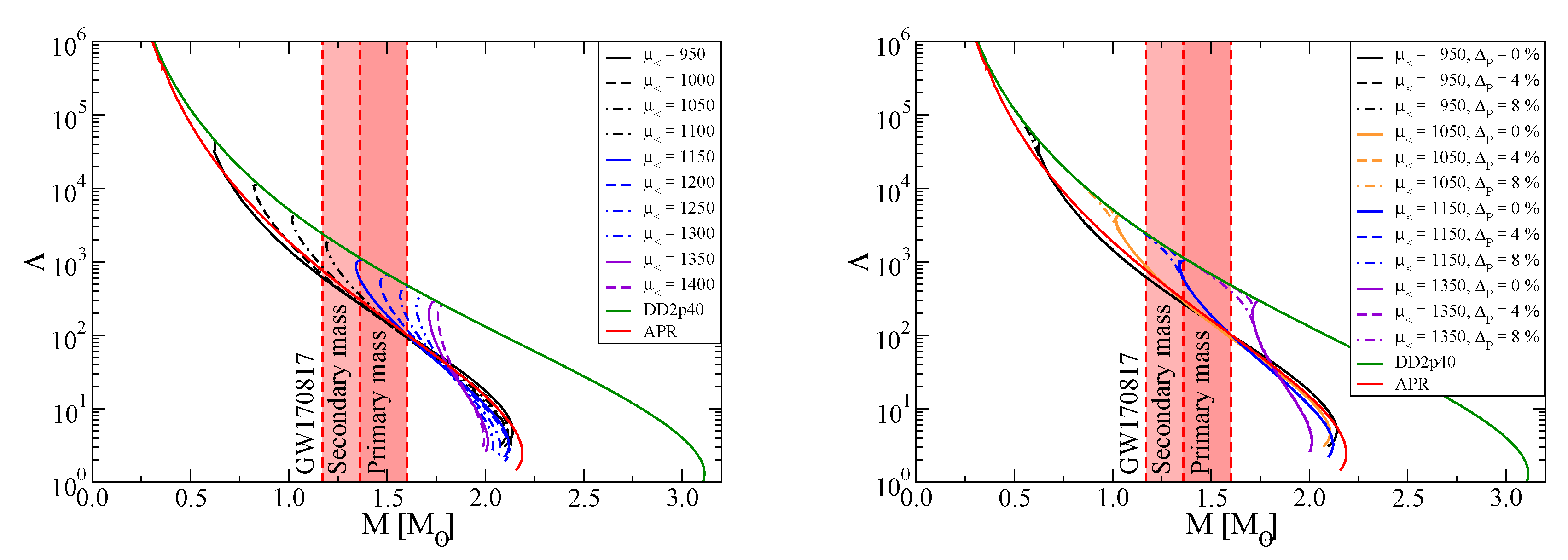
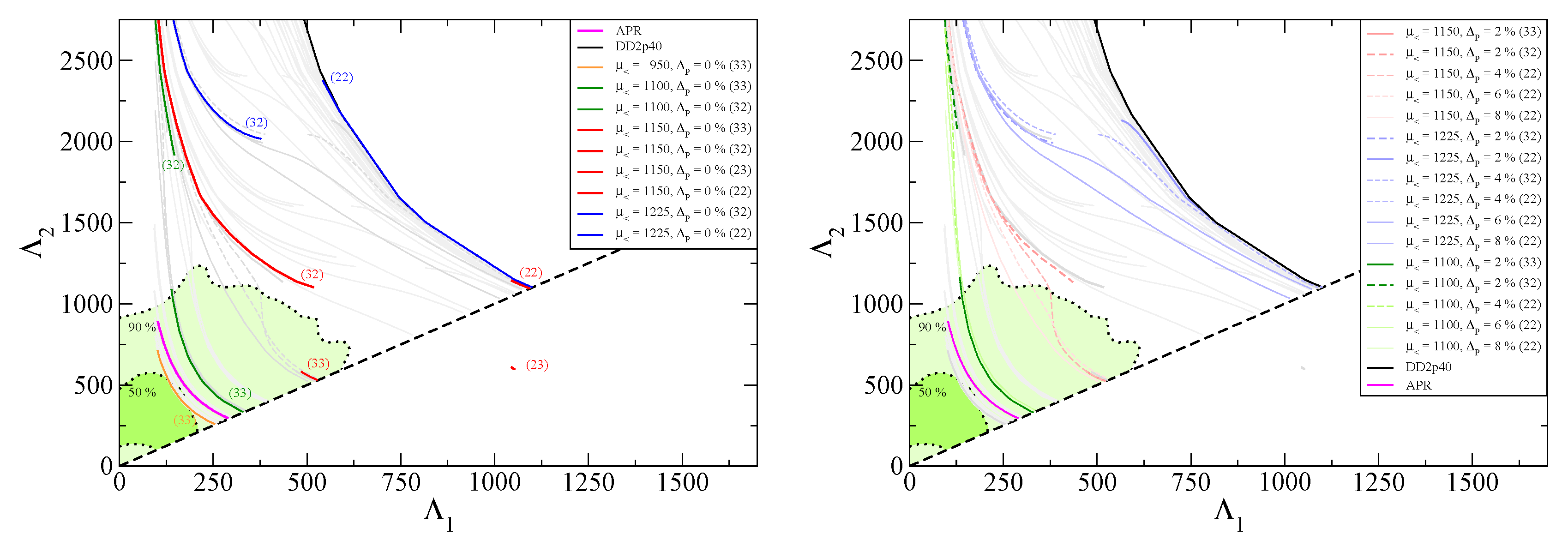
3.2. Tidal Deformabilities and GW170817
4. Bayesian Inference for the EoS Models
4.1. Vector of Parameters
4.2. Likelihood of a Model under the – Constraint from GW170817
4.3. Likelihood of a Model under the Constraint on the Lower Limit of the Maximum Mass
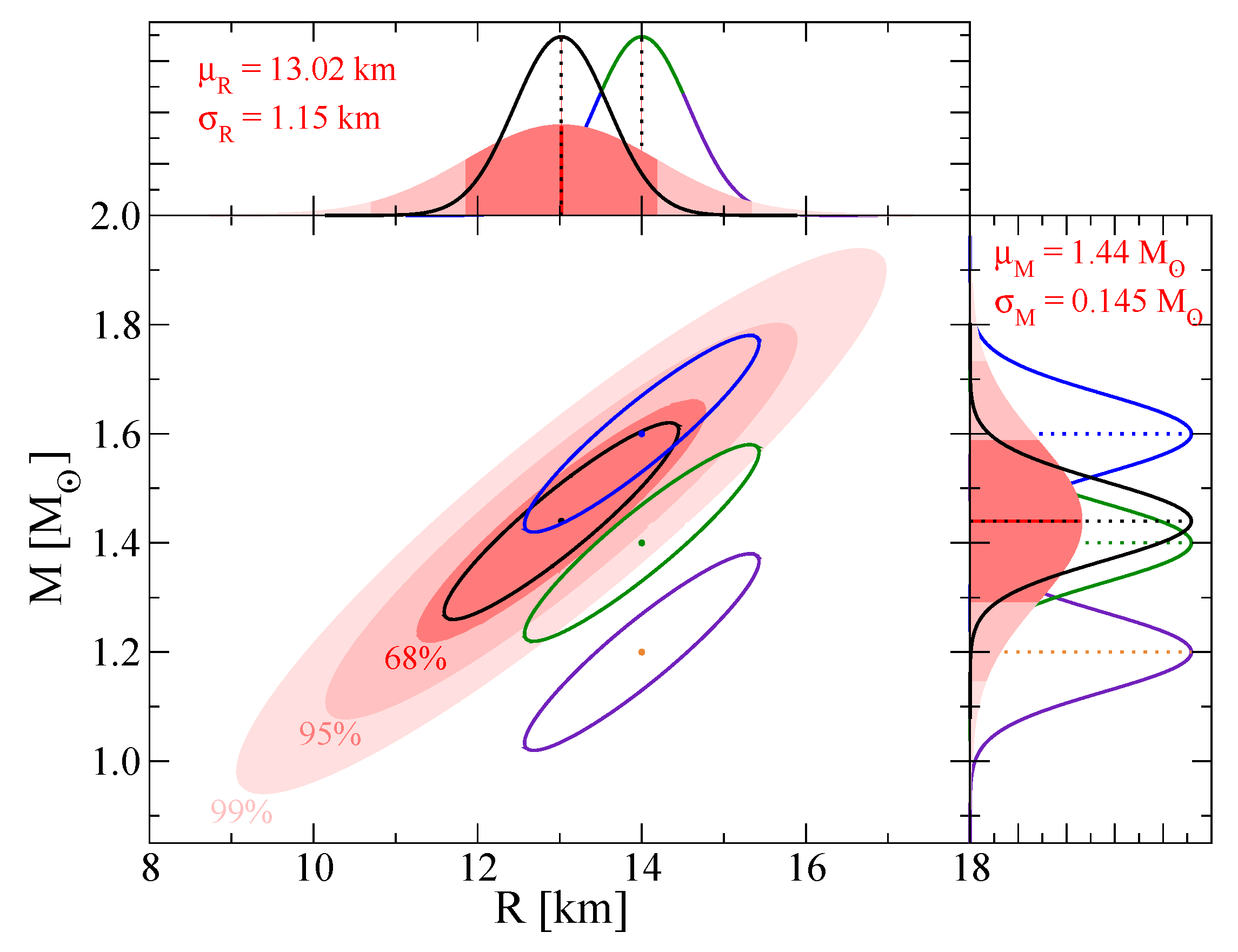
4.4. Likelihood of a Model under the Combined M-R Constraint of the NICER Experiment
4.5. Posterior Distribution
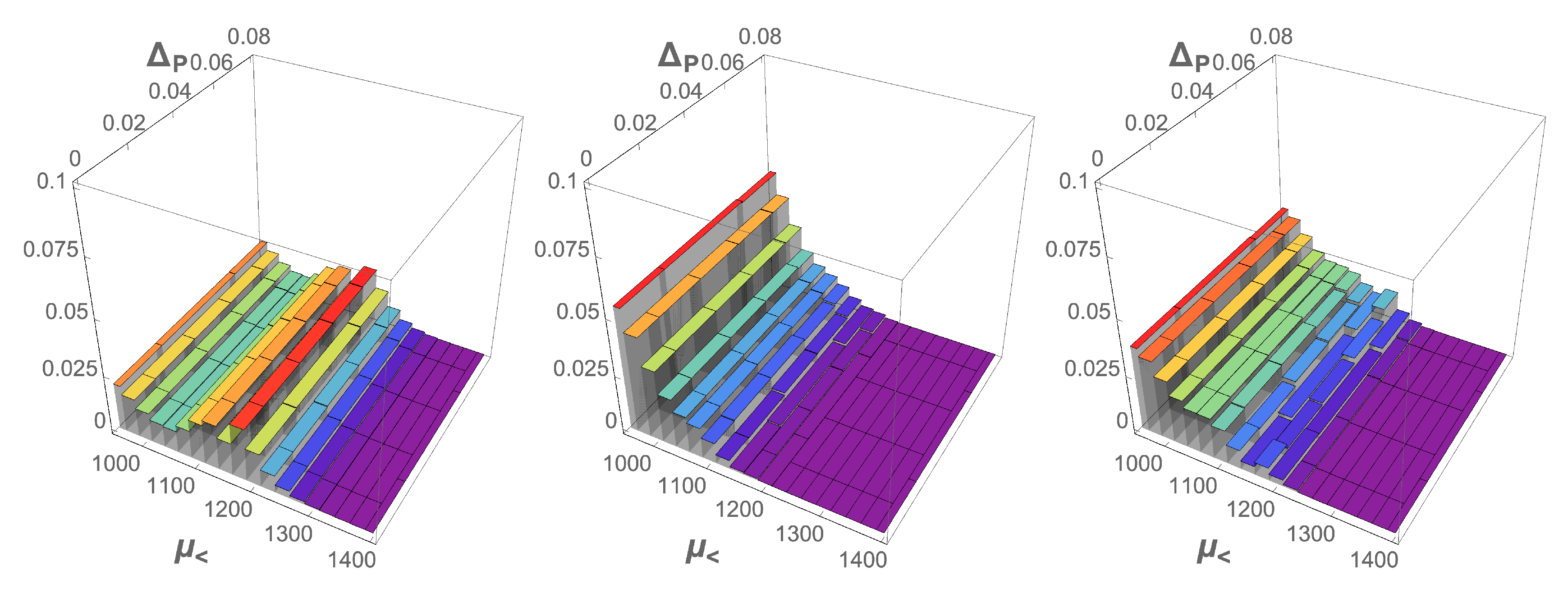
4.6. Results of the Bayesian Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; LIGO Scientific Collaboration and Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef] [PubMed]
- Weih, L.R.; Hanauske, M.; Rezzolla, L. Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Mergers. Phys. Rev. Lett. 2020, 124, 171103. [Google Scholar] [CrossRef] [PubMed]
- Gerlach, U.H. Equation of State at Supranuclear Densities and the Existence of a Third Family of Superdense Stars. Phys. Rev. 1968, 172, 1325–1330. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.T.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhilon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4M⊙. arXiv 2020, arXiv:astro-ph.HE/2001.01761. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmenn, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; Ludlam, R.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guilllot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33–54. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Neutron Star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Nättilä, J.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Equation of state constraints for the cold dense matter inside neutron stars using the cooling tail method. Astron. Astrophys. 2016, 591, A25. [Google Scholar] [CrossRef]
- Nättilä, J.; Miller, M.C.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Neutron star mass and radius measurements from atmospheric model fits to X-ray burst cooling tail spectra. Astron. Astrophys. 2017, 608, A31. [Google Scholar] [CrossRef]
- Salmi, T.; Nättilä, J.; Poutanen, J. Bayesian parameter constraints for neutron star masses and radii using X-ray timing observations of accretion-powered millisecond pulsars. Astron. Astrophys. 2018, 618, A161. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. From Neutron Star Observables to the Equation of State. II. Bayesian Inference of Equation of State Pressures. Astrophys. J. 2017, 844, 156. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Ayriyan, A.; Benic, S.; Blaschke, D.; Grigorian, H.; Typel, S. New class of hybrid EoS and Bayesian M-R data analysis. Eur. Phys. J. A 2016, A52, 69. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the neutron-star equation of state with gravitational-wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2015, 91, 043002. [Google Scholar] [CrossRef]
- Ayriyan, A.; Alvarez-Castillo, D.; Blaschke, D.; Grigorian, H. Bayesian Analysis for Extracting Properties of the Nuclear Equation of State from Observational Data including Tidal Deformability from GW170817. Universe 2019, 5, 61. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Ayriyan, A.; Barnaföldi, G.G.; Posfay, P. Studying the Landau mass parameter of the extended sigma-model for neutron star matter. arXiv 2020, arXiv:astro-ph.HE/2004.04210. [Google Scholar]
- Alvarez-Castillo, D.E.; Ayriyan, A.; Barnaföldi, G.G.; Grigorian, H.; Posfay, P. Studying the parameters of the extended σ-ω model for neutron star matter. arXiv 2020, arXiv:astro-ph.HE/2006.03676. [Google Scholar]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Signals in the tidal deformability for phase transitions in compact stars with constraints from GW170817. Phys. Rev. D 2019, 99, 023009. [Google Scholar] [CrossRef]
- Montana, G.; Tolos, L.; Hanauske, M.; Rezzolla, L. Constraining twin stars with GW170817. Phys. Rev. D 2019, 99, 103009. [Google Scholar] [CrossRef]
- Christian, J.E.; Schaffner-Bielich, J. Twin stars and the stiffness of the nuclear equation of state: Ruling out strong phase transitions below 1.7n0 with the new NICER radius measurements. arXiv 2019, arXiv:astro-ph.HE/1912.09809. [Google Scholar]
- Chatziioannou, K.; Han, S. Studying strong phase transitions in neutron stars with gravitational waves. Phys. Rev. D 2020, 101, 044019. [Google Scholar] [CrossRef]
- Miller, M.C.; Chirenti, C.; Lamb, F.K. Constraining the equation of state of high-density cold matter using nuclear and astronomical measurements. Astrophys. J. 2020, 888, 12. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L. A pitfall of piecewise-polytropic equation of state inference. Mon. Not. R. Astron. Soc. 2018, 478, 2177–2192. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- Raaijmakers, G.; Greif, S.K.; Riley, T.E.; Hinderer, T.; Hebeler, K.; Schwenk, A.; Watts, A.; Nissanke, S.; Guillot, S.; Lattimer, J.M.; et al. Constraining the dense matter equation of state with joint analysis of NICER and LIGO/Virgo measurements. Astrophys. J. 2020, 893, L21. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multi-messenger observations and nuclear theory. Nat. Astron. 2019, 3, 1–8. [Google Scholar]
- Lim, Y.; Holt, J.W. Bayesian modeling of the nuclear equation of state for neutron star tidal deformabilities and GW170817. Eur. Phys. J. 2019, A55, 209. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; Murase, K. Mapping neutron star data to the equation of state using the deep neural network. Phys. Rev. D 2020, 101, 054016. [Google Scholar] [CrossRef]
- Tews, I.; Carlson, J.; Gandolfi, S.; Reddy, S. Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys. J. 2018, 860, 149. [Google Scholar] [CrossRef]
- Reed, B.; Horowitz, C. Large Sound Speed in Dense Matter and the Deformability of Neutron Stars. Phys. Rev. C 2020, 101, 045803. [Google Scholar] [CrossRef]
- Zdunik, J.; Haensel, P. Maximum mass of neutron stars and strange neutron-star cores. Astron. Astrophys. 2013, 551, A61. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Quark-Matter Cores in Neutron Stars. Available online: https://www.nature.com/articles/s41567-020-0914-9 (accessed on 7 June 2020).
- Essick, R.; Landry, P.; Holz, D.E. Nonparametric Inference of Neutron Star Composition, Equation of State, and Maximum Mass with GW170817. Phys. Rev. D 2020, 101, 063007. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Model comparison from LIGO?Virgo data on GW170817?s binary components and consequences for the merger remnant. Class. Quantum Gravity 2020, 37, 045006. [Google Scholar] [CrossRef]
- Traversi, S.; Char, P.; Pagliara, G. Bayesian Inference of Dense Matter Equation of State within Relativistic Mean Field Models using Astrophysical Measurements. arXiv 2020, arXiv:astro-ph.HE/2002.08951. [Google Scholar]
- Blaschke, D.; Alvarez-Castillo, D.E.; Benic, S. Mass-radius constraints for compact stars and a critical endpoint. PoS 2013, CPOD2013, 063. [Google Scholar]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics—I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D. Mixed phase effects on high-mass twin stars. Phys. Part. Nucl. 2015, 46, 846–848. [Google Scholar] [CrossRef]
- Bejger, M.; Blaschke, D.; Haensel, P.; Zdunik, J.L.; Fortin, M. Consequences of a strong phase transition in the dense matter equation of state for the rotational evolution of neutron stars. Astron. Astrophys. 2017, 600, A39. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Classifications of Twin Star Solutions for a Constant Speed of Sound Parameterized Equation of State. Eur. Phys. J. 2018, A54, 28. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D.B. High-mass twin stars with a multipolytrope equation of state. Phys. Rev. 2017, C96, 045809. [Google Scholar] [CrossRef]
- Kaltenborn, M.A.R.; Bastian, N.U.F.; Blaschke, D.B. Quark-nuclear hybrid star equation of state with excluded volume effects. Phys. Rev. 2017, D96, 056024. [Google Scholar] [CrossRef]
- Ayriyan, A.; Bastian, N.U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. Robustness of third family solutions for hybrid stars against mixed phase effects. Phys. Rev. C 2018, 97, 045802. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, D97, 084038. [Google Scholar] [CrossRef]
- Alford, M.G.; Sedrakian, A. Compact stars with sequential QCD phase transitions. Phys. Rev. Lett. 2017, 119, 161104. [Google Scholar] [CrossRef] [PubMed]
- Sieniawska, M.; Turczanski, W.; Bejger, M.; Zdunik, J.L. Tidal deformability and other global parameters of compact stars with strong phase transitions. Astron. Astrophys. 2019, 622, A174. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D.B.; Grunfeld, A.G.; Pagura, V.P. Third family of compact stars within a nonlocal chiral quark model equation of state. Phys. Rev. D 2019, 99, 063010. [Google Scholar] [CrossRef]
- Maslov, K.; Yasutake, N.; Ayriyan, A.; Blaschke, D.; Grigorian, H.; Maruyama, T.; Tatsumi, T.; Voskresensky, D.N. Hybrid equation of state with pasta phases and third family of compact stars. Phys. Rev. C 2019, 100, 025802. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars with sequential first-order phase transitions and heavy-baryon envelopes. Phys. Rev. D 2020, 101, 063022. [Google Scholar] [CrossRef]
- Bozzola, G.; Espino, P.L.; Lewin, C.D.; Paschalidis, V. Maximum mass and universal relations of rotating relativistic hybrid hadron-quark stars. Eur. Phys. J. 2019, A55, 149. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez-Castillo, D.E.; Ayriyan, A.; Grigorian, H.; Khosravi Largani, N. Astrophysical aspects of general relativistic mass twin stars. arXiv 2019, arXiv:1906.02522. [Google Scholar]
- Jakobus, P.; Motornenko, A.; Gomes, R.O.; Steinheimer, J.; Stoecker, H. The possibility of twin star solutions in a model based on lattice QCD thermodynamics. arXiv 2020, arXiv:2004.07026. [Google Scholar]
- Glendenning, N.K. First order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 1274–1287. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, A.; Mishustin, I.N.; Greiner, W. Deconfinement Phase Transition in Compact Stars: Maxwell vs. Gibbs Construction of the Mixed Phase. J. Phys. G Nucl. Part. Phys. 2010, 37, 025201. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. Inner edge of neutron star crust with SLY effective nucleon-nucleon interactions. Phys. Lett. B 2000, 485, 107–114. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y. Analytical representations of unified equations of state of neutron-star matter. Astron. Astrophys. 2004, 428, 191–197. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Goriely, S.; Ducoin, C. Inner crust of neutron stars with mass-fitted Skyrme functionals. Phys. Rev. C 2012, 85, 065803. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klahn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Typel, S. Variations on the excluded-volume mechanism. Eur. Phys. J. 2016, A52, 16. [Google Scholar] [CrossRef]
- Blaschke, D.; Grigorian, H.; Röpke, G. Chirally improved quark Pauli blocking in nuclear matter and applications to quark deconfinement in neutron stars. arXiv 2020, arXiv:nucl-th/2005.10218. [Google Scholar]
- Blaschke, D.B.; Gomez Dumm, D.; Grunfeld, A.G.; Klähn, T.; Scoccola, N.N. Hybrid stars within a covariant, nonlocal chiral quark model. Phys. Rev. C 2007, 75, 065804. [Google Scholar] [CrossRef]
- Benic, S.; Horvatic, D.; Klaric, J. Recovering the chiral critical endpoint via delocalization of quark interactions. Phys. Rev. D 2014, 89, 054025. [Google Scholar] [CrossRef]
- Buballa, M. The Problem of matter stability in the Nambu-Jona-Lasinio model. Nucl. Phys. A 1996, 611, 393–408. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Grigorian, H.; Blaschke, D.; Aguilera, D.N. Hybrid stars with color superconductivity within a non local chiral quark model. Phys. Rev. C 2004, 69, 065802. [Google Scholar] [CrossRef]
- Blaschke, D.; Berdermann, J.; Lastowiecki, R. Hybrid neutron stars based on a modified PNJL model. Prog. Theor. Phys. Suppl. 2010, 186, 81–86. [Google Scholar] [CrossRef]
- Ayriyan, A.; Grigorian, H. Model of the Phase Transition Mimicking the Pasta Phase in Cold and Dense Quark-Hadron Matter. EPJ Web Conf. 2018, 173, 03003. [Google Scholar] [CrossRef]
- Abgaryan, V.; Alvarez-Castillo, D.; Ayriyan, A.; Blaschke, D.; Grigorian, H. Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars. Universe 2018, 4, 94. [Google Scholar] [CrossRef]
- Yudin, A.; Razinkova, T.; Nadyozhin, D.; Dolgov, A. Special point on the mass radius diagram of hybrid stars. Astron. Lett. 2014, 40, 201. [Google Scholar] [CrossRef]
- Blaschke, D.; Klähn, T.; Lastowiecki, R.; Sandin, F. How strange are compact star interiors ? J. Phys. G Nucl. Part. Phys. 2010, 37, 094063. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Confronting gravitational-wave observations with modern nuclear physics constraints. Eur. Phys. J. A 2019, A55, 97. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; The NANOGrav Collaboration. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.; Ravenhall, D. The Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- GW190412: Observation of a Binary-Black-Hole Coalescence with Asymmetric Masses. Available online: https://dcc.ligo.org/LIGO-P1800115/public (accessed on 8 June 2020).
- Seidov, Z. The Stability of a Star with a Phase Change in General Relativity Theory. Sov. Astron. 1971, 15, 347. [Google Scholar]
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, D88, 083013. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.W.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969–978. [Google Scholar] [CrossRef]
- Logoteta, D.; Vidana, I.; Bombaci, I. Impact of chiral hyperonic three-body forces on neutron stars. Eur. Phys. J. A 2019, 55, 207. [Google Scholar] [CrossRef]
- Lonardoni, D.; Lovato, A.; Gandolfi, S.; Pederiva, F. Hyperon Puzzle: Hints from Quantum Monte Carlo Calculations. Phys. Rev. Lett. 2015, 114, 092301. [Google Scholar] [CrossRef] [PubMed]
- Shahrbaf, M.; Blaschke, D.; Grunfeld, A.G.; Moshfegh, H.R. First-order phase transition from hypernuclear matter to deconfined quark matter obeying new constraints from compact star observations. Phys. Rev. C 2020, 101, 02580. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Blaschke, D.; Khanmohamadi, S. Mixed phase transition from hypernuclear matter to deconfined quark matter fulfilling mass-radius constraints of neutron stars. arXiv 2020, arXiv:nucl-th/2004.14377. [Google Scholar]
- Bastian, N.U.F.; Blaschke, D.; Fischer, T.; Röpke, G. Towards a Unified Quark-Hadron Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe 2018, 4, 67. [Google Scholar] [CrossRef]
- Marczenko, M.; Blaschke, D.; Redlich, K.; Sasaki, C. Chiral symmetry restoration by parity doubling and the structure of neutron stars. Phys. Rev. D 2018, 98, 103021. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.B. A unified quark-nuclear matter equation of state from the cluster virial expansion within the generalized Beth-Uhlenbeck approach. arXiv 2018, arXiv:nucl-th/1812.11766. [Google Scholar]
- Marczenko, M.; Blaschke, D.; Redlich, K.; Sasaki, C. Towards a unified equation of state for multi-messenger astronomy. arXiv 2020, arXiv:astro-ph.HE/2004.09566. [Google Scholar]
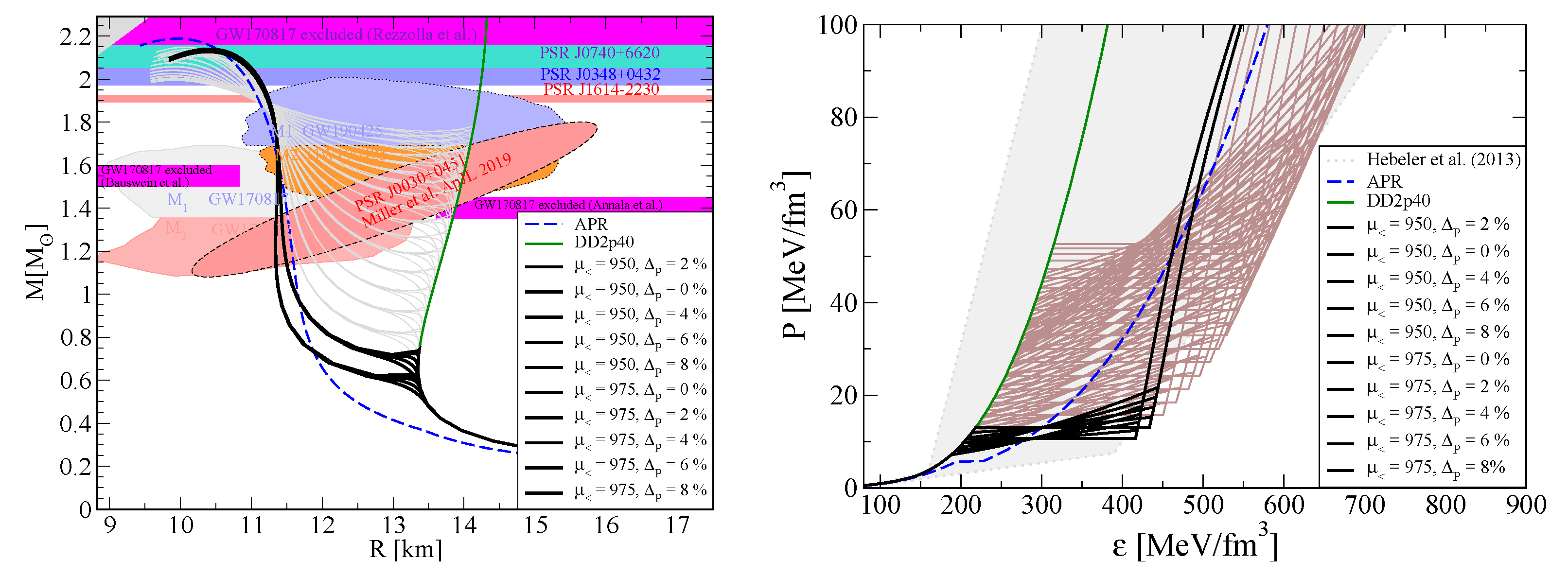
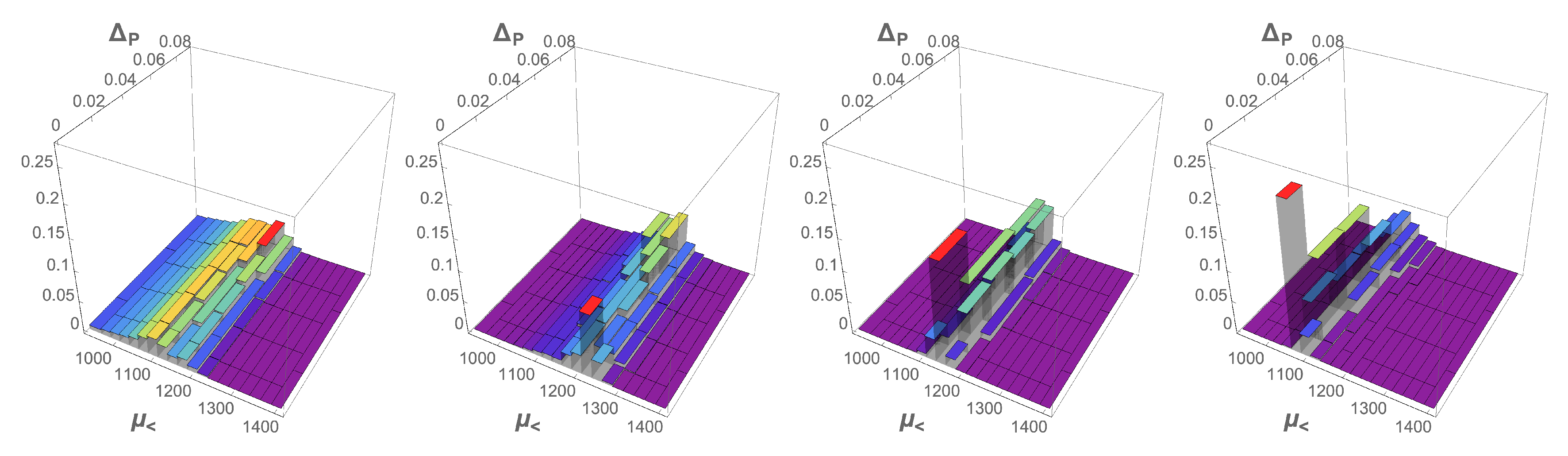
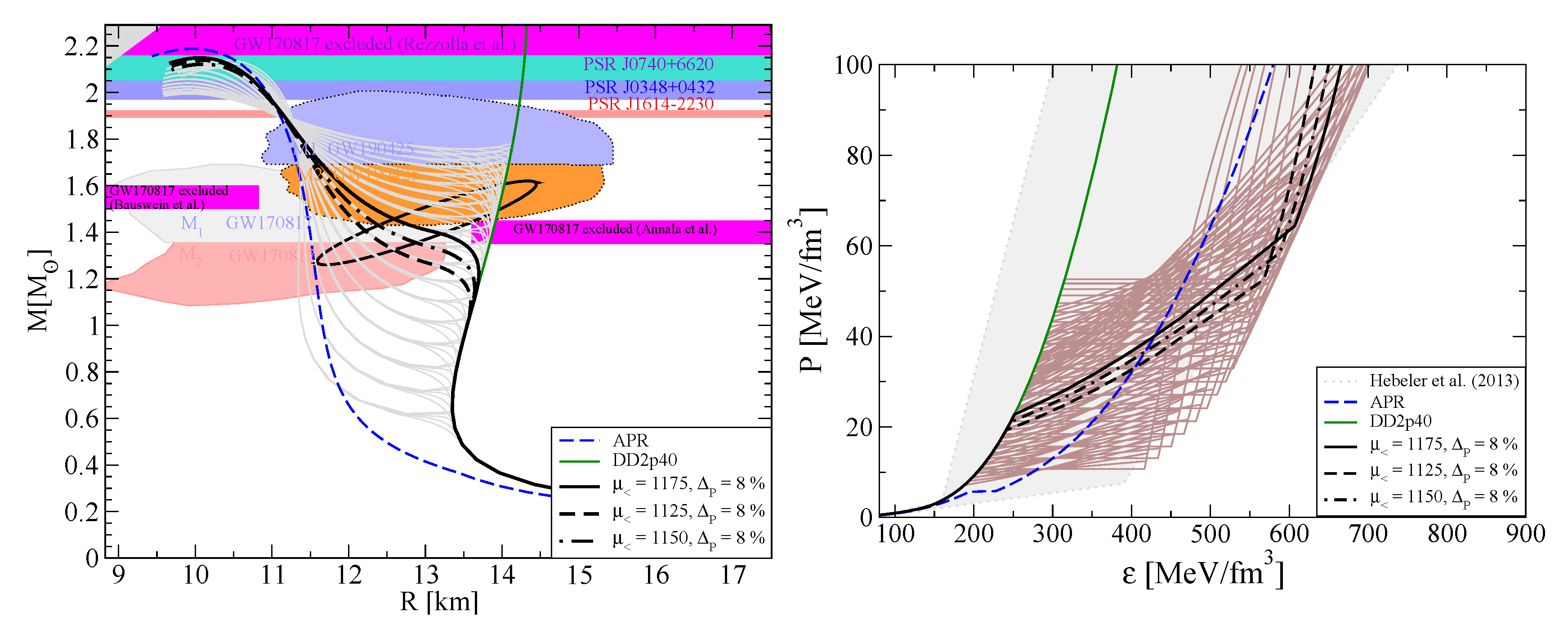
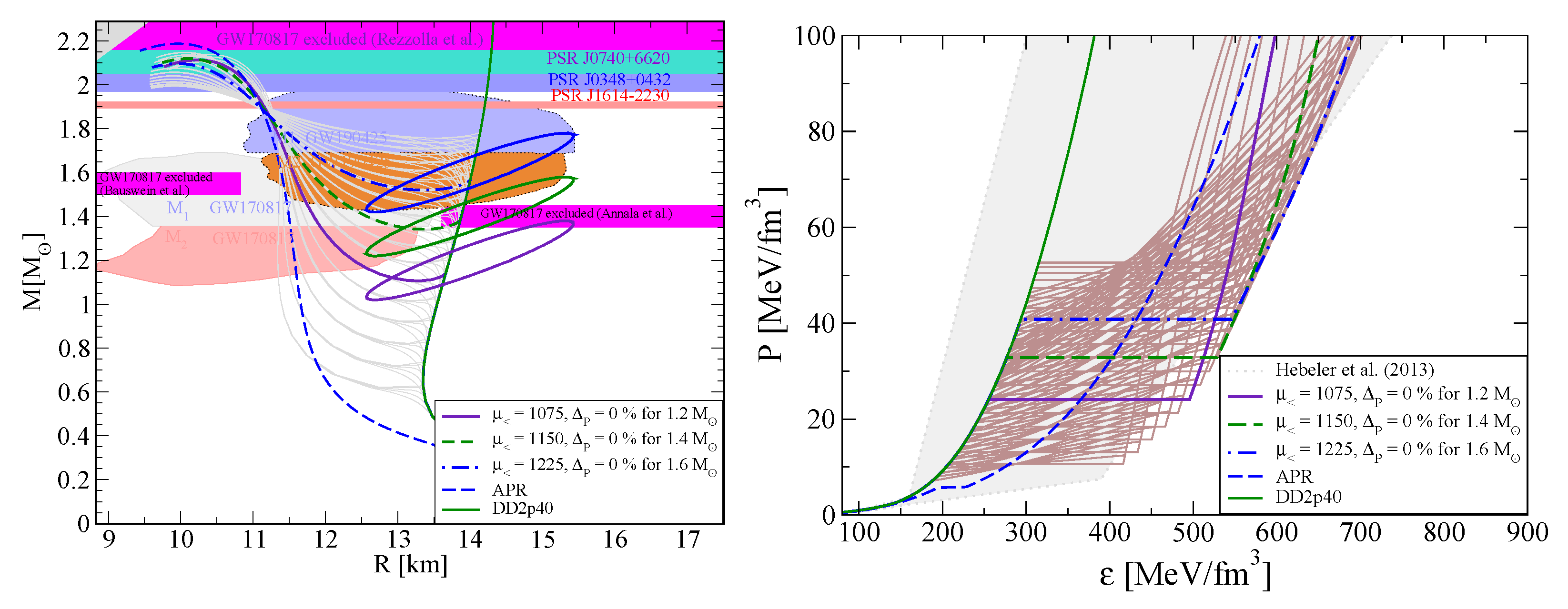
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blaschke, D.; Ayriyan, A.; Alvarez-Castillo, D.E.; Grigorian, H. Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars. Universe 2020, 6, 81. https://doi.org/10.3390/universe6060081
Blaschke D, Ayriyan A, Alvarez-Castillo DE, Grigorian H. Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars. Universe. 2020; 6(6):81. https://doi.org/10.3390/universe6060081
Chicago/Turabian StyleBlaschke, David, Alexander Ayriyan, David Edwin Alvarez-Castillo, and Hovik Grigorian. 2020. "Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars" Universe 6, no. 6: 81. https://doi.org/10.3390/universe6060081
APA StyleBlaschke, D., Ayriyan, A., Alvarez-Castillo, D. E., & Grigorian, H. (2020). Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars. Universe, 6(6), 81. https://doi.org/10.3390/universe6060081