Search for Double Beta Decay of ¹⁰⁶Cd with an Enriched ¹⁰⁶CdWO₄ Crystal Scintillator in Coincidence with CdWO₄ Scintillation Counters

Abstract

Studies on double beta decay processes in ${}^{106}$Cd were performed by using a cadmium tungstate scintillator enriched in ${}^{106}$Cd at 66% (${}^{106}$CdWO${}_4$) with two CdWO${}_4$ scintillation counters (with natural Cd composition). No effect was observed in the data that accumulated over 26,033 h. New improved half-life limits were set on the different channels and modes of the ${}^{106}$Cd double beta decay at level of $lim{T}_{1/2}\sim {10}^{20}-{10}^{22}$ yr. The limit for the two neutrino electron capture with positron emission in ${}^{106}$Cd to the ground state of ${}^{106}$Pd, $T_{1/2}^{2\nu \mathrm{EC}{\beta }^{+}}\ge 2.1\times {10}^{21}$ yr, was set by the analysis of the ${}^{106}$CdWO${}_4$ data in coincidence with the energy release 511 keV in both CdWO${}_4$ counters. The sensitivity approaches the theoretical predictions for the decay half-life that are in the range $T_{1/2}\sim {10}^{21}-{10}^{22}$ yr. The resonant neutrinoless double-electron capture to the 2718 keV excited state of ${}^{106}$Pd is restricted at the level of $T_{1/2}^{0\nu 2\mathrm{K}}\ge 2.9\times {10}^{21}$ yr.

1. Introduction

Observations of the neutrino oscillations suggest that the neutrinos are massive, which calls for an extension of the Standard Model of particles and fields (SM). However, oscillation experiments cannot determine the neutrino mass and the neutrino mass hierarchy. One of the most promising tools for determining the absolute neutrino mass scale and the neutrino mass hierarchy, the nature of the neutrino (Dirac or Majorana particle?), in order to check the lepton number conservation is double beta ($2\beta$) decay of atomic nuclei, a process in which two electrons (or positrons) are simultaneously emitted and nuclear charge changes by two units: (A,Z)→(A,Z$\pm 2$) [1,2,3]. The neutrinoless mode of the decay ($0\nu 2\beta$) violates the lepton number conservation law and it is possible if the neutrinos are Majorana particles (particle is equal to its antiparticle). Being a process beyond the SM, the $0\nu 2\beta$ decay has the potential to test the SM [4,5,6]. Moreover, the Majorana nature of the neutrino might shed light on the Universe baryon asymmetry problem [7,8].

The two-neutrino $2\beta$ decay ($2\nu 2\beta$) is a radioactive process that is allowed in the SM with the longest half-lives ever observed: ${10}^{18}$–${10}^{24}$ yr. The $2\nu 2{\beta }^{-}$ decay mode has been detected in several nuclides [9]. The $0\nu 2\beta$ decay is not observed. The most sensitive $2{\beta }^{-}$-decay experiments quote half-life limits at level of $T_{1/2}>({10}^{24}-{10}^{26}$) yr, which correspond to Majorana neutrino mass limits in the range $⟨m_{\nu }⟩<(0.1-0.7)$ eV. Probing the inverted hierarchy region of the neutrino mass requires improved sensitivities of $2{\beta }^{-}$ experiments at the level of $⟨m_{\nu }⟩\sim (0.02-0.05)$ eV (i.e., half-life sensitivity in the range: $T_{1/2}\sim {10}^{27}-{10}^{28}$ yr).

The sensitivity of the experiments in the search for “double beta plus” processes: double electron capture (2EC), electron capture with positron emission (EC${\beta }^{+}$), and double positron decay ($2{\beta }^{+}$) is substantially lower, while the physical lepton-number violating mechanisms of the neutrinoless 2EC, EC${\beta }^{+}$ and $2{\beta }^{+}$ processes are considered to be essentially the same as for the decay with electrons emission. At the same time, there is a motivation to search for the $0\nu$EC${\beta }^{+}$ and $0\nu 2{\beta }^{+}$ decays owing to the potential to clarify the possible contribution of the right-handed currents to the $0\nu 2{\beta }^{-}$ decay rate [10], and an interesting possibility of a resonant $0\nu$2EC process [11,12,13,14].

As for the allowed two-neutrino mode of the double beta plus decay, there are claims of positive results (indication) for the $2\nu$2EC radioactivity of three nuclides. The $2\nu$2EC decay of ${}^{130}$Ba was claimed in two geochemical experiments where anomaly in the isotopic concentrations of daughter xenon traces in old barite (BaSO${}_4$) minerals was interpreted as the sought effect with the half-life $T_{1/2}=(2.16\pm 0.52)\times {10}^{21}$ yr [15], and with $T_{1/2}=(6.0\pm 1.1)\times {10}^{20}$ yr in [16]. In the analysis [17], the disagreement was explained by a possible cosmogenic contribution with a conclusion that the result of [15] is a more reliable one. An indication on the $2\nu$2EC process in ${}^{78}$Kr with the half-life $T_{1/2}=9.2_{-2.9}^{+5.7}\times {10}^{21}$ yr was obtained with a proportional counter with a volume of 49 lt filled by gas enriched in ${}^{78}$Kr to 99.81% [18]. The value was then updated to $1.9_{-0.8}^{+1.3}\times {10}^{22}$ yr in [19]. Recently, a detection of the $2\nu$2EC of ${}^{124}$Xe with the half-life $(1.8\pm 0.5)\times {10}^{22}$ yr was claimed in [20]. However, the indications of ${}^{130}$Ba 2EC decay should be confirmed in direct counting experiments, while the results for ${}^{78}$Kr and ${}^{124}$Xe need to be confirmed with bigger statistics and very stable experiments. Other allowed $2\nu$ decay channels with decrease of the nuclear charge by two units, $2\nu$EC${\beta }^{+}$ and $2\nu 2{\beta }^{+}$, are not observed yet.

The nuclide ${}^{106}$Cd is one of the most appealing candidates to search for 2EC, EC${\beta }^{+}$, and $2{\beta }^{+}$ decays with a long history of studies (a review of the previous investigations reader can find in Ref. [21]). The interest to ${}^{106}$Cd can be explained by one of the biggest decay energy $Q_{2\beta }=2775.39\left(10\right)$ keV [22], comparatively high isotopic abundance $\delta =1.245\left(22\right)$% [23], and possibility of gas centrifugation for enrichment, existing technologies of cadmium purification, the availability of Cd-containing detectors to realize calorimetric experiments with a high detection efficiency.

Presently, there are three running experiments searching for the double beta decay of ${}^{106}$Cd: COBRA, TGV-2, and the present one.

The COBRA collaboration utilizes CdZnTe semiconductor detectors at the Gran Sasso underground laboratory (Laboratori Nazionali del Gran Sasso, LNGS). The experiment started with one Cd${}_{0.9}$Zn${}_{0.1}$Te detector with mass of ≃3 g, and one CdTe detector (≃6 g) [24]. CdZnTe detectors are used in the current stage of the experiment [25,26]. The measurements resulted in the half-life limits for several channels of ${}^{106}$Cd double beta decay at the level of ∼${10}^{18}$ yr.

The main goal of the TGV-2 experiment, which is located at the Modane underground laboratory, is the search for $2\nu 2$EC decay of ${}^{106}$Cd (a decay channel expected to be the fastest one) with the help of 32 planar HPGe detectors with a total sensitive volume $\approx 400$ cm${}^3$. In the first stage of the experiment, foils of cadmium enriched in ${}^{106}$Cd to (60–75)% were used [27,28,29]; now, 23.2 g of cadmium sample enriched in ${}^{106}$Cd to 99.57% are installed in the set-up [30]. The experiment gives the strongest limit on the $2\nu 2$EC decay: $T_{1/2}>4.7\times {10}^{20}$ yr. For other decay modes and channels, the sensitivity is at level of ${10}^{20}$ yr [31].

A cadmium tungstate crystal scintillator from cadmium enriched in ${}^{106}$Cd to 66% (${}^{106}$CdWO${}_4$) was developed in 2010 [32]. The experiments with that detector are carried out at the LNGS in the DAMA/CRYS, DAMA/R&D set-ups, and in an ultra-low background GeMulti HPGe $\gamma$ spectrometer of the STELLA (SubTErranean Low Level Assay) facility [33] at the LNGS. The first stage of the experiment with the ${}^{106}$CdWO${}_4$ detector gave the half-life limits on $2\beta$ processes in ${}^{106}$Cd at level of ∼${10}^{20}$ yr [21]. In the second stage, the ${}^{106}$CdWO${}_4$ scintillator was installed between four HPGe detectors (with volume $\simeq 225$ cm${}^3$ each) of the GeMulti HPGe $\gamma$ spectrometer to detect $\gamma$ quanta expected in the most of the ${}^{106}$Cd decay channels, including the annihilation $\gamma$’s emitted in decay modes with positron(s) emission (a simplified decay scheme of ${}^{106}$Cd is presented in Figure 1). The experiment improved the ${}^{106}$Cd half-life limits to the level of $T_{1/2}\ge ({10}^{20}-{10}^{21})$ yr [34]. In the third stage, described in the present report, the ${}^{106}$CdWO${}_4$ detector was running in coincidence (anti-coincidence) with two large volume CdWO${}_4$ crystal scintillators in a close geometry in order to increase the detection efficiency to $\gamma$ quanta expected to be emitted from the ${}^{106}$CdWO${}_4$ crystal in the double beta decay processes in ${}^{106}$Cd. Preliminary results of the experiment stage were reported in [35].

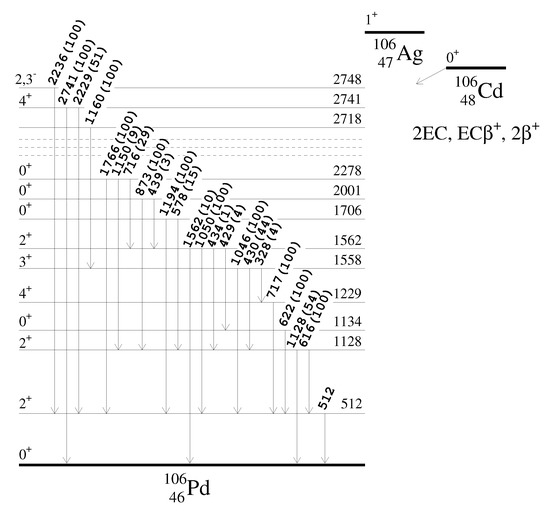
Figure 1. Simplified decay scheme of ${}^{106}$Cd [36] (levels with energies in the energy interval (2283–2714) keV are omitted). The energies of the excited levels are in keV. Relative intensities of $\gamma$ quanta are given in parentheses.

2. The Experiment

The ${}^{106}$CdWO${}_4$ crystal scintillator of roughly cylindrical shape (approximate sizes $\oslash 27$ mm × 50 mm, mass 215.4 g) was viewed by a three inches low radioactive photo-multiplier tube (PMT) Hamamatsu R6233MOD through a lead tungstate (PbWO${}_4$) crystal light-guide ($\oslash 40$ mm × 83 mm). The PbWO${}_4$ crystal has been developed from the highly purified [37] archaeological lead [38]. Two CdWO${}_4$ crystal scintillators $\oslash 70$ mm × 38 mm include a cylindrical cut-out to house the ${}^{106}$CdWO${}_4$ crystal. They were viewed by two three-inch low radioactive PMTs EMI9265B53/FL through light-guides glued in two parts: low radioactive quartz ($\oslash 66$ mm × 100 mm, close to the CdWO${}_4$ scintillators) and optical quality polystyrene ($\oslash 66$ mm × 100 mm). Figure 2 shows a schematic of the set-up. The detector system was surrounded by four high purity copper bricks (referred hereinafter as “internal copper”) and by layers of high purity copper (11 cm, hereinafter referred as “external copper”), low radioactive lead (10 cm), cadmium (2 mm), and polyethylene (10 cm) in order to reduce the external background. The inner volume of the set-up with the detector system was continuously flushed by high-purity nitrogen gas to remove environmental radon. The grade of the high-purity N${}_2$ gas is at least 5.5, for what concerns the presence of other possible gases. However, the possible presence in trace of Radon gas in the Nitrogen atmosphere inside the copper box, housing the detector, has been checked with another set-up, by searching for the double coincidences of the $\gamma$-rays (609 and 1120 keV) from ${}^{214}$Bi Radon daughter. The obtained upper limit on the possible Radon concentration in the high-purity Nitrogen atmosphere has been measured to be: <$5.8\times {10}^{-2}$ Bq/m${}^3$ (90% C.L.) [39]. Figure 3 shows photographs of the detector system.

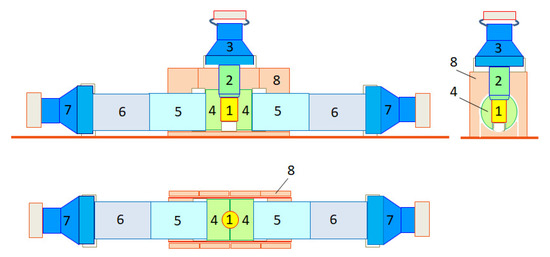
Figure 2. Schematic of the experimental set-up with the ${}^{106}$CdWO${}_4$ scintillation detector. ${}^{106}$CdWO${}_4$ crystal scintillator (1) is viewed through PbWO${}_4$ light-guide (2) by photo-multiplier tube (3). Two CdWO${}_4$ crystal scintillators (4) are viewed through light-guides glued from quartz (5) and polystyrene (6) by photo-multiplier tubes (7). The detector system was surrounded by passive shield made from copper, lead, polyethylene, and cadmium (not shown). Only part of the copper details (8, “internal copper”), used to reduce the direct hits of the detectors by $\gamma$ quanta from the PMTs, are shown.

Figure 3. Left photograph: the ${}^{106}$CdWO${}_4$ crystal scintillator (1), Teflon support of the ${}^{106}$CdWO${}_4$ crystal (2), CdWO${}_4$ crystal scintillators (3), quartz light-guide (4), “internal copper” brick (5). Right photograph: the detector system installed in the passive shield: PMT of the ${}^{106}$CdWO${}_4$ detector (1), light-guides of the CdWO${}_4$ counters wrapped by reflecting foil (2), PMT of the CdWO${}_4$ counters (3), “internal copper” bricks (4), “external copper” bricks (5), lead bricks (6), and polyethylene shield (7). The copper, lead and polyethylene shields are not completed.

An event-by-event data acquisition system that is based on a 100 MS/s 14 bit transient digitizer (DT5724 by CAEN) recorded the amplitude, the arrival time, and the pulse shape of each event. To reduce the data volume due to presence in the ${}^{106}$CdWO${}_4$ crystal of ${}^{113}$Cd and ${}^{113m}$Cd $\beta$ active nuclides [21,32], the energy threshold for the set-up was set at level of ≈510 keV for the anti-coincidence mode, while the energy threshold of the ${}^{106}$CdWO${}_4$ detector in the coincidence with the CdWO${}_4$ counters was ≈200 keV. The energy thresholds of the CdWO${}_4$ counters were ≈70 keV. The energy scale and energy resolution of the detectors were measured with ${}^{22}$Na, ${}^{60}$Co, ${}^{133}$Ba, ${}^{137}$Cs, and ${}^{228}$Th $\gamma$ sources at the beginning, in the middle and end of the experiment.

The energy resolution of the ${}^{106}$CdWO${}_4$ detector for the total exposure can be described by the function $\mathrm{FWHM}=6.85\times \sqrt{E_{\gamma }}$, where FWHM (full width at half maximum) and $E_{\gamma }$ are given in keV. The poor energy resolution of the enriched detector (despite excellent optical properties of the material [32]) is caused by the elongated shape of the enriched scintillator that results in a rather low and non-uniform light collection, and by the using of not perfectly transparent PbWO${}_4$ crystal light-guide. The performance of the CdWO${}_4$ counters is substantially better. The energy spectra that were accumulated by one of the counters with ${}^{22}$Na, ${}^{60}$Co and ${}^{228}$Th $\gamma$ sources are presented in Figure 4. The energy resolution of the counters was estimated by using the results of the three energy calibration campaigns as $\mathrm{FWHM}=a\times \sqrt{E_{\gamma }}$ with the coefficient a equal to 2.97 and 3.13 for the two detectors. The resolution formulas also take into account energy scale shifts during the data taking over the experiment.

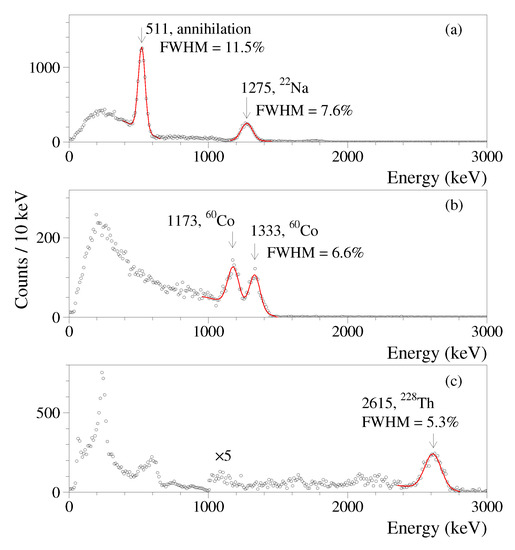
Figure 4. Energy spectra of ${}^{22}$Na (a), ${}^{60}$Co (b) and ${}^{228}$Th (c) $\gamma$ quanta measured by one of the CdWO${}_4$ detectors. Fits of intensive $\gamma$ peaks by Gaussian functions are shown by solid lines. Energies of $\gamma$ quanta are in keV.

The energy spectra of ${}^{22}$Na source were simulated by the EGSnrc code [40]. The data measured with ${}^{22}$Na source without coincidence selection and in coincidence with energy 511 keV in at least one of the CdWO${}_4$ counters is compared with the simulated distribution in Figure 5. The experimental data are in reasonable agreement with the results of simulations.

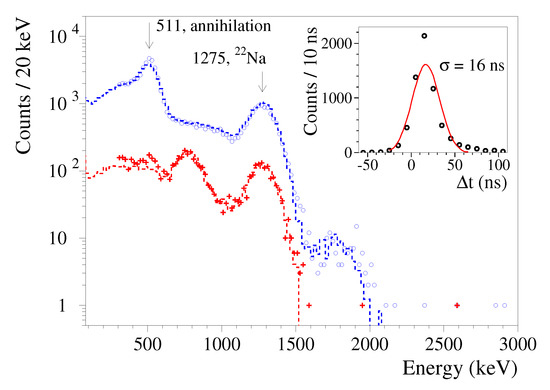
Figure 5. Energy spectra of ${}^{22}$Na $\gamma$ quanta measured by the ${}^{106}$CdWO${}_4$ detector: with no coincidence cuts (blue circles) and in coincidence with energy 511 keV in at least one of the CdWO${}_4$ counters (red crosses). The data simulated by using the EGSnrc Monte Carlo code are drawn by dashed lines. (Inset) Distribution of the ${}^{106}$CdWO${}_4$ detector pulses start positions relative to the CdWO${}_4$ signals with the energy 511 keV.

The inset of Figure 5 shows a distribution of the ${}^{106}$CdWO${}_4$ detector pulses start positions relative to the CdWO${}_4$ signals with energy 511 keV. The time resolution of the detector system is rather high (the standard deviation of the distribution is 16 ns) due to the fast rise time of the CdWO${}_4$ scintillation pulses.

3. Results and Discussion

3.1. Backgrounds Reduction and Model of the Backgrounds

The difference in CdWO${}_4$ scintillation pulse shape for $\beta$ particles ($\gamma$ quanta) and $\alpha$ particles can be used in order to suppress the background caused by $\alpha$ radioactive contamination of the detector due to the residual contamination in ${}^{232}$Th and ${}^{238}$U with their daughters. The mean time method was applied to the data in order to discriminate signals of different origin by pulse shape. For each signal $f\left(t\right)$, the numerical characteristic of its shape (mean time, $\zeta$) was defined using the following equation:

$$\zeta =\sum f\left(t_k\right)·t_k/\sum f\left(t_k\right),$$

(1)

where the sum is over the time channels k, starting from the origin of signal up to 35 $\mathsf{\mu }$s; $f\left(t_k\right)$ is the digitized amplitude (at the time $t_k$) of a given signal. The energy dependence of the parameter $\zeta$ and its standard deviation (the distributions of $\zeta$ for $\beta$ particles ($\gamma$ quanta) and $\alpha$ particles are well described by a Gaussian function) was determined by using the data of the calibration measurements with ${}^{228}$Th gamma source. The obtained parameters were then used to discriminate $\beta$ ($\gamma$) events from $\alpha$ events in the data of the low-background experiment. We refer the reader to our previous works [21,34], where the pulse-shape discrimination (PSD) method was described in detail.

By using the PSD, the $\alpha$ events were statistically separated from $\gamma \left(\beta \right)$ events. In addition the method discarded from the data events of the ${}^{212}$Bi – ${}^{212}$Po sub-chain from the ${}^{232}$Th family (due to the short decay time of ${}^{212}$Po $\approx 0.3$ $\mathsf{\mu }$s these decays are treated by the data acquisition system as a single event), PMT noise, pile-ups of signals in the ${}^{106}$CdWO${}_4$ detector, ${}^{106}$CdWO${}_4$ plus PbWO${}_4$ events, etc. Figure 6 shows the results of the PSD method application to the background data gathered for 26,033 h in the low-background set-up. The mean time method reduced the background mainly in the energy region (800–1300) keV (by a factor ∼1.6), where $\alpha$ events of the ${}^{232}$Th and ${}^{238}$U with their daughters are expected.

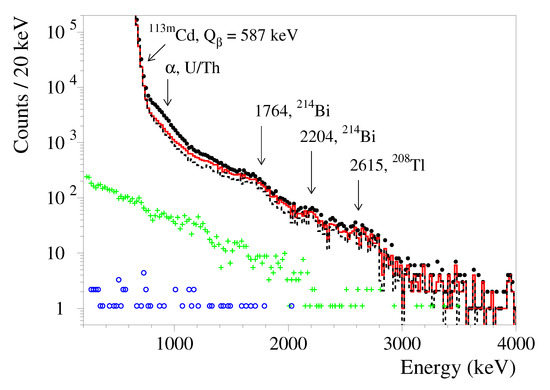
Figure 6. Energy spectra measured by the ${}^{106}$CdWO${}_4$ detector for 26,033 h in the low-background set-up without selection cuts (black dots), after selection of $\gamma$ and $\beta$ events by PSD using the mean time method (solid red line), the $\gamma$ and $\beta$ events in anti-coincidence with the CdWO${}_4$ counters (dashed black line), the $\gamma$ and $\beta$ events in coincidence with event(s) in at least one of the CdWO${}_4$ counters with the energy $E=511\pm 2\sigma$ keV (green crosses), the $\gamma$, and $\beta$ events in coincidence with events in both the CdWO${}_4$ counters with the energy $E=511\pm 2\sigma$ keV (blue circles).

Further reduction of the background counting rate (by a factor ∼1.3 in the energy interval (1000–3000) keV) was achieved by exploiting the anti-coincidence with the CdWO${}_4$ counters. The background was significantly suppressed by the selection of events in the ${}^{106}$CdWO${}_4$ detector in coincidence with the event(s) in at least one of the CdWO${}_4$ counters with the energy release $E=511\pm 2\sigma$ keV (by a factor ∼17 in the same energy interval; here, $\sigma$ is the energy resolution of the CdWO${}_4$ counters for 511 keV $\gamma$ quanta), and by selection of events in coincidence with the events in both the CdWO${}_4$ counters with the energy $E=511\pm 2\sigma$ keV (by a further factor ∼42). Figure 6 presents the stages of the background spectra reduction.

The counting rate of the ${}^{106}$CdWO${}_4$ detector below the energy of ∼0.8 MeV is mainly caused by the $\beta$ decay of ${}^{113}$Cd with the energy $Q_{\beta }=323.83\left(27\right)$ keV [22] and of ${}^{113m}$Cd ($Q_{\beta }=587.37\left(27\right)$ keV [22,41]). A background model to describe the experimental data after the ${}^{113m}$Cd $\beta$ spectrum was constructed from distributions of “internal” (radioactive contamination of the ${}^{106}$CdWO${}_4$ crystal) and “external” (radioactive contamination of the set-up details) sources. The equilibrium of the ${}^{238}$U and ${}^{232}$Th chains in all the materials is assumed to be broken1. The sub-chains ${}^{228}$Ra${\to }^{228}$Th, ${}^{228}$Th${\to }^{208}$Pb (the ${}^{232}$Th family) and ${}^{238}$U${\to }^{234}$U, ${}^{226}$Ra${\to }^{210}$Pb, ${}^{210}$Pb${\to }^{206}$Pb (${}^{238}$U) were assumed to be in secular equilibrium.

The following “internal” sources were simulated in the ${}^{106}$CdWO${}_4$ crystal scintillator:

• ${}^{40}$K, ${}^{228}$Ra${\to }^{228}$Th, ${}^{228}$Th${\to }^{208}$Pb, ${}^{226}$Ra${\to }^{210}$Pb, and ${}^{210}$Pb${\to }^{206}$Pb with activities estimated in the earlier stages of the experiment [45,46];
• distribution of $\alpha$ particles of ${}^{232}$Th and ${}^{238}$U with their daughters not discarded by the pulse-shape analysis; and,
• two-neutrino double beta decay of ${}^{116}$Cd with the half-life $T_{1/2}=2.63\times {10}^{19}$ yr [47].

The following “external” sources were simulated in the materials of the set-up:

• ${}^{40}$K, ${}^{228}$Ra${\to }^{228}$Th, ${}^{228}$Th${\to }^{208}$Pb, ${}^{226}$Ra${\to }^{210}$Pb in the internal and external copper details, the quartz light guides, the PbWO${}_4$ crystal light-guide, the PMTs;
• ${}^{210}$Pb${\to }^{206}$Pb in the PbWO${}_4$ crystal light-guide;
• ${}^{228}$Th${\to }^{208}$Pb and ${}^{226}$Ra${\to }^{210}$Pb in the CdWO${}_4$ crystal scintillators; and,
• ${}^{56}$Co and ${}^{60}$Co in the internal copper bricks.

The background components were simulated using the EGSnrc package with initial kinematics given by the DECAY0 event generator [48]. The distribution of residual $\alpha$ particles of ${}^{232}$Th and ${}^{238}$U with their daughters was constructed from the experimental data using the pulse-shape analysis.

The simulated models were used to fit the energy spectra of $\gamma$ and $\beta$ events in anti-coincidence with the CdWO${}_4$ counters and in coincidence with event(s) in at least one of the CdWO${}_4$ counters with the energy release $E=511\pm 2\sigma$ keV. The data were fitted in the energy intervals (940–4000) keV (anti-coincidence data) and (240–3940) keV (coincidence with 511 keV). The fit quality is reasonable (${\chi }^2=457$ for 235 degrees of freedom). Figure 7 shows the results of the fit and the main components of the background.

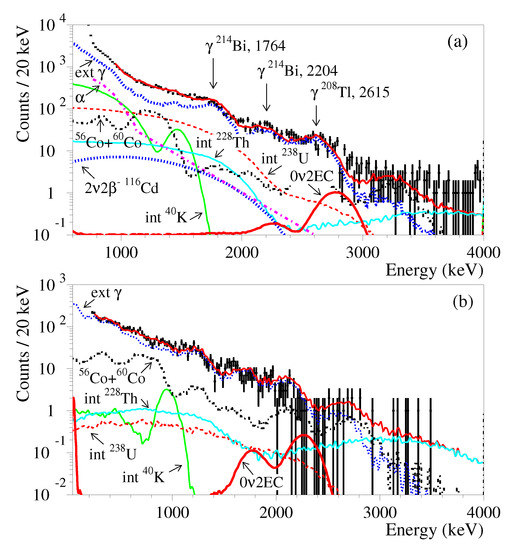
Figure 7. Energy spectra of the $\gamma$ and $\beta$ events accumulated for 26,033 h by the ${}^{106}$CdWO${}_4$ scintillation detector in anti-coincidence with the CdWO${}_4$ counters (a) and in coincidence with the 511 keV annihilation $\gamma$ quanta in at least one of the CdWO${}_4$ counters (b) (points) together with the background model (red line). The main components of the background are shown: the distributions of internal contaminations (“int ${}^{40}$K”, “int ${}^{232}$Th”, and “int ${}^{238}$U”) and external $\gamma$ quanta (“ext $\gamma$”), residual $\alpha$ particles in the ${}^{106}$CdWO${}_4$ crystal ($\alpha$), cosmogenic ${}^{56}$Co and ${}^{60}$Co in the copper shield details, and the $2\nu 2\beta$ decay of ${}^{116}$Cd. The excluded distributions of the $0\nu 2$EC decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd with the half-life $T_{1/2}=6.8\times {10}^{20}$ yr are shown by red solid line.

The fit allowed to estimate limits on radioactive contamination of the materials of the low-background set-up. Table 1 presents the data.

Table 1. Radioactive contamination (mBq/kg) of the materials of the low-background set-up estimated by using the fit of the energy spectra that are presented in Figure 7. Upper limits are given at 68% C.L.

Material	${}^{40}$K	${}^{56}$Co	${}^{60}$Co	${}^{88}$Y	${}^{210}$Pb	${}^{226}$Ra	${}^{228}$Ac	${}^{228}$Th
PbWO${}_4$ crystal	≤0.09	–	–	–	≤$12\times {10}^3$	≤ 0.07	≤0.28	≤0.23
CdWO${}_4$ crystals	–	–	–	–	–	≤0.27	–	≤0.014
Quartz light-guides	≤18	–	–	–	–	≤3.3	≤0.6	≤0.6
Copper internal	≤0.8	≤0.26	≤0.5	≤0.005	–	≤3.0	≤1.3	≤0.019
Copper external	≤1.4	–	–	–	–	≤1.5	≤3.2	≤0.026
PMTs	≤1060	–	–	–	–	≤140	≤1030	≤250

3.2. Limits on 2EC, EC${\beta }^{+}$ and $2{\beta }^{+}$ Processes in ${}^{106}$Cd

There are no peculiarities in the experimental data that could be ascribed to $2\beta$ processes in ${}^{106}$Cd. Lower limits on the half-life of ${}^{106}$Cd relatively to different $2\beta$ decay channels and modes can be estimated using the following formula:

$$lim{T}_{1/2}=N·ln2·{\eta }_{\det }·{\eta }_{\mathrm{sel}}·t/limS,$$

(2)

where N is the number of ${}^{106}$Cd nuclei in the ${}^{106}$CdWO${}_4$ crystal ($2.42\times {10}^{23}$), ${\eta }_{\det }$ is the detection efficiency for the process of decay (calculated as a ratio of the events number in a simulated distribution to the number of generated events), ${\eta }_{\mathrm{sel}}$ is the selection cuts efficiency (selection by PSD, time coincidence, energy interval), t is the time of measurements, and $limS$ is the number of events of the effect searched for, which can be excluded at a given confidence level (C.L.). The responses of the detector system to different modes and channels of ${}^{106}$Cd double beta decay were simulated while using the EGSnrc package with initial kinematics that were given by the DECAY0 event generator. Approximately $5\times {10}^6$ events were generated for each decay channel.

Different data were analyzed in order to estimate limits on the $2\beta$ processes in ${}^{106}$Cd. Fit of the anti-coincidence spectrum by the above described model plus a simulated distribution of the $0\nu 2$EC decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd returns the area of the distribution $(205\pm 99)$ counts that is no evidence for the effect searched for. According to [49], we took 367 events as $limS$ at 90% C.L.2 The detection efficiency for the decay was simulated as ${\eta }_{\det }=0.522$. Taking into account the selection cut efficiency due to application of the PSD to select $\gamma$ and $\beta$ events ${\eta }_{\mathrm{sel}}=0.955$, we got a lower limit on the half-life of ${}^{106}$Cd relative to the $0\nu 2$EC decay to the ground state of ${}^{106}$Pd $T_{1/2}\ge 6.8\times {10}^{20}$ yr (the excluded distribution of the $0\nu$2EC decay is shown in Figure 7). The limit is slightly worse than the one that was obtained in the previous stage of the experiment ($T_{1/2}\ge 1.0\times {10}^{21}$ yr [21], also see Table 2).

Table 2. Half-life limits on $2\beta$ processes in ${}^{106}$Cd. The experimental selection is also reported (AC, anti-coincidence; CC, in coincidence, at the given energy (energies) with CdWO${}_4$; CC 511&511, in coincidence with energies 511 keV in both of the CdWO${}_4$ counters). ${\eta }_{\det }$ denotes the detection efficiency, ${\eta }_{\mathrm{sel}}$ is the selection cuts efficiency. The results of the most sensitive previous experiments are given for comparison.

Decay,	Exp.	${\mathit{\eta }}_{\mathbf{det}}$	${\mathit{\eta }}_{\mathbf{sel}}$	$lim\mathit{S}$	$lim{\mathit{T}}_{1/2}$ (yr) at 90% C.L.
Level of ${}^{106}$Pd	Selection				Present Work	Best Previous
$2\nu 2$EC 2${}^{+}$ 1128	CC 616	0.135	0.909	92	≥$6.6\times {10}^{20}$	≥$5.5\times {10}^{20}$ [34]
$2\nu 2$EC 0${}^{+}$ 1134	CC 622	0.188	0.909	86	≥$9.9\times {10}^{20}$	≥$1.0\times {10}^{21}$ [34]
$2\nu 2$EC 2${}^{+}$ 1562	CC 1050	0.138	0.909	80	≥$7.8\times {10}^{20}$	≥$7.4\times {10}^{20}$ [34]
$2\nu 2$EC 0${}^{+}$ 1706	CC 1194	0.134	0.909	90	≥$6.7\times {10}^{20}$	≥$7.1\times {10}^{20}$ [34]
$2\nu 2$EC 0${}^{+}$ 2001	CC 873	0.153	0.909	46	≥$1.5\times {10}^{21}$	≥$9.7\times {10}^{20}$ [34]
$2\nu 2$EC 0${}^{+}$ 2278	CC 1766	0.091	0.909	131	≥$3.1\times {10}^{20}$	≥$1.0\times {10}^{21}$ [34]
$0\nu 2$EC g.s.	AC	0.522	0.955	367	≥$6.8\times {10}^{20}$	≥$1.0\times {10}^{21}$ [21]
$0\nu 2$EC 2${}^{+}$ 512	AC	0.319	0.955	443	≥$3.4\times {10}^{20}$	≥$5.1\times {10}^{20}$ [21]
$0\nu 2$EC 2${}^{+}$ 1128	CC 616	0.118	0.909	110	≥$4.9\times {10}^{20}$	$\ge 5.1$$\times {10}^{20}$ [34]
$0\nu 2$EC 0${}^{+}$ 1134	CC 622	0.155	0.909	109	≥$6.4\times {10}^{20}$	≥$1.1\times {10}^{21}$ [34]
$0\nu 2$EC 2${}^{+}$ 1562	CC 1050	0.136	0.909	45	≥$1.4\times {10}^{21}$	≥$7.3\times {10}^{20}$ [34]
$0\nu 2$EC 0${}^{+}$ 1706	CC 1194	0.120	0.909	27	≥$2.0\times {10}^{21}$	≥$1.0\times {10}^{21}$ [34]
$0\nu 2$EC 0${}^{+}$ 2001	CC 873	0.135	0.909	177	≥$3.5\times {10}^{20}$	≥$1.2\times {10}^{21}$ [34]
$0\nu 2$EC 0${}^{+}$ 2278	CC 1766	0.079	0.909	29	≥$1.2\times {10}^{21}$	≥$8.6\times {10}^{20}$ [34]
Res. $0\nu 2$K 2718	CC 1046 + 1160	0.215	0.909	33	≥$2.9\times {10}^{21}$	≥$1.1\times {10}^{21}$ [34]
Res. $0\nu K{L}_1$ 4${}^{+}$ 2741	AC	0.454	0.952	663	≥$3.2\times {10}^{20}$	≥$9.5\times {10}^{20}$ [21]
Res. $0\nu K{L}_3$ 2,3${}^{-}$ 2748	AC	0.318	0.955	432	≥$3.5\times {10}^{20}$	≥$1.4\times {10}^{21}$ [34]
$2\nu$EC${\beta }^{+}$ g.s.	CC 511&511	0.040	0.703	6.7	≥$2.1\times {10}^{21}$	≥$1.1\times {10}^{21}$ [34]
$2\nu$EC${\beta }^{+}$ 2${}^{+}$ 512	CC 511&511	0.047	0.459	4.0	≥$2.7\times {10}^{21}$	≥$1.3\times {10}^{21}$ [34]
$2\nu$EC${\beta }^{+}$ 2${}^{+}$ 1128	CC 511&511	0.029	0.509	5.6	≥$1.3\times {10}^{21}$	≥$1.0\times {10}^{21}$ [34]
$2\nu$EC${\beta }^{+}$ 0${}^{+}$ 1134	CC 511&511	0.031	0.603	11	≥$8.5\times {10}^{20}$	≥$1.1\times {10}^{21}$ [34]
$0\nu$EC${\beta }^{+}$ g.s.	CC 511	0.376	0.909	12	$\ge 1.4$$\times {10}^{22}$	≥$2.2\times {10}^{21}$ [21]
$0\nu$EC${\beta }^{+}$ 2${}^{+}$ 512	CC 511	0.384	0.909	18	$\ge 9.7$$\times {10}^{21}$	≥$1.9\times {10}^{21}$ [34]
$0\nu$EC${\beta }^{+}$ 2${}^{+}$ 1128	CC 511	0.314	0.909	14	≥$1.0\times {10}^{22}$	≥$1.3\times {10}^{21}$ [34]
$0\nu$EC${\beta }^{+}$ 0${}^{+}$ 1134	CC 511&511	0.030	0.385	5.0	≥$1.2\times {10}^{21}$	≥$1.9\times {10}^{21}$ [34]
$2\nu 2{\beta }^{+}$ g.s.	CC 511&511	0.052	0.385	5.8	≥$1.7\times {10}^{21}$	≥$2.3\times {10}^{21}$ [34]
$2\nu 2{\beta }^{+}$ 2${}^{+}$ 512	CC 511&511	0.048	0.323	3.4	≥$2.3\times {10}^{21}$	≥$2.5\times {10}^{21}$ [34]
$0\nu 2{\beta }^{+}$ g.s.	CC 511	0.391	0.909	30	≥$5.9\times {10}^{21}$	≥$3.0\times {10}^{21}$ [34]
$0\nu 2{\beta }^{+}$ 2${}^{+}$ 512	CC 511	0.370	0.909	39	≥$4.0\times {10}^{21}$	≥$2.5\times {10}^{21}$ [34]

Fit of the ${}^{106}$CdWO${}_4$ detector data in coincidence with signal(s) in the CdWO${}_4$ counters by the above described background model was more sensitive to the most of the modes and channels of the decay searched for. An example of such an analysis for the $0\nu$EC${\beta }^{+}$ and $0\nu 2{\beta }^{+}$ decays of ${}^{106}$Cd to the ground state of ${}^{106}$Pd using the data that were measured with the ${}^{106}$CdWO${}_4$ detector in coincidence with 511 keV events in at least one of the CdWO${}_4$ counters is shown in Figure 8. The selection cuts efficiency, e.g., for the $0\nu$EC${\beta }^{+}$ process was calculated to be ${\eta }_{\mathrm{sel}}=0.909$ as a product of the PSD to select $\gamma$ and $\beta$ events in the interval $\pm 2\sigma$ of the mean time values (0.9546), the time coincidence efficiency in the interval $\pm 3\sigma$ (0.9973), and the energy interval $\pm 2\sigma$ to select 511 keV events in the CdWO${}_4$ counters (0.9545). Table 2 provides the data on the efficiencies, values of $limS$, and the obtained half-life limits.

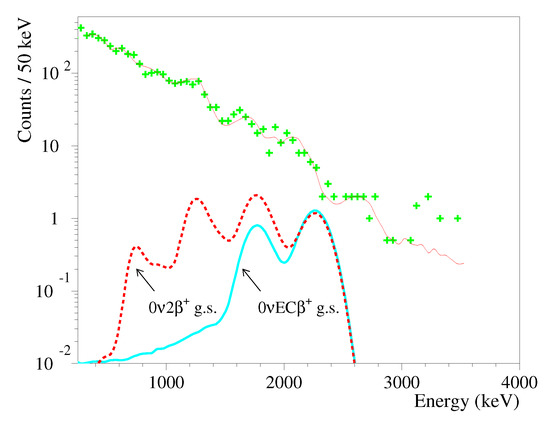
Figure 8. Energy spectrum of the $\gamma$ and $\beta$ events measured for 26,033 h by the ${}^{106}$CdWO${}_4$ detector in coincidence with events in at least one of the CdWO${}_4$ counters with energy $E=511\pm 2\sigma$ keV (crosses). The solid red line shows the fit of the data by the background model (see Section 3.1). Excluded distributions of $0\nu$EC${\beta }^{+}$ and $0\nu 2{\beta }^{+}$ decays of ${}^{106}$Cd to the ground state of ${}^{106}$Pd with the half-lives $T_{1/2}=1.4\times {10}^{22}$ yr and $T_{1/2}=5.9\times {10}^{21}$ yr, respectively, are shown.

Another example is the search for $0\nu 2$EC transition of ${}^{106}$Cd to the 2718 keV excited level of ${}^{106}$Pd (considered as one of the most promising decay channels from the point of view of a possible resonant process [14]). The search was realized by analysis of the ${}^{106}$CdWO${}_4$ detector data in coincidence with event(s) in at least one of the CdWO${}_4$ counters in the energy interval $(1046-1.5\sigma$) − ($1160+1.7\sigma$) keV. The interval should contain two intensive $\gamma$ quanta with energies 1046 keV and 1160 keV being expected in the decay searched for (see the decay scheme in Figure 1). Figure 9 presents the spectrum and its fit, consisting of the background model and excluded distribution of the resonant process searched for.

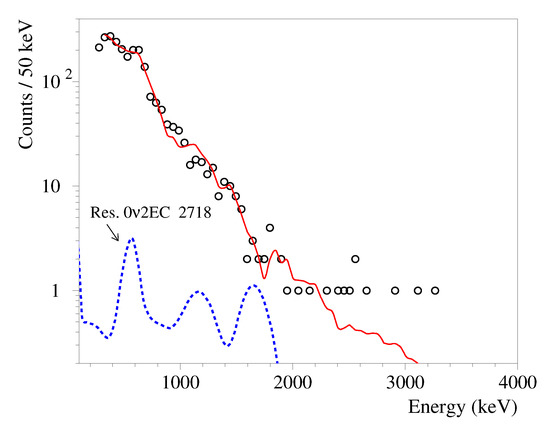
Figure 9. Energy spectrum of $\gamma$ and $\beta$ events measured by the ${}^{106}$CdWO${}_4$ detector for 26,033 h in coincidence with event(s) in at least one of the CdWO${}_4$ counters in the energy interval $(1046-1.5\sigma$) − ($1160+1.7\sigma$) keV (circles) and its fit by the model of background (red line). The excluded distribution of a possible resonant $0\nu 2$EC decay of ${}^{106}$Cd to the 2718 keV excited level of ${}^{106}$Pd with the half-life $T_{1/2}=2.9\times {10}^{21}$ yr is shown.

The highest sensitivity to several decay channels with positron(s) emission was achieved using the data that were gathered by the ${}^{106}$CdWO${}_4$ detector in coincidence with 511 keV annihilation $\gamma$ quanta in both of the CdWO${}_4$ counters thanks to a rather high detection efficiency of the CdWO${}_4$ counters and a very low background counting rate (see Figure 10). However, the fit of the spectrum by the background components is not reliable enough, due to the very low statistics of the data. Thus, the method of comparison of the measured background with the expected one was applied for the analysis. The expected background was estimated from the results of the fit that is shown in Figure 7. There are 54 counts in the whole spectrum, while the estimated background is 55.3 counts, confirming a correct background modelling. In the energy interval (250–1000) keV, the measured background is 33 counts, while the estimated one is 37.4 counts that leads to $limS=6.7$ counts in accordance with the recommendations [49]. Taking into account the detection and the selections efficiencies for the $2\nu$EC${\beta }^{+}$ decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd (0.040 and 0.703, respectively), one can obtain a half-life limit $T_{1/2}=2.1\times {10}^{21}$ yr that is about two times higher than the limit ($T_{1/2}=1.1\times {10}^{21}$ yr) that was obtained in the previous stage of the experiment [34].

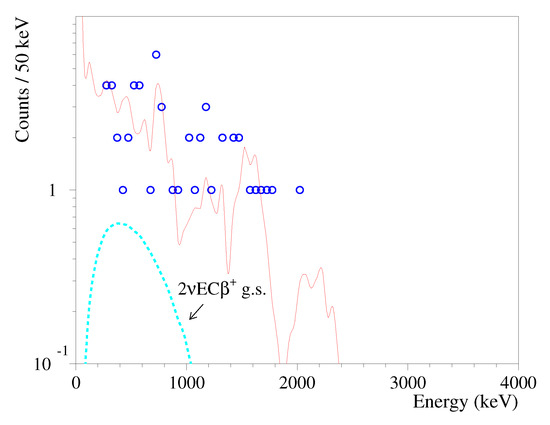
Figure 10. Energy spectrum of $\gamma$ and $\beta$ events measured by the ${}^{106}$CdWO${}_4$ detector for 26,033 h in coincidence with 511 keV annihilation $\gamma$ quanta in both of the CdWO${}_4$ counters (circles). The expected background, which was built on the basis of the fit presented in Figure 7, is shown by a red solid line. The excluded distribution of the $2\nu$EC${\beta }^{+}$ decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd with the half-life $T_{1/2}=2.1\times {10}^{21}$ yr is shown.

Limits on other $2\beta$ decay processes in ${}^{106}$Cd were obtained in a similar way. They are presented in Table 2, where the results of the most sensitive previous experiments are given for comparison.

A limit on effective nuclear matrix elements for the $2\nu$EC${\beta }^{+}$ decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd could be estimated using the calculations of the phase-space factors for the decay [50,51] with the formula $1/T_{1/2}=G^{2\nu \mathrm{EC}{\beta }^{+}}\times {\left|M^{eff}\right|}^2$. The effective matrix nuclear element $M^{eff}$ is expressed by $M^{eff}=g_A^2\times M^{2\nu \mathrm{EC}{\beta }^{+}}$, where $g_A$ is the axial-vector coupling constant, $M^{2\nu \mathrm{EC}{\beta }^{+}}$ is nuclear matrix element. An upper limit on the value of the effective matrix nuclear element for the process can be estimated as $M^{eff}\le$ (0.80–0.82).

The half-life limit on the $2\nu$EC${\beta }^{+}$ decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd, $T_{1/2}\ge 2.1\times {10}^{21}$ yr, approaches the region of the theoretical predictions that are in the range ${10}^{21}$–${10}^{22}$ yr [10,52,53,54,55]. The sensitivity to the double beta decay processes presented in ${}^{106}$Cd is expected to be improved in the currently running experiment with reduced background thanks to the utilization of ultra-radiopure PMTs, longer quartz light-guides for the CdWO${}_4$ counters, a more powerful passive shield of the detector system. Additionally, the energy resolution of the ${}^{106}$CdWO${}_4$ detector was improved, roughly by a factor ∼1.8, thanks to the replacement of the PbWO${}_4$ light-guide by a plastic scintillator light-guide with substantially better optical transmittance. This replacement became possible due to an extremely low radioactive contamination of the specially developed R11065-20 MOD Hamamatsu PMT [56] used for the ${}^{106}$CdWO${}_4$ detector.

4. Conclusions

The experiment to search for double beta decay of ${}^{106}$Cd with enriched ${}^{106}$CdWO${}_4$ scintillator in coincidence with two large volume CdWO${}_4$ scintillation counters was performed at the Gran Sasso underground laboratory of INFN (Italy). New improved limits are set on the different channels of ${}^{106}$Cd double beta decay at the level of ${10}^{20}-{10}^{22}$ yr. The new improved limit on half-life of ${}^{106}$Cd relative to the $2\nu$EC${\beta }^{+}$ decay was estimated as $T_{1/2}\ge 2.1\times {10}^{21}$ yr. The sensitivity is within the region of the theoretical predictions for the decay probability that are in the range of $T_{1/2}\sim {10}^{21}-{10}^{22}$ yr. A new improved limit was set for the resonant neutrinoless double-electron capture to the 2718 keV excited level of ${}^{106}$Pd, as $T_{1/2}^{0\nu 2\mathrm{K}}\ge 2.9\times {10}^{21}$ yr.

The next stage of experiment is running at LNGS in the DAMA/R&D set-up with an improved sensitivity to all of the decay channels, thanks to a reduction of the background approximately by a factor 3–5 with utilization of ultra-radiopure PMTs, longer quartz light-guides for the CdWO${}_4$ counters, and a more powerful passive shield of the detector system. The energy resolution of the ${}^{106}$CdWO${}_4$ detector was also improved thanks to replacement of the PbWO${}_4$ light-guide by a plastic scintillator light-guide with a substantially better optical transmittance. As a result, the sensitivity to the $2\nu$EC${\beta }^{+}$ decay of ${}^{106}$Cd is expected to be high enough to detect the process with the half-life at level of ∼$(0.5-1)\times {10}^{22}$ yr over five yr of measurements.