Identifying Quark Matter in Hybrid Stars through Relativistic Tidal Deformations
Abstract
1. Introduction
2. Relativistic Tidal Deformations
2.1. Gravitational Radiation
2.2. Modeling Tidal Deformations
3. Hybrid Equation of the State Model
3.1. Nuclear Matter
3.2. Phase Transitions
3.3. Quark Matter
4. Constraints from the Tidal Contributions of Gravitational Radiation
4.1. GW170817 Results
4.2. Constraints
5. Results
5.1. Mass-Radii Relation
5.2. Tidal Relations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics and General Relativity, 2nd ed.; Springer: New York, NY, USA, 2000; p. 468. [Google Scholar]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.; Reddy, S. Hybrid Stars That Masquerade as Neutron Stars. Astrophys. J. 2005, 629, 969–978. [Google Scholar] [CrossRef]
- Wei, W.; Irving, B.; Klähn, T.; Jaikumar, P. Camouflage of the phase transition to quark matter in neutron stars. arXiv 2018, arXiv:1811.09441. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.W.; Wang, Y.Z.; Shen, Z.Q.; Liang, Y.F.; Li, X.; Liao, N.H.; Jin, Z.P.; Yuan, Q.; Zou, Y.C.; et al. The GW170817/GRB 170817A/AT 2017gfo Association: Some Implications for Physics and Astrophysics. Astrophys. J. Lett. 2017, 851, L18. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Signals in the tidal deformability for phase transitions in compact stars with constraints from GW170817. Phys. Rev. D 2019, 99, 023009. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Nandi, R.; Char, P. Hybrid Stars in the Light of GW170817. Astrophys. J. 2018, 857, 12. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Flanagan, E.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2009, 80, 084035. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
- Bini, D.; Damour, T.; Faye, G. Effective action approach to higher-order relativistic tidal interactions in binary systems and their effective one body description. Phys. Rev. D 2012, 85, 124034. [Google Scholar] [CrossRef]
- Gralla, S.E. On the ambiguity in relativistic tidal deformability. Class. Quantum Gravity 2018, 35, 085002. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Landry, P.; Poisson, E. Relativistic theory of surficial Love numbers. Phys. Rev. D 2014, 89, 124011. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Ageev, A.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Araya, M.; Armandula, H.; et al. Analysis of LIGO data for gravitational waves from binary neutron stars. Phys. Rev. D 2004, 69, 122001. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2010, 81, 123016. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves: Volume 2: Astrophysics and Cosmology, 1st ed.; Oxford University Press: Oxford, UK, 2018; p. 752. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.; Volkoff, G. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Love, A. The yielding of the earth to disturbing forces. R. Soc. Publ. 1909, 82, 73–88. [Google Scholar] [CrossRef]
- Van Dalen, E.N.E.; Fuchs, C.; Faessler, A. Effective Nucleon Masses in Symmetric and Asymmetric Nuclear Matter. Phys. Rev. Lett. 2005, 95, 022302. [Google Scholar] [CrossRef] [PubMed]
- Van Dalen, E.N.E.; Fuchs, C.; Faessler, A. The relativistic Dirac-Brueckner approach to asymmetric nuclear matter. Nucl. Phys. A 2004, 744, 227–248. [Google Scholar] [CrossRef]
- Gross-Boelting, T.; Fuchs, C.; Faessler, A. Covariant representations of the relativistic Brueckner T-matrix and the nuclear matter problem. Technical report. Nucl. Phys. A 1999, 648, 105–137. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Fuchs, C.; Wolter, H.H. Modelization of the EOS. Eur. Phys. J. A 2006, 30, 5–21. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; Van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C—Nucl. Phys. 2006, 74, 35802. [Google Scholar] [CrossRef]
- Glendenning, N.K. First-order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 15. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector Interaction Enhanced Bag Model for Astrophysical Applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Binary, R.; Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; et al. A Massive Pulsar in a Compact. Sci. New Ser. 2013, 340, 448. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef]
- Radice, D.; Dai, L. A Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 2019, 55. [Google Scholar] [CrossRef]
- Wei, W.; Barry, M.; Klähn, T.; Jaikumar, P. Lifting the veil on quark matter in compact stars with core g-mode oscillations. arXiv 2018, arXiv:1811.11377. [Google Scholar]
| 1 | The factor of serves as a normalization factor, such that for , . |
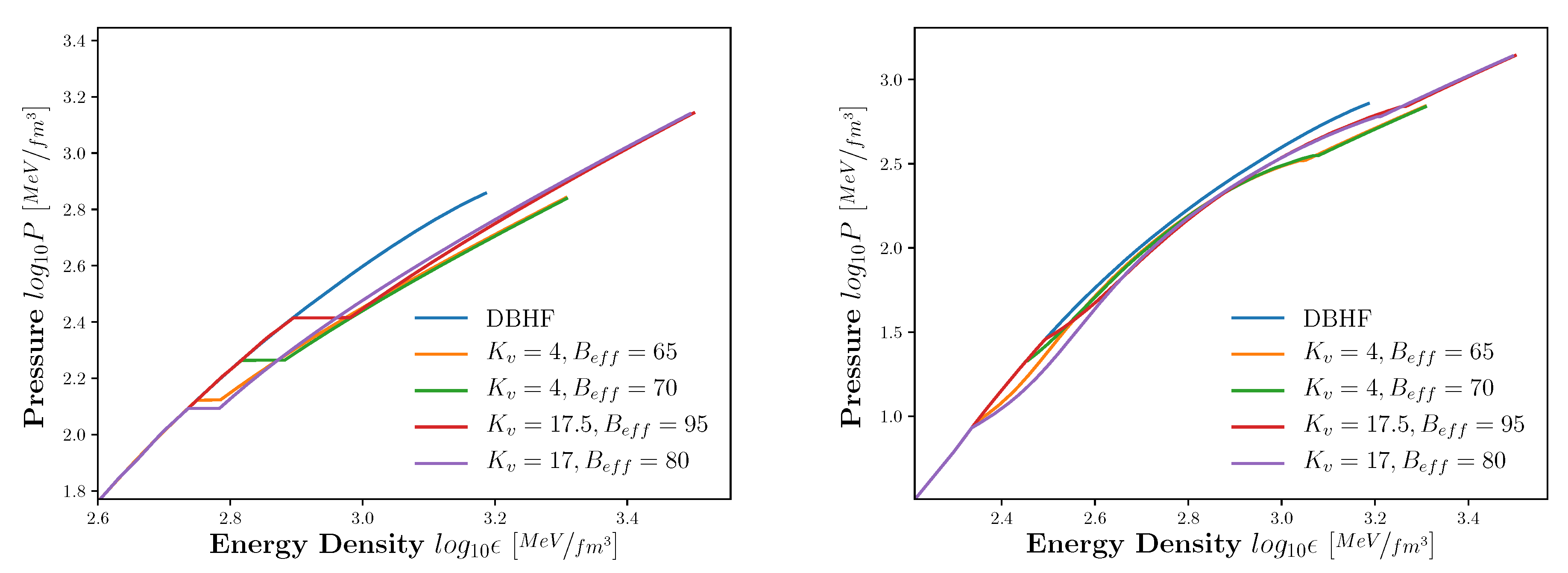
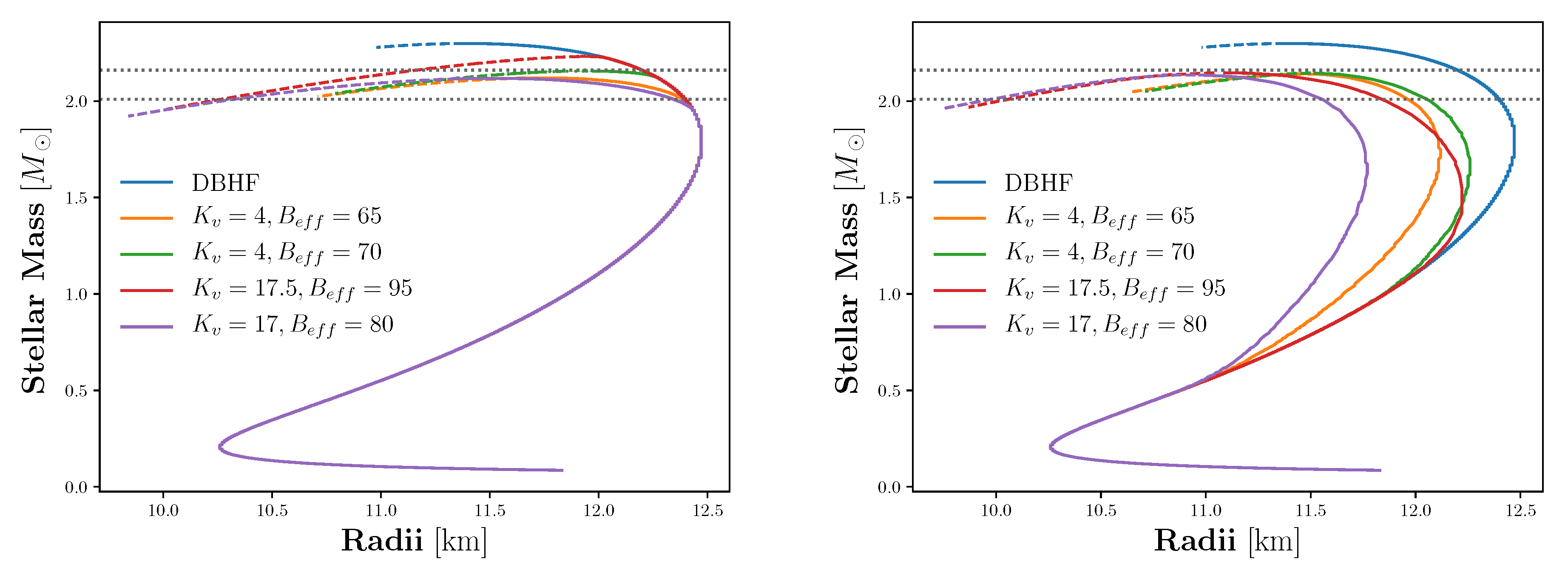
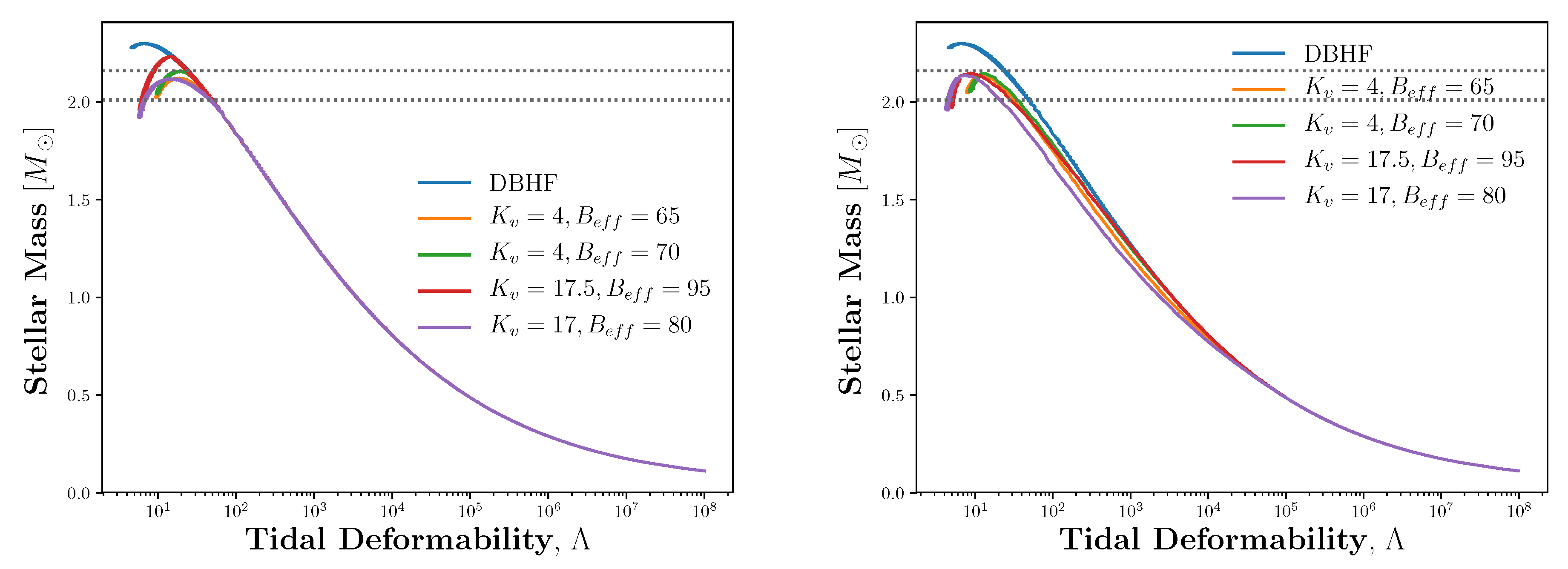
| Maxwell Construction | Gibbs Construction | |
|---|---|---|
| Maxwell Construction | Gibbs Construction | |||||
|---|---|---|---|---|---|---|
| 2.120 | 12.470 | 603 | 2.141 | 12.120 | 449 | |
| 2.156 | 12.470 | 603 | 2.145 | 12.260 | 544 | |
| 2.231 | 12.470 | 603 | 2.145 | 12.220 | 570 | |
| 2.118 | 12.470 | 603 | 2.135 | 11.830 | 345 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irving, B.; Klähn, T.; Jaikumar, P.; Salinas, M.; Wei, W. Identifying Quark Matter in Hybrid Stars through Relativistic Tidal Deformations. Universe 2019, 5, 193. https://doi.org/10.3390/universe5090193
Irving B, Klähn T, Jaikumar P, Salinas M, Wei W. Identifying Quark Matter in Hybrid Stars through Relativistic Tidal Deformations. Universe. 2019; 5(9):193. https://doi.org/10.3390/universe5090193
Chicago/Turabian StyleIrving, Bryen, Thomas Klähn, Prashanth Jaikumar, Marc Salinas, and Wei Wei. 2019. "Identifying Quark Matter in Hybrid Stars through Relativistic Tidal Deformations" Universe 5, no. 9: 193. https://doi.org/10.3390/universe5090193
APA StyleIrving, B., Klähn, T., Jaikumar, P., Salinas, M., & Wei, W. (2019). Identifying Quark Matter in Hybrid Stars through Relativistic Tidal Deformations. Universe, 5(9), 193. https://doi.org/10.3390/universe5090193






