Abstract
We construct a set of equations of state (EoS) of dense and hot matter with a 1st order phase transition from a hadronic system to a deconfined quark matter state. In this two-phase approach, hadrons are described using the relativistic mean field theory with different parametrisations and the deconfined quark phase is modeled using vBag, a bag–type model extended to include vector interactions as well as a simultaneous onset of chiral symmetry restoration and deconfinement. This feature results in a non–trivial connection between the hadron and quark EoS, modifying the quark phase beyond its onset density. We find that this unique property has an impact on the predicted hybrid (quark core) neutron star mass–radius relations.
PACS:
12.39.Ba; 26.60.Kp
1. Introduction
The current state-of-the-art in the description of strongly interacting matter is the theory of Quantum Chromodynamics (QCD). Its elementary degrees of freedom are quarks, spin 1/2 fermions with an electric charge of +2/3 or −1/3 and gluons, spin 1 bosons with an electric charge of 0 acting as strong interaction force carriers. Each of those particles has a chromodynamic charge called color. Given the QCD feature of running coupling, i.e., rapidly increasing interaction strength with respect to interaction range (cf. [1]) and, due to the fact that only color-neutral particles are being observed in nature, it is believed that color charged particles cannot be separated and can only exist in bound states. This is called confinement. Additionally, QCD exhibits a phenomenon called dynamic chiral symmetry breaking () along with chiral symmetry restoration at high densities and temperatures. This feature gives rise to approximately massless Nambu–Goldstone bosons (pions) as well as generates most of the quark mass. is believed to account for roughly of the mass of a proton [1].
The first-principle calculations of QCD (i.e., lattice QCD) produce reliable results for baryon chemical potentials up to about twice the given temperature (c.f. [2,3,4,5,6]). They predict a cross-over phase transition at the temperature of MeV [6] to the deconfined and chiraly restored quark–gluon plasma (QGP). This transition was analyzed up to a baryon chemical potential of about 300 MeV [4,5]. Astrophysical systems are characterized by high densities up to and beyond nuclear saturation and lower temperatures, reaching from 0 to not more than 60 MeV. Asymptotic freedom implies that a phase transition to the QGP will eventually occur. The nature of this transition, its relevance for the study of such systems, and the QGP matter afterwards is one of the pressing issues of contemporary studies of compact stars.
Due to the unavailability of first-principle calculations of cold dense QCD, studies that require the description of dense strongly interacting matter have to rely on effective models. Such models should exhibit all the properties of QCD, i.e., chiral symmetry breaking (and restoration) as well as confinement. Currently, there are only a few approaches that attempt to consistently describe hadron matter at the level of quarks and gluons at high density (cf. for example [7,8,9,10,11]), with the majority of studies relying on models constructed using the two-phase approach [12], i.e., with a separate hadron and quark matter models and a transition between them emulating the effect of deconfinement. A general review of recent developments concerning the EoS in astrophysical applications can be found in [13,14].
A common quark matter model for such studies is the tdBag model [15]. It approximates the effect of quark confinement but does not exhibit and lacks repulsive vector interactions necessary to reach the two solar mass neutron star limit in agreement with recent observations of PSRJ1614-2230 and PSRJ0348+0432 with masses of [16,17] and [18], respectively. vBag, a novel extension of the tdBag approach is an effective model for astrophysical studies with both vector repulsion, chiral symmetry restoration and deconfinement (cf. [19,20,21,22]). The two latter properties are assumed to be simultaneous. This is achieved via a correction to the quark EoS based on the hadron EoS at the chiral transition. The results of some Dyson–Schwinger studies justify this assumption in the cross-over domain of the QCD phase diagram; however, this is far from certain in the desired high density domain (cf. [23,24]), therefore it will be considered a model assumption of vBag.
The manuscript is organized as follows. In Section 2, we introduce vBag and its derivation from the Dyson–Schwinger equations (DSE) of QCD. In Section 3, the temperature–density phase diagrams of vBag will be discussed and Section 4 will focus on the resulting hybrid neutron star mass–radius relations. A summary of the findings will be presented in Section 5.
2. vBag
The general QCD in-medium single flavor quark propagator has the form [25,26]
with , and being the chemical potential. The gap functions A, B and C account for non-ideal behavior due to interactions. They can be derived by using the quark DSE,
with the self-energy term
where m is the bare mass, is the dressed–gluon propagator and is the dressed quark–gluon vertex. One solves this equation by imposing a specific set of approximations [19] to the self energy term . The first of them is the so-called rainbow truncation [27], the leading order in a systematic, symmetry-preserving DSE truncation scheme [28,29],
The second is an effective gluon propagator which is set to be constant in momentum space up to a hard cut-off ,
equivalent to a quark-quark contact interaction in configuration space analogous to the Nambu– Jona–Lasino model (NJL, cf. [30]). The Heaviside function provides a three-momentum cutoff for all momenta . represents a regularization mass scale which, in a realistic treatment, would be removed from the model by taking the limit . For the NJL model, this procedure fails and is typically used as a simple UV cutoff. Different regularization procedures are available; in fact, the regularization scheme does not have to affect UV divergences only, e.g., infra-red (IR) cutoff schemes can be used to remove unphysical implications [31].
The term in the gluon propagator refers to the gluon mass scale and defines the coupling strength. These approximations allow us to derive the gap equations. The A gap function has a trivial solution, the rest takes the form
where . Both equations can be recast in terms of scalar and vector densities of an ideal spin-degenerate Fermi gas,
where
with and . The integrals have no explicit external momentum dependence (p), therefore the gap solutions are constant for a given . Typically, for DSE calculations, the pressure is determined in the steepest descent approximation. It consists of an ideal Fermi gas and interaction contributions:
The merit of the NJL model is the ability to describe chiral symmetry breaking as the formation of a scalar condensate and the restoration of chiral symmetry as melting of the same. The chosen hard cutoff scheme reproduces standard NJL model results and allows for describing quarks as a quasi ideal gas of fermions (assuming constant mass equal to the quarks bare mass) shifted by a constant factor (denoted as ), as seen in Figure 1 of [19]. This is similar to the standard tdBag model approach (cf. [15]). Therefore, we can express the single-flavor pressure as
The second term corresponds to the vector condensate, where relates to the vector current–current interaction coupling constant. In our approach, it is defined in terms of the gluon mass scale:
In combination with the modification of the effective chemical potential , it causes stiffening of the EoS with increasing density. This effect is illustrated in Figure 2 of [22].
From Equation (8), it is evident that a corresponding scalar current–current interaction coupling constant can be defined as . The relation of the coupling constants is consistent with the result obtained after Fierz transformation of the one-gluon exchange interaction [30]. However, we absorbed the effect of scalar interactions in and vary as an independent model parameter. This procedure is common for NJL-type model studies. Taking the vector interaction into account then results in a modification of the effective chemical potential and pressure as evident from Equations (9) and (14). This term is not included in the standard tdBag model. Chiral symmetry is restored when , and therefore the critical chemical potential can be defined as
For two-flavor quark matter, this condition is redefined as
to avoid sequential chiral symmetry restoration. This is done so that we can impose simultaneous chiral symmetry restoration and deconfinement, which can be achieved by exploiting the fact that the total pressure is fixed only up to a constant. Therefore, we can impose
By defining as the hadron pressure at the point of quark chiral symmetry restoration, one easily sees that both transitions would coincide. We can now write the full set of equations that define vBag
where denotes energy density and n is the particle number density.
Since the vBag EoS is defined in terms of a free gas of quasiparticle fermions, its temperature extension follows by simply taking the full temperature-dependent terms of this free Fermi gas instead of its ground state (cf. [20]), with
being the entropy density of the system. In considering isospin asymmetry, it is useful to introduce the baryon and charge chemical potentials
and the associated densities
Furthermore, the assumption of isospin-independent chiral symmetry restoration (Equation (17)) allows us to define the (critical) chiral baryon chemical potential , such that
The deconfinement bag constant is therefore defined in term of as
The treatment of chiral symmetry restoration and deconfinement as simultaneous allows us to keep the description of chiral physics on the quark side of the EoS while avoiding the problem of using a nuclear EoS insensitive to the quark chiral restoration. This, however, results in being a function of both temperature and charge chemical potential. Thermodynamic consistency requires that additional terms be included in the expressions for charge density and entropy to account for this fact (as well as , due to the Euler equation, cf. [20]), i.e.,
where is the charge of the given quark flavor (, ) while and are functions of both quark and hadron equations of state.
This non–trivial relation is not present in any standard two-phase equations of state and is unique to vBag. Obviously, the impact on the deconfined quark matter is largely dependent on the choice of hadronic EoS and will be explored in the following chapter.
3. The Phase Diagram
Having an equation of state dependent on both the baryon and charge chemical potential, as well as temperature, one can compare the resulting phase diagrams of hot and dense matter. For this purpose, two hadronic equations of state based on the relativistic mean field theory (denoted DD2 [32] and NL3 [33]) have been selected. The choice of these EoS was made such that they produce sufficiently different thermodynamic quantities for given chemical potentials. A summary of their properties can be found in Table 1.

Table 1.
Selected properties of the hadronic equations of state (, ) and their experimental constraints (cf. [34,35,36]).
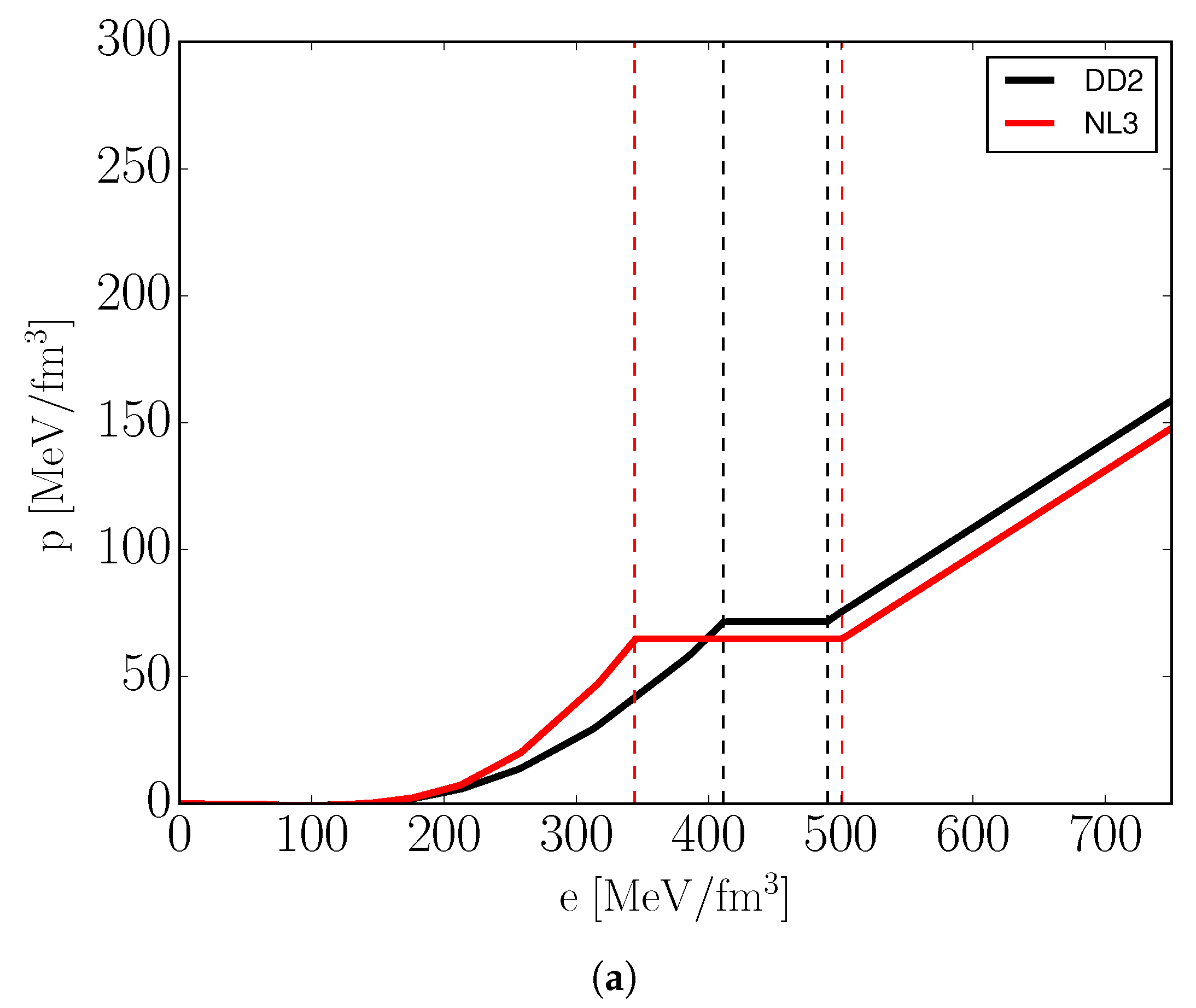
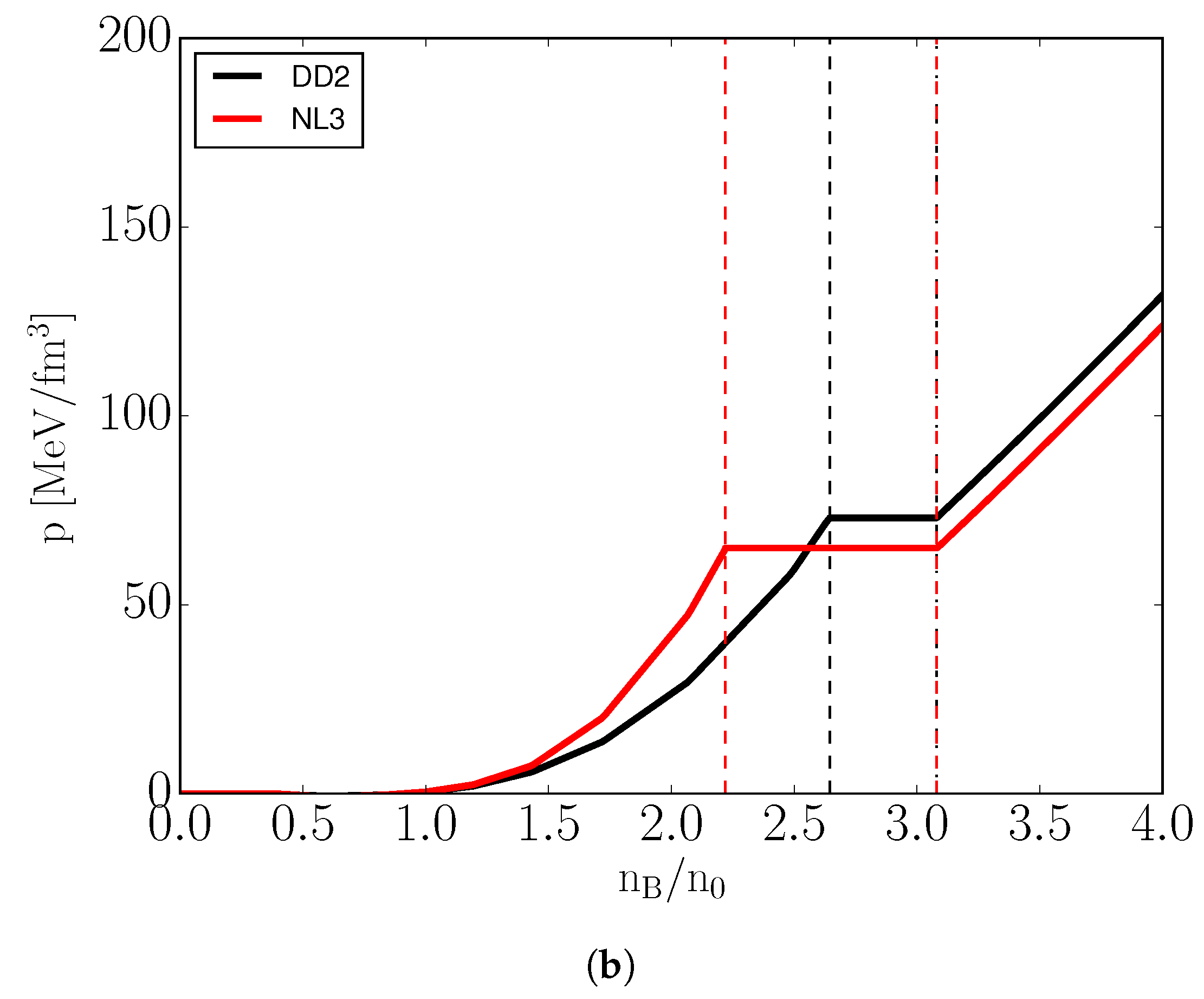
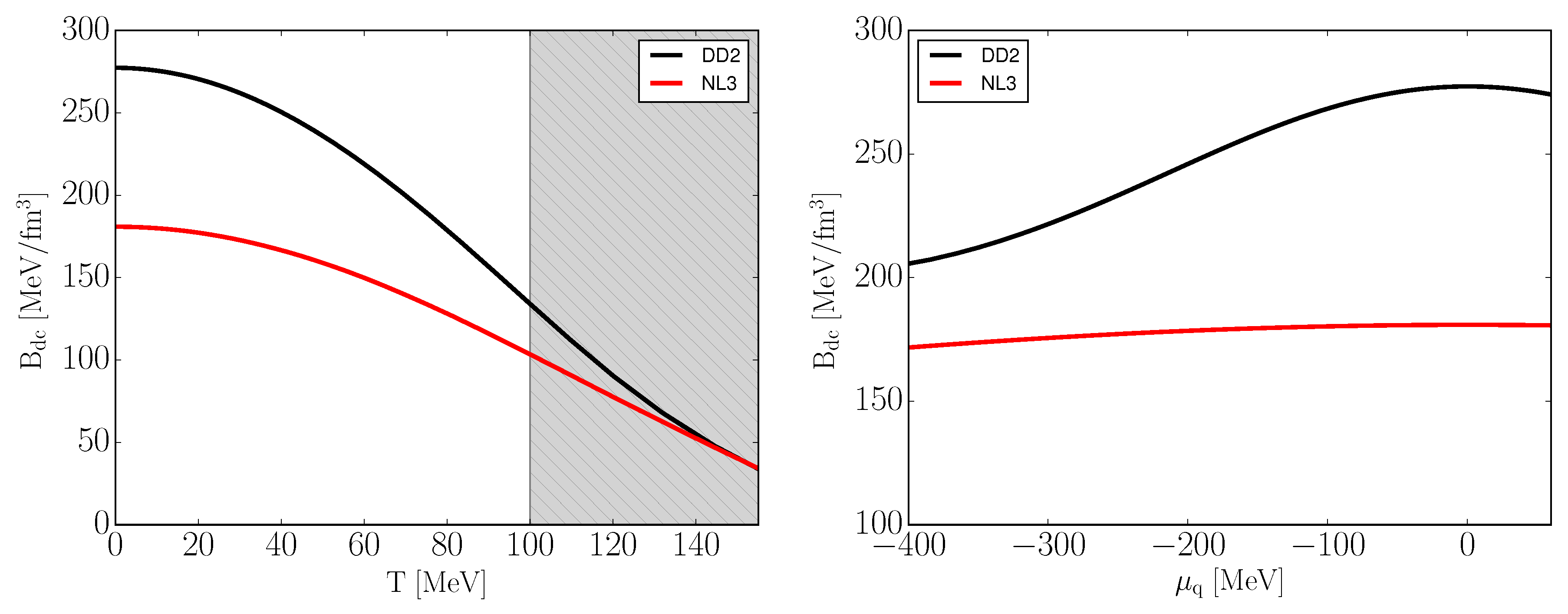
As evident from Figure 1, the quark matter EoS differ depending on the choice of hadronic EoS. This difference is constant for a given temperature and charge chemical potential, as to be expected from Equations (31), (35) and (36). It is also evident from Figure 2 that the hadronic EoS and resulting correction terms have no impact on the critical baryon chemical potential. This is imposed by Equation (30).
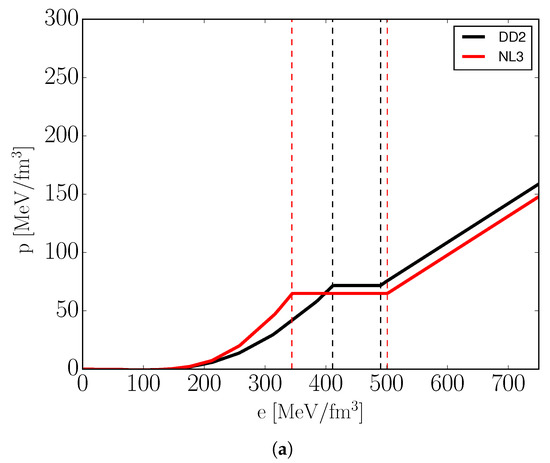
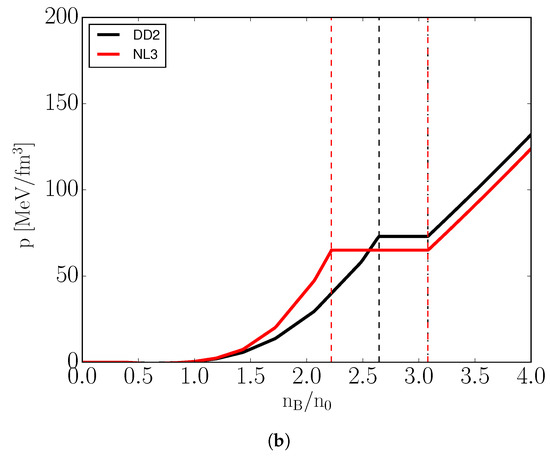
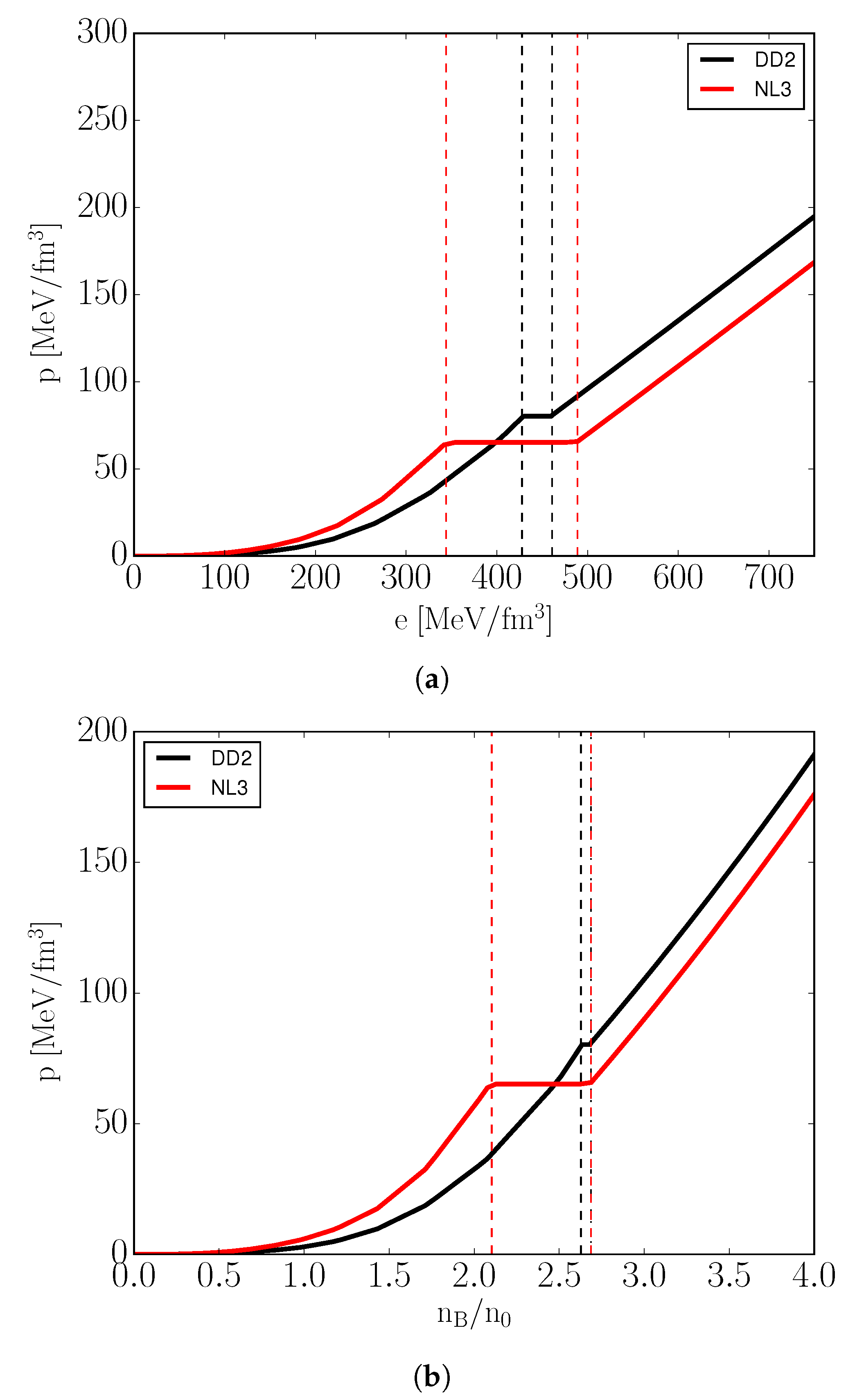
Figure 1.
Pressure as a function of energy density (a) and baryon density (b) for cold isospin symmetric matter () modeled using vBag ( MeV, ) with different hadronic EoS. Dashed lines highlight mixed phase regions.
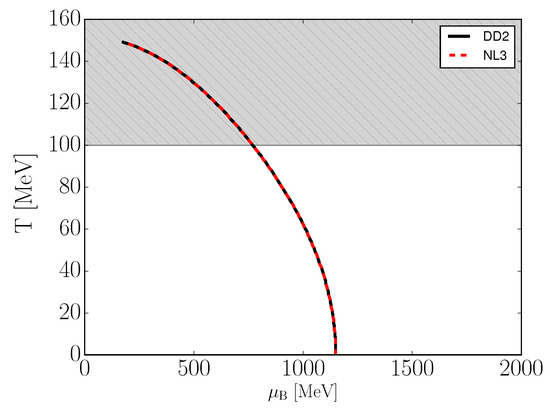
Figure 2.
The T– phase space of vBag ( MeV, ) for . The grey region lies outside of the models expected applicability domain. See text for details.
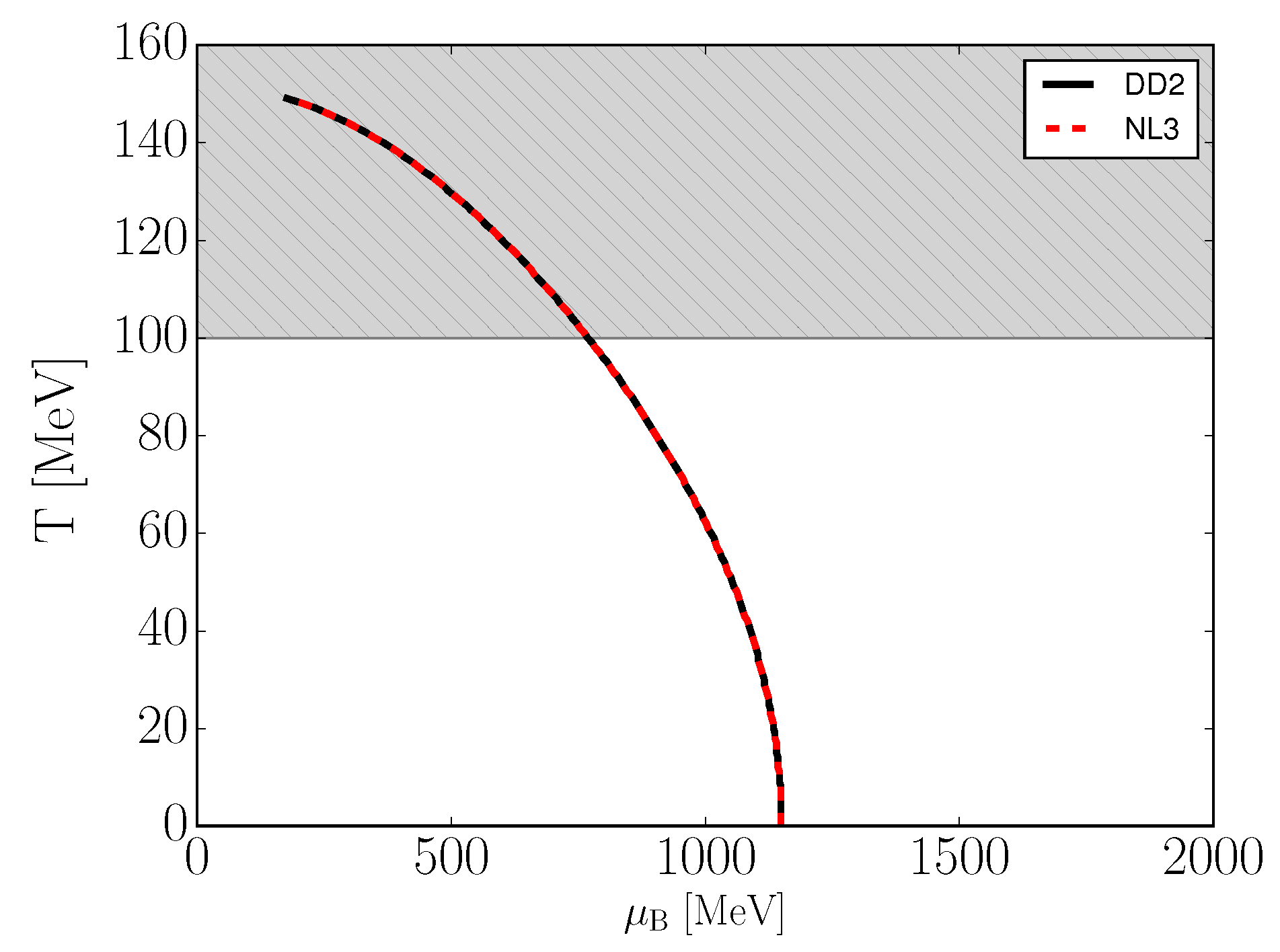
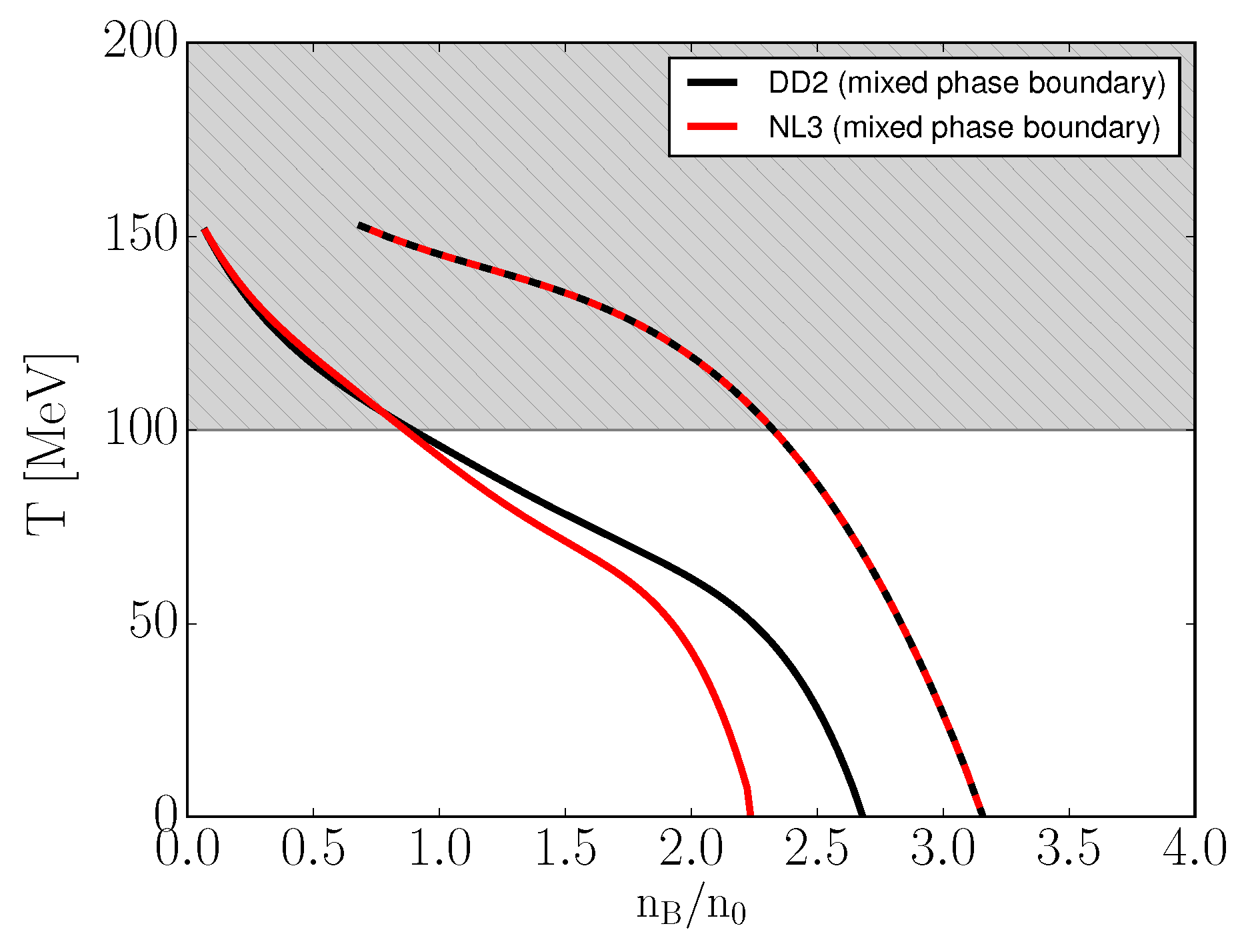
The biggest difference in the phase diagram can be seen in Figure 3. The difference in the mixed phase onset density is to be expected given the change in stiffness of the hadronic EoS. The overall shape of the mixed phase is a direct result of the temperature dependence of (i.e., ).
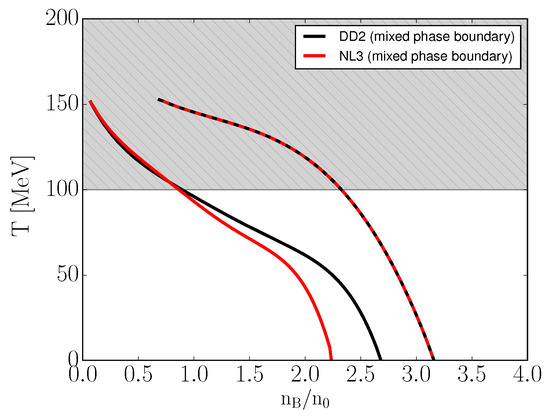
Figure 3.
The T– phase space of vBag ( MeV, ) for . The grey region lies outside of the models expected applicability domain. See text for details.
One needs to recognize that these phase diagrams cannot be considered accurate at temperatures of above 100 MeV [20]. This is caused by (the quark scalar condensate) and its temperature dependence, which at an excess of a 100 MeV is no longer negligible. On top of that, the phase transition is 1st order by construction, while at vanishing densities this transition should become a smooth crossover. These limitations are of no concern for static neutron star mass–radius relations; however, this might not be the case for neutron star mergers and therefore one needs to keep them in mind in future studies of neutron star phenomenology.
In the region below MeV, we can clearly see significant differences in the phase structure of our model resulting from the choice of hadronic EoS (as evident from Figure 4). This fact is expected to have an impact on the derived astrophysical observables.
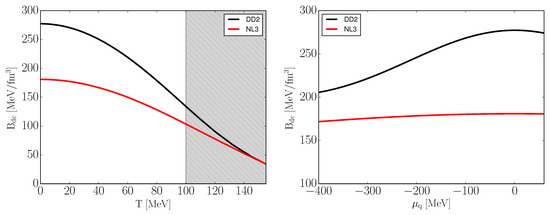
Figure 4.
The deconfinement bag constant (Equation (31)) as a function of temperature for (left) and the charge chemical potential for (right). The grey region lies outside of the models expected applicability domain. See text for details.
4. Hybrid Neutron Stars
In order to derive the mass-radius relations of neutron stars, we need to consider dense matter under -equilibrium and charge neutrality. These conditions will result in an EoS with strong isospin asymmetry (shown in Figure 5).
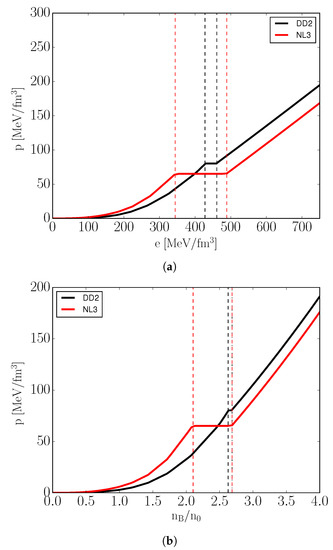
Figure 5.
Pressure as a function of energy density (a) and baryon density (b) for cold dense matter in -equilibrium modeled using vBag ( MeV, ) with different hadronic EoS. Dashed lines highlight mixed phase regions.
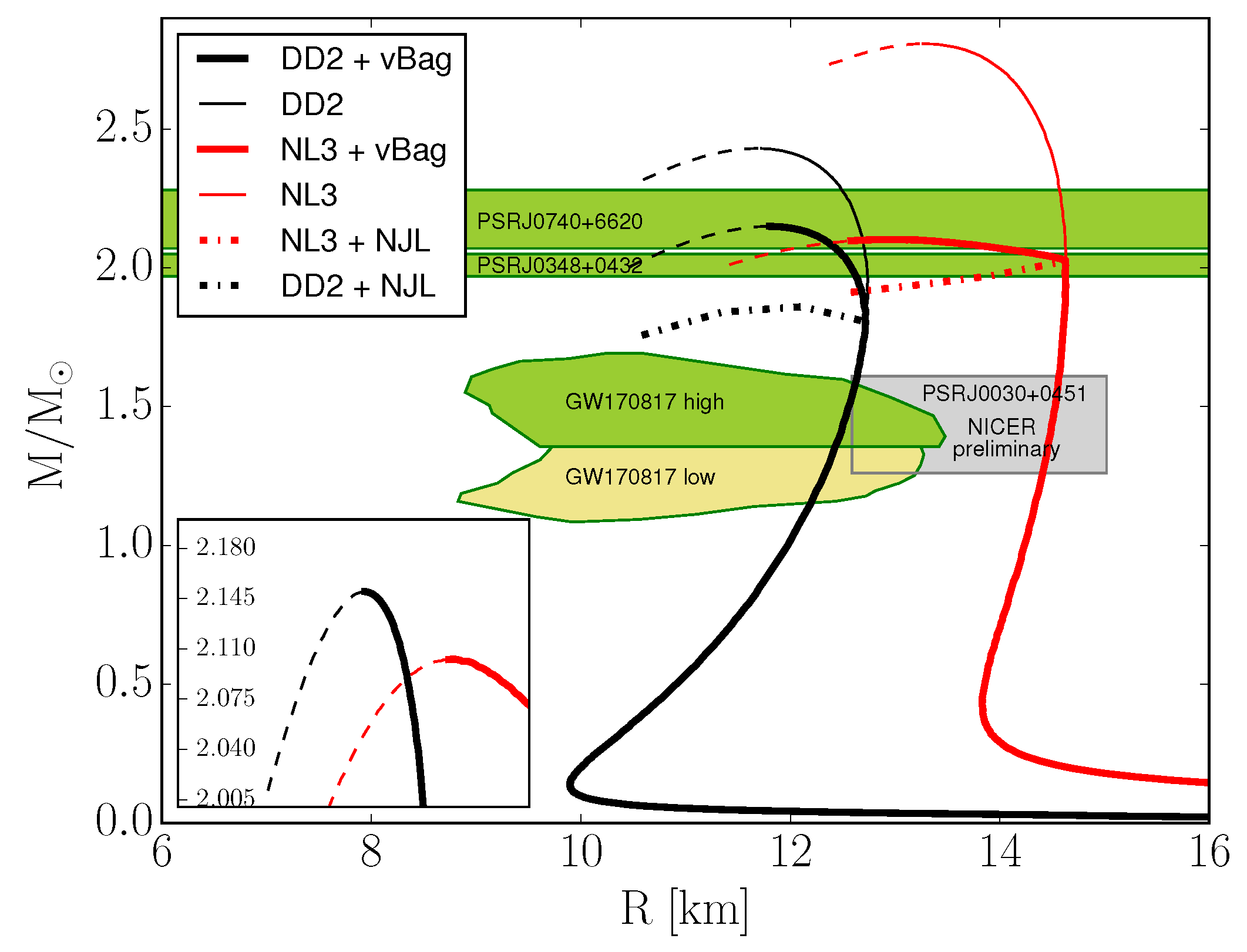
The resulting mass–radius curves shown in Figure 6 illustrate the impact of the underlying hadronic EoS on the quark matter in neutron stars. While Figure 3 indicates one should expect different onset densities for hybrid stars (and also different onset star masses, due to the stiffness of the hadronic EoS), what is unexpected is the difference in maximum neutron star masses. Given that the free parameters of vBag are kept constant (specifically the vector repulsion strength , which directly impacts the maximum mass of stable neutron stars), the quark phase of DD2+vBag would not be able to support a heavier neutron star without the modification caused by and .
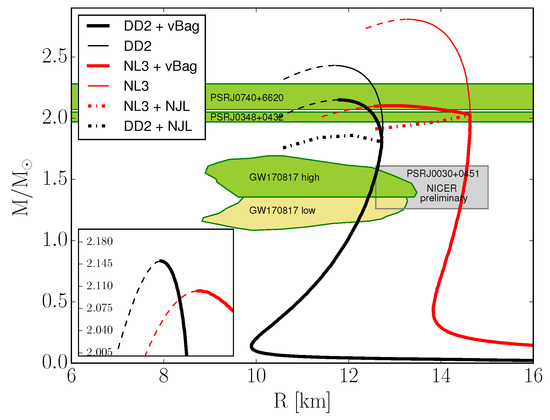
Figure 6.
Neutron star mass–radius curves obtained using vBag ( MeV, = 6 × 10 ) with two different hadronic EoS. The lower green, yellow and grey regions represent the mass–radius constraints of the neutron star merger event GW170817 for high and low mass posteriors (cf. [37,38]) and the preliminary radius measurement of PSRJ0030+0451 from the NICER experiment [39], respectively. The topmost green bands represent the mass measurements of the neutron star PSRJ0348+0432 [40] and the recent PSRJ0740+6620 [41]. Thin lines represent neutron stars with a purely hadronic core. Thick lines are hybrid neutron stars. Dashed lines show unstable mass–radius configurations. Dash-dotted lines represent hybrid EoS for (equivalent to a pure NJL model, cf. [19]). The vector interaction strength was kept constant between all hybrid branches.
5. Conclusions
The interior of neutron stars attains conditions that are presently inaccessible in nuclear physics and heavy-ion collision experiments. These astrophysical objects, together with core-collapse supernovae [14] and binary neutron star mergers [42], enable us to probe the possible existence of exotic phases of dense matter such as the transition from ordinary nuclear (in general hadronic) matter to the quark–gluon plasma. How this quark–gluon plasma behaves in the high density domain is largely uncertain. The current state-of-the-art in dense matter modeling is a two-phase approach, which, at its core, is inconsistent due to the separate treatment of hadronic and quark degrees of freedom. Nevertheless, since the unified approach to the hadron–quark matter EoS is still not available based on QCD degrees of freedom at high baryon density, in order to study the potential impact of a first-order hadron–quark phase transition at the interior of neutron stars, the two-phase approach has been commonly employed.
Furthermore, such a two-phase approach enables us to quantify the EoS in light of recent observations (see Figure 6). In particular, we focus on the recently available constraints obtained from the analysis of GW170817, which seems to favour not too large neutron star radii, and the preliminary data of NICER, which seem to agree with the latter only marginally. Nevertheless, both of them are likely to have only a minor impact on properties of hybrid stars with hadron–quark transition densities corresponding to neutron star masses in excess of 1.5 M. In fact, within vBAG, the latter is a direct consequence in order to obtain hybrid stars with a maximum mass of ∼2.1 M or above. Note that, within our setting, twin solutions were not obtained [43]. Here, we select two vastly different hadronic EoS, DD2 and NL3, both of which belong to the class of relativistic mean-field models, which result in very different radii of low- and intermediate-mass neutron stars (entirely determined by the hadronic EoS) but rather similar maximum masses though not identical. The differences arise exclusively from different correction terms related with . It remains to be explored by future observations, in particular the confirmed analysis of NICER data also for more massive pulsars on the order of 2 M, if it will become eventually possible to further constrain the supersaturation density EoS in the light of the appearance of exotic phase at high densities.
Another aspect of dense matter under the conditions found in the interior of neutron stars is the onset of strangeness, expected to occur already at supersaturation density in hadronic matter (cf. [13,44,45,46] and references therein). Since hyperons are more massive than baryons, the appearance of hyperons tends to soften the EoS with increasing density, which gave rise to the so-called hyperon puzzle in order to explain the existence of massive neutron stars with 2 M. However, little is presently known about hyperon–nucleon as well as hyperon–hyperon interactions. In particular, the repulsive vector interaction may ’cure’ the hyperon puzzle. Another solution has been proposed in terms of hadron–quark phase transition before hyperon degrees of freedom could substantially soften the EoS. However, studying this interesting scenario self-consistently requires not only strangeness as an explicit degree of freedom in the deconfined quark matter phase as was done in [19] but also in the hadronic EoS. This will allow us also to explore the hypothesis of absolutely stable strange matter [47,48], which has to be reviewed taking the restoration of chiral symmetry into account [19]. However, this extends beyond the scope of the present paper. We leave the exploration of strangeness for a future more focused study.
Author Contributions
Conceptualization, M.C. and T.F.; data curation, M.C. and N.-U.B.; formal analysis, M.C.; investigation, M.C.; methodology, M.C.; project administration, M.C.; resources, M.C., T.F., N.-U.B., T.K. and M.S.; software, M.C., N.-U.B., T.K. and M.S.; supervision, T.F.; validation, M.C., T.F., N.-U.B., T.K. and M.S.; visualization, M.C.; writing—original draft, M.C.; writing—review and editing, M.C., T.F., N.-U.B., T.K. and M.S.
Funding
This research received no external funding.
Acknowledgments
N.-U.B. and T.F. acknowledge support from the Polish National Science Center (NCN) under Grant No. UMO-2016/23/B/ST2/00720.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roberts, C.D. Three Lectures on Hadron Physics. J. Phys. Conf. Ser. 2016, 706, 022003. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S.D. Critical point of QCD at finite T and mu, lattice results for physical quark masses. JHEP 2004, 2004, 050. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. The QCD Equation of State to from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Guenther, J.N.; Bellwied, R.; Borsanyi, S.; Fodor, Z.; Katz, S.D.; Pasztor, A.; Ratti, C.; Szabó, K.K. The QCD equation of state at finite density from analytical continuation. Nucl. Phys. A 2017, 967, 720–723. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; Li, S.-T.; et al. Chiral crossover in QCD at zero and non-zero chemical potentials. arXiv 2018, arXiv:1812.08235. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.; Fischer, T.; Röpke, G. Towards a Unified Quark-Hadron Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe 2018, 4, 67. [Google Scholar] [CrossRef]
- Dexheimer, V.A.; Schramm, S. A Novel Approach to Model Hybrid Stars. Phys. Rev. C 2010, 81, 045201. [Google Scholar] [CrossRef]
- Steinheimer, J.; Schramm, S.; Stocker, H. An Effective chiral Hadron-Quark Equation of State. J. Phys. G 2011, 38, 035001. [Google Scholar] [CrossRef]
- Marczenko, M.; Sasaki, C. Net-baryon number fluctuations in the Hybrid Quark-Meson-Nucleon model at finite density. Phys. Rev. D 2018, 97, 036011. [Google Scholar] [CrossRef]
- Marczenko, M.; Blaschke, D.; Redlich, K.; Sasaki, C. Chiral symmetry restoration by parity doubling and the structure of neutron stars. Phys. Rev. D 2018, 98, 103021. [Google Scholar] [CrossRef]
- Cleymans, J.; Gavai, R.V.; Suhonen, E. Quarks and Gluons at High Temperatures and Densities. Phys. Rept. 1986, 130, 217. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cierniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The state of matter in simulations of core-collapse supernovae—Reflections and recent developments. Publ. Astron. Soc. Aust. 2017, 34, 67. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector interaction enhanced bag model for astrophysical applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T.; Hempel, M. Simultaneous chiral symmetry restoration and deconfinement—Consequences for the QCD phase diagram. Astrophys. J. 2017, 836, 89. [Google Scholar] [CrossRef]
- Fischer, T.; Klähn, T.; Hempel, M. Consequences of simultaneous chiral symmetry breaking and deconfinement for the isospin symmetric phase diagram. Eur. Phys. J. A 2016, 52, 225. [Google Scholar] [CrossRef]
- Cierniak, M.; Klähn, T.; Fischer, T.; Bastian, N.U. Vector-Interaction-Enhanced Bag Model. Universe 2018, 4, 30. [Google Scholar] [CrossRef]
- Qin, S.x.; Chang, L.; Chen, H.; Liu, Y.x.; Roberts, C.D. Phase diagram and critical endpoint for strongly-interacting quarks. Phys. Rev. Lett. 2011, 106, 172301. [Google Scholar] [CrossRef] [PubMed]
- Fischer, C.S.; Luecker, J.; Welzbacher, C.A. Phase structure of three and four flavor QCD. Phys. Rev. D 2014, 90, 034022. [Google Scholar] [CrossRef]
- Rusnak, J.J.; Furnstahl, R.J. Two point fermion correlation functions at finite density. Z. Phys. A Hadrons Nucl. 1995, 352, 345–350. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1–S103. [Google Scholar] [CrossRef]
- Gutierrez-Guerrero, L.X.; Bashir, A.; Cloet, I.C.; Roberts, C.D. Pion form factor from a contact interaction. Phys. Rev. C 2010, 81, 065202. [Google Scholar] [CrossRef]
- Munczek, H.J. Dynamical chiral symmetry breaking, Goldstone’s theorem and the consistency of the Schwinger-Dyson and Bethe-Salpeter Equations. Phys. Rev. D 1995, 52, 4736–4740. [Google Scholar] [CrossRef]
- Bender, A.; Roberts, C.D.; Von Smekal, L. Goldstone theorem and diquark confinement beyond rainbow ladder approximation. Phys. Lett. B 1996, 380, 7–12. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Ebert, D.; Feldmann, T.; Reinhardt, H. Extended NJL model for light and heavy mesons without q- anti-q thresholds. Phys. Lett. B 1996, 388, 154–160. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Konig, J.; Ring, P. A New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Motohiro, Y.; Kim, Y.; Harada, M. Asymmetric nuclear matter in a parity doublet model with hidden local symmetry. Phys. Rev. C 2015, 92, 025201. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Kortelainen, M.; McDonnell, J.; Nazarewicz, W.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S.M. Nuclear energy density optimization: Large deformations. Phys. Rev. C 2012, 85, 024304. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Guillot, S. First results on the equation of state constraints from NICER. In Proceedings of the Neutron Stars and Their Environments Workshop MODE-SNR-PWN, Orléans, France, 8–10 April 2019. [Google Scholar]
- Arzoumanian, Z.; Adam, B.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. A very massive neutron star: Relativistic Shapiro delay measurements of PSR J0740+6620. arXiv 2019, arXiv:1904.06759. [Google Scholar]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics - I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J.; Greiner, C.; Diener, A.; Stoecker, H. Detectability of strange matter in heavy ion experiments. Phys. Rev. C 1997, 55, 3038–3046. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802. [Google Scholar] [CrossRef]
- Fortin, M.; Oertel, M.; Providência, C. Hyperons in hot dense matter: What do the constraints tell us for equation of state? Publ. Astron. Soc. Austral. 2018, 35, 44. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaeffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).