A Theory of Inertia Based on Mach’s Principle
Abstract
:1. Introduction
- The universe, as represented by the average motion of distant galaxies, does not appear to rotate relative to local inertial frames.
- An isolated body in otherwise empty space has no inertia.
- Local inertial frames are affected by the cosmic motion and distribution of matter.
- Inertial mass is affected by the global distribution of matter.
- Overall rigid rotations and translations of a system [universe] are unobservable.
2. Results
2.1. Assumptions
- Assumption 1: A single point mass in an otherwise empty universe has no defined movement, i.e., no inertia, no acceleration, no momentum or kinetic energy.
- Assumption 2: Two-point masses in an otherwise empty universe can have a defined movement only along their connecting line. Any movement at a constant distance between the masses cannot be defined. This comprises rotation about each other (no tangential inertia) and collective translation. No kinetic energy or momentum arises due to such movement: Inertia, acceleration, momentum or kinetic energy can only be defined with respect to increasing/reducing the distance between the masses, i.e., for radial movement. We would like to have a theory where the sign of this radial movement does not matter.
- Assumption 3: Since the inertia of a test particle is ’created’ by the gravitational forces of other masses, it will depend on the direction. Therefore the angle between the direction of the test particle movement and the connecting line to any inducing mass will be crucial.
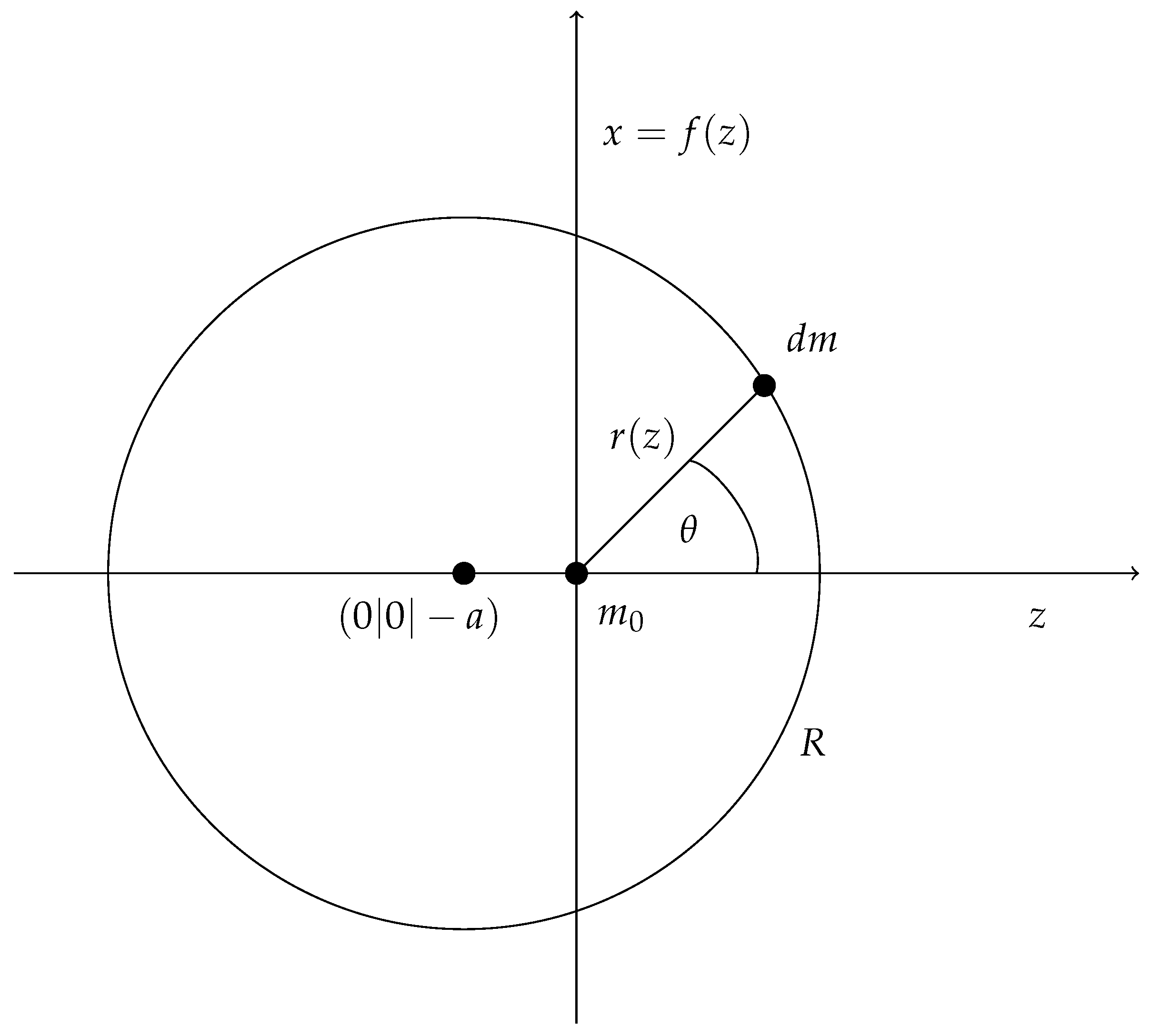
- Assumption 4: The size of the induced inertia should decrease with increasing distance r between test particle and inducing mass as with . Here guarantees vanishing inertia at infinite distance (which, of course, is an assumption itself). would lead to large effects perceivable in daily life, since anisotropy of inertia would balance or even excel the effects of Newton’s gravity. In fact, is a standard assumption in literature, see e.g., [8], where, however, isotropy of inertia is postulated.
- Assumption 5: The inertia of a test particle within a hollow sphere of constant mass density is isotropic and constant. If the mass distribution is largely isotropic within our universe, this assumption guarantees that this theory is very similar to our daily experience.
2.2. Theory
2.3. Check of Assumptions
3. Conclusions
Funding
Conflicts of Interest
Appendix A. Calculation of M within a Sphere
References
- Mach, E. Die Geschichte und die Wurzel des Satzes von der Erhaltung der Arbeit; Calve: Prague, Czech Republic, 1872. [Google Scholar]
- Bouquiaux, L. Leibniz Against the Unreasonable Newtonian Physics. In Leibniz: What Kind of Rationalist; Dascal, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; p. 104. [Google Scholar]
- Barbour, J.; Pfister, H. Mach’s Principle. From Newton’s Bucket to Quantum Gravity; Birkhäuser: Basel, Switzerland, 1995. [Google Scholar]
- Bondi, H.; Samuel, J. The Lense-Thirring effect and Mach’s principle. Phys. Lett. A 1997, 228, 121–126. [Google Scholar] [CrossRef]
- Huges, V.W. Gravitation and Relativity; Chiu, H., Hoffmann, W., Eds.; W. A. Benjamin, Inc.: New York, NY, USA, 1964; Chapter 6; pp. 106–120. [Google Scholar]
- Anderson, J. Principles of Relativity Physics; Academic Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Dicke, R.H. Experimental tests of Mach’s principle. Phys. Rev. Lett. 1961, 7, 359–360. [Google Scholar] [CrossRef]
- Treder, H.-J. Die Relativität der Trägheit; Akademie: Berlin, Germany, 1972. [Google Scholar]
- Treder, H.-J.; Mücket, J.-P. Große Kosmische Systeme; Akademie: Berlin, Germany, 1981. [Google Scholar]
- Bartsch, H.-J. Taschenbuch mathematischer Formeln. Fachbuchverlag Leipzig 1997, 633. [Google Scholar]
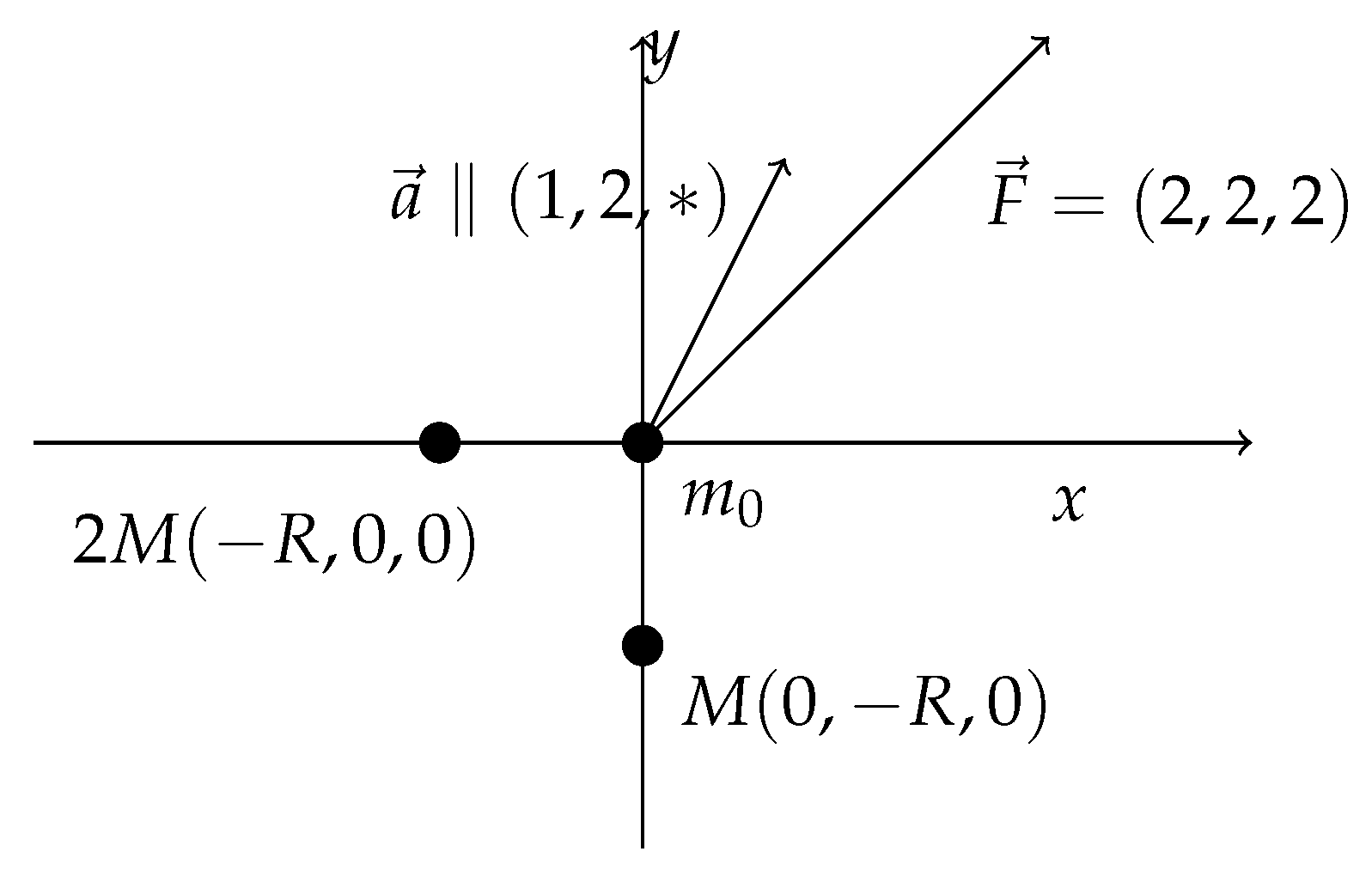
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putz, V. A Theory of Inertia Based on Mach’s Principle. Universe 2019, 5, 188. https://doi.org/10.3390/universe5080188
Putz V. A Theory of Inertia Based on Mach’s Principle. Universe. 2019; 5(8):188. https://doi.org/10.3390/universe5080188
Chicago/Turabian StylePutz, Volkmar. 2019. "A Theory of Inertia Based on Mach’s Principle" Universe 5, no. 8: 188. https://doi.org/10.3390/universe5080188
APA StylePutz, V. (2019). A Theory of Inertia Based on Mach’s Principle. Universe, 5(8), 188. https://doi.org/10.3390/universe5080188




