Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe
Abstract
1. Introduction
2. Dynamical Equations
3. Coupled Phantom Field
3.1. Coupling
3.2. Coupling
3.3. Coupling
4. Coupled Tachyon Dynamics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. A 2000, 9, 373. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 03501. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than −1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas, and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. Tachyons, scalar fields, and cosmology. Phys. Rev. D 2004, 69, 123512. [Google Scholar] [CrossRef]
- Debnath, U.; Banerjee, A.; Chakraborty, S. Role of modified Chaplygin gas in accelerated universe. Class. Quantum Grav. 2004, 21, 5609. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Zimdahl, W.; Pavon, D.; Chimento, L.P. Interacting quintessence. Phys. Lett. B 2001, 521, 133. [Google Scholar] [CrossRef]
- Chimento, L.P. Linear and nonlinear interactions in the dark sector. Phys. Rev. D 2010, 81, 043525. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. A Tachyonic scalar field with mutually interacting components. Int. J. Theor. Phys. 2012, 51, 2370. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. Shifted cosmological parameter and shifted dust matter in a two-phase tachyonic field universe. Astrophys. Space Sci. 2013, 344, 505. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, S.N. Dynamics of quintom and hessence energies in loop quantum cosmology. Phys. Rev. D 2007, 76, 063005. [Google Scholar] [CrossRef]
- Setare, M.R.; Saridakis, E.N. Coupled oscillators as models of quintom dark energy. Phys. Lett. B 2008, 668, 177. [Google Scholar] [CrossRef]
- Setare, M.R.; Saridakis, E.N. Quintom cosmology with general potentials. Int. J. Mod. Phys. D 2009, 18, 549. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S.; Pavón, D.; Zimdahl, W. Interacting quintessence solution to the coincidence problem. Phys. Rev. D 2003, 67, 083513. [Google Scholar] [CrossRef]
- Chimento, L.P.; Pavón, D. Dual interacting cosmologies and late accelerated expansion. Phys. Rev. D 2006, 73, 063511. [Google Scholar] [CrossRef]
- Shahalam, M.; Pathak, S.D.; Verma, M.M.; Khlopov, M.Y.; Myrzakulov, R. Dynamics of interacting quintessence. Eur. Phys. J. C 2015, 75, 395. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzie, S.; Motag, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Bogoyavlensky, O.I. Methods in the Qualitative Theory of Dynamical Systems in Astrophysics and Gas Dynamics; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Xiao, K.; Zhu, J. Stability analysis of an autonomous system in loop quantum cosmology. Phys. Rev. D 2011, 83, 083501. [Google Scholar] [CrossRef]
- Shahalam, M.; Pathak, S.D.; Li, S.; Myrzakulov, R.; Wang, A. Dynamics of coupled phantom and tachyon fields. Eur. Phys. J. C 2017, 77, 686. [Google Scholar] [CrossRef]
- Sharif, M.; Mughani, Q.A.T. Stability analysis of coupled phantom and tachyon field models in nonlinear electrodynamics. Int. J. Mod. Phys. D 2019, 28, 1950076. [Google Scholar] [CrossRef]
- Sharif, M.; Mumtaz, S. Stability of the universe model coupled with phantom and tachyon fields. Adv. High Energy Phys. 2019, 2019, 6582470. [Google Scholar]
- Waga, I.; Falcão, R.C.; Chanda, R. Bulk-viscosity-driven inflationary model. Phys. Rev. D 1986, 33, 1839. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Chitre, S.M. Viscous universes. Phys. Lett. A 1987, 120, 433. [Google Scholar] [CrossRef]
- Cheng, B. Bulk viscosity in the early universe. Phys. Lett. A 1991, 160, 329. [Google Scholar] [CrossRef]
- Zimdahl, W. Bulk viscous cosmology. Phys. Rev. D 1996, 53, 5483. [Google Scholar] [CrossRef]
- Acquaviva, G.; Beesham, A. Nonlinear bulk viscosity and the stability of accelerated expansion in FRW spacetime. Phys. Rev. D 2014, 90, 023503. [Google Scholar] [CrossRef]
- Sasidharan, A.; Mathew, T.K. Phase space analysis of bulk viscous matter dominated universe. J. High Energy Phys. 2016, 2016, 138. [Google Scholar] [CrossRef]
- Sharif, M.; Mumtaz, S. Stability analysis of bulk viscous anisotropic universe model. Astrophys. Space Sci. 2017, 362, 205. [Google Scholar] [CrossRef]
- Disconzi, M.M. On the well-posedness of relativistic viscous fluids. Nonlinearity 2014, 27, 1915. [Google Scholar] [CrossRef][Green Version]
- Disconzi, M.M.; Kephart, T.W.; Scherrer, R.J. New approach to cosmological bulk viscosity. Phys. Rev. D 2015, 91, 043532. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J.; Turner, M.S.; Wilczek, F. Reheating an inflationary universe. Phys. Rev. Lett. 1982, 48, 1437. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141. [Google Scholar] [CrossRef]
- Gumjudpai, B.; Naskar, T.; Sami, M.; Tsujikawa, S. Coupled dark energy: Towards a general description of the dynamics. J. Cosmol. Astropart. Phys. 2005, 2005, 0506. [Google Scholar] [CrossRef]
- Campo, S.D.; Herrera, R.; Pavon, D. H(z) Diagnostics on the nature of dark eneryg. Int. J. Mod. Phys. D 2011, 20, 561. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.G. K-chameleon and the coincidence problem. Phys. Rev. D 2005, 71, 043504. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23. [Google Scholar] [CrossRef]
- Sen, A. Rolling tachyon. J. High Energy Phys. 2002, 2002, 048. [Google Scholar] [CrossRef]
- Marra, V.; Amendola, L.; Sawicki, I.; Valkenburg, W. Cosmic variance and the measurement of the local Hubble parameter. Phys. Rev. Lett. 2013, 110, 241305. [Google Scholar] [CrossRef]
- Battye, R.A.; Charnock, T.; Moss, A. Tension between the power spectrum of density perturbations measured on large and small scales. Phys. Rev. D 2015, 91, 103508. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Copi, C.J.; Huterer, D.; Starkman, G.D. CMB Anomalies after Planck. Class. Quant. Grav. 2016, 33, 184001. [Google Scholar] [CrossRef]
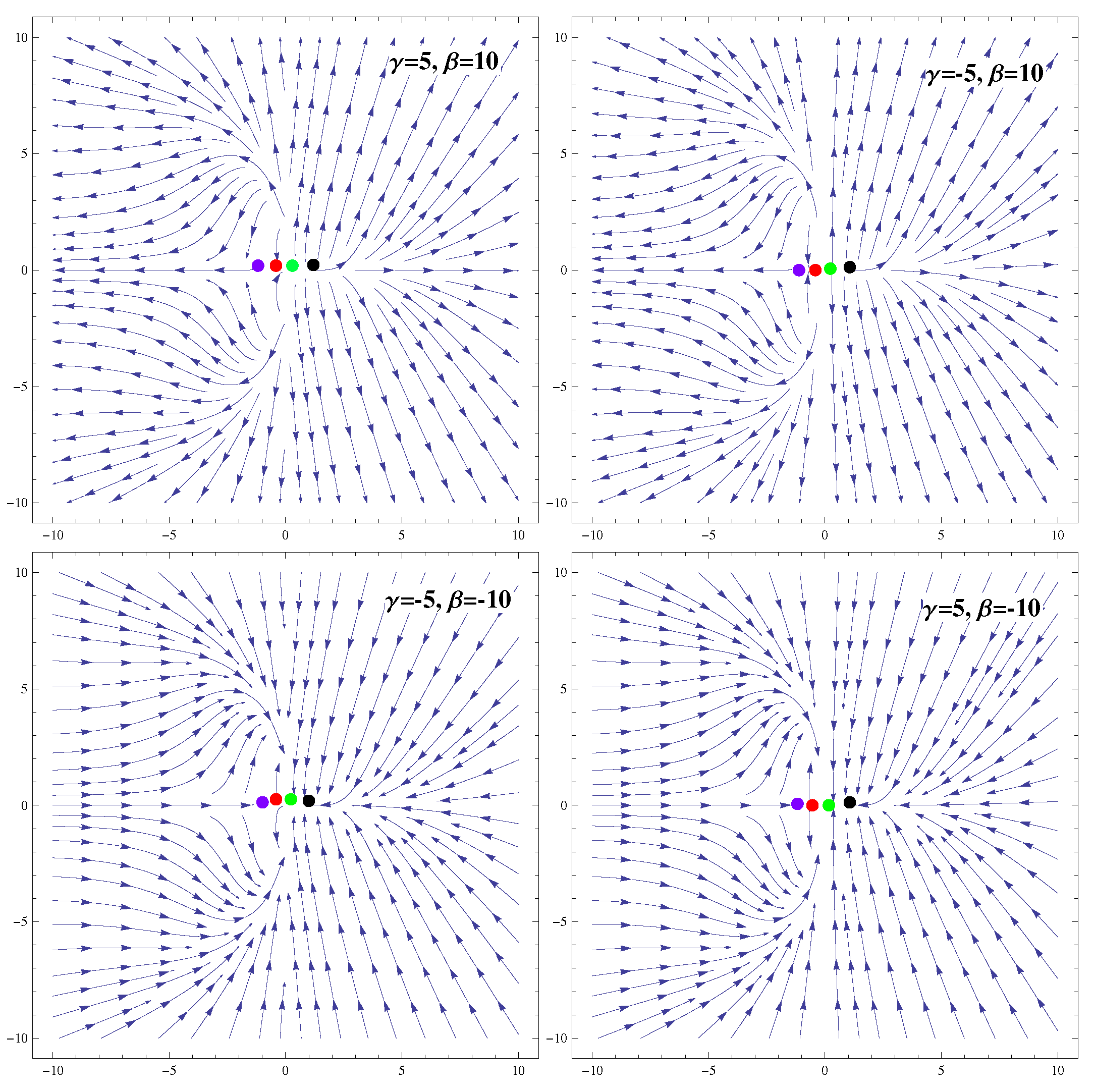

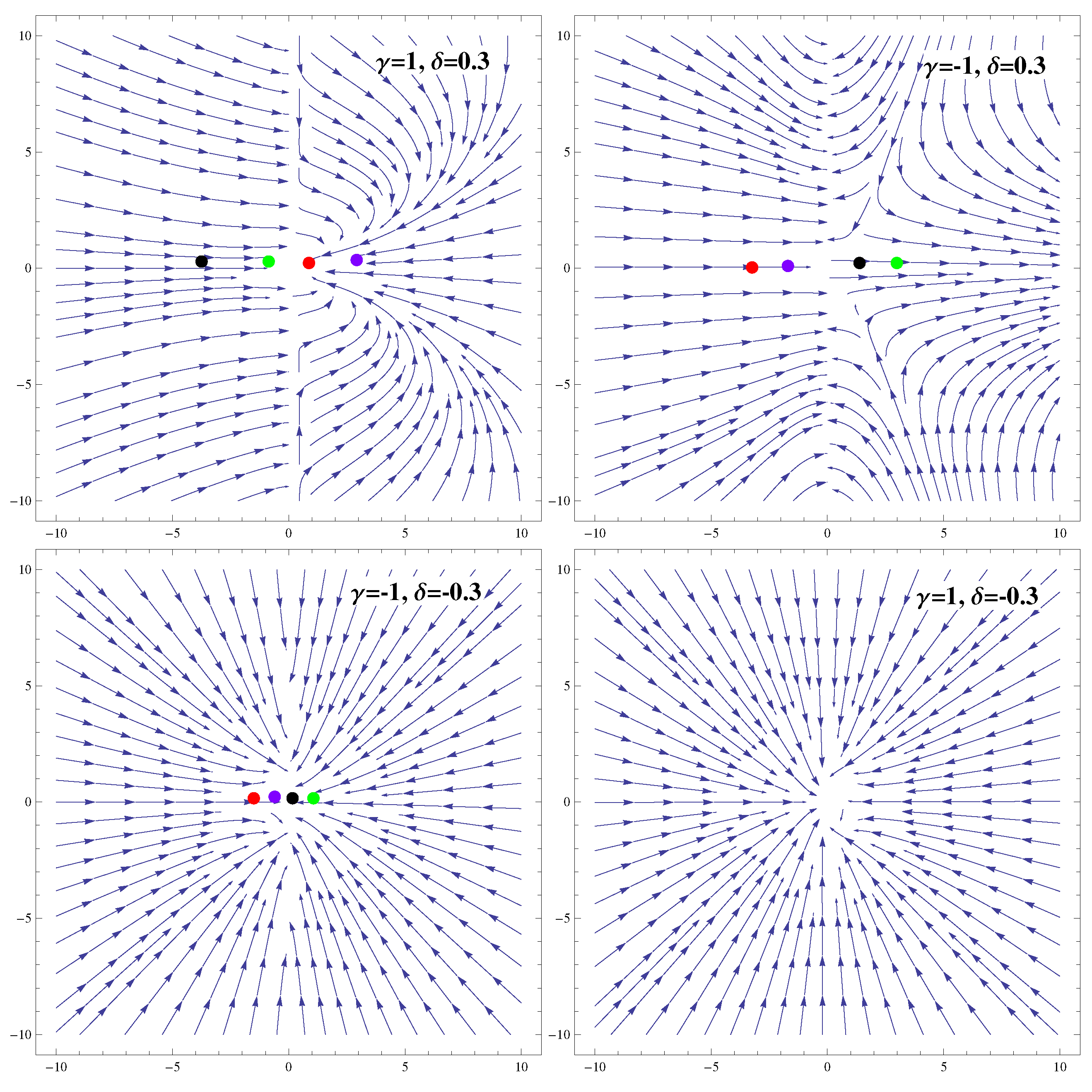
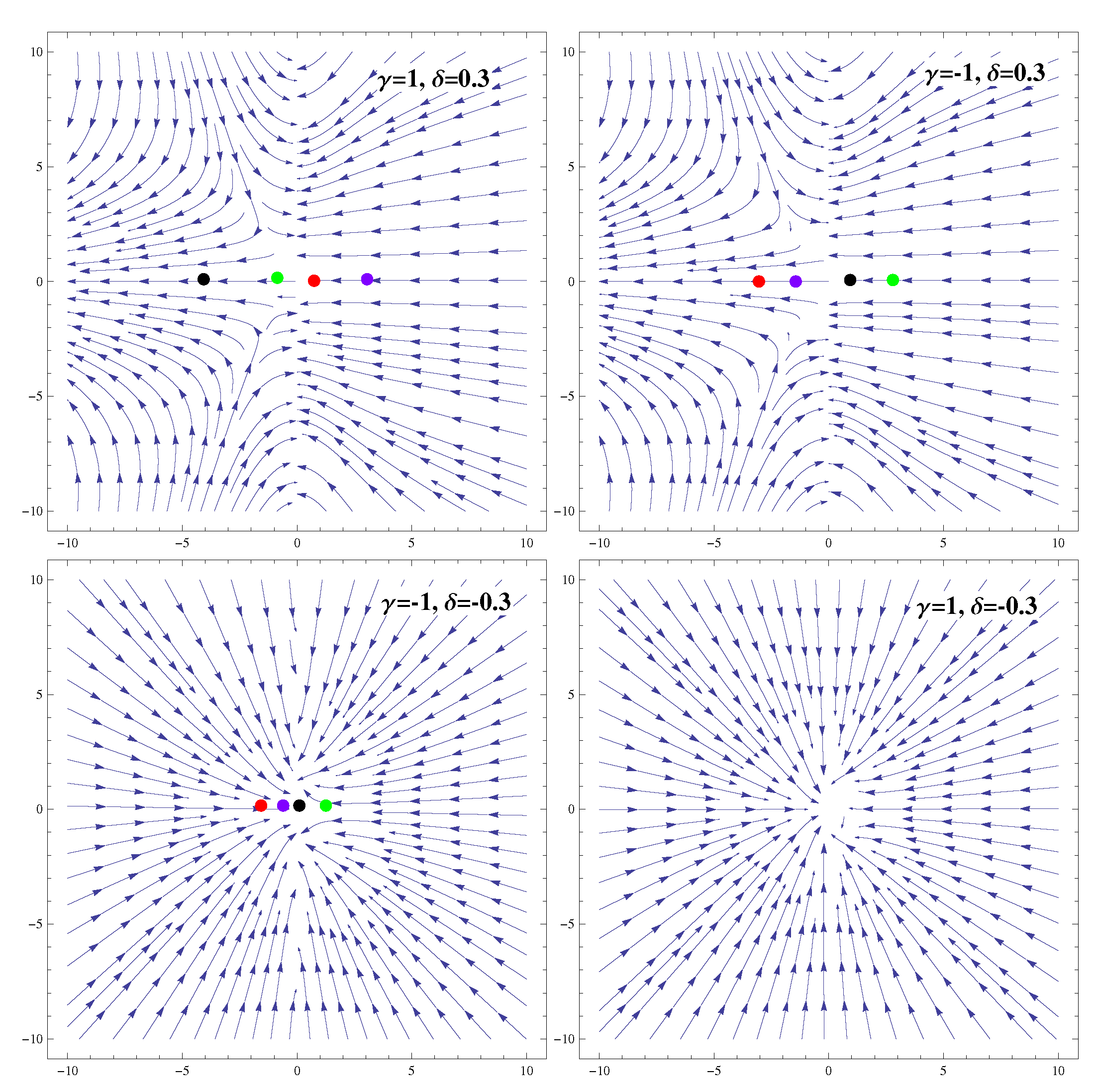
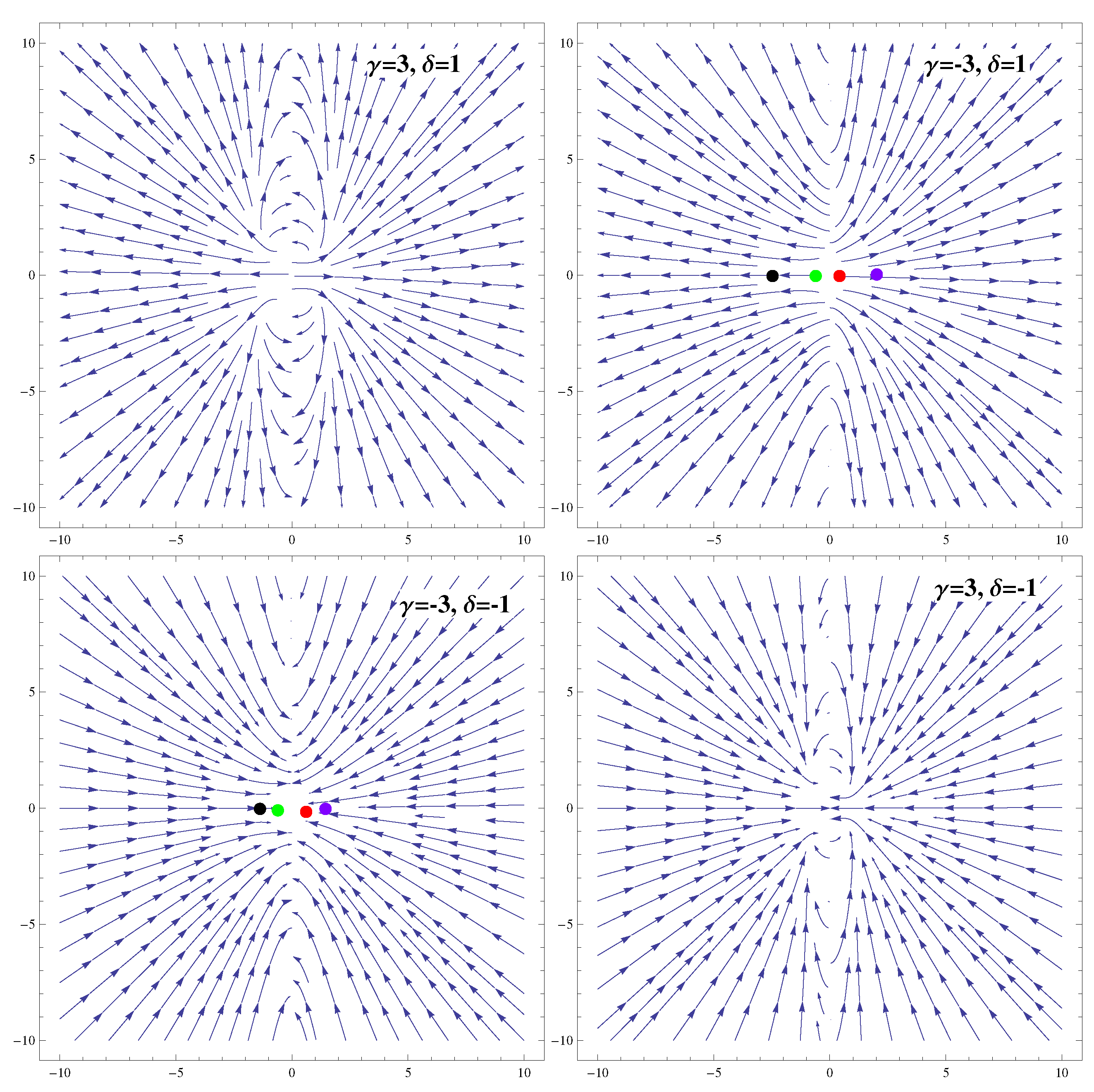

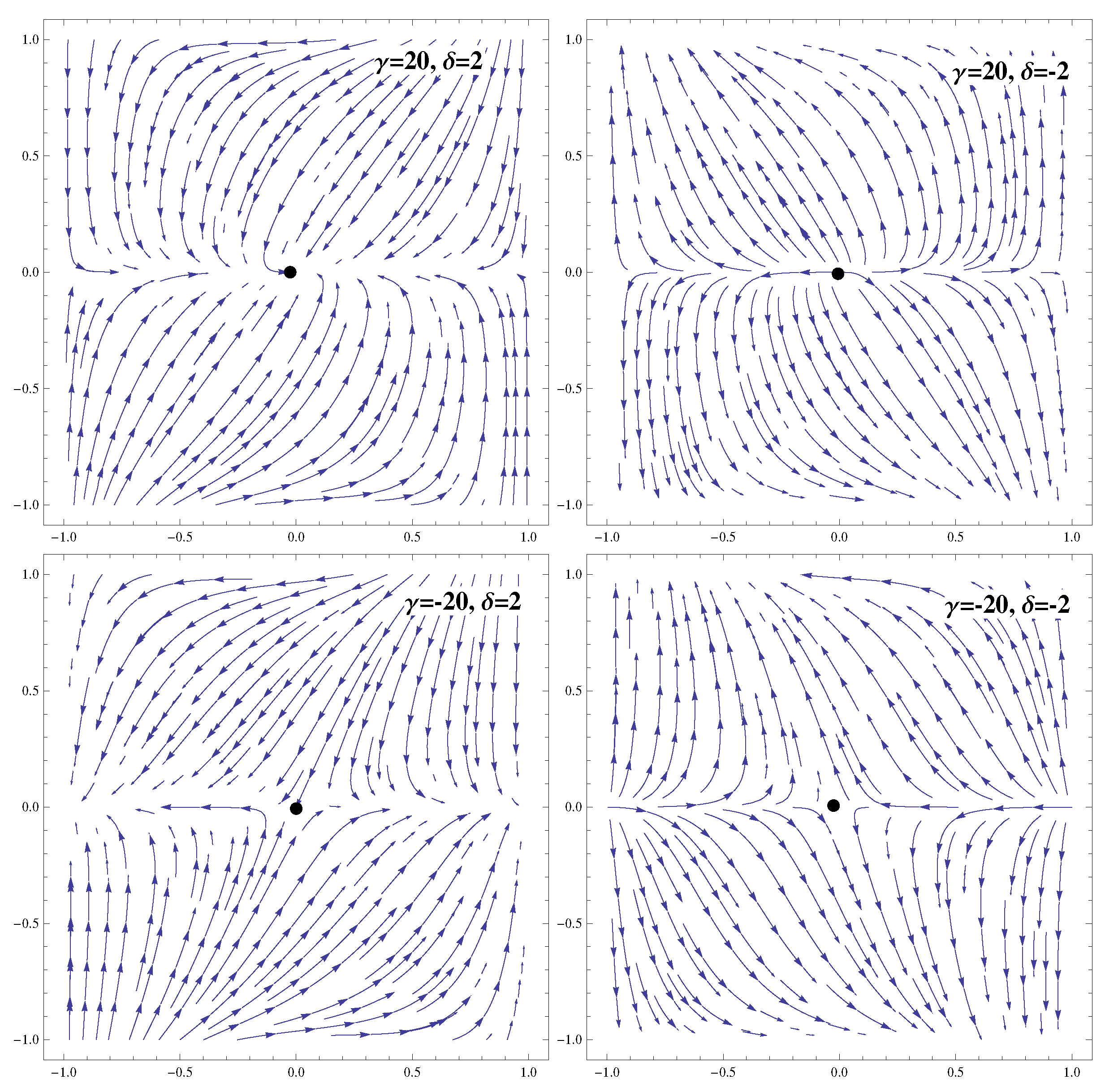
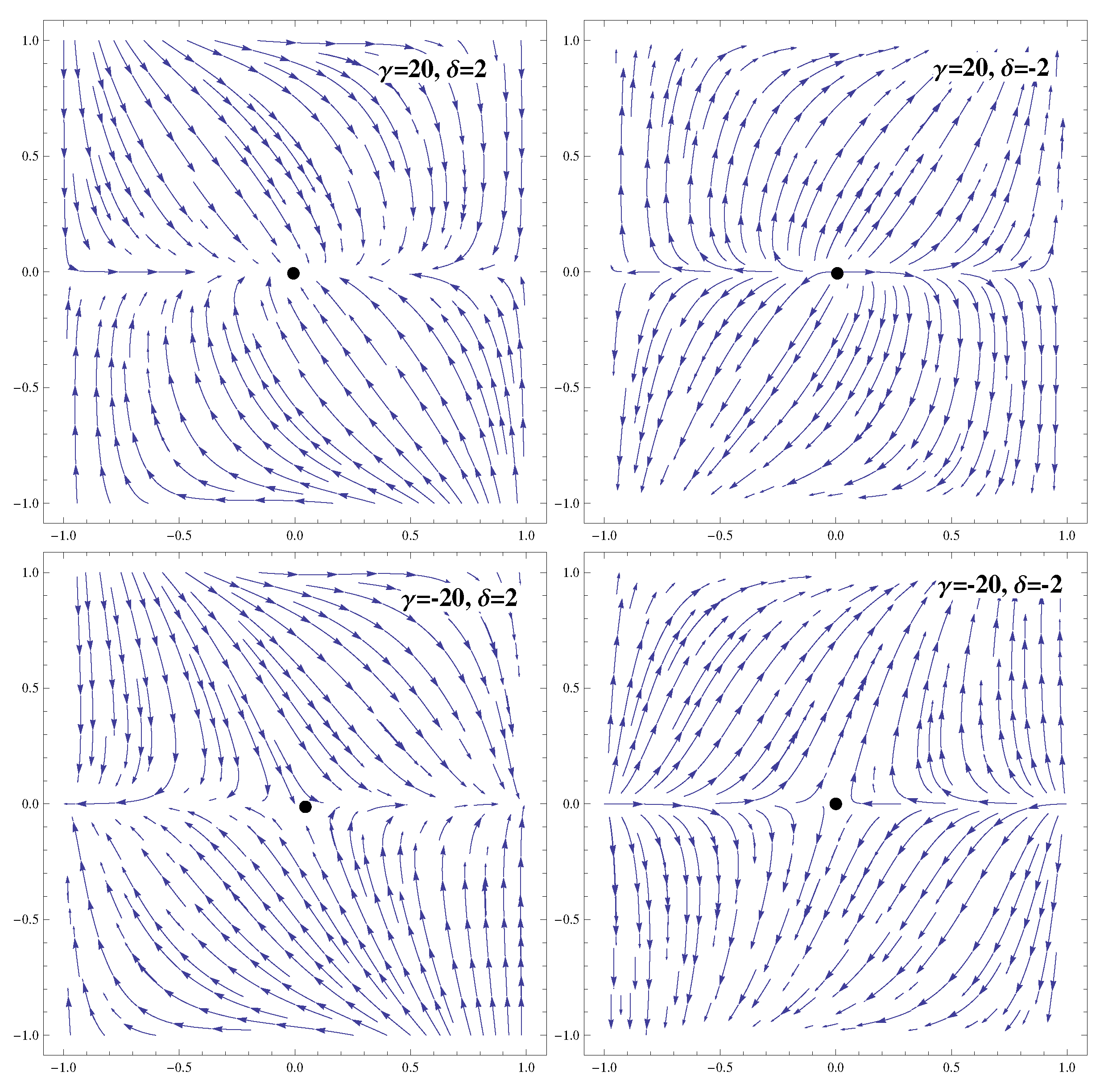
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| unstable | Yes | |
| stable | Yes | |
| stable | Yes | |
| unstable | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | Yes | |
| unstable | Yes | |
| stable | No | |
| stable | No | |
| unstable | Yes | |
| stable | Yes | |
| unstable | No | |
| unstable | No | |
| stable | Yes | |
| For, | ||
| unstable | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | Yes | |
| unstable | Yes | |
| stable | Yes | |
| stable | Yes | |
| unstable | Yes | |
| stable | Yes | |
| unstable | No | |
| unstable | No | |
| stable | Yes | |
| unstable | Yes | |
| stable | No | |
| stable | No | |
| unstable | Yes |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| stable | Yes | |
| stable if | No | |
| stable if | Yes | |
| stable for | - | |
| stable | Yes | |
| unstable for | No | |
| saddle for | ||
| saddle | Yes | |
| stable | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - | |
| For, | ||
| stable | Yes | |
| unstable for | No | |
| saddle for | ||
| saddle | Yes | |
| stable for , | - | |
| saddle for | ||
| stable | Yes | |
| stable for , | No | |
| stable | Yes | |
| stable | - | |
| saddle | Yes | |
| stable for , | Yes | |
| unstable for | ||
| unstable | No | |
| stable for | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| stable | - | |
| stable for , | Yes | |
| saddle/unstable | No | |
| stable | - | |
| stable | - | |
| saddle/unstable | Yes | |
| saddle/unstable | No | |
| stable | - | |
| unstable | - | |
| saddle/unstable | No | |
| saddle | Yes | |
| stable for , | - | |
| saddle | - | |
| stable | No | |
| stable | Yes | |
| stable for | - | |
| For, | ||
| stable | - | |
| stable/saddle | Yes | |
| saddle | No | |
| stable | - | |
| stable | - | |
| stable | Yes | |
| saddle/unstable | No | |
| stable | - | |
| saddle | - | |
| stable for , | No | |
| stable | Yes | |
| stable for , | - | |
| unstable | - | |
| saddle/unstable | No | |
| saddle | Yes | |
| stable/saddle | - |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| saddle | Yes for | |
| saddle/unstable for | No | |
| unstable | No | |
| saddle for , | Yes for | |
| stable for |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharif, M.; Ama-Tul-Mughani, Q. Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe 2019, 5, 185. https://doi.org/10.3390/universe5080185
Sharif M, Ama-Tul-Mughani Q. Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe. 2019; 5(8):185. https://doi.org/10.3390/universe5080185
Chicago/Turabian StyleSharif, Muhammad, and Qanitah Ama-Tul-Mughani. 2019. "Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe" Universe 5, no. 8: 185. https://doi.org/10.3390/universe5080185
APA StyleSharif, M., & Ama-Tul-Mughani, Q. (2019). Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe, 5(8), 185. https://doi.org/10.3390/universe5080185






