1. Introduction
The basic objective of theories of quantum gravity is to calculate transition amplitudes between configurations of the gravitational field. The most straightforward approach to the problem is provided by the Feynman’s path integral
where
and
are the gravitational and matter actions respectively. While the formula (
1) is easy to write, it is not very practical for the case of continuous gravitational field, characterized by infinite number of degrees of freedom. One of the approaches to determine (
1) utilizes discretization of the gravitational field associated with some cut-off scale. The expectation is that continuous limit of such discretized theory can be recovered at the second order phase transition [
1,
2]. The essential step in this challenge is to generate different discrete space-time configurations (triangulations) contributing to the path integral (
1). In Causal Dynamical Triangulations (CDT) [
1] which is one of the approaches to the problem, Markov chain of elementary moves is used to explore different triangulations between initial and final state. In practice, the Markov chain is implemented after performing Wick rotation in Equation (
1). In the last 20 years, the procedure has been extensively studied running computer simulations [
3]. However, in 1+1 D case analytical methods of generating allowed triangulations are also available. In particular, it has been shown that Feynman diagrams of auxiliary random matrix theories generate graphs dual to the triangulations [
4]. An advantage of the method is that in the large
N (color) limit of such theories, symmetry factors associated with given triangulations can be recovered [
5].
Another path to the problem of determining (
1) is provided by the Loop Quantum Gravity (LQG) [
6,
7] approach to the Planck scale physics. Here, discreteness of space is not due to the applied by hand cut-off but is a consequence of the procedure of quantization. Accordingly, the spatial configuration of the gravitational is encoded in the so-called
spin network states [
8]. In consequence, the transition amplitude (
1) is calculated between two spin network states. The geometric structures (2-complexes) representing the path integral are called
Spin Foams [
9,
10]. The elementary processes contributing to the spin foam amplitudes are associated with vertices of the spin foams and are called
vertex amplitudes [
11,
12]. The employed terminology of spin networks and spin foams is clarified in
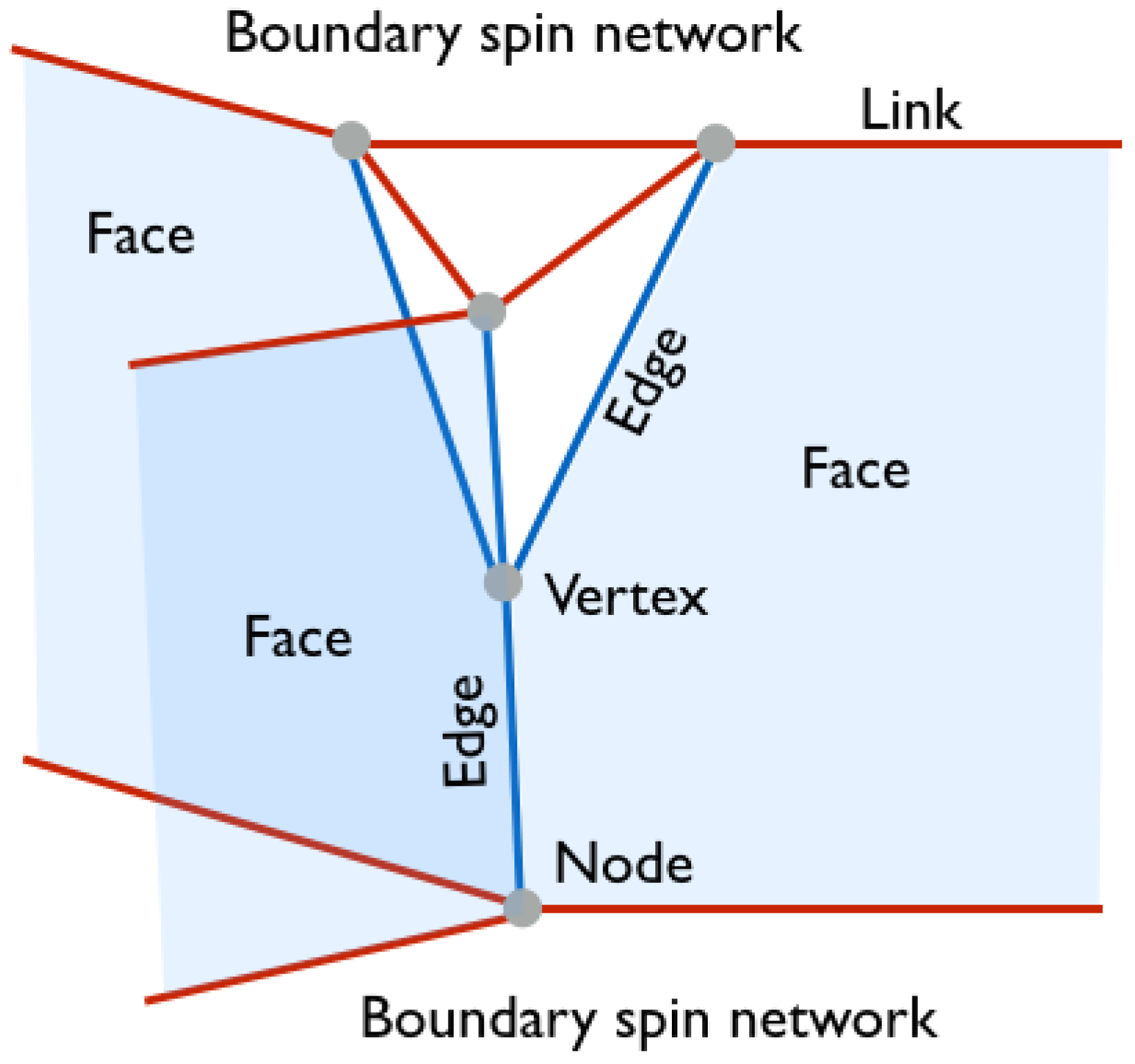
Figure 1 in an example of 2+1 D gravity.
In
Figure 1 two boundary spin networks with 3-valent nodes are shown. Such nodes are dual to two-dimensional triangles. In this article we will focus on the 3+1 D case in which the spin network nodes (related with non-vanishing volumes) are 4-valent. The nodes are dual to tetrahedra (3-simplex). In the example presented in
Figure 1, the four edges of the 2-complex meet at the vertex. However, in the 3+1 D case the valence of the vertex is higher and equal to 5. For the purpose of this article it is crucial to note that such 5-valent vertices can be enclosed by a boundary represented by a spin network containing five nodes. Each of the nodes is placed on one of the five edges entering the vertex. The boundary has topology of a three-sphere,
. This is higher dimensional extension of the 2+1 D case, where a vertex can be enclosed by the two-sphere,
.
In analogy to the random matrix theories in case of the 2D triangulations, the spin foams (2-complexes) can also be obtained as Feynman diagrams of some auxiliary field theory. Namely, the so-called Group Field Theories (GFTs) have been introduced to generate structure of vertices and edges associated with spin foams [
13,
14,
15]. In particular, the 3+1 D theory with 5-valent vertices requires GFT with five-order interaction terms, known as Ooguri’s model [
16]. There has recently been great progress in the field of GFTs with many interesting results (see e.g., [
17,
18]).
The aim of this article is to investigate a possibility of employing universal quantum computers to compute vertex amplitudes of 3+1 D spin foams. The idea has been suggested in Ref. [
19], however, it is not investigated there. Here, we make the first attempt to materialize this concept. In our studies, we consider a special case of spin networks with spin labels corresponding to fundamental representations of the
group, for which
intertwiner qubits [
19,
20,
21] can be introduced. The qubits will be implemented on IBM Q 5-qubit quantum computer (
ibmqx4) as well as with the use of quantum computer simulator provided by the same company [
22]. In the case of real 5-qubit quantum computer the qubits are physically realized as superconducting circuits [
23] operating at millikelvin temperatures. Furthermore, the QX quantum computer simulator [
24], available on the Quantum Inspire [
25] platform, will be employed.
The studies contribute to our broader research program focused on exploring the possibility of simulating Planck scale physics with the use of quantum computers. The research is in the spirit of the original Feynman’s idea [
26] of performing the so-called
exact simulations of quantum systems with the use of quantum information processing devices. In our previous articles [
21,
27] we have preliminary explored the possibility of utilizing Adiabatic Quantum Computers [
28] to simulate quantum gravitational systems. Here, we are making the first steps towards the application of Universal Quantum Computers [
29,
30].
2. Intertwiner Qubit
The basic question a skeptic can ask is why it is worth considering quantum computers to study Planck scale physics at all? Can we not just do it employing classical supercomputers as in the case of CDT approach to quantum gravity? Let me answer these questions by giving two arguments. The first concerns the huge dimensionality of a Hilbert space for many-body quantum system. For a single spin-1/2 (qubit) Hilbert space
the dimension is equal to 2. However, considering
N such spins (qubits) the resulting Hilbert space is a tensor product of N copies of the qubit Hilbert space. The dimension of such space grows exponentially with N:
This exponential behavior is the main obstacle behind simulating quantum systems on classical computers. With the present most powerful classical supercomputers we can simulate quantum systems with
at most [
31]. The difficulty is due to the fact that quantum operators acting on
dimensional Hilbert space are represented by
matrices. Operating with such matrices for
is challenging to the currently available supercomputers. On the other hand, such companies as IBM or Rigetti Computing are developing quantum chips with
and certain topologies of couplings between the qubits. The possibility of simulating quantum systems which are unattainable to classical supercomputers may, therefore, emerge in the coming decade leading to the so-called
quantum supremacy [
32]. See
Appendix A for more detailed discussion of the state of the art of the quantum computing technologies and prospects for the near future. The second argument concerns
quantum speed-up leading to reduction of computational complexity of some classical problems. Such possibility is provided by certain quantum algorithms (e.g., Deutsch, Grover, Shor, …) thanks to the so-called
quantum parallelism. For more information on quantum algorithms please see
Appendix B, where elementary introduction to quantum computing can be found.
Taking the above arguments into account we are convinced that it is justified to explore the possibility of simulating quantum gravitational physics on quantum computers. The fundamental question is, however, whether gravitational degrees of freedom can be expressed with qubits, which are used in the current implementations of quantum computers
1. Fortunately, it has recently been shown that at least in Loop Quantum Gravity approach to quantum gravity notion of qubit degrees of freedom can be introduced and is associated with the intertwiner space of a certain class of spin networks (see Refs. [
19,
20,
21,
27]).
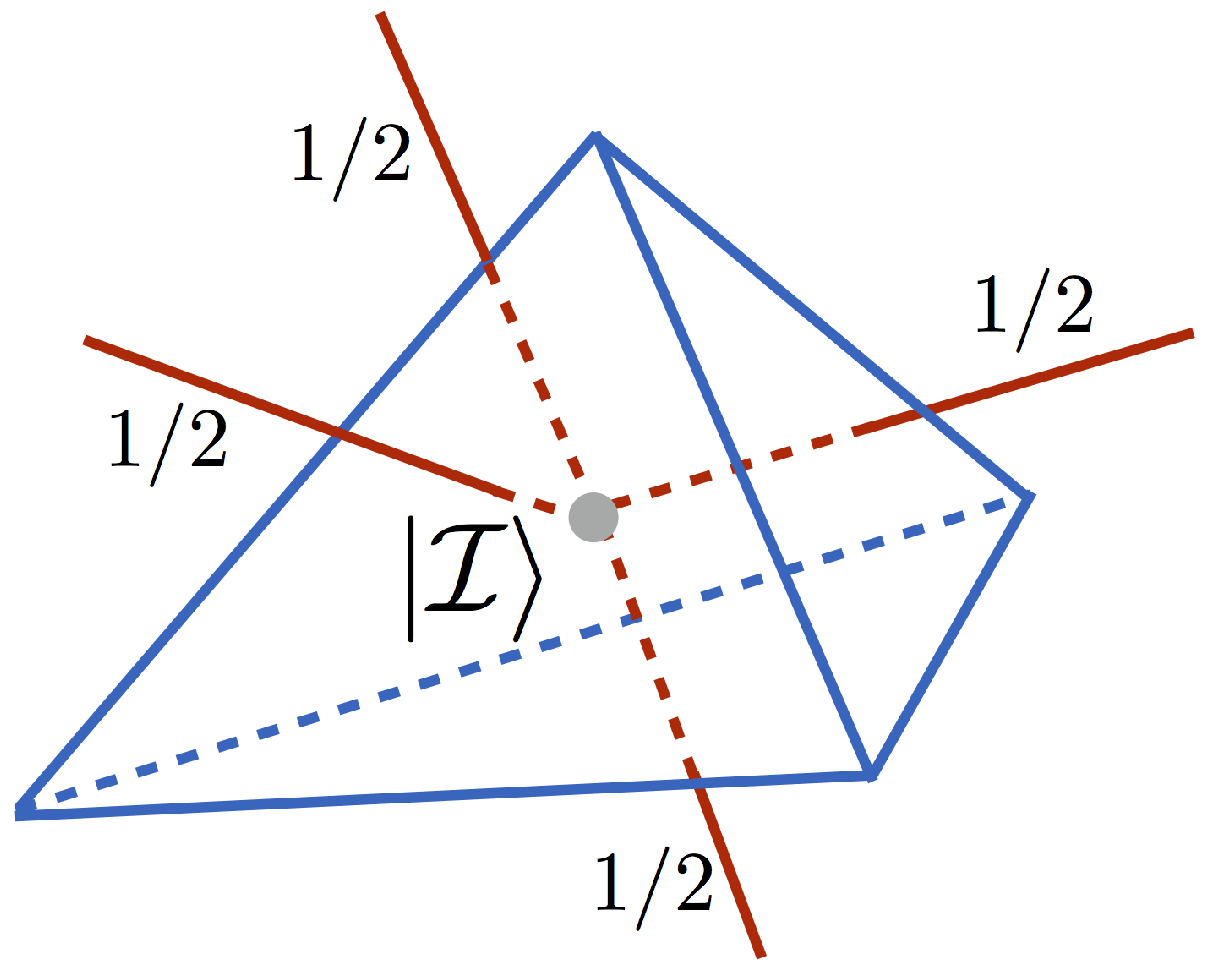
Let us briefly explain it. Namely, nodes of the spin networks are where Hilbert spaces associated with the links meet. The gauge invariance (enforced by the Gauss constraint) implies that the total spin at the node has to be equal zero. The 4-valent nodes are of special interest since they are associated with the non-vanishing eigenvalues of the volume operator (see e.g., Ref. [
7]). As already mentioned in the introduction, in the picture of discrete geometry, the 4-valent nodes are dual to tetrahedra. The class of spin networks that we are focused on here are those with links of the spin networks labelled by fundamental representations of the
group (i.e., the spin labels are equal
) and the nodes are 4-valent. For such spin networks the Hilbert spaces at the nodes are given by the following tensor products:
The Gauss constraint implies that only singlet configurations (
) are allowed. Because there are two copies of the spin-zero configurations in the tensor product (
3), the so-called intertwiner Hilbert space is two-dimensional:
We associate the two-dimensional invariant subspace with the
intertwiner qubit . The 4-valent node (at which the intertwiner qubit is defined) together with the entering links is dual to the tetrahedron in a way shown in
Figure 2.
The two basis states of the intertwiner qubit
are basically the two singlets we can obtain for a system of four spins
. The basis states can be expressed composing familiar singlets and triplet states for two spin-1/2 particles:
Namely, in the
s-channel (which is one of the possible superpositions) the intertwiner qubit basis states can be expressed as follows:
The
state is simply a tensor product of two singlets for two spin-1/2 particles, while the state
does not have such a simple product structure. The states
and
form an orthonormal basis of the intertwiner qubit. Worth stressing is that other bases being linear superpositions of
and
might be considered. In particular, the eigenbasis of the volume operator turns out to be useful (see Ref. [
27]). Here we stick to the
s-channel basis
in which a general intertwiner state (neglecting the total phase) can be expressed as
where
and
are angles parametrizing the Bloch sphere.
In the context of quantum computations it is crucial to define a quantum algorithm (a unitary operation
acting on the input state) which will allow us to create the intertwiner state (
11) from the input state
, i.e.,
The general construction of the operator
can be performed applying the procedure introduced in Ref. [
33], and will be discussed in a sequel to this article [
34]. Here, for the purpose of illustration of the method of computing vertex amplitude we will focus on the special case of the intertwiner states being the first basis state:
. The contributing two-particle singlet states can easily be generated as a sequence of elementary gates used to construct quantum circuits (see also
Appendix B):
Here, the
is the so-called
bit-flip (NOT) operator (Pauli
matrix) which transforms
into
and
into
(i.e.,
and
). The
is the Hadamard operator defined as
and
. Finally, the
is the Controlled NOT 2-qubit gate defined as
, where
and ⊕ is the XOR (exclusive or) logical operation, such that
,
,
and
. In consequence, the
basis state can be expressed as follows:
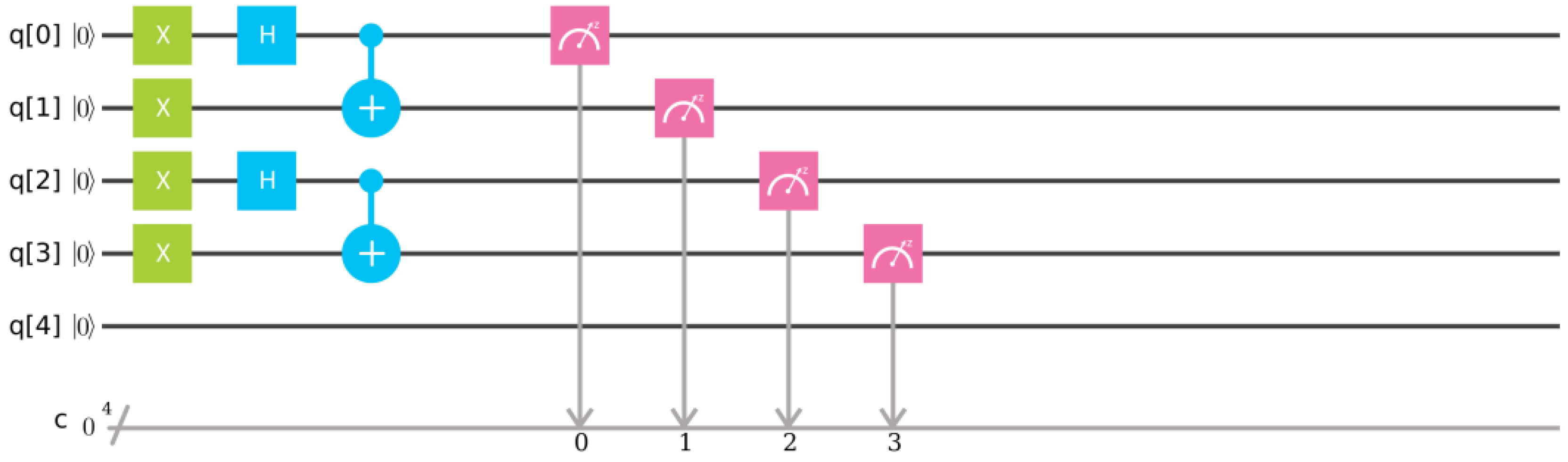
In
Figure 3 a quantum circuit generating (and measuring) the intertwiner state
has been presented.
The final state can be written as a superposition of 16 basis states in the product space of four qubit Hilbert spaces:
where the normalization condition implies that
.
We have executed the quantum algorithm (
14) with the use of both the IBM simulator of quantum computer and the real IBM Q 5-qubit quantum chip ibmqx4. In both cases the algorithm has been executed 1024 times. Moreover, the algorithm (
14) has also been executed (1024 times) on the QX quantum computer simulator. Results of the measurements of probabilities
are summarized in
Table 1.
Clearly, the results obtained from the simulator match well with the values predicted in Equation (
14). By increasing the number of shots, the accuracy of the results can be improved. In fact, because the number of shots in a single round was limited (either to 8192 in the case of the IBM simulator or to 1024 in the case of the QX simulator) the computational rounds had to be repeated in order to achieve better convergence to theoretical predictions. Furthermore, the results were also verified with the use of two other publicly available quantum simulators of quantum circuits, i.e., Quirk [
35] and Q-Kit [
36].
On the other hand, the errors of the
ibmqx4 quantum processor are more significant, leading even to
contribution from the undesired states, such as
and
. The errors have two main sources. The first are instrumental errors associated with uncertainty of gates, uncertainty of initial state preparation and uncertainty of readouts. For the IBM Q
ibmqx4 quantum processor the single-qubit gate errors are at the level of
and the errors of readouts are reaching even
for some of the qubits. The two-qubit gates are less accurate than the single quibit gates, with the errors approximately equal to
. The concrete values for every qubit and pairs of qubits are provided via the IBM website [
22]. The second source of error is due to statistical nature of quantum mechanics and the limited number of measurements. For a single qubit, the problem of estimating corresponding error is equivalent to the 1D random walk, which leads to uncertainty of the estimation of probability equal
, where
n is the number of measurements and
p is a probability of one of the two basis states. As an example, for
and
we obtain
. In the considered case of 16 basis states the uncertainty is expected to be lower roughly by the factor
2, leading to an approximate error equal
(the value is smaller because the average number of counts per basis states decreased). Summing up both the instrumental error and the uncertainty of measurement, we may estimate the cumulative uncertainty to be at the level of ∼15%, which is in agreement with the experimental data. With the current setup, the errors can be slightly reduced by increasing the number of measurements and by optimization of the quantum circuit, e.g., by placing (less noisy) single-qubit gates after (more noisy) two-qubit gates. In further studies, the circuits should also be equipped with quantum error correction algorithms. This will, however, require additional qubits to be involved. Moreover, reduction of the instrumental error will be a crucial challenge for the future utility of the quantum processors.
Let us end this section with quantitative comparison of the results from the
Table 1 with the use of classical Fidelity (Bhattacharyya distance)
, where
and
are two sets of probabilities. Comparison of the theoretical values with the results obtained from the IBM Simulator gives us
. However, comparing the theoretical values with the results of IBM Q ibmqx4 quantum computer we find much smaller Fidelity
. Worth keeping in mind is that the employed Fidelity function concerns classical probabilities and further analysis of the quantum state obtained from the quantum computer should include also analysis of the quantum Fidelity
, where
and
are density matrices of the compared states [
37]. For this purpose (i.e., reconstruction of the density matrix), full tomography of the obtained quantum state has to be performed.
3. Vertex Amplitude
Gravity is a theory of constraints. Specifically, in LQG three types of constraints are involved. The first is the mentioned Gauss constraint, which has already been imposed at the stage of constructing spin networks states. The second is the spatial diffeomorphism constraint which is satisfied by introducing equivalence relation between all spin-networks characterized by the same topology. The third is the so-called scalar or Hamiltonian constraint, which encodes temporal dynamics and is the most difficult to satisfy. In quantum theory, this constraint takes a form of an operator. Let us denote this operator as
. Following the Dirac procedure for constrained quantum systems, the physical states are those belonging to the kernel of the constraints, i.e.,
. Due to the complicated form of the gravitational scalar constraint (see e.g., [
6]), finding the physical states is in general a difficult task. However, for certain simplified scalar constraints, such as for the symmetry reduced cosmological models, the physical states are possible to extract. Furthermore, it has recently been proposed in Ref. [
21] that the problem of solving simple constraints can be implemented on Adiabatic Quantum Computers.
Another approach to the problem of constraints is to consider a projection operator
which projects kinematical states onto physical subspace. In particular, the Formula (
16) is valid for
characterized by discrete spectrum of eigenvalues. Specifically, the projection operator (
16) can be used to evaluate transition amplitude between any two kinematical states
and
:
The state
might correspond to the initial and
to the final boundary spin network states (confront with
Figure 1). While the notion of the boundary initial and final hypersurfaces is well defined in the case with preferred time foliation, the general relativistic case deserves generalization of the transition amplitude to the form being independent of the background time variable. This leads to the concept of
boundary formulation [
38] of transition amplitudes in which the transition amplitude is a function of boundary state only. Taking the particular boundary physical spin network state
the transition amplitude can be, therefore, written as
where the state
corresponds to representation in which the amplitude is evaluated. Worth stressing at this point is that physical interpretation of the transition amplitude (
18) is still under debate. In particular, very little is known about relation of the amplitude with the physical states of the theory under consideration.
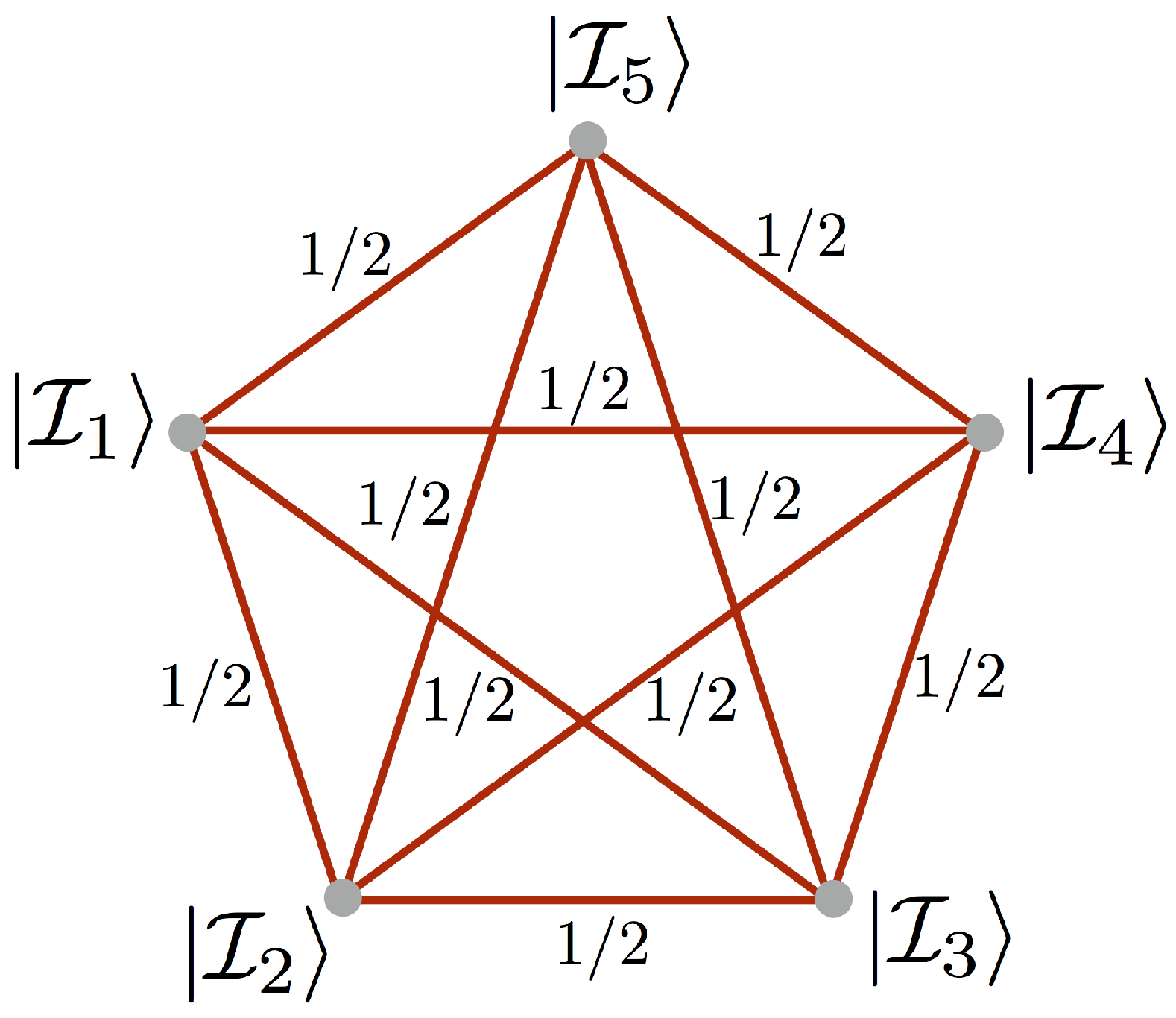
The object of our interest in this article, namely the vertex amplitude, is the amplitude (
18) of boundary enclosing a single vertex. As we have already explained in the introduction, the spin network enclosing the single vertex has pentagram structure and can be written as:
The associated spin network is shown in
Figure 4.
The pentagram spin network state is a tensor product of the five intertwiner qubits:
Since in the vertex amplitude (
18) physical states have to be considered the intertwiner qubits
have to be selected such that the state is annihilated by the scalar constraint:
. Due to the difficulty of the issue for general form of the scalar constraint operator, we do not address the problem of selecting
states here. As we have mentioned, for either symmetry reduced or simplified scalar constraints the physical states can be identified with the use of existing methods.
Another issue is the choice of the state
. Usually the representation of holonomies associated with the links of the spin networks are considered. Here, following Ref. [
19] we will evaluate the boundary spin network state in the state:
where
are Bell states associated with the links. This choice is interesting since the Bell states introduce entanglement between faces of the adjacent tetrahedra. Such a way of “gluing” tetrahedra by quantum entanglement has been recently studied in Ref. [
39], where it was shown that the
state is a superposition of spin network states (with
symbols as coefficients of the decomposition). Since the spin network state
is disentangled one can also interpret
as an amplitude of transition between disentangled and maximally entangled piece of quantum geometry. Going further, possibly the quantum entanglement is the key ingredient which merges the chunks of space associated with the nodes of spin networks into a geometric structure. This reasoning is consistent with the recent advances in the domain of entanglement/gravity duality, an example of which is provided by the AdS/CFT correspondence [
40], ER = EPR conjecture [
41] and considerations of holographic entanglement entropy [
42,
43,
44]. Interestingly, it has recently been argued that indeed the spin networks may represent structure of quantum entanglement [
45], indicating relation between spin networks and tensor networks [
46]. This is actually not very surprising since the holonomies associated with links of the spin-networks can be interpreted as “mediators” of entanglement.
Namely, the holonomies are maps between two vector (Hilbert) spaces at the ends of a curve
, where the affine parameter
. Let us denote the initial point as
and the final one as
. Then, holonomy
is a map between two Hilbert spaces
and
associated with two (in general) different spatial locations:
In the case considered in this article, the Hilbert spaces are related with the elementary qubits
“living” at the ends of the links of the spin-networks (keep in mind that these are not the intertwiner qubits but the elementary qubits out of which the intertwiner qubits are built). As an example of the holonomy of the Ashtekar connection
considered in LQG (i.e.,
, see e.g., Ref. [
6]) let us consider
where
is an angle variable and
is the Pauli matrix. The holonomies as the one given by Equation (
24) are associated with homogeneous models and are considered in Loop Quantum Cosmology [
47] and Spinfoam Cosmology [
48,
49]. The special case is when
for which
, which written as an operator
where
is the bit-flip operator introduced earlier. Therefore, having, e.g., the elementary qubit
at point
a, the operator (
25) maps this state into
at the point
b3. This introduces a relation between the quantum states at distant points
a and
b, which possibly can be associated with entanglement. However, the issue of relation between holonomies and entanglement requires further more detailed studies, also in the spirit of the recent proposal of
Entanglement holonomies [
50].
4. A Quantum Algorithm
Having the vertex amplitude (
19) defined we may proceed to the task of determining
with the use of quantum computers. Here, we will show how to obtain amplitude modulus square (the probability), while extraction of the phase factor will be a subject of our further investigations.
Let us begin with preparation of a suitable quantum register. Because each of the intertwiner qubits is a superposition of four elementary qubits, evaluation of the spin network with
N nodes requires
qubits in the quantum register
4. The corresponding Hilbert space is spanned by
basis states
, where
. The initial state for the quantum algorithm is:
Now, we have to find unitary operators
and
defined such that
where
is given by Equation (
26). Utilizing the operators
and
we introduce an operator
. Action of this operator on the initial state (
26) can be expressed as a superposition of the basis states with some amplitudes
:
It is now easy to show that the
coefficient in this superposition is the transition amplitude we are looking for. Namely:
By performing measurements on the final state we find the probabilities . The first of these probabilities is the modulus square of the vertex amplitude.
Before we will proceed to the discussion of the pentagram spin network associated with the vertex amplitude, let us first demonstrate the algorithm on two simpler examples of spin networks with one and two nodes.
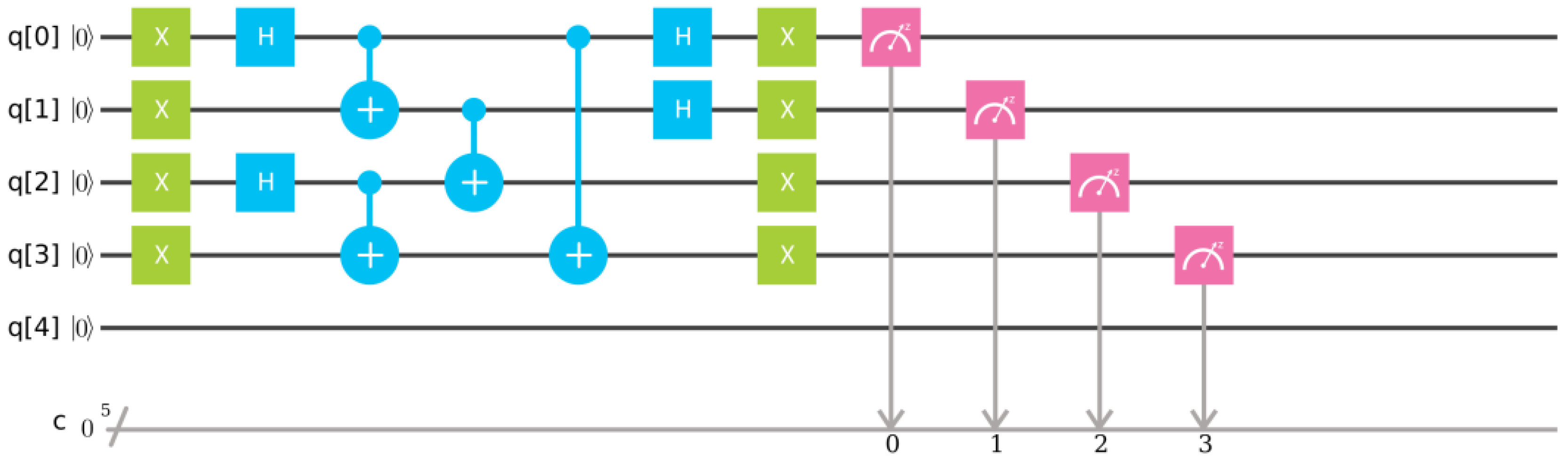
4.1. Example 1—Single Tetrahedron
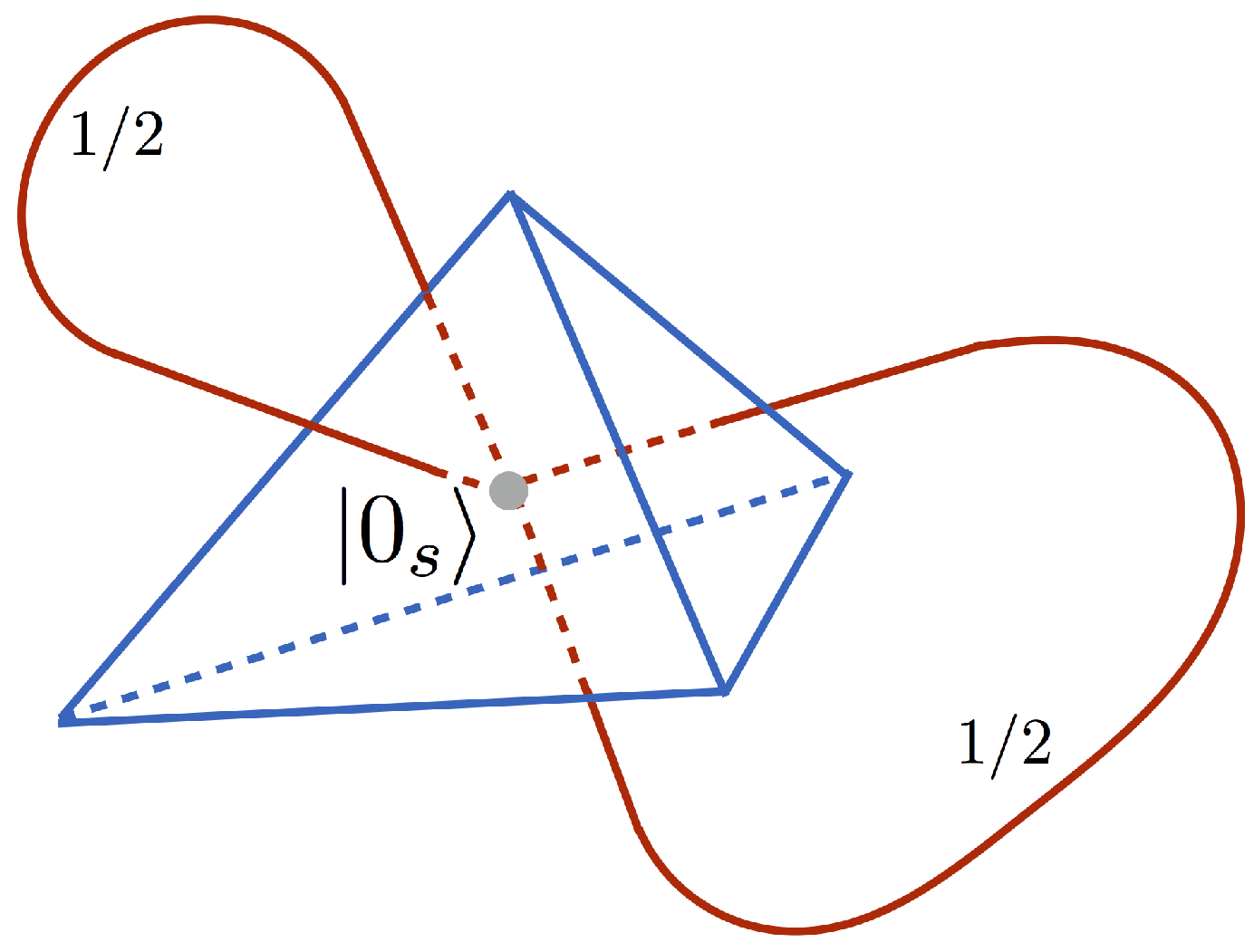
As a first example let us consider the case of a single-node spin network presented in
Figure 5.
Here, the intertwiner qubit is in the
state composed out of the four elementary qubits according to Equation (
14). The representation state
is a tensor product of two Bell states (
22). There are basically two different choices of pairing faces of the tetrahedron. The first choice is according to the pairing of qubits entering to the two-qubit singlets
out of which the
state is built. The second choice is by linking qubits contributing to the two different singlets. The first choice is trivial since in that case
and in consequence the amplitude
. Therefore, we will consider the second case for which the quantum circuit associated with the
operator is presented in
Figure 6.
The simulations were performed on both the IBM simulator and the QX simulator, with 1024 shots in each computational round. The rounds have been repeated 10 times. The results obtained are collected in
Table 2.
Averaging over the 10 rounds, the following values of modulus square of the amplitudes are obtained:
The results are consistent with the theoretically expected value . Finally, worth mentioning is that the algorithm cannot directly be executed using the IBM Q 5-qubit quantum chip due to the topological constraints of the structure of coupling between qubits. Additional ancilla qubits have to be involved for this purpose.
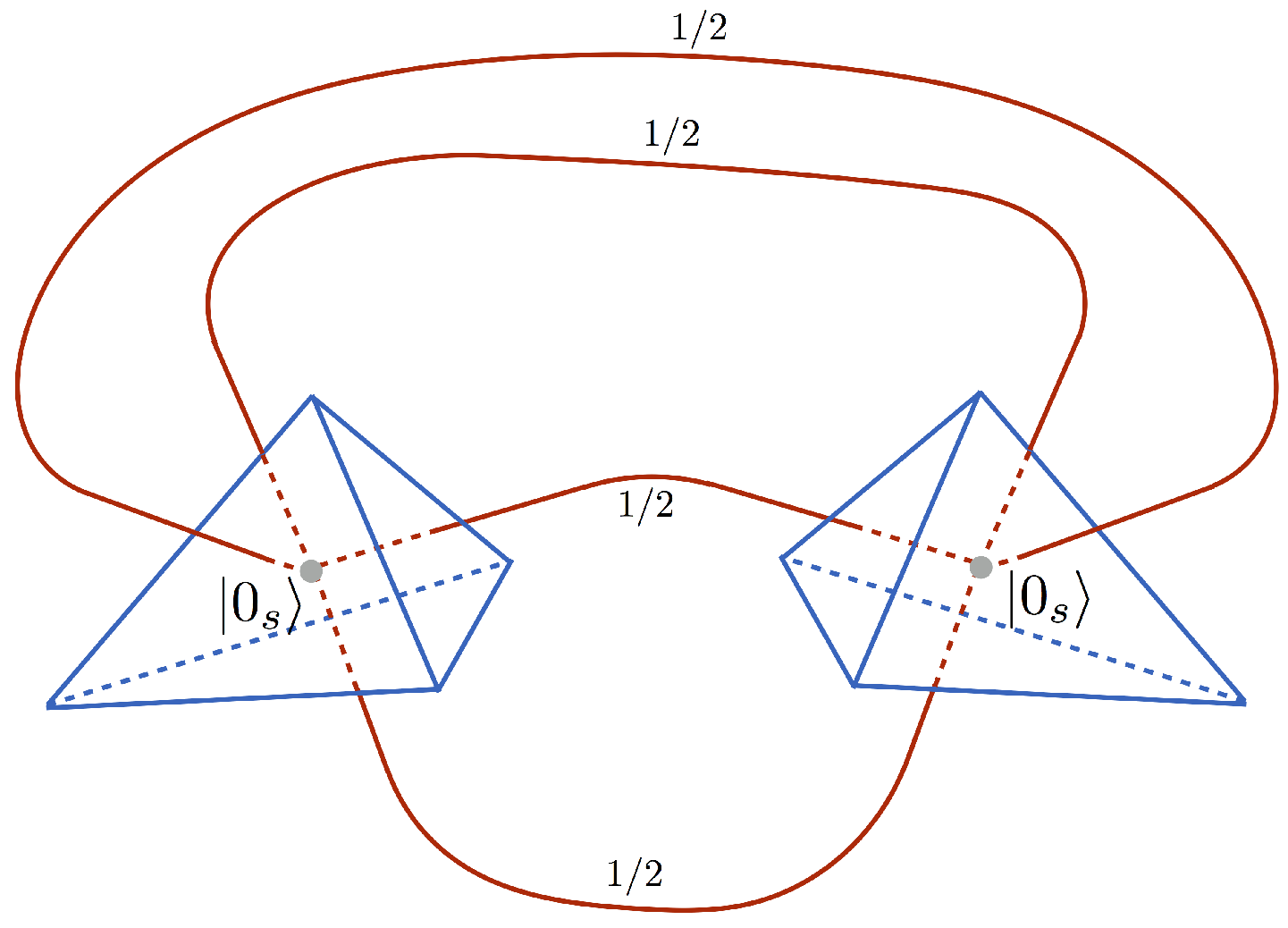
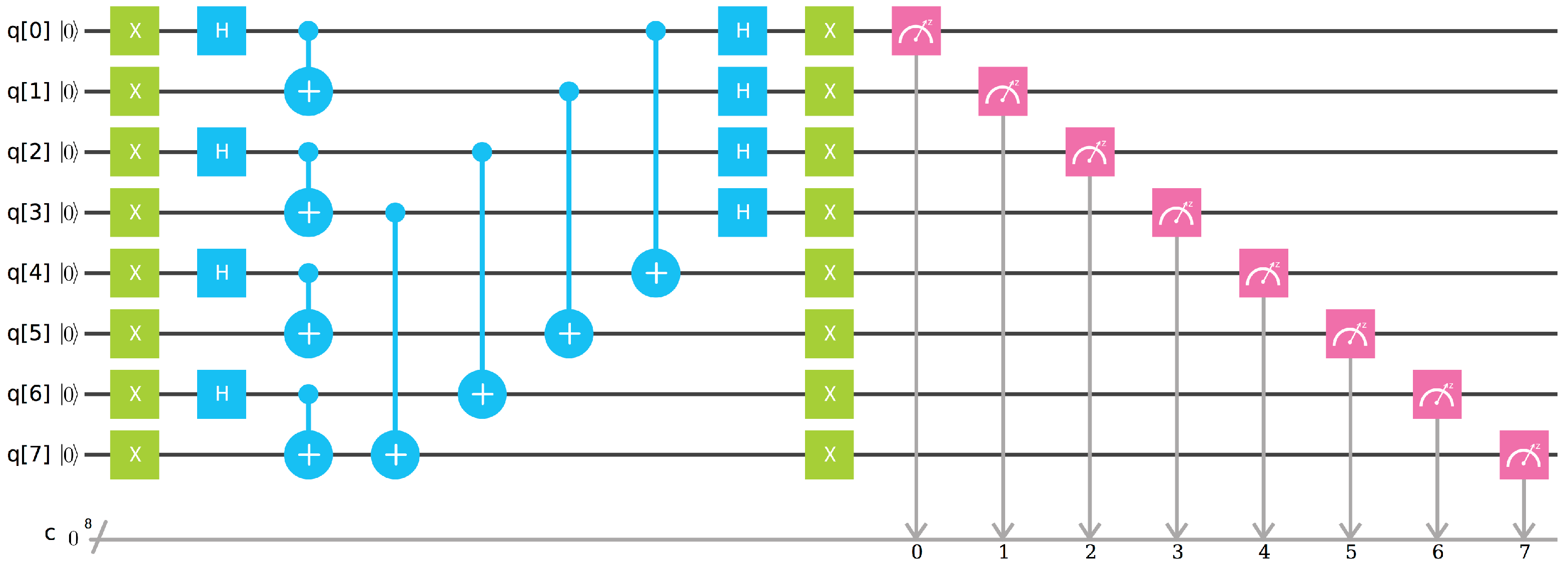
4.2. Example 2—Two Tetrahedra
The second example concerns a bit more complex situation with two-node spin network presented in
Figure 7.
Here, the representation state
similarly to the previous example is associated with the Bell sates (
22) entangling faces of the two tetrahedra one into another. The corresponding choice of the quantum circuit used to evaluate the boundary amplitude is presented in
Figure 8.
The simulations were performed on both the IBM simulator and the QX simulator, with 1024 shots in each round. As in the previous example, the computational rounds have been repeated 10 times. The results obtained are collected in
Table 3.
Performing averaging over the computational rounds the following values of
are obtained:
The results are in agreement with the theoretically expected value
(obtained using Quirk [
35]).
5. Evaluation of Vertex Amplitude
We are now ready to address the task of determining the vertex amplitude (
19) associated with the boundary spin network state:
The other possible choices of the spin network state will be discussed in our further work [
34].
The
is given by Equation (
21), representing entanglement between faces of tetrahedra being connected by the links of the spin network. Due to anti-symmetricity of the Bell states (
22) for the 10 links under consideration we have in general
ways to order the states between the nodes of the spin network. Here, in order to not distinguish any of the nodes, the configuration in which every node is entangled with two other nodes by the state
and another two nodes by the state
is considered. The resulting quantum circuit corresponding to the operator
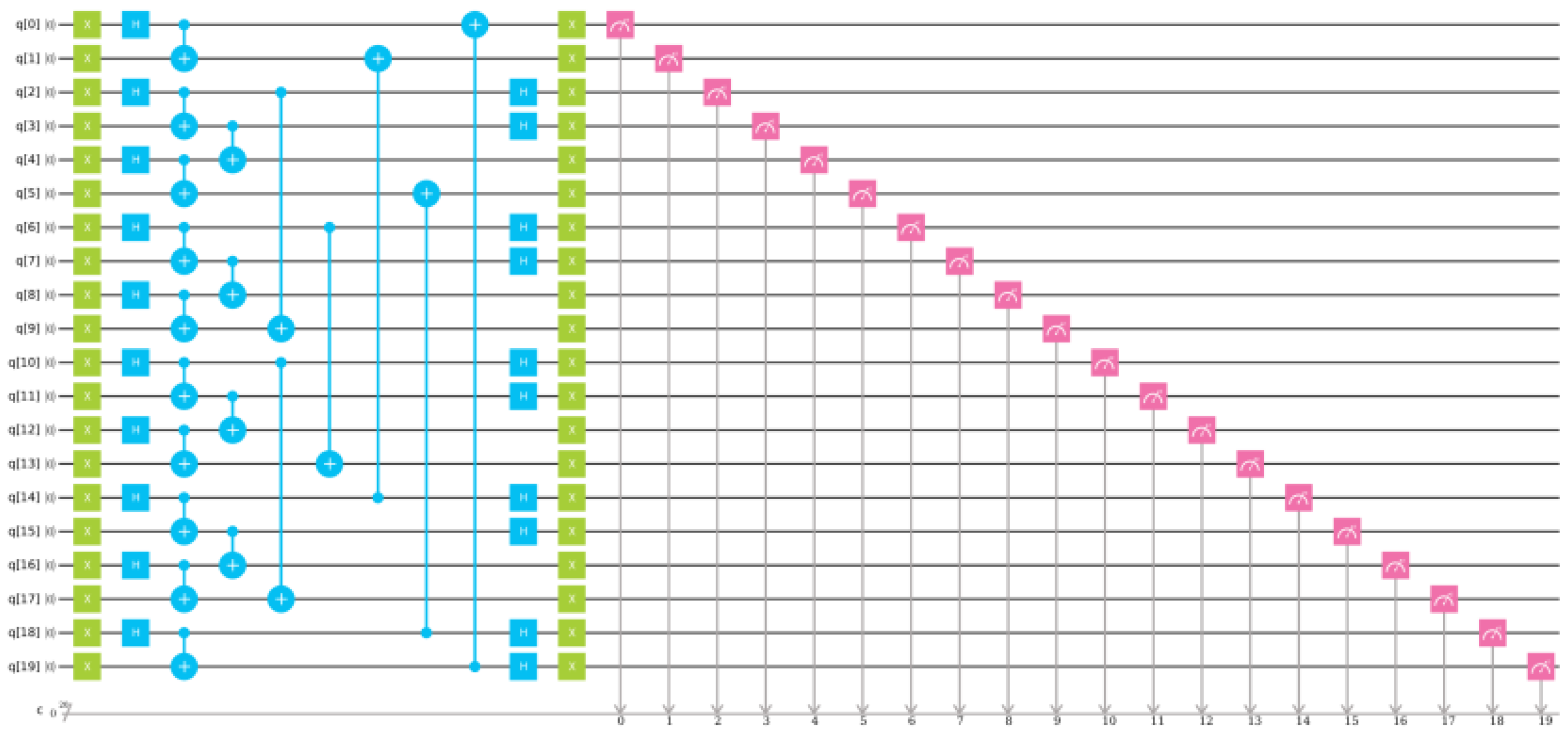
, together with the measurements necessary to find
is shown in
Figure 9.
The quantum circuit employs 20-qubit quantum register with the initial state:
The algorithm introduced in
Section 4 requires finding amplitude of the initial state (
34) in the final state. One has to keep in mind that the Hilbert space of the 20-qubit system is spanned by over 1,000,000 basis states:
. Therefore, selecting amplitude of one of the basis states (i.e.,
) is not an easy task.
The first attempt to determine the value of has been made by using the IBM simulator of quantum computer. Ten rounds of simulation, each of 1024 shots, have been performed. However, no single event with the state in the final state has been observed. Assuming that the probability is evenly distributed between the basis states, the probability per basis states can be expected. With the 10,240 measurements made, this gives roughly chance to observe the state.
The second attempt to determine value of the vertex amplitude has been made with the use of the QX quantum computer simulator. Similarly to the simulations performed on the IBM simulator, 10 computational rounds, each of 1024 shots, have been performed. In this case, the events with
have been observed and are collected in
Table 4.
By averaging the results from
Table 4, the following value of the modulus square of the vertex amplitude
can be found:
The results obtained from the IBM and QX simulators are contradictory. However, the QX simulator result (
35) is much closer to the theoretically expected value. Namely, the spin foam amplitude considered in this section can be determined using recoupling theory for
group. Following the discussion in Ref. [
39] on can find that the amplitude (
19) is given by the
symbol. Employing definition of the symbol (see e.g., Equation (
17) in Ref. [
51]) for all the spin labels
and the intertwiners
(which correspond to the
states), where
, one can find that
. In consequence,
. The difference between this prediction and the result of simulations (
35) goes beyond the statistical error and, therefore, one can expect that systematic error was involved. Resolution of this issue requires further investigation, especially analysis of the sampling methods used in the quantum simulator. The same concerns the IBM quantum simulator, where discrepancy between the theoretically predicted value and the results of measurements is even more serious. Certainly, the employed publicly available platforms exhibit significant limitations. Nevertheless, they can be overcome by using more advanced simulators run on up-to-date computational clusters.
A more serious challenge is that the algorithm, in its current form, requires making measurements on all qubits involved in the circuit. In consequence, the number of measurements is growing exponentially with the number of quibits. Therefore, proposals of new algorithms, which will allow to reduce the number of measurements, are welcome (one of the possibilities is to use Quantum Phase Estimation Algorithm).
Taking the above into account, a comment on utility of the applied methodology is desirable. First of all, we already used the fact that the vertex amplitude discussed in this section can easily be evaluated without the need of quantum circuits. The vertex amplitude, associated with the pentagram spin network is given by the
symbol. Recently, significant progress has been made in the development of numerical methods of evaluation of spin foam vertex amplitudes [
52,
53,
54]. However, there are still some obstacles, e.g., oscillating nature of the spin foam amplitudes, which motivate search for alternative computational methods.
The aim of our study was to provide the proof of the concept of applicability of quantum circuits to determine quantities being of relevance in Loop Quantum Gravity and Spin Foam approaches. We have shown that indeed, despite the current hardware limitations (see
Appendix A), interesting quantities can already be evaluated on simulators of quantum computers. As we demonstrated, 2 qubits per link of a spin network are needed for this purpose. Therefore, in case of the 5-node pentargam spin network (with 10 links) studied here, 20 qubit register was used. Utilizing the available commercial quantum simulators (e.g., 37 qubit QX multi-node simulator SurfSara [
25]), amplitudes of spin networks with up to nine 4-valent nodes can potentially be computed.
Our plan is to perform such simulations in our further studies. Furthermore, our goal is to extend computational capabilities to 40 qubits using academic and commercial supercomputing resources. This will allow to simulate spin networks with 10 nodes. Worth mentioning is that while scaling the system size is straightforward for the method based on quantum circuits, application of the standard methods based on recoupling theory may turn out to be inefficient. This will become even more evident when advantageous quantum computers will become available (as expected) in the second half on the coming decade (see
Appendix A), providing 100 and more fault tolerant qubits. Until that time, there is still a lot of potential for improving simulator-based computations and development of methods which will ultimately be applied on real quantum processors.
Furthermore, the introduced circuits for spin networks not only allow to study amplitudes but also other relevant quantities. In particular, analysis of quantum fluctuations and quantum entanglement between subsystems is possible to investigate. One of the open problems which is becoming possible to study by extending the methodology introduced here is the entanglement entropy between subsystems of spin networks and the issue of area law for entropy of entanglement.
In addition, while in the current setup we considered the spin labels
, the case of higher spins can potentially also be implemented. This would be relevant especially from the point of view of the semi-classical, large
j limit. Taking into account the restricted computational resources, this can be done only by the cost of keeping the number of nodes small. Therefore, basically we have two domains which seem to be plausible to investigate in the coming decade. The first is the one with the small spin labels (e.g.,
) and the increasing number of nodes of a spin network—the direction towards the thermodynamic limit of a quantum system. The second is the case with small number of nodes (e.g., dipole spin network) and increasing values of the spin labels. This corresponds to a semi-classical limit of a microscopic chunk of space. On the other hand, the case where both the number of nodes and the spin labels are large is the most interesting one. Analysis of this limit will allow to investigate emergence of classical space(time) in loop quantum gravity and spin foam approaches. This will provide an opportunity to (at least partially) verify physical relevance of the candidates for theory of quantum gravity. However, sufficient quantum computational resources are not expected to be available earlier than in the fourth decade of this century (see
Appendix A).