A HERO for General Relativity
Abstract
1. Introduction
2. Two Different Orbital Configurations for HERO
3. Summary and Overview
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Tables and Figures
| Physical Parameter | Numerical Value | Units |
|---|---|---|
| Newtonian constant of gravitation G | ||
| Speed of light in vacuum c | ||
| Gravitational parameter | ||
| Angular speed | ||
| Equatorial radius | ||
| Polar radius | ||
| Angular momentum S | ||
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Normalized Stokes coefficient | - | |
| Formal error | - | |
| Formal error | - | |
| Formal error | - | |
| Formal error | - | |
| Formal error | - | |
| Formal error | - | |
| Formal error | - |
| Orbital and Physical Parameter | Numerical Value | Units |
|---|---|---|
| Semimajor axis a | 13,500 | km |
| Orbital period | hr | |
| Orbital eccentricity e | - | |
| Perigee height | 1046.86 | km |
| Apogee height | 13,196.9 | km |
| Orbital inclination I | deg | |
| Argument of perigee | 45 | deg |
| Period of the node | yr | |
| Period of the perigee | −1363.4 | yr |
| Gravitational redshift | − |
| Effect | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 |
| Coefficient of | − | |
| Coefficient of | − | |
| Coefficient of | − | |
| 30,254.2 |
| Orbital and Physical Parameter | Numerical Value | Units |
|---|---|---|
| Semimajor axis a | 39,000 | km |
| Orbital period | hr | |
| Orbital eccentricity e | - | |
| Perigee height | km | |
| Apogee height | 64,601.9 | km |
| Orbital inclination I | deg | |
| Argument of perigee | 45 | deg |
| Period of the node | yr | |
| Period of the perigee | −8186.71 | yr |
| Gravitational redshift | − |
| Effect | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 |
| Coefficient of | − | |
| Coefficient of | − | |
| Coefficient of | − | |
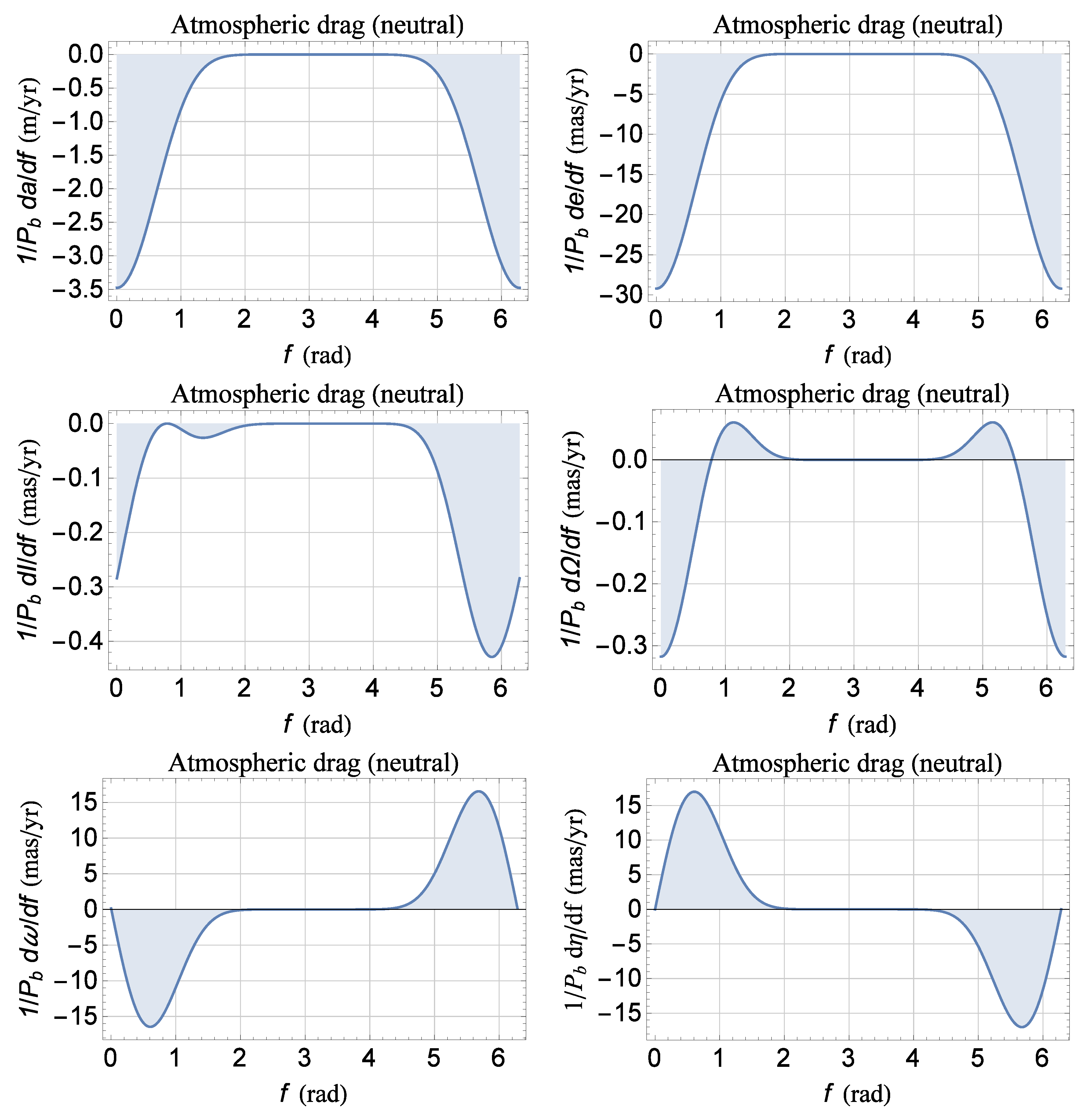
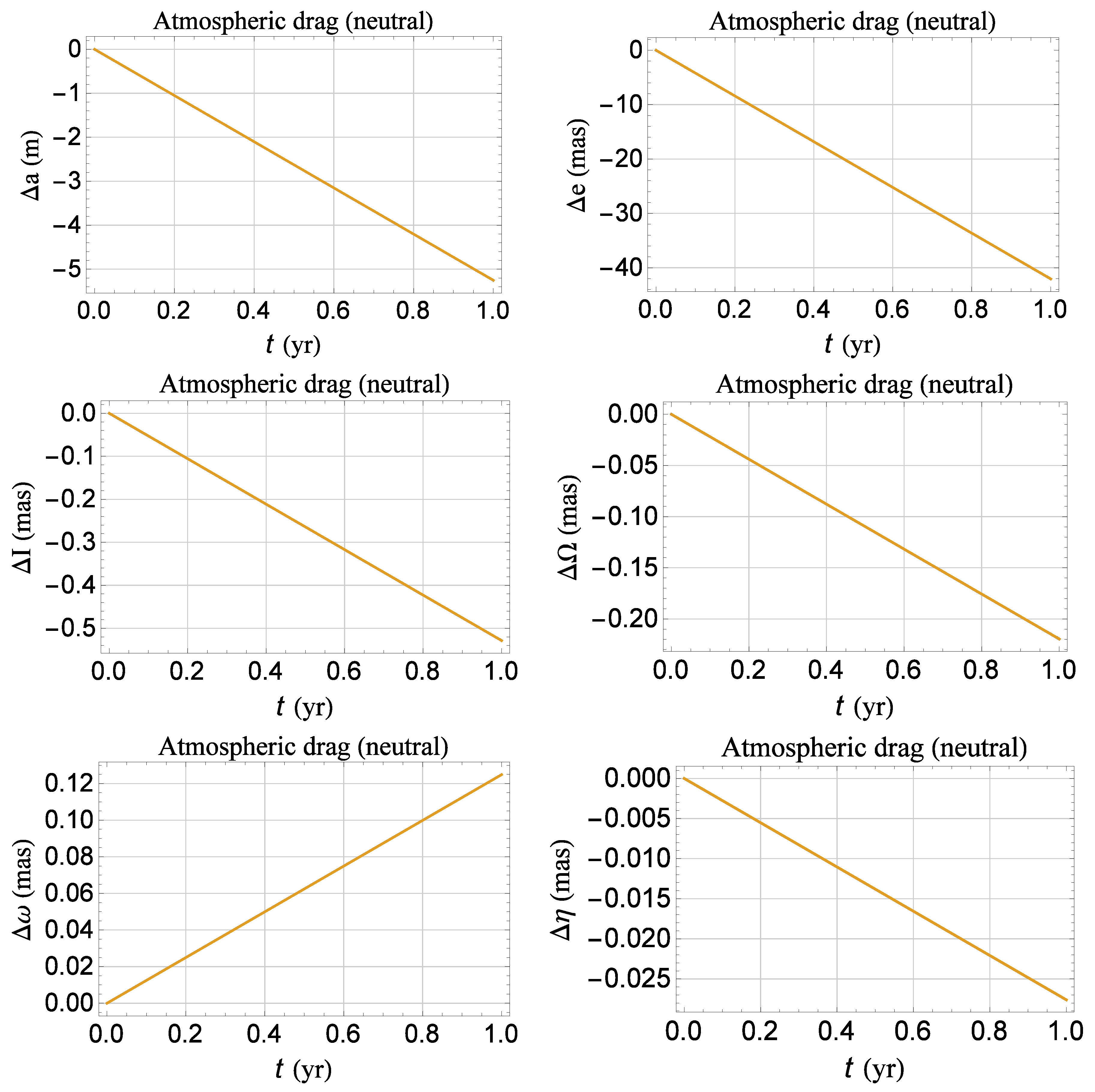
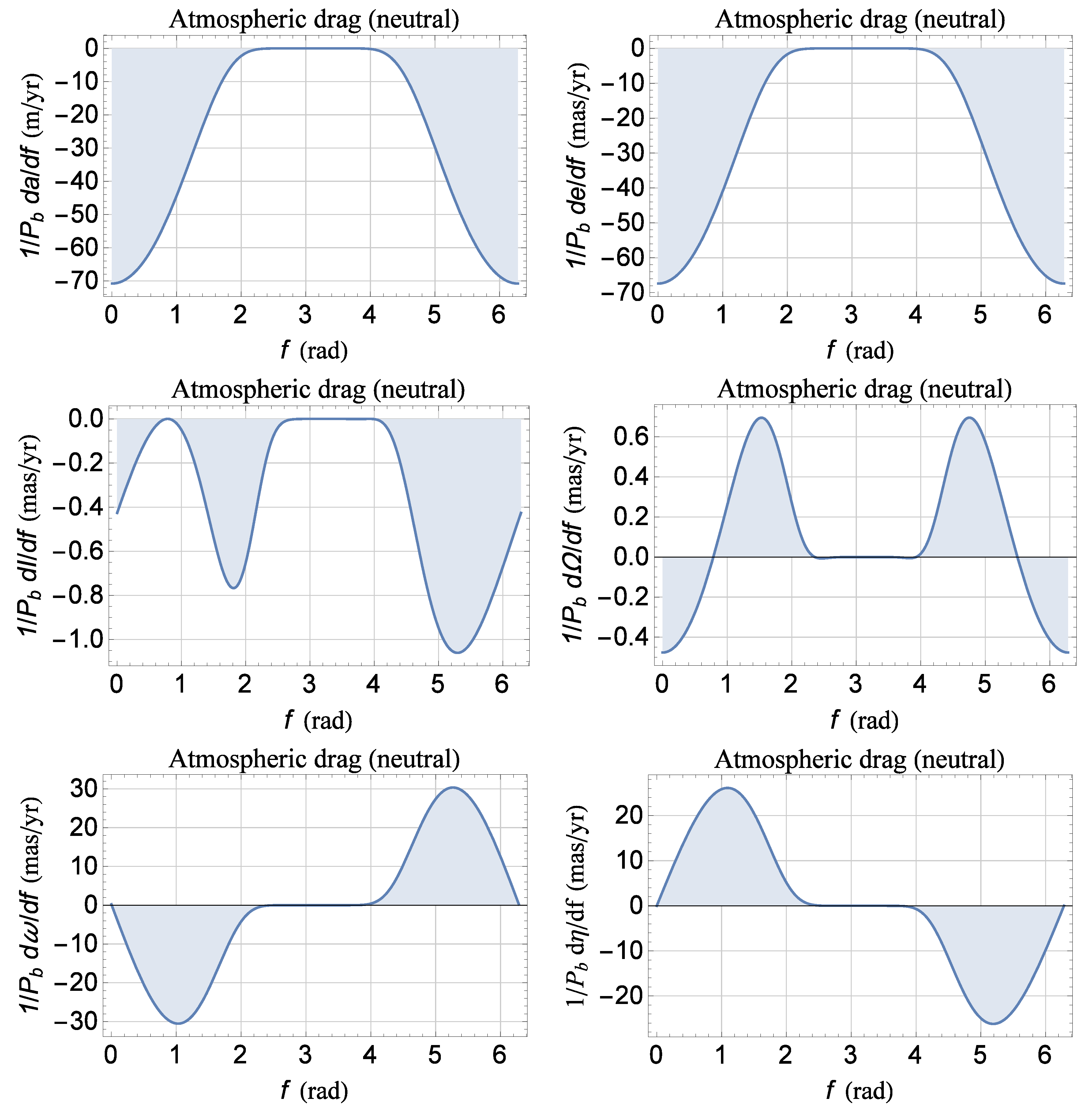
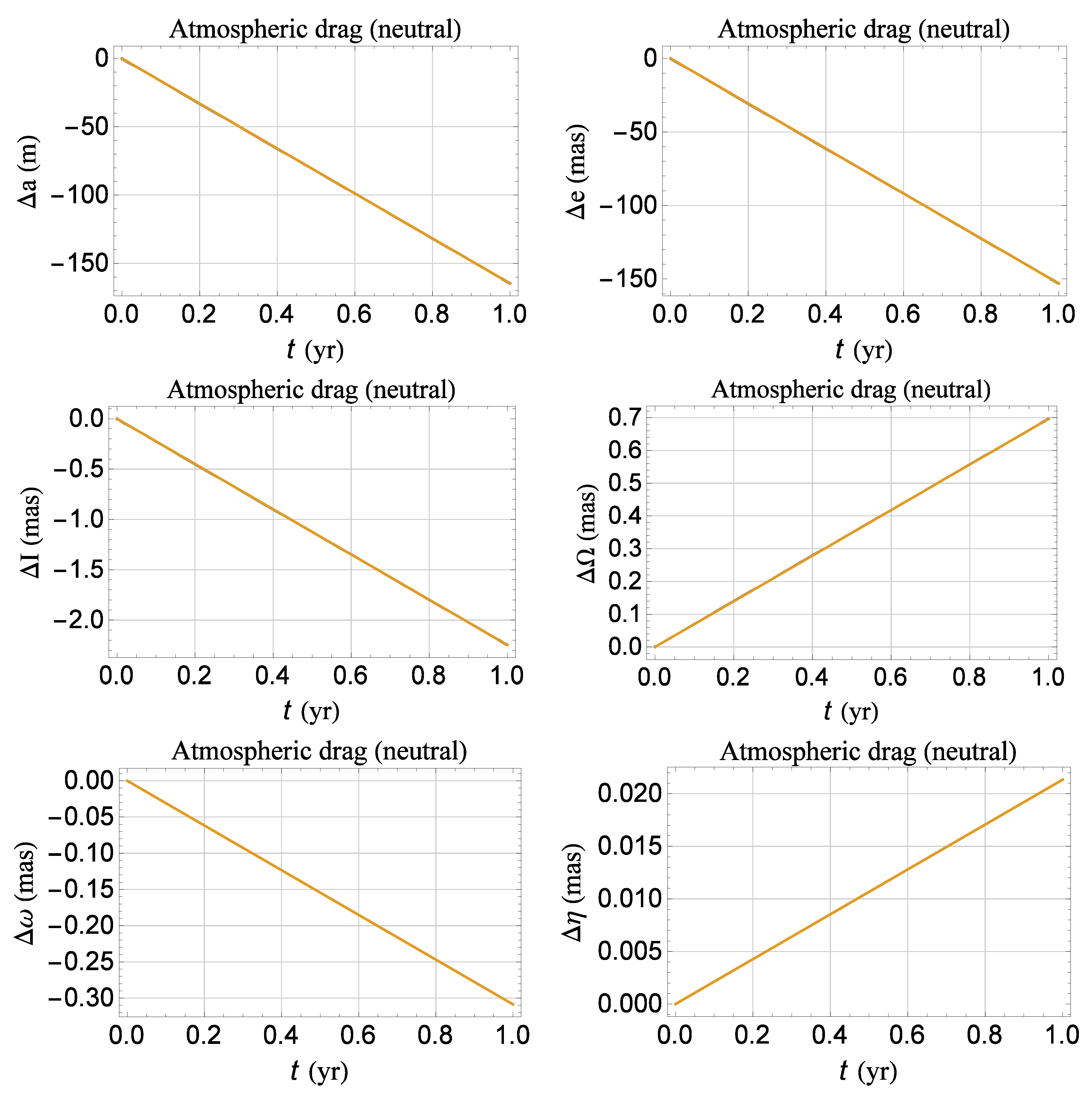
Appendix B. Classical Long-Term Rates of Change of the Keplerian Orbital Elements up to Degree ℓ = 8
Appendix B.1. The Eccentricity
Appendix B.2. The Inclination
Appendix B.3. The Longitude of the Ascending Node
Appendix B.4. The Argument of Perigee
Appendix B.5. The Mean Anomaly at Epoch
Appendix C. The Atmospheric Drag
References
- Brumberg, V.A. Essential Relativistic Celestial Mechanics; Adam Hilger: Bristol, UK, 1991. [Google Scholar]
- Meichsner, J.; Soffel, M.H. Effects on satellite orbits in the gravitational field of an axisymmetric central body with a mass monopole and arbitrary spin multipole moments. Celest. Mech. Dyn. Astr. 2015, 123, 1. [Google Scholar] [CrossRef][Green Version]
- Soffel, M.H. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer: Heidelberg, Germany, 1989. [Google Scholar]
- Will, C.M. Incorporating post-Newtonian effects in -body dynamics. Phys. Rev. D 2014, 89, 044043. [Google Scholar] [CrossRef]
- Panhans, M.; Soffel, M.H. Gravito-magnetism of an extended celestial body. Class. Quantum Gravity 2014, 31, 245012. [Google Scholar] [CrossRef]
- Soffel, M.; Wirrer, R.; Schastok, J.; Ruder, H.; Schneider, M. Relativistic effects in the motion of artificial satellites: The oblateness of the central body I. Celest. Mech. Dyn. Astr. 1987, 42, 81. [Google Scholar] [CrossRef]
- Le Verrier, U.; de Lettre, M.; Le Verrier à, M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète. Cr. Hebd. Acad. Sci. 1859, 49, 379. [Google Scholar]
- Einstein, A. Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. Sitzungsberichte der Preußischen Akademie der Wissenschaften 1915, 47, 831–839. [Google Scholar]
- Shapiro, I.I. General Relativity and Gravitation; Ashby, N., Bartlett, D.F., Wyss, W., Eds.; Cambridge University Press: Cambridge, UK, 1990; pp. 313–330. [Google Scholar]
- Shapiro, I.I.; Pettengill, G.H.; Ash, M.E.; Ingalls, R.P.; Campbell, D.B.; Dyce, R.B. Mercury’s perihelion advance: determination by radar. Phys. Rev. Lett. 1972, 28, 1594. [Google Scholar] [CrossRef]
- Anderson, J.D.; Campbell, J.K.; Jurgens, R.F.; Lau, E.L.; Newhall, X.X.; Slade, M.A., III; Standish, E.M., Jr. Recent developments in Solar system tests of general relativity. In Proceedings of the Sixth Marcel Grossmann Meeting on General Relativity; Satō, F., Nakamura, T., Eds.; World Scientific: Singapore, 1992; pp. 353–355. [Google Scholar]
- Anderson, J.D.; Keesey, M.S.W.; Lau, E.L.; Standish, E.M., Jr.; Newhall, X.X. Tests of general relativity using astrometric and radio metric observations of the planets. Acta Astronaut. 1978, 5, 43–61. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Ash, M.E.; Smith, W.B. Icarus: further confirmation of the relativistic perihelion precession. Phys. Rev. Lett. 1968, 20, 1517. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Smith, W.B.; Ash, M.E.; Herrick, S. General relativity and the orbit of Icarus. Astron. J. 1971, 76, 588. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of general relativity from timing the double pulsar. Science 2006, 314, 97. [Google Scholar] [CrossRef] [PubMed]
- Lucchesi, D.M.; Peron, R. Accurate measurement in the field of the earth of the general-relativistic precession of the LAGEOS II pericenter and new constraints on non-newtonian gravity. Phys. Rev. Lett. 2010, 105, 231103. [Google Scholar] [CrossRef] [PubMed]
- Lucchesi, D.M.; Peron, R. LAGEOS II pericenter general relativistic precession (1993–2005): Error budget and constraints in gravitational physics. Phys. Rev. D 2014, 89, 082002. [Google Scholar] [CrossRef]
- Lense, J.; Thirring, H. Über den Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 156. [Google Scholar]
- Pfister, H. On the history of the so-called Lense-Thirring effect. Gen. Relativ. Gravit. 2007, 39, 1735. [Google Scholar] [CrossRef]
- Pfister, H. Eleventh Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories; Kleinert, H., Jantzen, R.T., Ruffini, R., Eds.; World Scientific: Singapore, 2008; pp. 2456–2458. [Google Scholar]
- Pfister, H. Editorial note to: Hans Thirring, On the formal analogy between the basic electromagnetic equations and Einstein’s gravity equations in first approximation. Gen. Relativ. Gravit. 2012, 44, 3217. [Google Scholar] [CrossRef]
- Pfister, H. Relativity and Gravitation; Springer Proceedings in Physics; Bičák, J., Ledvinka, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 157, pp. 191–197. [Google Scholar]
- Renzetti, G. History of the attempts to measure orbital frame-dragging with artificial satellites. Open Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Anselmo, L.; Bassan, M.; Magnafico, C.; Pardini, C.; Peron, R.; Pucacco, G.; Visco, M. General Relativity Measurements in the Field of Earth with Laser-Ranged Satellites: State of the Art and Perspectives. Universe 2019, 5, 141. [Google Scholar] [CrossRef]
- Pugh, G. Proposal for a Satellite Test of the Coriolis Prediction of General Relativity; Research Memorandum 11, Weapons Systems Evaluation Group; The Pentagon: Washington, DC, USA, 1959. [Google Scholar]
- Schiff, L. Gravity probe B: final results of a space experiment to test general relativity. Phys. Rev. Lett. 1960, 4, 215. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity probe B: final results of a space experiment to test general relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B test of general relativity. Class. Quantum Gravity 2015, 32, 224001. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Buchman, S.; Debra, D.B.; Keiser, G.M.; Lockhart, J.M.; Muhlfelder, B.; Parkinson, B.W.; Turneaure, J.P. Gyros, Clocks, Interferometers …: Testing Relativistic Gravity in Space. In Lecture Notes in Physics; Lämmerzahl, C., Everitt, C.W.F., Hehl, F.W., Eds.; Springer: Berlin, Germany, 2001; Volume 562, p. 52. [Google Scholar]
- Iorio, L. Post-Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 2015, 24, 1550067. [Google Scholar] [CrossRef]
- Iorio, L. The post-Newtonian gravitomagnetic spin-octupole moment of an oblate rotating body and its effects on an orbiting test particle; are they measurable in the Solar system? Mon. Not. R. Astron. Soc. 2019, 484, 4811. [Google Scholar] [CrossRef]
- Iorio, L. A possible new test of general relativity with Juno. Class. Quantum Gravity 2013, 30, 195011. [Google Scholar] [CrossRef]
- Abbas, U.; Bucciarelli, B.; Lattanzi, M.G. Differential astrometric framework for the Jupiter relativistic experiment with Gaia. Mon. Not. Roy. Astron. Soc. 2019, 485, 1147. [Google Scholar] [CrossRef]
- Crosta, M.T.; Mignard, F. Microarcsecond light bending by Jupiter. Class. Quantum Gravity 2006, 23, 4853. [Google Scholar] [CrossRef][Green Version]
- Kopeikin, S.M.; Makarov, V.V. Gravitational bending of light by planetary multipoles and its measurement with microarcsecond astronomical interferometers. Phys. Rev. D 2007, 75, 062002. [Google Scholar] [CrossRef]
- Le Poncin-Lafitte, C.; Teyssandier, P. Influence of mass multipole moments on the deflection of a light ray by an isolated axisymmetric body. Phys. Rev. D 2008, 77, 044029. [Google Scholar] [CrossRef]
- Angélil, R.; Saha, P.; Bondarescu, R.; Jetzer, P.; Schärer, A.; Lundgren, A. Spacecraft clocks and relativity: Prospects for future satellite missions. Phys. Rev. D 2014, 89, 064067. [Google Scholar] [CrossRef]
- Schärer, A.; Angélil, R.; Bondarescu, R.; Jetzer, P.; Lundgren, A. Testing scalar-tensor theories and parametrized post-Newtonian parameters in Earth orbit. Phys. Rev. D 2014, 90, 123005. [Google Scholar] [CrossRef]
- Schärer, A.; Bondarescu, R.; Saha, P.; Angélil, R.; Helled, R.; Jetzer, P. Prospects for Measuring Planetary Spin and Frame-Dragging in Spacecraft Timing Signals. Front. Astron. Space Sci. 2017, 4, 11. [Google Scholar] [CrossRef]
- Delva, P.; Puchades, N.; Schönemann, E.; Dilssner, F.; Courde, C.; Bertone, S.; Gonzalez, F.; Hees, A.; Le Poncin-Lafitte, C.; Meynadier, F.; et al. Gravitational Redshift Test Using Eccentric Galileo Satellites. Phys. Rev. Lett. 2018, 121, 231101. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, S.; Finke, F.; Lülf, M.; Kichakova, O.; Puetzfeld, D.; Knickmann, D.; List, M.; Rievers, B.; Giorgi, G.; Günther, C.; et al. Test of the Gravitational Redshift with Galileo Satellites in an Eccentric Orbit. Phys. Rev. Lett. 2018, 121, 231102. [Google Scholar] [CrossRef] [PubMed]
- Altschul, B.; Bailey, Q.G.; Blanchet, L.; Bongs, K.; Bouyer, P.; Cacciapuoti, L.; Capozziello, S.; Gaaloul, N.; Giulini, D.; Hartwi, J.; et al. Quantum tests of the Einstein Equivalence Principle with the STE–QUEST space mission. Adv. Space Res. 2015, 55, 501. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar] [CrossRef]
- Rubincam, D.P. On the secular decrease in the semimajor axis of LAGEOS’s orbit. Celest. Mech. Dyn. Astr. 1982, 26, 361. [Google Scholar] [CrossRef]
- Sośnica, K. Determination of Precise Satellite Orbits and Geodetic Parameters Using Satellite Laser Ranging; ETH Zürich, Swiss Geodetic Commission: Zürich, Switzerland, 2014; pp. 94–95. [Google Scholar]
- Sośnica, K.; Baumann, C.; Thaller, D.; Jäggi, A.; Dach, R. Combined LARES-LAGEOS Solutions. In Proceedings of the 18th International Workshop on Laser Ranging, Fujiyoshida, Japan, 11–15 November 2013. 13-Po-57. [Google Scholar]
- Ciufolini, I.; Lucchesi, D.; Vespe, F.; Mandiello, A. Measurement of dragging of inertial frames and gravitomagnetic field using laser-ranged satellites. Nuovo Cimento A 1996, 109, 575. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Francis, O.; Chen, W.; Zhang, X.; Hsu, H.J. Tongji-Grace02s and Tongji-Grace02k: High-Precision Static GRACE-Only Global Earth’s Gravity Field Models Derived by Refined Data Processing Strategies. Geophys. Res. 2018, 123, 6111. [Google Scholar] [CrossRef]
- Sheard, B.S.; Heinzel, G.; Danzmann, K.; Shaddock, D.A.; Klipstein, W.M.; Folkner, W.M.J. Intersatellite laser ranging instrument for the GRACE follow-on mission. Geodesy 2012, 86, 1083. [Google Scholar] [CrossRef]
- Sehnal, L. Effects of the terrestrial infrared radiation pressure on the motion of an artificial satellite. Celest. Mech. Dyn. Astr. 1981, 25, 169. [Google Scholar] [CrossRef]
- Durand-Manterola, H.J. Dipolar magnetic moment of the bodies of the solar system and the Hot Jupiters. Planet. Space Sci. 2009, 57, 1405. [Google Scholar] [CrossRef][Green Version]
- Petit, G.; Luzum, B. IERS Conventions (2010). IERS Techn. Note 2010, 36, 1. [Google Scholar]
- Pardini, C.; Anselmo, L.; Lucchesi, D.M.; Peron, R. On the secular decay of the LARES semi-major axis. Acta Astronaut. 2017, 140, 469. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Anselmo, L.; Bassan, M.; Pardini, C.; Peron, R.; Pucacco, G.; Visco, M. Testing the gravitational interaction in the field of the Earth via satellite laser ranging and the Laser Ranged Satellites Experiment (LARASE). Class. Quantum Gravity 2015, 32, 155012. [Google Scholar] [CrossRef]
- Bertotti, B.; Farinella, P.; Vokrouhlický, D. Physics of the Solar System; Kluwer Academic Press: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Capderou, M. Satellites: Orbits and Missions; Springer: Berlin, Germany, 2005. [Google Scholar]
- Kopeikin, S.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Xu, G. Orbits; Springer: Berlin, Germany, 2008. [Google Scholar]
- Membrado, M.; Pacheco, A.F. Decrease of the atmospheric co-rotation with height. Eur. J. Phys. 2010, 31, 1013. [Google Scholar] [CrossRef]
- Brito, T.P.; Celestino, C.C.; Moraes, R.V. Study of the decay time of a CubeSat type satellite considering perturbations due to the Earth’s oblateness and atmospheric drag. J. Phys. Conf. Ser. 2015, 641, 012026. [Google Scholar] [CrossRef]
| 1. | |
| 2. | In that case, the aliasing Newtonian effect which must be disentangled from the pN perihelion precessions is due to the quadrupole mass moment of the Sun. |
| 3. | |
| 4. | At least one of them must be affected by the pN effect one is looking for. In principle, the N orbital elements may be different from one another belonging to the same satellite, or some of them may be identical belonging to different spacecraft (e.g., the nodes of two different vehicles). |
| 5. | In general, it is not necessarily one of the parameters of the parameterized post-Newtonian (PPN) formalism, being possibly a combination of some of them. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iorio, L. A HERO for General Relativity. Universe 2019, 5, 165. https://doi.org/10.3390/universe5070165
Iorio L. A HERO for General Relativity. Universe. 2019; 5(7):165. https://doi.org/10.3390/universe5070165
Chicago/Turabian StyleIorio, Lorenzo. 2019. "A HERO for General Relativity" Universe 5, no. 7: 165. https://doi.org/10.3390/universe5070165
APA StyleIorio, L. (2019). A HERO for General Relativity. Universe, 5(7), 165. https://doi.org/10.3390/universe5070165





