Accretion into Black Hole, and Formation of Magnetically Arrested Accretion Disks
Abstract
1. Introduction
1.1. Black Holes and Accretion
1.2. Accretion of Magnetized Matter
1.3. Accretion in the Presence of a Large-Scale Magnetic Field
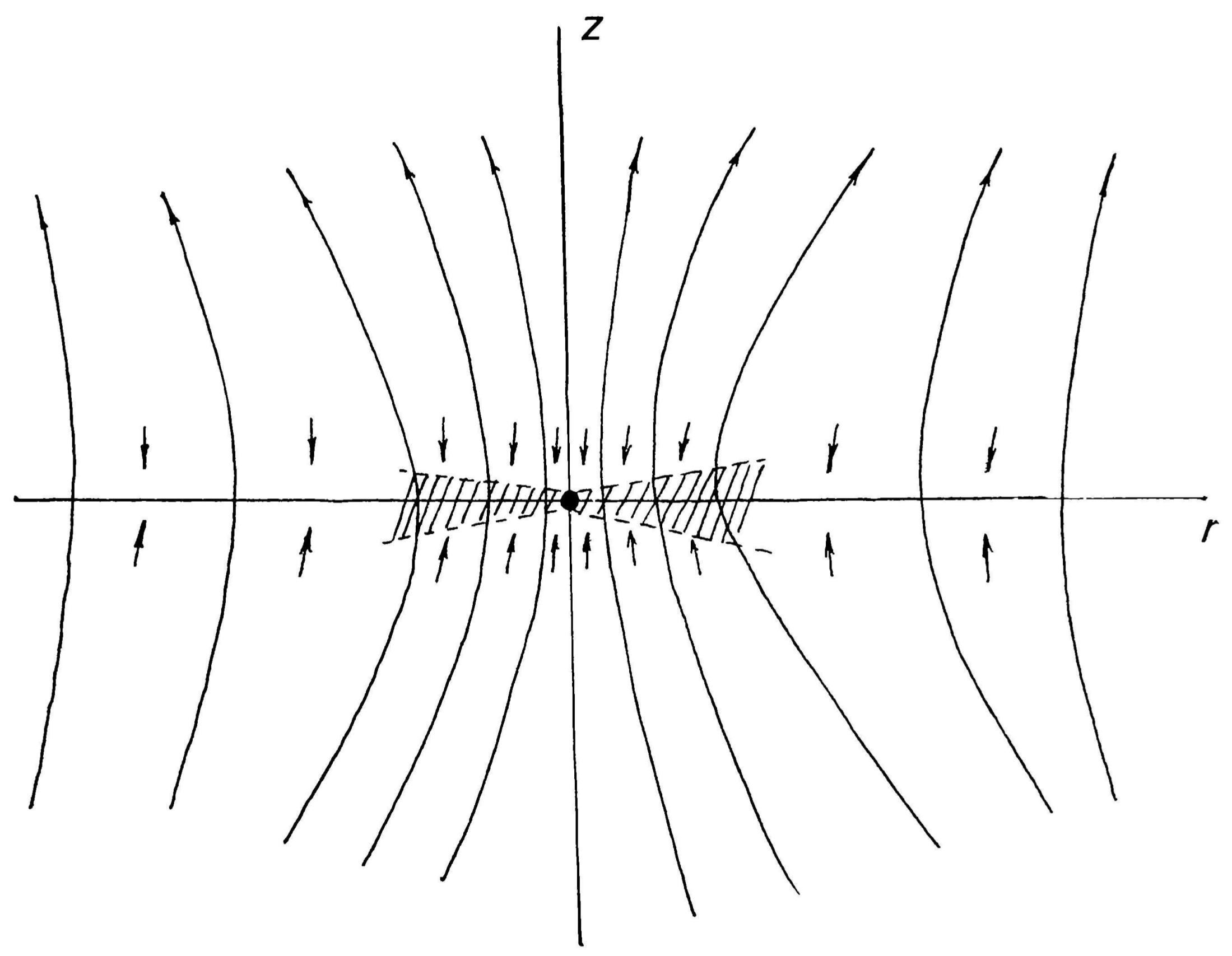
2. The Non-Stationary Solution for a Magnetic Field Evolution during a Radial Accretion onto BH
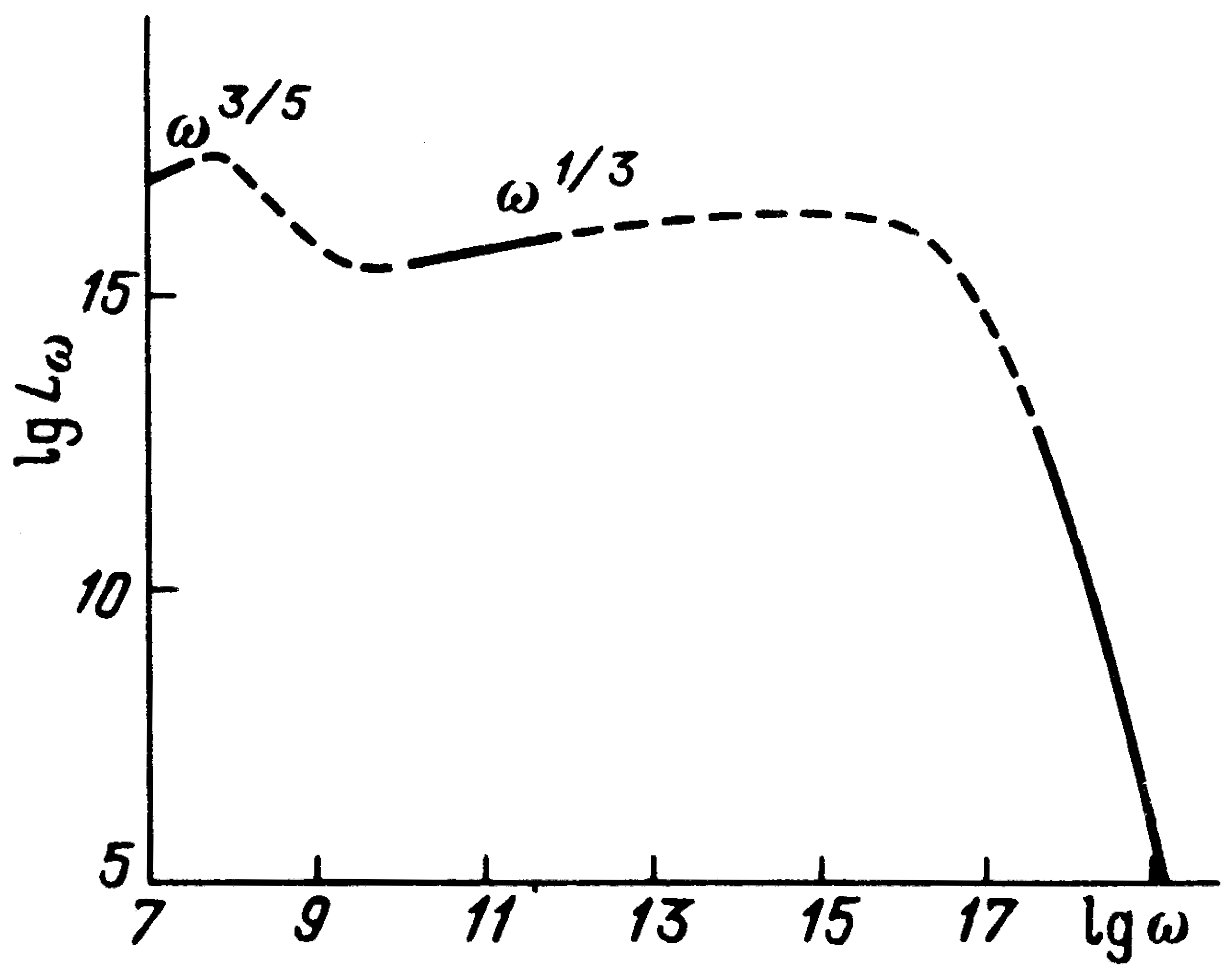
3. Radiation Flux and Spectrum at a Radial Accretion of Matter with Chaotic Magnetic Field onto a Black Hole
4. Accretion at an Ordered Magnetic Field
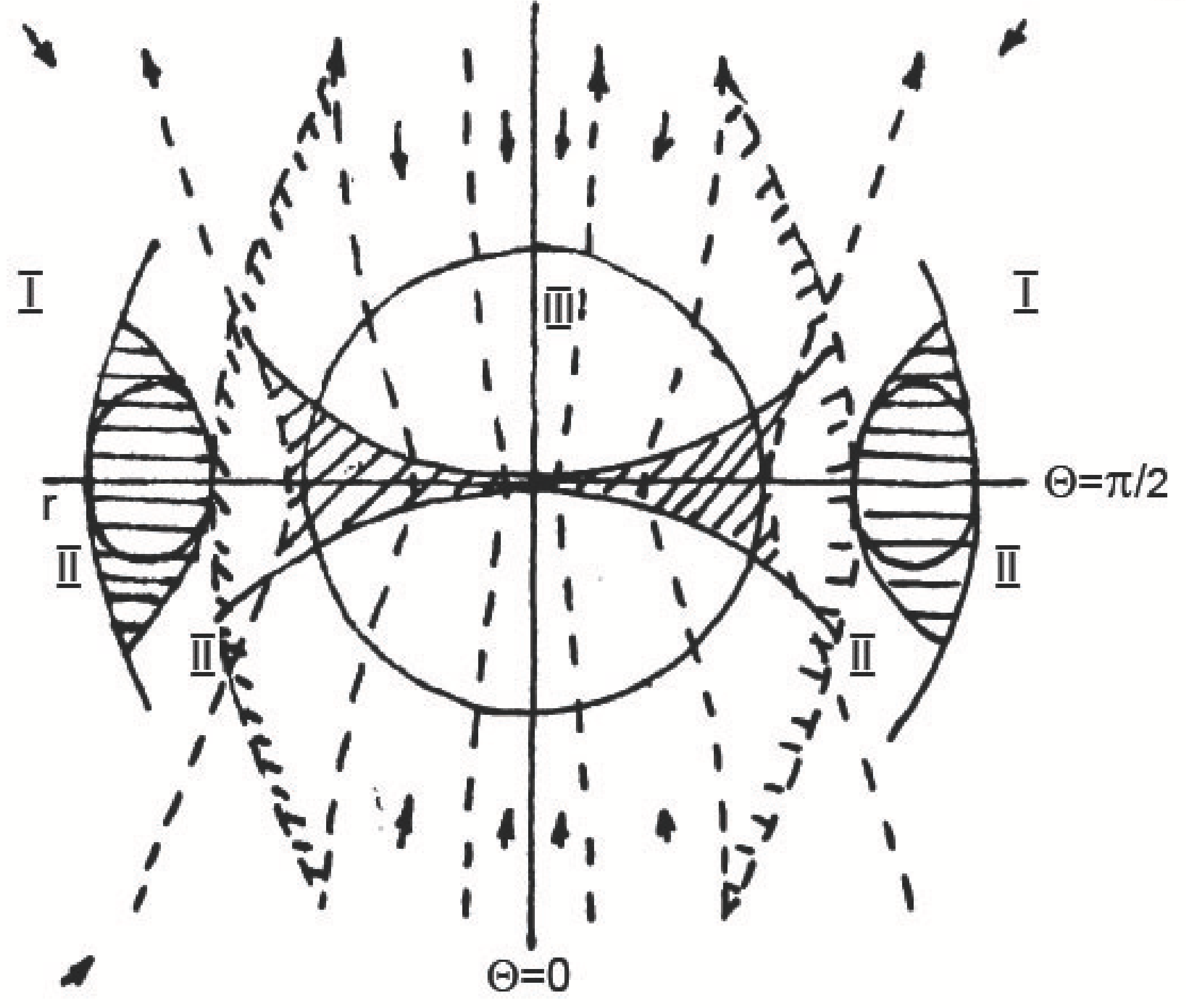
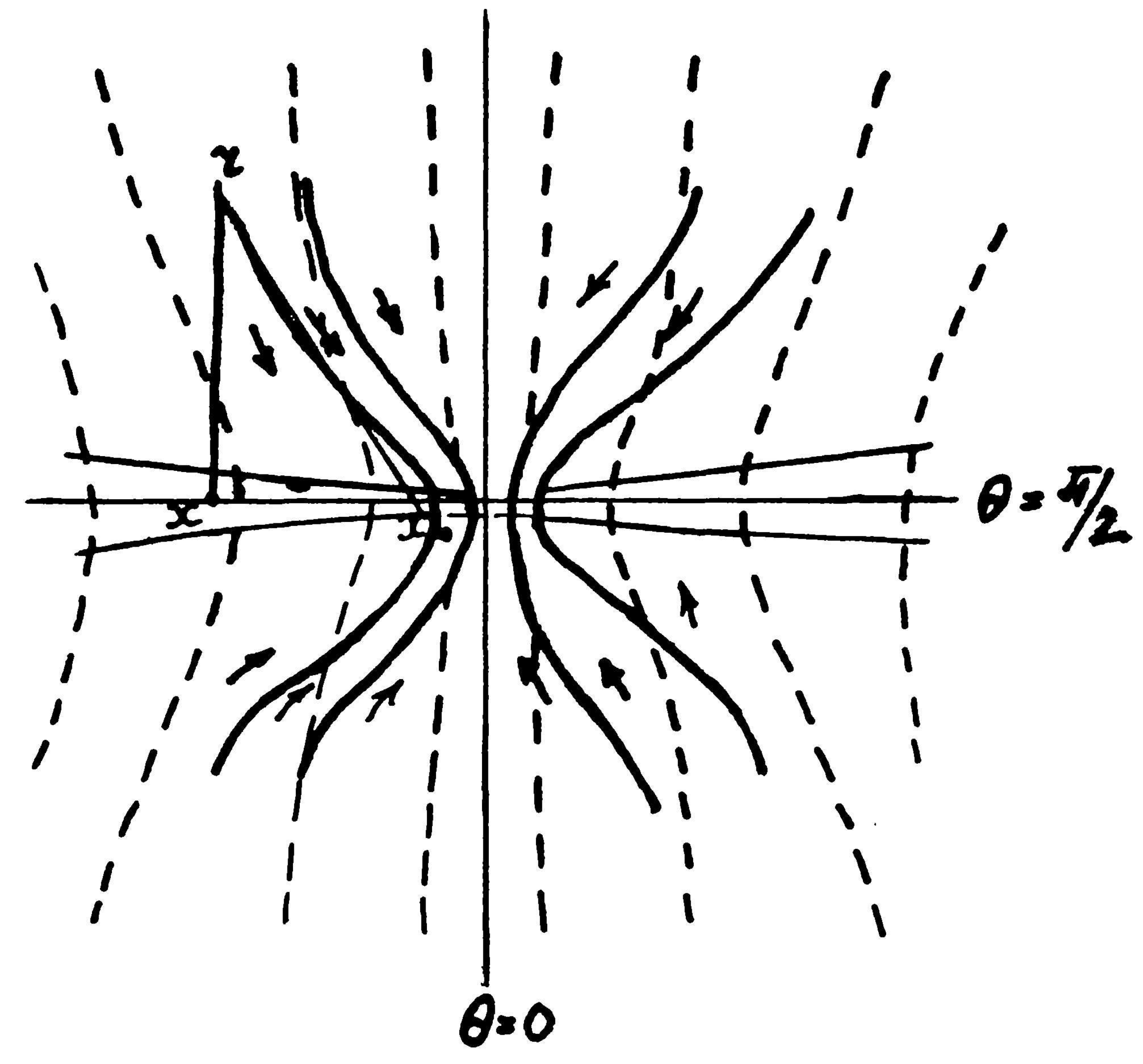
4.1. Self-Similar Solution for the Stationary Flow Outside the Symmetry Plane
4.2. Stationary Accretion Disk in Presence of a Large-Scale Magnetic Field
4.3. High Energy Radiation from the Shock on the Disk Surface and Radiation Spectrum
5. Numerical Simulations of Magnetically Arrested Disk
6. Magnetized Disk Levitation and Mad
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The Accretion of Matter by a Collapsing Star in the Presence of a Magnetic Field. Astrophys. Space Sci. 1974, 28, 45–59. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The accretion of matter by a collapsing star in the presence of a magnetic field. II - Selfconsistent stationary picture. Astrophys. Space Sci. 1976, 42, 401–424. [Google Scholar] [CrossRef]
- Chael, A.; Narayan, R.; Johnson, M.D. Two-temperature, Magnetically Arrested Disc simulations of the jet from the supermassive black hole in M87. arXiv 2018, arXiv:1810.01983. [Google Scholar] [CrossRef]
- Igumenshchev, I.V. Magnetically arrested disks and the origin of poynting jets: A numerical study. Astrophys. J. 2008, 677, 317–326. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. Lett. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon: Oxford, UK, 1983. [Google Scholar]
- Novikov, I.D.; Frolov, V.P. Physics of Black Holes; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Zeldovich, Ya.B.; Novikov, I.D. Relativistic Astrophysics, Volume 1; Chicago University Press: Chicago, IL, USA, 1971. [Google Scholar]
- Cherepashchuk, A.M. (Ed.) Catalog of Close Binary Systems at Late Evolutionary Stages; MGU Press: Moscow, Russia, 1988. [Google Scholar]
- Cherepashchuk, A.M. Masses of black holes in binary systems. Soviet. Phys. Uspekhi 1996, 39, 759–780. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M. X-ray nova binary systems. Space Sci. Rev. 2000, 93, 473–580. [Google Scholar] [CrossRef]
- Makishima, K.; Maejima, Y.; Mitsuda, K.; Bradt, H.V.; Remillard, R.A.; Tuohy, I.R.; Hoshi, R.; Nakagawa, M. Simultaneous X-ray and optical observations of GX 339–4 in an X-ray high state. Astrophys. J. 1986, 308, 635–643. [Google Scholar] [CrossRef]
- Shvartsman, V.F. Halos around “Black Holes”. Sov. Astron. 1971, 48, 479–488. [Google Scholar]
- Kaplan, S.A.; Pikel’ner, S.B. The Interstellar Medium; Fizmatgiz: Moscow, Russia, 1963. [Google Scholar]
- Bisnovatyi-Kogan, G.S. Magnetohydrodynamical processes near compact objects. Nuovo C. Riv. 1979, 2, 1–37. [Google Scholar] [CrossRef]
- Anderson, J.; Cohen, J. Gravitational Collapse of Magnetic Neutron Stars. Astrophys. Space Sci. 1970, 9, 146–152. [Google Scholar] [CrossRef]
- Ginzburg, V.L. The Magnetic Fields of Collapsing Masses and the Nature of Superstars. Sov. Phys. Dokl. 1964, 9, 329. [Google Scholar]
- Balbus, S.A.; Hawley, J.F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 1998, 70, 1–53. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. Disk accretion onto a black hole at subcritical luminosity. Astron. Astrophys. 1977, 59, 111–125. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E.; Belinski, V.A. A Cosmic Battery Reconsidered. Astrophys. J. 2002, 580, 380–388. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kazanas, D. A Cosmic Battery. Astrophys. J. 1998, 508, 859–863. [Google Scholar] [CrossRef]
- Amnuel, P.R.; Guseinov, O.H. The X-ray emission from neutron stars in the accretion process. Izv. Akad. Nauk Azerb. SSR 1968, 3, 70. [Google Scholar]
- Pringle, J.; Rees, M. Accretion Disc Models for Compact X-ray Sources. Astron. Astrophys. 1972, 21, 1–9. [Google Scholar]
- Shakura, N.I. Disk Model of Gas Accretion on a Relativistic Star in a Close Binary System. Sov. Astron. 1972, 49, 921–929. [Google Scholar]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Lichnerowicz, A. Relativistic Hydrodynamics and Magnetohydrodynamics; 1967. Available online: https://www.osti.gov/biblio/5096753#biblio-cite-chi (accessed on 10 June 2019).
- Michel, F.C. Accretion of Matter by Condensed Objects. Astrophys. Space Sci. 1972, 15, 153–160. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Field Theory; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195–204. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Gammie, C.F. Efficiency of Magnetized Thin Accretion Disks in the Kerr Metric. Astrophys. J. 1999, 522, L57–L60. [Google Scholar] [CrossRef]
- Mondal, T.; Mukhopadhyay, B. Magnetized advective accretion flows: Formation of magnetic barriers in magnetically arrested discs. Mon. Not. R. Astron. Soc. 2018, 476, 2396–2409. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Friedmann, A.M. A Mechanism for Emission of X Rays by a Neutron Star. Sov. Astron. 1969, 46, 721–724. [Google Scholar]
- Bisnovatyi-Kogan, G.S. Stellar Physics: 2: Stellar Evolution and Stability; Astronomy and Astrophysics Library, Springer-Verlag: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Park, M.-G. Self-consistent models of spherical accretion onto black holes. I. One-temperature solutions. Astrophys. J. 1990, 354, 64–82. [Google Scholar] [CrossRef]
- Park, M.-G. Self-consistent models of spherical accretion ontoblack holes. II. Two-temperature solutions with pairs. Astrophys. J. 1990, 354, 83–97. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. Spherical accretion onto compact X-ray source with preheating: No thermal limits for the luminosity. Mon. Not. R. Astron. Soc. 1980, 191, 711–719. [Google Scholar] [CrossRef][Green Version]
- Spiegel, E.E. The Gas Dynamics of Accretion. In Interstellar Gas Dynamics; Habing, H.J., Ed.; D. Reidel Publishing Company: Dordrecht-Holland, The Netherlands, 1970. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Kazhdan, Y.M.; Klypin, A.A.; Lutskii, A.E.; Shakura, N.I. Accretion onto a rapidly moving gravitating center. Sov. Astron. 1979, 23, 201–205. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. The Equilibrium, Stability and Evolution of a Rotating Magnetized Gaseous Disk. Astrophys. Space Sci. 1972, 19, 119–144. [Google Scholar] [CrossRef]
- Pikelner, S.B. Foundations of Space Electrodynamics; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Bisnovatyi-Kogan, G.S. Stellar Physics. Vol.1: Fundamental Concepts and Stellar Equilibrium; Astronomy and Astrophysics Library; Springer: Berlin, Germany, 2001. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. A hot corona around a black-hole accretion disk as a model for Cygnus X-1. Sov. Astron. Lett. 1976, 2, 191–193. [Google Scholar]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Lovelace, R.V.E. Dynamo model of double radio sources. Nature 1976, 262, 649–652. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869–880. [Google Scholar] [CrossRef]
- Paczyński, B.; Wiita, P.J. Thick accretion disks and supercritical luminosities. Astron. Astrophys. 1980, 88, 23–31. [Google Scholar]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. Astrophys. J. 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E. Influence of ohmic heating on advection-dominated accretion flows. Astrophys. J. 1997, 486, L43–L48. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The Piecewise Parabolic Method (PPM) for Gas-Dynamical Simulations. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef]
- Machida, M.; Nakamura, K.E.; Matsumoto, R. Formation of Magnetically Supported Disks during Hard-to-Soft Transitions in Black Hole Accretion Flows. Publ. Astron. Soc. Jpn. 2006, 58, 193–202. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo C. Riv. Ser. 1969, 1, 252. [Google Scholar]
- Ruffini, R.; Wilson, J.R. Relativistic magnetohydrodynamical effects of plasma accreting into a black hole. Phys. Rev. D 1975, 12, 2959–2962. [Google Scholar] [CrossRef]
- Oda, H.; Machida, M.; Nakamura, K.E.; Matsumoto, R. Thermal Equilibria of Optically Thin, Magnetically Supported, Two-temperature, Black Hole Accretion Disks. Astrophys. J. 2010, 712, 639–652. [Google Scholar] [CrossRef]
- Ikhsanov, N.R.; Kim, V.Y.; Beskrovnaya, N.G. A Scenario of the Formation of Isolated X-ray Pulsars with Anomalously Long Period. Astron. Rep. 2015, 59, 25–32. [Google Scholar] [CrossRef]
- Ikhsanov, N.R.; Beskrovnaya, N.G. Signs of Magnetic Accretion in X-ray Pulsars. Astron. Rep. 2012, 56, 589–594. [Google Scholar] [CrossRef]
- Ikhsanov, N.R.; Finger, M.H. Signs of magnetic accretion in the X-ray pulsar binary GX 301–2. Astrophys. J. 2012, 753, 1. [Google Scholar] [CrossRef]
- Ikhsanov, N.; Beskrovnaya, N.; Likh, Y. Evidence for magneto-levitation accretion in long-period X-ray pulsars. Int. J. Mod. Phys. Conf. Ser. 2014, 28, 1460187. [Google Scholar] [CrossRef]
- Ikhsanov, N.R.; Likh, Y.S.; Beskrovnaya, N.G. Spin Evolution of Long-Period X-ray Pulsars. Astron. Rep. 2014, 58, 376–385. [Google Scholar]
- Ikhsanov, N.R.; Beskrovnaya, N.G. The Spin-Down Mechanism of the X-ray Pulsar 4U 2206+54. Astron. Rep. 2013, 57, 287–293. [Google Scholar] [CrossRef]
- Ikhsanov, N.R. Signs of magnetic accretion in the young Be/X-ray pulsar SXP 1062. Mon. Not. R. Astron. Soc. 2012, 424, L39–L43. [Google Scholar] [CrossRef]
- Ikhsanov, N.R.; Kim, V.Y.; Beskrovnaya, N.G.; ·Pustil’nik, L.A. A new look at the origin of the 6.67 hr period X-ray pulsar 1E 161348–5055. Astrophys. Space Sci. 2013, 346, 105–109. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Ikhsanov, N.R. A New Look at Anomalous X-ray Pulsars. Astron. Rep. 2014, 58, 217–227. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Chechetkin, V.M. Nucleosynthesis in Supernova Outbursts and the Chemical Composition of the Envelopes of Neutron Stars. Astrophys. Space Sci. 1974, 26, 25–46. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Chechetkin, V.M. Nonequilibrium shells of neutron stars and their role in sustaining X-ray emission and nucleosynthesis. Sov. Phys. Uspekhi 1979, 22, 89–108. [Google Scholar] [CrossRef]
- Mondal, T.; Mukhopadhyay, B. FSRQ/BL Lac dichotomy as the magnetized advective accretion process around black holes: A unified classification of blazars. Mon. Not. R. Astron. Soc. 2019, 486, 3465–3472. [Google Scholar] [CrossRef]
- Mondal, T.; Mukhopadhyay, B. Ultraluminous X-ray sources as magnetically powered sub-Eddington advective accretion flows around stellar mass black holes. Mon. Not. R. Astron. Soc. 2019, 482, L24–L28. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.; Lei, W.; Xie, W. An MAD explanation for the correlation between bulk Lorentz factor and minimum variability time-scale. Mon. Not. R. Astron. Soc. 2018, 478, 3525–3529. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Dolence, J.C.; Fryer, C.L. A MAD model for gamma-ray burst variability. Month. Not. R. Astron. Soc. 2016, 461, 1045–1052. [Google Scholar] [CrossRef][Green Version]
| 1 | Protons are always non-relativistic. |

| 1 | 1/3 | 1/10 | |
| 0.2 | 0/4 | 0.6 | 0.8 | 1 | 1.2 | 1.4 | |||
| z | 0.15 | 0.30 | 0.46 | 0.62 | 0.78 | 0.96 | 1.2 | 1.4 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bisnovatyi-Kogan, G.S. Accretion into Black Hole, and Formation of Magnetically Arrested Accretion Disks. Universe 2019, 5, 146. https://doi.org/10.3390/universe5060146
Bisnovatyi-Kogan GS. Accretion into Black Hole, and Formation of Magnetically Arrested Accretion Disks. Universe. 2019; 5(6):146. https://doi.org/10.3390/universe5060146
Chicago/Turabian StyleBisnovatyi-Kogan, Gennady S. 2019. "Accretion into Black Hole, and Formation of Magnetically Arrested Accretion Disks" Universe 5, no. 6: 146. https://doi.org/10.3390/universe5060146
APA StyleBisnovatyi-Kogan, G. S. (2019). Accretion into Black Hole, and Formation of Magnetically Arrested Accretion Disks. Universe, 5(6), 146. https://doi.org/10.3390/universe5060146




