Study of Jet Shape Observables in Au+Au Collisions at
s
N
N
= 200 GeV with JEWEL
Abstract
:1. Introduction
2. Jet Shape Observables
3. The Anti- Algorithm
4. JEWEL
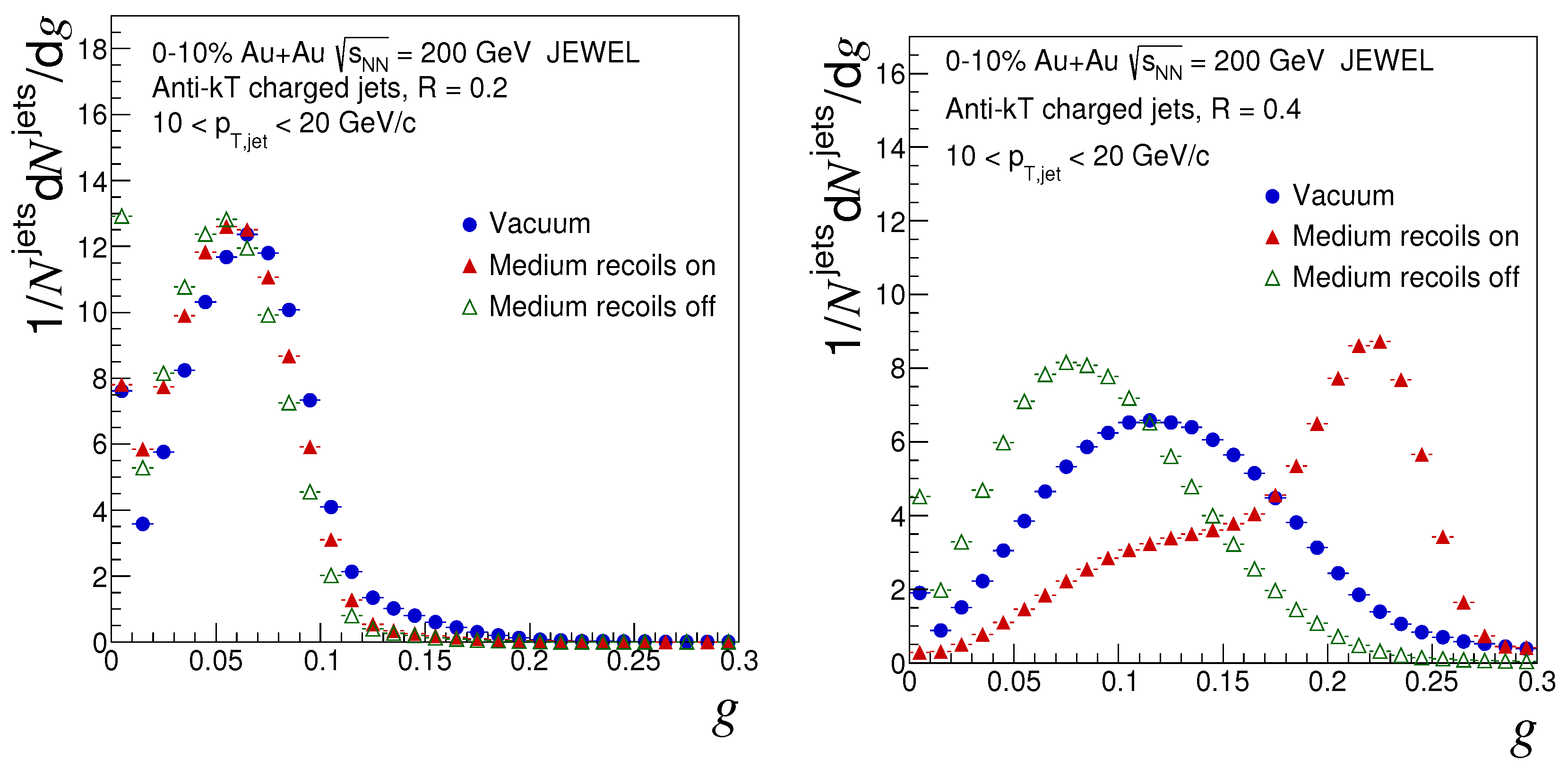
5. Results
6. Conclusions
Funding
Conflicts of Interest
Abbreviations
| LHC | Large Hadron Collider |
| RHIC | Relativistic Heavy-Ion Collider |
| CERN | Conseil européen pour la recherche nucléaire |
| QGP | Quark Gluon Plasma |
| QCD | Quantum Chromodynamics |
| CMS | center-of-mass |
| JEWEL | Jet Evolution With Energy Loss |
| IRC safe | Infrared and Collinear safe |
| ALICE | A Large Ion Collider Experiment |
References
- Agafonova, V. Study of Jet Shape Observables at RHIC. Available online: https://physics.fjfi.cvut.cz/publications/ejcf/bp_ejcf_17_agafonova.pdf (accessed on 11 May 2019).
- Aad, G.; Abbott, B.; Abdallah, J.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; Abramowicz, H.; Abreu, H.; et al. Observation of a Centrality-Dependent Dijet Asymmetry in Lead-Lead Collisions at = 2.77 TeV with the ATLAS Detector at the LHC. Phys. Rev. Lett. 2010, 105, 252303. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S. et al. [CMS Collaboration] Observation and studies of jet quenching in PbPb collisions at nucleon-nucleon center-of-mass energy = 2.76 TeV. Phys. Rev. C 2011, 84, 024906. [Google Scholar] [CrossRef]
- Vitev, I.; Wicks, S.; Zhang, B.W. A Theory of jet shapes and cross sections: From hadrons to nuclei. J. High Energy Phys. 2008, 11, 93. [Google Scholar] [CrossRef]
- Cunqueiro, L. et al. [ALICE Collaboration] Jet shapes in pp and Pb–Pb collisions at ALICE. Nucl. Phys. A 2016, 956, 593–596. [Google Scholar] [CrossRef] [Green Version]
- Salam, G.P. Towards Jetography. Eur. Phys. J. C 2010, l67, 637–686. [Google Scholar] [CrossRef]
- Cacciari, M.; Salam, G.P.; Soyez, G. The Anti-k(t) jet clustering algorithm. J. High Energy Phys. 2008, 4, 63. [Google Scholar] [CrossRef]
- Zapp, K.C. JEWEL 2.0.0: Directions for use. Eur. Phys. J. 2014, 74, 2762. [Google Scholar] [CrossRef]
- Zapp, K.C. Geometrical aspects of jet quenching in JEWEL. Phys. Lett. B 2014, 735, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Zapp, K.C.; Ingelman, G.; Rathsman, J.; Stachel, J.; Wiedemann, U.A. A Monte Carlo Model for ‘Jet Quenching’. Eur. Phys. J. C 2009, 60, 617–632. [Google Scholar] [CrossRef]
- Zapp, K.C.; Kunnawalkam Elayavalli, R. Medium response in JEWEL and its impact on jet shape observables in heavy ion collisions. J. High Energy Phys. 2017, 7, 141. [Google Scholar] [CrossRef]
- Cacciari, M.; Salam, G.P.; Soyez, G. FastJet user manual. Eur. Phys. J. C 2012, 72, 1896. [Google Scholar] [CrossRef]
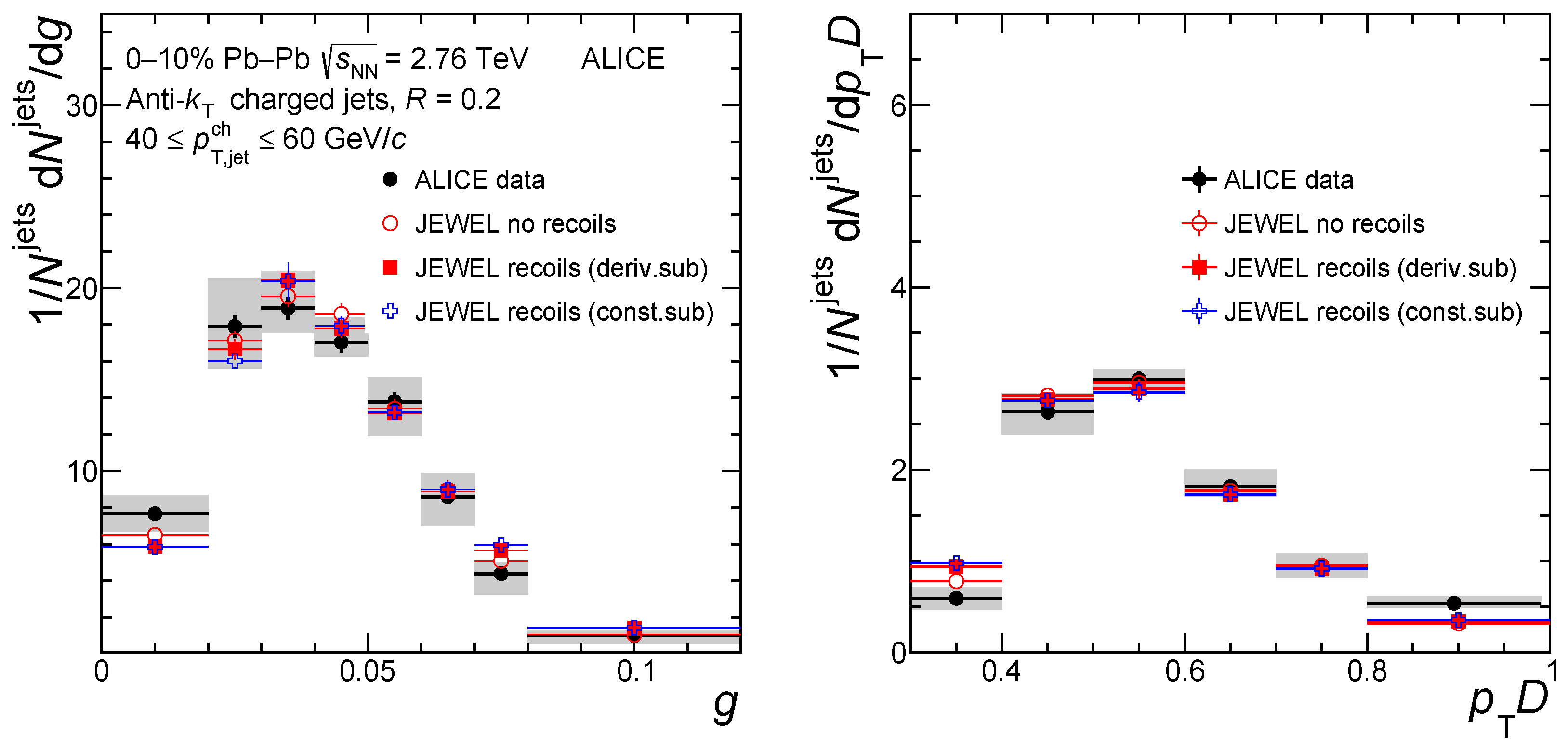
- Acharya, S.; Adamová, D.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; et al. Medium modification of the shape of small-radius jets in central Pb-Pb collisions at = 2.76 TeV. J. High Energy Phys. 2018, 10, 139. [Google Scholar] [CrossRef]





| Name of Parameter | Name in JEWEL | Value |
|---|---|---|
| Parton Distribution Function set | PDFSET | 10,100 |
| Number of events | NEVENT | 100,000 |
| Mass number of Au nucleus | MASS | 197 |
| The CMS energy of the colliding system | SQRTS, [GeV] | 200 |
| Minimum in matrix element | PTMIN, [GeV] | 3 |
| Maximum in matrix element | PTMAX, [GeV] | −1 |
| The rapidity range | ETAMAX | 2.5 |
| Name of Parameter | Name in JEWEL | Value | |
|---|---|---|---|
| The initial (mean) temperature | TI, [GeV] | 0.28 | |
| The initial time | TAUI, [fm] | 0.6 | |
| An integer mass number of colliding nuclei | A | 197 | |
| The lower end of centrality range | CENTRMIN, [%] | 0 | 60 |
| The upper end of centrality range | CENTRMAX, [%] | 10 | 80 |
| The switch of keeping recoils | KEEPRECOLIS | T | F |
| The nucleus–nucleus cross-section | SIGMANN, [fm] | 4.2 | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agafonova, V.
Study of Jet Shape Observables in Au+Au Collisions at
Agafonova V.
Study of Jet Shape Observables in Au+Au Collisions at
Agafonova, Veronika.
2019. "Study of Jet Shape Observables in Au+Au Collisions at
Agafonova, V.
(2019). Study of Jet Shape Observables in Au+Au Collisions at




