Taming the Energy Rise of the Total Proton-Proton Cross-Section
Abstract
:1. Introduction
2. Multiparton Interactions: “Minijet” Approach and Beyond
2.1. MPIs: “Minijet” Approach
2.2. MPIs: Role of Color Fluctuations
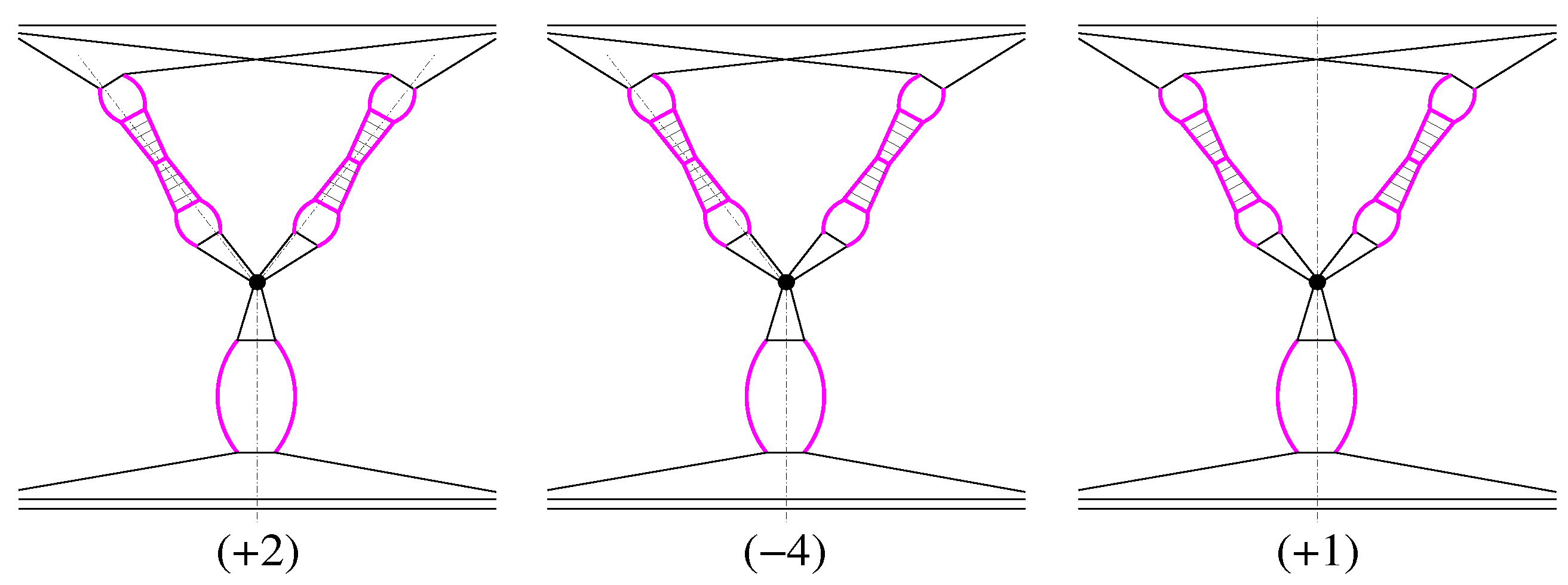
2.3. MPIs: Role of Multiparton Correlations
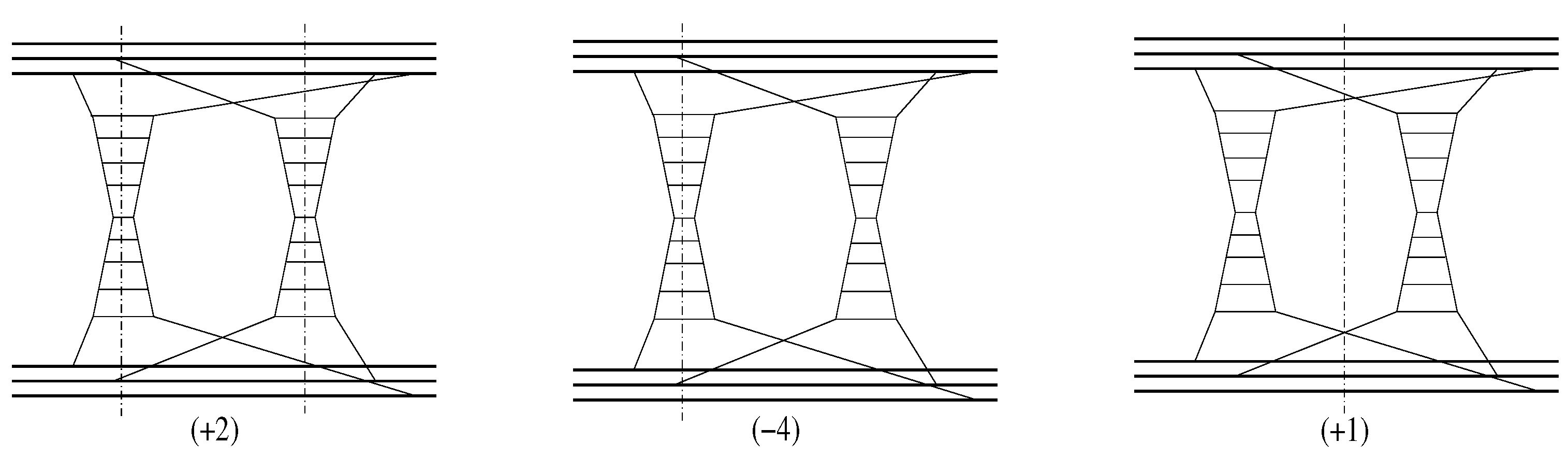
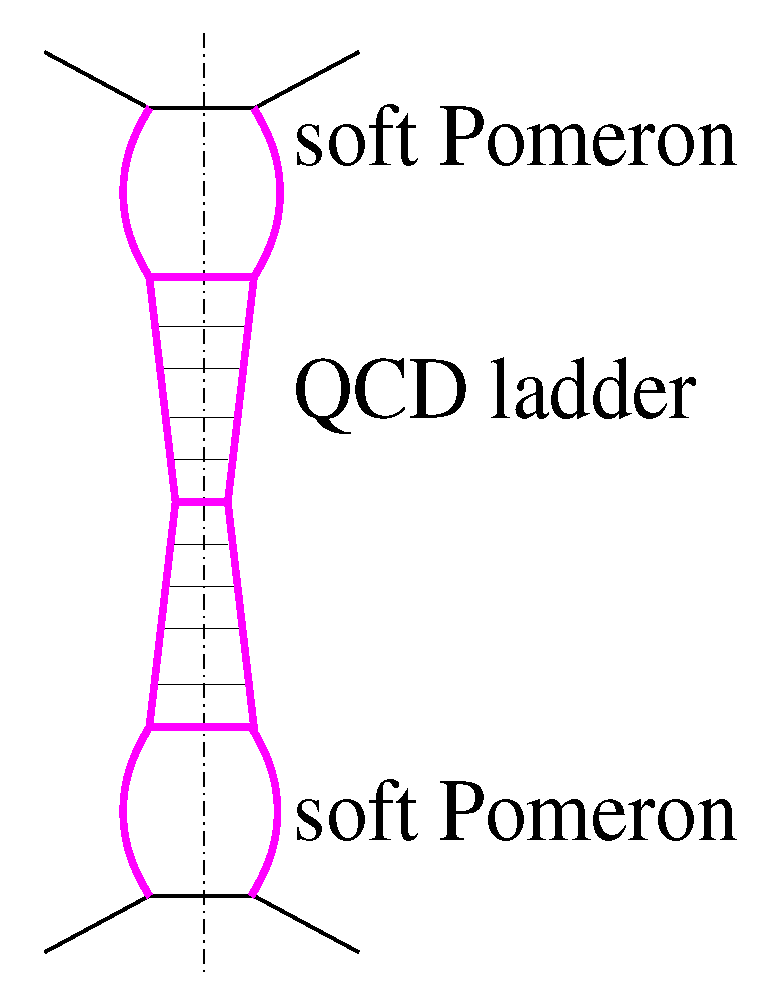
3. Potential Importance of Dynamical Higher Twist Corrections
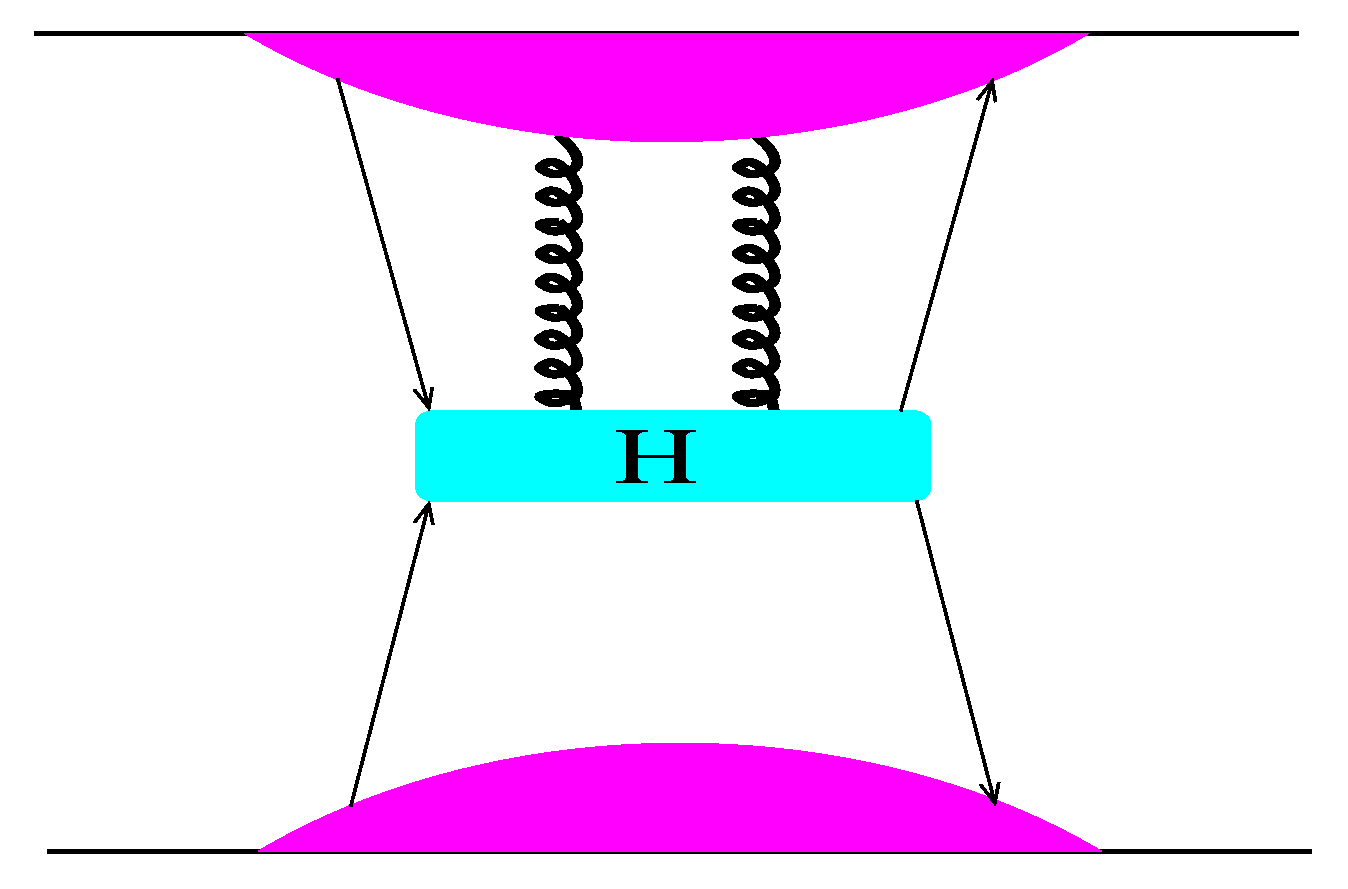
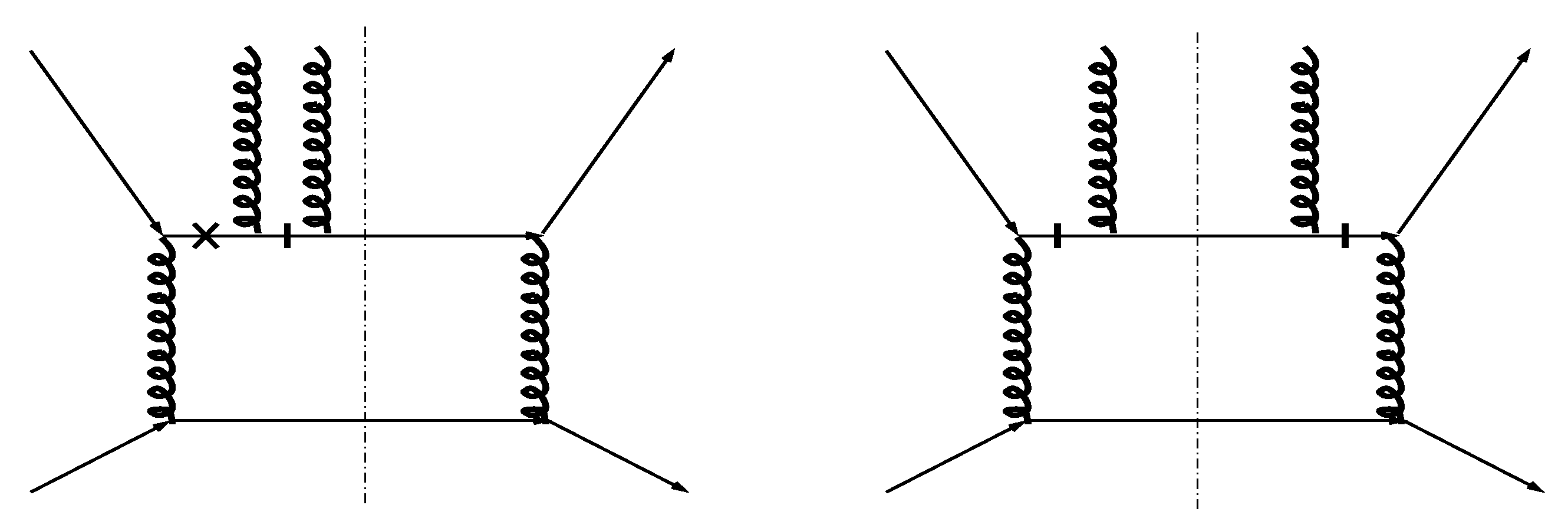
3.1. Resummed Power Corrections to High-Energy Scattering
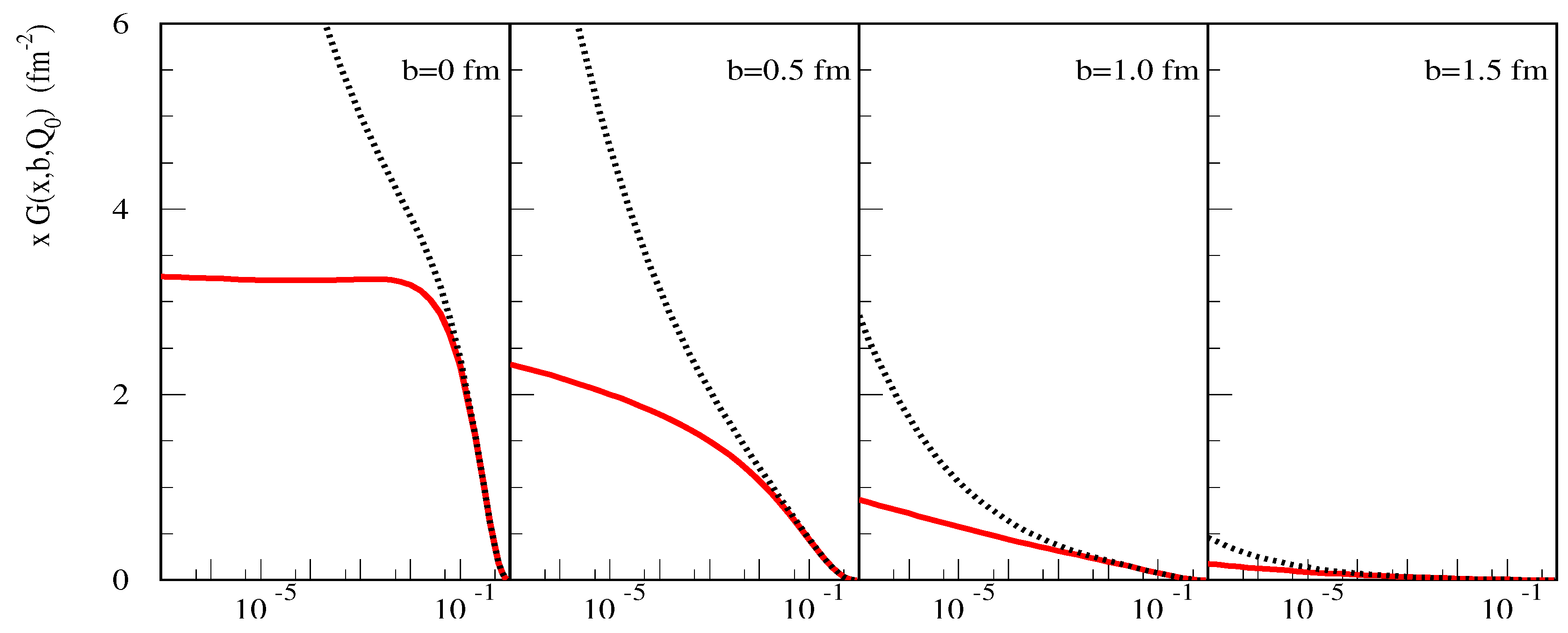
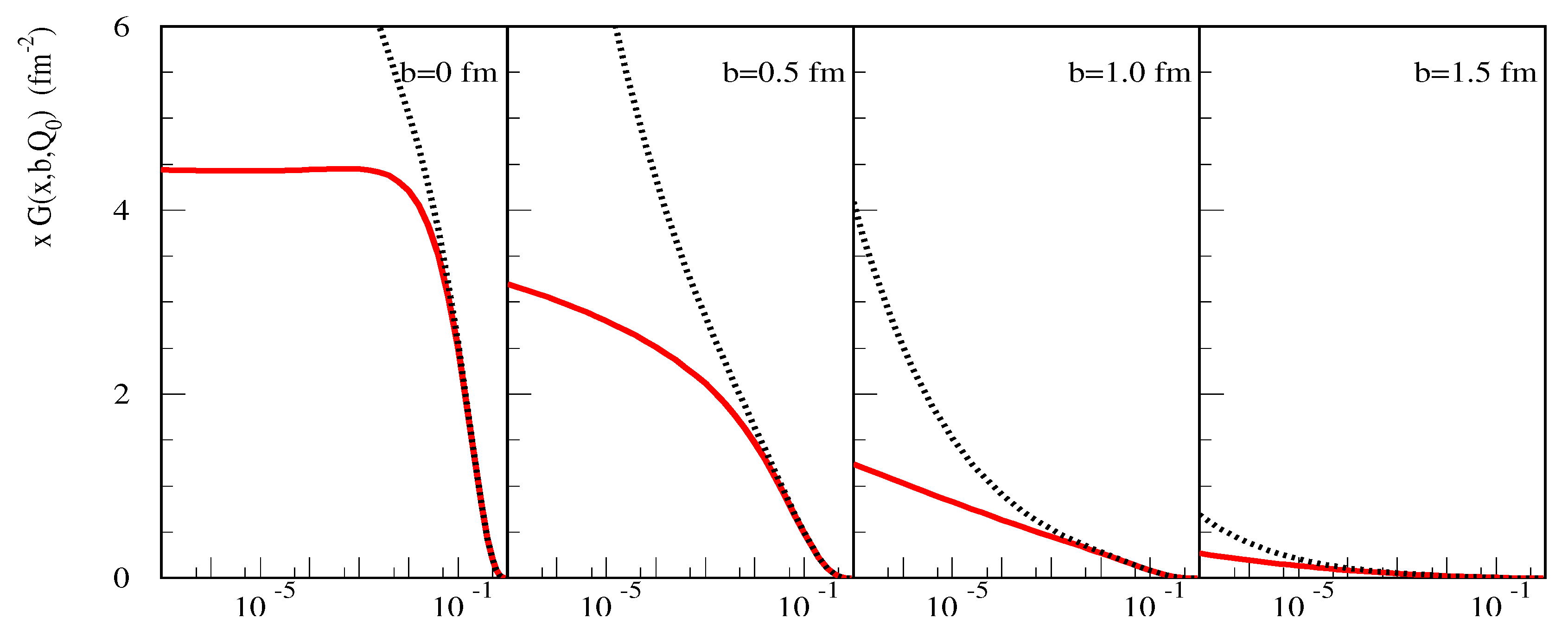
3.2. Additional Assumptions and Model Implementation
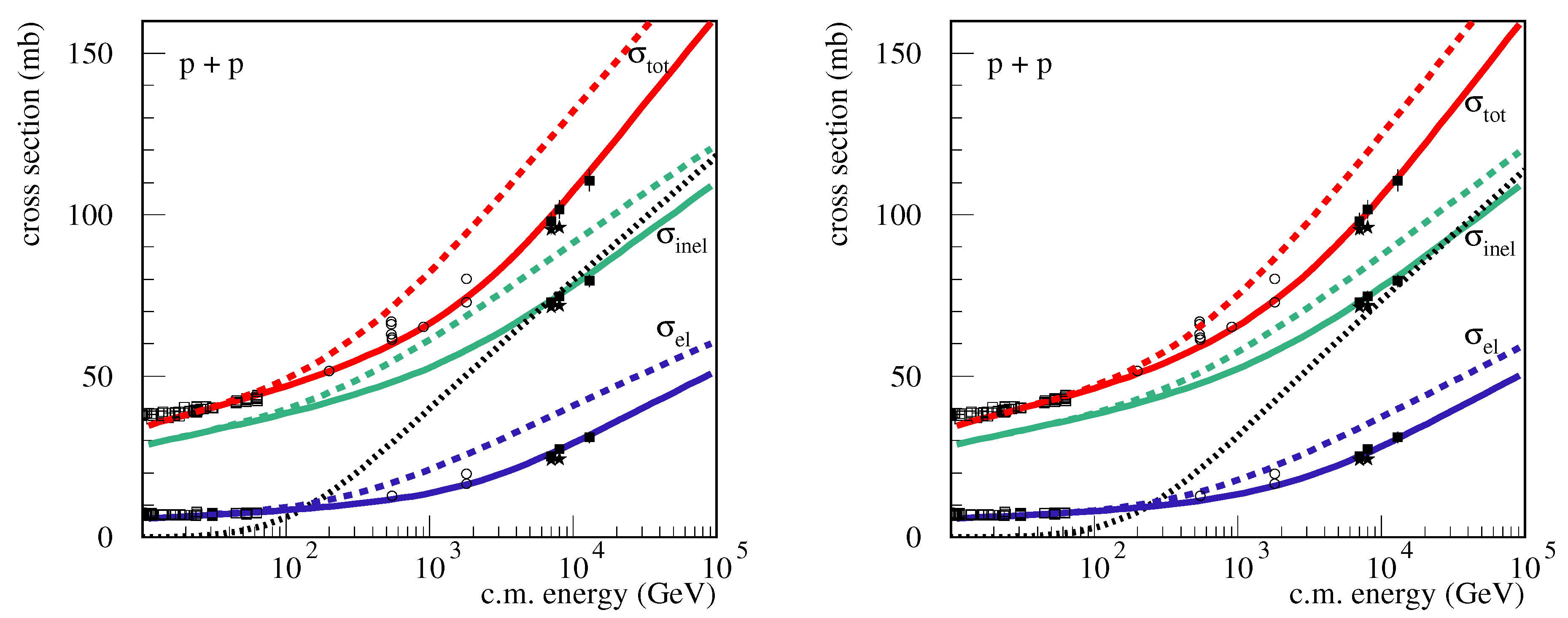
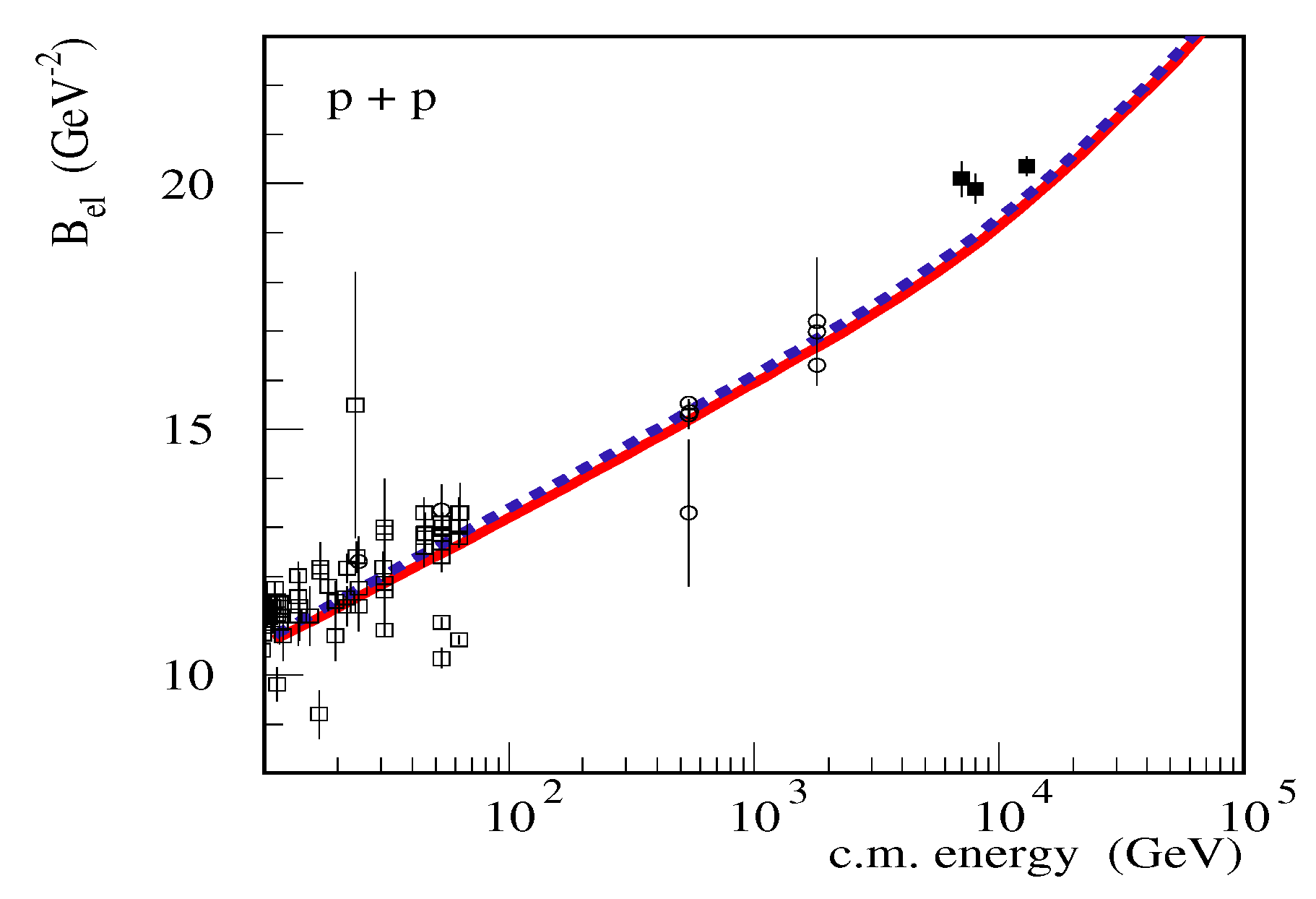
3.3. Impact on the Energy Rise of pp Cross Sections
4. Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| MC | Monte Carlo |
| pQCD | perturbative quantum chromodynamics |
| parton distribution function | |
| LC | light cone |
| c.m. | center-of-mass |
| DGLAP | Dokshitzer-Gribov-Lipatov-Altarelli-Parisi |
| MPI | multiparton interaction |
| GPD | generalized parton distribution |
| DPS | double parton scattering |
| AGK | Abramovskii-Gribov-Kancheli |
| DIS | deep inelastic scattering |
| LHC | Large Hadron Collider |
| HT | higher twist |
References
- Engel, R.; Heck, D.; Pierog, T. Extensive air showers and hadronic interactions at high energy. Ann. Rev. Nucl. Part. Sci. 2011, 61, 467–489. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Soft Gluons and Factorization. Nucl. Phys. B 1988, 308, 833–856. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Factorization of Hard Processes in QCD. Adv. Ser. Direct. High Energy Phys. 1989, 5, 1–91. [Google Scholar]
- Gribov, V.N.; Lipatov, L.N. Deep inelastic e p scattering in perturbation theory. Sov. J. Nucl. Phys. 1972, 15, 438–450. [Google Scholar]
- Altarelli, G.; Parisi, G. Asymptotic Freedom in Parton Language. Nucl. Phys. B 1977, 126, 298–318. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L. Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e− Annihilation by Perturbation Theory in Quantum Chromodynamics. Sov. Phys. JETP 1977, 46, 641–653. [Google Scholar]
- Akiba, K.; Akbiyik, M.; Albrow, M.; Arneodo, M.; Avati, V.; Baechler, J.; Baillie, O.V.; Bartalini, P.; Bartels, J.; Baur, S.; et al. LHC Forward Physics. J. Phys. G 2016, 43, 110201. [Google Scholar] [CrossRef]
- Calucci, G.; Treleani, D. Incoherence and multiple parton interactions. Phys. Rev. D 2009, 80, 054025. [Google Scholar] [CrossRef]
- Blok, B.; Dokshitzer, Y.; Frankfurt, L.; Strikman, M. The Four jet production at LHC and Tevatron in QCD. Phys. Rev. D 2011, 83, 071501. [Google Scholar] [CrossRef]
- Blok, B.; Dokshitzer, Y.; Frankfurt, L.; Strikman, M. pQCD physics of multiparton interactions. Eur. Phys. J. C 2012, 72, 1963. [Google Scholar] [CrossRef]
- Diehl, M.; Ostermeier, D.; Schafer, A. Elements of a theory for multiparton interactions in QCD. JHEP 2012, 1203, 89. [Google Scholar] [CrossRef]
- Abramovsky, V.A.; Gribov, V.N.; Kancheli, O.V. Character of Inclusive Spectra and Fluctuations Produced in Inelastic Processes by Multi-Pomeron Exchange. Sov. J. Nucl. Phys. 1974, 18, 308–316. [Google Scholar]
- Rogers, T.C.; Stasto, A.M.; Strikman, M.I. Unitarity Constraints on Semi-hard Jet Production in Impact Parameter Space. Phys. Rev. D 2008, 77, 114009. [Google Scholar] [CrossRef]
- Durand, L.; Pi, H. Semihard QCD and High-energy pp and p¯p Scattering. Phys. Rev. D 1989, 40, 1436. [Google Scholar] [CrossRef]
- Wang, X.-N. pQCD based approach to parton production and equilibration in high-energy nuclear collisions. Phys. Rept. 1997, 280, 287–371. [Google Scholar] [CrossRef]
- Frankfurt, L.; Strikman, M.; Treleani, D.; Weiss, C. Evidence for color fluctuations in the nucleon in high-energy scattering. Phys. Rev. Lett. 2008, 101, 202003. [Google Scholar] [CrossRef]
- Khoze, V.A.; Martin, A.D.; Ryskin, M.G. Elastic and diffractive scattering at the LHC. Phys. Lett. B 2018, 784, 192. [Google Scholar] [CrossRef]
- Antchev, G.; Berretti, M.; Bozzo, M.; Brogi, P.; Robutti, E.; Smajek, J.; Radicioni, E.; Atanassov, I.; Ferretti, R.; Eggert, K.; et al. Measurement of proton-proton inelastic scattering cross-section at = 7 TeV. Europhys. Lett. 2013, 101, 21003. [Google Scholar]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bossini, E.; Bottigli, U.; Bozzo, M.; et al. Double diffractive cross-section measurement in the forward region at the LHC. Phys. Rev. Lett. 2013, 111, 262001. [Google Scholar] [CrossRef]
- Rogers, T.C.; Strikman, M. Multiple Hard Partonic Collisions with Correlations in Proton-Proton Scattering. Phys. Rev. D 2010, 81, 016013. [Google Scholar] [CrossRef]
- Ostapchenko, S. Nonlinear screening effects in high energy hadronic interactions. Phys. Rev. D 2006, 74, 014026. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar] [CrossRef]
- Drescher H, J.; Hladik, M.; Ostapchenko, S.; Werner, K. A Unified treatment of high-energy interactions. J. Phys. G 1999, 25, L91. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton based Gribov-Regge theory. Phys. Rep. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Ostapchenko, S.; Drescher, H.J.; Liu, F.M.; Pierog, T.; Werner, K. Consistent treatment of soft and hard processes in hadronic interactions. J. Phys. G 2002, 28, 2597. [Google Scholar] [CrossRef]
- Ostapchenko, S. On the re-summation of enhanced Pomeron diagrams. Phys. Lett. B 2006, 636, 40–45. [Google Scholar] [CrossRef]
- Ostapchenko, S. Enhanced Pomeron diagrams: Re-summation of unitarity cuts. Phys. Rev. D 2008, 77, 034009. [Google Scholar] [CrossRef]
- Ostapchenko, S. Total and diffractive cross sections in enhanced Pomeron scheme. Phys. Rev. D 2010, 81, 114028. [Google Scholar] [CrossRef]
- Ryskin, M.G.; Martin, A.D.; Khoze, V.A. Soft processes at the LHC. II. Soft-hard factorization breaking and gap survival. Eur. Phys. J. C 2009, 60, 265–272. [Google Scholar] [CrossRef]
- Ostapchenko, S.; Bleicher, M. Double parton scattering: Impact of nonperturbative parton correlations. Phys. Rev. D 2016, 93, 034015. [Google Scholar] [CrossRef]
- Blok, B.; Strikman, M. Interplay of soft and perturbative correlations in multiparton interactions at central rapidities. Phys. Lett. B 2017, 772, 219–224. [Google Scholar] [CrossRef]
- Ostapchenko, S.; Bleicher, M. A dynamical cutoff on low pt jet production from higher twist effects. 2019; paper in preparation. [Google Scholar]
- Jaffe, R.L.; Soldate, M. Twist Four in the QCD Analysis of Leptoproduction. Phys. Lett. B 1981, 105B, 467–472. [Google Scholar] [CrossRef]
- Jaffe, R.L.; Soldate, M. Twist Four in Electroproduction: Canonical Operators and Coefficient Functions. Phys. Rev. D 1982, 26, 49. [Google Scholar] [CrossRef]
- Ellis, R.K.; Furmanski, W.; Petronzio, R. Power Corrections to the Parton Model in QCD. Nucl. Phys. B 1982, 207, 1–14. [Google Scholar] [CrossRef]
- Ellis, R.K.; Furmanski, W.; Petronzio, R. Unraveling Higher Twists. Nucl. Phys. B 1983, 212, 29. [Google Scholar] [CrossRef]
- Qiu, J.-W. Twist Four Contributions to the Parton Structure Functions. Phys. Rev. D 1990, 42, 30. [Google Scholar] [CrossRef]
- Qiu, J.-W.; Vitev, I. Resummed QCD power corrections to nuclear shadowing. Phys. Rev. Lett. 2004, 93, 262301. [Google Scholar] [CrossRef]
- Qiu, J.-W.; Vitev, I. Coherent QCD multiple scattering in proton-nucleus collisions. Phys. Lett. B 2006, 632, 507–511. [Google Scholar] [CrossRef]
- Qiu, J.-W.; Vitev, I. Nuclear shadowing in neutrino nucleus deeply inelastic scattering. Phys. Lett. B 2004, 587, 52–61. [Google Scholar] [CrossRef]
- Qiu, J.-W.; Sterman, G. Power corrections in hadronic scattering. 1. Leading 1/Q**2 corrections to the Drell-Yan cross-section. Nucl. Phys. B 1991, 353, 105–136. [Google Scholar] [CrossRef]
- Qiu, J.-W.; Sterman, G. Power corrections to hadronic scattering. 2. Factorization. Nucl. Phys. B 1991, 353, 137–164. [Google Scholar] [CrossRef]
- Doria, R.; Frenkel, J.; Taylor, J.C. Counter Example to Nonabelian Bloch-Nordsieck Theorem. Nucl. Phys. B 1980, 168, 93. [Google Scholar] [CrossRef]
- Basu, R.; Ramalho, A.J.; Sterman, G. Factorization at Higher Twist in Hadron—Hadron Scattering. Nucl. Phys. B 1984, 244, 221–246. [Google Scholar] [CrossRef]
- Nakamura, K.; Hagiwara, K.; Hikasa, K.; Murayama, H.; Tanabashi, M.; Watari, T.; Amsler, C.; Antonelli, M.; Asner, D.M.; Baer, H.; et al. Review of particle physics. J. Phys. G 2010, 37, 075021. [Google Scholar] [CrossRef]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bossini, E.; Bozzo, M.; Brogi, P.; et al. Luminosity-independent measurements of total, elastic and inelastic cross-sections at = 7 TeV. Europhys. Lett. 2013, 101, 21004. [Google Scholar]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bossini, E.; Bottigli, U.; Bozzo, M.; et al. Luminosity-Independent Measurement of the Proton-Proton Total Cross Section at = 8 TeV. Phys. Rev. Lett. 2013, 111, 012001. [Google Scholar] [CrossRef]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Barrera, C.B.; Berardi, V.; Berretti, M.; Bossini, E.; Bottigli, U.; et al. First measurement of elastic, inelastic and total cross-section at = 13 TeV by TOTEM and overview of cross-section data at LHC energies. Eur. Phys. J. C 2019, 79, 103. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Measurement of the total cross section from elastic scattering in pp collisions at = 7 TeV with the ATLAS detector. Nucl. Phys. B 2014, 889, 486. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Measurement of the total cross section from elastic scattering in pp collisions at = 8 TeV with the ATLAS detector. Phys. Lett. B 2016, 761, 158. [Google Scholar] [CrossRef]
- Ostapchenko, S. Non-linear effects in high energy hadronic interactions. arXiv 2005, arXiv:hep-ph/0501093. [Google Scholar]
- CMS Collaboration. Production of leading charged particles and leading charged-particle jets at small transverse momenta in pp collisions at = 8 TeV. Phys. Rev. D 2015, 92, 112001. [Google Scholar] [CrossRef]
| 1 | For the chosen factorization scale, , this corresponds to the transverse momentum cutoff GeV. |

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostapchenko, S.; Bleicher, M. Taming the Energy Rise of the Total Proton-Proton Cross-Section. Universe 2019, 5, 106. https://doi.org/10.3390/universe5050106
Ostapchenko S, Bleicher M. Taming the Energy Rise of the Total Proton-Proton Cross-Section. Universe. 2019; 5(5):106. https://doi.org/10.3390/universe5050106
Chicago/Turabian StyleOstapchenko, Sergey, and Marcus Bleicher. 2019. "Taming the Energy Rise of the Total Proton-Proton Cross-Section" Universe 5, no. 5: 106. https://doi.org/10.3390/universe5050106
APA StyleOstapchenko, S., & Bleicher, M. (2019). Taming the Energy Rise of the Total Proton-Proton Cross-Section. Universe, 5(5), 106. https://doi.org/10.3390/universe5050106



