Bose–Einstein Correlations in pp and pPb Collisions at LHCb †
Abstract
1. Introduction
2. Materials and Methods
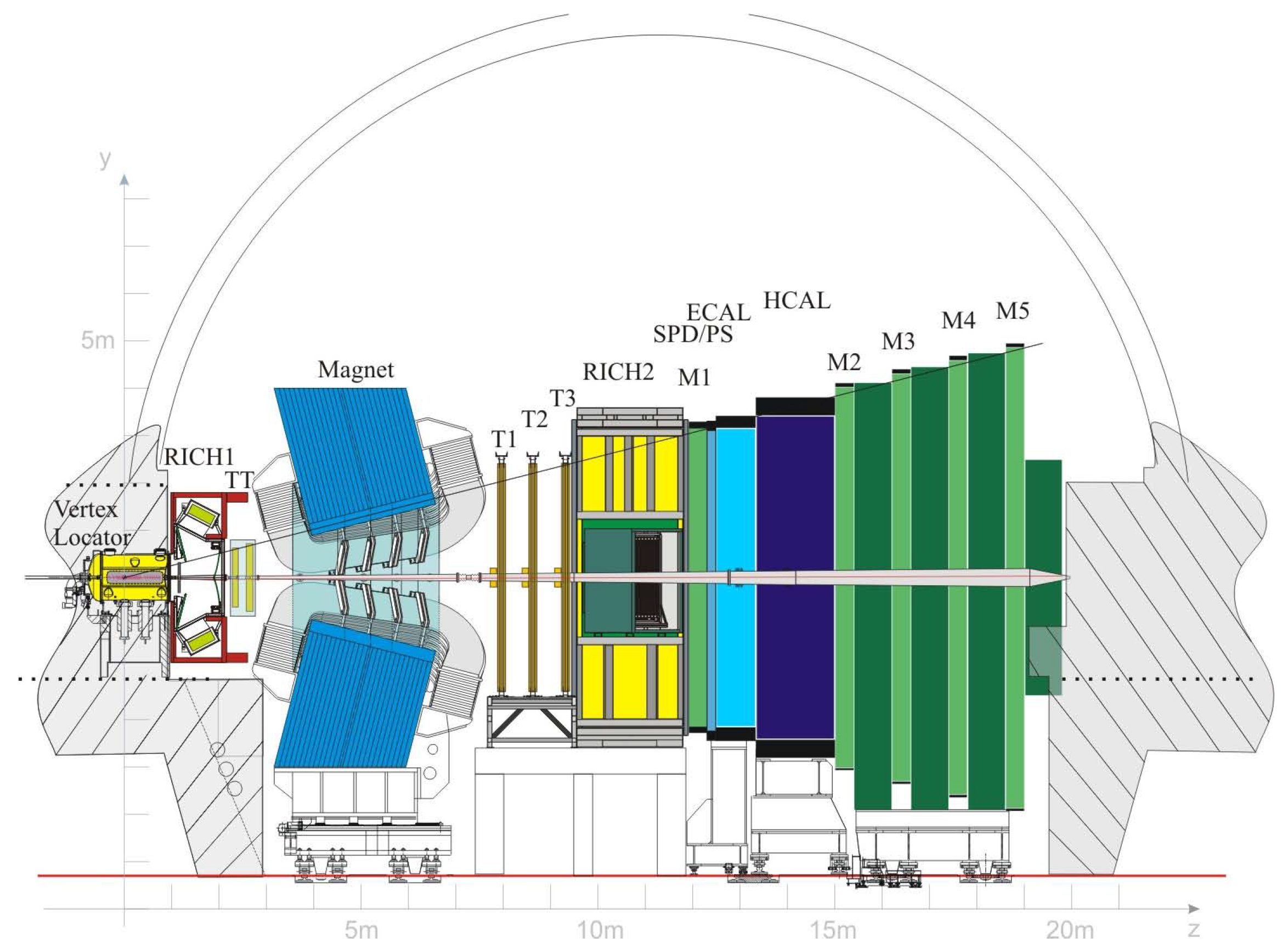
2.1. LHCb Detector
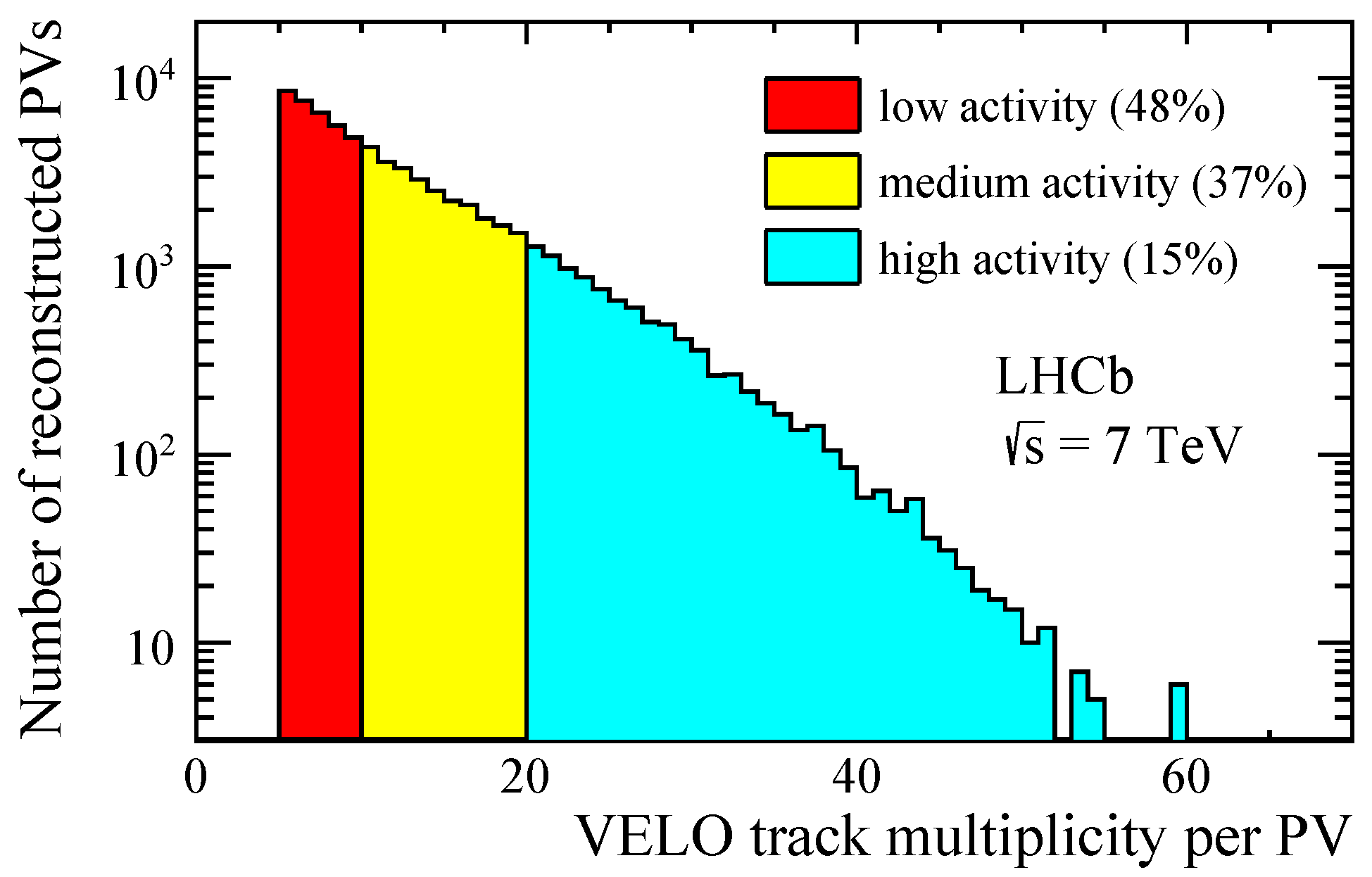
2.2. Data Sample
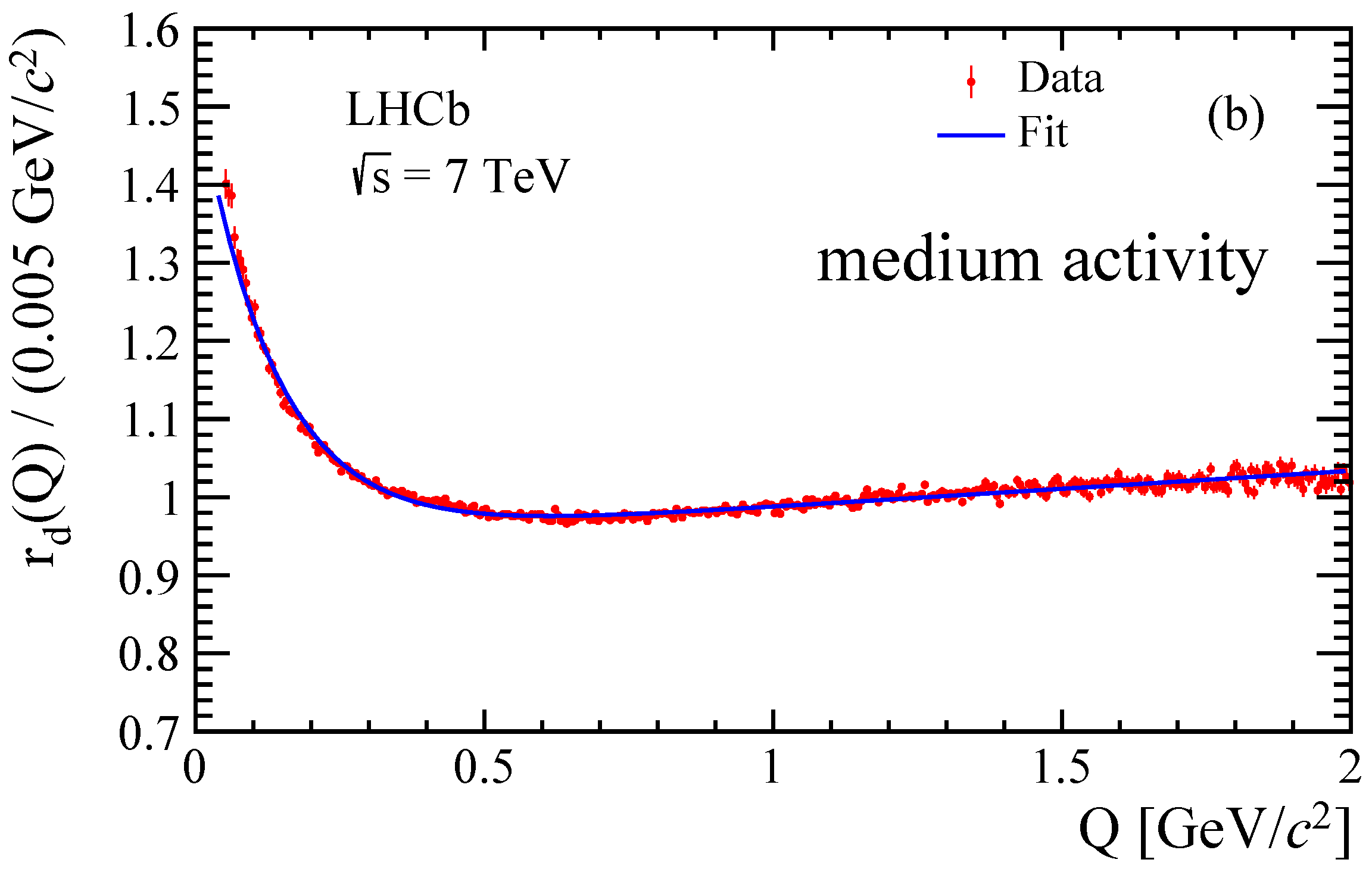
2.3. Analysis Method
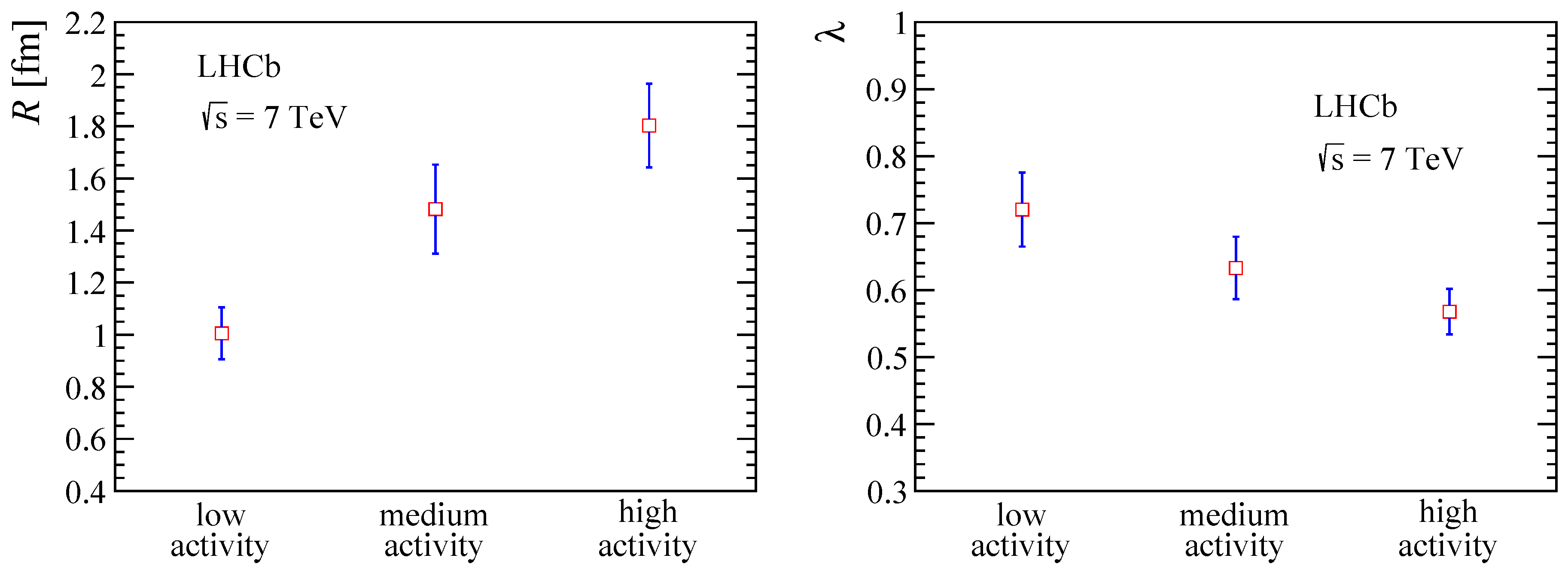
3. Results
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, R.H.; Twiss, R.Q. LXXIV. A new type of interferometer for use in radio astronomy. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 663–682. [Google Scholar] [CrossRef]
- Shapoval, V.M.; Braun-Munzinger, P.; Karpenko, I.A.; Sinyukov, Y.M. Femtoscopic scales in p+p and p+Pb collisions in view of the uncertainty principle. Phys. Lett. B 2013, 725, 139–147. [Google Scholar] [CrossRef][Green Version]
- Bożek, P.; Broniowski, W. Size of the emission source and collectivity in ultra-relativistic p–Pb collisions. Phys. Lett. B 2013, 720, 250–253. [Google Scholar] [CrossRef]
- Bzdak, A.; Schenke, B.; Tribedy, P.; Venugopalan, R. Initial-state geometry and the role of hydrodynamics in proton-proton, proton-nucleus, and deuteron-nucleus collisions. Phys. Rev. C 2013, 87, 064906. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Comparison of the color glass condensate to dihadron correlations in proton-proton and proton-nucleus collisions. Phys. Rev. D 2013, 87, 094034. [Google Scholar] [CrossRef]
- Goldhaber, G.; Goldhaber, S.; Fowler, W.B.; Hoang, T.F.; Kalogeropoulos, T.E.; Powell, W.M. Pion-Pion Correlations in Antiproton Annihilation Events. Phys. Rev. Lett. 1959, 3, 181–183. [Google Scholar] [CrossRef]
- ALEPH Collaboration. Fermi–Dirac correlations in Λ pairs in hadronic Z decays. Phys. Lett. B 2000, 475, 395–406. [Google Scholar] [CrossRef]
- ALEPH Collaboration. Two-dimensional analysis of Bose-Einstein correlationsin hadronic Z decays at LEP. Eur. Phys. J. C 2004, 36, 147–159. [Google Scholar] [CrossRef]
- DELPHI Collaboration. Bose-Einstein correlations in the hadronic decays of the Z0. Phys. Lett. B 1992, 286, 201–210. [Google Scholar] [CrossRef]
- DELPHI Collaboration. Kaon interference in the hadronic decays of the Z0. Phys. Lett. B 1996, 379, 330–340. [Google Scholar] [CrossRef][Green Version]
- L3 Collaboration. Measurement of an elongation of the pion source in Z decays. Phys. Lett. B 1999, 458, 517–528. [Google Scholar] [CrossRef]
- L3 Collaboration. Test of the τ-model of Bose–Einstein correlations and reconstruction of the source function in hadronic Z-boson decay at LEP. Eur. Phys. J. C 2011, 71, 1648. [Google Scholar] [CrossRef]
- OPAL Collaboration. Transverse and longitudinal Bose-Einstein correlations in hadronic Z0 decays. Eur. Phys. J. C 2000, 16, 423–433. [Google Scholar] [CrossRef][Green Version]
- OPAL Collaboration. Bose-Einstein correlations in K±K± pairs from Z0 decays into two hadronic jets. Eur. Phys. J. C 2001, 21, 23–32. [Google Scholar] [CrossRef][Green Version]
- ALICE Collaboration. Femtoscopy of pp collisions at and 7 TeV at the LHC with two-pion Bose-Einstein correlations. Phys. Rev. D 2011, 84, 112004. [Google Scholar] [CrossRef]
- ALICE Collaboration. Ks0Ks0 correlations in pp collisions at TeV from the LHC ALICE experiment. Phys. Lett. B 2012, 717, 151–161. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Two-particle Bose–Einstein correlations in pp collisions at = 0.9 and 7 TeV measured with the ATLAS detector. Eur. Phys. J. C 2015, 75, 466. [Google Scholar] [CrossRef]
- CMS Collaboration. First Measurement of Bose-Einstein Correlations in Proton-Proton Collisions at = 0.9 and 2.36 TeV at the LHC. Phys. Rev. Lett. 2010, 105, 032001. [Google Scholar] [CrossRef]
- CMS collaboration. Measurement of Bose-Einstein correlations in pp collisions at = 0.9 and 7 TeV. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- ALICE Collaboration. Two-pion Bose-Einstein correlations in central Pb-Pb collisions at = 2.76 TeV. Phys. Lett. B 2011, 696, 328–337. [Google Scholar] [CrossRef]
- STAR Collaboration. Pion interferometry in Au + Au and Cu + Cu collisions at = 62.4 and 200 GeV. Phys. Rev. C 2009, 80, 024905. [Google Scholar] [CrossRef]
- ALICE Collaboration. Two-pion femtoscopy in p-Pb collisions at = 5.02 TeV. Phys. Rev. C 2015, 91, 034906. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Femtoscopy with identified charged pions in proton-lead collisions at = 5.02 TeV with ATLAS. Phys. Rev. C 2017, 96, 064908. [Google Scholar] [CrossRef]
- CMS Collaboration. Bose-Einstein correlations in pp, pPb, and PbPb collisions at = 0.9 − 7 TeV. Phys. Rev. C 2018, 97, 064912. [Google Scholar] [CrossRef]
- Alexander, G.; Cohen, I.; Levin, E. The dependence of the emission size on the hadron mass. Phys. Lett. B 1999, 452, 159–166. [Google Scholar] [CrossRef]
- Bialas, A.; Kucharczyk, M.; Palka, H.; Zalewski, K. Mass dependence of HBT correlations in e+e− annihilation. Phys. Rev. D 2000, 62, 114007. [Google Scholar] [CrossRef]
- AFS Collaboration. Bose-Einstein correlations in αα, pp and pp interactions. Phys. Lett. B 1983, 129, 269–272. [Google Scholar] [CrossRef][Green Version]
- LHCb Collaboration. Bose-Einstein correlations of same-sign charged pions in the forward region in pp collisions at TeV. J. High Energy Phys. 2017, 2017, 25. [Google Scholar] [CrossRef]
- LHCb Collaboration. The LHCb Detector at the LHC. J. Instrum. 2008, 3, S08005. [Google Scholar] [CrossRef]
- LHCb Collaboration. LHCb detector performance. Int. J. Mod. Phys. A 2015, 30, 1530022. [Google Scholar] [CrossRef]
- Belyaev, I.; Brambach, T.; Brook, N.H.; Gauvin, N.; Corti, G.; Harrison, K.; Harrison, P.F.; He, J.; Ilten, P.H.; Jones, C.R.; et al. Handling of the generation of primary events in Gauss, the LHCb simulation framework. J. Phys. Conf. Ser. 2011, 331, 032047. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Mrenna, S.; Skands, P. A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 2008, 178, 852–867. [Google Scholar] [CrossRef]
- GEANT4 Collaboration. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrom. Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrom. Detect. Assoc. Equip. 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Alexander, G. Bose Einstein and Fermi Dirac interferometry in particle physics. Rep. Prog. Phys. 2003, 66, 481–522. [Google Scholar] [CrossRef]
- Pratt, S. Coherence and Coulomb effects on pion interferometry. Phys. Rev. D 1986, 33, 72–79. [Google Scholar] [CrossRef]
- Csörgő, T.; Hegyi, S.; Zajc, W.A. Bose-Einstein correlations for Lévy stable source distributions. Eur. Phys. J. C 2004, 36, 67–78. [Google Scholar] [CrossRef]
- Csörgő, T.; Zimányi, J. Pion interferometry for strongly correlated spacetime and momentum space. Nucl. Phys. A 1990, 517, 588–598. [Google Scholar] [CrossRef]
| Activity | R (fm) | (GeV) | ||
|---|---|---|---|---|
| Low | [8, 18] | 1.01 ± 0.01 ± 0.10 | 0.72 ± 0.01 ± 0.05 | 0.089 ± 0.002 ± 0.044 |
| Medium | [19, 35] | 1.48 ± 0.02 ± 0.17 | 0.63 ± 0.01 ± 0.05 | 0.049 ± 0.001 ± 0.009 |
| High | [36, 96] | 1.80 ± 0.03 ± 0.16 | 0.57 ± 0.01 ± 0.03 | 0.026 ± 0.001 ± 0.010 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malecki, B. Bose–Einstein Correlations in pp and pPb Collisions at LHCb. Universe 2019, 5, 95. https://doi.org/10.3390/universe5040095
Malecki B. Bose–Einstein Correlations in pp and pPb Collisions at LHCb. Universe. 2019; 5(4):95. https://doi.org/10.3390/universe5040095
Chicago/Turabian StyleMalecki, Bartosz. 2019. "Bose–Einstein Correlations in pp and pPb Collisions at LHCb" Universe 5, no. 4: 95. https://doi.org/10.3390/universe5040095
APA StyleMalecki, B. (2019). Bose–Einstein Correlations in pp and pPb Collisions at LHCb. Universe, 5(4), 95. https://doi.org/10.3390/universe5040095





