Influence of Finite Volume Effect on the Polyakov Quark–Meson Model
Abstract
1. Introduction
2. The Polyakov Quark–Meson (PQM) Model
3. Results
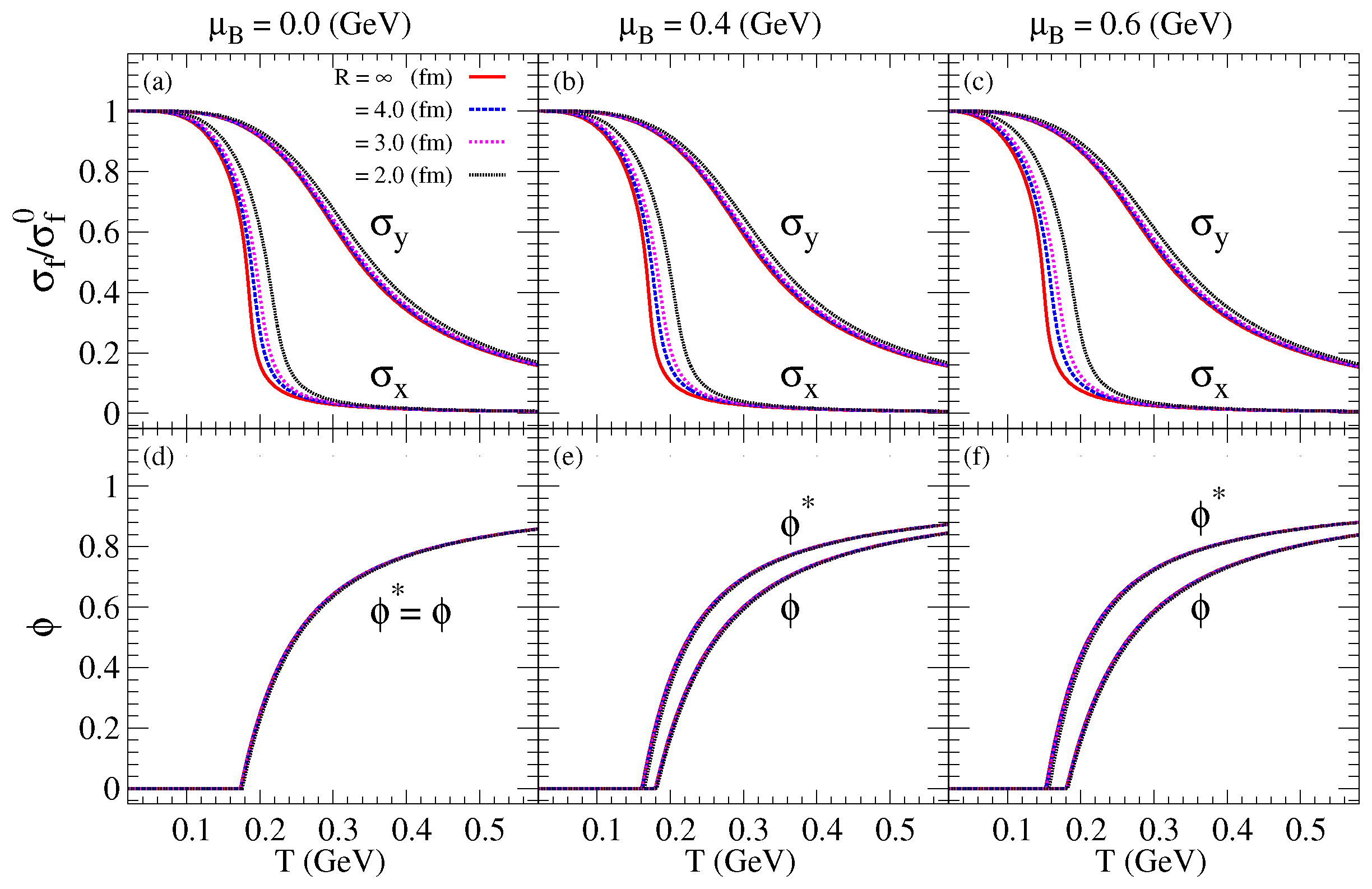
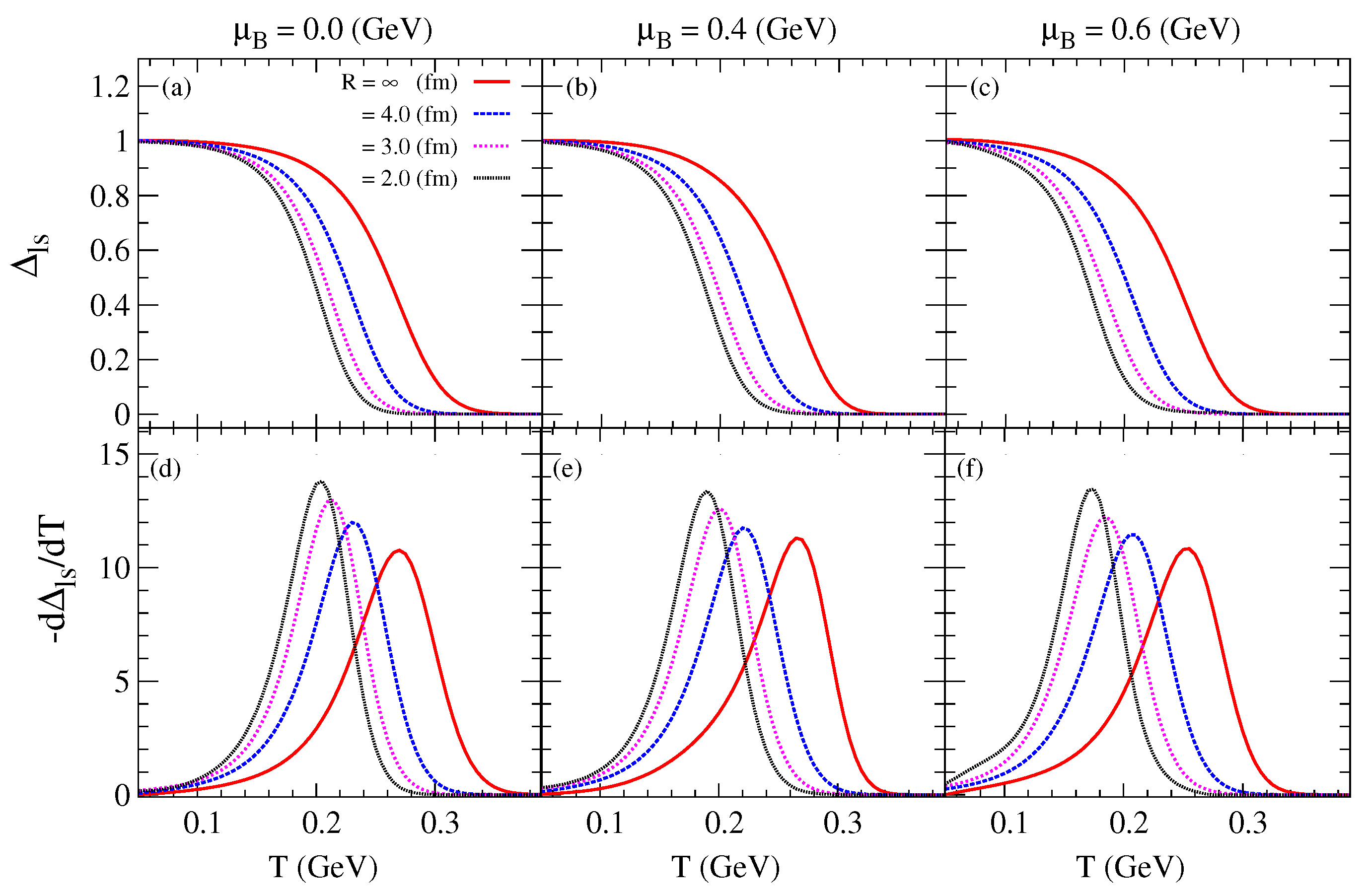
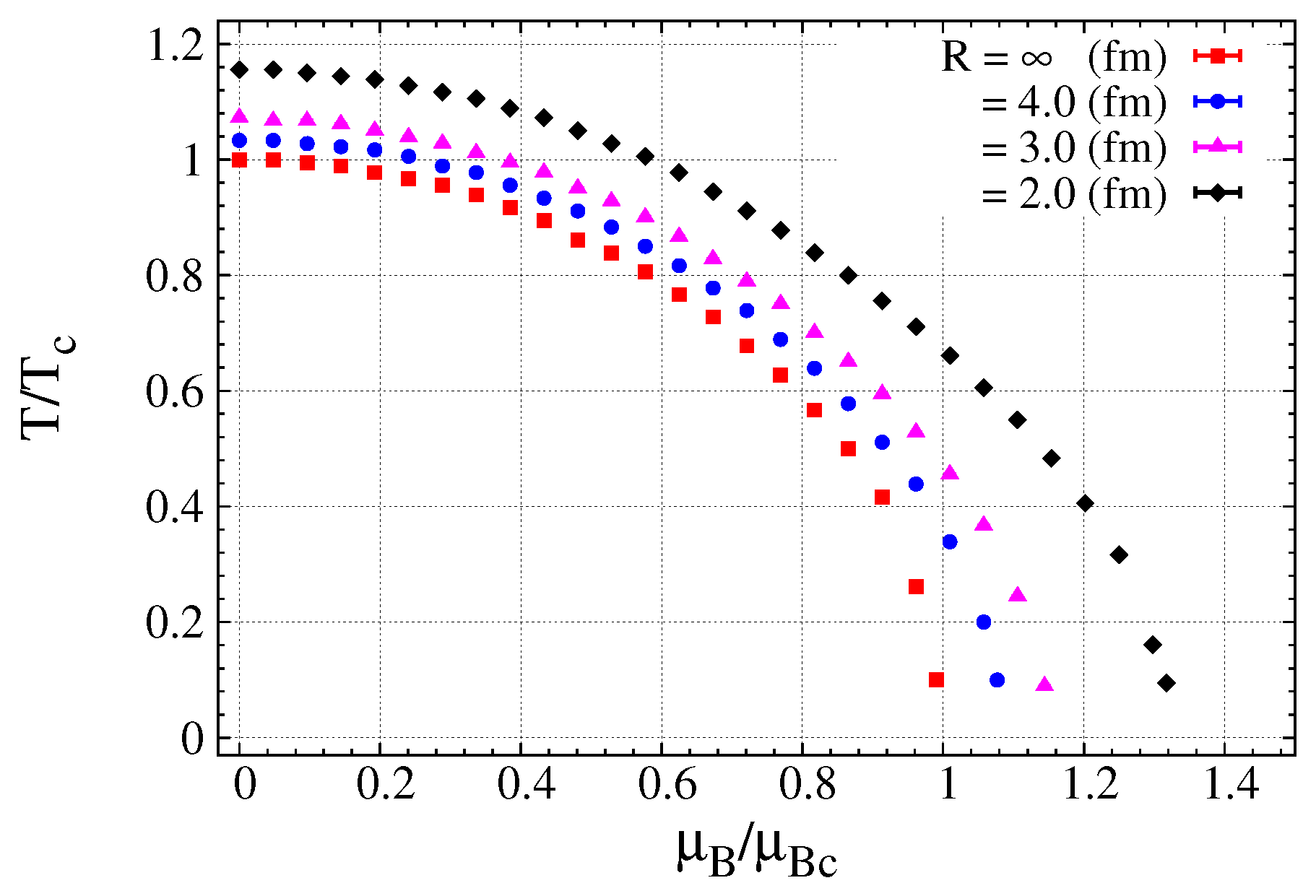
3.1. Order Parameters and Phase Transition
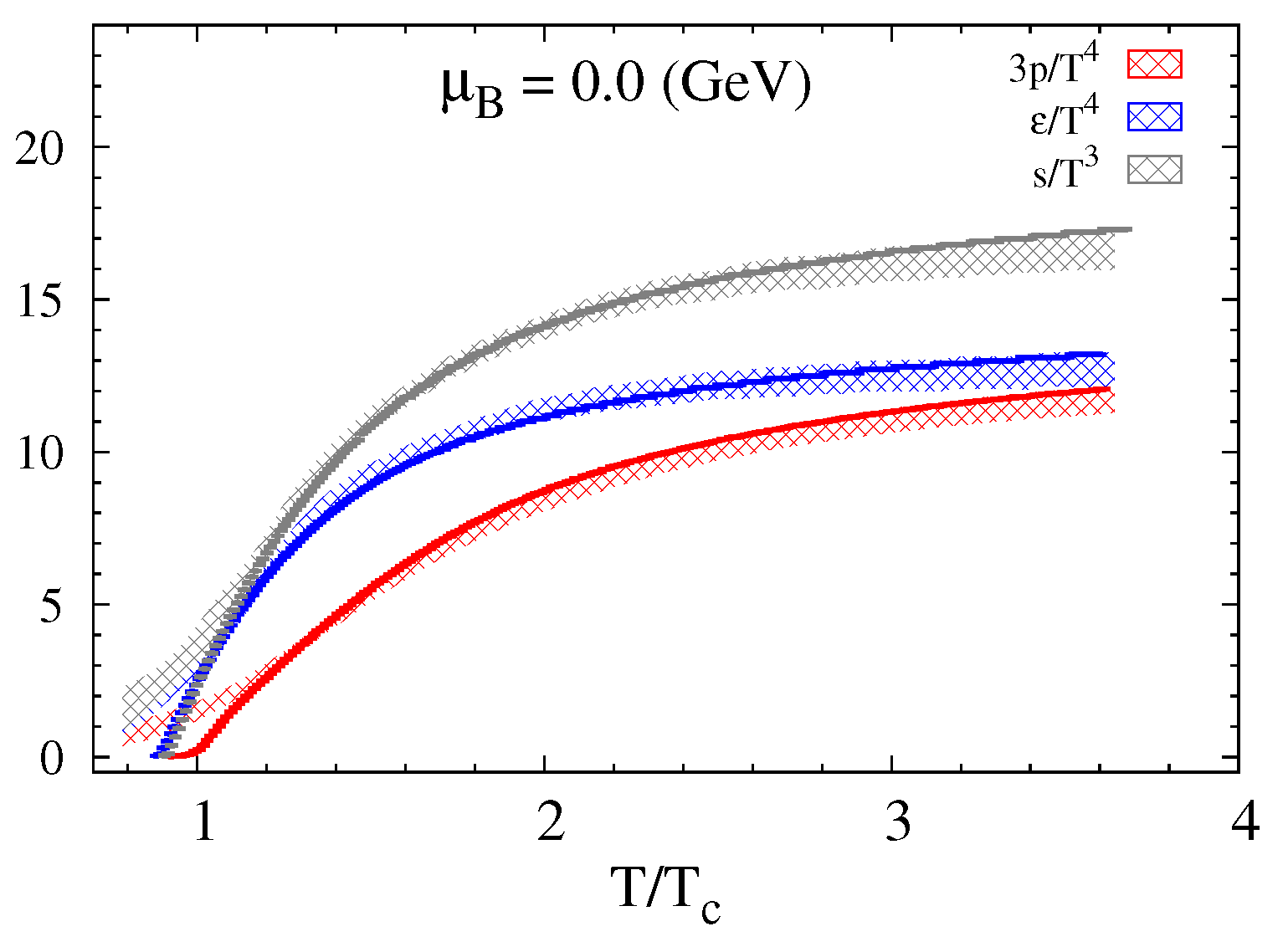
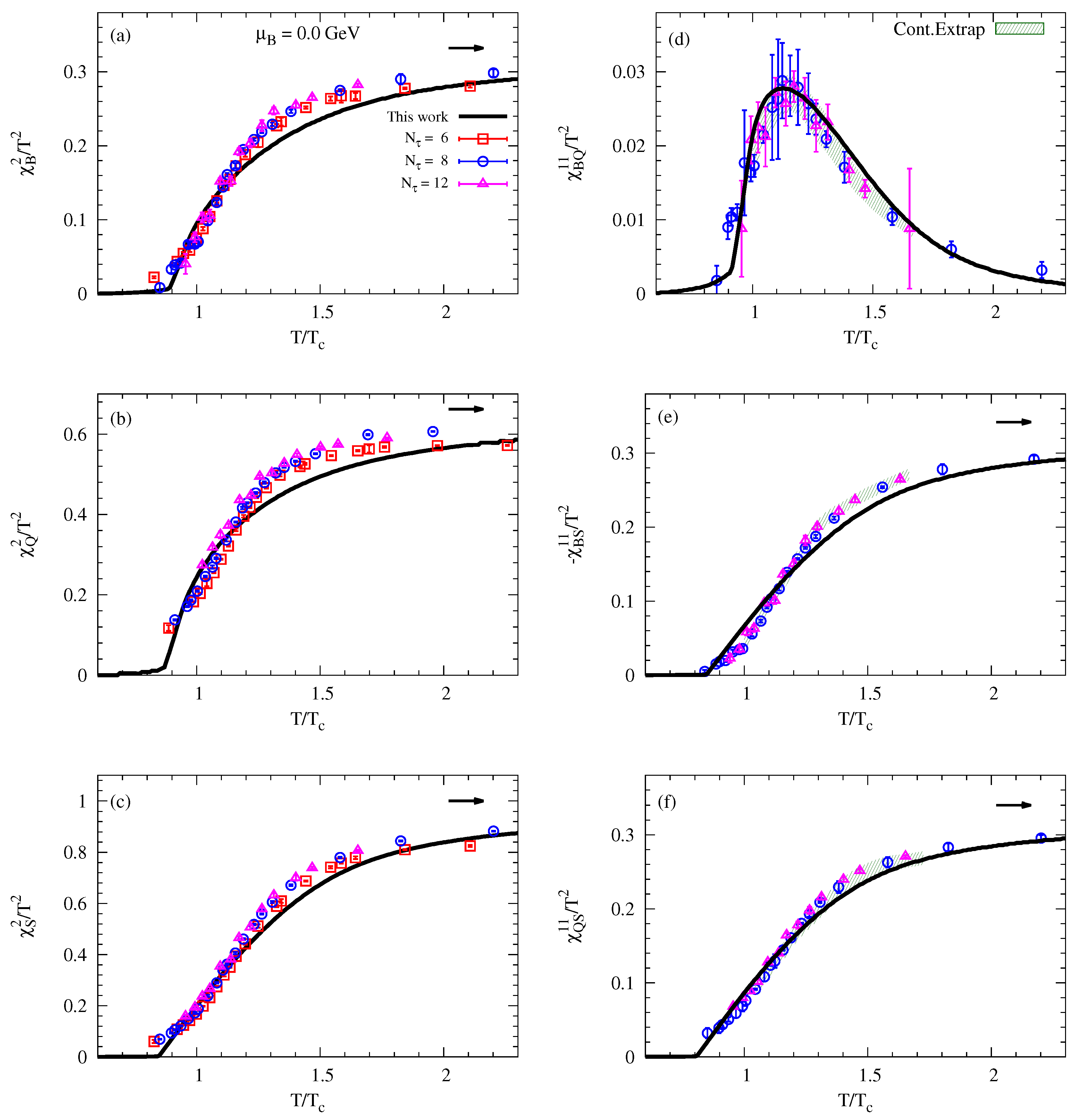
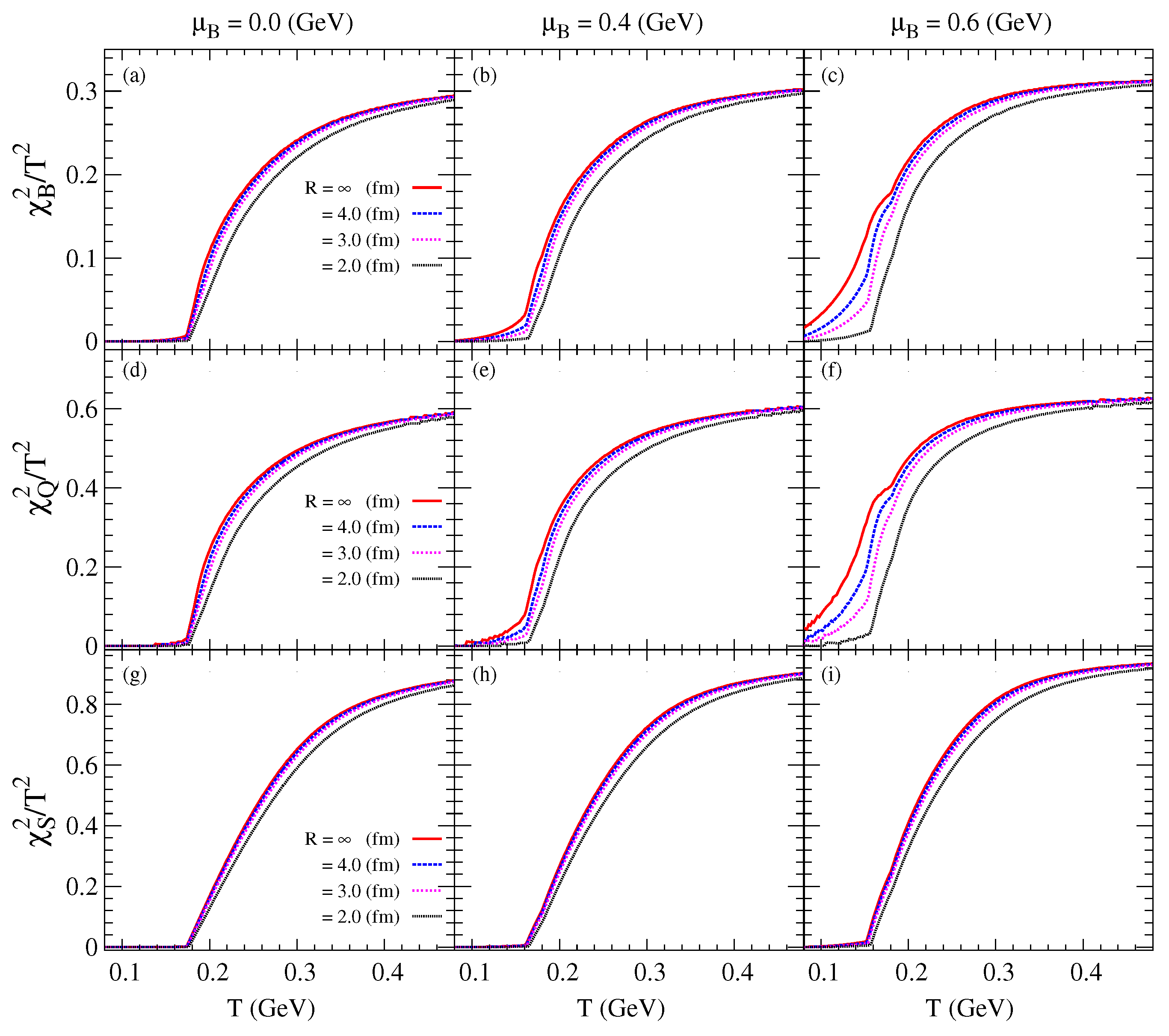
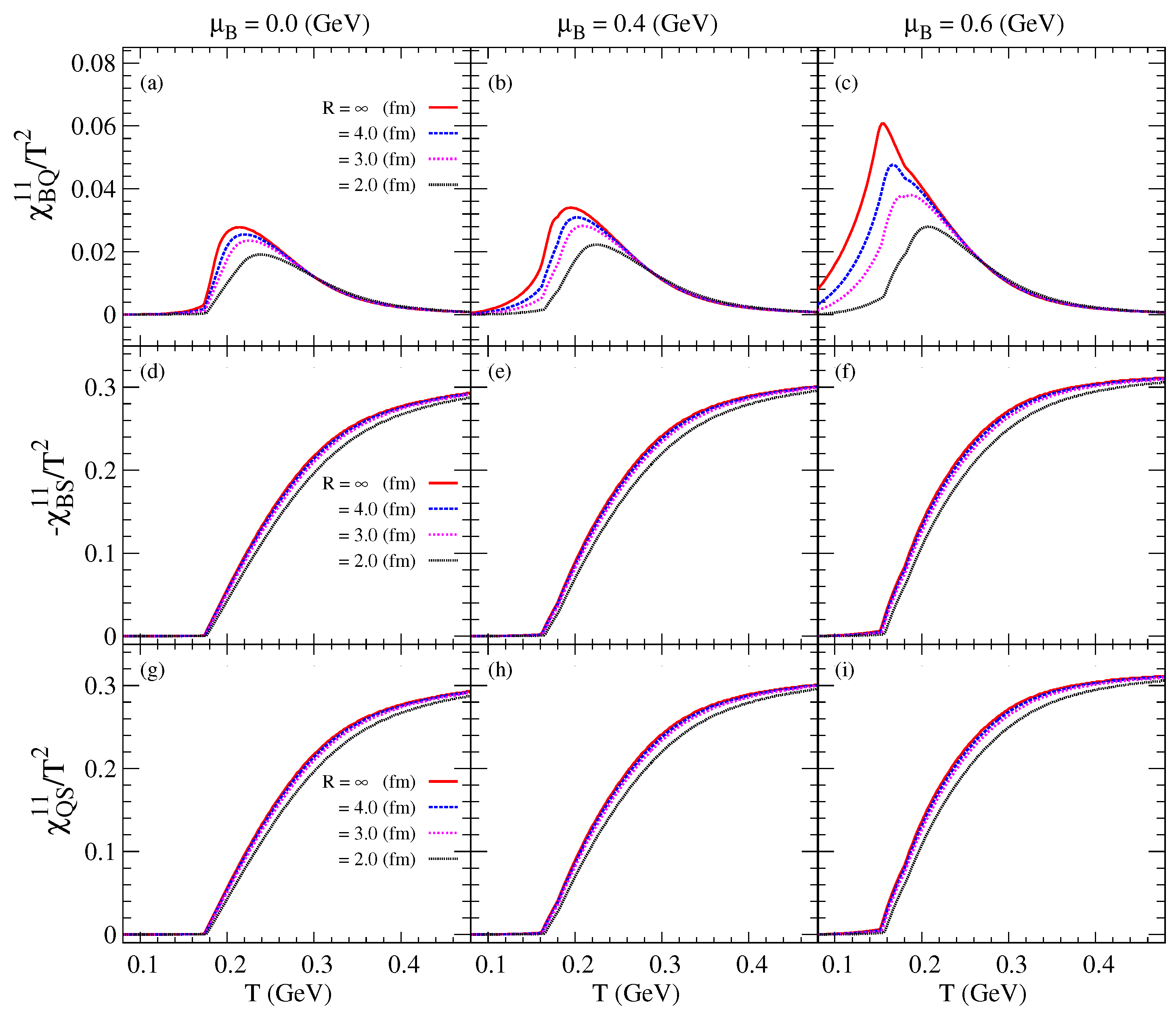
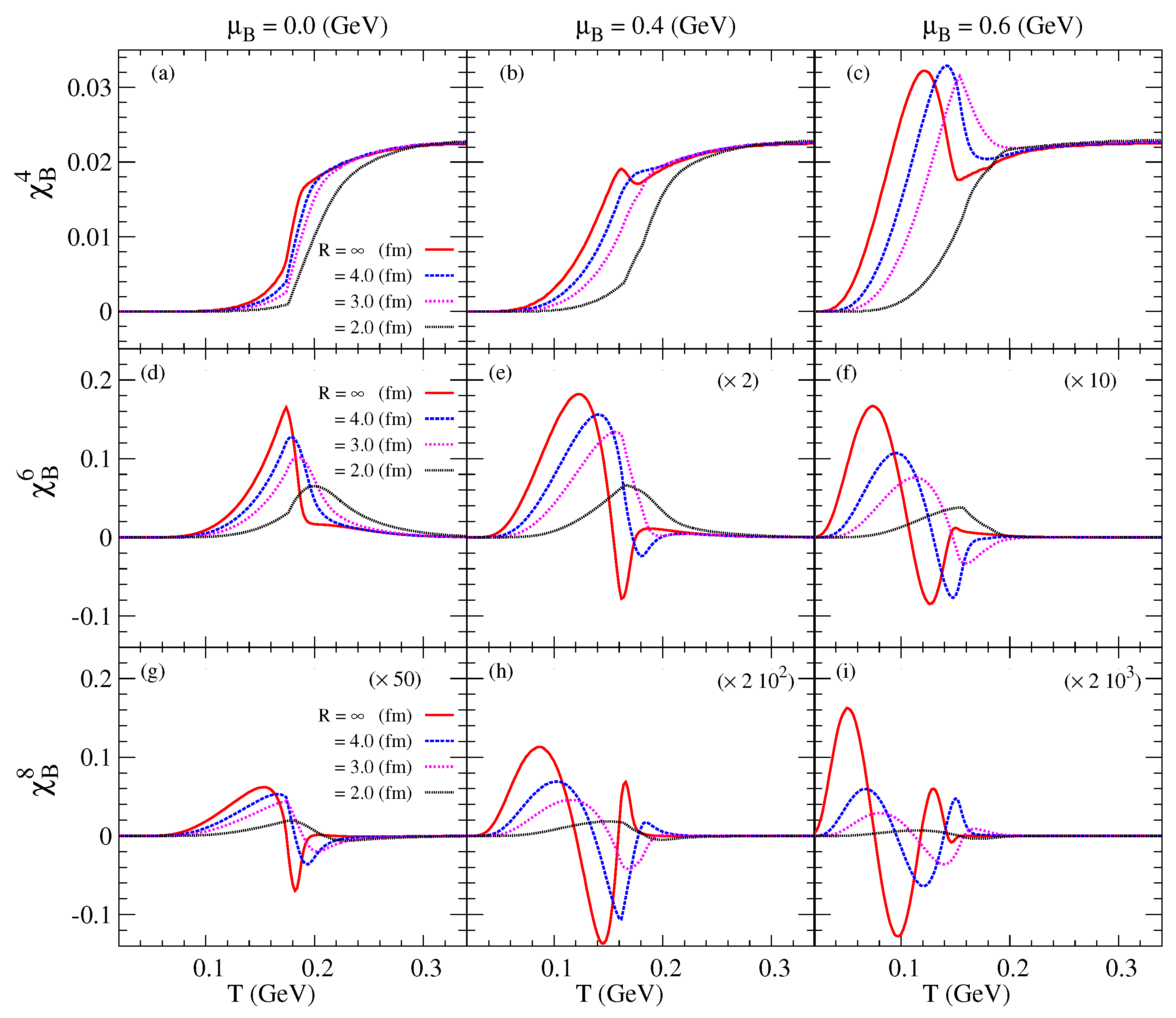
3.2. Fluctuations and Correlations of Conserved Charges
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Fachini, P. Experimental highlights of the RHIC program. In Proceedings of the PARTICLES AND FIELDS: X Mexican Workshop on Particles and Fields, Morelia, Mexico, 6–12 November 2005; AIP: New York, NY, USA, 2006; pp. 62–75. [Google Scholar]
- Monteno, M. The physics programme of the ALICE experiment at the LHC. Nucl. Phys. A 2007, 782, 283–290. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Ejiri, S. Canonical partition function and finite density phase transition in lattice QCD. Phys. Rev. D 2008, 78, 074507. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Wilczek, F. Remarks on the Chiral Phase Transition in Chromodynamics. Phys. Rev. D 1984, 29, 338. [Google Scholar] [CrossRef]
- Lee, B.W. Chiral Dynamics; Gordon and Breach: New York, NY, USA, 1972; Volume B591, 129p. [Google Scholar]
- Kovacs, P.; Szep, Z. The critical surface of the SU(3)L × SU(3)R chiral quark model at non-zero baryon density. Phys. Rev. D 2007, 75, 025015. [Google Scholar] [CrossRef]
- Kovacs, P.; Szep, Z. Influence of the isospin and hypercharge chemical potentials on the location of the CEP in the μB − T phase diagram of the SU(3)L × SU(3)R chiral quark model. Phys. Rev. D 2008, 77, 065016. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Kahara, T.; Tuominen, K. Degrees of freedom and the phase transitions of two flavor QCD. Phys. Rev. D 2008, 78, 034015. [Google Scholar] [CrossRef]
- Wambach, J.; Schaefer, B.J.; Wagner, M. QCD Thermodynamics: Confronting the Polyakov–Quark–Meson Model with Lattice QCD. Acta Phys. Polon. Suppl. 2010, 3, 691–700. [Google Scholar]
- Schaefer, B.J.; Wagner, M. On the QCD phase structure from effective models. Prog. Part. Nucl. Phys. 2009, 62, 381–385. [Google Scholar] [CrossRef]
- Mao, H.; Jin, J.; Huang, M. Phase diagram and thermodynamics of the Polyakov linear sigma model with three quark flavors. J. Phys. G Nucl. Part. Phys. 2010, 37, 035001. [Google Scholar] [CrossRef]
- Fisher, M.E.; Barber, M.N. Scaling Theory for Finite-Size Effects in the Critical Region. Phys. Rev. Lett. 1972, 28, 1516–1519. [Google Scholar] [CrossRef]
- Abreu, L.M.; Gomes, M.; da Silva, A.J. Finite-size effects on the phase structure of the Nambu-Jona-Lasinio model. Phys. Lett. B 2006, 642, 551–562. [Google Scholar] [CrossRef][Green Version]
- Palhares, L.F.; Fraga, E.S.; Kodama, T. Chiral transition in a finite system and possible use of finite size scaling in relativistic heavy ion collisions. J. Phys. G Nucl. Part. Phys. 2011, 38, 085101. [Google Scholar] [CrossRef]
- Fraga, E.S.; Palhares, L.F.; Sorensen, P. Finite-size scaling as a tool in the search for the QCD critical point in heavy ion data. Phys. Rev. C 2011, 84, 011903. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Ghosh, S.K.; Ray, R.; Sur, S. Thermodynamic Properties of Strongly Interacting Matter in Finite Volume using Polyakov-Nambu-Jona-Lasinio Model. Phys. Rev. D 2013, 87, 054009. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ray, R.; Sur, S. Fluctuation of strongly interacting matter in the Polyakov–Nambu–Jona-Lasinio model in a finite volume. Phys. Rev. D 2015, 91, 051501. [Google Scholar] [CrossRef]
- Magdy, N.; Csanád, M.; Lacey, R.A. Influence of finite volume and magnetic field effects on the QCD phase diagram. J. Phys. G Nucl. Part. Phys. 2017, 44, 025101. [Google Scholar] [CrossRef]
- Almasi, G.; Pisarski, R.; Skokov, V. Volume dependence of baryon number cumulants and their ratios. Phys. Rev. D 2017, 95, 056015. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.E.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Fluctuations and Correlations of net baryon number, electric charge, and strangeness: A comparison of lattice QCD results with the hadron resonance gas model. Phys. Rev. D 2012, 86, 034509. [Google Scholar] [CrossRef]
- Lenaghan, J.T.; Rischke, D.H.; Schaffner-Bielich, J. Chiral symmetry restoration at nonzero temperature in the SU(3)L × SU(3)R linear sigma model. Phys. Rev. D 2000, 62, 085008. [Google Scholar] [CrossRef]
- Schaefer, B.J.; Wagner, M. The Three-flavor chiral phase structure in hot and dense QCD matter. Phys. Rev. D 2009, 79, 014018. [Google Scholar] [CrossRef]
- Polyakov, A.M. Thermal Properties of Gauge Fields and Quark Liberation. Phys. Lett. B 1978, 72, 477–480. [Google Scholar] [CrossRef]
- Susskind, L. Lattice Models of Quark Confinement at High Temperature. Phys. Rev. D 1979, 20, 2610–2618. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. PNJL model with a Van der Monde term. Phys. Rev. D 2008, 77, 094024. [Google Scholar] [CrossRef]
- Haas, L.M.; Stiele, R.; Braun, J.; Pawlowski, J.M.; Schaffner-Bielich, J. Improved Polyakov-loop potential for effective models from functional calculations. Phys. Rev. D 2013, 87, 076004. [Google Scholar] [CrossRef]
- Schaefer, B.J.; Wagner, M.; Wambach, J. QCD thermodynamics with effective models. PoS 2009, CPOD2009, 017. [Google Scholar]
- Tawfik, A.; Magdy, N.; Diab, A. Polyakov linear SU(3) σ model: Features of higher-order moments in a dense and thermal hadronic medium. Phys. Rev. C 2014, 89, 055210. [Google Scholar] [CrossRef]
- Kovács, P.; Wolf, G. Chiral phase transition scenarios from the vector meson extended Polyakov quark meson model. arXiv 2015, arXiv:1507.02064. [Google Scholar]
- Kovács, P.; Szép, Z.; Wolf, G. Existence of the critical endpoint in the vector meson extended linear sigma model. Phys. Rev. D 2016, 93, 114014. [Google Scholar] [CrossRef]
- Fu, W.j. Fluctuations and correlations of hot QCD matter in an external magnetic field. Phys. Rev. D 2013, 88, 014009. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ray, R.; Samanta, S.; Sur, S. Thermodynamics and fluctuations of conserved charges in a hadron resonance gas model in a finite volume. Phys. Rev. C 2015, 91, 041901. [Google Scholar] [CrossRef]
- Schaefer, B.J.; Wagner, M.; Wambach, J. Thermodynamics of (2 + 1)-flavor QCD: Confronting Models with Lattice Studies. Phys. Rev. D 2010, 81, 074013. [Google Scholar] [CrossRef]
| c (MeV) | (MeV) | (MeV) | (MeV) | ||
|---|---|---|---|---|---|
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magdy, N. Influence of Finite Volume Effect on the Polyakov Quark–Meson Model. Universe 2019, 5, 94. https://doi.org/10.3390/universe5040094
Magdy N. Influence of Finite Volume Effect on the Polyakov Quark–Meson Model. Universe. 2019; 5(4):94. https://doi.org/10.3390/universe5040094
Chicago/Turabian StyleMagdy, Niseem. 2019. "Influence of Finite Volume Effect on the Polyakov Quark–Meson Model" Universe 5, no. 4: 94. https://doi.org/10.3390/universe5040094
APA StyleMagdy, N. (2019). Influence of Finite Volume Effect on the Polyakov Quark–Meson Model. Universe, 5(4), 94. https://doi.org/10.3390/universe5040094





