2.1. Fast Scramblers
Black holes have been proven to be the fastest scramblers [
6,
9,
10]. Scrambling, a form of strong thermalization, is a process which stores information in highly nontrivial correlations between subsystems. When chaotic thermal quantum systems of large number of degrees of freedom undergo scrambling, their initial state, although not lost, is very computationally costly to be recovered. In this paper we assume that although the modes are scrambled, they are still localized in a certain way across the horizon, as seen in
Figure 1. However, because of the strong thermalization, they remain indistinguishable from the rest of the black hole degrees of freedom as far as Alice is concerned. Suppose Alice is outside the black hole, and throws a few qubits inside. From her perspective, those extra modes will be effectively diffused, i.e., smeared across the horizon in a scrambling time
where
is the inverse temperature, and
N is the number of degrees of freedom.
As a result, a scrambling time after perturbing the black hole, Alice will not be able to distinguish those extra qubits. This statement is similar to the upper chaos bound for general thermal systems in the large
N limit [
11]. In particular, the large
N factor is what initially keeps the commutators small. However, for
, scrambling yields rapid commutator growth, and so the distance between the initial and perturbed states in complexity geometry increases non-trivially, Equations (12) and (13).
In strongly coupled thermal quantum systems chaos and scrambling are intimately related, which is why (1) is of particular interest to both quantum cloning, and retention time scales, i.e., the minimum time for information to begin leaking via Hawking radiation.
Imagine Bob crosses the horizon carrying a qubit, and Alice hovers outside the black hole. It was shown [
6] that by the time Alice recovers the perturbed qubit by collecting the outgoing modes, and enters the black hole, Bob will have already hit the singularity. So retention time scale of order the logarithm of the entropy (2) is just enough to save black hole complementarity from paradoxes
Thus quantum cloning cannot be verified given the above bound is respected.
Recent studies of quantum information and quantum gravity [
6,
7,
8,
12,
13,
14,
15,
16] support the scrambling time as the appropriate time scale at which black holes begin releasing information via Hawking radiation. Note that in such generic early evaporation scenarios where quantum information begins leaking out of order the scrambling time, not every Hawking particle carries information as this would make the retention time scale
, which would violate the no-cloning bound (2).
2.2. Qubit Description of Black Holes
A quantum circuit is composed of gates, and describes the evolution of a quantum system of qubits. The gates may be defined to act on an arbitrary number of qubits, and to couple any given pair of them. The gates may act in succession or in parallel, where series-type quantum circuits are not good scramblers.
Here, we present a random quantum circuit with time-dependent Hamiltonian which has been proved to scramble in time logarithmic in the entropy [
17,
18].
Consider a
K-qubit analog of a Schwarzschild black hole in 3 + 1 dimensions, where
here
A is horizon area, and
is Newton’s constant.
Let the
K qubits be in some initial pure state of the form
where
is the amplitude, and
is the Hilbert space basis. The state lives in a Hilbert space of
dimensions.
In this framework the Hamiltonian is given as [
17]
where
denote the independent Gaussians,
are Pauli matrices, and the eigenenergies live in a
dimensional state space.
Thus the evolution between two successive time-steps is
Here, there is an inverse relation between the time-step and the strength of the interactions. It was thus demonstrated by Hayden et al. in [
17] that the time required to scramble an arbitrary number of degrees of freedom scales like
.
The evolution of the
K-qubit system is controlled by a random quantum circuit, composed of a universal gate set of two-local gates, where we assume the gate set approximates Hamiltonian time evolution
Suppose k-local gates with are strictly penalized. In addition to the k-local restriction, we assume the gates have non-zero couplings only with respect to the nearest qubits, similar to ordinary lattice Hamiltonians. Of course, in principle, nothing demands this particular locality constraint, and we could have easily allowed any arbitrary pair of qubits to couple.
The evolution is divided into time steps , where at each time-step a random gate set is chosen. The choice is random because at each time-step the gate set is picked via a time-dependent Hamiltonian governed by a stochastic probability distribution. Furthermore, the random choice has to also determine which k qubits the gate set will act on. Note that the random quantum circuit that we use is bounded from above by gates which are allowed to act in parallel every time-step.
We suggest a natural time scale to associate with the time intervals between successive time steps would be the Schwarzschild radius
(i.e., light crossing time). One does not have to look further than elementary black hole mechanics to see why this is the case. For instance, in a freely evaporating black hole,
is adiabatically decreasing. Consequently, the time intervals between successive time steps are shorter, and thus black hole evaporates at a faster rate. This fits well with classical black hole thermodynamics
where
denotes the inverse temperature.
Since this random quantum circuit scrambles information logarithmically, throughout the paper we consider it to be an effective analog of general early evaporation models.
2.3. Relative State Complexity
In this section we argue that calculating retention time scales for systems controlled by random quantum circuits is a question of relative state complexity. We show that calculating relative state complexity is extremely difficult, and in order for Alice to carry out the computation she would need to either act with an exponentially complex unitary operator or apply a future precursor operator to the perturbed state, and rely on extreme fine-tuning.
We can simply define circuit (gate) complexity as the minimum number of gates required to implement a particular state. The evolution of a quantum state via time-dependent Hamiltonian resembles the motion of a non-relativistic particle through the homogeneous
space [
19]. That is, the particle defines a trajectory between a pair of points, where one point corresponds to some initial state
, while the second point corresponds to a perturbed state
, where
. The particle thus moves on a
dimensional state space. Without loss of generality, the state evolution can be straightforwardly given by the Schrodinger equation
Given two states are different to begin with, their relative state complexity naturally increases with time.
A compelling argument was made in [
19] that the naive way of defining the distance between two states does not capture the whole story. The classical Fubini metric bounds the state distance as
. Obviously, the upper bound can be easily saturated and we need a different measure to quantify the relative state complexity between two states. Due to the exponential upper bound of complexity,
, quantifying relative state complexity necessitates the use of complexity metric. That is the notion of distance between states on the non-standard
, see refs. [
20,
21]. Intuitively, the farther apart two states are on
, the higher their relative state complexity is. Geometrically, we can think of relative state complexity as the minimum geodesic length in
which connects two states.
In light of the proposed random quantum circuit, and following the definition of circuit complexity, we define relative state complexity as the minimum number of time steps required to go from one quantum state to another.
Keep in mind that every time step a random set of two-local gates is chosen following a time-dependent Hamiltonian controlled by a stochastic probability distribution. So essentially, using Nielsen’s approach [
20], we are interested in assigning a notion of distance (geodesic length) to the gate sets. Here the minimum length increase in complexity geometry sets a lower bound for the minimum complexity growth, which corresponds to acting with a single 2-local gate.
More precisely, suppose Alice perturbs the
K-qubit system immediately after its formation by
n qubits, where
,
Figure 1. We ask: what is the relative state complexity of
and
? In other words, what is the minimum number of time steps
in which Alice could time-reverse the perturbation
where
K-qubit system,
-qubit system.
Let us now turn to the main objective of this paper which is to address the question:
In a young black hole, can Alice calculate the relative state complexity of and in time less than ?
In our case calculating the relative state complexity means counting the number of time steps in which the extra n qubits are radiated to infinity.
Our claim is that in implementing U, Alice cannot beat because of the causal structure of the black hole spacetime. Alice does not have access to all the relevant degrees of freedom which dramatically increases the computational complexity. Therefore, the inability of implementing U faster than not only renders the computation unrealizable for astrophysical black holes, but also takes away Alice’s predictive power.
We will now look at the two ways Alice could hope to estimate (9). Namely, she could either apply gate sets to the radiated qubits, or act with an extremely fine-tuned precursor.
2.3.1. How Fast Can Alice Calculate the Relative State Complexity?
In this subsection we consider the Harlow–Hayden reasoning [
15] but for the case of a young black hole. Recall that in [
15] Harlow and Hayden argued that Almheiri, Marolf, Polchinski and Sully (AMPS)’ conjectured violation of the equivalence principle after page time is computationally unrealizable for black holes formed by sudden collapse since it requires complicated measurements on the emitted Hawking cloud. We now study the limit of the proposed
complexity bound, and demonstrate that it is strong enough to hold even for the case where (i) entanglement entropy is still low, and (ii)
.
Here we employ a standard Hilbert space decomposition where k are the black hole qubits in , m are the qubits of the black hole atmosphere in , and r are the emitted qubits in , whose dimensionality grows as the black hole evaporates. We assume Alice can only manipulate the r qubits, and that all outside observers must agree on . For her this is essentially a decoding problem, where she acts with the unitary transformation U to . Alice’s goal is to decode in search for the extra n qubits, and count the number of time steps in which they were radiated away.
To demonstrate more clearly the robustness of the
complexity bound, suppose we violate the fast scrambling conjecture [
17]. The violation is in the sense that Alice can recognize the perturbed
n qubits easier, and does not need to decode a significant part of all the system’s degrees of freedom. Even in this case, however, we argue there is an overwhelming probability Alice cannot beat
.
Since the scrambling time is the shortest time-scale compatible with the no-cloning bound (2), one might naively expect Alice can time-reverse the perturbation in time comparable to the scrambling time. Considering the exponentially high upper bound of complexity, however, we can easily see that this is not the case [
2]. Even though the scrambling time is negligible compared to the time-scale associated with reaching maximum complexity, in a scrambling time the complexity of the system scales as
Although nowhere near the upper bound of
, the scrambling complexity is high enough to make the computation extremely difficult. From a geometry perspective, by the scrambling time, due to quantum chaos, the trajectories of the two points on
diverge exponentially,
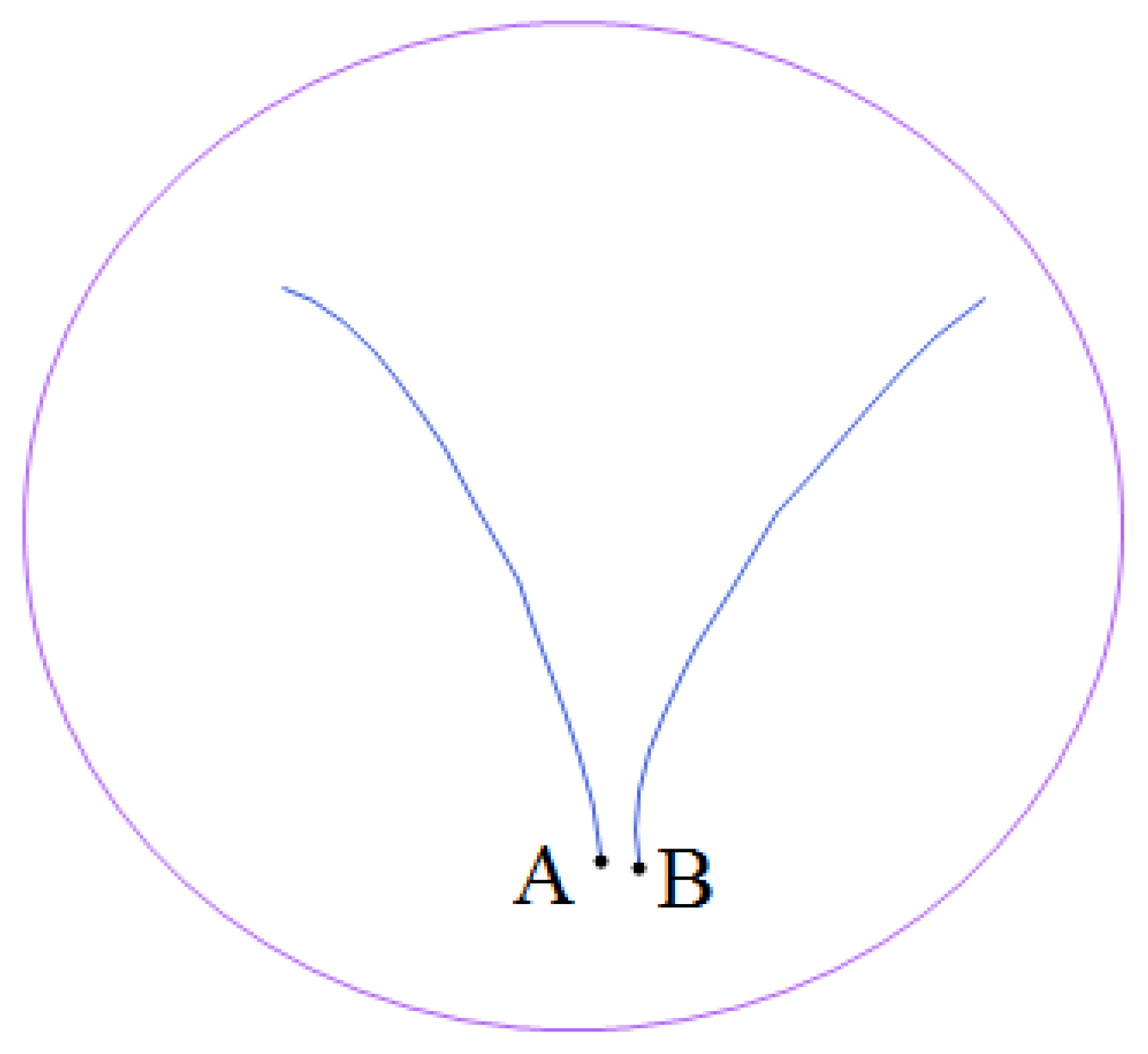
Figure 2.
Despite being initially arbitrarily close, given they are separated to begin with, in just a scrambling time the distance (i.e., relative state complexity) between them grows exponentially.
Let us further illustrate the point with the use of an out-of-time-order correlator (OTOC)
. OTOCs are used for measuring quantum chaos [
22,
23]. In particular, OTOCs describe how initially commuting operators develop into non-commuting ones. Suppose
and
are simple Hermitian operators, where
B is just a time-evolved
A. Initially, for
the correlator is approximately constant. Then at the scrambling time, due to quantum chaos [
11]
After the scrambling time, regardless of
A and
B, the correlator takes the form
This exponential decay is associated with the initial rapid growth of the commutator, which becomes highly non-trivial at the scrambling time. Note that for small t, the large number of black hole degrees of freedom suppress the commutator. Therefore, the scrambling time is enough to make the operators very complicated, and thus the distinguishablity between them non-trivial. So what can Alice do?
The obvious thing to do would be to brute-force. In this case Alice will have to first artificially group the
r qubits in
into different sets, and then apply a complex unitary transformation to those sets in search for the extra
n qubits. The difficulty here is to have a unitary transformation which acts on a particular set of qubits [
15]. Unlike the Harlow-Hayden argument where Alice tries to decode a subfactor of
in order to verify entanglement with
, here the decoding task is especially complicated given Alice will have to engineer multiple such unitary transformations because of the monotonically growing dimensionality of
. It seems that even with the assumption we made that Alice need not probe a significant part of all the initial degrees of freedom to recognize the extra qubits, the computation remains extremely non-trivial.
Of course, Alice could try to use some clever tricks to carry out the computation faster than . For instance, she could try to impose some special structure to the unitary transformation, and in particular, on how it evolves with time. She could engineer U to allow specific sequences of gate sets to act every time-step on preferred qubit sets. However, such modifications can only account for very small changes which are not enough to speed up the computation to reasonable time scales.
Another possibility is for Alice to manipulate the adiabatically growing number of r qubits and make them interact in a preferred manner. By making use of the smaller dimensionality of , she could form sets of qubits, establish certain connection between them, and choose which sets to interact every time step. However, despite engineering such a connection between the r qubits would obviously require introducing additional degrees of freedom which would scale like an exponential in r. Thus the computation becomes very complex even for relatively small r. In fact, by trying to fine-tune the qubits in this way, Alice makes her decoding task harder.
Clearly, even in the case of a young black hole, and making the unphysical assumption that Alice need not decode a large part of the entropy, the computation remains very hard. Even though there is nothing, in principle, that prevents the first n emitted qubits to be the perturbed one, this is exponentially unlikely. So even with weak violations of the fast scrambling conjecture the bound holds with an overwhelming probability.
What about black holes which have evaporated more than half of their initial degrees of freedom? One could hope to speed up the computation by letting the black hole evaporate passed its Page time, and apply certain gate sets on . For example, once , ancillary qubits could be introduced and entangled with subfactors of . Then one could apply gates to those subfactors in effort to implement U faster than . Unfortunately, as long as the extra qubits scale like r, the computation does not get any faster.
Therefore, unless Alice finds a way to calculate the relative state complexity in a way which does not involve exponential number of gates, the time-scale remains solid.
2.3.2. Precursors and Extreme Fine-Tuning
Here we examine Alice’s second attempt of calculating the relative state complexity which now involves applying a future precursor operator to the late-time state. For simplicity, we study the case using a generic time-independent Hamiltonian but expect the main conclusions to hold for the time-dependent ones, too.
Alice’s task here is to adjust the late-time state and time reverse it. Effectively, this means running the chaotic black hole dynamics backwards. We show that this process of time-reversing (10) by applying a future precursor operator to the perturbed state is notoriously difficult, and Alice still cannot beat . The particular argument should be considered in the context of complexity geometry on .
The laws of physics are time-reversible, so any state perturbation that we introduce could be reversed. Naturally, however, for complexity tends to increase linearly in K until it saturates the bound of . Therefore, after the scrambling time we expect linear increase of the relative state complexity between and as t grows. Geometrically, this corresponds to a linear growth of the minimum geodesic length connecting the two states in .
Let us analyze the same example of Alice perturbing the
K-qubit system immediately after its formation with
n qubits. As we already saw, whatever Alice does, she cannot carry out the computation faster than
. Determined to calculate the relative state complexity before the complexity bound is saturated, however, imagine she now acts with a specific operator, namely a future precursor operator [
24].
A future precursor operator
is a highly non-local operator which when applied at a certain time simulates acting with a local operator
P at an earlier time
where
.
Generally, calculating a precursor operator for
is extremely difficult as one has to keep track of all the interactions of the degrees of freedom of the system. The computational costs grow immensely in cases involving black holes because they not only have a large number of degrees of freedom but also saturate the chaos bound [
11]. For the first scrambling time after perturbing a black hole, the complexity growth is governed by the Lyapunov exponent, and hence grows exponentially [
25]. Black holes are the fastest scramblers in Nature, and due to their chaotic dynamics, only a scrambling time after the perturbation, all of the degrees of freedom (
for a solar mass black hole) will have indirectly interacted. Evidently, the precursor operator quickly becomes extremely difficult to calculate. Whatever Alice does to implement the precursor, she must time-reverse all of the interactions between the degrees of freedom of the black hole which requires an extreme degree of fine-tuning. Regardless of the exponential complexity, however, individual interactions remain well defined.
In our case acting with the precursor operator takes the general form
Similar to the evolution of a quantum state via a time-dependent Hamiltonian, the action of a future precursor resembles a backward motion of a particle through complexity geometry.
The high complexity of (14) corresponds to the complexity associated with constructing a thermofield-double state using only
degrees of freedom, see Ref. [
24]. In both cases, due to the large number of degrees of freedom an extreme fine-tuning is required. Even a mistake of order a single qubit will accumulate, and result in a completely different end-state. The system only becomes more sensitive to errors as the time separation increases. Therefore, unlike regular unitary operators which need not always be complex, precursors are typically extremely complex and unstable to perturbations (the butterfly effect) whenever the time separation is at least of order the scrambling time.
Expanding (15) for
yields
where
is the initial time when the
K-qubit system was perturbed.
Notice we have restricted our analysis not to include cases when either
or
. The former case was discussed in ref. [
25], where it was argued that before the scrambling time the distance in complexity geometry between the initial and perturbed states remains approximately constant. Initially, for
, the large
N terms keep the commutators relatively small. So scrambling is what drives the rapid distance growth in
. On the other hand, the latter case is unnecessary since, as we showed, the computation becomes unmanageable in just
.
Therefore, due to the chaotic black hole dynamics, and the great deal of fine-tuning required, the probability of Alice implementing the precursor (and thus calculating the relative state complexity) without making a mistake of even a single qubit is exponentially small.
In conclusion, we can see that due to the causal structure of the black hole geometry, and the chaotic dynamics there is nothing Alice can do that would allow her to calculate the relative state complexity faster than
. This exponential time scale, however, is only applicable for AdS black holes since astrophysical black hole evaporate much before the complexity bound is saturated. So in the case of black hole formed by a sudden collapse there are two very general scenarios, associated with minimum and maximum retention time scales,
and
, respectively. Obviously, the fastest retention time possible which obeys the no-cloning bound (2) is
up to some constant.
This is similar to the Hayden–Preskill result [
6] concerning the mirror-like dynamics of an old black hole. On the other hand, the longest retention time for astrophysical black holes would be of order the evaporation time
Usually, such retention time scales are associated with remnants which have been seriously questioned due to the apparent violation of the Bekenstein entropy bound.