4.2. WKB
Given the considerations presented in the previous section, it is interesting to calculate the Wigner function of a WKB state since the WKB approximation is often viewed as a way to study the classical limit in Quantum Mechanics. Surprisingly, the calculation of the WKB Wigner function is not as straightforward as one might think at first sight. In Cosmology, it has even a controversial and rich history. The WKB Wigner function has indeed been applied to various questions in Cosmology such as the interpretation of the wavefunction of the Universe (Quantum Cosmology) and the quantum-to-classical transition of inflationary perturbations, this last topic being obviously especially relevant for the present article.
Although the original calculation of the semi-classical Wigner function was performed by M. Berry in 1976 [
48], it started to be applied in Cosmology only at the end of the 1980s in Ref. [
49]. The question of how to interpret the wavefunction of the Universe in Quantum Cosmology was the issue tackled in this article. Usually, the solution of the Wheeler-de Witt equation makes sense only in the WKB approximation because this is the regime where positive probabilities can be extracted from this formalism (recall that the Wheeler–de Witt equation is similar to a Klein–Gordon equation and, hence, does not always lead to positive probabilities). Then, the idea was to look for correlations in the WKB Wigner function. The calculation of Ref. [
49] proceeds as follows. Inserting the WKB wavefunction,
where we have provisionally re-established
ℏ and where
is the classical action of the system, into the definition of the Wigner function, one arrives at
Expanding the amplitude and the phase in
ℏ, one obtains
that is to say, by performing the integration over
xTherefore, the conclusion of Ref. [
49] was that the WKB approximation is really a classical limit in the sense that the Wigner function is positive definite and peaked over the classical trajectories
with a weight given by the squared amplitude
.
However, after the publication of Ref. [
49], it was pointed out in Refs. [
50,
51] that the calculation of the WKB Wigner function (
69) is in fact unjustified and that, moreover, the correct formula was derived, as already mentioned, by M. Berry in Ref. [
48]. The trouble with Equation (
69) is that one cannot truncate the expansion of the phase and, then, perform the integration over
x. It is true that the higher order terms are proportional to powers of
ℏ (which goes to zero) but also to powers of
x (the range of which is the entire real axis) so that it is unclear whether the contributions of higher order terms are really negligible. The correct method consists in fact in using the saddle point approximation. This leads to
where
is a Airy function [
52]. In the above expression,
E is the energy shell, namely the quantity such that the Hamiltonian of the system satisfies
. The points 1 and 2 are the points of coordinates
,
satisfying the stationary phase condition
. They lie on the classical trajectory and their position is determined such that the arithmetic mean of their momentum is
p. Finally,
is the area comprised between the chords 1–2 and the classical torus
. One can show that, when the Wigner function is known, the above formula (
70) matches very well the exact result in the regime where the WKB condition is valid. However, the most important property of Equation (
70) is that it is not positive definite and usually displays oscillations in phase space. This shows that the semi-classical limit cannot be viewed as being a truly classical regime.
The WKB approximation has also been applied to the quantum-to-classical transition of cosmological perturbations in Ref. [
53]. In that paper, it is claimed that this transition is achieved because the quantum state of the perturbations precisely satisfies the WKB approximation on super Hubble scales. Based on what we have just seen about the WKB Wigner function, this last statement should be taken with great care. In fact, as we are going to see, the behavior of cosmological perturbations on large scales is especially relevant when it comes to semi-classical methods in phase space.
Based on the fact that the quantum state of the perturbations is a squeezed state, Ref. [
53] considers a simplified model consisting in an inverted harmonic oscillator whose Lagrangian is given by
where the potential term has the “wrong” sign,
. As we are going to see, the state of the oscillator evolves into a strongly squeezed state which justifies considering this simple system. The corresponding Hamiltonian reads
, with
, and is not bounded from below. Then, creation and annihilation operators can be introduced in the standard fashion
where
. This allows us to express the Hamiltonian as
Of course, the most striking property of this Hamiltonian is the presence of an overall minus sign which is just the consequence of the inverted nature of the oscillator. Then, the equations of motion are given by
As usual, they can be solved by mean of a Bogoliubov transformation, namely
where the functions
and
satisfy the following equations:
with initial conditions
and
(here, for simplicity, we have taken
). Combining these two first order differential equations, one can obtain one second order equation for
u (and/or
v), which reads
which gives
and
. As a consequence, the operator
can be rewritten as
where we have written
and where the operator
is defined by
with squeezing parameter and angle given by
and
.
is the squeezing operator and is responsible, as announced above, for the appearance of squeezed states in the problem.
In order to mimic the behavior of cosmological perturbations, we assume that the initial state of the system is the vacuum
. Then, the state at a subsequent time
t can be found using techniques based on the operator ordering theorem [
54], which allows us to rewrite the operator
as
from which it follows that
This state is a one-mode squeezed state. It slightly differs from the two-mode squeezed state considered before in Equation (
21). In particular, we see that the sum is only on states with an even number of particles. Since
, the squeezing goes to infinity in the large time limit.
Our next move is to calculate the wavefunction. It reads
where
is a Hermite polynomial of order
[
52] and appears in the
q-representation of the state
. Then, using
(here, one has
) and, recalling that
, one arrives at
where one verifies that this wavefunction is correctly normalized.
As noticed in Ref. [
53], it can be written in a WKB form (
66) with
and, in the large time limit or, equivalently, strong squeezing limit, the semi-classical approximation is extremely well-verified since the WKB condition is satisfied
. Hence, the claim that cosmological perturbations on super Hubble scales, which is equivalent to strong squeezing, are “semi-classical”. It is then tempting to go from “semi-classical” to “classical” and consider that the quantum-to-classical transition has been achieved. However, as seen above, given that the WKB Wigner function is not positive definite, one should a priori resist to this temptation.
However, as it is often the case, Cosmology introduces a new twist in this question. Using Equation (
83), one can calculate the Wigner function. The result reads
One obtains a Gaussian, which is consistent with the fact that the wavefunction (
83) is a Gaussian. This means that this Wigner function, contrary to the WKB Wigner function (
70), is positive definite, which, at first sight, seems surprising since
in Equation (
83) satisfies the WKB approximation. Moreover, writing
which, in the strong squeezing limit, goes to zero, representing the Dirac function by
and, finally, noticing that
, the Wigner function (
85) can be re-written as
where
C is given in Equation (
84). This equation is nothing but Equation (
69) which was, as discussed in Refs. [
50,
51], supposed to be incorrect! What happened is in fact very simple. It was pointed out before that the expansion of the phase performed in Ref. [
49] is not justified because the order of the various terms of this expansion is in fact indeterminate. There is of course one exception to this claim which is when the calculation of Ref. [
49] is not an expansion but is exact. This is exactly what happens here since the phase is quadratic in
q. Thus, ignoring higher order terms, which is usually unjustified, is, in the present case, totally valid simply because these higher order terms are just not present. This is consistent with the fact that the Wigner function of Gaussian is a Gaussian and, therefore, is positive definite. This shows how peculiar and subtle is the quantum-to-classical transition of cosmological perturbations is.
4.3. Bell’s Paper on the Wigner Function
After these preliminary considerations, let us now come back to the letter written by J. Bell in 1986 [
27]. Based on the original EPR article [
43], Bell imagines a situation where there are two free particles traveling in space along a given axis (the particles can propagate in both directions). Then, Bell assumes that one can measure position (of the two particles) only. As he notices himself, this slightly differs from the standard EPR argument where it is also assumed that momenta can be measured. The article makes use of the “two-time” Wigner function defined by
where
is the wavefunction of the system. If one considers two freely-moving particles, then
satisfies the Schrödinger equations,
and, as a consequence, the Wigner function obeys
. This means that
and this allows us to calculate the Wigner function at any times from the sole knowledge of the initial wavefunction. Of course, the calculation of
still requires the knowledge of the wavefunction and, in the following, several possibilities are considered.
Then, Bell proceeds and shows how his famous inequality can be implemented in the situation described before. More precisely, he does so in the so-called Clauser, Horne, Shimony and Holt (CHSH) formulation
3, which supposes to deal with quantities that can only take the values
. This is why, usually, the CHSH inequality is experimentally tested with spin variables. However, in the case considered by Bell, the particles are spinless and, as already mentioned, we only have access to position measurements. Although he does not present it exactly in this way, what Bell does to circumvent this problem is to introduce the two following operators:
which represent the sign of
and
at times
and
, respectively,
being an arbitrary position. Clearly, the spectra of
and
only consist of two values, namely
, as required. Interestingly enough, this is exactly what is done in Refs. [
56,
57,
58] and, then in the context of Cosmology, in Refs. [
25,
26]. Therefore, remarkably, Bell’s paper already contains the idea of fictitious spin operators that, as we will see later on, can be used in order to design a cosmic Bell experiment.
Then, once we have discrete variables, one can just mimic the usual approach, which, as reminded above, is formulated in terms of spins. The first step consists of defining the two-point correlators
where
is the quantum state in which the system is placed. Let us also remark that the two times
and
play the role of the polarizers settings in the standard CHSH formulation. Following the usual considerations, one can then prove that
if the correlators are interpreted as stochastic averages and if locality holds [
59]. On the contrary, in Quantum Mechanics, one just has
, hence the idea to look for experimental configurations for which
. In the following, Bell inequality violation (or CHSH inequality violation, we use the two expressions indifferently) will refer to as a situation where
.
As discussed at the beginning of this section, Bell wants to relate the non-positivity of the Wigner function to a violation of the CHSH inequality. Technically, the link between the inequality and the Wigner function is expressed as follows. It is easy to check that the quantities
and
are such that
and
—see the discussion above in
Section 3.1—and, as a consequence, thanks to Equations (
43) and (
44), the expression of the correlator
can be rewritten as
where the two-time distribution probability
is defined by
. The above equations exactly represent the relation needed as it allows us to estimate the left-hand side of Equation (
90) in terms of the Wigner function. Using the definition of
and
, one can also show that
where we used the fact that the Wigner function is normalized to one.
To go further and concretely calculate the correlators, and, hence, verify whether the CHSH inequality is violated or not, one needs to specify the state in which the system is placed. The first example considered by Bell is simply the original EPR wavefunction [
43] (supposed to hold at initial times),
, where
is a normalization constant. Then, he calculates the corresponding Wigner function and finds
Bell remarks that this Wigner function is positive everywhere and that “the EPR correlations are precisely those between two classical particles in independent free classical motion. With the wave function (8) (namely the EPR wavefunction), then, there is no non-locality problem when the incompleteness of the wave function description is admitted”. Therefore, Bell explicitly relates classicality (namely no violation of the CHSH inequality) and positivity of the Wigner function.
However, it is interesting to notice that he does not explicitly verify the violation of the CHSH inequality in that case (namely, he does not explicitly calculate the two-point correlators for the EPR wavefunction nor the combination (
90)), despite the fact that he clearly suggests it is not violated. Although he does not explain why, one can maybe guess the reason. If one takes the EPR Wigner function (
95) and tries to calculate
one finds an infinite result. Indeed, the first integration, say on
, kills the Dirac delta function
. Then, it remains an integral over
of something which does not depend on
, which gives an infinite result. This remark is interesting because it turns out to be at the core of all the literature that is devoted to this question and to the Bell’s paper: this will be discussed at length in the following sections. The reason for this problem is in fact related to the normalization
. Indeed, the wavefunction
is not properly normalized. A correct way to normalize it is to modify the wavefunction such that it now reads
This is suggested by Bell himself in the continuation of his article. Strictly speaking, in Bell’s paper, this trick is not applied to the EPR wavefunction but to another wavefunction considered later on in his article (and, in the present paper as well, see Equation (
108)). Here, we have just anticipated his guess and have applied it to the EPR wavefunction. We will comment more about this point in the following. The “new” wavefunction (
96) is made of three pieces: a normalization factor, a new factor depending on a new parameter
b,
and the last factor depending on another new parameter
,
. This last factor is just a finite representation of the Dirac function
which is recovered in the limit
. The second factor is necessarily present to make the wavefunction normalizable. Even if one uses the finite representation of the Dirac function, it is not possible to make
finite without the factor
as it is easy to see by introducing new variables
in the previous integral. Finally, the first factor is the normalization coefficient implied by the two other factors.
In his article, Bell claims
4 that the second factor can be ignored by taking the limit
. However, we see that this limit, as well as the limit
, are very problematic due to the normalization factor. For this reason, in the following, we work with Equation (
96) without taking any limit. Since the wavefunction is Gaussian, the calculations are tractable. Indeed, using the wavefunction (
96), it is easy to calculate the Wigner function, which reads
Of course, since the state (
96) is Gaussian, we find that the Wigner function is also a Gaussian—see
Section 2.5. One checks that the Wigner function is properly normalized,
, which is a consistency check of Equation (
97). The next move consists in calculating the distribution
. Recall that this requires the calculation of
. Using Equation (
97), this can be expressed as
where one has defined
and
and
.
Then, the distribution
can then be straightforwardly evaluated by applying well-known formula for Gaussian integrals. This leads to
We are now in a position where the correlator
can be calculated. Plugging the above Equation (
101) into Equation (
94), one obtains
We see that, in the arguments of all exponentials,
cancel out and makes the correlation function independent of
. This makes sense since this quantity is arbitrary and, therefore, a physical result cannot depend on its value. This also implies that the arguments of the exponentials are in fact quadratic in
and
. As a consequence, by a simple change of variable, the second term in the square bracket is in fact equal to the first one. Finally, one obtains
where the coefficients
,
and
are defined by
The integral (
103) can easily be performed and one obtains
As required,
varies between
and 1. It is interesting to notice that the form of the correlator is really typical of what one obtains with pseudo spin operators—see, for instance, Equation (26) of Ref. [
26]: the resemblance is striking.
Having obtained the correlators, it is now easy to verify whether the CHSH inequality (
90) is violated or not. In
Figure 4, we have represented the quantity
defined in Equation (
90) and evaluated with the correlator obtained above. We see that this quantity is always smaller than two so that Bell inequality is never violated.
Therefore, we have confirmed Bell’s suggestion that the EPR state, which has a positive Wigner function, does not lead to any Bell inequality violation. This was done with a method that avoided the technical issues present in Bell’s letter. In short, we conclude that Bell calculations are problematic, but, despite those issues, the overall result, at least for the example of the EPR state, is correct.
After this description of the warm-up example in Bell’s paper, we now come to the core of it. As noticed by Bell and as we have seen in detail previously, the EPR state corresponds to a positive Wigner function. However, Bell remarks that this is not always the case and that, for other wavefunctions, the Wigner distribution can take negative values—see, for instance, the case of the Schrödinger cat state (
60). The next and crucial step of Bell’s paper is then to study the CHSH inequality for states corresponding to Wigner functions that are not positive definite. In particular, Bell considers the case of the following initial wavefunction
where
a is a free parameter. Bell notices that this wavefunction is not properly normalized, but he suggests that it could be easily made so by including a factor
, where
b is a new parameter
5. Notice that, while only the difference
appeared in Equation (
108), considering this extra factor introduces an additional dependence in
in the wavefunction. It can be checked that the wavefunction
is indeed correctly normalized. However, Bells argues that the limit
can be taken from the very beginning so that we can work with (
108) and ignore the more complicated form (
109). The justification given by Bell is that only relative probabilities will be calculated in the rest of his article. Thus, for all practical purposes, he argues that one can work with Equation (
108), replacing the proportionality symbol by a
and
independent “normalization constant”
. In other words,
which, according to Equation (
109), reads
, is treated as a simple constant. Then, it is easy to calculate the corresponding Wigner function, which, if the choice
is made (namely the value considered by Bell in his letter), reads
This equation is in perfect agreement with Equation (13) of Bell’s letter [
27] and, in addition, allows us to identify “
K” the “
unimportant constant” introduced by Bell in the above equation. Comparing with Equation (13) of Ref. [
27], we have
. The main point of this example is that the Wigner function (
110) can be negative in some region as can be seen in
Figure 5.
Then, we follow the same procedure as the one already used and explained for the EPR wavefunction: the next step consists of calculating the distribution
. Using the definition of this quantity, see below Equation (
93), one arrives at
where
. This expression coincides with Equation (15) of Ref. [
27] and, again, we can identify the constant
in Ref. [
27], namely
. The final step consists of using the distribution
in Equation (
94) in order to calculate the two-point correlators of the pseudo spin operators. This leads to
This expression is identical to Equation (18) of Ref. [
27] and, therefore, is in perfect agreement with Bell calculations. Once more, this allows us to identify the constant called
by Bell and we have
. Finally, one can compute the quantity
given in Equation (
90). One arrives at
which is our final result. We have an explicit form of the Bell operator mean value which allows us to test the CHSH inequality.
In his paper, Bell calculates
for
,
,
and
. If, given Equation (
112), one writes, as Bell does,
, which defines
, then one has
. In fact, since
is a function of
only, the previous equation reduces to
or, more explicitly,
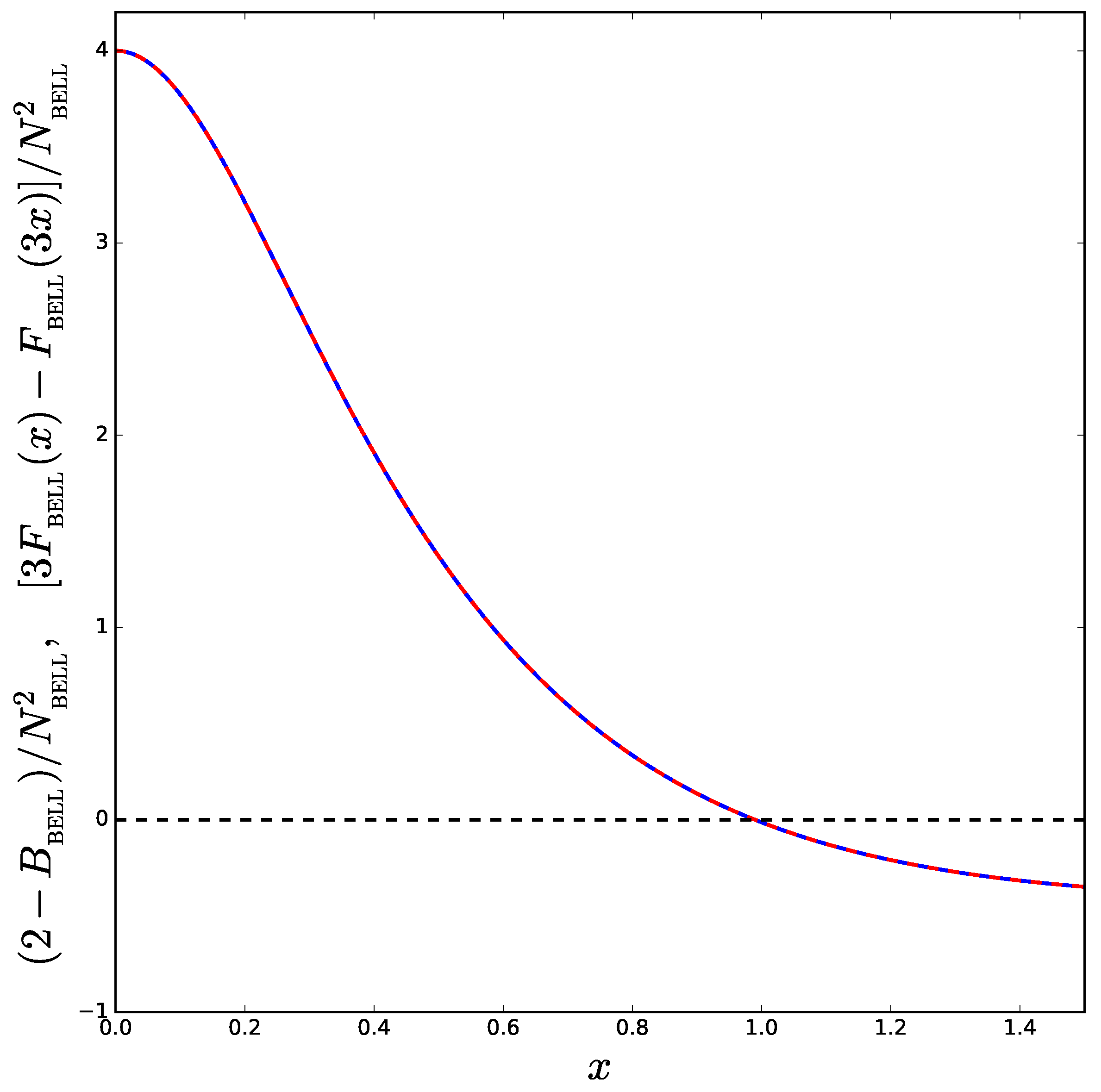
In
Figure 6, we have have plotted the quantity
(solid blue line). When this quantity is negative, the CHSH inequality is violated. We see on the plot that this is indeed the case provided
, a conclusion also reached by Bell. Notice that one can obtain this result regardless of the value of
. In
Figure 6, we have also represented the quantity
(dashed red line), where
has been defined above. Evidently, according to the previous considerations, it should exactly coincide with
and one checks that this is indeed the case. The condition
for a non violation of the CHSH inequality is Equation (25) of Bell’s paper.
Based on the previous considerations, Bell concludes that the non-positivity of the Wigner function (
110) implies a violation of the CHSH inequality. He also adds that “
I do not know that the failure of W to be non-negative is a sufficient condition in general for a locality paradox”. Although it is fair to say that the main message is not explicitly expressed in this way, it is however clear that Bell’s letter suggests a (one-to-one?) correspondence between a violation of the CHSH inequality and the non-positivity of the Wigner distribution. This argument seems to be supported by the EPR example (positive Wigner function and no violation of CHSH) and by the example we have just studied (no positive definite Wigner function and violation of CHSH). After all, the non-positivity of the Wigner function certainly signals that some genuine quantum effects are at play and, when this is the case, it is natural to think that Bell inequality could be violated. Therefore, at first sight, this conclusion appears to be meaningful and correct. It has very important consequences for Cosmology. Indeed, as we have already seen, cosmological perturbations are placed in a two-mode squeezed state, which is a Gaussian state, and, therefore, has a positive definite Wigner function. As a consequence, Bell’s result, if true, would imply that no violation of his inequality can be observed in the CMB.
4.4. Is Bell’s Paper Wrong?
In 1997, the article [
30] was published by L. Johansen in
Physics Letters A. In brief, this article claims that Bell’s paper is wrong. The main argument is that working with Equation (
108), namely with a wave function
, where
is just viewed as a constant, is incorrect because, as we have already noticed in the previous section, this wavefunction is not correctly normalized. Ref. [
30] quotes the book by A. Peres, “
Quantum Theory: Concepts and Methods” where, on p. 80, one is warned that not normalizing properly the wavefunction can lead to negative probabilities or to probabilities larger than one.
Then, Ref. [
30] makes his argument more precise and states that Bell’s mistake is in fact to treat the normalization factor
as time independent. However, what Ref. [
30] does in practice is in fact much more interesting for the question discussed here. The idea is to consider a Wigner function which is positive definite, then use Bell’s mathematical trick described above and, finally, show that this implies of violation of the CHSH inequality. Since, according to Ref. [
30], one cannot have a CHSH inequality violation if the Wigner function is positive definite, it follows that Bell’s mathematical trick and, therefore, Bell’s result must be incorrect. This is a
reductio ad absurdum proof. What is especially interesting is the fact that the correspondence positivity of the Wigner distribution versus impossibility to violate Bell inequality is taken for granted or is considered as obvious by the author.
Let us now study in detail the results of Ref. [
30]. The starting point is the following Wigner function
which is obviously positive definite. In fact, this is the product of the Wigner function of a coherent state with the Wigner function of a squeezed state. One can also check that this Wigner function is correctly normalized. Then, Ref. [
30] proceeds and applies Bell’s trick consisting in working with unnormalized states to the Wigner function (
115). In order to see what it means in the present context, the best is to calculate the Wigner function associated with the wavefunction (
109). Recall that the wavefunction (
109) is the correctly normalized version of the unnormalized wavefunction (
108) considered before and used by Bell to show that a non-positive Wigner function may cause a CHSH inequality violation. Assuming the wavefunction (
109), the corresponding Wigner function reads
As discussed before, Bell claims that one can take the limit
from the very beginning, which consists of killing the term proportional to
and boosting the term proportional to
in the argument of the first exponential. In the limit
, one has
and recalling that
, we see that we exactly arrive at the Wigner function considered by Bell in his article, namely Equation (
110) (for
, which is the choice made in Bell’s article). The conclusion is that Bell’s limit or trick is equivalent to killing the term proportional to
and boosting the term
in the Wigner function.
Therefore, coming back to Equation (
115) and to the article [
30], this corresponds to taking the limit
, leading to
where
. We see that this Wigner function also contains a Dirac function of
as in Equation (
110), which confirms that Bell’s limit has indeed been correctly implemented in Equation (
115). As already noticed before, Ref. [
30] remarks that
K is what Bell calls an “
an unimportant constant”. Here, we have calculated
K in term of
s, which is not done in Ref. [
30].
Then, we repeat once more the standard procedure. We first calculate
by integrating the Wigner function over
and
. We find
where
(recall that Bell defines
as
) and
. This expression exactly coincides with Equation (10) of Ref. [
30]. The only difference is that the constant
K is divided by
instead of
in the above expression. This factor
is just due to the fact that Ref. [
30] has a slightly different definition of
K: according to its Equation (3), it is indeed the overall constant for the Wigner function (
117) if the Dirac function appearing is written as
, while in our case the Dirac function is simply written
. This difference accounts for the
between the two expressions.
Although Ref. [
30] is supposed to mimic Bell’s paper exactly, there are other differences between the two articles. One, which is only a detail, is that Ref. [
30] defines the sign operators, or pseudo spin operators, with
, namely
and
. However, this does not affect the discussion since it was shown before that Bell’s result does not depend on
. This also means that Equation (
94) now reads
. Inserting Equation (
118) in this last expression, one finds that
which coincides with Equation (14) of Ref. [
30] (up to the factor
already mentioned above). Following Bell, Ref. [
30] simply defines
by
, which means that
in agreement with Equation (14) of this paper.
Finally, Ref. [
30] computes the mean value of the Bell operator given in Equation (
114), namely for
,
,
,
. Following Bell, Ref. [
30] studies the function
which, if it takes negative values, signals a violation of the CHSH inequality—see the discussion around Equation (
114). Ref. [
30] notices that, if, for instance, one chooses
and
, this is precisely the case in the limit
—see
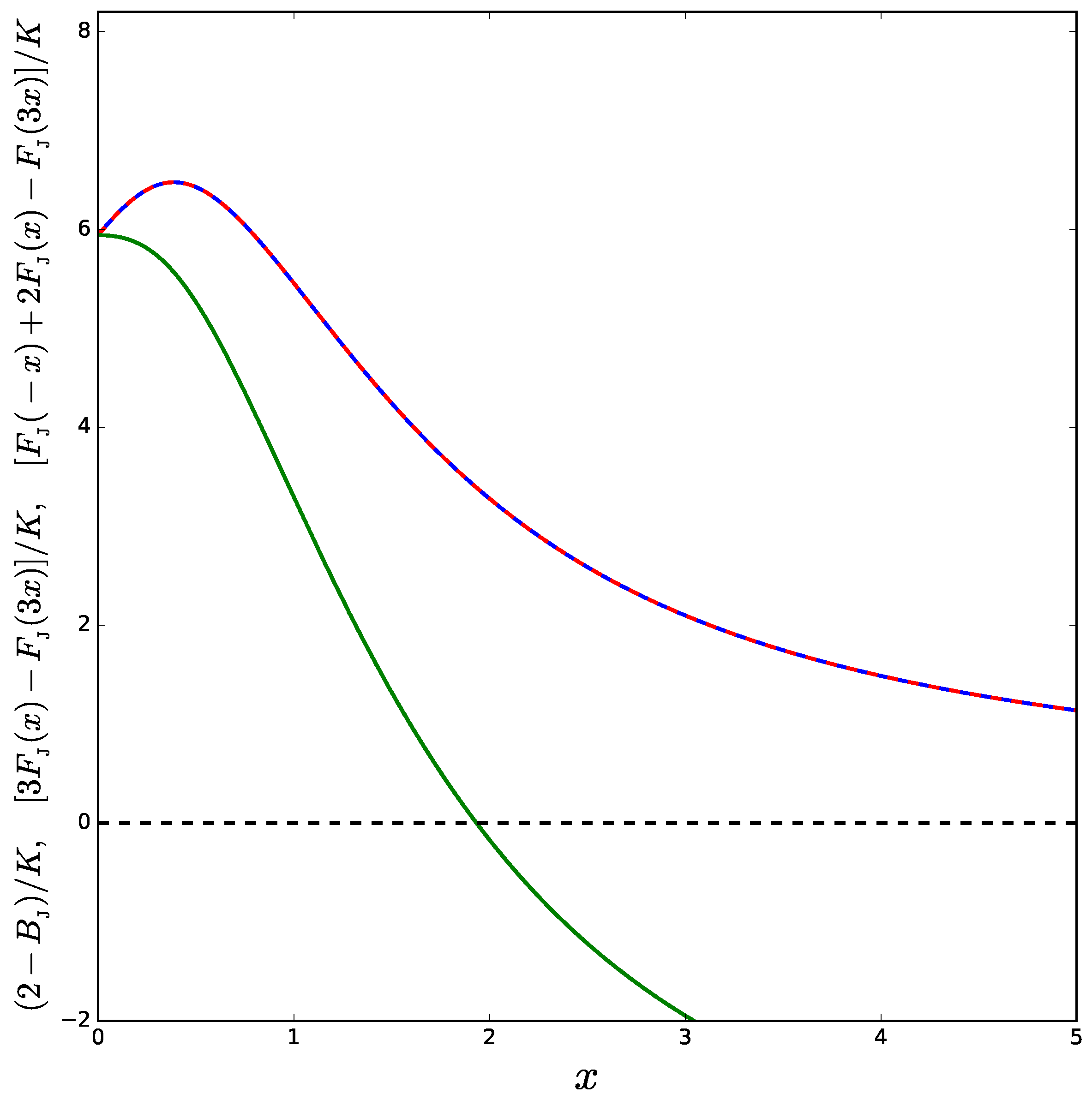
Figure 1 of this article. In
Figure 7, we have checked that, indeed, the function
can be negative—see the green solid line. Notice that the scales in
Figure 7 and in Figure 1 of Ref. [
30] do not coincide because of the slight difference in the definition of
already signaled before.
Therefore, by using Bell’s trick, Ref. [
30] arrives at a violation of the CHSH inequality starting with a Wigner function which is positive definite. According to this paper, this is impossible because a positive Wigner function necessarily implies that the CHSH inequality cannot be violated. As a consequence, Ref. [
30] concludes that the only way out is that Bell’s trick, and therefore his entire paper, is incorrect. The deep reason for this mistake is that “
one is not allowed to assume that K is time independent”.
4.7. Revzen’s Theorem
We are apparently in a complex situation: we have found that Bell’s paper establishing a connection between the non-positivity of the Wigner function and a CHSH inequality violation is incorrect, but we have also reached the conclusion that the criticisms expressed against that paper are wrong as well! Moreover, all these authors seem to agree that, if the Wigner function is positive definite, then no CHSH inequality violation can occur, which, we recall, would have important conceptual consequences for Cosmology.
In fact, the situation was clarified in 2004 in Refs. [
60,
61]. In these papers, Revzen establishes that, under certain conditions that we are going to describe, Bell inequality can be violated even if the Wigner distribution is positive definite. Notice that this both invalidates Bell’s paper [
27], since Revzen’s result shows that a Bell inequality violation is not necessarily associated with a negative Wigner function, but also Ref. [
30] since its reasoning was entirely based on the fact that violating Bell’s inequality is impossible if the Wigner function is positive. In his paper, Revzen mentions Bell’s paper [
27] but says that “
Bell’s original argument that nonnegativity of Wigner’s function suffices to preclude Bell inequality violation was shown to be inaccurate” in Ref. [
30]. He adds that “
Difficulties in handling normalization of the EPR state considered by Bell were shown to involve a misleading factor”. As explained in the last section, this description is not very accurate since we have just shown that the criticisms of Ref. [
30] are in fact not valid.
Let us now come to the main result obtained by Revzen. In brief, Revzen shows that Bell inequality can be violated even if the Wigner function is positive definite provided the variables considered are “improper”, namely if the Weyl transform (defined in Equation (
42)) of an operator takes different values than the spectrum of that operator. Let us give an example of a proper and improper operators. First, let us consider the pseudo spin operators used by Bell, namely
. Its Weyl transform is given by
Therefore, this operator is proper since its Weyl transform takes values
which are exactly the values taken by the spectrum of the operator. This explains why, in the EPR state, Bell inequality was not violated in
Section 4.3. This was a situation where the Wigner function was positive and the operator used to construct the Bell operator was proper.
Let us now give an example of an improper operator. Let us consider the following operator
The reason for the notation
will be clarified below. Here,
is an eigenvector of the number operator. It is easy to show that the spectrum of this operator is
because
. The matrix element of
is given by
with a plus sign if
m is odd and a minus sign if m is even. This allows us to rewrite
as
Indeed, one can show that this leads to the same matrix element, namely
where
is a Hermite polynomial of order
n [
52]. It follows that
Clearly, the Weyl transform of does not take values and, as a consequence, this operator is improper.
The Revzen theorem rests on Equations (
43) and (
44). Indeed, according to these equations, the mean value of an operator is the average of its Weyl transform weighted by the Wigner function. If the Weyl transform takes the same values as the spectrum of the operator, it means that any quantum average can be obtained through the usual, classical, laws of random variables. However, if this is so, Bell’s theorem precisely tells us that its inequality cannot be violated.
We conclude that the history of the relationship between the possibility of violating Bell inequality and the positivity of the Wigner function is a long, chaotic and rich one. For Cosmology, this question is absolutely crucial since the Wigner function is, in this case, positive definite. The Revzen theorem establishes the possibility of a Bell inequality violation in the sky, a fascinating possibility indeed. In his paper, Revzen precisely discusses his theorem with the help of a two-mode squeezed state. What was not realized before is that Cosmology provides a perfect situation to illustrate this problem. It was not realized by the cosmology community because the issues related to quantum foundations are, usually, far from its everyday interests and it was not realized by people working on Quantum Mechanics because the inflationary mechanism and the fact that cosmological perturbations are placed in a two-mode squeezed state was largely ignored by people working in this field. In fact, given that Cosmology is the part of physics where the largest squeezing is achieved, one can even argue that it is the most interesting situation to discuss the issues tackled in this section.