Tripartite Entanglement: Foundations and Applications
Abstract
1. Introduction
2. Overview of Bipartite Entanglement
2.1. Pure States
2.2. Some Special Families of Mixed States
2.2.1. Werner States
2.2.2. Isotropic States
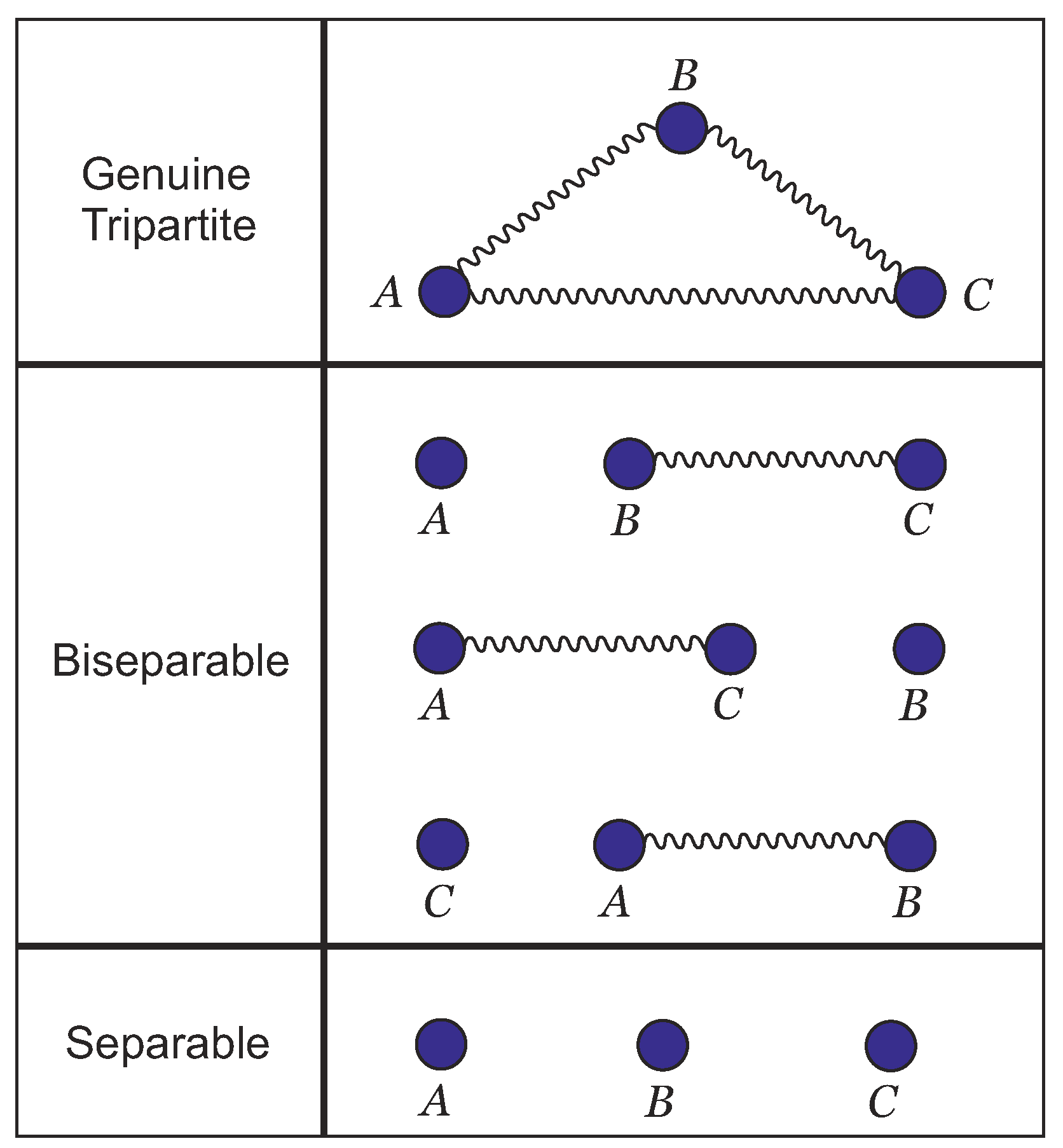
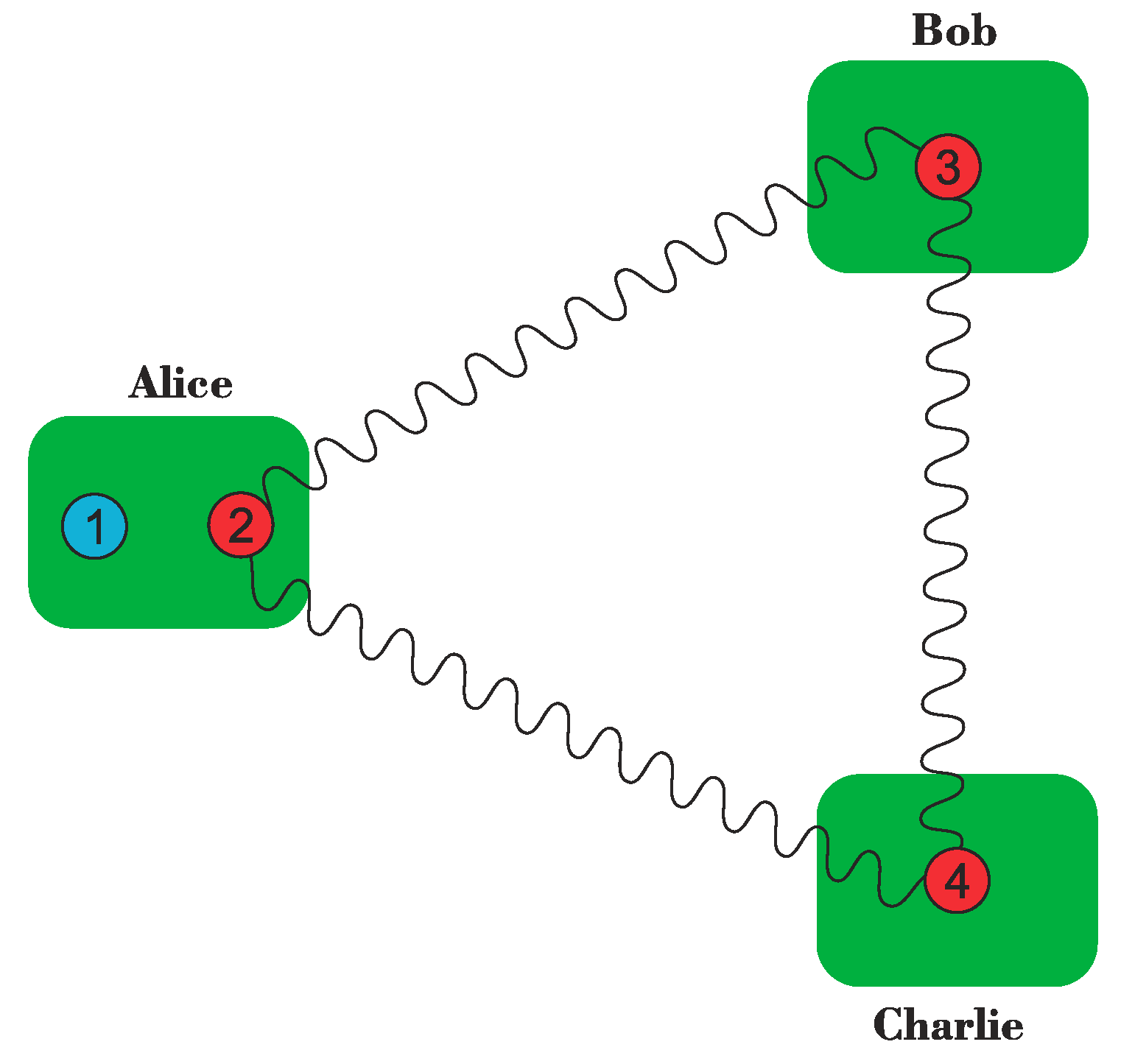
3. Tripartite Entanglement
3.1. Genuine Tripartite Pure States
3.2. Other Instances of Tripartite Entanglement
3.3. Tripartite Entanglement in Other Areas
4. Non-Locality, Bell’s Theorem and GHZ States
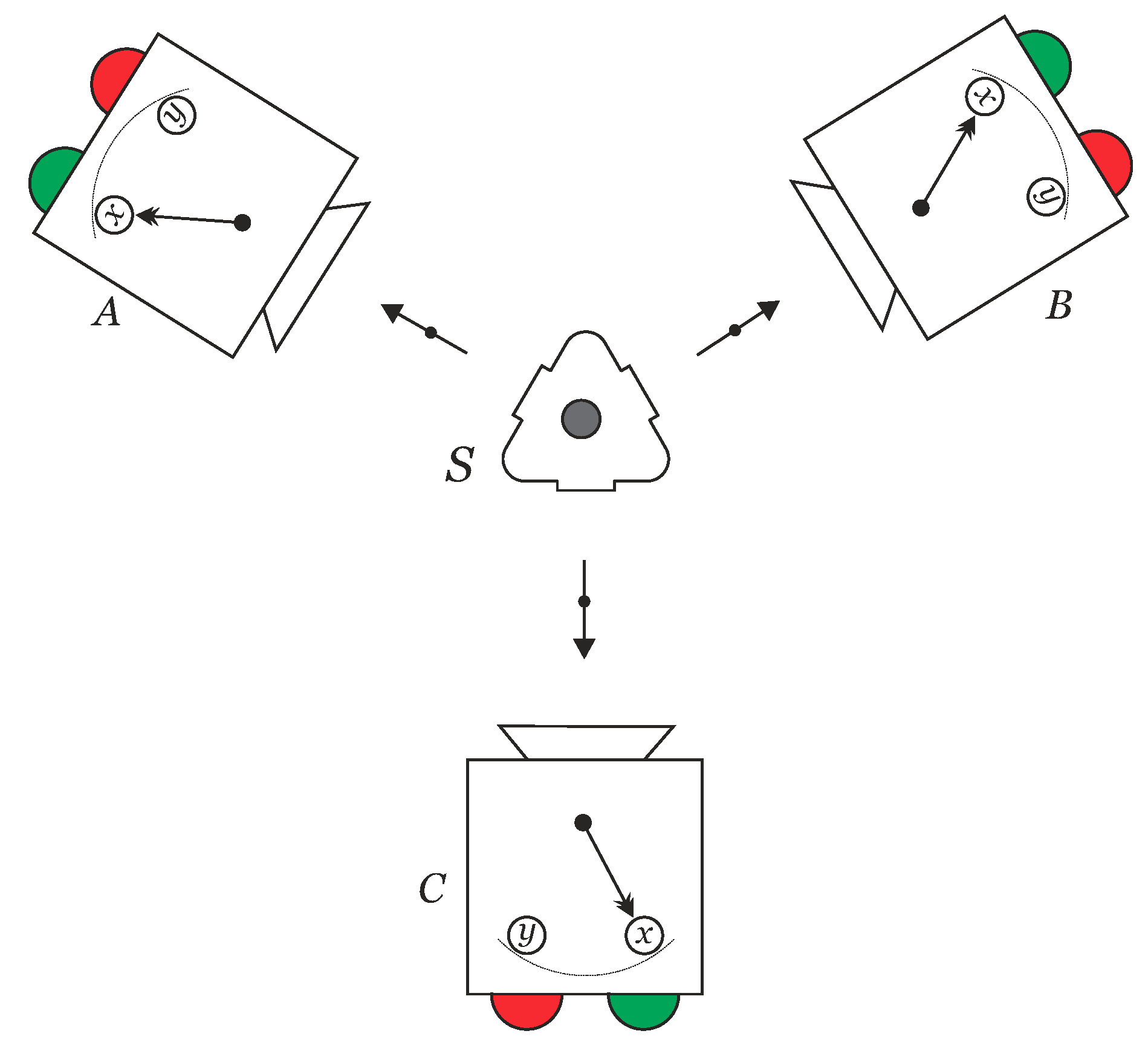
5. Quantum Information Protocols Using Three-Partite Entanglement
5.1. Teleportation of a Single-Qubit State by Using a GHZ Channel and EPR Measurements
5.2. Teleportation of a Single-Qubit State: GHZ Channel and Measurement
5.3. Teleportation of a Two-Qubit State
5.4. Teleportation of a GHZ State
5.5. Teleportation of a Single-Qubit State Using a W Channel
5.6. Teleportation of a W State
5.7. Dense Coding
5.8. Quantum Cryptography and Quantum Secure Communication
5.9. Other Developments
6. Production of Three-Partite Entanglement
7. Detection and Characterization of Tripartite Entanglement
8. Remote Preparation
9. Continuous-Variable Systems
10. Noisy Environments
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Gabriel, C.; Aiello, A.; Zhong, W.; Euser, T.G.; Joly, N.Y.; Banzer, P.; Förtsch, M.; Elser, D.; Andersen, U.L.; Marquardt, C.; et al. Entangling different degrees of freedom by quadrature squeezing cylindrically polarized modes. Phys. Rev. Lett. 2011, 106, 060502. [Google Scholar] [CrossRef]
- Barnett, S. Quantum Information; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Luo, Y.H.; Zhong, H.S.; Erhard, M.; Wang, X.L.; Peng, L.C.; Krenn, M.; Jiang, X.; Li, L.; Liu, N.L.; Lu, C.Y.; et al. Quantum teleportation in high dimensions. Phys. Rev. Lett. 2019, 123, 070505. [Google Scholar] [CrossRef]
- Chen, P.X.; Zhu, S.Y.; Guo, G.C. General form of genuine multipartite entanglement quantum channels for teleportation. Phys. Rev. A 2006, 74, 032324. [Google Scholar] [CrossRef]
- De, A.S.; Sen, U. Quantum Advantage in Communication Networks. Available online: https://arxiv.org/abs/1105.2412 (accessed on 26 September 2019).
- Raussendorf, R.; Briegel, H.J. A one-way quantum computer. Phys. Rev. Lett. 2001, 86, 5188–5191. [Google Scholar] [CrossRef]
- Li, M.; Jia, L.; Wang, J.; Shen, S.; Fei, S.M. Measure and detection of genuine multipartite entanglement for tripartite systems. Phys. Rev. A 2017, 96, 052314. [Google Scholar] [CrossRef]
- Briegel, H.J.; Browne, D.E.; Dür, W.; Raussendorf, R.; Van den Nest, M. Measurement-based quantum computation. Nat. Phy. 2009, 5, 19. [Google Scholar] [CrossRef]
- Bengtsson, I.; Zyczkowski, K. A Brief Introduction to Multipartite Entanglement. Available online: https://arxiv.org/abs/1612.07747 (accessed on 26 September 2019).
- Enríquez, M.; Wintrowicz, I.; Życzkowski, K. Maximally entangled multipartite states: A brief survey. J. Phys. Conf. Ser. 2016, 698, 012003. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Walter, M.; Gross, D.; Eisert, J. Multi-Partite Entanglement. Available online: https://arxiv.org/abs/1612.02437 (accessed on 26 September 2019).
- Fortes, R.; Rigolin, G. Fighting noise with noise in realistic quantum teleportation. Phys. Rev. A 2015, 92, 012338. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 2008, 4, 282. [Google Scholar] [CrossRef]
- Takesue, H.; Dyer, S.D.; Stevens, M.J.; Verma, V.; Mirin, R.P.; Nam, S.W. Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors. Optica 2015, 2, 832–835. [Google Scholar] [CrossRef]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277–4281. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 1999, 59, 4206–4216. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Hirsch, F.; Quintino, M.T.; Vértesi, T.; Navascués, M.; Brunner, N. Better local hidden variable models for two-qubit Werner states and an upper bound on the Grothendieck constant $K_G(3)$. Quantum 2016, 1, 3. [Google Scholar] [CrossRef]
- Zhao, M.J.; Zhang, T.G.; Li-Jost, X.; Fei, S.M. Identification of three-qubit entanglement. Phys. Rev. A 2013, 87, 012316. [Google Scholar] [CrossRef]
- Bose, S.; Vedral, V.; Knight, P.L. Purification via entanglement swapping and conserved entanglement. Phys. Rev. A 1999, 60, 194–197. [Google Scholar] [CrossRef]
- Vidal, G. Entanglement of pure states for a single copy. Phys. Rev. Lett. 1999, 83, 1046–1049. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Shimony, A.; Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 1990, 58, 1131–1143. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Going beyond Bell’s theorem. In Bell’s Theorem, Quantum Theory and Conceptions of the Universe; Springer: Dordrecht, The Netherlands, 1989; pp. 69–72. [Google Scholar]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Żukowski, M.; Zeilinger, A.; Horne, M.; Weinfurter, H. Quest for GHZ states. Acta Phys. Pol. A 1998, 93, 187. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Schwemmer, C.; Knips, L.; Tran, M.C.; De Rosier, A.; Laskowski, W.; Paterek, T.; Weinfurter, H. Genuine multipartite entanglement without multipartite correlations. Phy. Rev. Lett. 2015, 114, 180501. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Zhao, S.M. Efficient two-step entanglement concentration for arbitrary W states. Phys. Rev. A 2012, 85, 042302. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L. Efficient W-state entanglement concentration using quantum-dot and optical microcavities. J. Opt. Soc. Am. B 2013, 30, 678–686. [Google Scholar] [CrossRef]
- Sheng, Y.; Pan, J.; Guo, R.; Zhou, L.; Wang, L. Efficient N-particle W state concentration with different parity check gates. Sci. Chin. Phy. Mech. Astron. 2015, 58, 1–11. [Google Scholar] [CrossRef]
- Sheng, Y.; Liu, J.; Zhao, S.; Zhou, L. Multipartite entanglement concentration for nitrogen-vacancy center and microtoroidal resonator system. Chin. Sci. Bull. 2013, 58, 3507–3513. [Google Scholar] [CrossRef]
- Zhou, L. Efficient entanglement concentration for electron-spin W state with the charge detection. Quantum Inf. Process. 2013, 12, 2087–2101. [Google Scholar] [CrossRef]
- Acín, A.; Andrianov, A.; Costa, L.; Jané, E.; Latorre, J.I.; Tarrach, R. Generalized schmidt decomposition and classification of three-quantum-bit states. Phys. Rev. Lett. 2000, 85, 1560–1563. [Google Scholar] [CrossRef]
- Acín, A.; Andrianov, A.; Jané, E.; Tarrach, R. Three-qubit pure-state canonical forms. J. Phys. A Math. Gen. 2001, 34, 6725–6739. [Google Scholar] [CrossRef]
- Acin, A.; Bruß, D.; Lewenstein, M.; Sanpera, A. Classification of mixed three-qubit states. Phys. Rev. Lett. 2001, 87, 040401. [Google Scholar] [CrossRef]
- Erhard, M.; Malik, M.; Krenn, M.; Zeilinger, A. Experimental Greenberger–Horne–Zeilinger entanglement beyond qubits. Nat. Photonics 2018, 12, 759. [Google Scholar] [CrossRef]
- Siewert, J.; Eltschka, C. Quantifying tripartite entanglement of three-qubit generalized Werner States. Phys. Rev. Lett. 2012, 108, 230502. [Google Scholar] [CrossRef]
- Aravind, P. Borromean entanglement of the GHZ state. In Potentiality, Entanglement and Passion-at-a-Distance; Springer: Dordrecht, The Netherlands, 1997; pp. 53–59. [Google Scholar]
- Kauffman, L.H.; Lomonaco, S.J., Jr. Quantum entanglement and topological entanglement. New J. Phys. 2002, 4, 73. [Google Scholar] [CrossRef]
- Asoudeh, M.; Karimipour, V.; Memarzadeh, L.; Rezakhani, A. On a suggestion relating topological and quantum mechanical entanglements. Phys. Lett. A 2004, 327, 380–390. [Google Scholar] [CrossRef][Green Version]
- Mironov, S. Topological entanglement and knots. Universe 2019, 5, 60. [Google Scholar] [CrossRef]
- Perseguers, S.; Cavalcanti, D.; Lapeyre, G., Jr.; Lewenstein, M.; Acín, A. Multipartite entanglement percolation. Phys. Rev. A 2010, 81, 032327. [Google Scholar] [CrossRef]
- McCutcheon, W.; Pappa, A.; Bell, B.; McMillan, A.; Chailloux, A.; Lawson, T.; Mafu, M.; Markham, D.; Diamanti, E.; Kerenidis, I.; et al. Experimental verification of multipartite entanglement in quantum networks. Nat. Commun. 2016, 7, 13251. [Google Scholar] [CrossRef]
- Duff, M. The black hole/qubit correspondence. J. Phys. Conf. Ser. 2013, 462, 012012. [Google Scholar] [CrossRef]
- Borsten, L.; Duff, M.J.; Lévay, P. The black-hole/qubit correspondence: an up-to-date review. Class. Quantum Gravity 2012, 29, 224008. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fizika 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682. [Google Scholar] [CrossRef]
- Mermin, N.D. Quantum mysteries revisited. Am. J. Phys. 1990, 58, 731–734. [Google Scholar] [CrossRef]
- Lo, H.K.; Spiller, T.; Popescu, S. Introduction to Quantum Computation and Information; World Scientific: Singapore, 1998. [Google Scholar]
- Cabello, A. Bell’s theorem with and without inequalities for the three-qubit Greenberger-Horne-Zeilinger and W states. Phys. Rev. A 2002, 65, 032108. [Google Scholar] [CrossRef]
- Hardy, L. Nonlocality for 2 Particles without Inequalities for Almost-All Entangled States. Phys. Rev. Lett. 1993, 71, 1665–1668. [Google Scholar] [CrossRef]
- Mermin, N.D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 1990, 65, 1838–1840. [Google Scholar] [CrossRef]
- Ardehali, M. Bell inequalities with a magnitude of violation that grows exponentially with the number of particles. Phys. Rev. A 1992, 46, 5375–5378. [Google Scholar] [CrossRef]
- Belinskiĭ, A.V.; Klyshko, D.N. Interference of light and Bell’s theorem. Phys. Usp. 1993, 36, 653–693. [Google Scholar] [CrossRef]
- Svetlichny, G. Distinguishing three-body from two-body nonseparability by a Bell-type inequality. Phys. Rev. D 1987, 35, 3066–3069. [Google Scholar] [CrossRef]
- Cereceda, J.L. Three-particle entanglement versus three-particle nonlocality. Phys. Rev. A 2002, 66, 024102. [Google Scholar] [CrossRef]
- Bancal, J.D.; Barrett, J.; Gisin, N.; Pironio, S. Definitions of multipartite nonlocality. Phys. Rev. A 2013, 88, 014102. [Google Scholar] [CrossRef]
- Paul, B.; Mukherjee, K.; Sarkar, D. Revealing hidden genuine tripartite nonlocality. Phys. Rev. A 2016, 94, 052101. [Google Scholar] [CrossRef]
- Pan, J.W.; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. Experimental test of quantum nonlocality in three-photon Greenberger–Horne–Zeilinger entanglement. Nature 2000, 403, 515–519. [Google Scholar] [CrossRef]
- Lavoie, J.; Kaltenbaek, R.; Resch, K.J. Experimental violation of Svetlichny’s inequality. New J. Phys. 2009, 11, 073051. [Google Scholar] [CrossRef]
- Erven, C.; Meyer-Scott, E.; Fisher, K.; Lavoie, J.; Higgins, B.; Yan, Z.; Pugh, C.; Bourgoin, J.P.; Prevedel, R.; Shalm, L.; et al. Experimental three-photon quantum nonlocality under strict locality conditions. Nat. Photonics 2014, 8, 292. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, C.J.; Huang, Y.F.; Hou, Z.B.; Liu, B.H.; Li, C.F.; Guo, G.C. Experimental test of genuine multipartite nonlocality under the no-signalling principle. Sci. Rep. 2016, 6, 39327. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, A. Analysing nonlocality robustness in multiqubit systems under noisy conditions and weak measurements. Quantum Inf. Process. 2018, 17, 249. [Google Scholar] [CrossRef]
- Swain, M.; Rai, A.; Behera, B.K.; Panigrahi, P.K. Experimental demonstration of the violations of Mermin’s and Svetlichny’s inequalities for W and GHZ states. Quantum Inf. Process. 2019, 18, 218. [Google Scholar] [CrossRef]
- Caban, P.; Trzcińska, K. Noise resistance of activation of the violation of the Svetlichny inequality. Quantum Inf. Process. 2019, 18, 139. [Google Scholar] [CrossRef]
- Chaves, R.; Cavalcanti, D.; Aolita, L. Causal hierarchy of multipartite Bell nonlocality. Quantum 2017, 1, 23. [Google Scholar] [CrossRef]
- Karlsson, A.; Bourennane, M. Quantum teleportation using three-particle entanglement. Phys. Rev. A 1998, 58, 4394. [Google Scholar] [CrossRef]
- Almeida, N.; Maia, L.; Villas-Bôas, C.; Moussa, M. One-cavity scheme for atomic-state teleportation through GHZ states. Phys. Lett. A 1998, 241, 213–217. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Samanta, S. Simultaneous perfect teleportation of three 2-qubit states. Quantum Inf. Process. 2017, 16, 230. [Google Scholar] [CrossRef]
- Moreno, M.; Fonseca, A.; Cunha, M.M. Using three-partite GHZ states for partial quantum error detection in entanglement-based protocols. Quantum Inf. Process. 2018, 17, 191. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; An, N.B. Quantum state sharing of an arbitrary multiqubit state using nonmaximally entangled GHZ states. Eur. Phys. J. D 2007, 42, 333–340. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Gou, Y.T.; Hou, J.X.; Cao, L.K.; Wang, X.H. Probabilistic resumable quantum teleportation of a two-qubit entangled state. Entropy 2019, 21, 352. [Google Scholar] [CrossRef]
- Gorbachev, V.; Trubilko, A. Quantum teleportation of an Einstein-Podolsy-Rosen pair using an entangled three-particle state. J. Exp. Theor. Phys. 2000, 91, 894–898. [Google Scholar] [CrossRef]
- Shi, B.S.; Jiang, Y.K.; Guo, G.C. Probabilistic teleportation of two-particle entangled state. Phys. Lett. A 2000, 268, 161–164. [Google Scholar] [CrossRef]
- Tsai, C.W.; Hwang, T. Teleportation of a pure EPR state via GHZ-like state. Int. J. Theor. Phys. 2010, 49, 1969–1975. [Google Scholar] [CrossRef]
- Li, D.f.; Wang, R.j.; Baagyere, E. Quantum teleportation of an arbitrary two-qubit state by using two three-qubit GHZ states and the six-qubit entangled state. Quantum Inf. Process. 2019, 18, 147. [Google Scholar] [CrossRef]
- Dai, H.Y.; Chen, P.X.; Li, C.Z. Probabilistic teleportation of an arbitrary two-particle state by a partially entangled three-particle GHZ state and W state. Opt. Commun. 2004, 231, 281–287. [Google Scholar] [CrossRef]
- Wang, K.; Yu, X.T.; Zhang, Z.C. Teleportation of two-qubit entangled state via non-maximally entangled GHZ state. Procedia Comput. Sci. 2018, 131, 1202–1208. [Google Scholar] [CrossRef]
- Hassanpour, S.; Houshmand, M. Bidirectional teleportation of a pure EPR state by using GHZ states. Quantum Inf. Process. 2016, 15, 905–912. [Google Scholar] [CrossRef]
- Zou, Z.Z.; Yu, X.T.; Gong, Y.X.; Zhang, Z.C. Multihop teleportation of two-qubit state via the composite GHZ–Bell channel. Phys. Lett. A 2017, 381, 76–81. [Google Scholar] [CrossRef]
- Wang, K.; Yu, X.T.; Cai, X.F.; Zhang, Z.C. Probabilistic teleportation of arbitrary two-qubit quantum state via non-symmetric quantum channel. Entropy 2018, 20, 238. [Google Scholar] [CrossRef]
- Xia, Y.; Song, J.; Lu, P.M.; Song, H.S. Teleportation of an N-photon Greenberger-Horne-Zeilinger (GHZ) polarization-entangled state using linear optical elements. J. Opt. Soc. Am. B 2010, 27, A1–A6. [Google Scholar] [CrossRef]
- Hong, L. Probabilistic teleportation of the three-particle entangled state via entanglement swapping. Chin. Phys. Lett. 2001, 18, 1004. [Google Scholar] [CrossRef]
- Xiu, L.; Hong-Cai, L. Probabilistic teleportation of a three-particle GHZ state via two three-particle entangled W states. Commun. Theor. Phys. 2006, 45, 1018. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Samanta, S. A Teleportation Protocol For Transfer of Arbitrary GHZ-states Using Intermediate Nodes. Int. J. Theor. Phys. 2018, 57, 2665–2675. [Google Scholar] [CrossRef]
- Jin-Ming, L.; Guang-Can, G. Quantum teleportation of a three-particle entangled state. Chin. Phys. Lett. 2002, 19, 456. [Google Scholar] [CrossRef]
- Fang, J.; Lin, Y.; Zhu, S.; Chen, X. Probabilistic teleportation of a three-particle state via three pairs of entangled particles. Phys. Rev. A 2003, 67, 014305. [Google Scholar] [CrossRef]
- Shi, B.S.; Tomita, A. Teleportation of an unknown state by W state. Phys. Lett. A 2002, 296, 161–164. [Google Scholar] [CrossRef]
- Joo, J.; Park, Y.J. Comment on “Teleportation of an unknown state by W states”:[Phys. Lett. A 296 (2002) 161]. Phys. Lett. A 2002, 300, 324–326. [Google Scholar] [CrossRef]
- Shi, B.S.; Tomita, A. Reply to“Comment on: Teleportation of an unknown state by W state”.[Phys. Lett. A 300 (2002) 324]. Phys. Lett. A 2002, 300, 538–539. [Google Scholar] [CrossRef]
- Gorbachev, V.; Trubilko, A.; Rodichkina, A.; Zhiliba, A. Can the states of the W-class be suitable for teleportation? Phys. Lett. A 2003, 314, 267–271. [Google Scholar] [CrossRef]
- Joo, J.; Park, Y.J.; Oh, S.; Kim, J. Quantum teleportation via a W state. New J. Phys. 2003, 5, 136. [Google Scholar] [CrossRef]
- Agrawal, P.; Pati, A. Perfect teleportation and superdense coding with W states. Phys. Rev. A 2006, 74, 062320. [Google Scholar] [CrossRef]
- Li, L.; Qiu, D. The states of W-class as shared resources for perfect teleportation and superdense coding. J. Phys. A Math. Theor. 2007, 40, 10871. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.H.; Shu, L.; Mo, Z.W. Quantum teleportation and superdense coding through the composite W-Bell channel. Quantum Inf. Process. 2013, 12, 1957–1967. [Google Scholar] [CrossRef]
- Zheng, Y.Z.; Gu, Y.J.; Guo, G.C. Teleportation of a three-particle entangled W state. Chin. Phys. 2002, 11, 537. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, Z.; Gong, Y.; Sheng, B.; Yu, X. Teleportation of entanglement using a three-particle entangled W state. J. Opt. Soc. Am. B 2017, 34, 142–147. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Advances in Quantum Dense Coding. Adv. Quantum Technol. 2019, 2, 1900011. [Google Scholar] [CrossRef]
- Hao, J.C.; Li, C.F.; Guo, G.C. Controlled dense coding using the Greenberger-Horne-Zeilinger state. Phys. Rev. A 2001, 63, 054301. [Google Scholar] [CrossRef]
- Huang, Y.B.; Li, S.S.; Nie, Y.Y. Controlled dense coding via GHZ-class state. Int. J. Mod. Phys. C 2008, 19, 1509–1514. [Google Scholar] [CrossRef]
- Yang, X.; Bai, M.Q.; Mo, Z.W. Controlled Dense Coding with the W State. Int. J. Theor. Phys. 2017, 56, 3525–3533. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Wang, F.; Luo, M.X. Efficient Superdense Coding with W States. Int. J. Theor. Phys. 2018, 57, 1935–1941. [Google Scholar] [CrossRef]
- Ye, L.; Yu, L.B. Scheme for implementing quantum dense coding using tripartite entanglement in cavity QED. Phys. Lett. A 2005, 346, 330–336. [Google Scholar] [CrossRef]
- Roy, S.; Chanda, T.; Das, T.; De, A.S.; Sen, U. Deterministic quantum dense coding networks. Phys. Lett. A 2018, 382, 1709–1715. [Google Scholar] [CrossRef]
- Wiesner, S. Conjugate coding. ACM Spec. Interest Group Algorithms Comput. Theor. News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Joo, J.; Lee, J.; Jang, J.; Park, Y.J. Quantum Secure Communication with W States. Available online: https://arxiv.org/abs/quant-ph/0204003 (accessed on 26 September 2019).
- Jin, X.R.; Ji, X.; Zhang, Y.Q.; Zhang, S.; Hong, S.K.; Yeon, K.H.; Um, C.I. Three-party quantum secure direct communication based on GHZ states. Phys. Lett. A 2006, 354, 67–70. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; An, N.B. Quantum secure direct communication by using GHZ states and entanglement swapping. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3855. [Google Scholar] [CrossRef]
- Chen, X.B.; Wen, Q.Y.; Guo, F.Z.; Sun, Y.; Xu, G.; Zhu, F.C. Controlled quantum secure direct communication with W state. Int. J. Quantum Inf. 2008, 6, 899–906. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Yin, H.L.; Chen, T.Y.; Chen, Z.B. Long-Distance Measurement-Device-Independent Multiparty Quantum Communication. Phys. Rev. Lett. 2015, 114, 090501. [Google Scholar] [CrossRef]
- Christandl, M.; Wehner, S. Quantum anonymous transmissions. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2005; pp. 217–235. [Google Scholar]
- Lipinska, V.; Murta, G.; Wehner, S. Anonymous transmission in a noisy quantum network using the W state. Phys. Rev. A 2018, 98, 052320. [Google Scholar] [CrossRef]
- Cruz, D.; Fournier, R.; Gremion, F.; Jeannerot, A.; Komagata, K.; Tosic, T.; Thiesbrummel, J.; Chan, C.L.; Macris, N.; Dupertuis, M.A.; et al. Efficient quantum algorithms for GHZ and W states, and implementation on the IBM quantum computer. Adv. Quantum Technol. 2019, 2, 1900015. [Google Scholar] [CrossRef]
- Hwang, M.R.; Park, D.; Jung, E. Tripartite entanglement in a noninertial frame. Phys. Rev. A 2011, 83, 012111. [Google Scholar] [CrossRef]
- Acin, A.; Jane, E.; Dür, W.; Vidal, G. Optimal distillation of a Greenberger-Horne-Zeilinger state. Phys. Rev. Lett. 2000, 85, 4811. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.N.; Li, C.F.; Guo, G.C. Distillation of the Greenberger-Horne-Zeilinger state from arbitrary tripartite states. Phys. Rev. A 2002, 65, 024301. [Google Scholar] [CrossRef]
- Yildiz, A. Optimal distillation of three-qubit W states. Phys. Rev. A 2010, 82, 012317. [Google Scholar] [CrossRef]
- Liao, X.P.; Fang, M.F.; Fang, J.S. Entanglement purification and amplification of three-qubit states using two-outcome weak measurements. J. Mod. Opt. 2014, 61, 1018–1026. [Google Scholar] [CrossRef]
- Yuan, J.; Tang, S.; Wang, X.; Zhang, D. One-step distillation of local-unitary-equivalent GHZ-type states. Quantum Inf. Process. 2018, 17, 259. [Google Scholar] [CrossRef]
- Gottesman, D.; Chuang, I.L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 1999, 402, 390. [Google Scholar] [CrossRef]
- Cai, Y.; Le, H.N.; Scarani, V. State complexity and quantum computation. Annalen der Physik 2015, 527, 684–700. [Google Scholar] [CrossRef]
- D’Hondt, E.; Panangaden, P. The Computational Power of the W And GHZ States. Quantum Inf. Comput. 2006, 6, 173–183. [Google Scholar]
- Rajan, D.; Visser, M. Quantum Blockchain using entanglement in time. Quantum Rep. 2019, 1, 2. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Y.A.; Zhang, A.N.; Yang, T.; Briegel, H.J.; Pan, J.W. Experimental demonstration of five-photon entanglement and open-destination teleportation. Nature 2004, 430, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Monz, T.; Schindler, P.; Barreiro, J.T.; Chwalla, M.; Nigg, D.; Coish, W.A.; Harlander, M.; Hänsel, W.; Hennrich, M.; Blatt, R. 14-qubit entanglement: Creation and coherence. Phys. Rev. Lett. 2011, 106, 130506. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Daniell, M.; Weinfurter, H.; Zeilinger, A. Observation of three-photon Greenberger-Horne-Zeilinger entanglement. Phys. Rev. Lett. 1999, 82, 1345. [Google Scholar] [CrossRef]
- Eibl, M.; Kiesel, N.; Bourennane, M.; Kurtsiefer, C.; Weinfurter, H. Experimental Realization of a Three-Qubit Entangled W State. Phys. Rev. Lett. 2004, 92, 077901. [Google Scholar] [CrossRef] [PubMed]
- Zeilinger, A.; Horne, M.A.; Weinfurter, H.; Żukowski, M. Three-particle entanglements from two entangled pairs. Phys. Rev. Lett. 1997, 78, 3031. [Google Scholar] [CrossRef]
- Laflamme, R.; Knill, E.; Zurek, W.; Catasti, P.; Mariappan, S. NMR Greenberger–Horne–Zeilinger states. Philos. Trans. R. Soc. Lond. Ser. A 1998, 356, 1941–1948. [Google Scholar] [CrossRef]
- Ju, L.; Yang, M.; Paunković, N.; Chu, W.J.; Cao, Z.L. Creating photonic GHZ and W states via quantum walk. Quantum Inf. Process. 2019, 18, 176. [Google Scholar] [CrossRef]
- Erdösi, D.; Huber, M.; Hiesmayr, B.C.; Hasegawa, Y. Proving the generation of genuine multipartite entanglement in a single-neutron interferometer experiment. New J. Phys. 2013, 15, 023033. [Google Scholar] [CrossRef]
- Yamamoto, T.; Tamaki, K.; Koashi, M.; Imoto, N. Polarization-entangled W state using parametric down-conversion. Phys. Rev. A 2002, 66, 064301. [Google Scholar] [CrossRef]
- Yu, C.S.; Yi, X.X.; Song, H.S.; Mei, D. Robust preparation of Greenberger-Horne-Zeilinger and W states of three distant atoms. Phys. Rev. A 2007, 75, 044301. [Google Scholar] [CrossRef]
- Deng, Z.J.; Feng, M.; Gao, K.L. Simple scheme for generating an n-qubit W state in cavity QED. Phys. Rev. A 2006, 73, 014302. [Google Scholar] [CrossRef]
- Gorbachev, V.; Rodichkina, A.; Trubilko, A.; Zhiliba, A. On preparation of the entangled W-states from atomic ensembles. Phys. Lett. A 2003, 310, 339–343. [Google Scholar] [CrossRef]
- Roos, C.F.; Riebe, M.; Häffner, H.; Hänsel, W.; Benhelm, J.; Lancaster, G.P.; Becher, C.; Schmidt-Kaler, F.; Blatt, R. Control and measurement of three-qubit entangled states. Science 2004, 304, 1478–1480. [Google Scholar] [CrossRef]
- Kang, Y.H.; Xia, Y.; Lu, P.M. Effective scheme for preparation of a spin-qubit Greenberger–Horne–Zeilinger state and W state in a quantum-dot-microcavity system. J. Opt. Soc. Am. B 2015, 32, 1323–1329. [Google Scholar] [CrossRef]
- Kang, Y.H.; Chen, Y.H.; Wu, Q.C.; Huang, B.H.; Song, J.; Xia, Y. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Sci. Rep. 2016, 6, 36737. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.X.; Shen, L.T. Tripartite entanglement of atoms trapped in coupled cavities via quantum Zeno dynamics. Phys. Lett. A 2011, 375, 3840–3844. [Google Scholar] [CrossRef]
- Miry, S.R.; Tavassoly, M.K.; Roknizadeh, R. Generation of some entangled states of the cavity field. Quantum Inf. Process. 2015, 14, 593–606. [Google Scholar] [CrossRef]
- Hamel, D.R.; Shalm, L.K.; Hübel, H.; Miller, A.J.; Marsili, F.; Verma, V.B.; Mirin, R.P.; Nam, S.W.; Resch, K.J.; Jennewein, T. Direct generation of three-photon polarization entanglement. Nat. Photonics 2014, 8, 801. [Google Scholar] [CrossRef]
- de Lima Bernardo, B.; Lencses, M.; Brito, S.; Canabarro, A. Greenberger–Horne–Zeilinger state generation with linear optical elements. Quantum Inf. Process. 2019, 18, 331. [Google Scholar] [CrossRef]
- Heo, J.; Hong, C.; Choi, S.G.; Hong, J.P. Scheme for generation of three-photon entangled W state assisted by cross-Kerr nonlinearity and quantum dot. Sci. Rep. 2019, 9, 10151. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; Lo Franco, R.; Compagno, G. N identical particles and one particle to entangle them all. Phys. Rev. A 2017, 96, 022319. [Google Scholar] [CrossRef]
- Yesilyurt, C.; Bugu, S.; Ozaydin, F.; Altintas, A.A.; Tame, M.; Yang, L.; Özdemir, S.K. Deterministic local doubling of W states. J. Opt. Soc. Am. B 2016, 33, 2313–2319. [Google Scholar] [CrossRef]
- Li, D.X.; Zheng, T.Y.; Shao, X.Q. Adiabatic preparation of Multipartite GHZ states via Rydberg ground-state blockade. Opt. Express 2019, 27, 20874–20885. [Google Scholar] [CrossRef] [PubMed]
- Omran, A.; Levine, H.; Keesling, A.; Semeghini, G.; Wang, T.T.; Ebadi, S.; Bernien, H.; Zibrov, A.S.; Pichler, H.; Choi, S.; et al. Generation and Manipulation of Schrödinger Cat States in Rydberg Atom Arrays. Available online: https://arxiv.org/abs/1905.05721 (accessed on 26 September 2019).
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef]
- Bruß, D.; Cirac, J.I.; Horodecki, P.; Hulpke, F.; Kraus, B.; Lewenstein, M.; Sanpera, A. Reflections upon separability and distillability. J. Mod. Opt. 2002, 49, 1399–1418. [Google Scholar] [CrossRef]
- Gerke, S.; Vogel, W.; Sperling, J. Numerical Construction of Multipartite Entanglement Witnesses. Phys. Rev. X 2018, 8, 031047. [Google Scholar] [CrossRef]
- Pan, J.W.; Zeilinger, A. Greenberger-Horne-Zeilinger-state analyzer. Phys. Rev. A 1998, 57, 2208. [Google Scholar] [CrossRef]
- Qian, J.; Feng, X.L.; Gong, S.Q. Universal Greenberger-Horne-Zeilinger-state analyzer based on two-photon polarization parity detection. Phys. Rev. A 2005, 72, 052308. [Google Scholar] [CrossRef]
- Ralph, T.C.; Bartlett, S.D.; O’Brien, J.L.; Pryde, G.J.; Wiseman, H.M. Quantum nondemolition measurements for quantum information. Phys. Rev. A 2006, 73, 012113. [Google Scholar] [CrossRef]
- Wang, X.W.; Zhang, D.Y.; Tang, S.Q.; Xie, L.J. Nondestructive Greenberger-Horne-Zeilinger-state analyzer. Quantum Inf. Process. 2013, 12, 1065–1075. [Google Scholar] [CrossRef]
- Barbieri, M.; Cinelli, C.; Mataloni, P.; De Martini, F. Polarization-momentum hyperentangled states: Realization and characterization. Phys. Rev. A 2005, 72, 052110. [Google Scholar] [CrossRef]
- Bhatti, D.; von Zanthier, J.; Agarwal, G.S. Entanglement of polarization and orbital angular momentum. Phys. Rev. A 2015, 91, 062303. [Google Scholar] [CrossRef]
- Song, S.; Cao, Y.; Sheng, Y.B.; Long, G.L. Complete Greenberger–Horne–Zeilinger state analyzer using hyperentanglement. Quantum Inf. Process. 2013, 12, 381–393. [Google Scholar] [CrossRef]
- Zheng, Y.Y.; Liang, L.X.; Zhang, M. Self-assisted complete analysis of three-photon hyperentangled Greenberger–Horne–Zeilinger states with nitrogen-vacancy centers in microcavities. Quantum Inf. Process. 2018, 17, 172. [Google Scholar] [CrossRef]
- Habibian, H.; Clark, J.W.; Behbood, N.; Hingerl, K. Greenberger-Horne-Zeilinger and W entanglement witnesses for the noninteracting Fermi gas. Phys. Rev. A 2010, 81, 032302. [Google Scholar] [CrossRef]
- Chen, X.Y.; Jiang, L.Z.; Yu, P.; Tian, M. Necessary and sufficient fully separable criterion and entanglement of three-qubit Greenberger–Horne–Zeilinger diagonal states. Quantum Inf. Process. 2015, 14, 2463–2476. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Shen, S.; Chen, Z.; Fei, S.M. Detection and measure of genuine tripartite entanglement with partial transposition and realignment of density matrices. Sci. Rep. 2017, 7, 17274. [Google Scholar] [CrossRef]
- Singh, A.; Singh, H.; Dorai, K. Experimental classification of entanglement in arbitrary three-qubit pure states on an NMR quantum information processor. Phys. Rev. A 2018, 98, 032301. [Google Scholar] [CrossRef]
- Singh, A.; Dorai, K. Experimentally identifying the entanglement class of pure tripartite states. Quantum Inf. Process. 2018, 17, 334. [Google Scholar] [CrossRef]
- Gross, D.; Liu, Y.K.; Flammia, S.T.; Becker, S.; Eisert, J. Quantum State Tomography via Compressed Sensing. Phys. Rev. Lett. 2010, 105, 150401. [Google Scholar] [CrossRef] [PubMed]
- Resch, K.J.; Walther, P.; Zeilinger, A. Full Characterization of a Three-Photon Greenberger-Horne-Zeilinger State Using Quantum State Tomography. Phys. Rev. Lett. 2005, 94, 070402. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.X.; Zhao, J.Q.; Wang, X.Q. Characterization of a high-intensity three-qubit GHZ state using state tomography and Gisins inequality. Phys. Lett. A 2011, 375, 1850–1854. [Google Scholar] [CrossRef]
- Mikami, H.; Li, Y.; Fukuoka, K.; Kobayashi, T. New High-Efficiency Source of a Three-Photon W State and its Full Characterization Using Quantum State Tomography. Phys. Rev. Lett. 2005, 95, 150404. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Zhan, Y.B. Scheme for Asymmetric and Deterministic Controlled Bidirectional Joint Remote State Preparation. Commun. Theor. Phys. 2018, 70, 515. [Google Scholar] [CrossRef]
- Sun, Y.R.; Chen, X.B.; Xu, G.; Yuan, K.G.; Yang, Y.X. Asymmetric controlled bidirectional remote preparation of two-and three-qubit equatorial state. Sci. Rep. 2019, 9, 2081. [Google Scholar] [CrossRef]
- Kurpiers, P.; Magnard, P.; Walter, T.; Royer, B.; Pechal, M.; Heinsoo, J.; Salathé, Y.; Akin, A.; Storz, S.; Besse, J.C.; et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 2018, 558, 264. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.Y.; Chen, P.X.; Liang, L.M.; Li, C.Z. Classical communication cost and remote preparation of the four-particle GHZ class state. Phys. Lett. A 2006, 355, 285–288. [Google Scholar] [CrossRef]
- Luo, M.X.; Chen, X.B.; Ma, S.Y.; Niu, X.X.; Yang, Y.X. Joint remote preparation of an arbitrary three-qubit state. Opt. Commun. 2010, 283, 4796–4801. [Google Scholar] [CrossRef]
- Zhan, Y.B.; Ma, P.C. Deterministic joint remote preparation of arbitrary two-and three-qubit entangled states. Quantum Inf. Process. 2013, 12, 997–1009. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Dhara, A. Joint remote state preparation for two-qubit equatorial states. Quantum Inf. Process. 2015, 14, 373–379. [Google Scholar] [CrossRef]
- Khosa, A.H.; Saif, F. Remote preparation of atomic and field cluster states from a pair of tri-partite GHZ states. Chin. Phys. B 2010, 19, 040309. [Google Scholar] [CrossRef]
- An, N.B. Joint remote state preparation via W and W-type states. Opt. Commun. 2010, 283, 4113–4117. [Google Scholar] [CrossRef]
- Wang, Z.Y. Classical communication cost and probabilistic remote two-qubit state preparation via POVM and W-type states. Quantum Inf. Process. 2012, 11, 1585–1602. [Google Scholar] [CrossRef]
- Wang, D.; Hoehn, R.; Ye, L.; Kais, S. Generalized remote preparation of arbitrary m-qubit entangled states via genuine entanglements. Entropy 2015, 17, 1755–1774. [Google Scholar] [CrossRef]
- Ra, Y.S.; Lim, H.T.; Kim, Y.H. Remote preparation of three-photon entangled states via single-photon measurement. Phys. Rev. A 2016, 94, 042329. [Google Scholar] [CrossRef]
- Lv, S.X.; Zhao, Z.W.; Zhou, P. Multiparty-controlled joint remote preparation of an arbitrary m-qudit state with d-dimensional Greenberger-Horne-Zeilinger states. Int. J. Theor. Phys. 2018, 57, 148–158. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, Q.Q.; An, N.B. Deterministic joint remote preparation of an arbitrary three-qubit state via Einstein–Podolsky–Rosen pairs with a passive receiver. J. Phys. A Math. Theor. 2012, 45, 335306. [Google Scholar] [CrossRef]
- Luo, M.X.; Chen, X.B.; Ma, S.Y.; Yang, Y.X.; Hu, Z.M. Deterministic remote preparation of an arbitrary W-class state with multiparty. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 065501. [Google Scholar] [CrossRef]
- Peng-Cheng, M.; You-Bang, Z. Scheme for probabilistic remotely preparing a multi-particle entangled GHZ state. Chin. Phys. B 2008, 17, 445. [Google Scholar] [CrossRef]
- Wang, D.; Hu, Y.D.; Wang, Z.Q.; Ye, L. Efficient and faithful remote preparation of arbitrary three-and four-particle $$$$-class entangled states. Quantum Inf. Process. 2015, 14, 2135–2151. [Google Scholar] [CrossRef]
- Wu, N.N.; Jiang, M. A highly efficient scheme for joint remote preparation of multi-qubit W state with minimum quantum resource. Quantum Inf. Process. 2018, 17, 340. [Google Scholar] [CrossRef]
- Sang, Z.W. Deterministic Joint Remote State Preparation of an Arbitrary Equatorial Three-Qubit State. Int. J. Theor. Phys. 2019, 58, 1157–1160. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Samanta, S. Remote Preparation of Some Three Particle Entangled States Under Divided Information. Int. J. Theor. Phys. 2019, 58, 83–91. [Google Scholar] [CrossRef]
- Eisert, J.; Plenio, M. Introduction to the basics of entanglement theory in continuous-variable systems. Int. J. Quantum Inf. 2003, 1, 479–506. [Google Scholar] [CrossRef]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: recent advances and current perspectives. J. Phys. A Math. Theor. 2007, 40, 7821. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Kimble, H.J. Teleportation of Continuous Quantum Variables. Phys. Rev. Lett. 1998, 80, 869–872. [Google Scholar] [CrossRef]
- Bowen, W.P.; Treps, N.; Buchler, B.C.; Schnabel, R.; Ralph, T.C.; Bachor, H.A.; Symul, T.; Lam, P.K. Experimental investigation of continuous-variable quantum teleportation. Phys. Rev. A 2003, 67, 032302. [Google Scholar] [CrossRef]
- Polkinghorne, R.E.S.; Ralph, T.C. Continuous Variable Entanglement Swapping. Phys. Rev. Lett. 1999, 83, 2095–2099. [Google Scholar] [CrossRef]
- Takeda, S.; Fuwa, M.; van Loock, P.; Furusawa, A. Entanglement Swapping between Discrete and Continuous Variables. Phys. Rev. Lett. 2015, 114, 100501. [Google Scholar] [CrossRef] [PubMed]
- van Loock, P.; Furusawa, A. Detecting genuine multipartite continuous-variable entanglement. Phys. Rev. A 2003, 67, 052315. [Google Scholar] [CrossRef]
- Adesso, G.; Ragy, S.; Lee, A.R. Continuous variable quantum information: Gaussian states and beyond. Open Syst. Inf. Dyn. 2014, 21, 1440001. [Google Scholar] [CrossRef]
- Teh, R.Y.; Reid, M.D. Criteria for genuine N-partite continuous-variable entanglement and Einstein-Podolsky-Rosen steering. Phys. Rev. A 2014, 90, 062337. [Google Scholar] [CrossRef]
- Adesso, G.; Serafini, A.; Illuminati, F. Multipartite entanglement in three-mode Gaussian states of continuous-variable systems: Quantification, sharing structure, and decoherence. Phys. Rev. A 2006, 73, 032345. [Google Scholar] [CrossRef]
- Aoki, T.; Takei, N.; Yonezawa, H.; Wakui, K.; Hiraoka, T.; Furusawa, A.; van Loock, P. Experimental creation of a fully inseparable tripartite continuous-variable state. Phys. Rev. Lett. 2003, 91, 080404. [Google Scholar] [CrossRef] [PubMed]
- Coelho, A.; Barbosa, F.; Cassemiro, K.; Villar, A.; Martinelli, M.; Nussenzveig, P. Three-color entanglement. Science 2009, 326, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Shalm, L.K.; Hamel, D.R.; Yan, Z.; Simon, C.; Resch, K.J.; Jennewein, T. Three-photon energy–time entanglement. Nat. Phys. 2013, 9, 19. [Google Scholar] [CrossRef]
- Valido, A.A.; Levi, F.; Mintert, F. Hierarchies of multipartite entanglement for continuous-variable states. Phys. Rev. A 2014, 90, 052321. [Google Scholar] [CrossRef]
- González, E.A.R.; Borne, A.; Boulanger, B.; Levenson, J.A.; Bencheikh, K. Continuous-Variable Triple-Photon States Quantum Entanglement. Phys. Rev. Lett. 2018, 120, 043601. [Google Scholar] [CrossRef]
- Liang, H.Q.; Liu, J.M.; Feng, S.S.; Chen, J.G. Quantum teleportation with partially entangled states via noisy channels. Quantum Inf. Process. 2013, 12, 2671–2687. [Google Scholar] [CrossRef]
- Fortes, R.; Rigolin, G. Probabilistic quantum teleportation in the presence of noise. Phys. Rev. A 2016, 93, 062330. [Google Scholar] [CrossRef]
- Zhao, J.Q.; Cao, L.Z.; Yang, Y.; Li, Y.D.; Lu, H.X. Tripartite entanglement and non-locality in three-qubit Greenberger–Horne–Zeilinger states with bit-flip noise. Can. J. Phys. 2018, 97, 248–251. [Google Scholar] [CrossRef]
- Aolita, L.; Chaves, R.; Cavalcanti, D.; Acín, A.; Davidovich, L. Scaling Laws for the Decay of Multiqubit Entanglement. Phys. Rev. Lett. 2008, 100, 080501. [Google Scholar] [CrossRef] [PubMed]
- Kenfack, L.T.; Tchoffo, M.; Fai, L.C. Decoherence and protection of entanglement of a system of three qubits driven by a classical Gaussian distributed fluctuating field. Phys. Lett. A 2018, 382, 2805–2818. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.M.; Zhang, C.J.; Oh, C. Quantum discord of a three-qubit w-class state in noisy environments. Quantum Inf. Comput. 2012, 12, 677. [Google Scholar]
- Mahdian, M.; Yousefjani, R.; Salimi, S. Quantum discord evolution of three-qubit states under noisy channels. Eur. Phys. J. D 2012, 66, 133. [Google Scholar] [CrossRef][Green Version]
- Metwally, N.; Almannaei, A. Dynamics of three-qubit systems in a noisy environment. Can. J. Phys. 2015, 94, 170–176. [Google Scholar] [CrossRef]
- Lionel, T.K.; Martin, T.; Collince, F.G.; Fai, L.C. Effects of static noise on the dynamics of quantum correlations for a system of three qubits. Int. J. Mod. Phys. B 2017, 31, 1750046. [Google Scholar] [CrossRef]
- Jung, E.; Hwang, M.R.; Ju, Y.H.; Kim, M.S.; Yoo, S.K.; Kim, H.; Park, D.; Son, J.W.; Tamaryan, S.; Cha, S.K. Greenberger-Horne-Zeilinger versus W states: Quantum teleportation through noisy channels. Phys. Rev. A 2008, 78, 012312. [Google Scholar] [CrossRef]
- Hu, M.L. Robustness of Greenberger–Horne–Zeilinger and W states for teleportation in external environments. Phys. Lett. A 2011, 375, 922–926. [Google Scholar] [CrossRef]
- Metwally, N. Entanglement and quantum teleportation via decohered tripartite entangled states. Ann. Phys. 2014, 351, 704–713. [Google Scholar] [CrossRef]
- Chun, M.; Ming, Y.; Zhuo-Liang, C. Controlled Quantum Teleportation Through Noisy GHZ Channel. Commun. Theor. Phys. 2010, 53, 489. [Google Scholar] [CrossRef]
- Khan, S. Entanglement of tripartite states with decoherence in non-inertial frames. J. Mod. Opt. 2012, 59, 250–258. [Google Scholar] [CrossRef]
- Zounia, M.; Shamirzaie, M.; Ashouri, A. Quantum teleportation via noisy bipartite and tripartite accelerating quantum states: beyond the single mode approximation. J. Phys. A Math. Theor. 2017, 50, 395302. [Google Scholar] [CrossRef]
- Yang, Y.G.; Gao, S.; Li, D.; Zhou, Y.H.; Shi, W.M. Three-party quantum secret sharing against collective noise. Quantum Inf. Process. 2019, 18, 215. [Google Scholar] [CrossRef]
- Liang, H.Q.; Liu, J.M.; Feng, S.S.; Chen, J.G. Remote state preparation via a GHZ-class state in noisy environments. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 115506. [Google Scholar] [CrossRef]
- Liang, H.Q.; Liu, J.M.; Feng, S.S.; Chen, J.G.; Xu, X.Y. Effects of noises on joint remote state preparation via a GHZ-class channel. Quantum Inf. Process. 2015, 14, 3857–3877. [Google Scholar] [CrossRef]
- Zhong-Fang, C.; Jin-Ming, L.; Lei, M. Deterministic joint remote preparation of an arbitrary two-qubit state in the presence of noise. Chin. Phys. B 2013, 23, 020312. [Google Scholar]
- Qu, Z.; Wu, S.; Wang, M.; Sun, L.; Wang, X. Effect of quantum noise on deterministic remote state preparation of an arbitrary two-particle state via various quantum entangled channels. Quantum Inf. Process. 2017, 16, 306. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Bai, M.Q.; Zhou, S.Q. Cyclic joint remote state preparation in noisy environment. Quantum Inf. Process. 2018, 17, 146. [Google Scholar] [CrossRef]
- Wang, X.W.; Yu, S.; Zhang, D.Y.; Oh, C. Effect of weak measurement on entanglement distribution over noisy channels. Sci. Rep. 2016, 6, 22408. [Google Scholar] [CrossRef] [PubMed]
- Singh, H.; Dorai, K. Evolution of tripartite entangled states in a decohering environment and their experimental protection using dynamical decoupling. Phys. Rev. A 2018, 97, 022302. [Google Scholar] [CrossRef]
- Jiang, S.X.; Zhou, R.G.; Xu, R.; Luo, G. Cyclic Hybrid Double-Channel Quantum Communication via Bell-State and GHZ-State in Noisy Environments. IEEE Access 2019, 7, 80530–80541. [Google Scholar] [CrossRef]
- Cunha, M.M.; Fonseca, E.; Moreno, M.; Parisio, F. Non-ideal teleportation of tripartite entanglement: Einstein–Podolsky–Rosen versus Greenberger–Horne–Zeilinger schemes. Quantum Inf. Process. 2017, 16, 254. [Google Scholar] [CrossRef]
- Wang, X.W.; Tang, S.Q.; Liu, Y.; Yuan, J.B. Improving the Robustness of Entangled States by Basis Transformation. Entropy 2019, 21, 59. [Google Scholar] [CrossRef]
| 1. | Note that entanglement is not the only nonclassical resource useful for computation, though. |
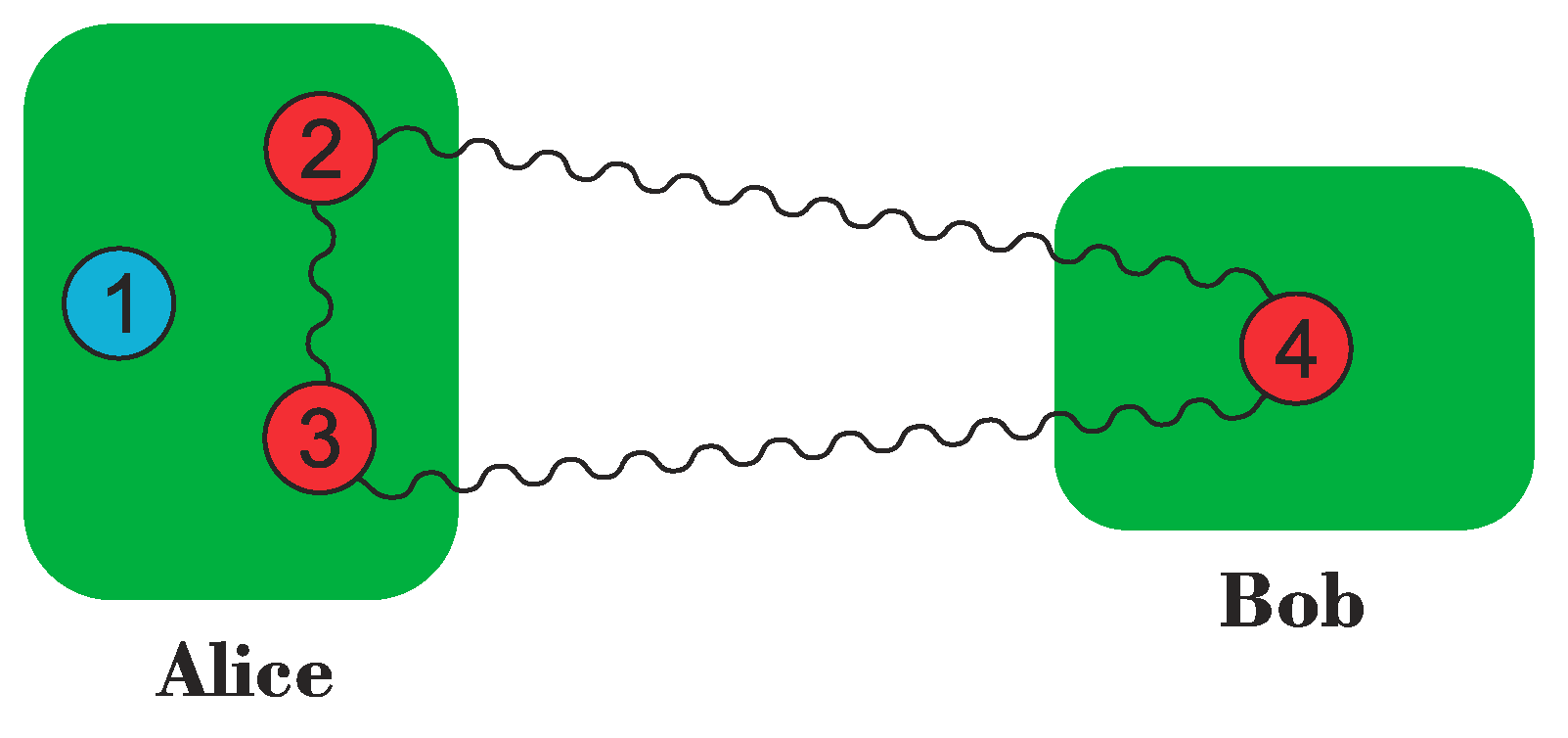
| 2. | It is important to keep in mind that bipartite entanglement does not necessarily imply two spatially separated parts. Instead, it can be generated between different degrees of freedom in a single part [2]. |
| 3. | EPR, after Einstein’s, Podolsky’s, and Rosen’s seminal paper [15]. |
| 4. | The symbol “*” indicates complex conjugation of the associated matrix elements. |
| 5. | In the case , in particular, p denotes the singlet fraction or, in other words, the degree of similarity of the state before () and after () applying twirling operations to the singlet state , i.e., . |
| 6. | Nevertheless, note that in contrast to the bipartite case, there is no unique way of measuring entanglement in multipartite quantum systems [31]. |
| 7. | The union of both premises is known as the assumption of local realism. |
| 8. | An alternative interesting proof of the violation local realism without using Bell inequalities is given by the Hardy paradox [56]. |
| 9. | Here, QND means Quantum Non-demolition related to the idea of a QND measurement [162]. |
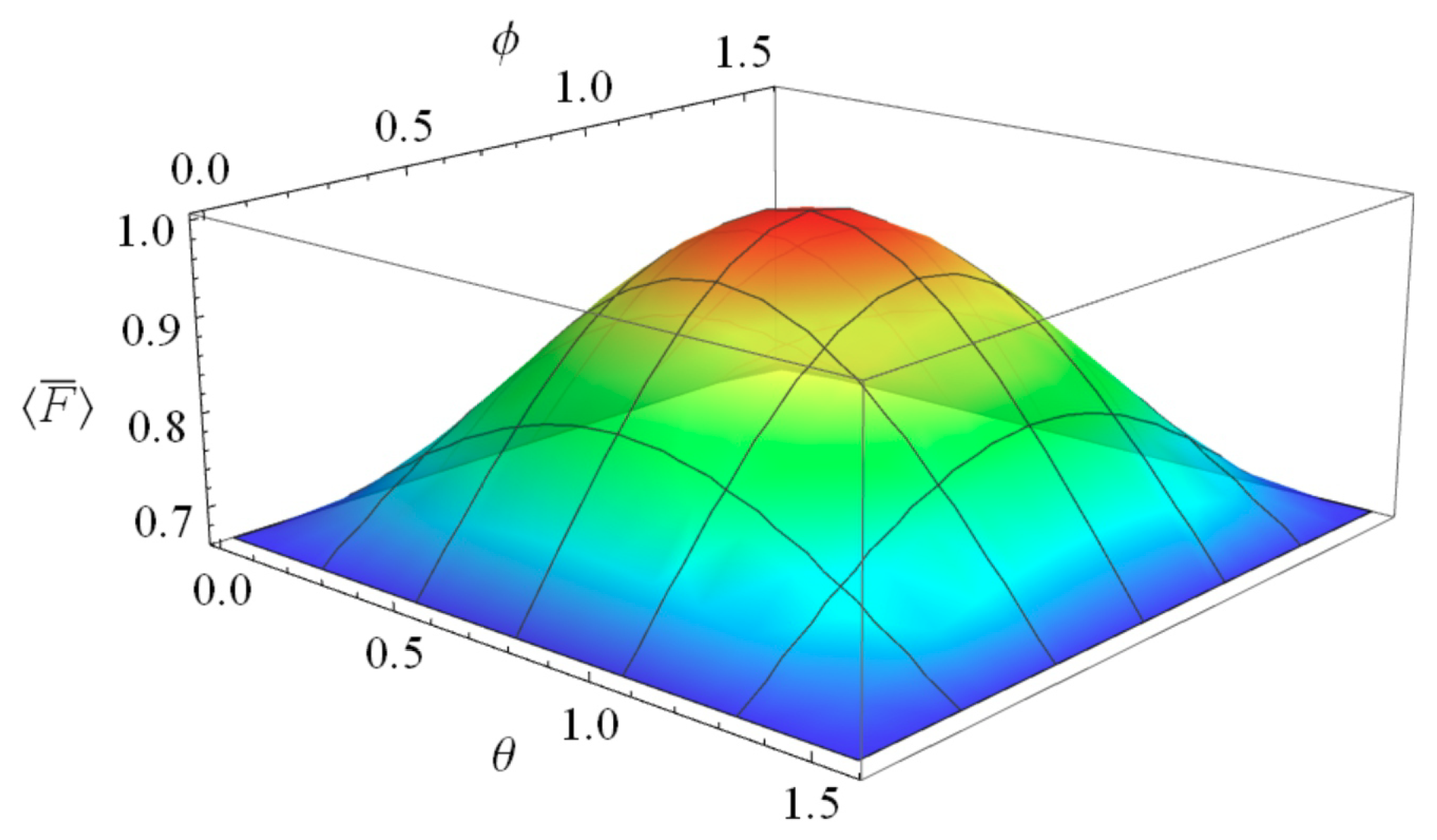
| 10. |
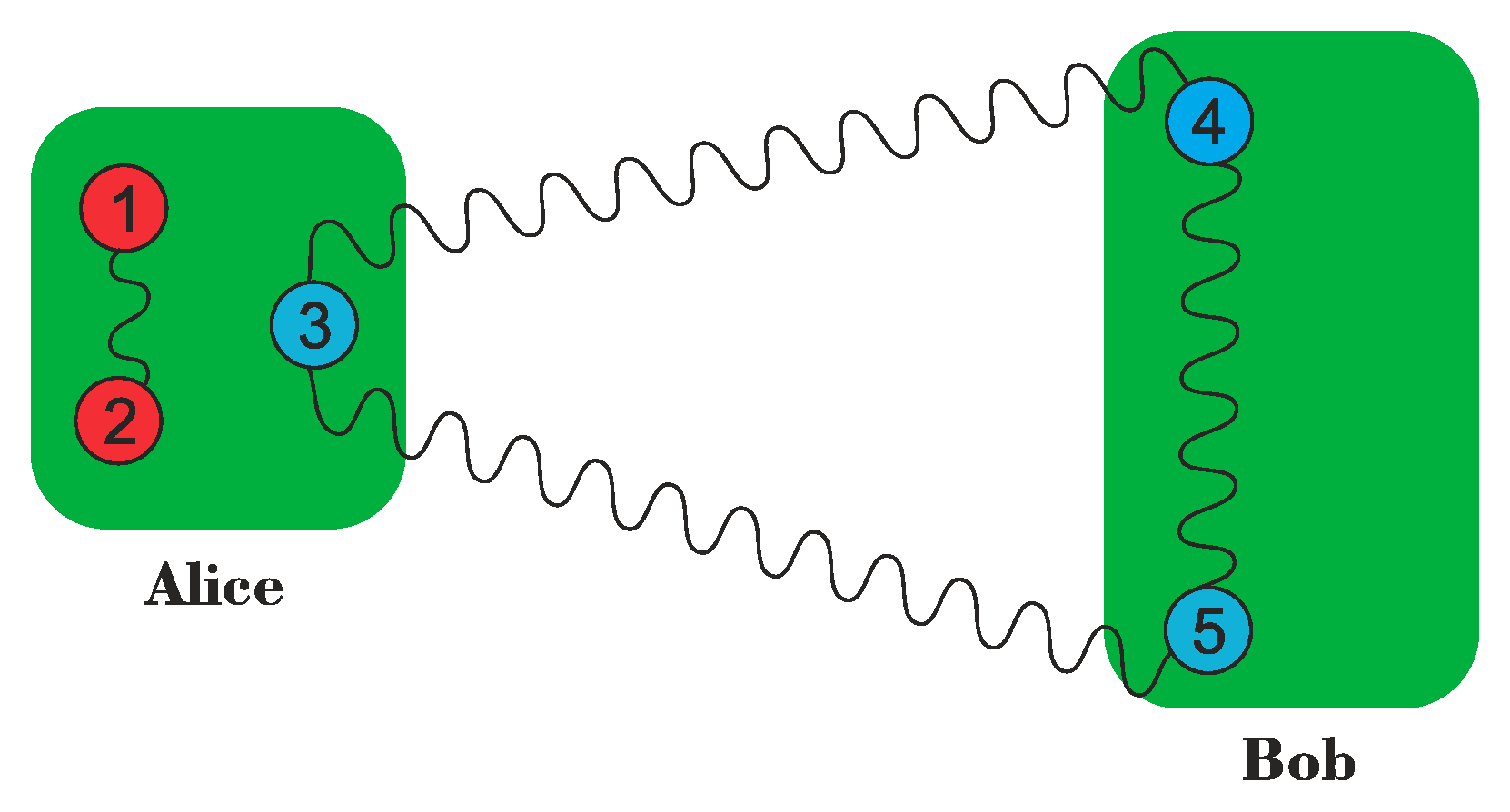
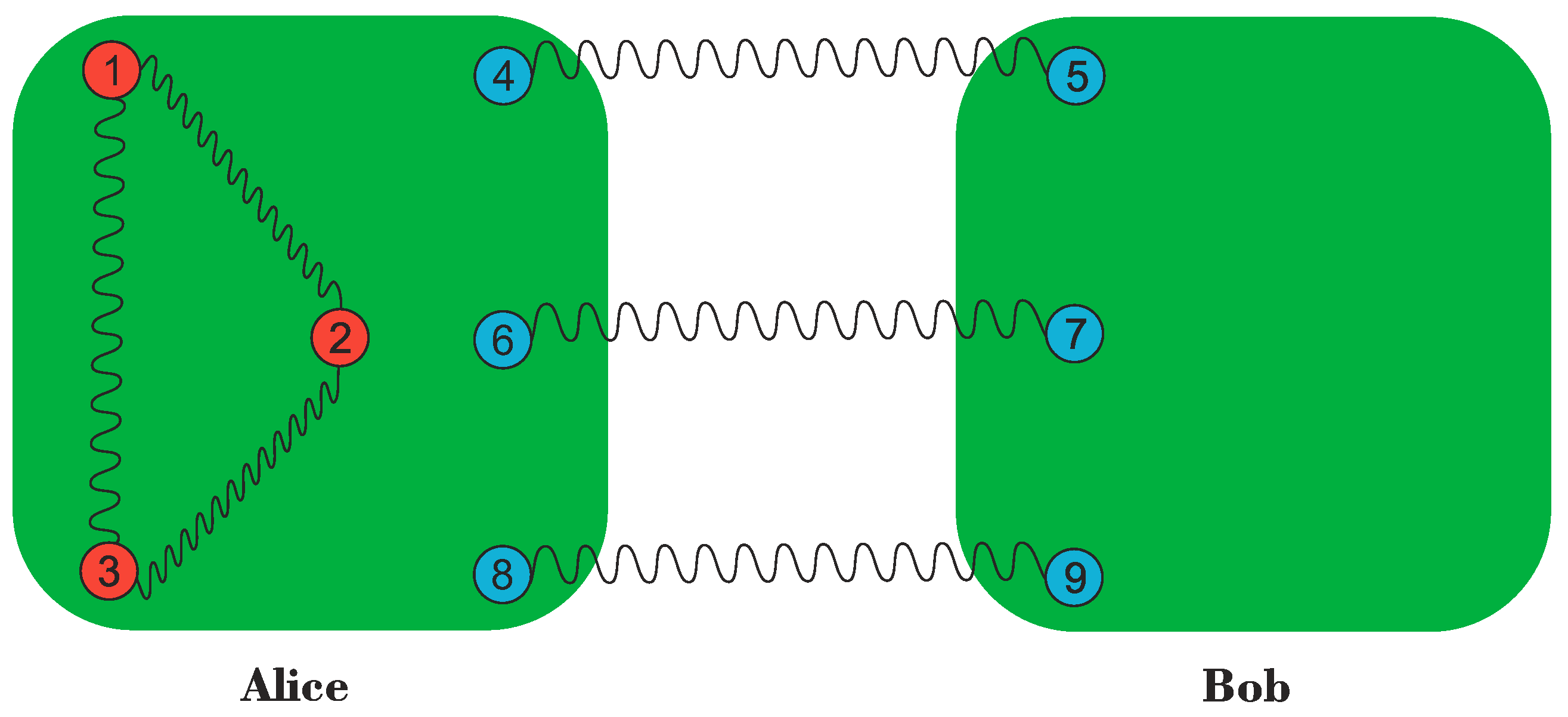
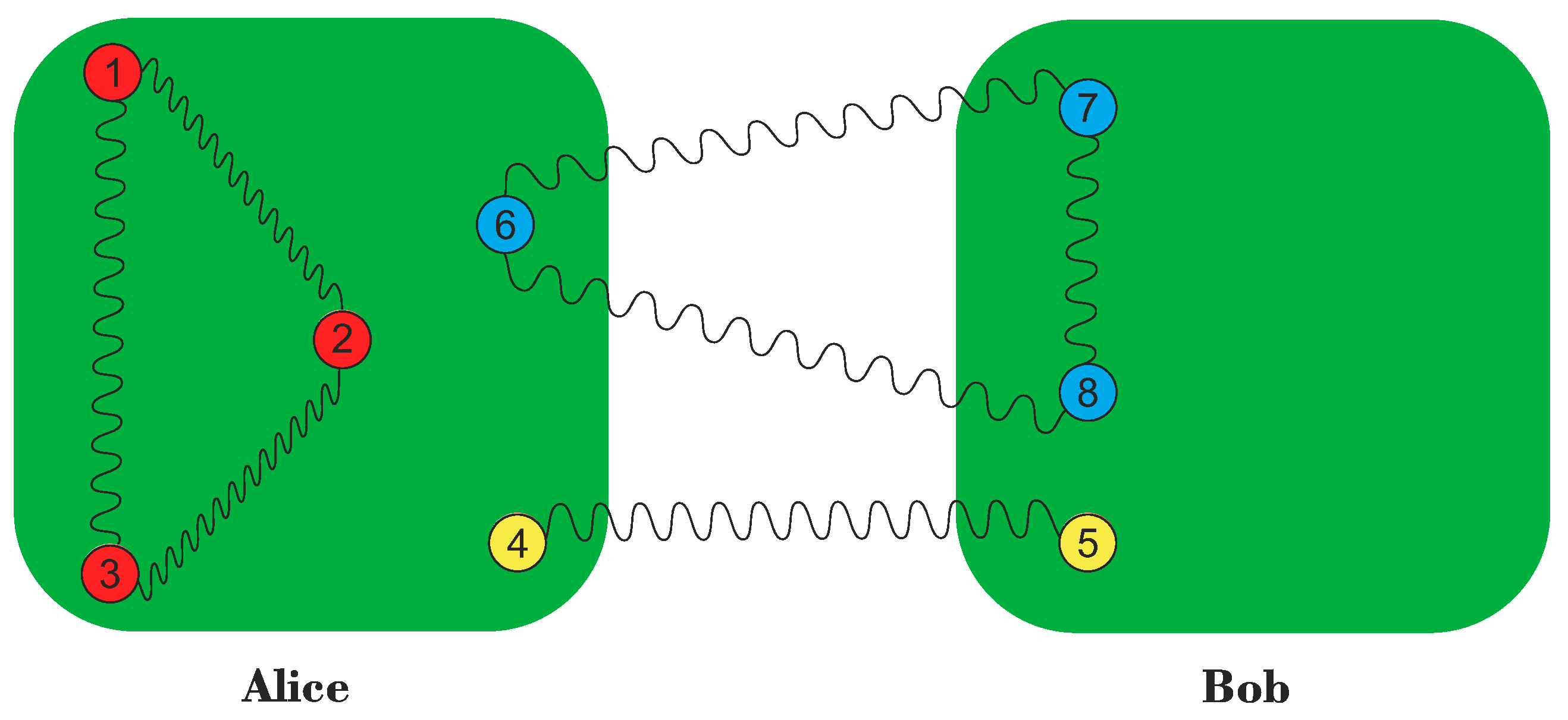
| Alice’s Result | State Shared by Bob and Charlie | |
|---|---|---|
| m | n | state |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
| Alice’s Result | Bob’s Result | Charlie’s Unnormalized State | |
|---|---|---|---|
| m | n | State | |
| 0 | 0 | ||
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 0 | ||
| 1 | 1 | ||
| 1 | 1 |
| Result: | Operation |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Cunha, M.; Fonseca, A.; O. Silva, E. Tripartite Entanglement: Foundations and Applications. Universe 2019, 5, 209. https://doi.org/10.3390/universe5100209
M. Cunha M, Fonseca A, O. Silva E. Tripartite Entanglement: Foundations and Applications. Universe. 2019; 5(10):209. https://doi.org/10.3390/universe5100209
Chicago/Turabian StyleM. Cunha, Márcio, Alejandro Fonseca, and Edilberto O. Silva. 2019. "Tripartite Entanglement: Foundations and Applications" Universe 5, no. 10: 209. https://doi.org/10.3390/universe5100209
APA StyleM. Cunha, M., Fonseca, A., & O. Silva, E. (2019). Tripartite Entanglement: Foundations and Applications. Universe, 5(10), 209. https://doi.org/10.3390/universe5100209






