Study of Very Forward Neutrons with the CMS Zero Degree Calorimeter
Abstract
1. Introduction
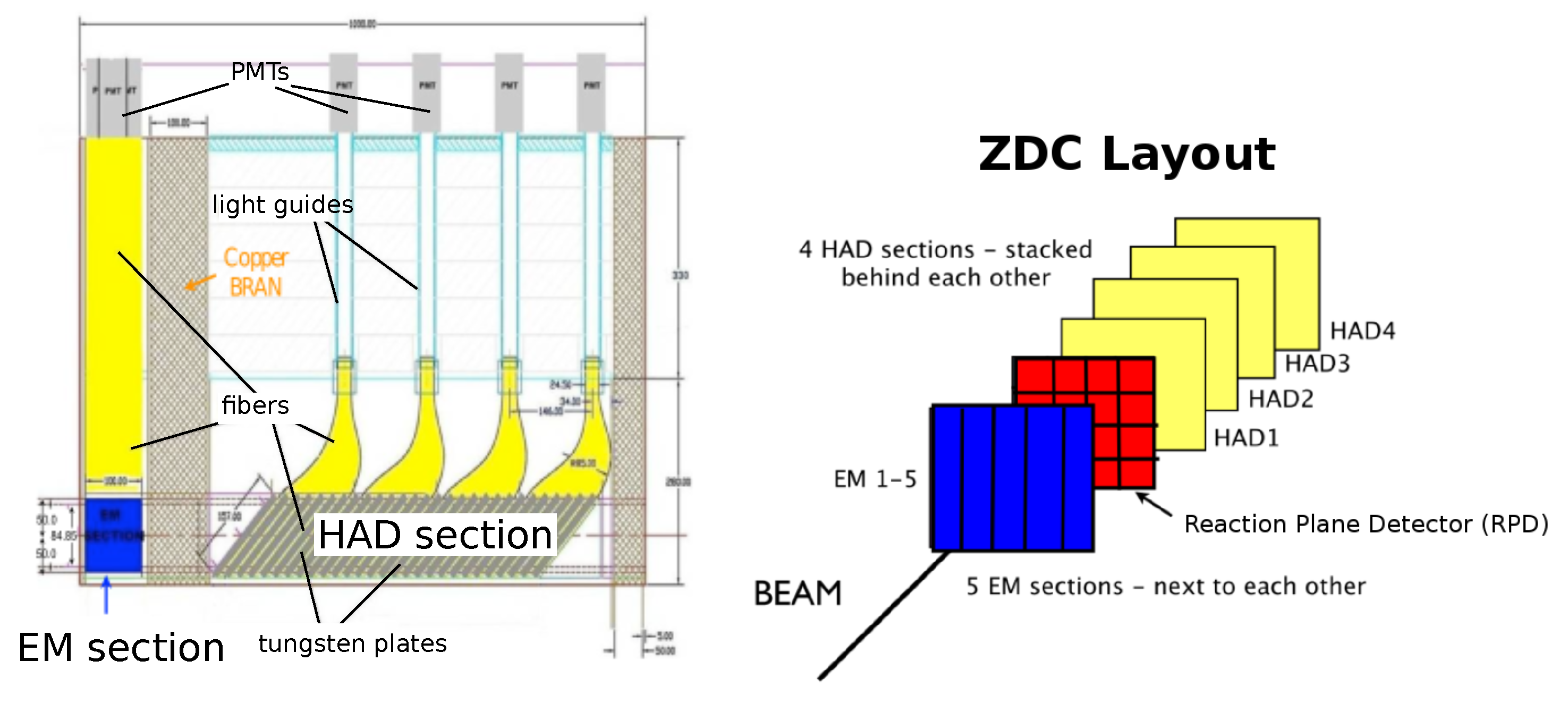
2. The Zero Degree Calorimeter of CMS Experiment
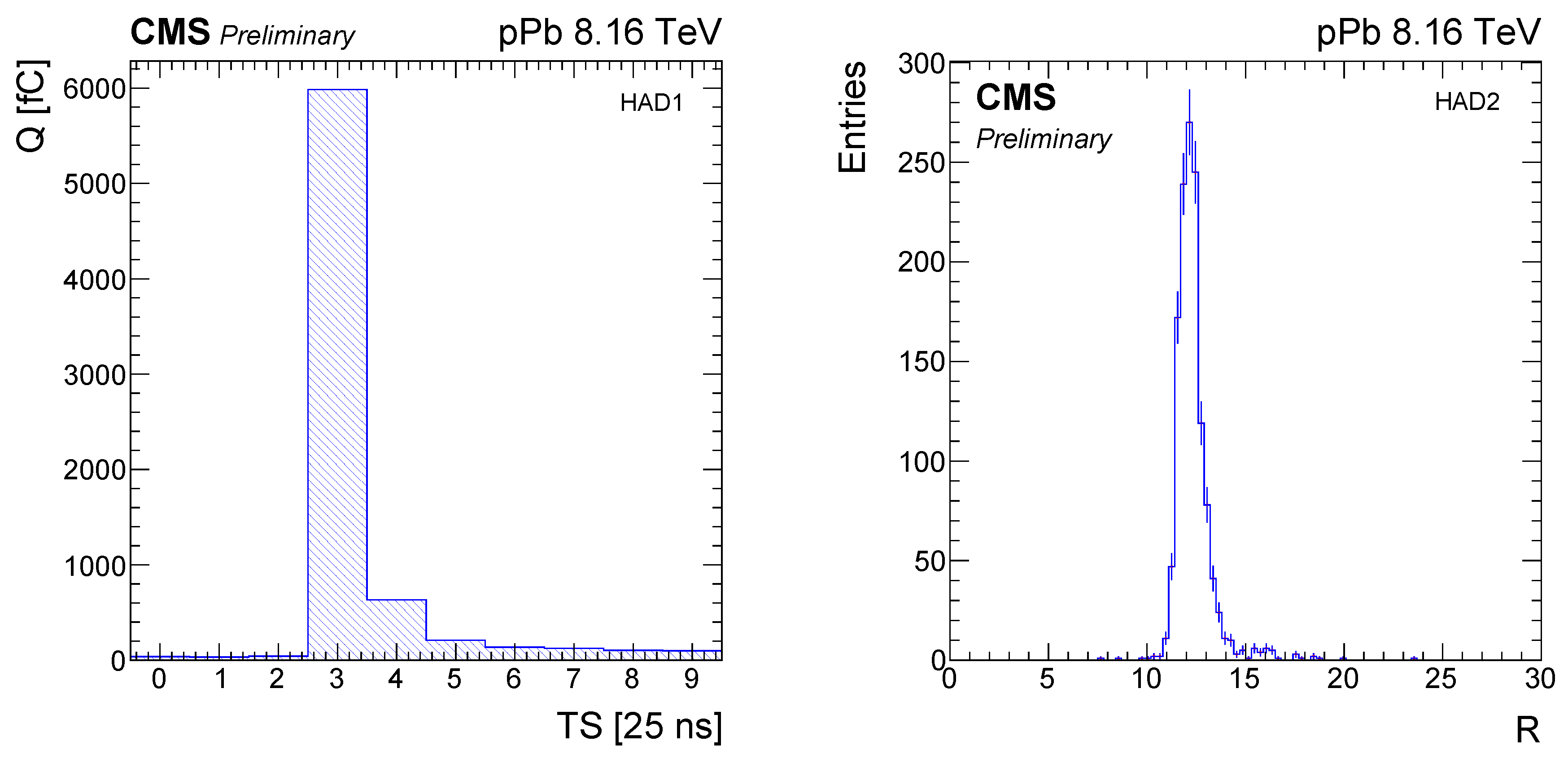
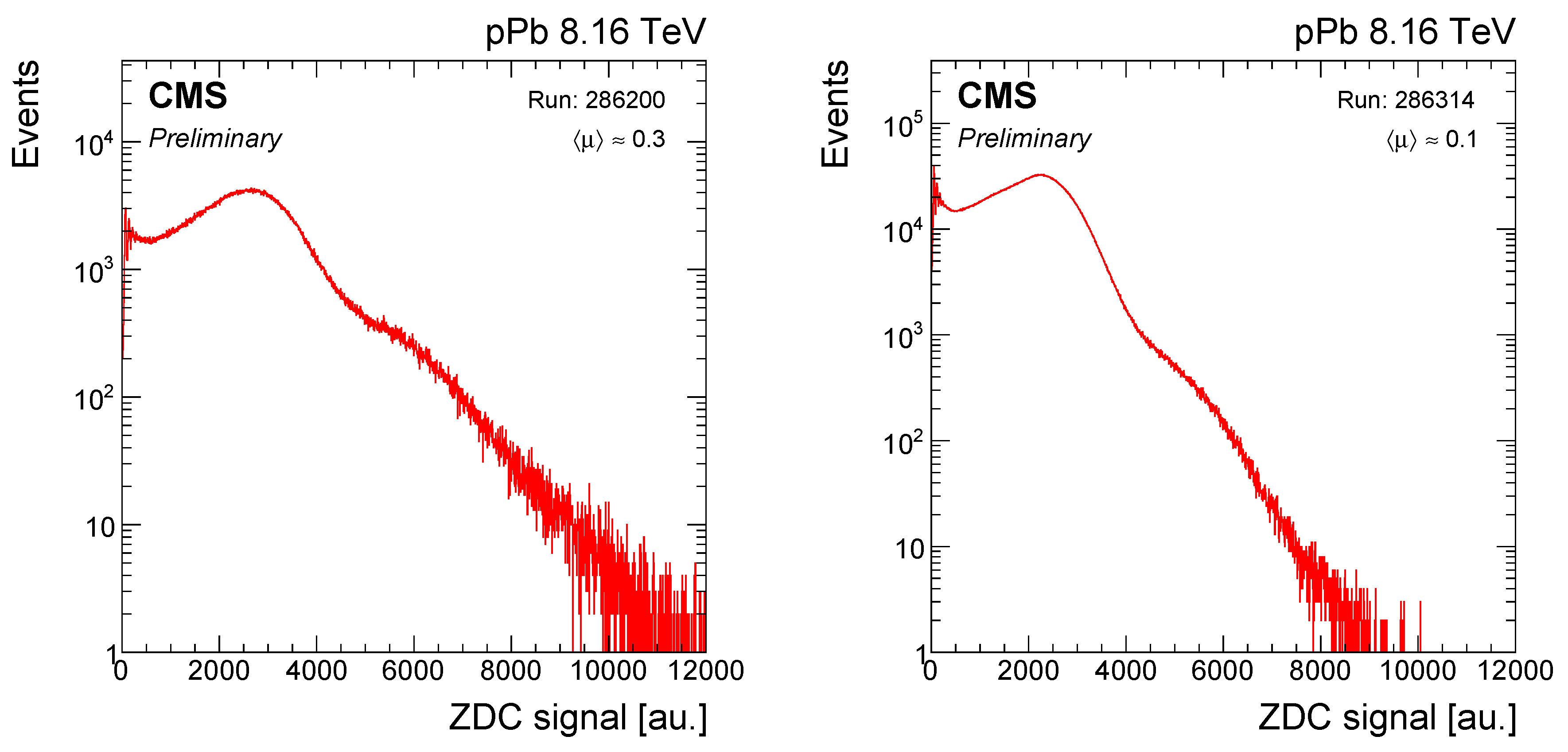
3. Calibration
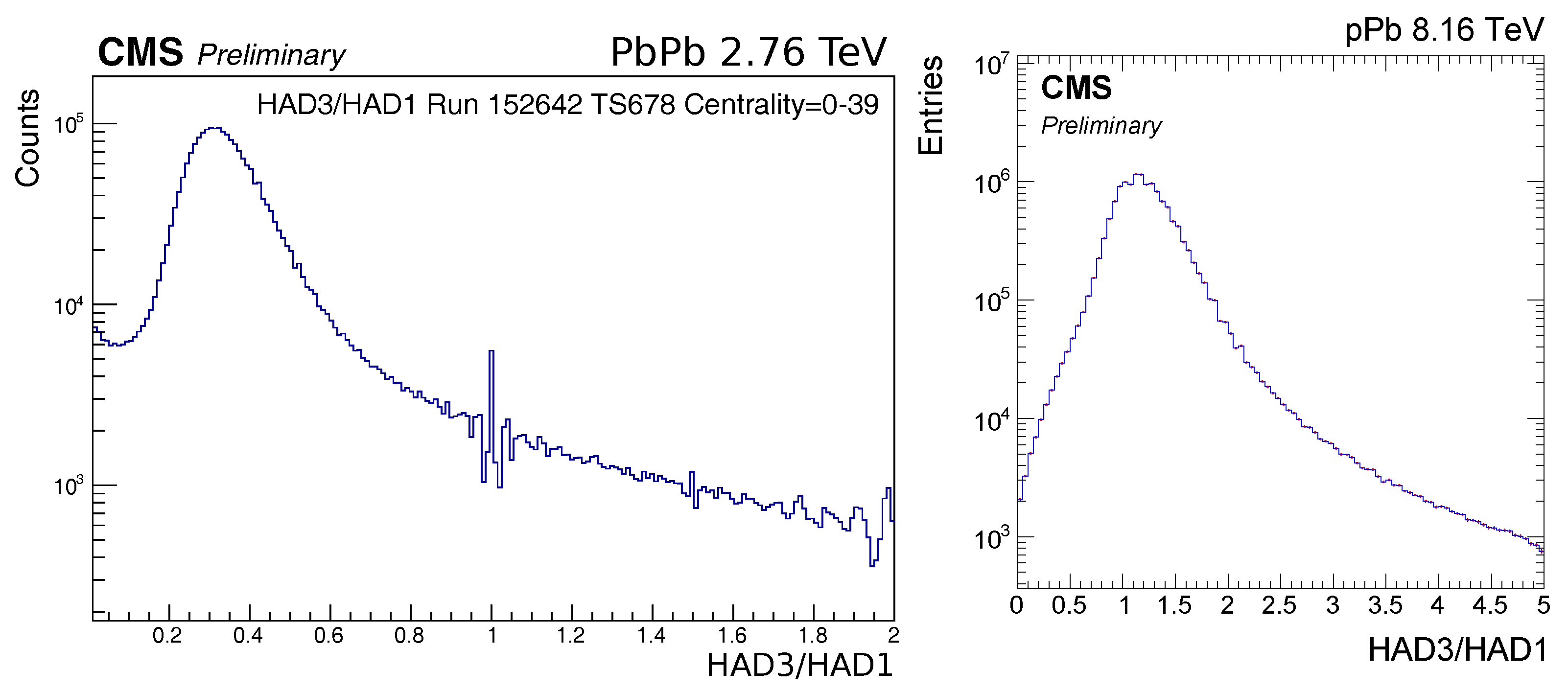
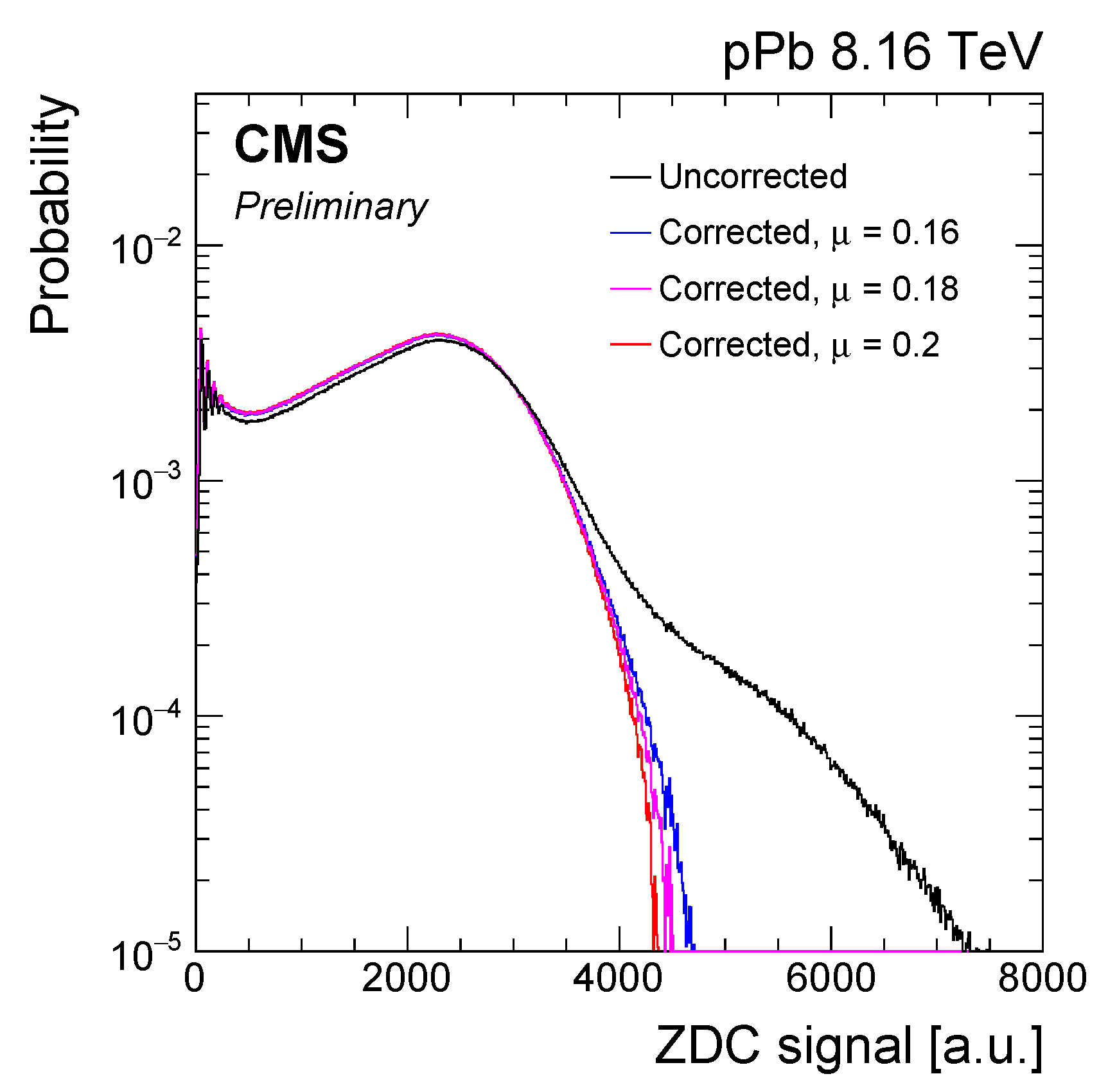
4. Pileup Correction
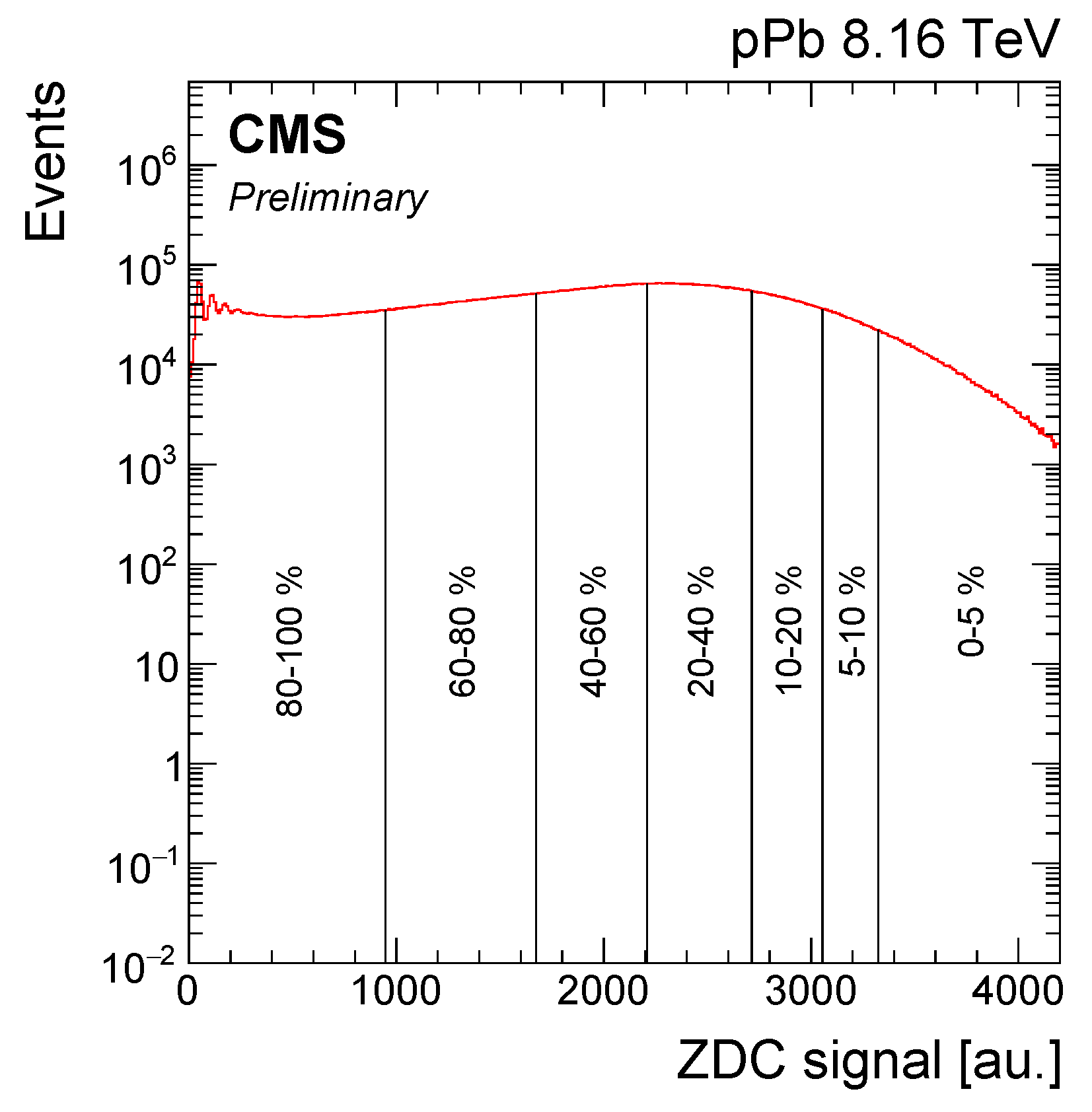
5. Using ZDC as a Centrality Estimator in pPb Collisions
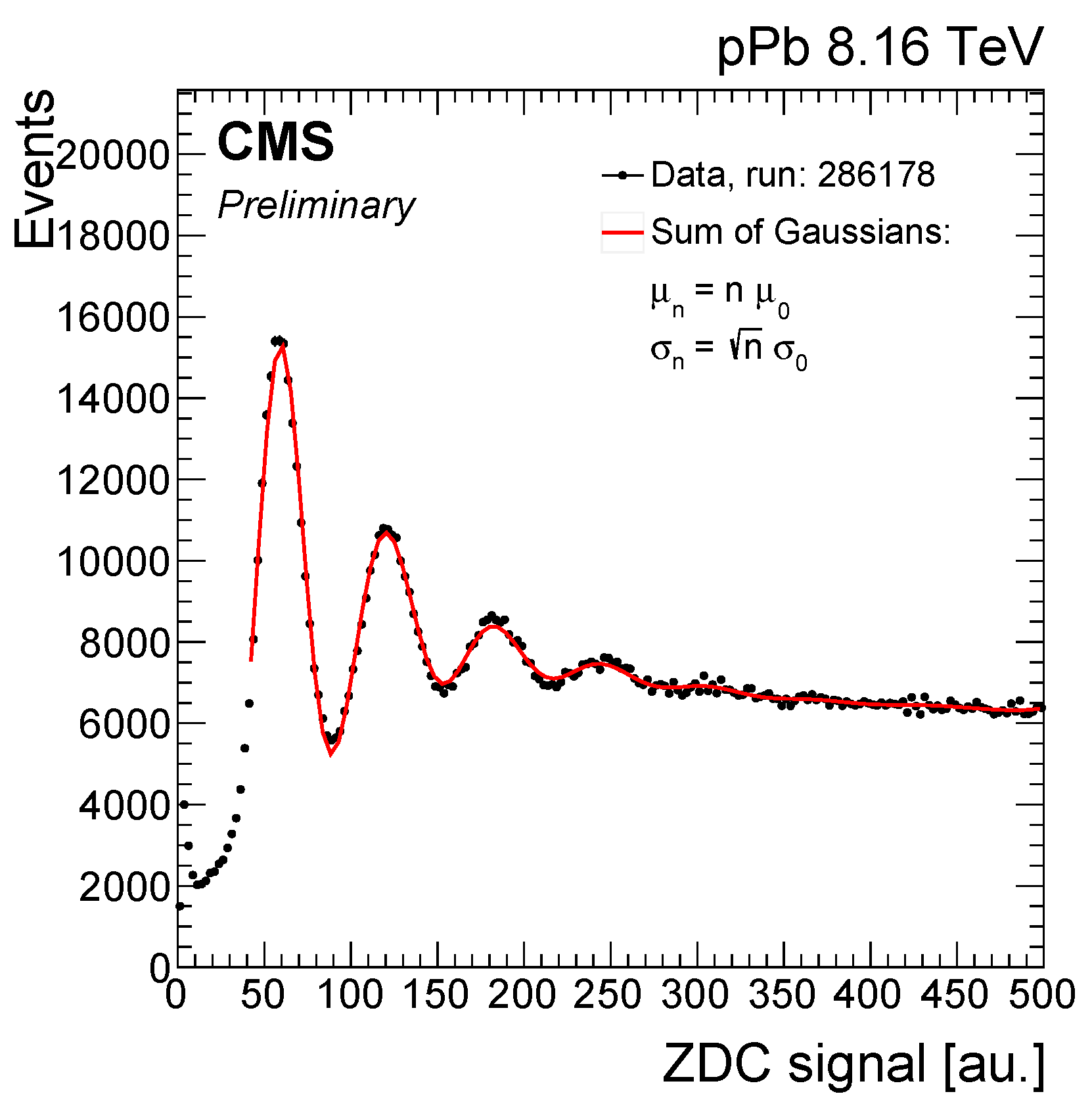
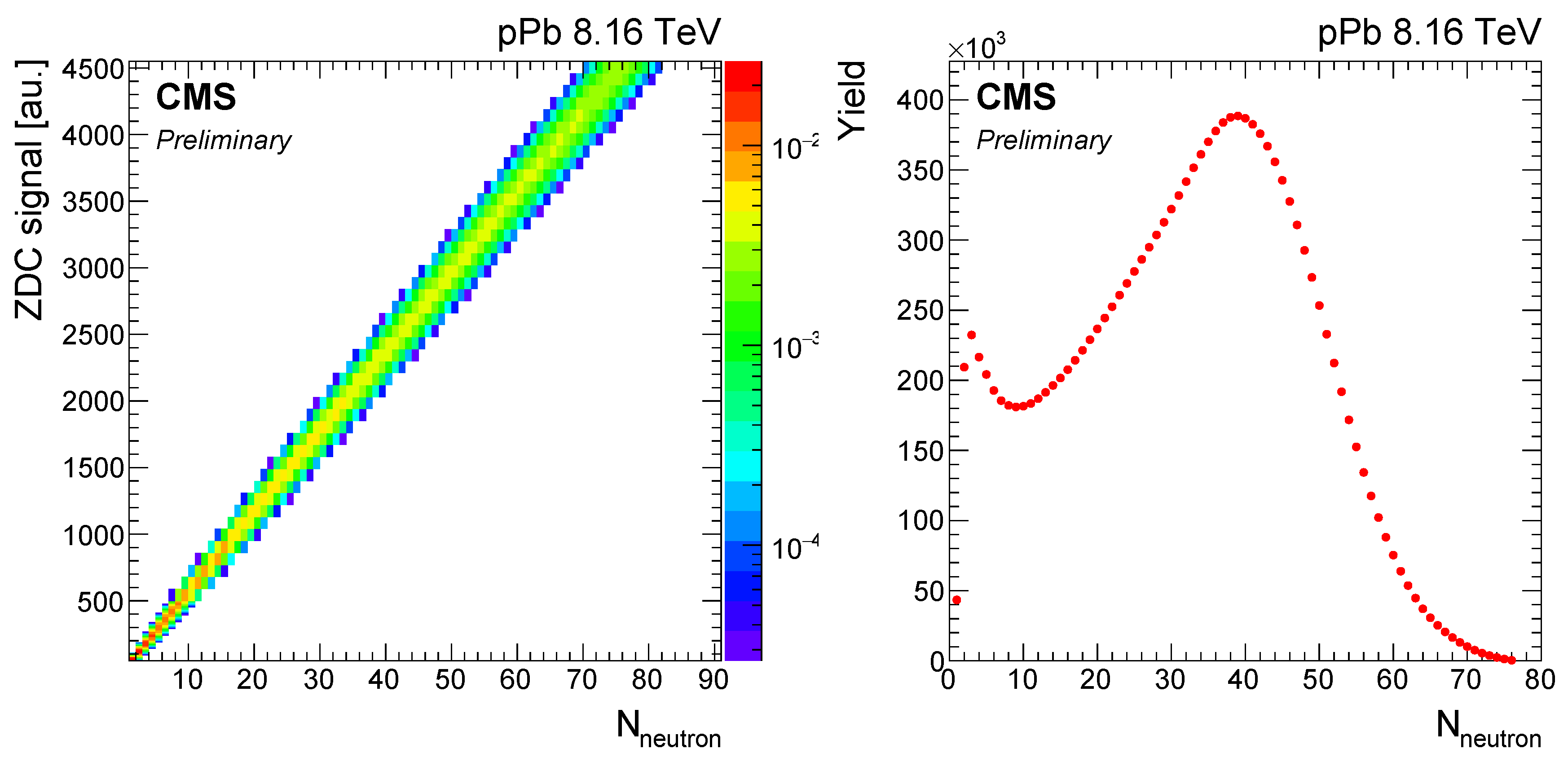
6. Unfolding Neutron Multiplicity Distribution
7. Conclusions
Funding
Conflicts of Interest
References
- Cugnon, J.; Volant, C.; Vuillier, S. Improved intranuclear cascade model for nucleon-nucleus interactions. Nucl. Phys. A 1997, 620, 475. [Google Scholar] [CrossRef]
- Ferrari, A.; Sala, P.R.; Ranft, J.; Roesler, S. Cascade particles, nuclear evaporation, and residual nuclei in high-energy hadron-nucleus interactions. Z. Phys. C Part. Fields 1996, C70, 413. [Google Scholar] [CrossRef][Green Version]
- Berman, B.L.; Fultz, S.C. Measurements of the giant dipole resonance with monoenergetic photons. Rev. Mod. Phys. 1975, 47, 713. [Google Scholar] [CrossRef]
- Sikler, F. Centrality Control of Hadron Nucleus Interactions by Detection of Slow Nucleons. Available online: https://arxiv.org/abs/hep-ph/0304065 (accessed on 5 October 2019).
- Adler, C.; et al.; [STAR Collaboration] Coherent ρ0 production in ultraperipheral heavy ion collisions. Phys. Rev. Lett. 2002, 89, 272302. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.; et al.; [STAR Collaboration] Production of e+e- pairs accompanied by nuclear dissociation in ultra-peripheral heavy ion collision. Phys. Rev. C 2004, 70, 031902. [Google Scholar] [CrossRef]
- Abelev, B.; et al.; [STAR Collaboration] Centrality determination of Pb-Pb collisions at sNN = 2.76 TeV with ALICE. Phys. Rev. C 2013, 88, 044909. [Google Scholar] [CrossRef]
- Adam, J.; et al.; [ALICE Collaboration] Centrality dependence of particle production in p-Pb collisions at sNN = 5.02 TeV. Phys. Rev. C 2015, 91, 064905. [Google Scholar] [CrossRef]
- Adriani, O.; Berti, E.; Bonechi, L.; Bongi, M.; Castellini, G.; D’Alessandro, R.; Del Prete, M.; Haguenauer, M.; Itow, Y.; Kasahara, K.; et al. Measurement of very forward neutron energy spectra for 7 TeV proton–proton collisions at the Large Hadron Collider. Phys. Lett. B 2015, 750, 360. [Google Scholar] [CrossRef]
- Ueno, M. Zero degree neutron energy spectra measured by the LHCf at s= 13 TeV proton-proton collision. PoS 2018, ICRC2017, 322. [Google Scholar]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255. [Google Scholar] [CrossRef]
- Galoyan, A.; Ribon, A.; Uzhinsky, V. Simulation of neutron production in hadron-nucleus and nucleus-nucleus interactions in Geant4. In Proceedings of the 24th International Baldin Seminar on High Energy Physics Problems: Relativistic Nuclear Physics and Quantum Chromodynamics (ISHEPP 2018), Dubna, Russia, 17–22 September 2018. [Google Scholar]
- Allison, J.; Amakoca, K.; Apostolakisd, J.; Arcee, P.; Asaif, M.; Asog, T.; Baglih, E.; Bagulyai, A.; Banerjeej, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Meth. A 2016, 835, 186. [Google Scholar] [CrossRef]
- Weil, J.; Steinberg, V.; Staudenmaier, J.; Pang, L.G.; Oliinychenko, D.; Mohs, J.; Kretz, M.; Kehrenberg, T.; Goldschmidt, A.; Bäuchle, B.; et al. Particle production and equilibrium properties within a new hadron transport approach for heavy-ion collisions. Phys. Rev. 2016, C94, 054905. [Google Scholar] [CrossRef]
- Nara, Y.; Otuka, N.; Ohnishi, A.; Niita, K.; Chiba, S. Study of relativistic nuclear collisions at AGS energies from p + Be to Au + Au with hadronic cascade model. Phys. Rev. C 2000, 61, 024901. [Google Scholar] [CrossRef]
- Cassing, W.; Bratkovskaya, E.L. Parton transport and hadronization from the dynamical quasiparticle point of view. Phys. Rev. 2008, C78, 034919. [Google Scholar] [CrossRef]
- Grachov, O.A.; Murray, M.J.; Ayan, A.S.; Debbins, P.; Norbeck, E.; Onel, Y.; d’Enterria, D.G. Status of zero degree calorimeter for CMS experiment. AIP Conf. Proc. 2006, 867, 258. [Google Scholar]
- Grachov, O.A.; Grachov, O.A.; Metzler, B.; Murray, M.; Snyder, J.; Stiles, L.; Wood, J.; Zhukova, V.; Beaumont, W.; Ochesanu, S.; et al. Measuring photons and neutrons at zero degrees in CMS. Int. J. Mod. Phys. E 2007, 16, 2137. [Google Scholar] [CrossRef]
- Grachov, O.A.; Murray, M.; Snyder, S.; Wood, J.; Zhukova, V.; Ayan, A.S.; Debbins, P.; Ingram, D.F.; Norbeck, E.; Onel, Y.; et al. Performance of the combined zero degree calorimeter for CMS. J. Phys. Conf. Ser. 2009, 160, 012059. [Google Scholar] [CrossRef]
- Grachov, O.; Murray, M.; Wood, J.; Onel, Y.; Sen, S.; Yetkin, T. Commissioning of the CMS zero degree calorimeter using LHC beam. J. Phys. Conf. Ser. 2011, 293, 012040. [Google Scholar] [CrossRef]
- CMS Collaboration. The Performance of CMS ZDC Detector in 2016. CMS Detector Performance Summary; CMS-DP-2018-025; CMS Collaboration: 2017. Available online: https://cds.cern.ch/record/2621978?ln=en (accessed on 9 October 2019).
- Jowett, J.M. The LHC as a Nucleus-Nucleus Collider. J. Phys. G 2008, 35, 104028. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of incorrectly formulated problems and the regularization method. Soviet Math. 1963, 4, 1035. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surányi, O., on Behalf of the CMS Collaboration. Study of Very Forward Neutrons with the CMS Zero Degree Calorimeter. Universe 2019, 5, 210. https://doi.org/10.3390/universe5100210
Surányi O on Behalf of the CMS Collaboration. Study of Very Forward Neutrons with the CMS Zero Degree Calorimeter. Universe. 2019; 5(10):210. https://doi.org/10.3390/universe5100210
Chicago/Turabian StyleSurányi, Olivér on Behalf of the CMS Collaboration. 2019. "Study of Very Forward Neutrons with the CMS Zero Degree Calorimeter" Universe 5, no. 10: 210. https://doi.org/10.3390/universe5100210
APA StyleSurányi, O., on Behalf of the CMS Collaboration. (2019). Study of Very Forward Neutrons with the CMS Zero Degree Calorimeter. Universe, 5(10), 210. https://doi.org/10.3390/universe5100210



