Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the UA(1) Symmetry
Abstract
1. Introduction
2. Connection with the Complex of the and Mesons
2.1. Some Generalities on the Influence of the Anomaly on and
2.2. On Some Possibilities of Modeling the Anomaly Influence
3. The Axion Mass from the Non-Abelian Axial Anomaly of QCD
3.1. The Axion as the Almost-Goldstone Boson of the Peccei–Quinn Symmetry
3.2. Axion Mass from the Topological Susceptibility from Condensates of Massive Quarks
3.3. Axion Mass and Topological Susceptibility—Results from the Rank-2 Separable Model in the Isosymmetric Limit
3.4. Axion Mass and Topological Susceptibility from Rank-1 and Rank-2 Models out of the Isosymmetric Limit
4. Summary and Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DChSB | Dynamical chiral symmetry breaking |
| DSE | Dyson–Schwinger equations |
| QCD | Quantum chromodynamics |
| ABJ | Adler-Bell-Jackiw |
| CKM | Cabibbo-Kobayashi-Maskawa |
| CP | charge conjugation parity |
Appendix A. Separable Interaction Models for Usage at T≥0
References
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. [Particle Data Group]. Review of Particle Physics. Phys. Rev. 2018, D98, 030001. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. 1977, D16, 1791–1797. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Peccei, R.D. The Strong CP problem and axions. Lect. Notes Phys. 2008, 741, 3–17. [Google Scholar] [CrossRef]
- Cabibbo, N. Unitary Symmetry and Leptonic Decays. Phys. Rev. Lett. 1963, 10, 531–533. [Google Scholar] [CrossRef]
- Kobayashi, M.; Maskawa, T. CP Violation in the Renormalizable Theory of Weak Interaction. Prog. Theor. Phys. 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Baker, C.A.; Doyle, D.D.; Geltenbort, P.; Green, K.; van der Grinten, M.G.D.; Harris, P.G.; Iaydjiev, P.; Ivanov, S.N.; May, D.J.R.; Pendlebury, J.M.; et al. An Improved experimental limit on the electric dipole moment of the neutron. Phys. Rev. Lett. 2006, 97, 131801. [Google Scholar] [CrossRef]
- Wantz, O.; Shellard, E.P.S. Axion Cosmology Revisited. Phys. Rev. 2010, D82, 123508. [Google Scholar] [CrossRef]
- Berkowitz, E.; Buchoff, M.I.; Rinaldi, E. Lattice QCD input for axion cosmology. Phys. Rev. 2015, D92, 034507. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. 1983, 120B, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. 1983, 120B, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. 1983, 120B, 137–141. [Google Scholar] [CrossRef]
- Kim, J.E.; Nam, S.; Semetzidis, Y.K. Fate of global symmetries in the Universe: QCD axion, quintessential axion and trans-Planckian inflaton decay-constant. Int. J. Mod. Phys. 2018, A33, 1830002. [Google Scholar] [CrossRef]
- Dvali, G.; Funcke, L. Domestic Axion. arXiv 2016, arXiv:1608.08969. [Google Scholar]
- Horvatić, D.; Kekez, D.; Klabučar, D. η′ and η mesons at high T when the UA(1) and chiral symmetry breaking are tied. Phys. Rev. 2019, D99, 014007. [Google Scholar] [CrossRef]
- Adler, S.L. Axial vector vertex in spinor electrodynamics. Phys. Rev. 1969, 177, 2426–2438. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0→γγ in the σ model. Nuovo Cim. 1969, A60, 47–61. [Google Scholar] [CrossRef]
- Feldmann, T. Quark structure of pseudoscalar mesons. Int. J. Mod. Phys. 2000, A15, 159–207. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D.; Scadron, M.D. Revisiting the U(A)(1) problems. J. Phys. 2000, G26, 1335–1354. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D. Two photon processes of pseudoscalar mesons in a Bethe-Salpeter approach. Phys. Lett. 1996, B387, 14–20. [Google Scholar] [CrossRef]
- Kekez, D.; Bistrović, B.; Klabučar, D. Application of Jain and Munczek’s bound state approach to gamma gamma processes of Pi0, eta(c) and eta(b). Int. J. Mod. Phys. 1999, A14, 161–194. [Google Scholar] [CrossRef]
- Klabučar, D.; Kekez, D. eta and eta-prime in a coupled Schwinger-Dyson and Bethe-Salpeter approach. Phys. Rev. 1998, D58, 096003. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D. Gamma* gamma —> pi0 transition and asymptotics of gamma* gamma and gamma* gamma* transitions of other unflavored pseudoscalar mesons. Phys. Lett. 1999, B457, 359–367. [Google Scholar] [CrossRef]
- Bistrović, B.; Klabučar, D. Anomalous gamma —> 3 pi amplitude in a bound state approach. Phys. Lett. 2000, B478, 127–136. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D. Eta and eta-prime in a coupled Schwinger-Dyson and Bethe-Salpeter approach: The gamma* gamma transition form-factors. Phys. Rev. 2002, D65, 057901. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D. Pseudoscalar q anti-q mesons and effective QCD coupling enhanced (A**2) condensate. Phys. Rev. 2005, D71, 014004. [Google Scholar] [CrossRef]
- Kekez, D.; Klabučar, D. Eta and eta’ mesons and dimension 2 gluon condensate < A**2 >. Phys. Rev. 2006, D73, 036002. [Google Scholar] [CrossRef]
- Horvatić, D.; Blaschke, D.; Kalinovsky, Y.; Kekez, D.; Klabučar, D. eta and eta-prime mesons in the Dyson-Schwinger approach using a generalization of the Witten-Veneziano relation. Eur. Phys. J. 2008, A38, 257–264. [Google Scholar] [CrossRef][Green Version]
- Horvatić, D.; Klabučar, D.; Radzhabov, A.E. eta and eta-prime mesons in the Dyson-Schwinger approach at finite temperature. Phys. Rev. 2007, D76, 096009. [Google Scholar] [CrossRef]
- Horvatić, D.; Blaschke, D.; Klabučar, D.; Radzhabov, A.E. Pseudoscalar Meson Nonet at Zero and Finite Temperature. Phys. Part. Nucl. 2008, 39, 1033–1039. [Google Scholar] [CrossRef]
- Alkofer, R.; von Smekal, L. The Infrared behavior of QCD Green’s functions: Confinement dynamical symmetry breaking, and hadrons as relativistic bound states. Phys. Rept. 2001, 353, 281. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1–S103. [Google Scholar] [CrossRef]
- Holl, A.; Roberts, C.D.; Wright, S.V. Hadron physics and Dyson-Schwinger equations. In Proceedings of the 20th Annual Hampton University Graduate Studies Program (HUGS 2005), Newport News, VA, USA, 31 May–17 June 2005. [Google Scholar]
- Fischer, C.S. Infrared properties of QCD from Dyson-Schwinger equations. J. Phys. 2006, G32, R253–R291. [Google Scholar] [CrossRef]
- Benić, S.; Horvatić, D.; Kekez, D.; Klabučar, D. A UA(1) symmetry restoration scenario supported by the generalized Witten-Veneziano relation and its analytic solution. Phys. Lett. 2014, B738, 113–117. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra Theorems for the U(1) Goldstone Boson. Nucl. Phys. 1979, B156, 269–283. [Google Scholar] [CrossRef]
- Veneziano, G. U(1) Without Instantons. Nucl. Phys. 1979, B159, 213–224. [Google Scholar] [CrossRef]
- Alles, B.; D’Elia, M.; Di Giacomo, A. Topological susceptibility at zero and finite T in SU(3) Yang-Mills theory. Nucl. Phys. 1997, B494, 281–292. [Google Scholar] [CrossRef]
- Boyd, G.; Engels, J.; Karsch, F.; Laermann, E.; Legeland, C.; Lutgemeier, M.; Petersson, B. Thermodynamics of SU(3) lattice gauge theory. Nucl. Phys. 1996, B469, 419–444. [Google Scholar] [CrossRef]
- Gattringer, C.; Hoffmann, R.; Schaefer, S. The Topological susceptibility of SU(3) gauge theory near T(c). Phys. Lett. 2002, B535, 358–362. [Google Scholar] [CrossRef]
- Di Vecchia, P.; Rossi, G.; Veneziano, G.; Yankielowicz, S. Spontaneous CP breaking in QCD and the axion potential: An effective Lagrangian approach. J. High Energy Phys. 2017, 12, 104. [Google Scholar] [CrossRef]
- Dick, V.; Karsch, F.; Laermann, E.; Mukherjee, S.; Sharma, S. Microscopic origin of UA(1) symmetry violation in the high temperature phase of QCD. Phys. Rev. 2015, D91, 094504. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. The QCD Equation of State to O() from Lattice QCD. Phys. Rev. 2017, D95, 054504. [Google Scholar] [CrossRef]
- Bazavov, A. An overview of (selected) recent results in finite-temperature lattice QCD. J. Phys. Conf. Ser. 2013, 446, 012011. [Google Scholar] [CrossRef]
- Stoecker, H.; Zhou, K.; Schramm, S.; Senzel, F.; Greiner, C.; Beitel, M.; Gallmeister, K.; Gorenstein, M.; Mishustin, I.; Vasak, D.; et al. Glueballs amass at RHIC and LHC Colliders! - The early quarkless 1st order phase transition at T=270 MeV - from pure Yang-Mills glue plasma to GlueBall-Hagedorn states. J. Phys. 2016, G43, 015105. [Google Scholar] [CrossRef]
- Benić, S.; Horvatić, D.; Kekez, D.; Klabučar, D. eta-prime Multiplicity and the Witten-Veneziano relation at finite temperature. Phys. Rev. 2011, D84, 016006. [Google Scholar] [CrossRef]
- Leutwyler, H.; Smilga, A.V. Spectrum of Dirac operator and role of winding number in QCD. Phys. Rev. 1992, D46, 5607–5632. [Google Scholar] [CrossRef]
- Di Vecchia, P.; Veneziano, G. Chiral Dynamics in the Large n Limit. Nucl. Phys. 1980, B171, 253–272. [Google Scholar] [CrossRef]
- Dürr, S. Topological susceptibility in full QCD: Lattice results versus the prediction from the QCD partition function with granularity. Nucl. Phys. 2001, B611, 281–310. [Google Scholar] [CrossRef]
- Bernard, V.; Descotes-Genon, S.; Toucas, G. Topological susceptibility on the lattice and the three-flavour quark condensate. JHEP 2012, 06, 051. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Wilczek, F. Remarks on the Chiral Phase Transition in Chromodynamics. Phys. Rev. 1984, D29, 338–341. [Google Scholar] [CrossRef]
- Höll, A.; Maris, P.; Roberts, C.D. Mean field exponents and small quark masses. Phys. Rev. 1999, C59, 1751–1755. [Google Scholar] [CrossRef]
- Kiriyama, O.; Maruyama, M.; Takagi, F. Current quark mass effects on chiral phase transition of QCD in the improved ladder approximation. Phys. Rev. 2001, D63, 116009. [Google Scholar] [CrossRef]
- Ikeda, T. Dressed quark propagator at finite temperature in the Schwinger-Dyson approach with the rainbow approximation: Exact numerical solutions and their physical implication. Prog. Theor. Phys. 2002, 107, 403–420. [Google Scholar] [CrossRef]
- Blank, M.; Krassnigg, A. The QCD chiral transition temperature in a Dyson-Schwinger-equation context. Phys. Rev. 2010, D82, 034006. [Google Scholar] [CrossRef]
- Fischer, C.S.; Mueller, J.A. Quark condensates and the deconfinement transition. PoS 2009, CPOD2009, 023. [Google Scholar] [CrossRef]
- Qin, S.x.; Chang, L.; Chen, H.; Liu, Y.x.; Roberts, C.D. Phase diagram and critical endpoint for strongly-interacting quarks. Phys. Rev. Lett. 2011, 106, 172301. [Google Scholar] [CrossRef]
- Gao, F.; Chen, J.; Liu, Y.X.; Qin, S.X.; Roberts, C.D.; Schmidt, S.M. Phase diagram and thermal properties of strong-interaction matter. Phys. Rev. 2016, D93, 094019. [Google Scholar] [CrossRef]
- Fischer, C.S. QCD at finite temperature and chemical potential from Dyson–Schwinger equations. Prog. Part. Nucl. Phys. 2019, 105, 1–60. [Google Scholar] [CrossRef]
- Ejiri, S.; Karsch, F.; Laermann, E.; Miao, C.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Soeldner, W.; Unger, W. On the magnetic equation of state in (2+1)-flavor QCD. Phys. Rev. 2009, D80, 094505. [Google Scholar] [CrossRef]
- Ding, H.T.; Hegde, P.; Karsch, F.; Lahiri, A.; Li, S.T.; Mukherjee, S.; Petreczky, P. Chiral phase transition of (2+1)-flavor QCD. Nucl. Phys. 2019, A982, 211–214. [Google Scholar] [CrossRef]
- Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Lahiri, A.; Li, S.T.; Mukherjee, S.; Petreczky, P. Chiral phase transition in (2 + 1)-flavor QCD. PoS 2019, LATTICE2018, 171. [Google Scholar] [CrossRef]
- Csorgo, T.; Vertesi, R.; Sziklai, J. Indirect observation of an in-medium η′ mass reduction in = 200 GeV Au+Au collisions. Phys. Rev. Lett. 2010, 105, 182301. [Google Scholar] [CrossRef]
- Vertesi, R.; Csorgo, T.; Sziklai, J. Significant in-medium η ’ mass reduction in = 200 GeV Au+Au collisions at the BNL Relativistic Heavy Ion Collider. Phys. Rev. 2011, C83, 054903. [Google Scholar] [CrossRef]
- Aoki, S.; Fukaya, H.; Taniguchi, Y. Chiral symmetry restoration, eigenvalue density of Dirac operator and axial U(1) anomaly at finite temperature. Phys. Rev. 2012, D86, 114512. [Google Scholar] [CrossRef]
- Buchoff, M.I.; Cheng, M.; Christ, N.; Ding, H.-T.; Jung, C.; Karsch, F.; Lin, Z.; Mawhinney, R.D.; Mukherjee, S.; Petreczky, P.; et al. QCD chiral transition, U(1)A symmetry and the dirac spectrum using domain wall fermions. Phys. Rev. 2014, D89, 054514. [Google Scholar] [CrossRef]
- Shore, G.M. Pseudoscalar meson decay constants and couplings, the Witten-Veneziano formula beyond large N(c), and the topological susceptibility. Nucl. Phys. 2006, B744, 34–58. [Google Scholar] [CrossRef][Green Version]
- Petreczky, P.; Schadler, H.P.; Sharma, S. The topological susceptibility in finite temperature QCD and axion cosmology. Phys. Lett. 2016, B762, 498–505. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; Redondo, J.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Mariti, M.; Martinelli, G.; Mesiti, M.; Negro, F.; Sanfilippo, F.; Villadoro, G. Axion phenomenology and θ-dependence from Nf = 2 + 1 lattice QCD. J. High Energy Phys. 2016, 03, 155. [Google Scholar] [CrossRef]
- Takahashi, F.; Yin, W.; Guth, A.H. QCD axion window and low-scale inflation. Phys. Rev. 2018, D98, 015042. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Martinelli, G.; Negro, F.; Sanfilippo, F.; Todaro, A. Topology in full QCD at high temperature: A multicanonical approach. J. High Energy Phys. 2018, 11, 170. [Google Scholar] [CrossRef]
- Grilli di Cortona, G.; Hardy, E.; Pardo Vega, J.; Villadoro, G. The QCD axion, precisely. J. High Energy Phys. 2016, 01, 034. [Google Scholar] [CrossRef]
- Gorghetto, M.; Villadoro, G. Topological Susceptibility and QCD Axion Mass: QED and NNLO corrections. J. High Energy Phys. 2019, 03, 033. [Google Scholar] [CrossRef]
- Blaschke, D.; Burau, G.; Kalinovsky, Y.L.; Maris, P.; Tandy, P.C. Finite T meson correlations and quark deconfinement. Int. J. Mod. Phys. 2001, A16, 2267–2291. [Google Scholar] [CrossRef]
- Alkofer, R.; Watson, P.; Weigel, H. Mesons in a Poincare covariant Bethe-Salpeter approach. Phys. Rev. 2002, D65, 094026. [Google Scholar] [CrossRef]
- Contant, R.; Huber, M.Q. Phase structure and propagators at nonvanishing temperature for QCD and QCD-like theories. Phys. Rev. 2017, D96, 074002. [Google Scholar] [CrossRef]
- Blaschke, D.; Kalinovsky, Y.L.; Radzhabov, A.E.; Volkov, M.K. Scalar sigma meson at a finite temperature in a nonlocal quark model. Phys. Part. Nucl. Lett. 2006, 3, 327–330. [Google Scholar] [CrossRef]
- Burger, F.; Ilgenfritz, E.M.; Kirchner, M.; Lombardo, M.P.; Muller-Preussker, M.; Philipsen, O.; Urbach, C.; Zeidlewicz, L. Thermal QCD transition with two flavors of twisted mass fermions. Phys. Rev. 2013, D87, 074508. [Google Scholar] [CrossRef]
- Kotov, A.Y.; Lombardo, M.P.; Trunin, A.M. Fate of the η′ in the quark gluon plasma. Phys. Lett. 2019, B794, 83–88. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Is there still any Tc mystery in lattice QCD? Results with physical masses in the continuum limit III. J. High Energy Phys. 2010, 09, 073. [Google Scholar] [CrossRef]
- Isserstedt, P.; Buballa, M.; Fischer, C.S.; Gunkel, P.J. Baryon number fluctuations in the QCD phase diagram from Dyson-Schwinger equations. arXiv 2019, arXiv:1906.11644. [Google Scholar] [CrossRef]
- Cahill, R.T.; Gunner, S.M. The Global color model of QCD for hadronic processes: A Review. Fizika 1998, B7, 171. [Google Scholar]
- Blaschke, D.; Horvatić, D.; Klabučar, D.; Radzhabov, A.E. Separable Dyson-Schwinger model at zero and finite T. In Proceedings of the Mini-Workshop Bled 2006 on Progress in Quark Models, Bled, Slovenia, 10–17 July 2006; pp. 20–26. [Google Scholar]
- Klabučar, D.; Horvatić, D.; Kekez, D. T-dependence of the axion mass when the UA(1) and chiral symmetry breaking are tied. In Proceedings of the Workshop on Excited QCD 2019, Schladming, Austria, 30 January–3 February 2019. [Google Scholar]
- Lu, Z.Y.; Ruggieri, M. Effect of the chiral phase transition on axion mass and self-coupling. Phys. Rev. 2019, D100, 014013. [Google Scholar] [CrossRef]
- Gu, X.W.; Duan, C.G.; Guo, Z.H. Updated study of the η-η′ mixing and the thermal properties of light pseudoscalar mesons at low temperatures. Phys. Rev. 2018, D98, 034007. [Google Scholar] [CrossRef]
- Fukaya, H. Can axial U(1) anomaly disappear at high temperature? EPJ Web Conf. 2018, 175, 01012. [Google Scholar] [CrossRef][Green Version]
| 1. | The mass eigenstate is approximated only roughly by the pure singlet state , due to the relatively large explicit breaking of the flavor symmetry by much heavier s-quark: [1]. |
| 2. | |
| 3. | |
| 4. | The combinations need not always pertain to physical mesons. The pseudoscalar hidden-flavor states , , are not physical as long as the symmetry is not restored ( i.e., the anomaly effectively turned off, see around Equation (2.6) in Ref. [43] for example), but build the states , and . |
| 5. |
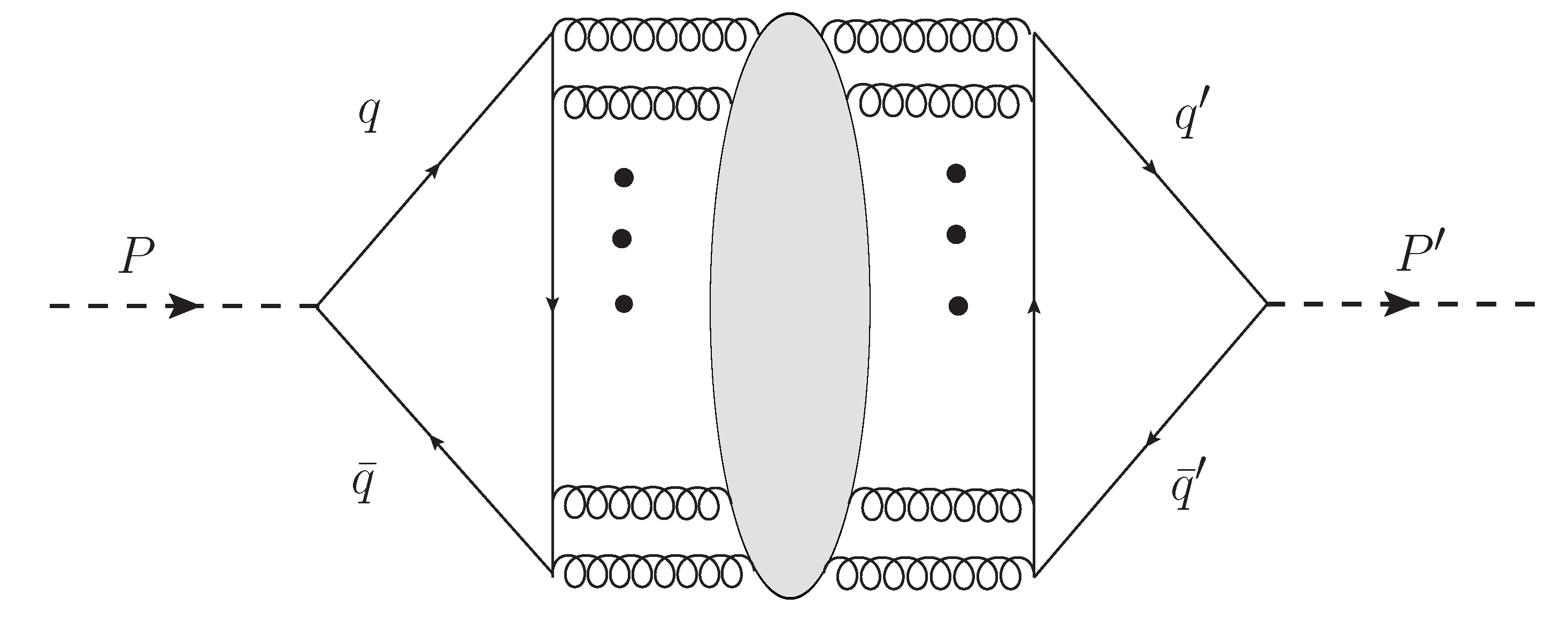
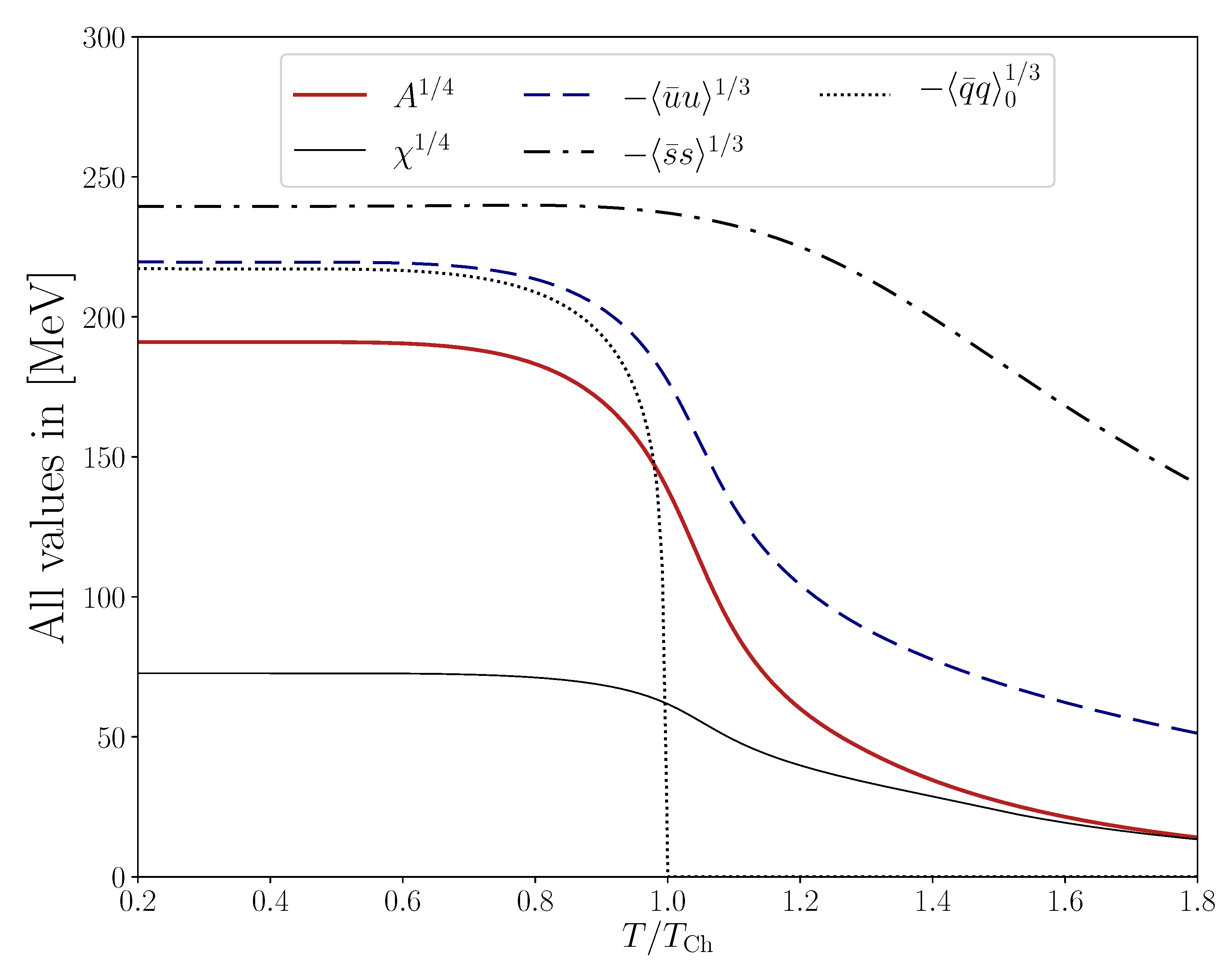
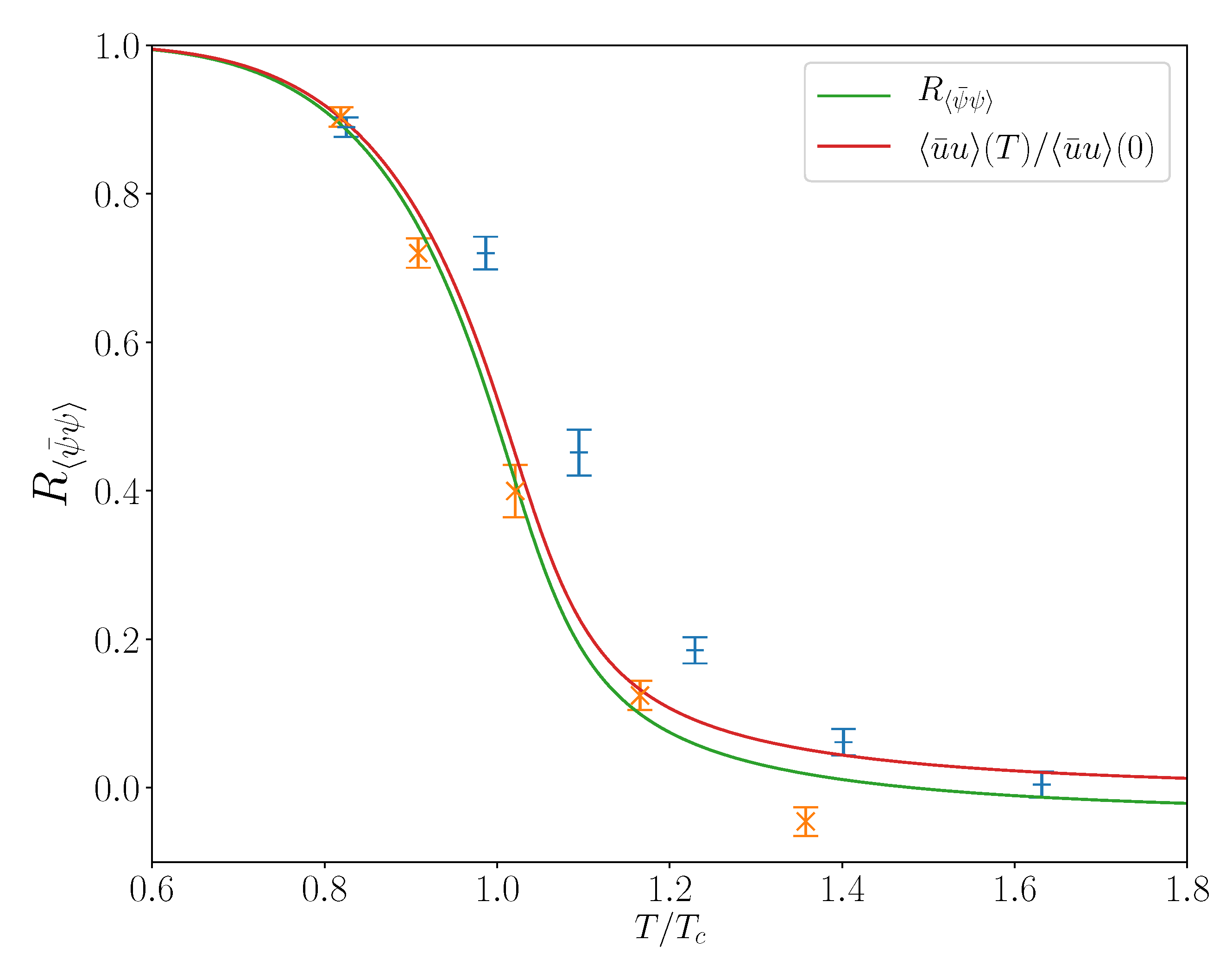
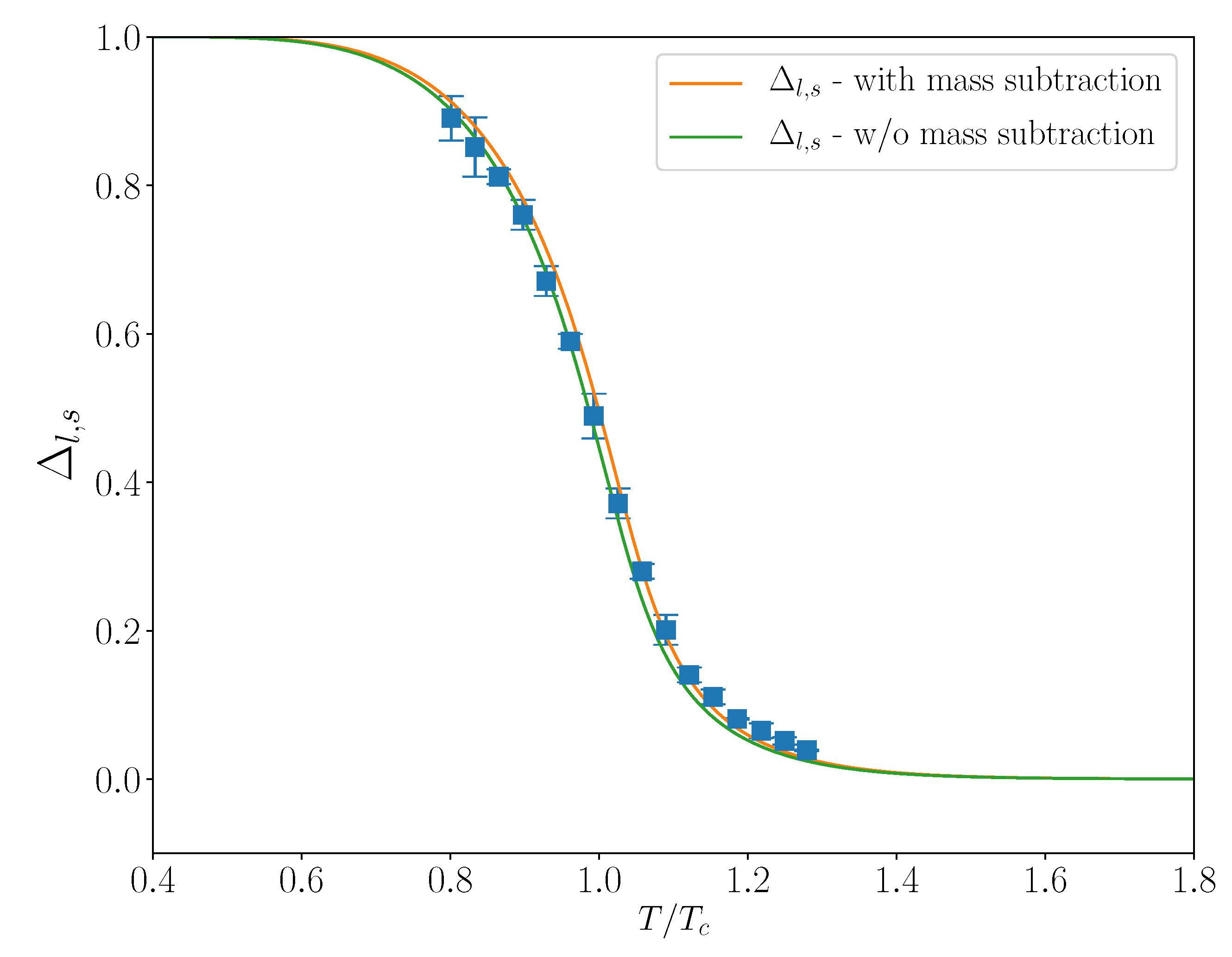

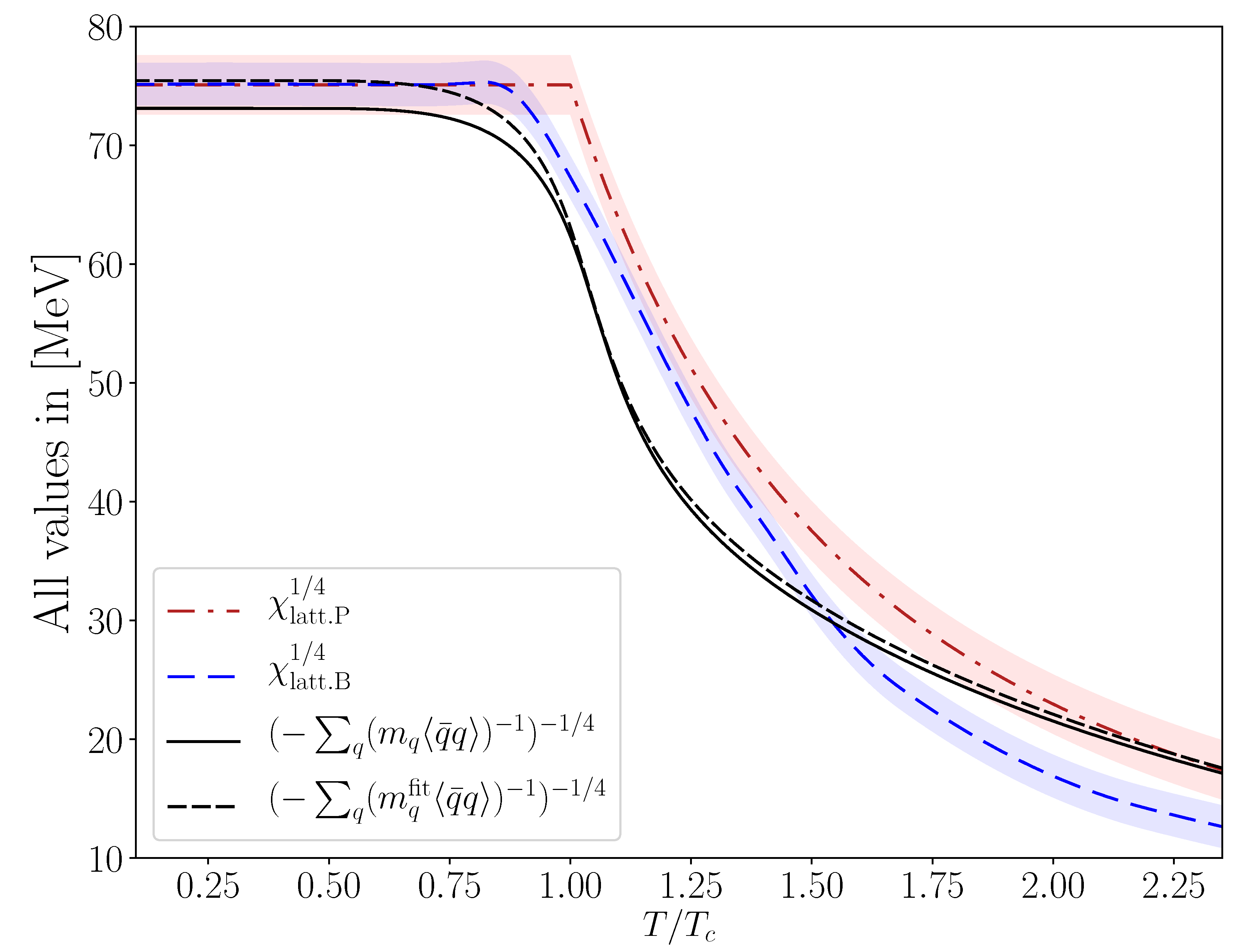
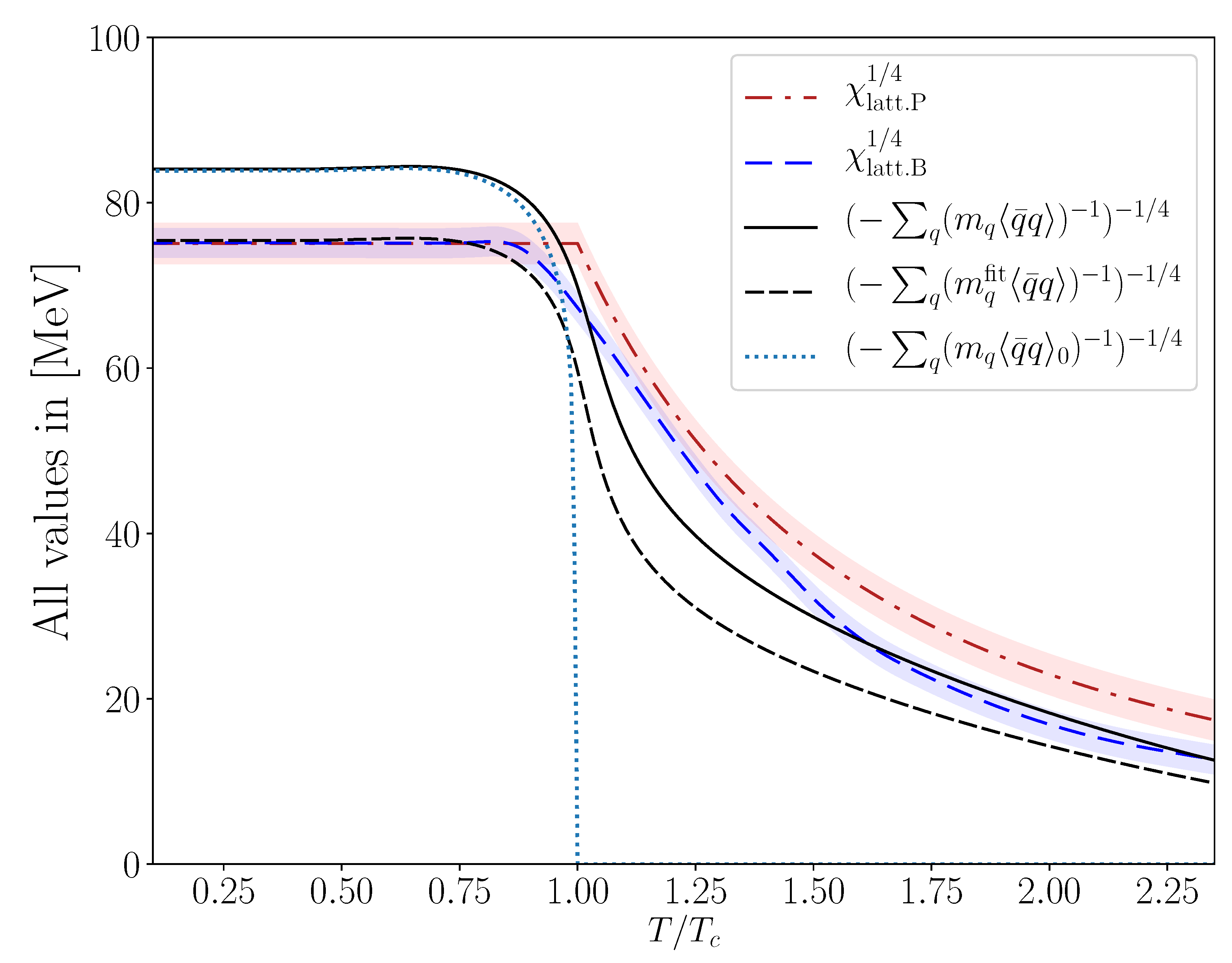
| (with ) | ||||||||
|---|---|---|---|---|---|---|---|---|
| rank-2 | ||||||||
| [17] | 5.49 | 5.49 | 115 | |||||
| with constraint | ||||||||
| [1], | 4.66 | 9.71 | 115 | |||||
| fitted & | ||||||||
| rank-1 | ||||||||
| 6.6 | 6.6 | 142 | ||||||
| with constraint | ||||||||
| [1], | 3.15 | 6.56 | 142 | |||||
| fitted & |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horvatić, D.; Kekez, D.; Klabučar, D. Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the UA(1) Symmetry. Universe 2019, 5, 208. https://doi.org/10.3390/universe5100208
Horvatić D, Kekez D, Klabučar D. Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the UA(1) Symmetry. Universe. 2019; 5(10):208. https://doi.org/10.3390/universe5100208
Chicago/Turabian StyleHorvatić, Davor, Dalibor Kekez, and Dubravko Klabučar. 2019. "Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the UA(1) Symmetry" Universe 5, no. 10: 208. https://doi.org/10.3390/universe5100208
APA StyleHorvatić, D., Kekez, D., & Klabučar, D. (2019). Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the UA(1) Symmetry. Universe, 5(10), 208. https://doi.org/10.3390/universe5100208





