Abstract
Neutron captures are likely to occur in the crust of accreting neutron stars (NSs). Their rate depends on the thermodynamic state of neutrons in the crust. At high densities, neutrons are degenerate. We find degeneracy corrections to neutron capture rates off nuclei, using cross sections evaluated with the reaction code TALYS. We numerically integrate the relevant cross sections over the statistical distribution functions of neutrons at thermodynamic conditions present in the NS crust. We compare our results to analytical calculations of these corrections based on a power-law behavior of the cross section. We find that although an analytical integration can simplify the calculation and incorporation of the results for nucleosynthesis networks, there are uncertainties caused by departures of the cross section from the power-law approach at energies close to the neutron chemical potential. These deviations produce non-negligible corrections that can be important in the NS crust.
1. Introduction
X-ray burst and superburst observations are attributed to accreting neutron stars (NSs) (see, e.g., [1,2]). In such a scenario, a NS drags matter from a companion star. This accreted proton-rich material undergoes nuclear reactions in the NS envelope [3,4]. The energy released during the reactions heats up the star material, triggering the bursts and contributing to the synthesis of proton-rich nuclei via rp-process nucleosynthesis. Despite several efforts, there are still open questions regarding the X-ray burst and superburst detonation mechanisms. The amount of energy released during nuclear reactions is the key to understanding the cooling and heating of the crust after periods of accretion and therefore the energy budget available for the bursts. Furthermore, how deep in the crust the energy is released can play an important role. The products of the rp-process reactions, or ashes, can be deposited further in the inner regions of the crust when more material is accreted [5]. These ashes could capture the highly degenerate neutrons present in the crust. If neutron degeneracy is important for changing the reactions rates, then this will impact the energy released or consumed during the reaction and the composition of the crust.
The importance of degeneracy in neutron capture reactions has been highlighted in previous works [6,7]. There, it has been shown that degeneracy increases the reaction rates on some nuclides under the NS crust conditions, in contrast to considering neutrons behaving classically as is usually done in reaction networks for astrophysical purposes (see, e.g., [8,9]). Besides the important effect of neutron degeneracy, a reliable calculation of capture rates strongly depends on the relevant cross sections. Because of the extreme conditions of the NS crust, however, many of the involved nuclei are out of experimental reach, and their capture cross sections need to be evaluated theoretically. To quantify the effect of neutron degeneracy on capture rates, Shternin et al. [6] assumed a power-law behavior of such cross sections that should be valid up to some neutron energy and thermodynamic conditions. With such behavior, the authors found an analytical correction to the neutron capture rates. They also compared this analytical method with numerical integration for some capture reactions and found slight discrepancies. An analytical correction allows for an easy implementation in nucleosynthesis calculations. In this contribution, we study the feasibility and validity of a power-law approximation by numerically integrating the absorption cross sections over the Fermi–Dirac distribution of the neutrons. We calculate capture cross sections with the specialized nuclear reaction code TALYS 1.9 [10,11] and follow a similar methodology as was done in Reference [7] to find the correction due to degeneracy. We do not include plasma effects in this work. Shternin et al. have showed that there will also be a correction to capture rates as a result of the electron plasma, and we will study this effect in later work.
2. Neutron Capture Rates
The reaction rate itself is determined by the average . The statistical average is calculated by weighting the total cross section, , over the velocity distribution function of the target and incident particle. The star denotes the fact that the cross section includes excited states of the target nuclei. By use of a unitary transformation into the center of mass and relative coordinates, and by integrating out the center of mass term, we obtain
where N is the normalization factor given by
with collision energy , where is the reduced mass of the system. Assuming a non-relativistic collision, then the reduced mass, average velocity v, and distribution function correspond to neutrons. This distribution function can take the form of the classical Maxwell–Boltzmann distribution, , where T is the temperature (MeV), or a Fermi–Dirac distribution, , where is the neutron chemical potential. We treat the neutrons within the crust as a free Fermi gas. To measure the degeneracy effects, as was done in Reference [6], we can define a ratio
As mentioned in Reference [6], plasma effects will affect this ratio, but for now, only the degeneracy effects are explored. We can further simplify this ratio by excluding the excited states of the cross section. The domain of temperatures investigated is smaller than the typical first excited state energy, and thus to a reasonable approximation .
3. Capture Cross Sections
The determination of neutron capture rates in the NS crust requires knowledge of the corresponding cross sections for nuclei currently out of experimental reach. Assuming the formation of a compound nucleus, a detailed calculation of the neutron capture cross section, of the reaction , can be done in the framework of the Hauser-Feshbach theory [12]. The compound nucleus model assumes that when a projectile particle is absorbed by the target, it will reach an internal equilibrium and then decay into a final state. The final state will be independent of the absorption reaction. In our case, the target nucleus is a neutron-rich nuclei X, the projectile is a neutron n, and an ejectile consists of gamma rays to conserve energy in the system.
Such theoretical calculations can be implemented with the nuclear reaction code TALYS [10], which allows the user to choose among several nuclear physics models as input. To compare our numerical results with those of [6], we adopt the nucleon optical model potential from Koning and Delaroche [13], the Hartree–Fock–Bogoliubov mass model HFB-17 [14], the level densities from the microscopic model of Goriely et al. [15], gamma-ray strength functions as in Reference [16], and the McFadden–Satchler alpha potential [17]. To account for correlations between incident and outgoing waves, we use width-factor corrections from Hofmann et al. [18,19]. Finally, we do not include pre-equilibrium effects. We note that in TALYS, the capture cross section of very low energy neutrons follows behavior, from 10 eV to a limit (with determined from nuclear model database or from the level density). A straight line joins the values from and , and therefore there are unresolved resonances (for more information, see Reference [11]).
Counting on knowledge of the neutron capture cross section for a given nucleus, the next step is to integrate Equation (1) to determine the absorption rate. Shternin et al. [6] proposed that given the low temperature of the NS crust, the relevant cross section follows a power-law behavior such that
with as a normalization constant (irrelevant in the analysis of R), as the threshold energy of the reaction, and as a power-law index, for a range of energies . This proposed approximation would be valid as long as , allowing the analytical integration of Equation (1) and therefore a study of the ratio R for different temperatures and neutron chemical potentials. This analytical approach can be very useful in nucleosynthesis calculations. However, determining the power-law index and for each reaction , where X is one of the many neutron-rich nuclei in the crust, can be involved. Furthermore, if large values of R emerge, it would be difficult to discriminate between whether they are produced as a result of the degenerate character of the neutrons or whether the thermodynamic conditions are such that the power-law approximation is no longer valid.
4. Results
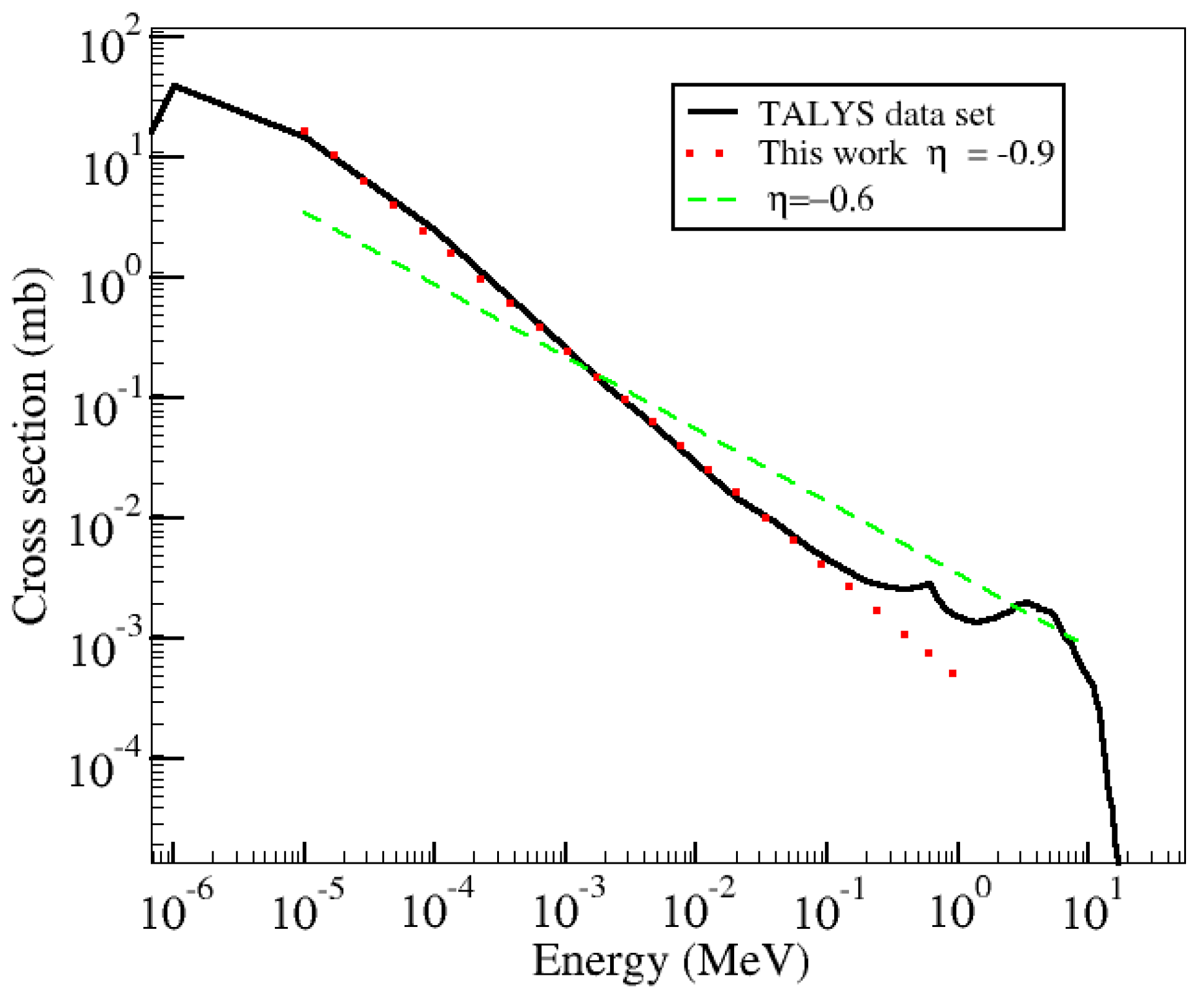
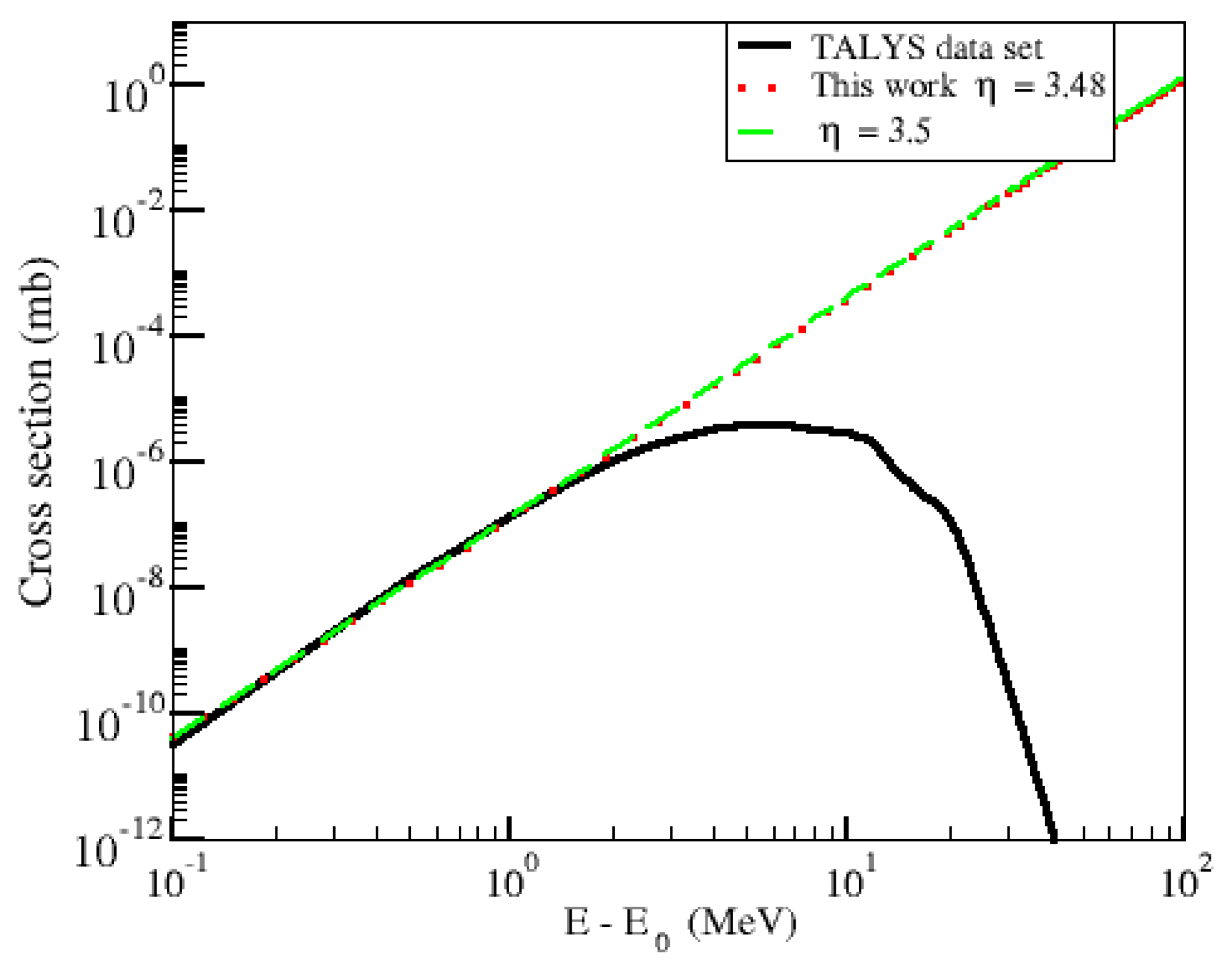
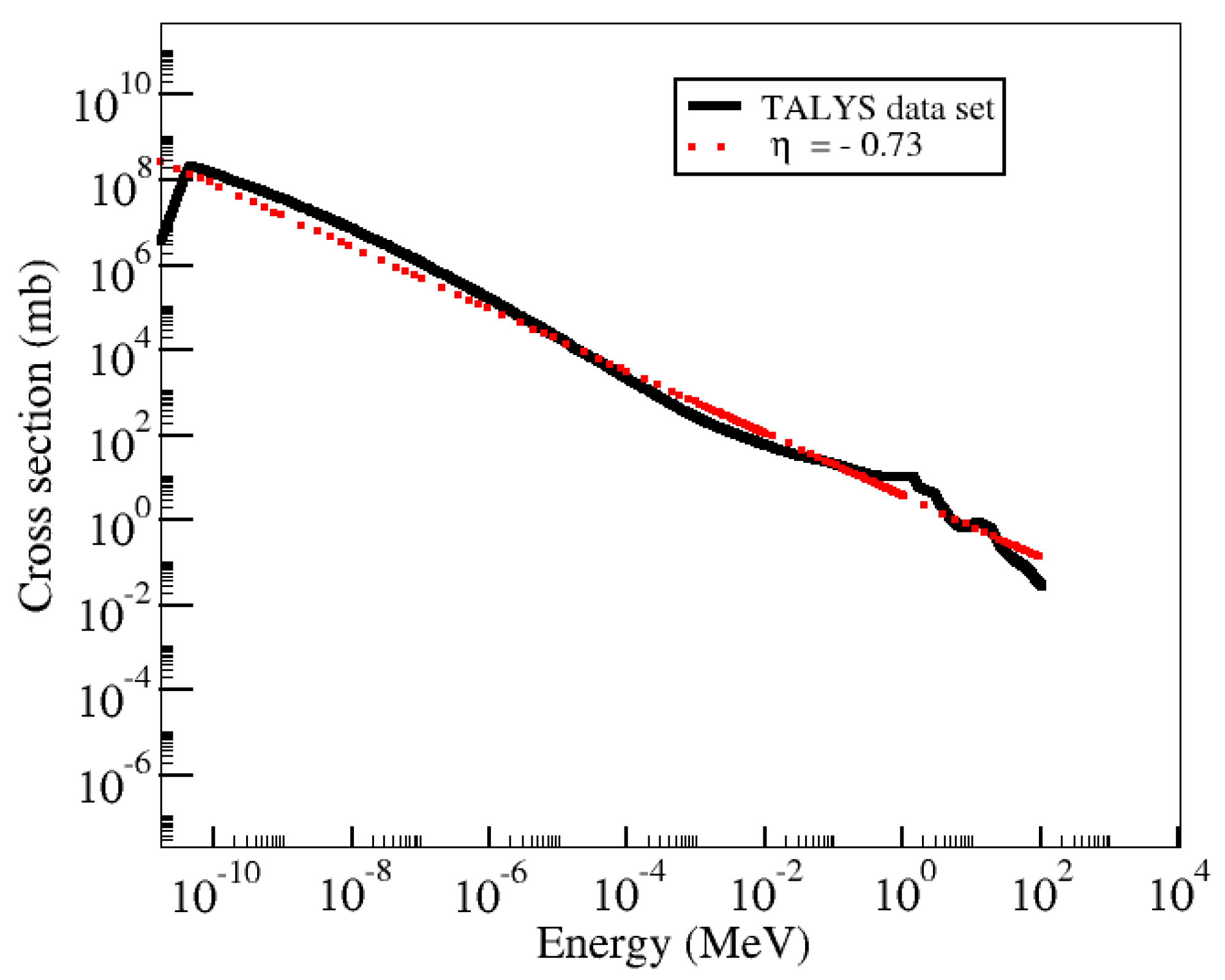
We study the behavior of R for Mg, Mg, and Ni using three different cross sections: (1) the results obtained directly with TALYS, (2) the power-law indexes and energy ranges as provided in Reference [6] (for the MgMg and MgMg reactions), and (3) our power-law fit to TALYS cross sections. Shternin et al. provided results for Mg and Mg, and therefore we use the same nuclei to compare our numerical results to theirs. However, Ni was not considered by these authors. We selected Ni as it provides an excellent example of how, even for a nucleus for which experimental data is available (and therefore TALYS cross sections more reliable) and for which a good fit to a power-law expression can be obtained, the integration over such an approximation still deviates from numerical results of the degeneracy correction R. Ni was also selected to allow easily reproducible results, as it is a common result of rp-process nucleosynthesis. Figure 1, Figure 2 and Figure 3 show the neutron capture cross sections for Mg, Mg, and Ni, respectively. The solid black lines are results from TALYS with the nuclear physics models discussed in the previous section. The dashed green lines are fits provided by Shternin et al., and the dotted red lines are our fits. We can see that for Mg and Ni, the power law follows the low-energy behavior of the cross sections well (and for large energies in the case of Ni). However, describing the cross section for Mg is more challenging.
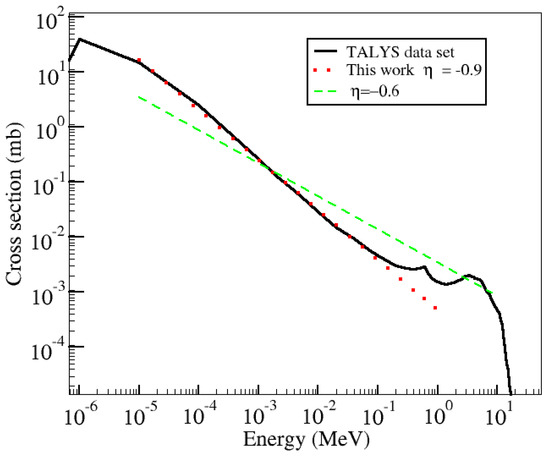
Figure 1.
Neutron capture cross section off Mg. The solid black line shows the full dataset obtained with TALYS 1.9 [10]. The dotted red line shows our fit to a power-law as in Equation (3). The dashed green line corresponds to a power index as discussed in Reference [6].
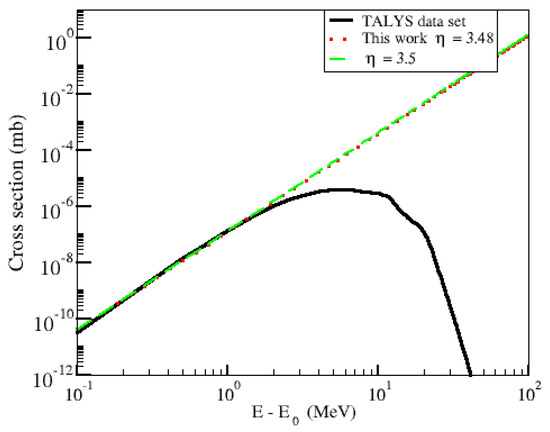
Figure 2.
The same as in Figure 1, except that neutrons are captured by Mg.
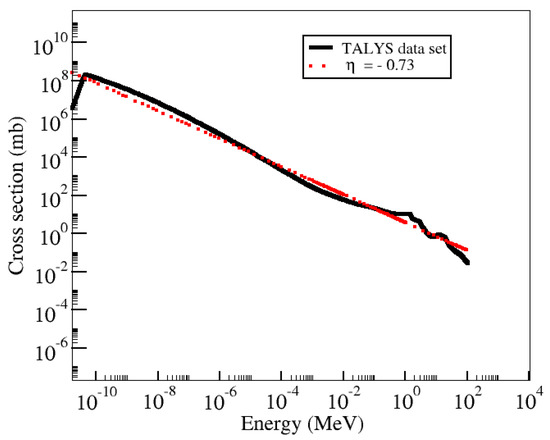
Figure 3.
Neutron capture cross section off Ni. The solid black line shows the full dataset obtained with TALYS 1.9 [10]. The dotted red line shows our fit to a power law as in Equation (3).
We note that for neutron-rich nuclei such as those presented in Figure 1 and Figure 2, there are uncertainties in their capture cross sections as a result of the use of theoretical nuclear physics inputs, for example, mass model, level densities, and so on. To explore the effect of a power-law approximation and possibly separate those uncertainties from the integration approach, we study the well-known isotope Ni. Figure 3 shows the cross section obtained with TALYS when a set of nuclear physics models are such that TALYS’s output agrees as much as possible to available experimental data in all channels. This set of adjusted nuclear model parameters is known as the “best” input, as described in the TALYS documentation [11]. The best input parameters are limited to some nuclei for which experimental data is available. Therefore there is no best input for neutron-rich nuclei such as Mg and Mg. In Figure 3, we also show a fit that follows Equation (3), with . It can be seen that this fit reproduces the neutron capture cross section for a large range of energies fairly well.
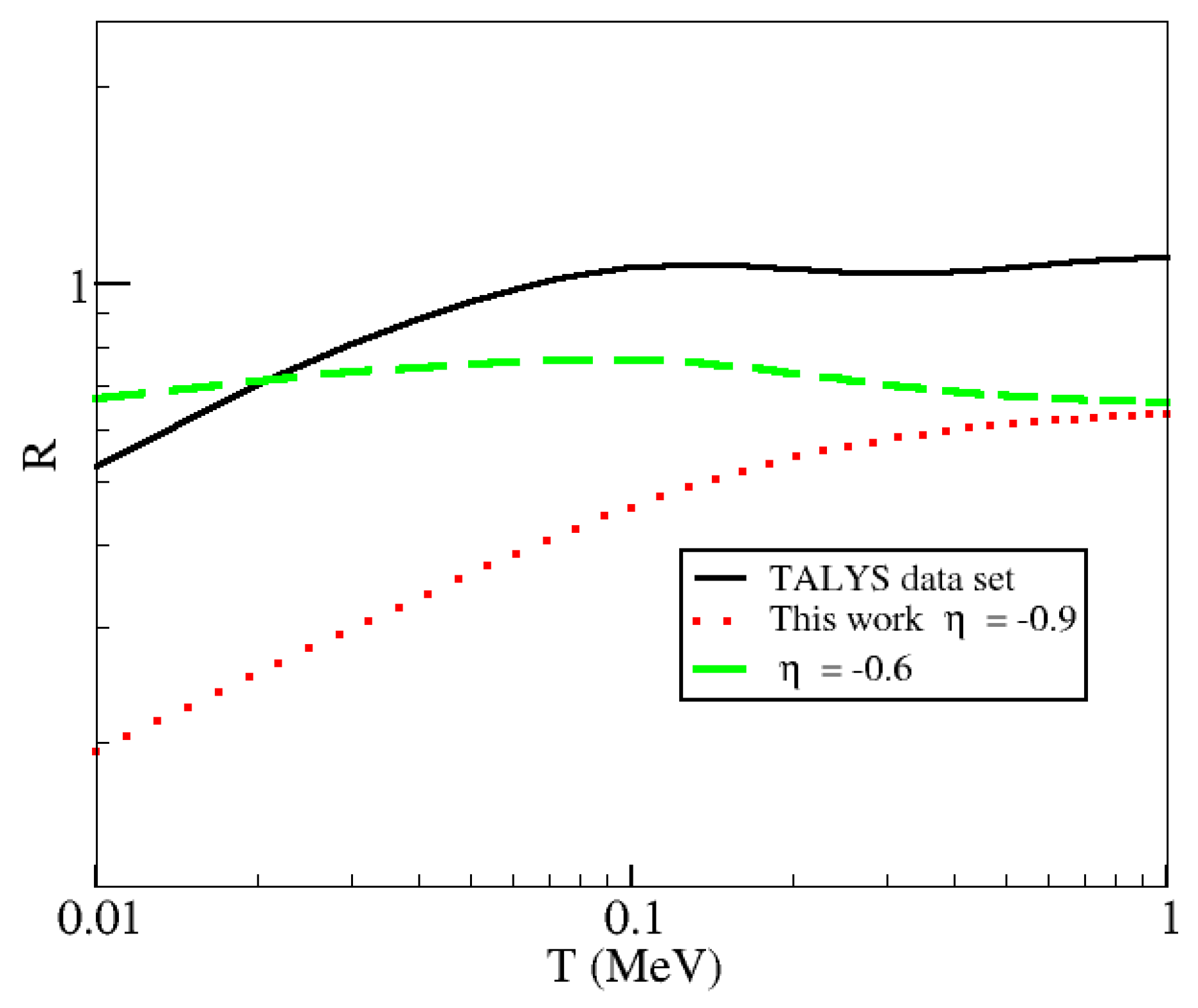
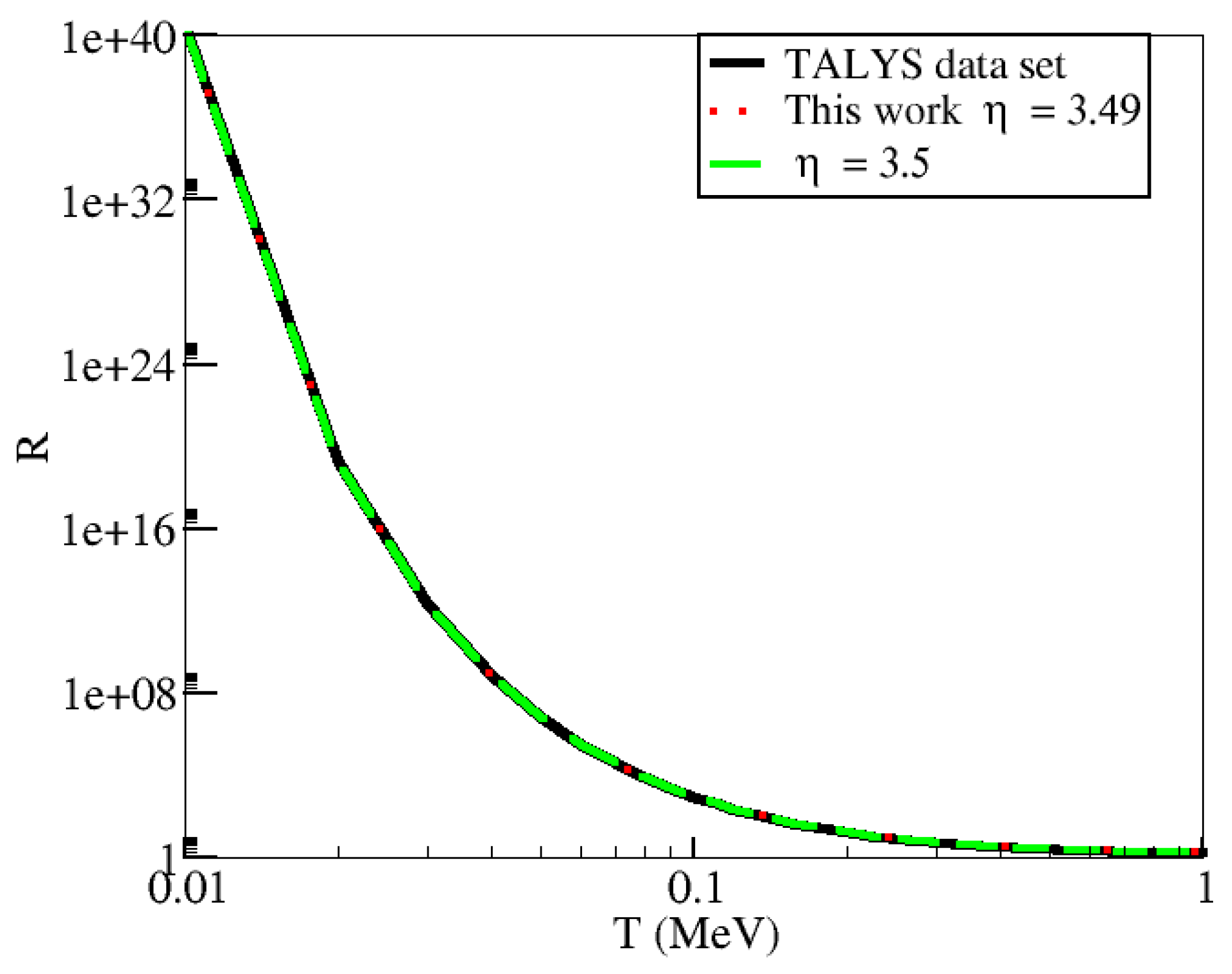
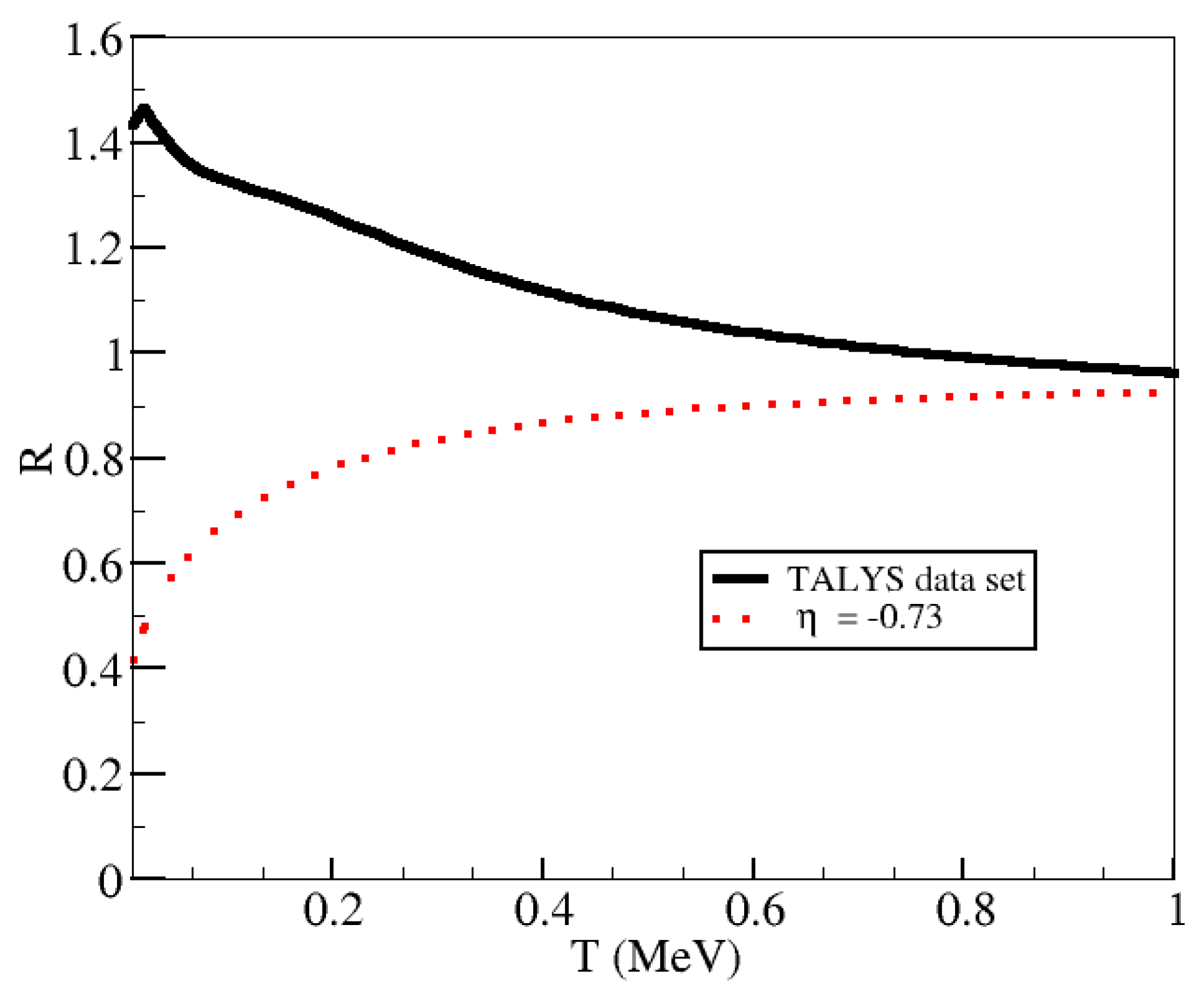
Figure 4, Figure 5 and Figure 6 show the results for R as a function of temperature, as defined in Equation (2), when the corresponding cross sections shown in Figure 1, Figure 2 and Figure 3 are integrated numerically. We have assumed a chemical potential MeV, a reasonable value for a free neutron gas within the crusts using a density of g/cm, and temperatures typical of the NS crust. These values are also in agreement with rp-process nucleosynthesis calculations [20].
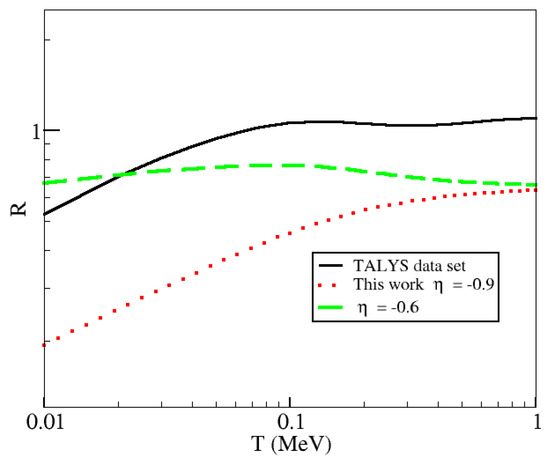
Figure 4.
R calculations for Mg. All integrals are done numerically with cross sections, as explained in the text.
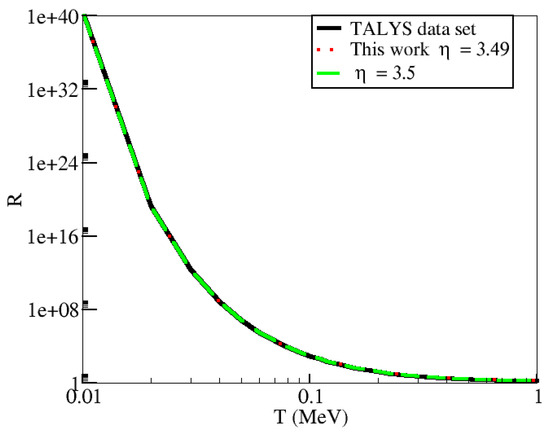
Figure 5.
The same as Figure 4 but for Mg.
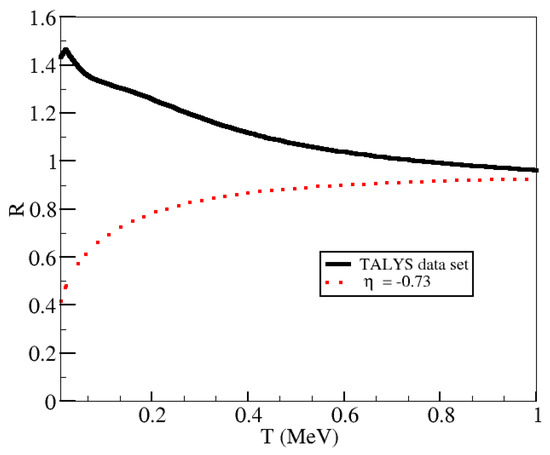
Figure 6.
The same as Figure 4 but for Ni.
5. Discussion and Conclusions
From Figure 1 and Figure 3, it can be seen that while the power-law approximations are good at predicting the linear regimes, the corresponding ratios R fluctuate. Both of these reactions are exothermic with a threshold energy . When integrating over a statistical distribution, the most critical values for R are those near the chemical potential, in our case MeV. If considering degenerate neutrons, there will be a few of them, but some will have energies greater than the chemical potential (for temperatures different from zero). Therefore, changes in the cross section (produced by, e.g., taking a different power index ) at those energies will change the absorption rates of degenerated neutrons more significantly compared to neutrons behaving classically, as, for those energies, the Maxwell–Boltzmann distribution predicts an almost zero occupancy number. In other words, the denominator in Equation (2) does not change much near MeV. We note that Shternin et al. also performed a numerical calculation for the Mg R value, with small deviation from our calculation. For example, their T = 0.01 MeV R value was 0.63, while our value was 0.58 at a chemical potential = 1 MeV. This deviation is likely a result of the different versions of TALYS used, and the results still appear to agree reasonably well. It is important to mention that their numerical and power-index results for this reaction disagreed as the neutron chemical potential was increased, as can be seen in Figure 4 of their paper.
The breakdown of the power-law approximation for exothermic reactions was pointed out in Reference [6]. As found by Shternin et al., in the case of the capture off Mg, given that , it is not possible to assure that the validity condition () for MeV holds (even for lower chemical potentials). However, one could argue that, for this neutron chemical potential, the changes in R are relatively small and degeneracy does not have a strong effect (as discussed in Reference [6]). The results for Ni bring an interesting point. This nucleus was not studied in Reference [6], and thus we do not present a power index from such work. Using the best input parameter set from TALYS, we calculated the cross section. As seen in Figure 3, a power-law index seems to agree well with the reaction code results. As in the previous case of Mg, we have again . However, now we could take a larger value for (2 MeV). In such a case, the power-law behavior should be valid in () for values of T less than 1 MeV. However, our results for R again show that slight changes in the cross section for values of energies around the neutron chemical potential can result in capture rates a factor of larger at very low temperatures. To what extent a factor of 2 affects the nucleosynthetic outcome or the energy liberation in the NS crust should be explored.
Capture on Mg corresponds to a non-zero threshold energy for the reaction with MeV. The validity of Equation (3) holds () in this case, as MeV and MeV for the temperatures studied here. The low-energy neutrons will not contribute to captures. This means that integrating over the power-law approximation and using the full set of the cross section from TALYS will give the same results for R, and therefore the enhancement in the values of R at low T correspond only to the degenerate character of neutrons in the crust instead of to an assumed approximation of the cross section, as was also discussed in Reference [6]. We anticipate that the power-law and numerical integration results will agree well for other endothermic reactions with large energy thresholds, as there would not be contribution from low-energy degenerate neutrons, while we expect larger discrepancies, between the two approaches, for nuclei capturing neutrons at low energies via exothermic reactions.
We find numerical corrections to capture rates of degenerate neutrons off Mg, Mg, and Ni. We do this by numerically integrating the capture cross section over Maxwell–Boltzmann and Fermi–Dirac distributions. We compare the changes, in these corrections, that occur by choosing a power-law approximation of the cross section and compare to the values that are obtained by directly using cross sections from the reaction code TALYS. We find that for the threshold reaction MgMg considered here, changes in the cross section have no influence on the correction to the degenerate rates (as was also found by Shternin et al.) at the temperature and chemical potential studied. In such a case, for large energy thresholds, a power-law behavior can be adequate and analytical correction of R is advantageous.
We find that for the exothermic reactions studied here, the power-law approximation breaks down (as also found in Reference [6]) for values of the neutron chemical potential relevant to the NS crust. However, our results suggest that finding a power-law index and determining the range of validity of the power-law behavior is not a trivial matter, and therefore we suggest a direct numerical integration of the cross section calculated from reaction codes to exclude uncertainties due to the power index.
The impact of neutron degeneracy on accreting NSs and the triggering of X-ray bursts, using a numerical integration such as that proposed here, have not yet been investigated. If very neutron rich nuclei (such as Mg) are present in the crust of NSs, the large value of R found here and in Reference [6] for Mg(n, )Mg (large corrections due to neutron degeneracy were also found in our previous work [7]) would affect the energy budget and the production of heavier nuclei in the crust. How this energy is consumed or transported in the star can change the detonation of X-ray bursts. On the other hand, our results also show that for some reactions (such as Mg(n, )Mg), R can achieve values of less than 1, and therefore the gamma-ray production will decrease compared to a classical statistical treatment of the neutrons in the crust. The study of the net effect requires a network calculation of the abundances of nuclei produced during the rp-process and will also depend on how deep in the crust the ashes are deposited. In this work, we propose a reduction in one of the many uncertainties involved in this kind of study.
Author Contributions
Authors contributed equally to this work.
Funding
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC).
Acknowledgments
L.C. thanks Hendrik Schatz for useful discussons.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Strohmayer, T.; Bildsten, L. Compact Stellar X-ray Sources; Lewin, W., van der Klis, M., Eds.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Liu, Q.Z.; van Paradijs, J.; Heuvel, E.P.J.V.D. A catalogue of low-mass X-ray binaries in the Galaxy, LMC, and SMC. Astron. Astrophys. 2007, 469, 807–810. [Google Scholar] [CrossRef]
- Schatz, H.; Bildsten, L.; Cumming, A.; Wiescher, M. The rp process ashes from stable nuclear burning on an accreting neutron star. Astrophys. J. 1999, 524, 1014. [Google Scholar] [CrossRef]
- Schatz, H.; Aprahamian, A.; Görres, J.; Wiescher, M.; Rauscher, T.; Rembges, J.F.; Thielemann, F.-K.; Pfeiffer, B.; Möller, P.; Kratz, K.-L.; et al. rp-process nucleosynthesis at extreme temperature and density conditions. Phys. Rep. 1998, 294, 167–263. [Google Scholar] [CrossRef]
- Gupta, S.; Brown, E.F.; Schatz, H.; Moeller, P.; Kratz, K.L. Heating in the Accreted Neutron Star Ocean: Implications for Superburst Ignition. Astrophys. J. 2007, 662, 1188. [Google Scholar] [CrossRef]
- Shternin, P.S.; Beard, M.; Wiescher, M.; Yakovlev, D.G. Neutron degeneracy and plasma physics effects on radiative neutron captures in neutron star crust. Phys. Rev. C 2012, 86, 015808. [Google Scholar] [CrossRef]
- Knight, B.; Graham, L.; Caballero, O.L. Weak processes in astrophysical nucleosynthesis. J. Phys. Conf. Ser. 2018, 1078, 012012. [Google Scholar] [CrossRef]
- Arlandini, C.; Kaeppeler, F.; Wisshak, K.; Gallino, R.; Lugaro, M.; Busso, M.; Straniero, O. Neutron capture in low mass asymptotic giant branch stars: Cross-sections and abundance signatures. Astrophys. J. 1999, 525, 886. [Google Scholar] [CrossRef]
- Arnould, M.; Goriely, S.; Takahashi, K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys. Rep. 2007, 450, 97–213. [Google Scholar] [CrossRef]
- Koning, A.J.; Hilaire, S.; Duijvestijn, M.C. TALYS-1.0. In Proceedings of the International Conference on Nuclear Data for Science and Technology, Nice, France, 22–27 April 2007; Bersillon, O., Gunsing, F., Bauge, E., Jacqmin, R., Leray, S., Eds.; EDP Sciences: Les Ulis, France, 2008. [Google Scholar]
- A Nuclear Reaction Program. Available online: ftp://ftp.nrg.eu/pub/www/talys/talys1.9.pdf (accessed on 17 January 2019).
- Hauser, W.; Feshbach, H. The Inelastic Scattering of Neutrons. Phys. Rev. 1952, 87, 366. [Google Scholar] [CrossRef]
- Koning, A.J.; Delaroche, J.P. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl. Phys. A 2003, 713, 231–310. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov nuclear mass formulas: Crossing the 0.6 MeV threshold with microscopically deduced pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef] [PubMed]
- Goriely, S.; Tondeur, F.; Pearson, J.M. A Hartree-Fock Nuclear Mass Table. Atomic Data Nucl. Data Tables 2001, 77, 311–381. [Google Scholar] [CrossRef]
- Capote, R.; Herman, M.; Obložinský, P.; Young, P.G.; Goriely, S.; Belgya, T.; Ignatyuk, A.V.; Koning, A.J.; Hilaire, S.; Plujko, V.A.; et al. RIPL—Reference Input Parameter Library for Calculation of Nuclear Reactions and Nuclear Data Evaluations. Nucl. Data Sheets 2009, 110, 3107–3214. [Google Scholar] [CrossRef]
- McFadden, L.; Satchler, G.R. Optical-model analysis of the scattering of 24.7 MeV alpha particles. Nucl. Phys. 1966, 84, 177–200. [Google Scholar] [CrossRef]
- Tepel, J.W.; Hofmann, H.M.; Weidenmüller, H.A. Hauser-Feshbach formulas for medium and strong absorption. Phys. Lett. B 1974, 49, 1–4. [Google Scholar] [CrossRef]
- Hofmann, H.M.; Richert, J.; Tepel, J.W.; Weidenmüller, H.A. Direct reactions and Hauser-Feshbach theory. Ann. Phys. 1975, 90, 403–437. [Google Scholar] [CrossRef]
- Lau, R.; Beard, M.; Gupta, S.S.; Schatz, H.; Afanasjev, A.V.; Brown, E.F.; Deibel, A.; Gasques, L.R.; Hitt, G.W.; Hix, W.R.; et al. Nuclear Reactions in the Crusts of Accreting Neutron Stars. Astrophys. J. 2018, 859, 62. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).