Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars
Abstract
1. Introduction
2. Hybrid Star EoS with a Third Family and High-Mass Twins
3. Mixed Phase Constructions
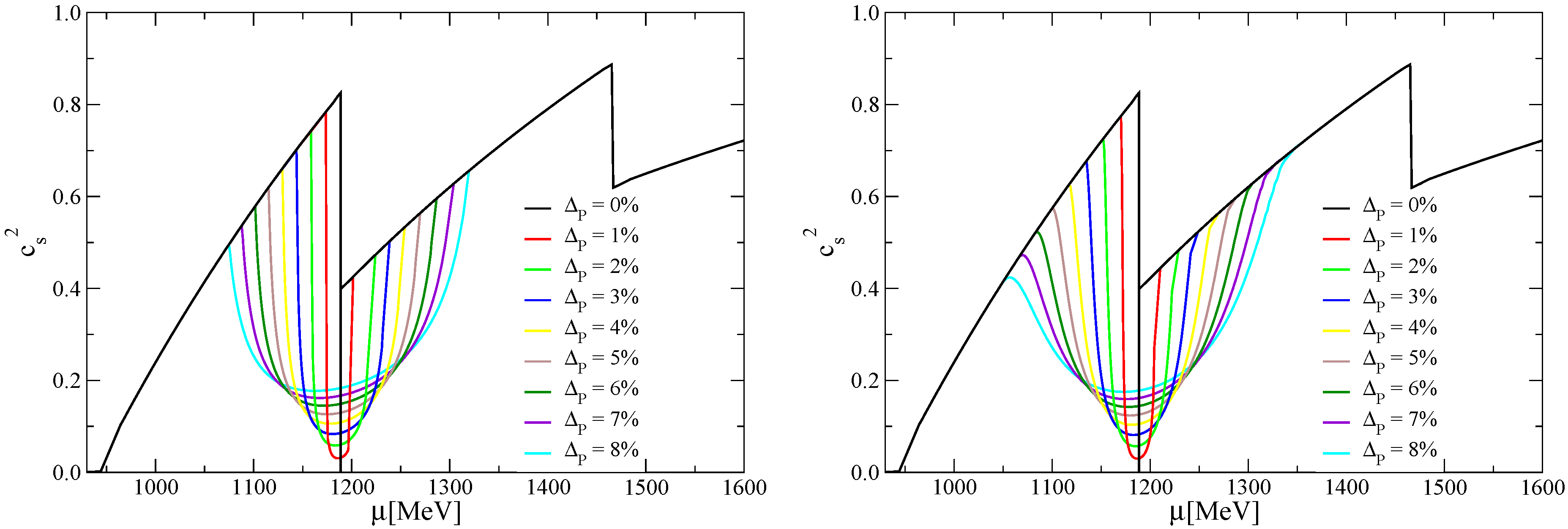
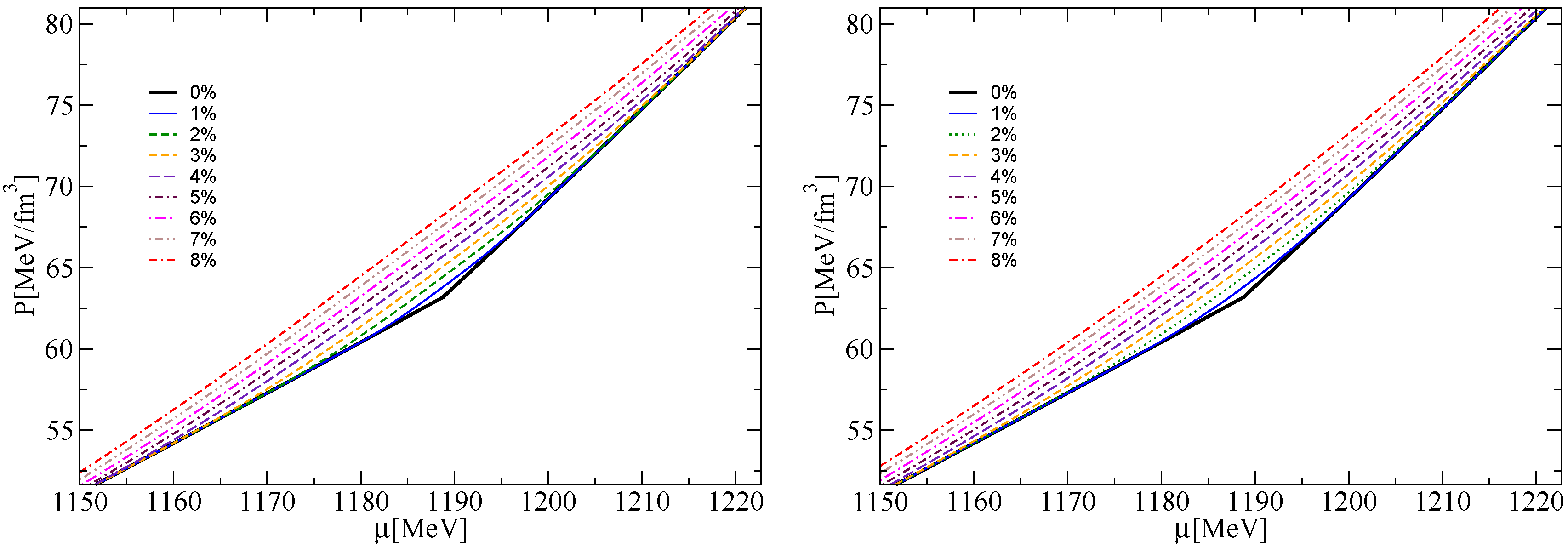
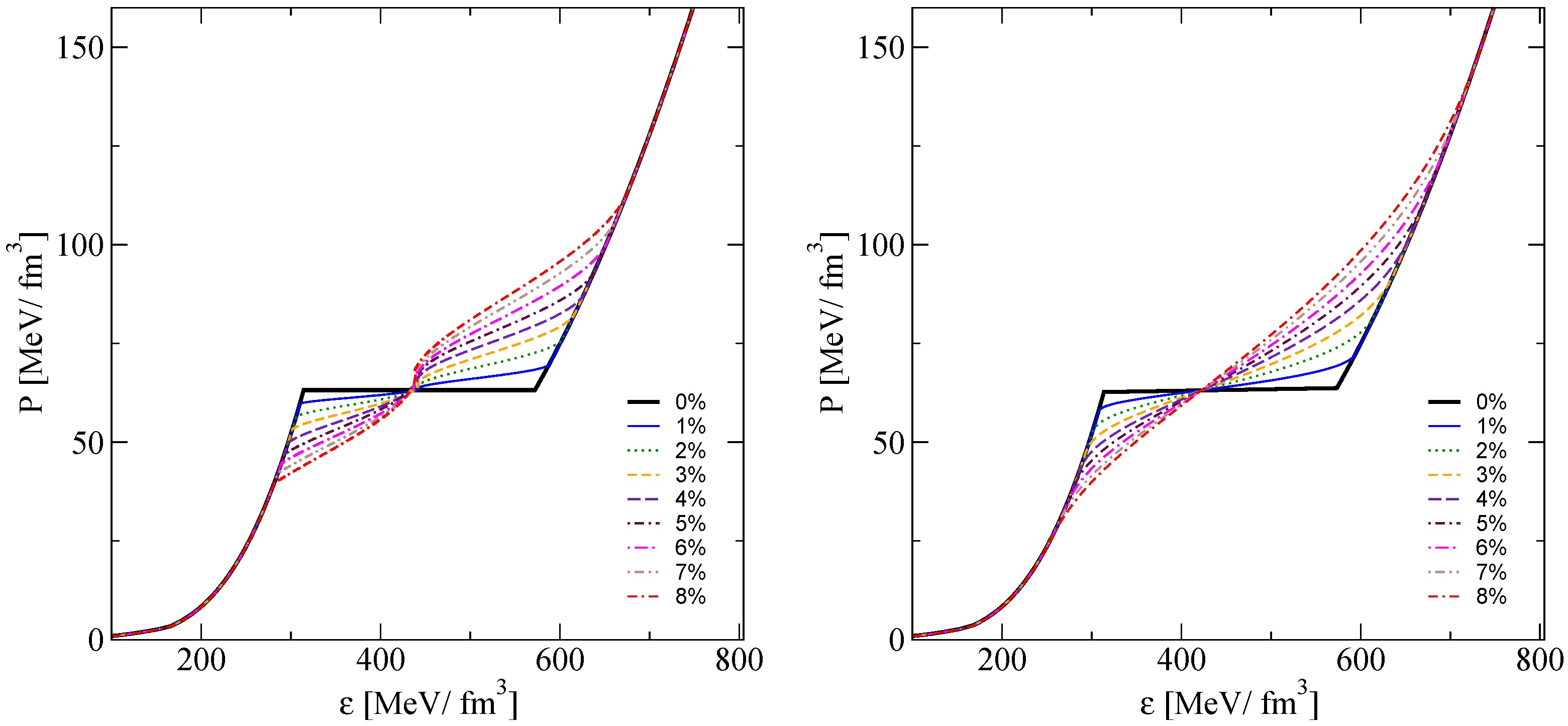
3.1. The Replacement Interpolation Method (RIM)
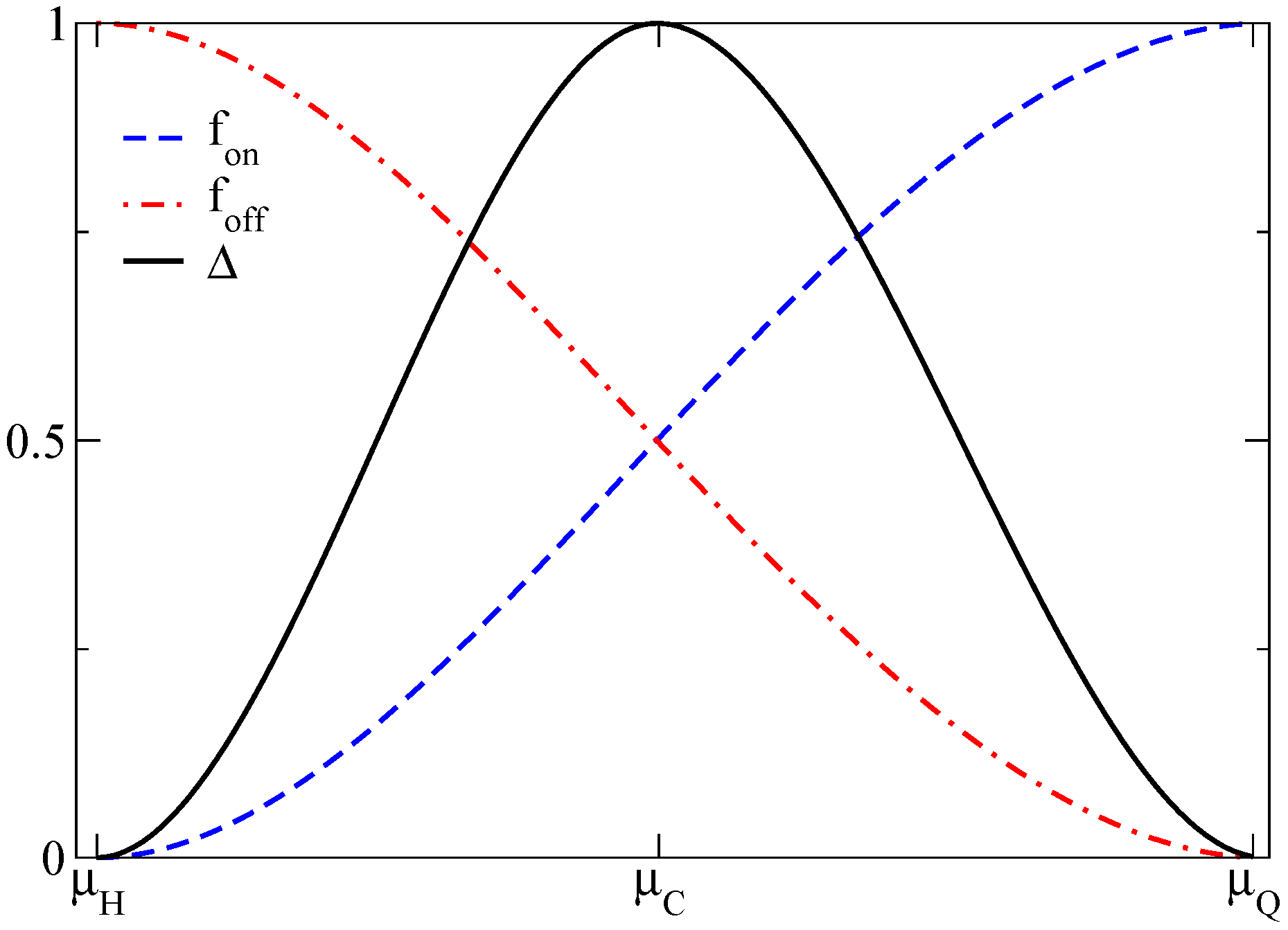
3.2. The Mixing Interpolation Method (MIM)
4. Results
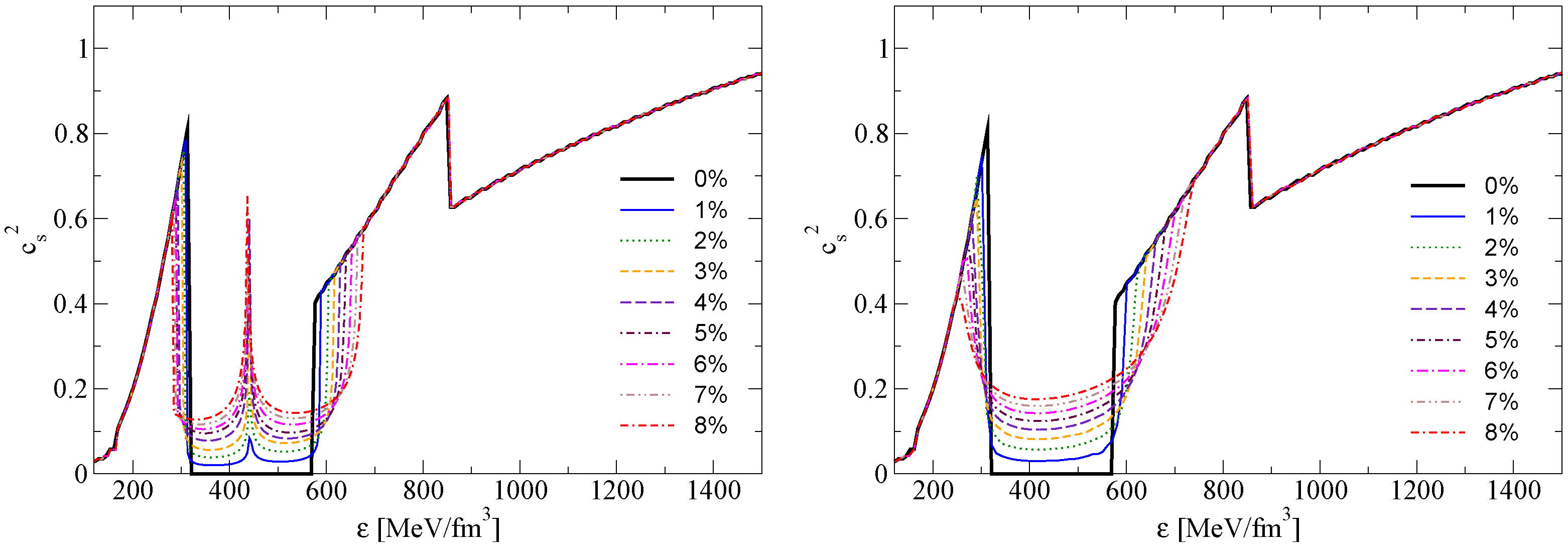
4.1. Hybrid Star EoS with Mixed Phases
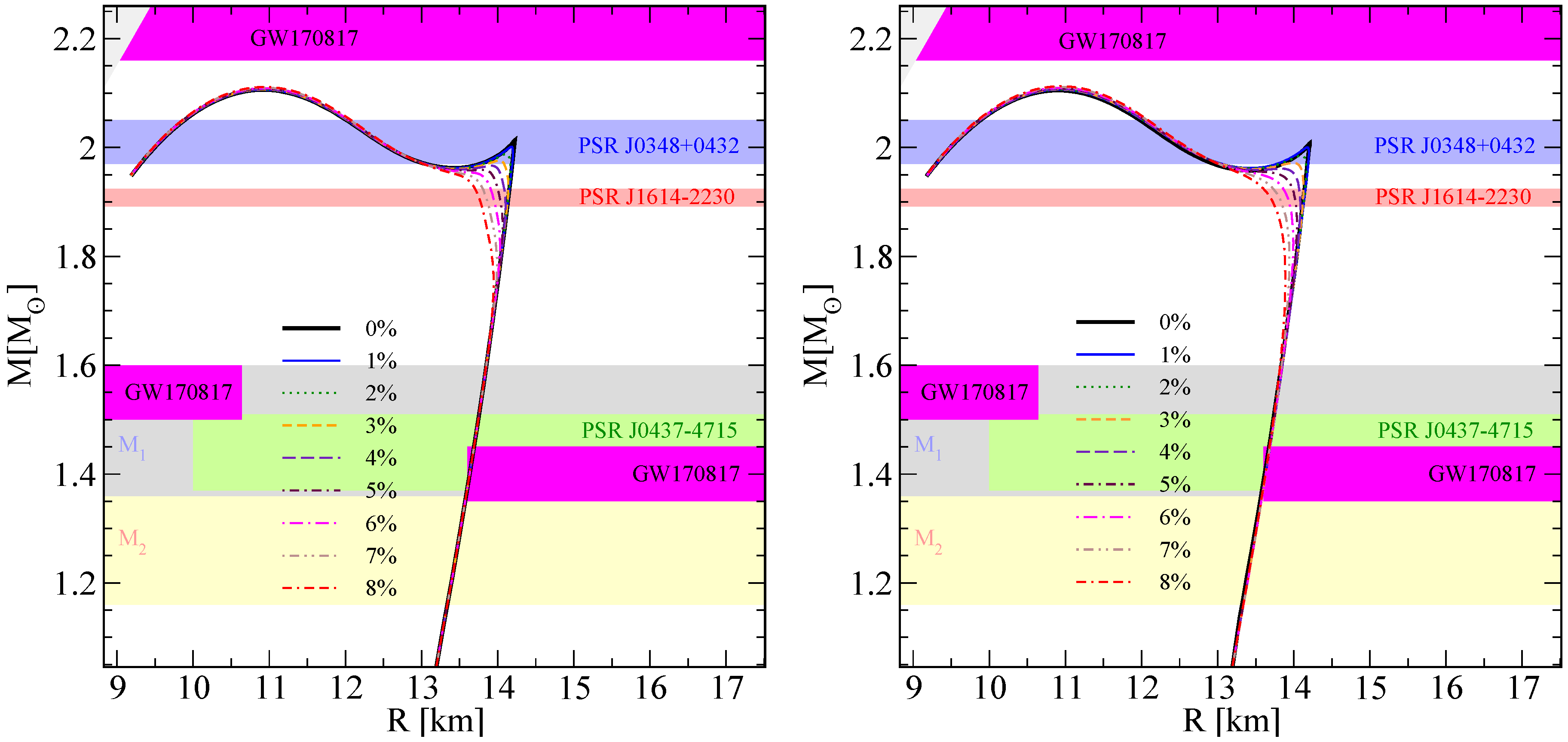
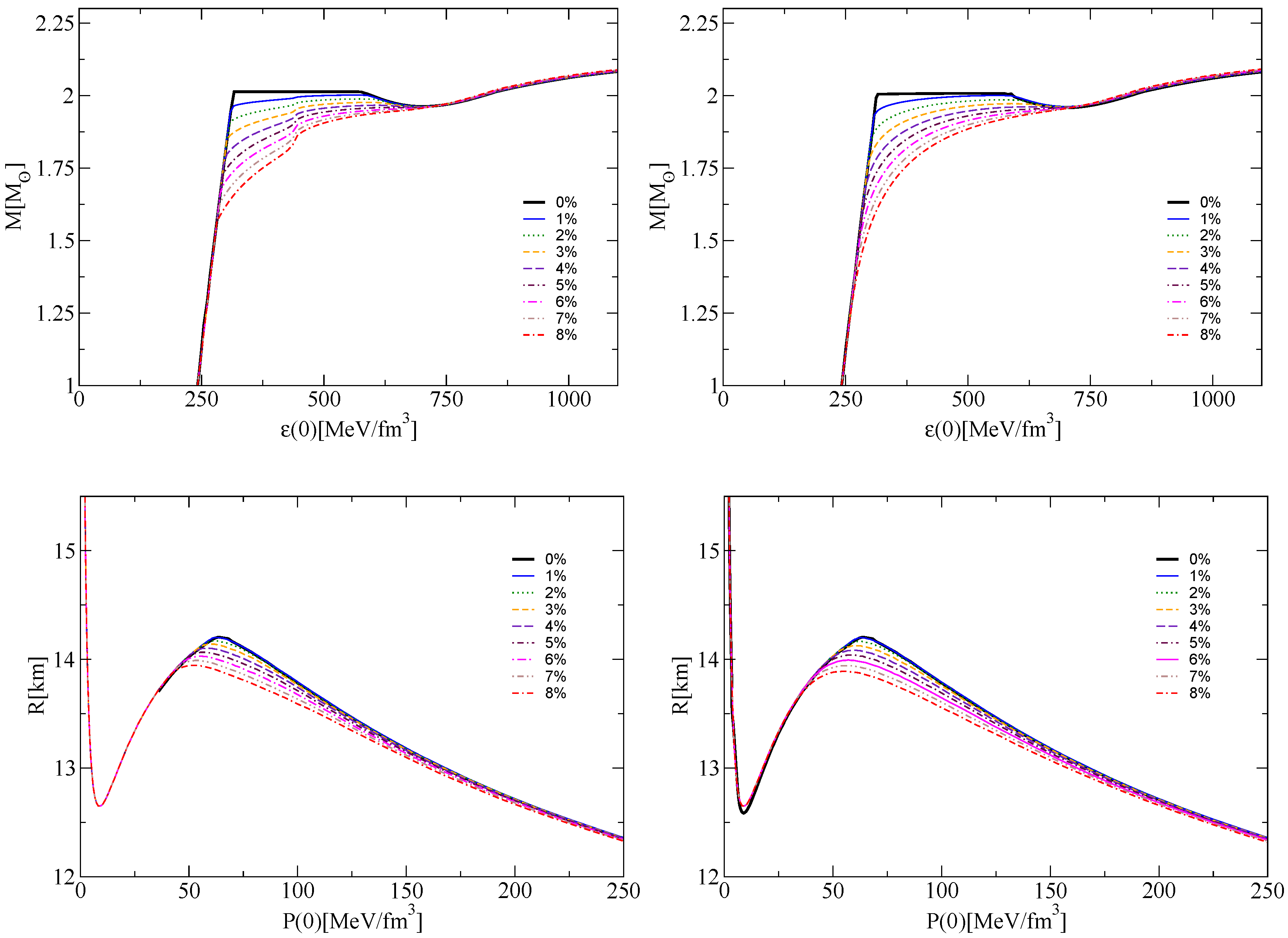
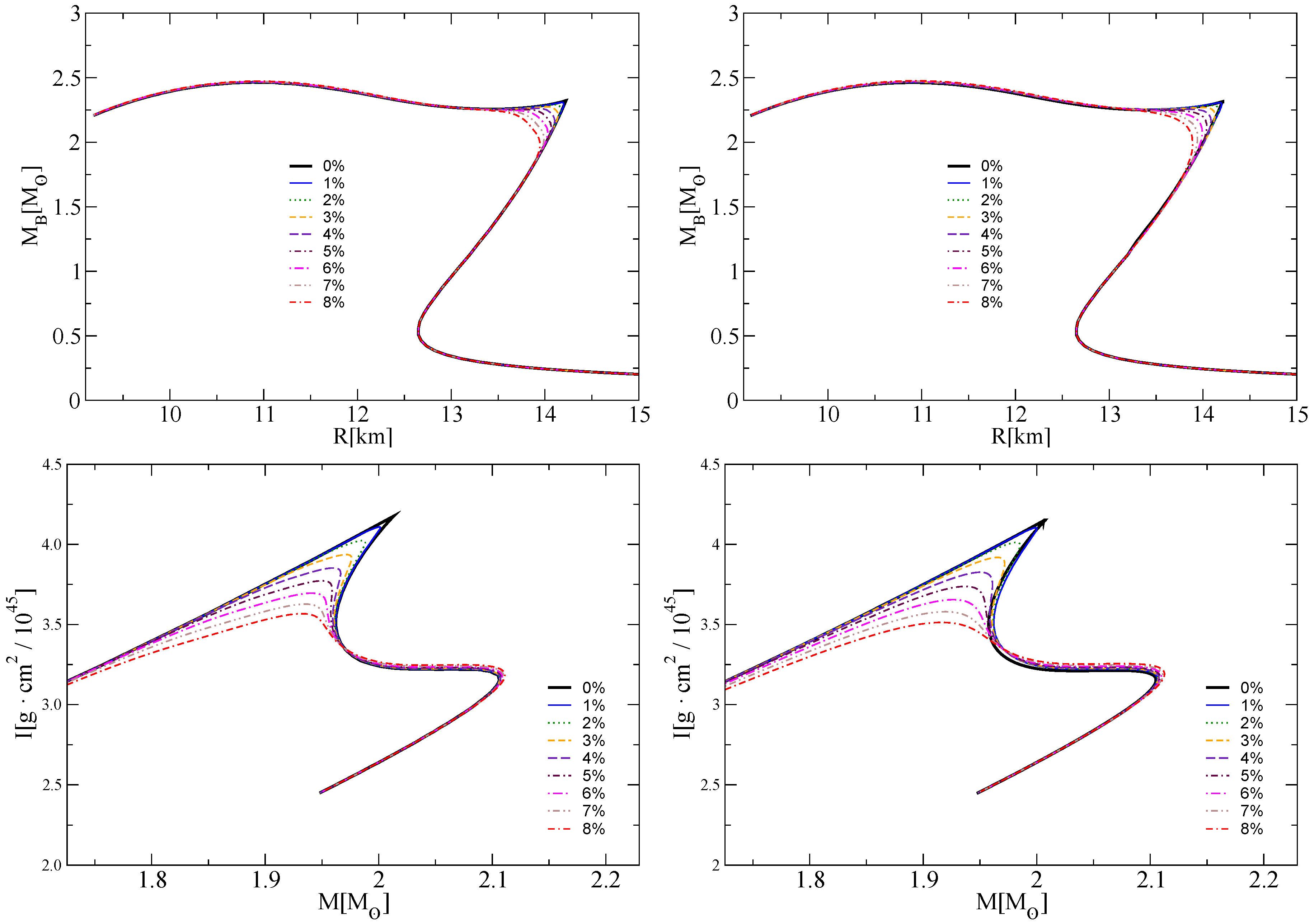
4.2. Compact Star Sequences
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. 2018, L25, 852. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, 88, 083013. [Google Scholar] [CrossRef]
- Kojo, T. Phenomenological neutron star equations of state: 3-window modeling of QCD matter. Eur. Phys. J. A 2016, 52, 51. [Google Scholar] [CrossRef]
- Glendenning, N.K. First order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 1274–1287. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066. [Google Scholar] [CrossRef]
- Voskresensky, D.N.; Yasuhira, M.; Tatsumi, T. Charge screening at first order phase transitions and hadron quark mixed phase. Nucl. Phys. A 2003, 723, 291–339. [Google Scholar] [CrossRef]
- Maruyama, T.; Chiba, S.; Schulze, H.J.; Tatsumi, T. Quark deconfinement transition in hyperonic matter. Phys. Lett. B 2008, 659, 192–196. [Google Scholar] [CrossRef]
- Watanabe, G.; Sato, K.; Yasuoka, K.; Ebisuzaki, T. Structure of cold nuclear matter at subnuclear densities by quantum molecular dynamics. Phys. Rev. C 2003, 68, 035806. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Perez-Garcia, M.A.; Berry, D.K.; Piekarewicz, J. Dynamical response of the nuclear ‘pasta’ in neutron star crusts. Phys. Rev. C 2005, 72, 035801. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Cumming, A.; Schneider, A.S. Disordered nuclear pasta, magnetic field decay, and crust cooling in neutron stars. Phys. Rev. Lett. 20015, 114, 031102. [Google Scholar] [CrossRef] [PubMed]
- Newton, W.G.; Stone, J.R. Modeling nuclear ‘pasta’ and the transition to uniform nuclear matter with the D-3 Skyrme-Hartree-Fock method at finite temperature: Core-collapse supernovae. Phys. Rev. C 2009, 79, 055801. [Google Scholar] [CrossRef]
- Yasutake, N.; Lastowiecki, R.; Benic, S.; Blaschke, D.; Maruyama, T.; Tatsumi, T. Finite-size effects at the hadron-quark transition and heavy hybrid stars. Phys. Rev. C 2014, 89, 065803. [Google Scholar] [CrossRef]
- Maruyama, T.; Chiba, S.; Schulze, H.J.; Tatsumi, T. Hadron-quark mixed phase in hyperon stars. Phys. Rev. D 2007, 76, 123015. [Google Scholar] [CrossRef]
- Maslov, K.; Yasutake, N.; Ayriyan, A.; Blaschke, D.; Grigorian, H.; Maruyama, T.; Tatsumi, T.; Voskresensky, D.N. Hybrid Equation of State with Pasta Phases and Third Family of Compact Stars. Unpublished work. 2018. [Google Scholar]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron–quark crossover and massive hybrid stars. Prog. Theor. Exp. Phys. 2013, 7, 073D01. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D. Mixed phase effects on high-mass twin stars. Phys. Part. Nucl. 2015, 46, 846–848. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Blaschke, D.; Typel, S. Mixed phase within the multi-polytrope approach to high-mass twins. Astron. Nachr. 2017, 338, 1048–1051. [Google Scholar] [CrossRef]
- Ayriyan, A.; Grigorian, H. Model of the Phase Transition Mimicking the Pasta Phase in Cold and Dense Quark-Hadron Matter. Eur. Phys. J. Web Conf. 2018, 173, 03003. [Google Scholar] [CrossRef]
- Ayriyan, A.; Bastian, N.-U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. Robustness of third family solutions for hybrid stars against mixed phase effects. Phys. Rev. C 2018, 97, 045802. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Blaschke, D. A mixing interpolation method to mimic pasta phases in compact star matter. arXiv, 2018; arXiv:1807.03258. [Google Scholar]
- Kojo, T.; Powell, P.D.; Song, Y.; Baym, G. Phenomenological QCD equation of state for massive neutron stars. Phys. Rev. D 2015, 91, 045003. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. 2017, 850, L34. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics—I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D. Supporting the existence of the QCD critical point by compact star observations. In Proceedings of the 9th International Workshop on Critical Point and Onset of Deconfinement (CPOD2014), Bielefeld, Germany, 17–21 November 2014. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Benic, S.; Blaschke, D.; Han, S.; Typel, S. Neutron star mass limit at 2 M⊙ supports the existence of a CEP. Eur. Phys. J. A 2016, 52, 232. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, K.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Raithel, C.A.; Ozel, F.; Psaltis, D. From Neutron Star Observables to the Equation of State: An Optimal Parametrization. Astrophys. J. 2016, 831, 44. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D.B. High-mass twin stars with a multipolytrope equation of state. Phys. Rev. C 2017, 96, 045809. [Google Scholar] [CrossRef]
- Seidov, Z.F. The Stability of a Star with a Phase Change in General Relativity Theory. Sov. Astron. Lett. 1971, 15, 347–348. [Google Scholar]
- Schaeffer, R.; Zdunik, L.; Haensel, P. Phase transitions in stellar cores. I-Equilibrium configurations. Astron. Astrophys. 1983, 126, 121–145. [Google Scholar]
- Zdunik, J.L.; Haensel, P.; Schaeffer, R. Phase transitions in stellar cores. II-Equilibrium configurations in general relativity. Astron. Astrophys. 1987, 172, 95–110. [Google Scholar]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crowter, K. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Bogdanov, S.; Cordes, J.; Gendreau, K.; Lai, D.; Lattimer, J.; Link, B.; Lommen, A.; Miller, C.; Ray, P.; et al. X-ray Timing of Neutron Stars, Astrophysical Probes of Extreme Physics. arXiv, 2009; arXiv:0902.3264. [Google Scholar]
- Ravenhall, D.G.; Pethick, C.J. Neutron star moments of inertia. Astrophys. J. 1994, 424, 846–851. [Google Scholar] [CrossRef]
- Chubarian, E.; Grigorian, H.; Poghosyan, G.S.; Blaschke, D. Deconfinement phase transition in rotating nonspherical compact stars. Astron. Astrophys. 2000, 357, 968. [Google Scholar]
- Zdunik, J.L.; Bejger, M.; Haensel, P.; Gourgoulhon, E. Phase transitions in rotating neutron stars cores: Back bending, stability, corequakes and pulsar timing. Astron. Astrophys. 2006, 450, 747–758. [Google Scholar] [CrossRef]
- Bejger, M.; Blaschke, D.; Haensel, P.; Zdunik, J.L.; Fortin, M. Consequences of a strong phase transition in the dense matter equation of state for the rotational evolution of neutron stars. Astron. Astrophys. 2017, 600, A39. [Google Scholar] [CrossRef]
| 1. | The word “crossover” is used generically for a transition that does not proceed like in a Maxwell construction at a strictly constant pressure with a jump in (energy) density, but rather by a varying pressure in the transition region. It can thus be a generic crossover transition like in ferromagnetic systens under external magnetic field, but also a first order transition for several globally conserved charges which proceeds via formation of structures of different shapes (pasta phases). |

| ACB | i | |||||
|---|---|---|---|---|---|---|
| [MeV/fm3] | [1/fm3] | [MeV] | [M⊙] | |||
| 4 | 1 | 4.921 | 2.1680 | 0.1650 | 939.56 | 2.01 |
| 2 | 0.0 | 63.178 | 0.3174 | 939.56 | – | |
| 3 | 4.000 | 0.5075 | 0.5344 | 1031.2 | 1.96 | |
| 4 | 2.800 | 3.2401 | 0.7500 | 958.55 | 2.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abgaryan, V.; Alvarez-Castillo, D.; Ayriyan, A.; Blaschke, D.; Grigorian, H. Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars. Universe 2018, 4, 94. https://doi.org/10.3390/universe4090094
Abgaryan V, Alvarez-Castillo D, Ayriyan A, Blaschke D, Grigorian H. Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars. Universe. 2018; 4(9):94. https://doi.org/10.3390/universe4090094
Chicago/Turabian StyleAbgaryan, Vahagn, David Alvarez-Castillo, Alexander Ayriyan, David Blaschke, and Hovik Grigorian. 2018. "Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars" Universe 4, no. 9: 94. https://doi.org/10.3390/universe4090094
APA StyleAbgaryan, V., Alvarez-Castillo, D., Ayriyan, A., Blaschke, D., & Grigorian, H. (2018). Two Novel Approaches to the Hadron-Quark Mixed Phase in Compact Stars. Universe, 4(9), 94. https://doi.org/10.3390/universe4090094







