The High-Density Symmetry Energy in Heavy-Ion Collisions and Compact Stars
Abstract
1. Introduction
2. Theoretical Considerations
2.1. Overview of Transport Theories
2.2. Fluctuations
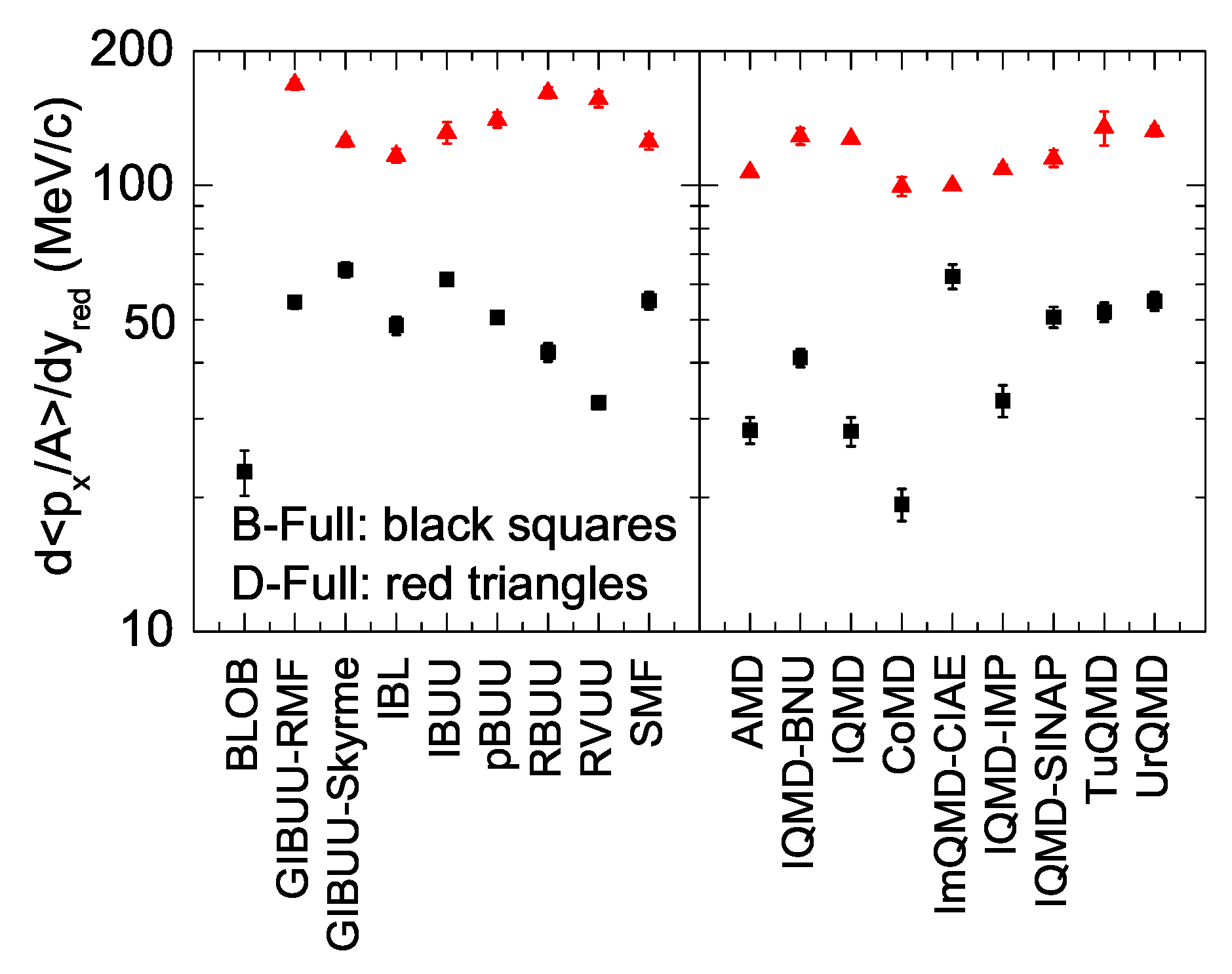
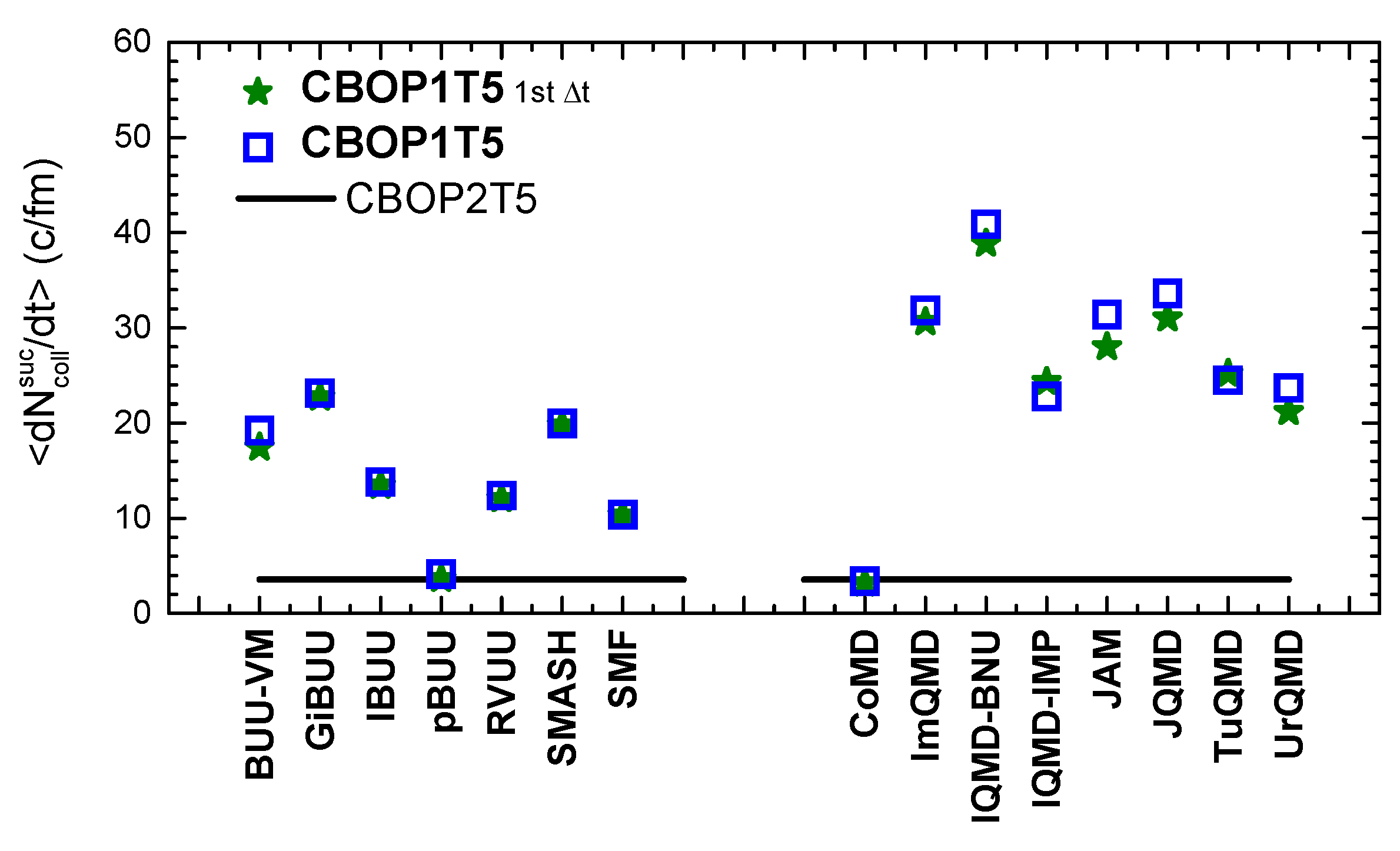
2.3. Code Comparison
3. Symmetry Energy in Heavy-Ion Collisions
3.1. Overview
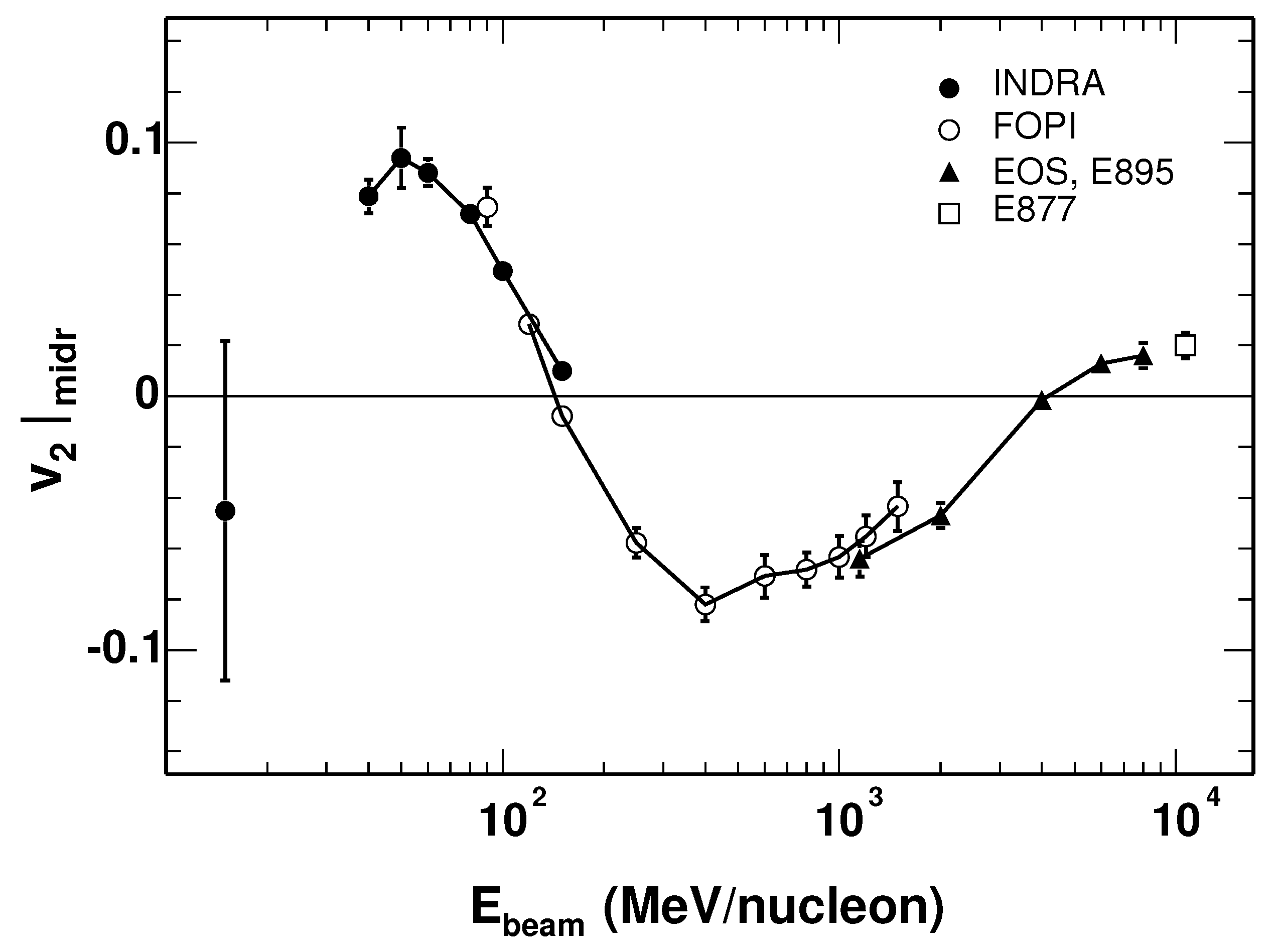
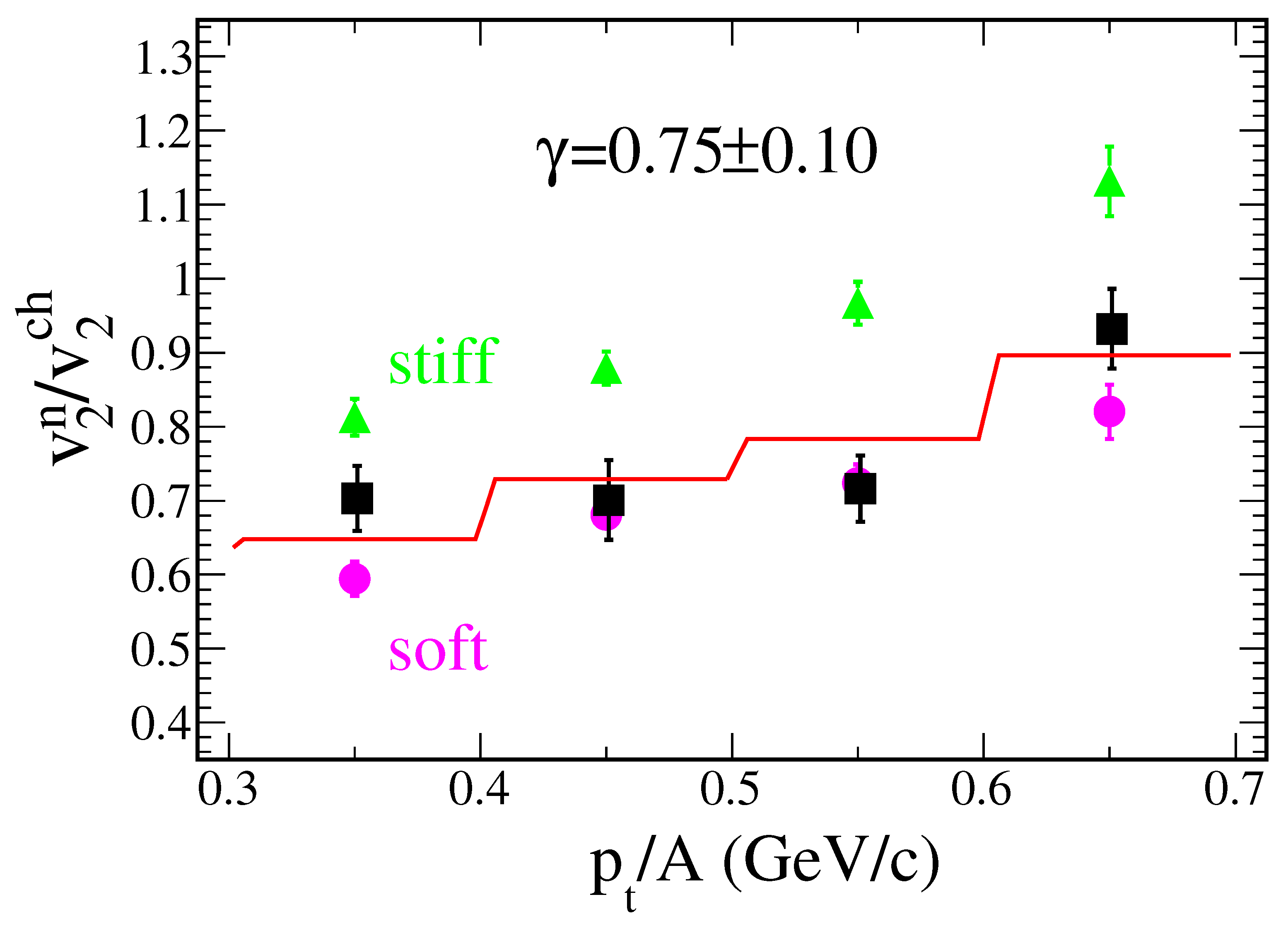
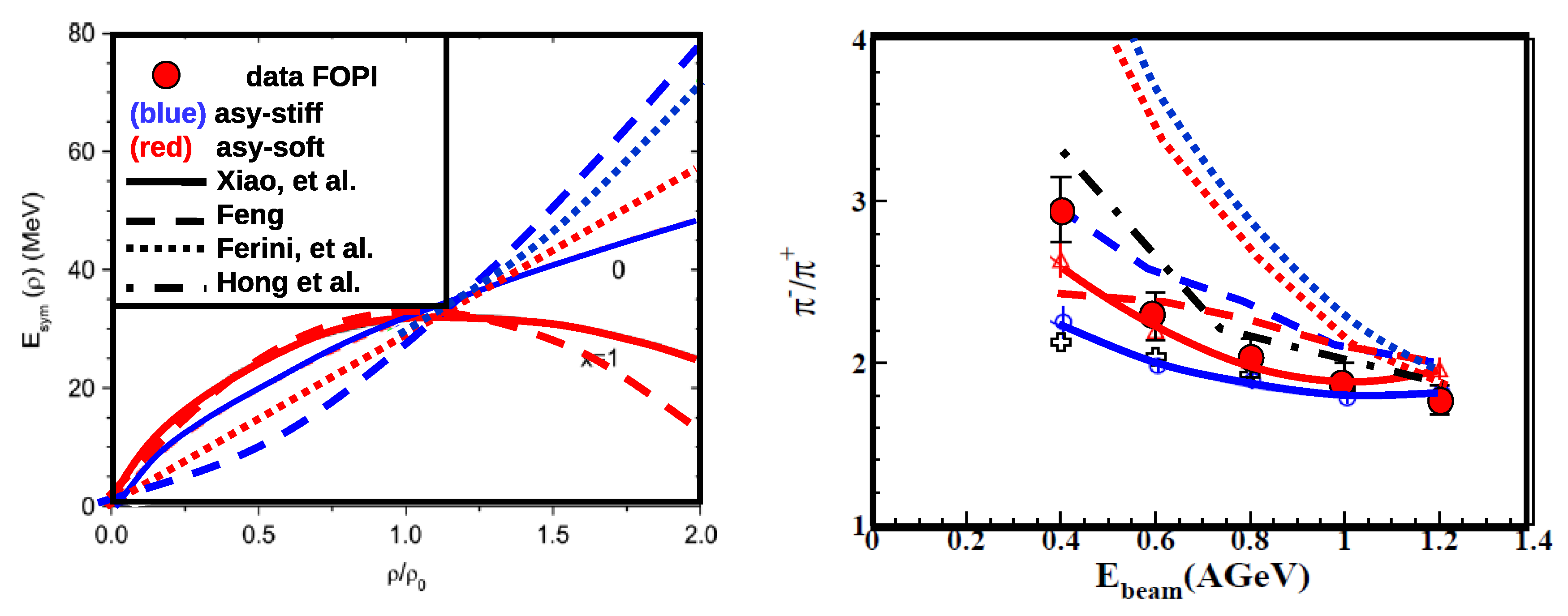
3.2. Collective Flow
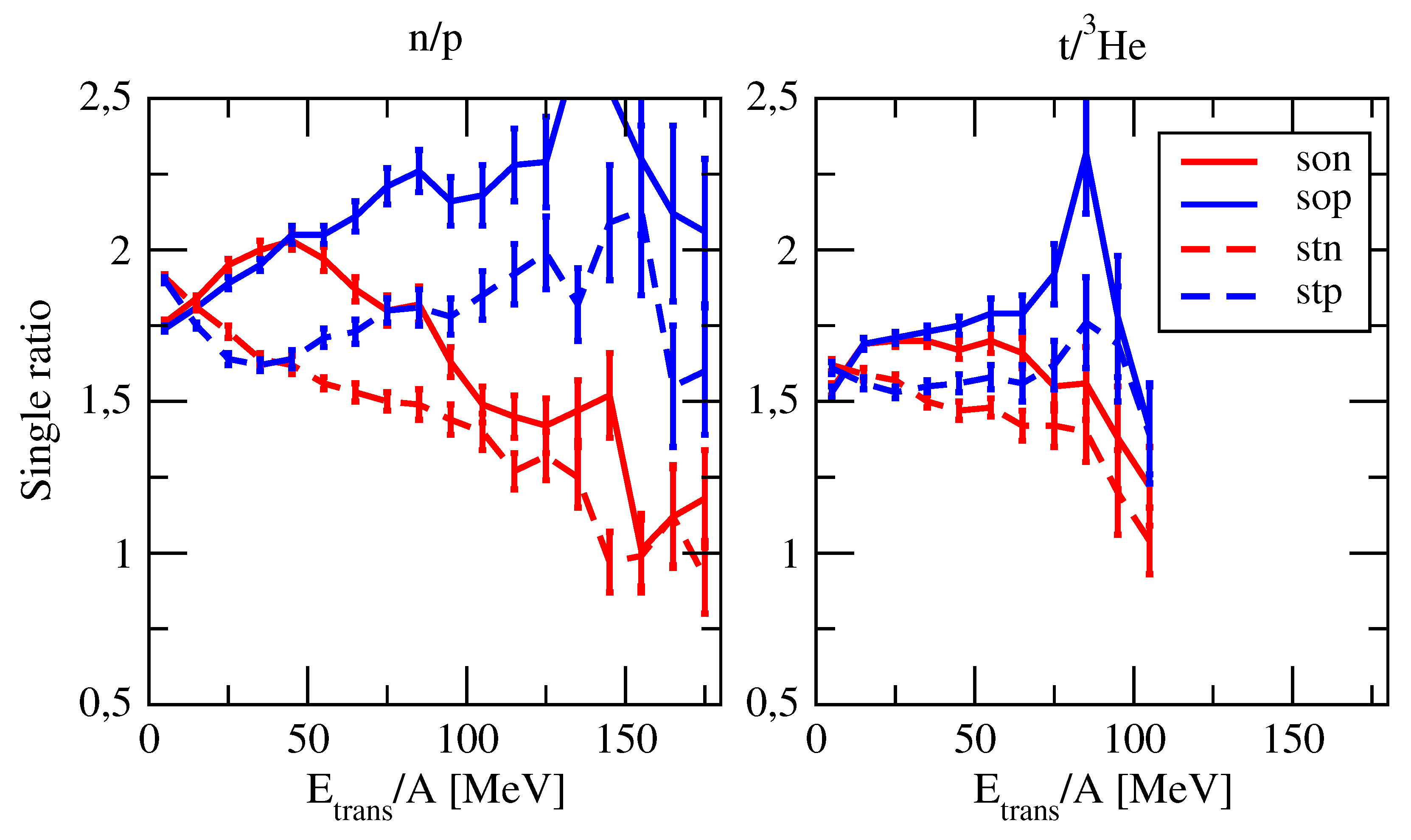
3.3. Light Cluster Emission
3.4. Particle Production
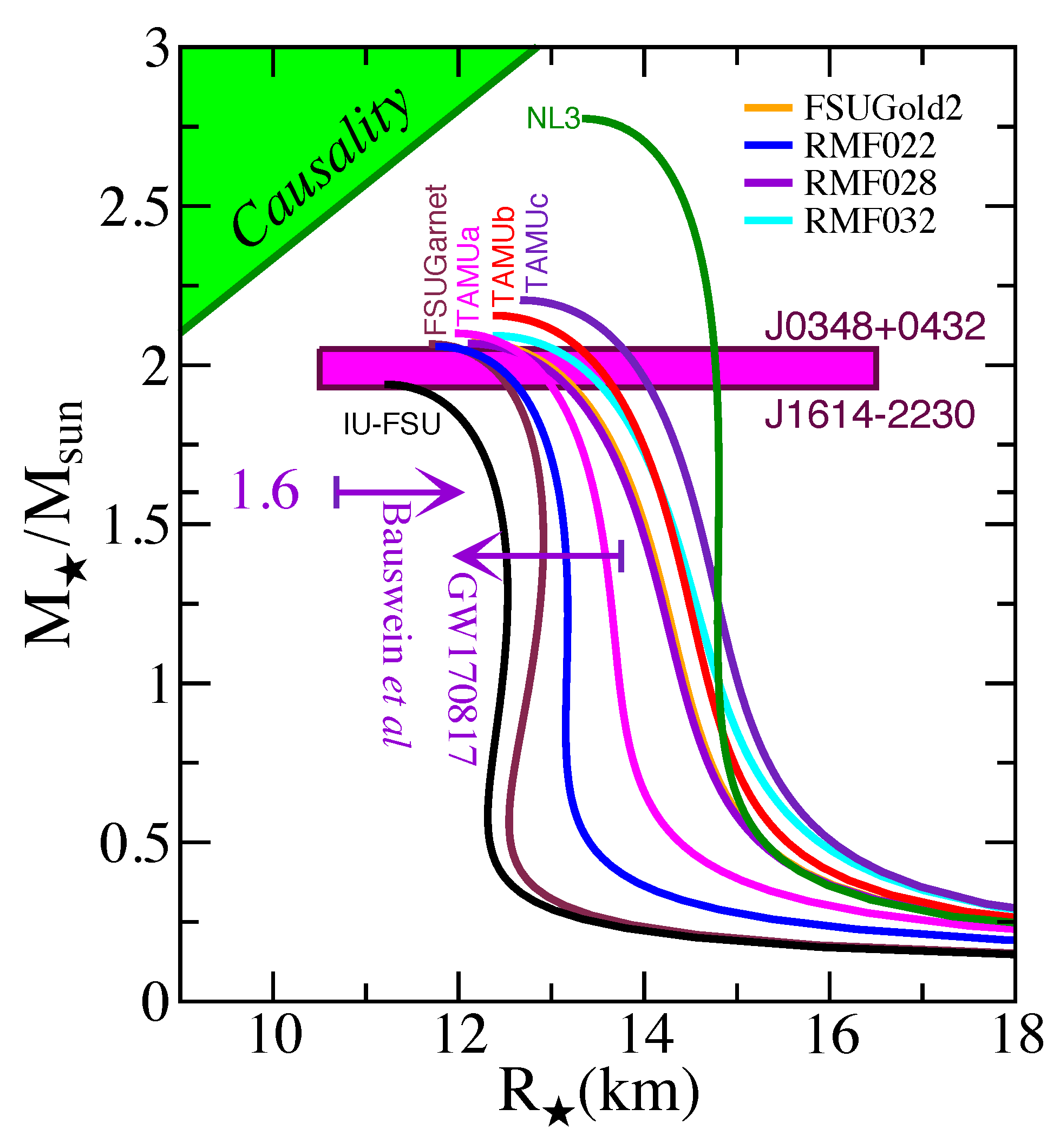
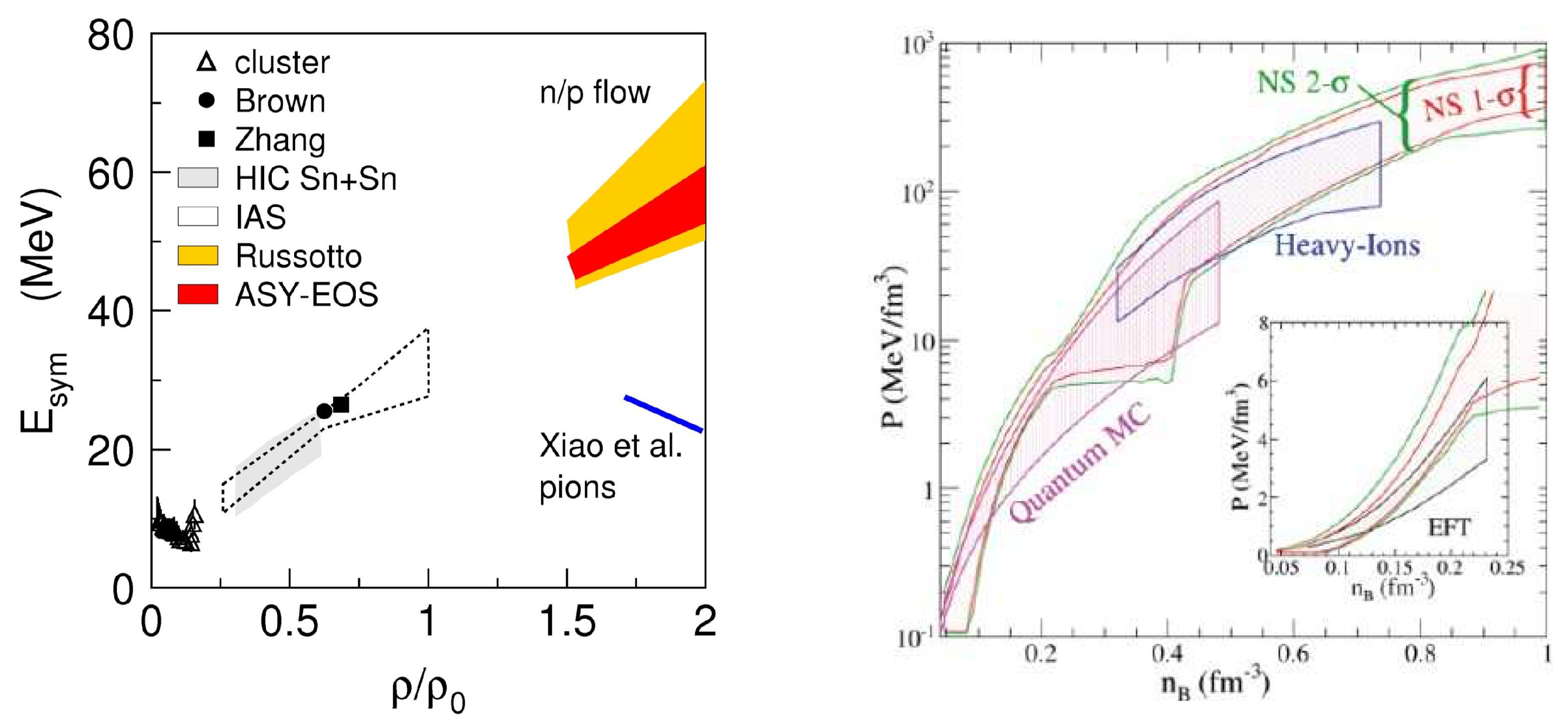
4. Discussion and Summary
Acknowledgments
Conflicts of Interest
References
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef] [PubMed]
- Li, B.A.; Ramos, À.; Verde, G.; Vidaña, I. Topical Issue on the Nuclear Symmetry Energy. Eur. Phys. J. A 2014, 50, 1–3. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: experiment, theory, and observation. J. Phys. G 2014, 41, 093001. [Google Scholar] [CrossRef]
- Demorest, P.D.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The equation of etate from observed masses and radii of neutron stars. Astrophys. J. 2010, 722, 33. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys. J. Lett. 2013, 765, L5. [Google Scholar] [CrossRef]
- Abott, P.B.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, B.; et al. GW170817: Implications for the stochastic gravitational-wave background from compact binary coalescences. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.K.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An ordinary short gamma-ray burst with extraordinary implications: Fermi-GBM detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E. INTEGRAL detection of the first prompt gamma-ray signal coincident with the gravitational-wave event GW170817. Astrophys. J. Lett. 2017, 848, L15. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal LOVE numbers of neutron stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron skins and neutron stars in the multimessenger era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef] [PubMed]
- Krastev, P.G.; Li, B.A. Imprints of the nuclear symmetry energy on the tidal deformability of neutron stars. arXiv, 2018; arXiv:1801.04620. [Google Scholar]
- Bauswein, A.; Just, O.; Janka, H.-T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- Paschalides, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Danielewicz, P. Quantum theory of nonequilibrium processes I. Ann. of Phys. 1984, 152, 239–304. [Google Scholar]
- Botermans, W.; Malfliet, R. Quantum transport theory of nuclear matter. Phys. Rep. 1990, 198, 115–194. [Google Scholar] [CrossRef]
- Hofmann, F.; Keil, C.M.; Lenske, H. Density dependent hadron field theory for asymmetric nuclear matter and exotic nuclei. Phys. Rev. C 2001, 64, 034314. [Google Scholar]
- Fuchs, C.; Lenske, H. Rearrangement in the density-dependent field theory of relativistic nuclei. Phys. Lett. B 1995, 345, 355. [Google Scholar]
- Fuchs, C.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C. 1995, 52, 3043. [Google Scholar] [CrossRef]
- Ono, A.; Horiuchi, H.; Maruyama, T.; Ohnishi, A. Antisymmetrized version of molecular dynamics with two-nucleon collisions and its application to heavy ion reactions. Prog. Theor. Phys. 1992, 87, 1185. [Google Scholar] [CrossRef]
- Bertsch, G.F.; Gupta, S.D. A guide to microscopic models for intermediate energy heavy ion collisions. Phys. Rep. 1988, 160, 189. [Google Scholar] [CrossRef]
- Aichelin, J. Quantum molecular dynamics: A dynamical microscopic n-body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys. Rep. 1991, 202, 233–360. [Google Scholar] [CrossRef]
- Napolitani, P.; Colonna, M. Bifurcations in Boltzmann—Langevin one body dynamics for fermionic systems. Phys. Lett. B 2013, 726, 382–386. [Google Scholar] [CrossRef]
- Napolitani, P.; Colonna, M. Frustrated fragmentation and re-aggregation in nuclei: A non-equilibrium description in spallation. Phys. Rev. C 2015, 92, 034607. [Google Scholar] [CrossRef]
- Colonna, M.; di Toro, M.; Guarnera, A.; Maccarone, S.; Zielinska-Pfabé, M.; Wolter, H.H. Fluctuations and dynamical instabilities in heavy-ion reactions. Nucl. Phys. A 1998, 642, 449–460. [Google Scholar] [CrossRef]
- Colonna, M. Fluctuations and Symmetry Energy in Nuclear Fragmentation Dynamics. Phys. Rev. Lett. 2013, 110, 042701. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Chen, L.-W.; Tsang, M.B.; Wolter, H.H.; Zhang, Y.-X.; Aichelin, J.; Colonna, M.; Cozma, D.; Danielewicz, P.; Feng, Z.-Q.; et al. Understanding transport simulations of heavy-ion collisions at 100 A and 400 A MeV: Comparison of heavy-ion transport codes under controlled conditions. Phys. Rev. C 2016, 93, 044609. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Wang, Y.-J.; Colonna, M.; Danielewicz, P.; Ono, A.; Tsang, M.B.; Wolter, H.H.; Xu, J.; Chen, L.-W.; Cozma, D.; et al. Comparison of heavy-ion transport simulations: Collision integral in a box. Phys. Rev. C. 2018, 97, 034625. [Google Scholar] [CrossRef]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.-M. Probing the nuclear equation of state by K+ production in heavy-ion collisions. Phys. Rev. Lett. 2001, 86, 1974. [Google Scholar] [CrossRef] [PubMed]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef]
- Poskanzer, A.M.; Voloshin, S.A. Methods for analyzing anisotropic flow in relativistic nuclear collisions. Phys. Rev. C 1998, 58, 1671. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Directed flow in heavy-ion collisions and its implications for astrophysics. Universe 2017, 3, 79. [Google Scholar] [CrossRef]
- Andronic, A.; Łukasik, J.; Reisdorf, W.; Trautmann, W. Systematics of stopping and flow in Au + Au collisions. Eur. Phys. J. A 2006, 30, 31–46. [Google Scholar] [CrossRef]
- Reisdorf, W.; Leifels, Y.; Andronic, A.; Averbeck, R.; Barret, V. Systematics of azimuthal asymmetries in heavy ion collisions in the 1A GeV regime. Nucl. Phys. A 2012, 876, 1–60. [Google Scholar] [CrossRef]
- Łukasik, J.; Auger, G.; Bellaize, M.L.; Be, N.; Bittiger, R.; Bocage, F.; Borderie, B.; Bougault, R.; Bouriquet, F.; Charvet, J.L.; Chbihi, A.; et al. Directed and elliptic flow in 197Au+197Au at intermediate energies. Phys. Lett. B 2005, 608, 223–230. [Google Scholar] [CrossRef]
- Trautmann, W.; Wolter, H.H. Elliptic flow and the symmetry energy at supra-saturation density. Int. J. Mod. Phys. E 2012, 21, 1230003. [Google Scholar] [CrossRef]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Amorini, F. Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Russotto, P.; Wu, P.Z.; Zoric, M.; Chartier, M.; Leifels, Y.; Lemmon, R.C.; Li, Q.; Łukasik, J.; Pagano, A.; Pawłowski, P.; et al. Symmetry energy from elliptic flow in 197Au + 197Au. Phys. Lett. B 2011, 697, 471–476. [Google Scholar] [CrossRef]
- Wolter, H.H.; Zielinska-Pfabe, M.; Decowski, P.; Colonna, M.; Bougault, R.; Chbihi, A. Symmetry energy dependence of light fragment production in heavy ion collisions. EPJ Web Conf. 2014, 66, 03097. [Google Scholar] [CrossRef]
- Giordano, V.; Colonna, M.; di Toro, M.; Greco, V.; Rizzo, J. Isospin emission and flow at high baryon density: A test of the symmetry potential. Phys. Rev. C 2010, 81, 064611. [Google Scholar] [CrossRef]
- Wolter, H.H. The nuclear symmetry energy in heavy ion collisions. Phys. Part. Nucl. 2015, 46, 781. [Google Scholar] [CrossRef]
- Coupland, D.D.S.; Youngs, M.; Chajecki, Z.; Lynch, W.G.; Tsang, M.B.; Zhang, Y.X.; Famiano, A.; Ghosh, T.K.; Giacherio, B.; Kilburn, M.A. et al. Probing effective nucleon masses with heavy-ion collisions. Phys. Rev. C 2016, 94, 011601. [Google Scholar] [CrossRef]
- Kowalski, S.; Natowitz, J.B.; Shlomo, S.; Wada, R.; Hagel, K.; Wang, J.; Materna, T.; Chen, Z.; Ma, Y.G.; Qin, L.; et al. Experimental determination of the symmetry energy of a-low density nuclear gas. Phys. Rev. C 2007, 75, 014601. [Google Scholar] [CrossRef]
- Tsang, M.B.; Friedman, W.A.; Gelbke, C.K.; Lynch, W.G.; Verde, G.; Xu, H.S. Isotopic scaling in nuclear reactions. Phys. Rev. Lett. 2001, 86, 5023. [Google Scholar] [CrossRef] [PubMed]
- Tsang, M.B.; Friedman, W.A.; Gelbke, C.K.; Lynch, W.G.; Verde, G.; Xu, H.S. Conditions for isoscaling in nuclear reactions. Phys. Rev. C 2001, 64, 041603. [Google Scholar] [CrossRef]
- Natowitz, J.B.; Röpke, G.; Typel, S.; Blaschke, D.; Bonasera, A.; Hagel, K.; Klähn, T.; Kowalski, S.; Qin, L.; Shlomo, S.; Wada, R.; Wolter, H.H. Symmetry energy of dilute warm nuclear matter. Phys. Rev. Lett. 2010, 104, 202501. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Bastian, N.-U.; Batyuk, P.; Blaschke, D.; Danielewicz, P.; Yu, B. Light cluster production at NICA. Eur. Phys. J. A 2016, 52, 244. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Ivanov, Y.B.; Karpenko, I.; Rogachevsky, O.V.; Wolter, H.H. Medium effects on freeze-out of light clusters at NICA energies. Phys. Part. Nucl. Lett. 2018, 15, 225. [Google Scholar] [CrossRef]
- Ferini, G.; Colonna, M.; Gaitanos, T.; di Toro, M. Aspects of particle production in isospin-asymmetric matter. Nucl. Phys. A 2005, 762, 147–166. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, B.A.; Chen, L.W.; Yong, G.C.; Zhang, M. Circumstantial evidence for a soft nuclear symmetry energy at suprasaturation densities. Phys. Rev. Lett. 2009, 102, 062502. [Google Scholar] [CrossRef] [PubMed]
- Prassa, V.; Ferini, G.; Gaitanos, T.; Wolter, H.H.; Lalazissis, G.; di Toro, M. In-medium effects on particle production in heavy ion collisions. Nucl. Phys. A 2007, 789, 311–333. [Google Scholar] [CrossRef]
- Feng, Z.Q.; Jin, G.M. Probing high-density behavior of symmetry energy from pion emission in heavy-ion collisions. Phys. Lett. B 2010, 683, 140–144. [Google Scholar] [CrossRef]
- Hong, J.; Danielewicz, P. Subthreshold pion production within a transport description of central Au + Au collisions. Phys. Rev. C 2014, 90, 024605. [Google Scholar] [CrossRef]
- Reisdorf, W. The FOPI Collaboration. Systematics of pion emission in heavy ion collisions in the 1 A GeV regime. Nucl. Phys. A 2007, 781, 459–508. [Google Scholar] [CrossRef]
- Tsang, M.B. Pion Production in Rare-Isotope Collisions; Nuclear Symmetry Energy 2017 (NuSYM2017); Grand Accélérateur National D’Ions Lourds: Caen, France, 2017. [Google Scholar]
- Ferini, G.; Gaitanos, T.; Colonna, M.; di Toro, M.; Wolter, H.H. Isospin effects on subthreshold kaon production at intermediate energies. Phys. Rev. Lett. 2006, 97, 202301. [Google Scholar] [CrossRef] [PubMed]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Brown, B.A. Constraints on the Skyrme Equations of State from Properties of Doubly Magic Nuclei. Phys. Rev. Lett. 2013, 111, 232502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, L.-W. Constraining the symmetry energy at subsaturation densities using isotope binding energy difference and neutron skin thickness. Phys. Lett. B 2013, 726, 234–238. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.-W.; Pethick, C.J.; Schwenk, A. Constraints on neutron star radii based on chiral effective field theory interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar]
- Gandolfi, S.; Carlson, J.; Reddy, S. Maximum mass and radius of neutron stars, and the nuclear symmetry energy. Phys. Rev. C 2012, 85, 032801. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolter, H. The High-Density Symmetry Energy in Heavy-Ion Collisions and Compact Stars. Universe 2018, 4, 72. https://doi.org/10.3390/universe4060072
Wolter H. The High-Density Symmetry Energy in Heavy-Ion Collisions and Compact Stars. Universe. 2018; 4(6):72. https://doi.org/10.3390/universe4060072
Chicago/Turabian StyleWolter, Hermann. 2018. "The High-Density Symmetry Energy in Heavy-Ion Collisions and Compact Stars" Universe 4, no. 6: 72. https://doi.org/10.3390/universe4060072
APA StyleWolter, H. (2018). The High-Density Symmetry Energy in Heavy-Ion Collisions and Compact Stars. Universe, 4(6), 72. https://doi.org/10.3390/universe4060072




