Abstract
Quantum resolutions of the space-time singularity at the end of gravitational collapse may provide hints towards the properties of a final theory of Quantum-Gravity. The mechanism by which the singularity is avoided and replaced by a bounce depends on the specific behaviour of gravity in the strong field and may have implications for the geometry of the space-time also in the weak field. In the last few decades, several scenarios for black hole bounces have been proposed and I shall argue that the times are now mature to ask the question of whether such bounces can be observed in astrophysical phenomena.
1. Introduction
The search for a viable theory of Quantum-Gravity (QG) has been ongoing for several decades [1]. It is now widely accepted that General Relativity (GR) is not a complete theory and that it needs modifications in the high energy (ultra-violet) regime [2]. One of the clearest indicators of the need for a theory that departs from GR in the strong field is the generic occurrence of singularities in the classical theory. It is today generally accepted that a theory of QG would be free of singularities. However, QG, like any good scientific theory, should be experimentally validated. This can happen either by explaining some observed phenomena in the universe that is lacking a valid explanation, or by predicting some new phenomena that can be observed in the universe or in a laboratory [3]. As of now, theoretical attempts to quantize gravitation always inevitably hit the brick wall of experimental tests. In most cases, the energy scales at which QG becomes relevant are well beyond what is presently achievable in particle accelerators [4], although there exist other proposed experiments that do not require high energy particle physics that may provide results in the future (see, for example, [5]). However, these may also run into difficulties due to the weakness of the gravitational field at low energy regimes. This situation has left us at an impasse, with several candidate theories of QG that are presently beyond the reach of man-made experiments.
At the same time, on the other side of the battlefield, the recent observation of gravitational waves from black hole and neutron star mergers (see [6,7]) has shown that Einstein’s theory holds well even when venturing into regions where the gravitational field becomes strong. However, the era of precision tests of gravity in astrophysics has just begun and it is possible that future observations will open new doors on unexpected phenomena. In this context, black holes provide the ideal test bed to study how QG could manifest in physical phenomena.
Within the ongoing research of quantum properties of black holes, in recent times, considerable interest has been devoted to the modification of existing models for collapse in order to describe the occurrence of a ‘quantum bounce’. The main idea is that QG must induce repulsive effects in the strong field regime that prevent the formation of singularities. Within models for gravitational collapse, such effects imply that a collapsing object (a ‘star’) does not produce a singularity but instead reaches a minimum size before entering a phase of re-expansion (see [8] for a review of existing models). In the classical collapse scenario, in the absence of rotation, once the singularity forms, the space-time is described by the Schwarzschild solution. In contrast, in the bouncing scenarios, the removal of the singularity implies that there is not a time after which the geometry can be described by a black hole solution. Obviously, this affects the nature of the horizon, which can not be the usual event horizon, and may also have implications for the weak field regions of the space-time. Interestingly, many different approaches to the application of QG to collapse produce similar qualitative results. This may be taken as a hint to the fact that there must be some common underlying feature. At the same time, different bouncing models, coming from different theories, provide different predictions, suggesting that it may be possible, at least in principle, to distinguish them experimentally.
In the following, I shall briefly review the history of models for collapse and bounces in Section 2, discuss some of the most important unsolved problems in Section 3 and suggest some phenomena where such models may produce observable effects in Section 4. Finally, in Section 5, I shall briefly discuss the future prospects for a phenomenology of QG.
2. History of Black Hole Bounces
Since Hawking and Penrose proved the famous theorems that show that singularities are an inevitable feature of GR [9], the general consensus has become that the occurrence of space-time singularities signals a regime where the usual classical relativistic description fails. Singularities generically appear in solutions of Einstein’s equations but are expected to be removed within a fully quantum gravitational description [10].
In order to understand how the singularity avoidance may occur, people have been looking at different approaches to QG and how they modify known classical solutions of physical interest. In this respect, analytical toy models describing the complete gravitational collapse of a matter cloud and the subsequent formation of a black hole, provide an ideal test bed for different approaches to singularity resolution.
In 1981, Frolov and Vilkoviski studied the first example (to my knowledge) of such singularity avoidance in the collapse of a thin null shell within a theory with a gravitational effective Lagrangian truncated at one loop [11].
Later, Hajicek and Kiefer considered the quantization of a collapsing light-like shell within the Hamiltonian formulation [12]. In this context, for the first time, it emerged the possible transition of the black hole solution, representing the exterior of the collapsing shell at early times, to a white hole solution, representing the exterior of the expanding shell at late times.
Other, more recent, approaches rely on the semi-classical approximation in order to circumvent the lack of a viable theory of QG. Namely, QG modifications to the geometrical side of Einstein’s equations are treated as an effective energy-momentum tensor [13]. This allows to solve the usual set of field equations of GR for an effective (i.e., unphysical) matter source that takes into account QG effects.
In this context, Barcelo et al. have studied how the occurrence of the bounce may induce a transition from the black hole solution to a white hole [14]. The transition, if it does occur for real collapse, would have important implications for astrophysical black holes.
Finally, it is worth mentioning an approach based on the bouncing models developed within Loop Quantum Cosmology (LQC) [15]. In this case, the bounce is induced by effective corrections to the energy momentum tensor that are quadratic in the density. The simplest toy model is a straightforward extension of the Oppenheimer–Snyder model to the bouncing case [16]. As a consequence of the singularity removal a remnant can be produced. Such object would have a density of the order of Planck density, and size larger than Planck size [17].
The general picture that has emerged is the following: collapse initially follows the classical description. At high densities, QG modifications to GR produce repulsive effects that halt collapse and cause the bounce (region I in Figure 1). The apparent horizon curve in the interior is also affected. QG effects may propagate in the exterior (region II in Figure 1) and possibly even outside the black hole horizon. After the bounce, the matter cloud re-expands. Matter eventually crosses the horizon and destroys the black hole (see Figure 1 for details). Depending on the approach used, the exterior region may be described by a black hole metric until the expanding matter crosses the horizon or may turn into a white hole metric around the time of the bounce.
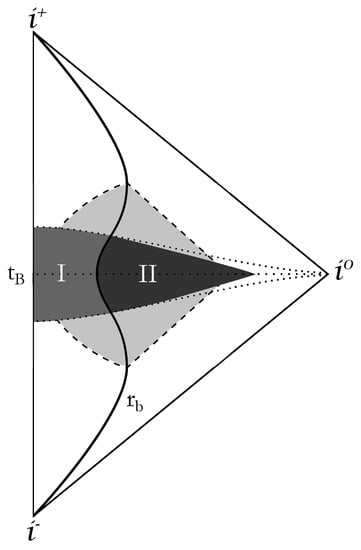
Figure 1.
Penrose diagram of a generic black hole bounce: the boundary of the cloud (thick line ) separates the interior from the exterior. Initially, there are no deviations from the classical scenario. The apparent horizon develops in the interior and the black hole horizon in the exterior (dashed lines). The QG dominated regime develops in the interior (region I, drawn here for an homogeneous matter cloud, for which the QG regime is reached by all shells at the same co-moving time) and possibly propagates in the exterior (region II). Depending on the model, region II may vanish, may extend to a finite distance outside or may even extend to spatial infinity. The way the horizons are affected depends on the specifics of the model. After the bounce (which, in the homogeneous case, occurs at the same co-moving time for all shells), the solution is described by the time reversal of the collapsing phase.
3. Some Open Questions
After nearly four decades since the first bounce model, the times are right for toy models describing singularity resolution and bounces to address the question of what would happen to real collapsing objects in the universe. In this context, there are several open issues that are addressed differently depending on the approach chosen. The answer to such questions, in principle, may indicate which models are more realistic, and in turn it could reveal some features of a viable theory of QG.
3.1. Timescales
One important unsolved problem concerns the timescales of the bounce, which is related to the lifetime of the black hole. How long does it take for the matter cloud to bounce and re-emerge from the horizon, as seen by a far away observer? This is an important issue because, in the absence of any measurable effects in the exterior of the horizon, the object would be indistinguishable from a black hole for any distant observer. A short enough timescale would imply a higher chance of experimental detection. On the other hand, if the timescales predicted by the model were to be too short, then we should not observe any black holes in the universe. Typically, the lifetime of the black hole is determined by the black hole mass M and the critical scale of the QG theory (typically the Planck time or the Planck mass ). For example, the black hole forming from null shell collapse in the Frolov–Vilkoviski model [11] has a lifetime of the order , the process investigated by Barcelo et al. in [18] has a lifetime of the order of , while the process discussed by Rovelli and Haggard in [19] produces a black hole with lifetime of the order of .
It is worth noting that, however long the above estimates may be, they are considerably shorter than the Hawking evaporation time, which goes like . This suggests that if black hole bounces do occur in the real universe then they would dominate over black hole evaporation via Hawking radiation.
3.2. Limitations of Toy Models
In order to find an exact analytical solution, a lot of physics must be neglected. This is true for classical collapse models as well as for bouncing models. Most of the scenarios that have been studied so far consider non rotating spherically symmetric matter clouds that are described by simple adiabatic fluid models with constant entropy. In this context, almost all the toy models studied in the literature exhibit a time-symmetric bounce, with the expanding phase being the time reversal of the collapsing phase. However, we can expect that in the collapse of a real object the scenario would be made more complicated by the presence of deformations, rotation and dissipative effects. Therefore, the time symmetry should be understood as arising from the simplifications made. What effects would rotation, deformations and the presence of dissipation in the fluids have on the bounce scenario?
- -
- Rotation: Numerical simulations have shown that during collapse within classical GR a rapidly rotating star disperses away the excess angular momentum to settle below the Kerr bound [20]. It is reasonable to expect that this behaviour is shared by bouncing models, since at the time of formation of the horizon the collapsing matter is still far from the QG regime. Then, after the bounce, the re-expanding cloud would be rotating slower than the original collapsing cloud.
- -
- Deformations: Similarly to what happens with angular momentum, it is usually believed that a collapsing `star’ (without charge) must get rid of all deformations that make it depart from the Kerr or Schwarzschild solutions before the horizon forms. Then, in the case of a bouncing scenario, the expanding cloud should be exactly spherical in shape at the moment in which matter passes the horizon. In principle, this should be a significant observable feature of the expanding cloud at late times.
- -
- Dissipation: It is reasonable to assume that, in a realistic fluid, entropy will increase during the collapsing phase as well as during the expanding phase. However, the increase in entropy in the expanding phase is not compatible with the time symmetry of the toy models studied in the literature, which typically consider fluids with constant entropy. For example, the presence of heat flow in the collapsing fluid would alter the structure of the horizon in the expanding phase, thus destroying the time symmetry [21].
3.3. Exterior Geometry
Another unresolved issue of bouncing models is the nature of the geometry in the exterior region. In most classical analytical models, as the cloud collapses, the exterior is described by either vacuum (i.e., typically the Schwarzschild solution) or outgoing radiation (i.e., typically the Vaidya solution). The introduction of QG corrections modifies the collapsing interior, which must be matched to the exterior geometry. For simplicity, let’s consider only the case where the exterior of the classical model is described by the Schwarzschild solution. Once QG corrections are introduced to modify the behaviour of the collapsing matter close to the formation of the singularity, there are several possibilities for what could happen to the exterior space-time:
- -
- Classical black holes: The exterior geometry is not affected by quantum corrections. The exterior space-time is described by the Schwarzschild solution, which means that a far away observer sees a classical black hole until the boundary of the `star’ in the expanding phase crosses the horizon.
- -
- White holes: If repulsive QG effects propagate in the exterior of the `star’, then the geometry outside may turn from a black hole solution to a white hole solution as the matter bounces going from the collapsing phase to the expanding phase.
- -
- Regular black holes: The exterior geometry may be described by a regular black hole, such as, for example, the one discussed in [22]. During the period of existence of the black hole, the horizon in the exterior space-time would then exhibit deviations from the classical event horizon. Such deviations are expected to be tiny as they would depend on the critical parameter governing quantum corrections.
- -
- Exotic compact objects: If the trapped region in the exterior is closed and exists for a finite time, then the process may eventually produce an exotic compact object visible to far away observers. This kind of exotic compact object would be extremely small and dense (typically at Planck scale) [23].
It is worth noticing that for the collapsing matter to be ejected in the expanding phase the causal behaviour of the space-time must change. Namely, the light cones in the trapped region must turn from ingoing to outgoing. This may happen close to the instant in which the boundary of the ‘star’ crosses the horizon, as explained in the first item above, or gradually from the moment in which the horizon forms until the moment in which matter is expelled, as explained in the second item above. In addition, in the first case, the phase transition may be confined in the interior of the ‘star’ or to the vicinity of its boundary, while in the second case the phase transition may affect the exterior geometry and extend to the horizon and its neighborhood [24].
4. Phenomenology
All of the above possibilities present specific features that may have phenomenological implications. In the case of a classical black hole exterior, for example, as the expanding matter crosses the horizon, one would expect to see some kind of explosion. In the case of the black hole to white hole transition, on the other hand, one important questions concerns the timescale of the transition and the behaviour of matter in accretion disks around the object as it turns from a black hole to a white hole. In the case of a regular black hole, it is worth asking whether it would be possible to measure deviations from the Schwarzschild geometry with astrophysical observations. Finally, in the case of exotic compact objects, the observable features of such objects would be completely different from those of black holes and it is worth asking if such hypothetical objects could be detected.
Astrophysical black hole candidates have been observed mostly in the stellar mass range, namely less than (with being the mass of the Sun) and in the supermassive range, namely above . Stellar mass black hole candidates can be detected via gravitational wave emission during a binary merger [6] or via the properties of light emitted by accretion disks when they are in a binary system with a regular companion star [25]. Two supermassive black hole candidates (Sgr-A*, located at the center of the Milky Way and the one located at the center of the galaxy M87) can potentially be observed directly and imaging of their shadow is within the experimental reach of the Event Horizon Telescope [26]. In the case of Sgr-A*, it has been possible also to track the motion of stars located in its vicinity. For example, the nearest star, S2, has its closest approach at a distance of abut 120 Astronomical Units (AU), which must be compared to the Schwarzschild radius of the black hole candidate which is around 0.3 AU. Other supermassive black hole candidates have been detected only via the emission of light from their accretion disks.
If black hole bounces can be observed, at least in principle, what features would they present that could distinguish them from classical black holes?
- -
- Explosions: How would the explosion produced by the expanding matter crossing the horizon look? In the context of astrophysics, the explosion would present some characteristic features that would distinguish it from a supernova explosion (for example, in the neutrino and gravitational wave emissions). In this direction, a speculative connection with Fast Radio Bursts (FRBs) has already been suggested [27].
- -
- White hole transitions: Accretion disks around white holes are unstable [28]. Therefore, if the bounce turns a black hole into a white hole, the process must affect the light emission of the surrounding accretion disk, if present.
- -
- Deviations from classical solutions: If the geometry in the exterior differs from the classical black hole geometry (such as in the case of regular black holes, for example), then such deviations could be observable in the motion of test particles. When thinking about astrophysical black hole candidates, this may translate into tiny deviations of the orbits of stars close to Sgr-A*, or in different features of its shadow [29].
- -
- Gravitational waves: If the collapsing ‘star’ sheds away all deformations and excess angular momentum in the collapsing phase, it is worth asking what kind of gravitational wave signal (if any) would be emitted by the expanding phase once it passes the horizon. Would it be possible to detect it and distinguish it from the gravitational waves emitted during the core collapse of a supernova?
- -
- Exotic compact objects: If the horizon disappears leaving behind an exotic compact object (see for example the toy model in [8]), then such an object would have some characteristic observational features that distinguish it from a black hole. However, its detection would be extremely hard due to the intrinsic small size of the object.
5. Conclusions
While it may seem depressing that, after many years of search, no new physics has appeared on either side of the experimental siege to QG (see Figure 2), we have to keep in mind that multi-messenger astronomy is just now starting to give its first fruits. If, on one hand, it is unlikely that any physics beyond the standard model will appear from particle accelerator experiments any time soon; on the other hand, it not so obvious that every new astrophysical observation of the strong gravity regime will confirm the predictions of GR. In this context, if one is hoping to find some deviation from Einstein’s gravity in astrophysical phenomena, there is one main aspect to keep in mind: the number of events detected and objects observed is still extremely small when compared to the statistical significance of the expected deviations.
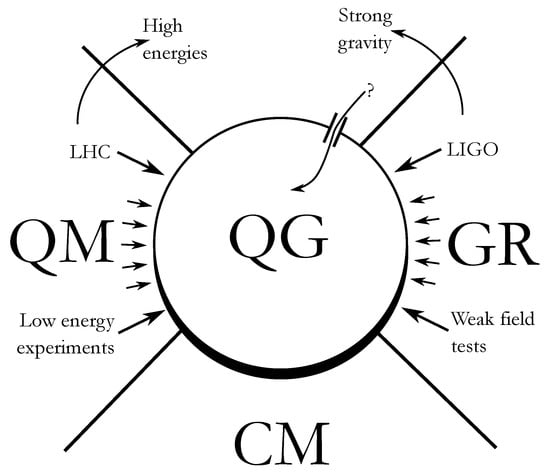
Figure 2.
The siege to Quantum Gravity: from the side of Classical Mechanics (CM), there are no cracks in the wall (no experimental evidence of QG). From the side of Quantum Mechanics (QM), high energy experiments in particle physics (such as those performed at LHC) have shown no conclusive hints at new physics. To open new lines of attack, higher energies are needed, but they may be hard to achieve in the near future. Low energy experiments have also been proposed. From the side of General Relativity (GR), weak field tests have shown no cracks in the wall. Data from black hole and neutron star mergers also have shown no hints at QG. However, more data and better precision are expected to be achieved in the near future for tests of gravity in the strong field regime. Will the crack in the wall appear there?
As of now, the number of observations for which we have sound experimental data is fairly limited: we have observed few black hole mergers through gravitational waves, one neutron star merger, few stellar mass black hole candidates and zero direct imaging of the black hole shadow (soon to become one). The number of observed supermassive black hole candidates is large, but such observations are very hard, and there are still many unsolved questions surrounding these objects. If deviations from GR do appear, it is likely that they will be statistically not very significant and so it is possible that they are there but have not passed the sieve of experimental detection yet.
Consider, for example, exotic compact objects: if such hypothetical objects do form from collapse, they are probably small in size, extremely dense and not as massive, as compared to neutron stars. Therefore, they would be extremely hard to detect. Such a family of objects, that are intrinsically quantum gravitational, could be living alongside black holes and neutron stars, just waiting to be detected.
Now, consider bouncing black holes: if the singularity resolution leads to a bounce that eventually destroys the black hole, the process, as seen by distant observers, could take millions or even billions of years for a stellar mass black hole. Therefore, at present, the probability of detecting it as it happens in one of the observed black hole candidates is low.
Finally, consider the observed black hole candidates: if some deviation, due to a bouncing scenario or some other quantum gravitational effect, from the classical solution occurs in the vicinity of the horizon, it is bound to be very small and most probably below the threshold for detection with current observations. However, the direct imaging of the shadow of Sgr-A* will give us the first optical image of light coming from the strong gravity region and will allow us to test GR in a regime where it has never been tested.
As new observations come, more constraints will be put on the scenarios discussed above. The hunt for experimental evidence of QG phenomena is on and there are good chances that such detection will come from space.
Funding
This research was funded by Nazarbayev University Faculty Development Competitive Research Grants: `Quantum gravity from outer space and the search for new extreme astrophysical phenomena’, Grant No. 090118FD5348 and by the Ministry of Education of Kazakhstan’s target program: `Center of Excellence for Fundamental and Applied Physics’, IRN: BR05236494.
Conflicts of Interest
The author declares no conflict of interest.
References
- Carlip, S.; Chiou, D.W.; Ni, W.T.; Woodard, R. Quantum Gravity: A Brief History of Ideas and Some Prospects. Int. J. Mod. Phys. D 2015, 24, 1530028. [Google Scholar] [CrossRef]
- Niedermaier, M.; Reuter, M. The Asymptotic Safety Scenario in Quantum Gravity. Living Rev. Rel. 2006, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Hossenfelder, S. Experimental Search for Quantum Gravity. In Classical and Quantum Gravity: Theory, Analysis and Applications; Frignanni, V.R., Ed.; Nova Publishers: Hauppauge, NY, USA, 2011. [Google Scholar]
- Calmet, X. A review of Quantum Gravity at the Large Hadron Collider. Mod. Phys. Lett. A 2010, 25, 1553–1579. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Gravitationally Induced Entanglement between Two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity. Phys. Rev. Lett. 2017, 119, 240402. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. [LIGO Scientific Collaboration and Virgo Collaboration] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. [LIGO Scientific Collaboration and Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Malafarina, D. Classical collapse to black holes and quantum bounces: A review. Universe 2017, 3, 48. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The Singularities of gravitational collapse and cosmology. Proc. Royal Soc. Lond. A 1970, 314, 529–548. [Google Scholar] [CrossRef]
- Bojowald, M. Singularities and Quantum Gravity. AIP Conf. Proc. 2007, 910, 294–333. [Google Scholar]
- Frolov, V.P.; Vilkovisky, G.A. Spherically Symmetric Collapse in Quantum Gravity. Phys. Lett. B 1981, 106, 307–313. [Google Scholar] [CrossRef]
- Hajicek, P.; Kiefer, C. Singularity avoidance by collapsing shells in quantum gravity. Int. J. Mod. Phys. D 2001, 10, 775–780. [Google Scholar] [CrossRef]
- Barceló, C.; Liberati, S.; Sonego, S.; Visser, M. Fate of gravitational collapse in semiclassical gravity. Phys. Rev. D 2008, 77, 044032. [Google Scholar] [CrossRef]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Black holes turn white fast, otherwise stay black: No half measures. J. High Energy Phys. 2016, 2016, 157. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Malafarina, D.; Modesto, L. Non-singular quantum-inspired gravitational collapse. Phys. Rev. D 2013, 88, 044009. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Planck stars. Int. J. Mod. Phys. D 2014, 23, 1442026. [Google Scholar] [CrossRef]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Where does the physics of extreme gravitational collapse reside? Universe 2016, 2, 7. [Google Scholar] [CrossRef]
- Haggard, H.M.; Rovelli, C. Black hole fireworks: Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef]
- Baiotti, L.; Hawke, I.; Montero, P.J.; Löffler, F.; Rezzolla, L.; Stergioulas, N.; Font, J.A.; Seidel, E. Three-dimensional relativistic simulations of rotating neutron-star collapse to a Kerr black hole. Phys. Rev. D 2005, 71, 024035. [Google Scholar] [CrossRef]
- Malafarina, D.; Satin, S. Unpublished work. 2018. (in progress) [Google Scholar]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Visser, M.; Barceló, C.; Liberati, S.; Sonego, S. Small, dark, and heavy: But is it a black hole? arXiv 2008, arXiv:0902.0346. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J.; Jannes, G. The lifetime problem of evaporating black holes: Mutiny or resignation. Class. Quantum Grav. 2015, 32, 035012. [Google Scholar] [CrossRef]
- Narayan, R.; McClintock, J.E. General Relativity and Gravitation: A Centennial Perspective; Ashtekar, A., Berger, B., Isenberg, J., MacCallum, M.A.H., Eds.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Psaltis, D. Testing General Relativity with the Event Horizon Telescope. arXiv 2018, arXiv:1806.09740. [Google Scholar]
- Christodoulou, M.; Rovelli, C.; Speziale, S.; Vilensky, I. Realistic Observable in Background-Free Quantum Gravity: The PlanckStar Tunnelling-Time. Phys. Rev. D 2016, 94, 084035. [Google Scholar] [CrossRef]
- Eardley, D.M. Death of white holes in the early universe. Phys. Rev. Lett. 1974, 33, 442–444. [Google Scholar] [CrossRef]
- Giddings, S.B. Possible observational windows for quantum effects from black holes. Phys. Rev. D 2014, 90, 124033. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).