Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †
Abstract
1. Introduction
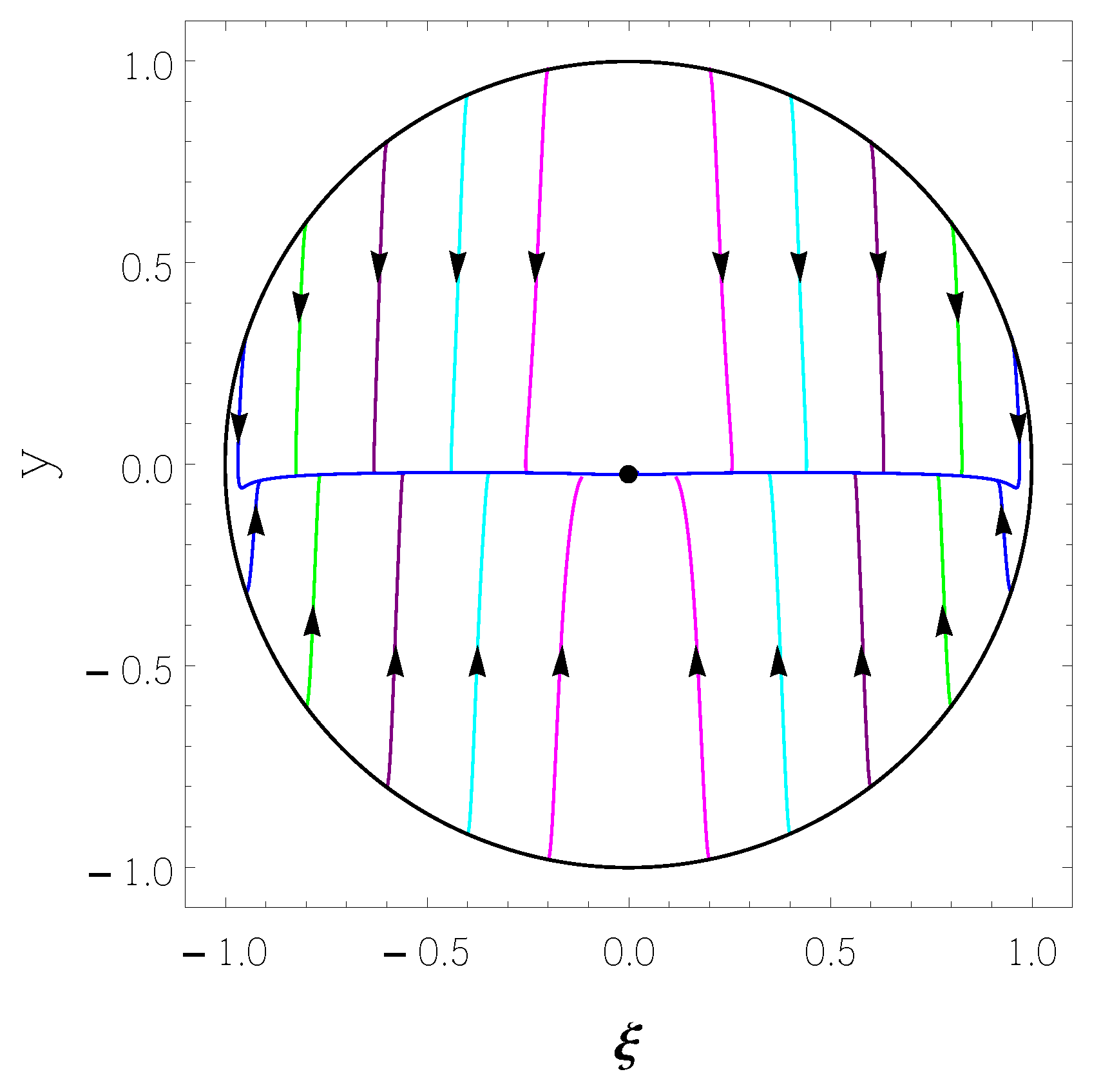
2. Background Evolution and Phase Space Analysis
- The equation of state for inflaton:
- The slow-roll parameter :
- The number of e-folds during the slow-roll inflation:
- In the bouncing regime, one can find an analytical solution of the expansion factor [27]:where is the Planck time and denotes a dimensionless constant.
3. Conclusions
Conflicts of Interest
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results-XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Borde, A.; Vilenkin, A. Eternal inflation and the initial singularity. Phys. Rev. Lett. 1994, 72, 3305. [Google Scholar] [CrossRef] [PubMed]
- Borde, A.; Guth, A.H.; Vilenkin, A. Inflationary Spacetimes Are Incomplete in Past Directions. Phys. Rev. Lett. 2003, 90, 151301. [Google Scholar] [CrossRef] [PubMed]
- Barrow, J.D.; Graham, A.A.H. Singular inflation. Phys. Rev. D 2015, 91, 083513. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop quantum cosmology: A status report. Class. Quantum Gravity 2011, 28, 213001. [Google Scholar] [CrossRef]
- Ashtekar, A.; Barrau, A. Loop quantum cosmology: From pre-inflationary dynamics to observations. Class. Quantum Gravity 2015, 32, 234001. [Google Scholar] [CrossRef]
- Barrau, A.; Bolliet, B. Some conceptual issues in loop quantum cosmology. Int. J. Mod. Phys. D 2016, 25, 1642008. [Google Scholar] [CrossRef]
- Yang, J.; Ding, Y.; Ma, Y. Alternative quantization of the Hamiltonian in loop quantum cosmology. Phys. Lett. B 2009, 682, 1–7. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 2012, 109, 251301. [Google Scholar] [CrossRef] [PubMed]
- Agullo, I.; Ashtekar, A.; Nelson, W. The pre-inflationary dynamics of loop quantum cosmology: Confronting quantum gravity with observations. Class. Quantum Gravity 2013, 30, 085014. [Google Scholar] [CrossRef]
- Agullo, I.; Morris, N.A. Detailed analysis of the predictions of loop quantum cosmology for the primordial power spectra. Phys. Rev. D 2015, 92, 124040. [Google Scholar] [CrossRef]
- Méndez, M.F.; Marugán, G.A.M.; Olmedo, J. Hybrid quantization of an inflationary model: The flat case. Phys. Rev. D 2013, 88, 044013. [Google Scholar] [CrossRef]
- Gomar, L.C.; Méndez, M.F.; Marugán, G.A.M.; Olmedo, J. Hybrid Cosmological perturbations in hybrid loop quantum cosmology: Mukhanov-Sasaki variables. Phys. Rev. D 2014, 90, 064015. [Google Scholar] [CrossRef]
- Gomar, L.C.; Méndez, M.F.; Marugán, G.A.M.; Blas, D.M.D.; Olmedo, J. Hybrid loop quantum cosmology and predictions for the cosmic microwave background. Phys. Rev. D 2017, 96, 103528. [Google Scholar] [CrossRef]
- Méndez, M.F.; Marugán, G.A.M.; Olmedo, J. Hybrid quantization of an inflationary universe. Phys. Rev. D 2012, 86, 024003. [Google Scholar] [CrossRef]
- Blas, D.M.D.; Olmedo, J. Primordial power spectra for scalar perturbations in loop quantum cosmology. J. Cosmol. Astropart. Phys. 2016, 6, 29. [Google Scholar] [CrossRef]
- Navascués, B.E.; Blas, D.M.D.; Marugán, G.A.M. Time-dependent mass of cosmological perturbations in the hybrid and dressed metric approaches to loop quantum cosmology. Phys. Rev. D 2018, 97, 043523. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Loop quantum cosmology and slow roll inflation. Phys. Lett. B 2010, 694, 108–112. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Probability of inflation in loop quantum cosmology. Gen. Relativ. Gravit. 2011, 43, 3619–3655. [Google Scholar] [CrossRef]
- Singh, P.; Vandersloot, K.; Vereshchagin, G.V. Non-singular bouncing universes in loop quantum cosmology. Phys. Rev. D 2006, 74, 043510. [Google Scholar] [CrossRef]
- Mielczarek, J.; Cailleteau, T.; Grain, J.; Barrau, A. Inflation in loop quantum cosmology: Dynamics and spectrum of gravitational waves. Phys. Rev. D 2010, 81, 104049. [Google Scholar] [CrossRef]
- Bonga, B.; Gupt, B. Phenomenological investigation of a quantum gravity extension of inflation with the Starobinsky potential. Phys. Rev. D 2016, 93, 063513. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Pre-inflationary universe in loop quantum cosmology. Phys. Rev. D 2017, 96, 083520. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. Universal features of quantum bounce in loop quantum cosmology. Phys. Lett. B 2017, 773, 196–202. [Google Scholar] [CrossRef]
- Shahalam, M.; Sharma, M.; Wu, Q.; Wang, A. Preinflationary dynamics in loop quantum cosmology: Power law potentials. Phys. Rev. D 2017, 96, 123533. [Google Scholar] [CrossRef]
- Shahalam, M.; Sami, M.; Wang, A. Preinflationary dynamics of α-attractor in loop quantum cosmology. arXiv, 2018; arXiv:1806.05815. [Google Scholar]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang: improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef]
- Meissne, K.A. Black hole entropy in loop quantum gravity. Class. Quantum Gravity 2004, 21, 5245. [Google Scholar] [CrossRef]
- Domagala, M.; Lewandowski, J. Black hole entropy from quantum geometry. Class. Quantum Gravity 2004, 21, 5233. [Google Scholar] [CrossRef]
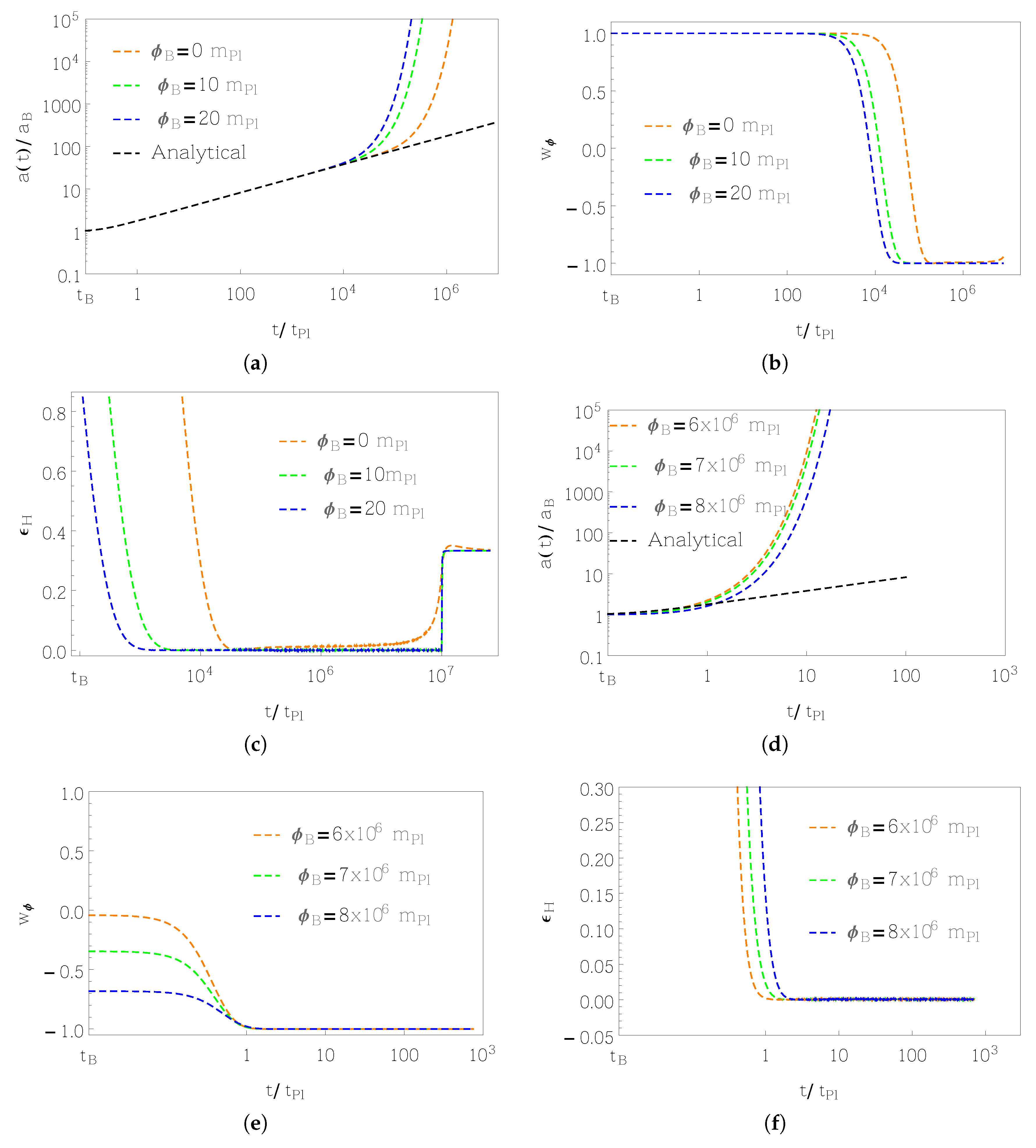
| Inflation | ||||
|---|---|---|---|---|
| >0 | 0 | starts | 40.32 | |
| ends | ||||
| 0.75 | starts | 60.01 | ||
| ends | ||||
| 0.80 | starts | 65.73 | ||
| ends | ||||
| starts | 709.81 | |||
| ends | ||||
| <0 | 4.5 | starts | 37.87 | |
| ends | ||||
| 5.27 | starts | 60.32 | ||
| ends | ||||
| 6.0 | starts | 78.21 | ||
| ends |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahalam, M. Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †. Universe 2018, 4, 87. https://doi.org/10.3390/universe4080087
Shahalam M. Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †. Universe. 2018; 4(8):87. https://doi.org/10.3390/universe4080087
Chicago/Turabian StyleShahalam, M. 2018. "Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †" Universe 4, no. 8: 87. https://doi.org/10.3390/universe4080087
APA StyleShahalam, M. (2018). Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †. Universe, 4(8), 87. https://doi.org/10.3390/universe4080087





