The Polarizations of Gravitational Waves ^†

Abstract

The gravitational wave provides a new method to examine General Relativity and its alternatives in the high speed, strong field regime. Alternative theories of gravity generally predict more polarizations than General Relativity, so it is important to study the polarization contents of theories of gravity to reveal the nature of gravity. In this talk, we analyze the polarization contents of Horndeski theory and $f\left(R\right)$ gravity. We find out that in addition to the familiar plus and cross polarizations, a massless Horndeski theory predicts an extra transverse polarization, and there is a mix of pure longitudinal and transverse breathing polarizations in the massive Horndeski theory and $f\left(R\right)$ gravity. It is possible to use pulsar timing arrays to detect the extra polarizations in these theories. We also point out that the classification of polarizations using Newman–Penrose variables cannot be applied to massive modes. It cannot be used to classify polarizations in Einstein-æther theory or generalized Tensor-Vector-Scalar (TeVeS) theory, either.

1. Introduction

The gravitational wave (GW) was detected by the Laser Interferometer Gravitational-Wave Observatory (LIGO) Scientific and Virgo collaborations, which further supports General Relativity (GR) [1,2,3,4,5,6]. It is also a new tool to probe gravitational physics in the high speed, strong field regime. To confirm that GR is the theory of gravity, the polarizations of GWs need be determined. It is well known that there are only two polarizations in GR, the plus and the cross. In contrast, a generic modified theory gravity predicts up to four extra polarizations [7], so it is possible to probe the nature of gravity by examining the polarization content of the GWs detected [8,9]. This can be done by Laser Interferometer Space Antenna (LISA) [10], TianQin [11], pulsar timing arrays (PTAs) [12,13], and the network of Advanced LIGO (aLIGO) and Virgo. Ref. [14] proposed to use spherical antenna to detect the massive GWs. In fact, GW170814 was the first GW event to test the polarization content of GWs. The analysis revealed that the pure tensor polarizations are favored against pure vector and pure scalar polarizations [4,15]. With the advent of more advanced detectors, there exists a better chance to pin down the polarization content and thus, the nature of gravity in the near future.

According to their transformation properties under the little group $E\left(2\right)$ of the Lorentz group, the six polarizations of the null plane GWs can be classified in terms of the Newman–Penrose (NP) variables: ${\mathsf{\Psi }}_2$, ${\mathsf{\Psi }}_3$, ${\mathsf{\Psi }}_4$ and ${\mathsf{\Phi }}_{22}$ [16,17,18]. Among them, ${\mathsf{\Psi }}_4$ represents the plus and the cross polarizations, ${\mathsf{\Phi }}_{22}$ donates the transverse breathing polarization, ${\mathsf{\Psi }}_3$ corresponds to the vector-x and vector-y polarizations, and ${\mathsf{\Psi }}_2$ is for the longitudinal polarization. This classification can be applied to any metric theory of gravity which respects the local Lorentz invariance and predicts null GWs, such as Brans–Dicke theory, the simplest scalar-tensor theory [19]. In this theory, there are plus and cross modes ${\mathsf{\Psi }}_4$ due to the massless graviton, and there also exists the transverse breathing mode ${\mathsf{\Phi }}_{22}$ induced by the massless scalar field [17].

The most general scalar-tensor theory of gravity is Horndeski theory, whose action contains derivatives of the metric tensor $g_{\mu \nu }$ and a scalar field $\varphi$ higher than the second order [20]. However, this theory has only three physical degrees of freedom (d.o.f.) because the equations of motion are at most of the second order. So, it is expected that there is one extra polarization state. Our analysis showed that the extra polarization state is the transverse breathing mode if the scalar field is massless, and it is a mix of the transverse breathing and the longitudinal modes if the scalar field is massive [21]. $f\left(R\right)$ gravity [22] is equivalent to a scalar-tensor theory of gravity [23,24]. The equivalent scalar field is massive, and it excites both the longitudinal and transverse breathing modes [25,26,27]. So, this theory has the similar polarization content to the massive Horndeski theory [28].

We show that the classification based on $E\left(2\right)$ symmetry cannot be applied to the massive Horndeski theory or $f\left(R\right)$ gravity, as there are massive modes in these two theories. In fact, it cannot be used to identify the polarizations in Einstein-æther theory [29] or generalized Tensor-Vector-Scalar (TeVeS) theory [30,31,32], as the local Lorentz invariance is violated in both theories [33].

The talk is organized in the following way. Section 2 quickly goes over $E\left(2\right)$ classification for identifying the polarization content of null GWs. In Section 3, the GW polarization content of $f\left(R\right)$ gravity is obtained. In Section 4, the polarization content of Horndeski theory is discussed. Section 5 discusses the polarizations of Einstein-æther theory as well as the generalized TeVeS theory. Finally, Section 6 is a brief summary. In this talk, natural units will be used and the speed of light is $c=1$.

2. Review of $\mathit{E}\mathbf{\left(}\mathbf{2}\mathbf{\right)}$ Classification

$E\left(2\right)$ classification is a framework [17,18] to categorize the null GWs in a generic, local Lorentz invariant metric theory of gravity using the Newman–Penrose variables [16]. For the GW traveling in the $+z$ direction, the suitable null tetrad basis, $E_a^{\mu }=(k^{\mu },l^{\mu },$$m^{\mu },{\overline{m}}^{\mu })$, is given by

$$k^{\mu }=\frac{1}{\sqrt{2}}(1,0,0,1),l^{\mu }=\frac{1}{\sqrt{2}}(1,0,0,-1),m^{\mu }=\frac{1}{\sqrt{2}}(0,1,i,0),{\overline{m}}^{\mu }=\frac{1}{\sqrt{2}}(0,1,-i,0),$$

(1)

where bar indicates the complex conjugation. They are normalized such that $-k^{\mu }{l}_{\mu }=m^{\mu }{\overline{m}}_{\mu }=1$, and the remaining inner products are zero. With this choice of coordinate system, the Riemann tensor is $R_{abcd}=R_{abcd}\left(u\right)$ with $u=t-z$, so $R_{abcd,p}=0$, where $(a,b,c,d)$ take values in $(k,l,m,\overline{m})$ and $(p,q,r,\cdots )$ take values in ($k,m,\overline{m}$). Using the Bianchi identity and the symmetries of $R_{abcd}$, one obtains that $R_{abcd}$ has only six independent nonzero components. In terms of the NP variables, they are

$${\mathsf{\Psi }}_2=-\frac{1}{6}{R}_{klkl},{\mathsf{\Psi }}_3=-\frac{1}{2}{R}_{kl\overline{m}l},{\mathsf{\Psi }}_4=-R_{\overline{m}l\overline{m}l},{\mathsf{\Phi }}_{22}=-R_{ml\overline{m}l}.$$

(2)

Other nonvanishing NP variables are ${\mathsf{\Phi }}_{11}=3{\mathsf{\Psi }}_2/2$, ${\mathsf{\Phi }}_{12}={\overline{\mathsf{\Phi }}}_{21}={\overline{\mathsf{\Psi }}}_3$ and $\mathsf{\Lambda }={\mathsf{\Psi }}_2/2$. Note that ${\mathsf{\Psi }}_2$ and ${\mathsf{\Phi }}_{22}$ are real, while ${\mathsf{\Psi }}_3$ and ${\mathsf{\Psi }}_4$ are complex.

These four NP variables $\{{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,{\mathsf{\Psi }}_4,{\mathsf{\Phi }}_{22}\}$ can be classified based on how they transform under the little group $E\left(2\right)$. Under $E\left(2\right)$ transformation,

$$\begin{array}{c}{\mathsf{\Psi }}_2^{\prime }={\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3^{\prime }=e^{-i\vartheta }({\mathsf{\Psi }}_3+3\overline{\rho }{\mathsf{\Psi }}_2),\end{array}$$

(3)

$$\begin{array}{c}{\mathsf{\Psi }}_4^{\prime }=e^{-i2\vartheta }({\mathsf{\Psi }}_4+4\overline{\rho }{\mathsf{\Psi }}_3+6{\overline{\rho }}^2{\mathsf{\Psi }}_2),{\mathsf{\Phi }}_{22}^{\prime }={\mathsf{\Phi }}_{22}+2\rho {\mathsf{\Psi }}_3+2\overline{\rho }{\overline{\mathsf{\Psi }}}_3+6\rho \overline{\rho }{\mathsf{\Psi }}_2,\end{array}$$

(4)

where $\vartheta \in [0,2\pi )$ and $\rho$ is complex [17]. Using these, six classes are defined below [17],

Class II${}_6$

${\mathsf{\Psi }}_2\ne 0$; for any observer, there is the same ${\mathsf{\Psi }}_2\ne 0$ mode, but all other modes are observer-dependent;

Class III${}_5$

${\mathsf{\Psi }}_2=0$, ${\mathsf{\Psi }}_3\ne 0$; for any observer, there are the ${\mathsf{\Psi }}_2=0$ mode and the same ${\mathsf{\Psi }}_3\ne 0$ mode, but the remaining modes ${\mathsf{\Psi }}_4$ and ${\mathsf{\Phi }}_{22}$ are observer-dependent;

Class N${}_3$

${\mathsf{\Psi }}_2={\mathsf{\Psi }}_3=0,{\mathsf{\Psi }}_4\ne 0\ne {\mathsf{\Phi }}_{22}$;

Class N${}_2$

${\mathsf{\Psi }}_2={\mathsf{\Psi }}_3={\mathsf{\Phi }}_{22}=0,{\mathsf{\Psi }}_4\ne 0$;

Class O${}_1$

${\mathsf{\Psi }}_2={\mathsf{\Psi }}_3={\mathsf{\Psi }}_4=0,{\mathsf{\Phi }}_{22}\ne 0$;

Class O${}_0$

${\mathsf{\Psi }}_2={\mathsf{\Psi }}_3={\mathsf{\Psi }}_4={\mathsf{\Phi }}_{22}=0$; no wave is observed.

For Classes N${}_3$, N${}_4$ and N${}_5$, the presence or absence of all modes depends on the observer. Note that by setting $\rho =0$ in Equation (3), one finds out that ${\mathsf{\Psi }}_2$ and ${\mathsf{\Phi }}_{22}$ have a helicity of 0, ${\mathsf{\Psi }}_3$ has a helicity of 1 and ${\mathsf{\Psi }}_4$ has a helicity of 2.

The relation between $\{{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,{\mathsf{\Psi }}_4,{\mathsf{\Phi }}_{22}\}$ and the polarizations of the GW can be found by examining the linearized geodesic deviation equation [17],

$${\ddot{x}}^j=\frac{d^2{x}^j}{d{t}^2}=-R_{tjtk}{x}^k,$$

(5)

where $x^j$ gives the deviation vector between two nearby test particles and $j,k=1,2,3$. The electric component $R_{tjtk}$ is important and given by the following matrix,

$$R_{tjtk}=\left(\begin{array}{ccc}-\frac{1}{2}(\mathsf{\Re }{\mathsf{\Psi }}_4+{\mathsf{\Phi }}_{22})& \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& -2\mathsf{\Re }{\mathsf{\Psi }}_3\\ \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& \frac{1}{2}(\mathsf{\Re }{\mathsf{\Psi }}_4-{\mathsf{\Phi }}_{22})& 2\mathsf{\Im }{\mathsf{\Psi }}_3\\ -2\mathsf{\Re }{\mathsf{\Psi }}_3& 2\mathsf{\Im }{\mathsf{\Psi }}_3& -6{\mathsf{\Psi }}_2\end{array}\right),$$

(6)

where ℜ and ℑ represent the real and imaginary parts, respectively. Therefore, $\mathsf{\Re }{\mathsf{\Psi }}_4$ and $\mathsf{\Im }{\mathsf{\Psi }}_4$ donate the plus and the cross polarizations, respectively; ${\mathsf{\Phi }}_{22}$ gives the transverse breathing polarization, and ${\mathsf{\Psi }}_2$ gives the longitudinal polarization; finally, $\mathsf{\Re }{\mathsf{\Psi }}_3$ and $\mathsf{\Im }{\mathsf{\Psi }}_3$ stand for vector-x and vector-y polarizations, respectively. Or, one can also use $R_{tjtk}$ to label different polarizations.Tthe plus mode is labeled by ${\widehat{P}}_{+}=-R_{txtx}+R_{tyty}$, the cross mode is by ${\widehat{P}}_{\times }=R_{txty}$, the transverse breathing mode is donated by ${\widehat{P}}_b=R_{txtx}+R_{tyty}$, the vector-x mode is donated by ${\widehat{P}}_{xz}=R_{txtz}$, the vector-y mode is given by ${\widehat{P}}_{yz}=R_{tytz}$, and the longitudinal mode is given by ${\widehat{P}}_l=R_{tztz}$. According to the $E\left(2\right)$ classification, the longitudinal mode (${\mathsf{\Psi }}_2\ne 0$) belongs to Class ${\mathrm{II}}_6$, so all six polarizations exist in some coordinate systems.

One can apply the $E\left(2\right)$ classification to some paricular modified theories of gravity. For Brans–Dicke theory, one gets

$$R_{tjtk}^{\mathrm{BD}}=\left(\begin{array}{ccc}-\frac{1}{2}(\mathsf{\Re }{\mathsf{\Psi }}_4+{\mathsf{\Phi }}_{22})& \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& 0\\ \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& \frac{1}{2}(\mathsf{\Re }{\mathsf{\Psi }}_4-{\mathsf{\Phi }}_{22})& 0\\ 0& 0& 0\end{array}\right).$$

(7)

In the next sections, the plane GW solutions are calculated for $f\left(R\right)$ gravity, Horndeski theory, Einstein-æther theory, and generalized TeVeS theory. Then, the polarization contents are determined. We show that $E\left(2\right)$ classification cannot be applied to the massive mode in $f\left(R\right)$ gravity or Horndeski theory. It cannot be applied to the local Lorentz violating theories, for instance, Einstein-æther theory and generalized TeVeS theory, either.

3. Gravitational Wave Polarizations in $\mathit{f}\mathbf{\left(}\mathit{R}\mathbf{\right)}$ Gravity

$f\left(R\right)$ gravity has an action taking the following form [22],

$$S=\frac{1}{2\kappa }\int d^{4}x\sqrt{-g}f\left(R\right),$$

(8)

which can be reexpressed as

$$S=\frac{1}{2\kappa }\int d^{4}x\sqrt{-g}[f\left(\phi \right)+(R-\phi )f^{\prime }\left(\phi \right)],$$

(9)

where $f^{\prime }\left(\phi \right)=df\left(\phi \right)/d\phi$. So $f\left(R\right)$ gravity is equivalent to a scalar-tensor theory [23,24]. One varies the action to calculate the equations of motion,

$$f^{\prime }\left(R\right)R_{\mu \nu }-\frac{1}{2}f\left(R\right)g_{\mu \nu }-{\nabla }_{\mu }{\nabla }_{\nu }{f}^{\prime }\left(R\right)+g_{\mu \nu }\square f^{\prime }\left(R\right)=0,$$

(10)

where $\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }$. The trace of Equation (10) is thus

$$f^{\prime }\left(R\right)R+3\square f^{\prime }\left(R\right)-2f\left(R\right)=0.$$

(11)

If $f\left(R\right)=R+\alpha R^2$, Equation (10) becomes

$$R_{\mu \nu }-\frac{1}{2}{\eta }_{\mu \nu }R-2\alpha \left({\partial }_{\mu }{\partial }_{\nu }R-{\eta }_{\mu \nu }\square R\right)=0,$$

(12)

Taking the trace of Equation (12) or using Equation (11), one gets

$$(\square -m^2)R=0,$$

(13)

where $m^2=1/\left(6\alpha \right)$ with $\alpha >0$. GW170104 puts an upper bound on the graviton mass $m<m_b=7.7\times {10}^{-23}\mathrm{eV}/c^2$ [3].

Before discussing the GW solutions, let us point it out that there are several constraints on $f\left(R\right)$ theory from experiments, notably from the observations of binary pulsars. Refs. [34,35,36,37,38] studied the rate of the orbital decay of the binary pulsar system using the parameterized post-Newtonian (PPN) or the parameterized post-Keplerian formalisms. Refs. [39,40] also studied the solar system tests of $f\left(R\right)$ gravity and calculated the PPN parameters $\gamma$ and $\beta$. However, all of these works ignore the chameleon mechanism, which was taken into account by Ref. [41]. In this work, the authors considered the solar system tests and various constraints from the observations of cosmology and the binary pulsars.

Now, we want to get the GW solutions in the Minkowski background, so we perturb $g_{\mu \nu }$ about the fundamental metric ${\eta }_{\mu \nu }$ such that $g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$ with $h_{\mu \nu }$ of the first order, and define a new tensor

$${\overline{h}}_{\mu \nu }=h_{\mu \nu }-\frac{1}{2}{\eta }_{\mu \nu }h-2\alpha {\eta }_{\mu \nu }R.$$

(14)

Under a gauge transformation $x^{\mu }\to x^{\prime }{}^{\mu }=x^{\mu }+{ϵ}^{\mu }$, this tensor transforms according to

$${\overline{h}}_{\mu \nu }^{\prime }={\overline{h}}_{\mu \nu }-{\partial }_{\mu }{ϵ}_{\nu }-{\partial }_{\nu }{ϵ}_{\mu }+{\eta }_{\mu \nu }{\partial }_{\rho }{ϵ}^{\rho }.$$

(15)

So, in the transverse traceless gauge

$${\partial }^{\mu }{\overline{h}}_{\mu \nu }=0,\overline{h}={\eta }^{\mu \nu }{\overline{h}}_{\mu \nu }=0.$$

(16)

In this gauge, one obtains

$$\square {\overline{h}}_{\mu \nu }=0.$$

(17)

Therefore, Equations (13) and (17) are the equations of motion.

The plane wave solutions are given below:

$$\begin{array}{c}{\overline{h}}_{\mu \nu }=e_{\mu \nu }\exp \left(i{q}_{\mu }{x}^{\mu }\right)+c.c.,\end{array}$$

(18)

$$\begin{array}{c}R={\varphi }_1\exp \left(i{p}_{\mu }{x}^{\mu }\right)+c.c.,\end{array}$$

(19)

where $c.c.$ indicates the complex conjugation, $e_{\mu \nu }$ and ${\varphi }_1$ are the amplitudes with $q^{\nu }{e}_{\mu \nu }=0$ and ${\eta }^{\mu \nu }{e}_{\mu \nu }=0$, and $q_{\mu }$ and $p_{\mu }$ are the wave numbers satisfying ${\eta }^{\mu \nu }{q}_{\mu }{q}_{\nu }=0,{\eta }^{\mu \nu }{p}_{\mu }{p}_{\nu }=-m^2$.

3.1. Physical Degrees of Freedom

The number of physical degrees of freedom (d.o.f.) in $f\left(R\right)$ gravity can be determined using the Hamiltonian analysis. The action (9) is used to carry out the Hamiltonian analysis. The metric written in the standard Arnowitt–Deser–Misner (ADM) form [42] is,

$$d{s}^2=-N^{2}d{t}^2+h_{jk}(d{x}^j+N^{j}dt)(d{x}^k+N^{k}dt),$$

(20)

where N is the lapse function, $N^j$ is the shift function and $h_{jk}$ is the induced metric on the constant t slice ${\mathsf{\Sigma }}_t$. Set $n_{\mu }=-N{\nabla }_{\mu }t$, then $K_{\mu \nu }={\nabla }_{\mu }{n}_{\nu }+n_{\mu }{n}^{\rho }{\nabla }_{\rho }{n}_{\nu }$ is the exterior curvature. In terms of the ADM variables and setting $\kappa =1$ for simplicity, Equation (9) becomes

$$S=\int d^{4}xN\sqrt{h}\left[\frac{1}{2}{f}^{\prime }(\mathcal{R}-\phi )+\frac{1}{2}f+\frac{1}{2}{f}^{\prime }(K_{jl}{K}^{jl}-K^2)+\frac{K}{N}(N_j{D}^j{f}^{\prime }-f^{″}\dot{\phi })+D_j{f}^{\prime }{D}^j\ln N\right],$$

(21)

where $\mathcal{R}$ is the spatial Ricci scalar calculated with $h_{jk}$ and $K=h^{jk}{K}_{jk}$. Note that the action contains 11 dynamical variables: $N,N_j,h_{jk}$ and $\phi$. The calculation shows that there are four primary constraints:

$${\pi }^N=\frac{\delta S}{\delta \dot{N}}\approx 0,{\pi }^j=\frac{\delta S}{\delta {\dot{N}}_j}\approx 0.$$

(22)

After obtaining the conjugate momenta for $h_{jk}$ and $\phi$, one finds the following Hamiltonian:

$$H={\int }_{{\mathsf{\Sigma }}_t}{d}^{3}x\sqrt{h}(NC+N_j{C}^j),$$

(23)

where the boundary terms have been ignored. Then, the consistency conditions are checked which lead to four secondary constraints, i.e., $C\approx 0$ and $C^j\approx 0$. Finally, it is checked whether these are all the constraints within this theory. Since all the constraints belong to the first class, there are ${\displaystyle \frac{22-8\times 2}{2}}=3$, as expected.

3.2. Polarization Content

The polarizations of GWs are contained in the geodesic deviation equations. Let the GWs travel in the $+z$ direction with the following wave vectors:

$$q^{\mu }=\omega (1,0,0,1),p^{\mu }=(\mathsf{\Omega },0,0,\sqrt{{\mathsf{\Omega }}^2-m^2}),$$

(24)

for ${\overline{h}}_{\mu \nu }$ and R, respectively. From Equation (14), $h_{\mu \nu }={\overline{h}}_{\mu \nu }(t-z)-2\alpha {\eta }_{\mu \nu }R(vt-z)$ is obtained with $v=\sqrt{{\mathsf{\Omega }}^2-m^2}/\mathsf{\Omega }$. So, clearly, ${\overline{h}}_{\mu \nu }$ excites the plus and the cross polarizations. Now, ${\overline{h}}_{\mu \nu }=0$ is set, so the geodesic deviation equations are

$$\ddot{x}=\alpha \ddot{R}x,\ddot{y}=\alpha \ddot{R}y,\ddot{z}=-\alpha m^{2}Rz=-\frac{1}{6}Rz,$$

(25)

which states that the massive scalar field induces a mix of the longitudinal and the transverse breathing modes.

The NP formalism [17,18] is not suitable for identifying the polarizations of $f\left(R\right)$ gravity. Indeed, ${\mathsf{\Psi }}_2=0$ is found, which implies the absence of the longitudinal polarization according to the NP formalism. However, Equation (25) clearly means that the longitudinal polarization exists. Nevertheless, the six polarizations can still be described by $R_{tjtk}$.

4. Gravitational Wave Polarizations in Horndeski Theory

The action of Horndeski theory is [20]

$$S=\int d^{4}x\sqrt{-g}({\mathcal{L}}_2+{\mathcal{L}}_3+{\mathcal{L}}_4+{\mathcal{L}}_5),$$

(26)

where

$$\begin{array}{c}{\mathcal{L}}_2=K(\varphi ,X),{\mathcal{L}}_3=-G_3(\varphi ,X)\square \varphi ,{\mathcal{L}}_4=G_4(\varphi ,X)R+G_{4,X}\left[{(\square \varphi )}^2-\left({\nabla }_{\mu }{\nabla }_{\nu }\varphi \right)\left({\nabla }^{\mu }{\nabla }^{\nu }\varphi \right)\right],\\ {\mathcal{L}}_5=G_5(\varphi ,X)G_{\mu \nu }{\nabla }^{\mu }{\nabla }^{\nu }\varphi -\frac{1}{6}{G}_{5,X}\left[{(\square \varphi )}^3-3(\square \varphi )\left({\nabla }_{\mu }{\nabla }_{\nu }\varphi \right)\left({\nabla }^{\mu }{\nabla }^{\nu }\varphi \right)\right.\\ \left.+2\left({\nabla }^{\mu }{\nabla }_{\rho }\varphi \right)\left({\nabla }^{\rho }{\nabla }_{\nu }\varphi \right)\left({\nabla }^{\nu }{\nabla }_{\mu }\varphi \right)\right].\end{array}$$

Here, $X=-{\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi /2$, $\square \varphi ={\nabla }_{\mu }{\nabla }^{\mu }\varphi$, the functions K, $G_3$, $G_4$ and $G_5$ depend on $\varphi$ and X, and $G_{j,X}(\varphi ,X)=\partial G_j(\varphi ,X)/\partial X$ with $j=4,5$. Note that $G_3=G_5=0$, $K=f\left(\varphi \right)-\varphi f^{\prime }\left(\varphi \right)$ and $G_4=f^{\prime }\left(\varphi \right)$ with $f^{\prime }\left(\varphi \right)=df\left(\varphi \right)/d\varphi$ can be set to reproduce $f\left(R\right)$ gravity.

Since the observation of GW170817 and GRB 170817A [5,43,44], many alternative theories of gravity have been highly constrained by the speed bound of the GW [45],

$$-3\times {10}^{-15}\le \frac{v_{\mathrm{GW}}-v_{\mathrm{EM}}}{v_{\mathrm{EM}}}\le 7\times {10}^{-16},$$

(27)

where $v_{\mathrm{GW}}$ is the speed of the GW, and $v_{\mathrm{EM}}$ is that of the photon, usually taken to be 1. This bound also severely constrains the Horndeski theory. The analyses done in Refs. [46,47,48,49] showed that $G_4=G_4\left(\varphi \right)$ and $G_5=0$. Ref. [50] discussed the constraints on Horndeski theory from the solar system test. For more constraints derived from the GW speed bound, please refer to Refs. [48,51,52].

4.1. Gravitational Wave Solutions

To find the GW solutions in the Minkowski background, the metric tensor and the scalar field are perturbed such that $g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$ and $\varphi ={\varphi }_0+\phi$ with ${\varphi }_0$ a constant. The consistence of the equations of motion leads to $K({\varphi }_0,0)=0$ and $K_{,{\varphi }_0}{=\partial K(\varphi ,X)/\partial \varphi |}_{\varphi ={\varphi }_0,X=0}=0$. The linearized equations of motion are

$$(\square -m^2)\phi =0,G_{\mu \nu }^{\left(1\right)}-\frac{G_{4,{\varphi }_0}}{G_4\left(0\right)}({\partial }_{\mu }{\partial }_{\nu }\phi -{\eta }_{\mu \nu }\square \phi )=0,$$

(28)

where $G_{\mu \nu }^{\left(1\right)}$ is the linear Einstein tensor, $G_4\left(0\right)=G_4({\varphi }_0,0)$, $K_{,X_0}{=\partial K(\varphi ,X)/\partial X|}_{\varphi ={\varphi }_0,X=0}$. The scalar field is generally massive, and its mass squared is

$$m^2=-\frac{K_{,{\varphi }_0{\varphi }_0}}{K_{,X_0}-2G_{3,{\varphi }_0}+3G_{4,{\varphi }_0}^2/G_4\left(0\right)}.$$

(29)

Analogously to Equation (14), a field ${\tilde{h}}_{\mu \nu }$ is introduced,

$${\tilde{h}}_{\mu \nu }=h_{\mu \nu }-\frac{1}{2}{\eta }_{\mu \nu }{\eta }^{\rho \sigma }{h}_{\rho \sigma }-\frac{G_{4,{\varphi }_0}}{G_4\left(0\right)}{\eta }_{\mu \nu }\phi ,$$

(30)

and in the transverse traceless gauge ${\partial }_{\mu }{\tilde{h}}^{\mu \nu }=0$, ${\eta }^{\mu \nu }{\tilde{h}}_{\mu \nu }=0$ by using the gauge freedom, Equation (28) become,

$$(\square -m^2)\phi =0,\square {\tilde{h}}_{\mu \nu }=0.$$

(31)

4.2. Polarization Content

The similarity between Equations (13), (17) and (31) makes it clear that there are plus and the cross polarizations, and the massive scalar field $\varphi$ excites a mix of the transverse breathing and the longitudinal polarizations. The electric component $R_{tjtk}$ can be calculated, given the below equation:

$$R_{tjtk}=\left(\begin{array}{ccc}-\frac{1}{2}{q}_t^2\sigma \phi +\frac{1}{2}{\mathsf{\Omega }}^2{\tilde{h}}_{xx}& \frac{1}{2}{\mathsf{\Omega }}^2{\tilde{h}}_{xy}& 0\\ \frac{1}{2}{\mathsf{\Omega }}^2{\tilde{h}}_{xy}& -\frac{1}{2}{q}_t^2\sigma \phi -\frac{1}{2}{\mathsf{\Omega }}^2{\tilde{h}}_{xx}& 0\\ 0& 0& -\frac{1}{2}{m}^2\sigma \phi \end{array}\right),$$

(32)

for a GW with wave vectors given by Equation (24), and $\sigma =G_{4,{\varphi }_0}/G_4\left(0\right)$. From this, it is found out that ${\tilde{h}}_{\mu \nu }$ excites the plus and the cross polarizations by setting $\phi =0$. Now, ${\tilde{h}}_{\mu \nu }=0$ is set. If the scalar field is massless ($m=0$), then $R_{tztz}=0$, so $\phi$ excites merely the transverse breathing polarization ($R_{txtx}=R_{tyty}$). If $m\ne 0$, in the rest frame of the scalar field ($q_z=0$), the geodesic deviation equations are,

$${\ddot{x}}^j=\frac{1}{2}{m}^2\sigma \phi x^j,j=1,2,3.$$

(33)

Integrating the above equations twice leads to

$$\delta x^j\approx -\frac{1}{2}\sigma \phi x_0^j$$

(34)

with $x_0^j$ being the initial deviation vector. Equation (34) implies that the massive scalar field induces the longitudinal polarization together with the breathing polarization.

In a generic frame where $q_z\ne 0$, one has

$$\delta x\approx -\frac{1}{2}\sigma \phi x_0,\delta y\approx -\frac{1}{2}\sigma \phi y_0,\delta z\approx -\frac{1}{2}\frac{m^2}{q_t^2}\sigma \phi z_0.$$

(35)

From this, it is clearly shown that when $m\ne 0$, the scalar field excites a mix of the longitudinal and transverse breathing polarizations, while when $m=0$, it excites merely the transverse breathing mode.

The NP variables can also be calculated. One obtains

$${\mathsf{\Psi }}_2=\frac{1}{12}(R_{txtx}+R_{tyty}-2R_{tztz}+2R_{xyxy}-R_{xzxz}-R_{yzyz})+\frac{1}{2}i{R}_{tzxy}=0,$$

(36)

as well as several nonvanishing NP variables:

$$\begin{array}{c}{\mathsf{\Psi }}_4=-{\omega }^2({\tilde{h}}_{xx}-i{\tilde{h}}_{xy}),{\mathsf{\Phi }}_{22}=\frac{{(\mathsf{\Omega }+\sqrt{{\mathsf{\Omega }}^2-m^2})}^2}{4}\sigma \phi ,\end{array}$$

(37)

$$\begin{array}{c}{\mathsf{\Phi }}_{00}=\frac{4{(\mathsf{\Omega }-\sqrt{{\mathsf{\Omega }}^2-m^2})}^2}{{(\mathsf{\Omega }+\sqrt{{\mathsf{\Omega }}^2-m^2})}^2}{\mathsf{\Phi }}_{22},{\mathsf{\Phi }}_{11}=-\mathsf{\Lambda }=\frac{4m^2}{{(\mathsf{\Omega }+\sqrt{{\mathsf{\Omega }}^2-m^2})}^2}{\mathsf{\Phi }}_{22}.\end{array}$$

(38)

Note that for null GWs, only ${\mathsf{\Psi }}_2=-R_{tztz}/6$, and in general cases, we should use Equation (36). Next, $R_{tjtk}$ is expressed in terms of NP variables,

$$R_{tjtk}=\left(\begin{array}{ccc}\mathsf{{\rm Y}}-\frac{1}{2}\mathsf{\Re }{\mathsf{\Psi }}_4& \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& 0\\ \frac{1}{2}\mathsf{\Im }{\mathsf{\Psi }}_4& \mathsf{{\rm Y}}+\frac{1}{2}\mathsf{\Re }{\mathsf{\Psi }}_4& 0\\ 0& 0& -2(\mathsf{\Lambda }+{\mathsf{\Phi }}_{11})\end{array}\right),$$

(39)

with $\mathsf{{\rm Y}}=-2\mathsf{\Lambda }-\frac{{\mathsf{\Phi }}_{00}+{\mathsf{\Phi }}_{22}}{2}$. The difference from Equation (7) is that the NP formalism fails to identify the polarization content of the massive mode.

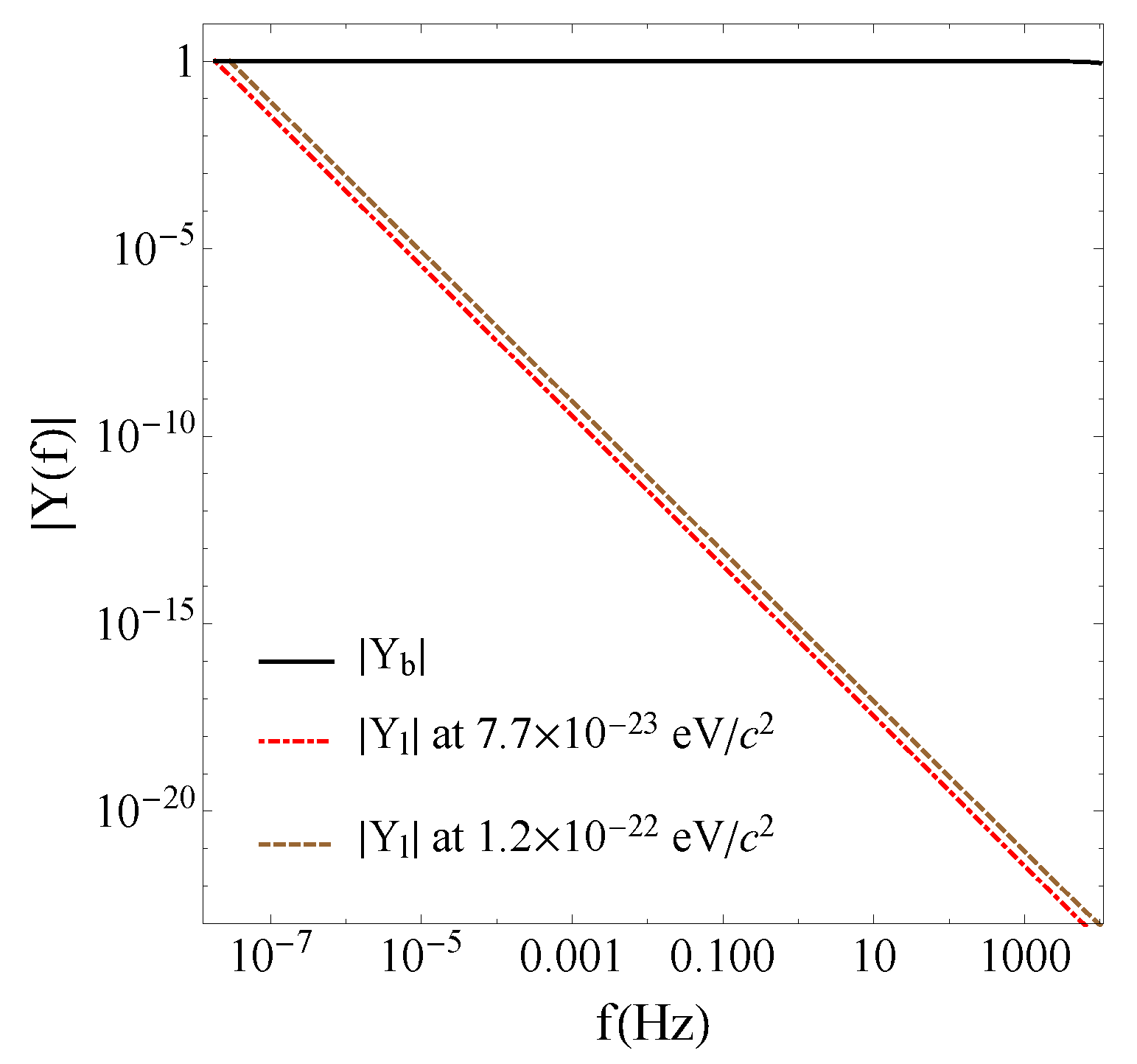
4.3. Experimental Tests

The detection of GWs by interferometers is done to measure the differences in the changes in the propagation times of photons traveling in the two arms. The interferometer response function is important [25,53]. It is defined to be the Fourier transform of the change in the round-trip propagation time of photons traveling in a single arm. To calculate it for the longitudinal polarization, we assume that the arm is pointing in the propagating direction of the GW, while, for the transverse breathing polarization, the arm is in the direction perpendicular to the propagating direction. Figure 1 displays the absolute values of the response functions for the longitudinal and the transverse breathing polarizations for aLIGO if the mass of $\phi$ is $1.2\times {10}^{-22}\mathrm{eV}/c^2$ [1] or $7.7\times {10}^{-23}$ eV/$c^2$ [3]. This graph shows that interferometers such as aLIGO are not suitable for testing the probe of longitudinal polarization.

A second method to detect GWs is to use pulsar timing arrays (PTAs) [54,55,56,57,58,59,60]. The propagation of radial pulses emanating from pulsars is affected by the stochastic GW background. It causes the timing residuals $\tilde{R}\left(t\right)$ which can be detected and measured by PTAs [54]. The timing residuals of two pulsars (labeled i and j) are correlated, which is characterized by the cross-correlation function $C\left(\theta \right)=\langle {\tilde{R}}_i\left(t\right){\tilde{R}}_j\left(t\right)\rangle$, where $\theta$ is the angle between the two pulsars. The brackets imply the ensemble average over the stochastic GW background. Figure 2 shows the behaviors of $\zeta \left(\theta \right)=C\left(\theta \right)/C\left(0\right)$ for different polarizations. The solid black curve shows $\zeta \left(\theta \right)$ induced by ${\tilde{h}}_{\mu \nu }$, and the dashed blue curve is for the massless scalar field $\phi$. The remaining three curves represent $\zeta \left(\theta \right)$, induced by the mixed polarization of the transverse and longitudinal ones when $m\ne 0$ at different values of $\alpha$, which is called the power–law index [55]. From Figure 2, it is possible to identify the polarizations of GWs. Note that Figure 2 shows the cross-correlation functions for the pure tensor and the pure scalar modes, while, in the actual detection, both modes exist. So in reality, the cross-correlation function should be some combination of these for the pure modes. In order to calculate it, one has to know the energy density of each mode, or at least, the ratio between the tensor and the scalar modes. However, the energy densities or their ratio depend on the processes that generate the stochastic GW background. Calculating them is beyond the scope of the present work. Nevertheless, Figure 2 shows the possibility of distinguishing different polarizations. The mass of the scalar field also affects the cross-correlation function for the mixed polarization of the transverse and the longitudinal polarizations. Figure 3 shows $\zeta \left(\theta \right)$ for the massless (labeled by Breathing) and the massive (five different masses in units of $m_b$) scalar field. It is shown that $\zeta \left(\theta \right)$ for $\phi$ is changes quite a lot with small masses ($m\le m_b$), while, for larger masses, $\zeta \left(\theta \right)$ remains almost the same.

5. Gravitational Wave Polarizations in Einstein-æther Theory and Generalized TeVeS Theory

Finally, we briefly talk about the GW polarizations in Einstein-æther theory [29] as well as generalized TeVeS Theory [30,31,32]. These theories have more d.o.f., which excite more polarizations. They both contain the unit timelike vector fields, so the local Lorentz invariance is violated. This allows superluminal propagation. Although all polarizations are massless, NP formalism cannot be applied either. The experimental constraints and the implications for the future experimental tests of these theories can be found in Refs. [33,61].

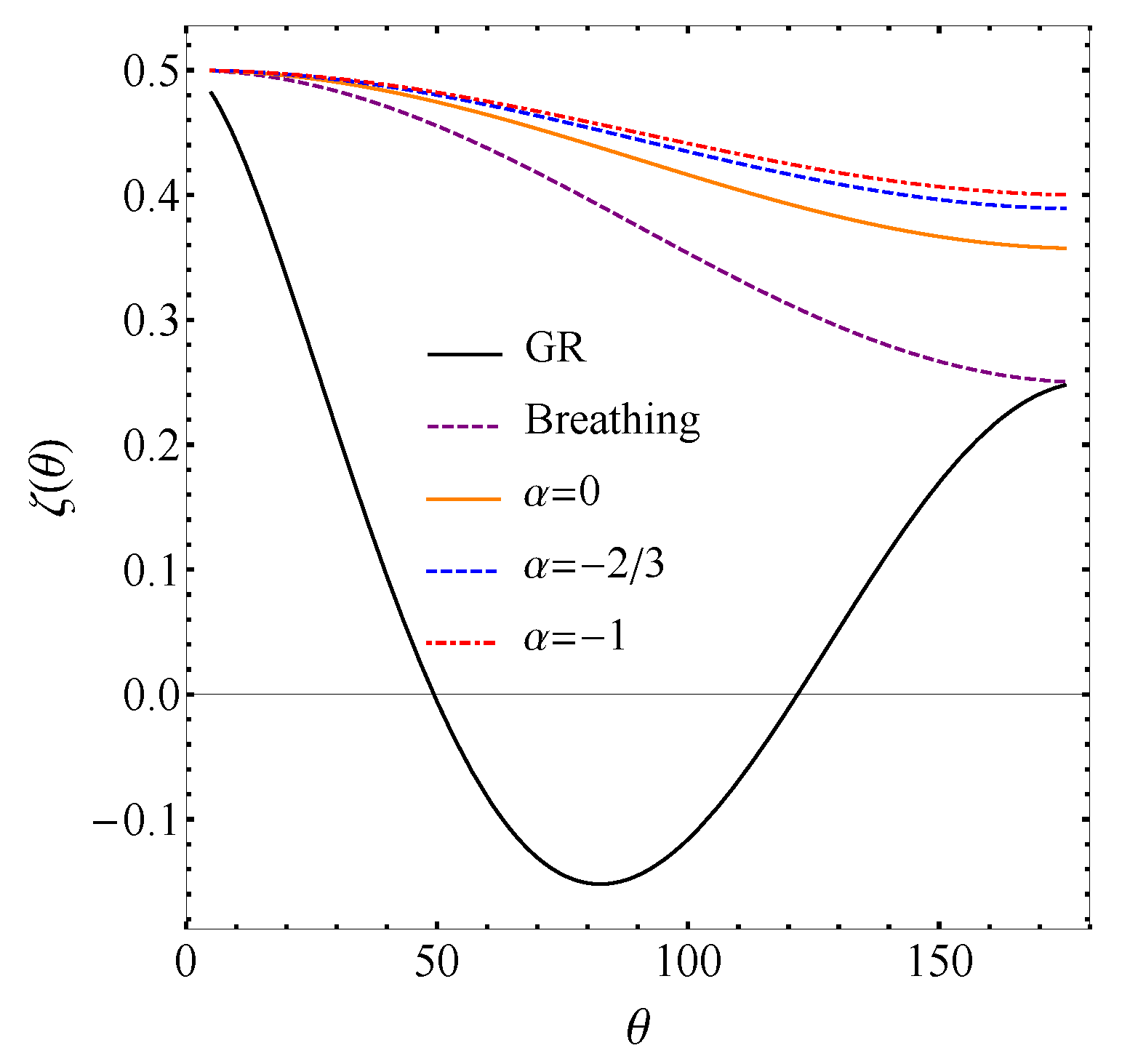
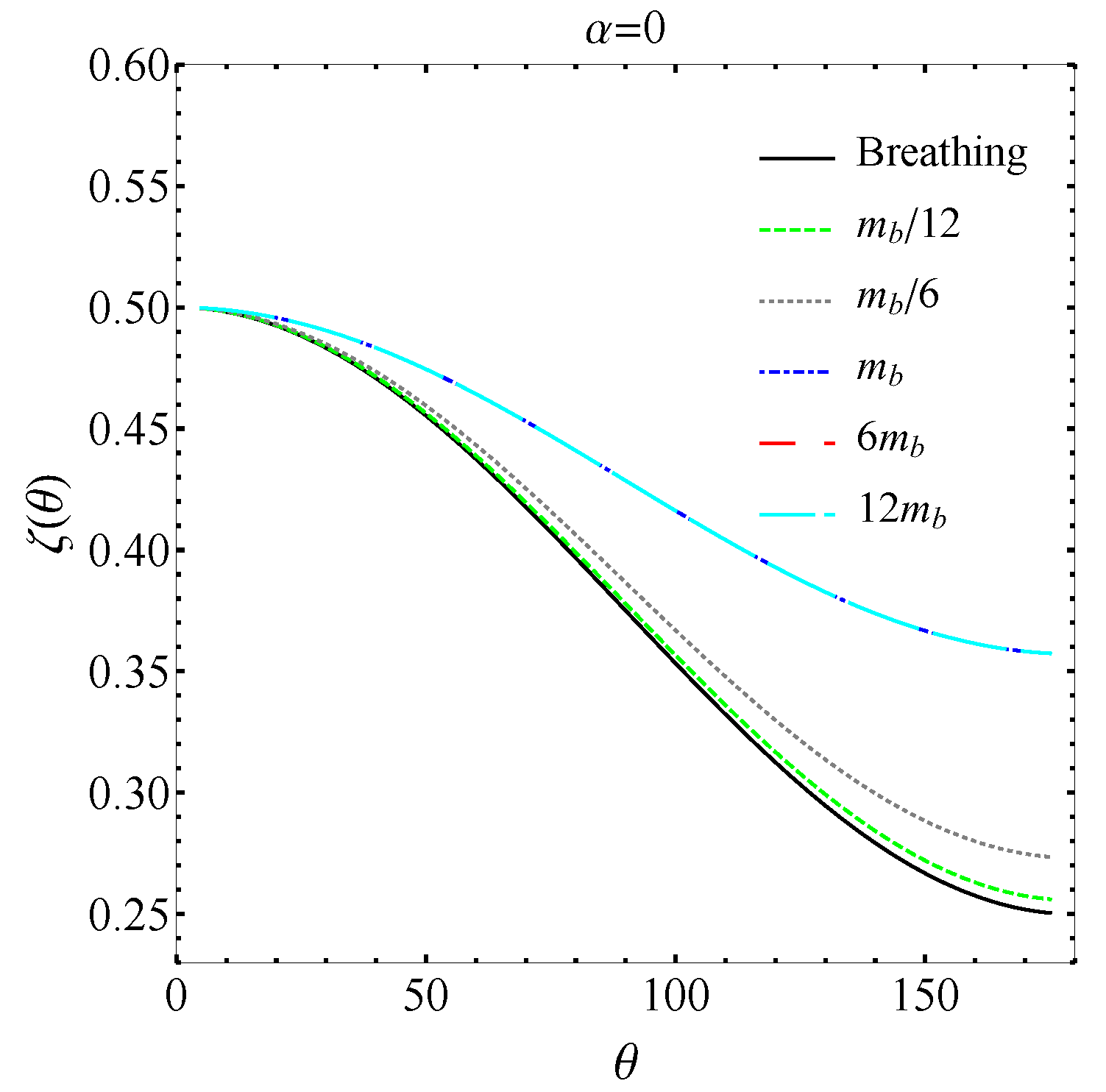
5.1. Einstein-æther Theory

Einstein-æther theory contains the metric tensor $g_{\mu \nu }$ and the æther field $u^{\mu }$ to mediate gravity. The action is

$$\begin{array}{cc}\hfill S_{\mathrm{EH}-\mathsf{\ae }}=& \frac{1}{16\pi G}\int {\mathrm{d}}^{4}x\sqrt{-g}[R-c_1\left({\nabla }_{\mu }{u}_{\nu }\right){\nabla }^{\mu }{u}^{\nu }-c_2{\left({\nabla }_{\mu }{u}^{\mu }\right)}^2-c_3\left({\nabla }_{\mu }{u}_{\nu }\right){\nabla }^{\nu }{u}^{\mu }\hfill \\ & +c_4\left(u^{\rho }{\nabla }_{\rho }{u}^{\mu }\right)u^{\sigma }{\nabla }_{\sigma }{u}_{\mu }+\lambda (u^{\mu }{u}_{\mu }+1)],\hfill \end{array}$$

(40)

where G is the gravitational constant, $\lambda$ is a Lagrange multiplier, and $c_i(i=1,2,3,4)$ are the coupling constants. A special solution solves the equations of motion, i.e., $g_{\mu \nu }={\eta }_{\mu \nu }$ and $u^{\mu }={\underline{u}}^{\mu }={\delta }_0^{\mu }$. Linearizing the equations of motion ($g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$ and $u^{\mu }={\underline{u}}^{\mu }+v^{\mu }$), and using the gauge-invariant variables defined in Ref. [33], one obtains the following equations of motion

$$\begin{array}{c}\frac{c_{14}}{2-c_{14}}[c_{123}(1+c_2+c_{123})-2{(1+c_2)}^2]\ddot{\mathsf{\Omega }}+c_{123}{\nabla }^2\mathsf{\Omega }=0,\end{array}$$

(41)

$$\begin{array}{c}{c}_{14}{\ddot{\mathsf{\Sigma }}}_j-\frac{c_1-c_1^2/2+c_3^2/2}{1-c_{13}}{\nabla }^2{\mathsf{\Sigma }}_j=0,\end{array}$$

(42)

$$\begin{array}{c}\frac{1}{2}(c_{13}-1){\ddot{h}}_{jk}^{\mathrm{TT}}+\frac{1}{2}{\nabla }^2{h}_{jk}^{\mathrm{TT}}=0,\end{array}$$

(43)

where $c_{13}=c_1+c_3$, $c_{14}=c_1+c_4$, and $c_{123}=c_1+c_2+c_3$. There are five propagating d.o.f., and they propagate at three speeds. The squared speeds are given by

$$s_g^2=\frac{1}{1-c_{13}},s_v^2=\frac{c_1-c_1^2/2+c_3^2/2}{c_{14}(1-c_{13})},s_s^2=\frac{c_{123}(2-c_{14})}{c_{14}(1-c_{13})(2+2c_2+c_{123})}.$$

(44)

These speeds generally differ from one another and 1. In fact, the lack of the gravitational Cherenkov radiation requires them to be superluminal [62].

The polarization content can be obtained in terms of the gauge-invariant variables [63],

$$R_{tjtk}=-\frac{1}{2}{\ddot{h}}_{jk}^{\mathrm{TT}}+{\dot{\mathsf{\Xi }}}_{(j,k)}+{\mathsf{\Phi }}_{,jk}-\frac{1}{2}\ddot{\mathsf{\Theta }}{\delta }_{jk}.$$

(45)

Again, it is assumed that the GWs have the following wave vectors:

$$k_s^{\mu }={\omega }_s(1,0,0,1/s_s),k_v^{\mu }={\omega }_v(1,0,0,1/s_v),k_g^{\mu }={\omega }_g(1,0,0,1/s_g),$$

(46)

for the scalar, vector and tensor GWs, respectively. The calculation reveals that there are five polarization states. The plus polarization is represented by ${\widehat{P}}_{+}=-R_{txtx}+R_{tyty}={\ddot{h}}_{+}$, and the cross polarization is ${\widehat{P}}_{\times }=R_{txty}=-{\ddot{h}}_{\times }$; the vector-x polarization is donated by ${\widehat{P}}_{xz}=R_{txtz}\propto {\partial }_3{\dot{\mathsf{\Sigma }}}_1$, and the vector-y polarization is ${\widehat{P}}_{yz}=R_{txty}\propto {\partial }_3{\dot{\mathsf{\Sigma }}}_2$; the transverse breathing polarization is specified by ${\widehat{P}}_b=R_{txtx}+R_{tyty}\propto \stackrel{⃛}{\mathsf{\Omega }}$, and the longitudinal polarization is ${\widehat{P}}_l=R_{tztz}\propto \stackrel{⃛}{\mathsf{\Omega }}$. Note that $\mathsf{\Omega }$ excites both the transverse breathing and the longitudinal modes, so $\mathsf{\Omega }$ excites a mixed state of ${\widehat{P}}_b$ and ${\widehat{P}}_l$ [21,64].

Although the five polarizations are null, the NP formalism cannot be applied, as they propagate at speeds other than 1. Indeed, the calculation showed that none of the NP variables vanish in general [33].

Finally, let us mention that Einstein-æther theory is highly constrained by various experimental observations, especially the speed bound derived from GW170817 and GRB 170817A [5,43,44,45]. Apart from this speed bound and the absence of the gravitational Cherenkov radiation, there are constraints from the observations of pulsars (such as the post-Newtonian parameters, $|{\alpha }_1|<4\times {10}^{-5}$ [65] and $|{\alpha }_2|<2\times {10}^{-9}$ [66,67]1), and the requirement that the energy carried by GW be positive ($(2c_1-c_1^2+c_3^2)(1-c_{13})>0$ and $c_{14}(2-c_{14})>0$ [68]), etc. In addition, Refs. [69,70] specifically obtained the constraints on this theory based on the orbital evolution of the binary pulsars. Combining all these observational constraints, it is found that all of the coupling constants ($c_i$s) are of the order of ${10}^{-9}\sim {10}^{-15}$ if all speeds are of the order 1. For more details, please refer to Refs. [33,71].

5.2. Generalized TeVeS Theory

Tensor-Vector-Scalar (TeVeS) theory is the relativistic realization of Milgrom’s modified Newtonian dynamics (MOND) [30,72,73,74]. It has an additional scalar field $\sigma$ to mediate gravity. The vector field $u^{\mu }$ has an action similar to that of the electromagnetic field. Later, it was generalized and replaced by the action for the æther field to solve some of the problems which TeVeS theory suffers from [31]. The new theory is simply called the generalized TeVeS theory, whose actions include Equation (40) and the one for the scalar field:

$$S_{\sigma }=-\frac{8\pi }{j^2{\ell }^{2}G}\int {\mathrm{d}}^{4}x\sqrt{-g}\mathcal{F}\left(j{\ell }^2{j}^{\mu \nu }{\sigma }_{,\mu }{\sigma }_{,\nu }\right),$$

(47)

where $j^{\mu \nu }=g^{\mu \nu }-u^{\mu }{u}^{\nu }$, $j>0$ is dimensionless, and ℓ is a constant with the dimension of length. The dimensionless function, $\mathcal{F}$, must have the property to reproduce the relativistic MOND phenomena.

We use a similar method to obtain the polarization content for this theory as for Einstein-æther theory. Compared with Einstein-æther theory, this theory has one additional polarization state: a mix polarization of the longitudinal and transverse breathing polarizations due to the new d.o.f. $\sigma$. This polarization state is also massless and travels at a fourth speed other than 1. So, the NP formalism cannot be applied to this theory, either.

Ref. [33] also discussed the constraints that the generalized TeVeS theory should satisfy. Similarly to Einstein-æther theory, it is also constrained by the solar system test (i.e., the constraints on ${\alpha }_1$ and ${\alpha }_2$2), the absence of the gravitational Cherenkov radiation, and the recent GW speed bound [45], etc. Taking all the constraints into account, it was found that the speed of the one of scalar d.o.f. is much greater than 1, in general. A very large scalar speed might lead to the strong coupling of the scalar field, and if that happens, the linearization cannot be applied. Ref. [33] discussed the conditions for the strong coupling to take place. The analysis showed that in some parameter regions, the strong coupling does not happen, so this theory should be excluded. However, in other parameter regions, the strong coupling exists, and the validity of the theory remains to be determined by further analysis. For details, please refer to Ref. [33].

6. Conclusions

In this talk, we discussed the polarization contents in several alternative theories of gravity: $f\left(R\right)$ gravity, Horndeski theory, Einstein-æther theory, and generalized TeVeS theory. Each theory predicts at least one extra polarization states due to the additional d.o.f. provided by it. In the case of the local Lorentz invariant theories, such as $f\left(R\right)$ gravity and Horndeski theory, the massive scalar field excites a mix of ${\widehat{P}}_l$ and ${\widehat{P}}_b$; the massless scalar field induces merely ${\widehat{P}}_b$. For the local Lorentz violating theories, such as Einstein-æther theory and generalized TeVeS theory, each of the scalar d.o.f. is massless, but it propagates at speeds different from 1, so it also excites a mix of ${\widehat{P}}_l$ and ${\widehat{P}}_b$. Einstein-æther theory and generalized TeVeS theory also have vector polarizations due to the presence of the vector fields. $E\left(2\right)$ classification was designed to categorize the polarizations for the null GWs in the local Lorentz invariant theories, so it cannot be applied to these theories discussed in this talk. The observational tests of the extra polarizations were also discussed. The analysis showed that the interferometers are not sensitive to the longitudinal polarization which might be detected using PTAs.