The Polarizations of Gravitational Waves †
Abstract
1. Introduction
2. Review of Classification
- Class II
- ; for any observer, there is the same mode, but all other modes are observer-dependent;
- Class III
- , ; for any observer, there are the mode and the same mode, but the remaining modes and are observer-dependent;
- Class N
- ;
- Class N
- ;
- Class O
- ;
- Class O
- ; no wave is observed.
3. Gravitational Wave Polarizations in Gravity
3.1. Physical Degrees of Freedom
3.2. Polarization Content
4. Gravitational Wave Polarizations in Horndeski Theory
4.1. Gravitational Wave Solutions
4.2. Polarization Content
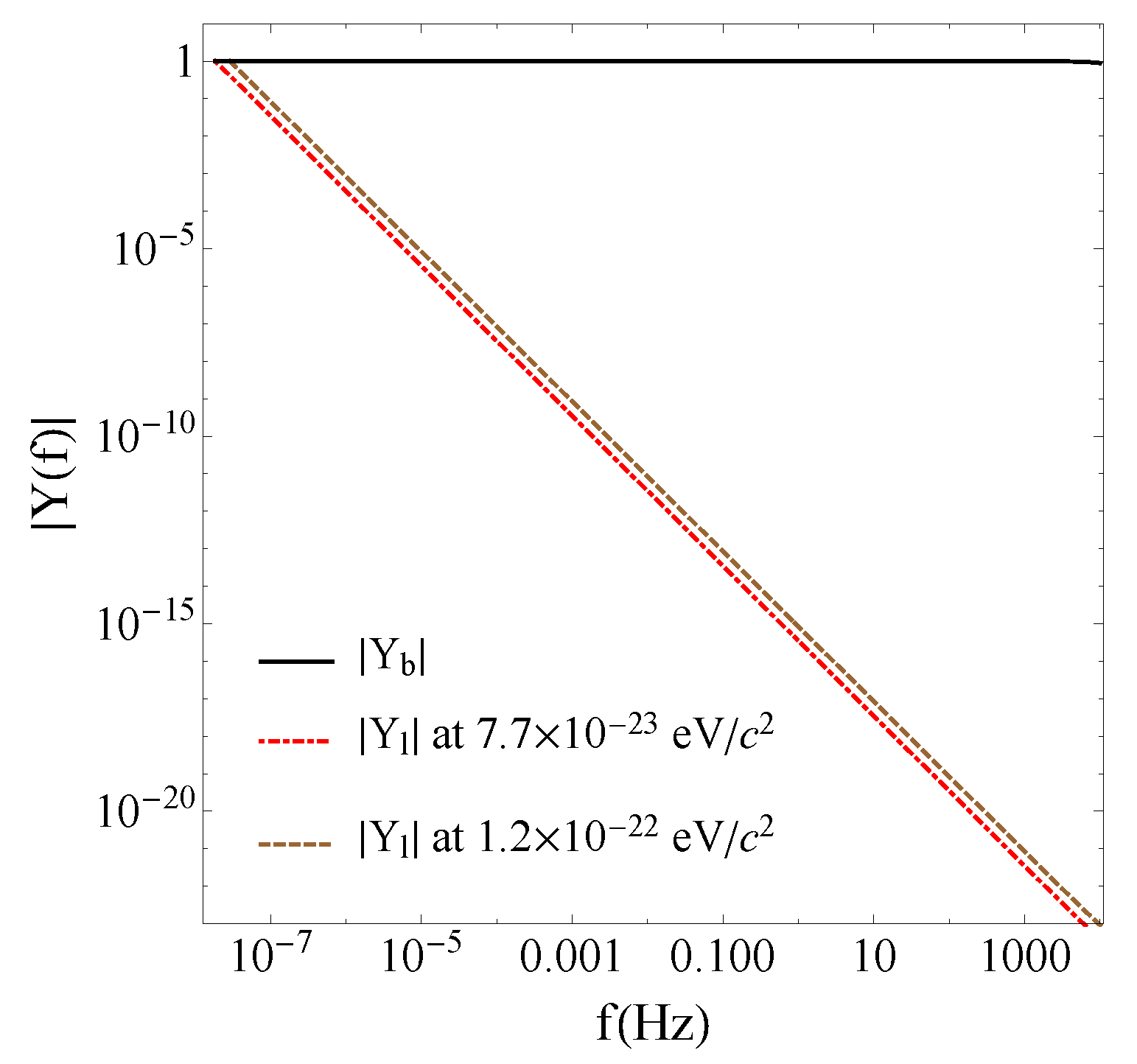
4.3. Experimental Tests
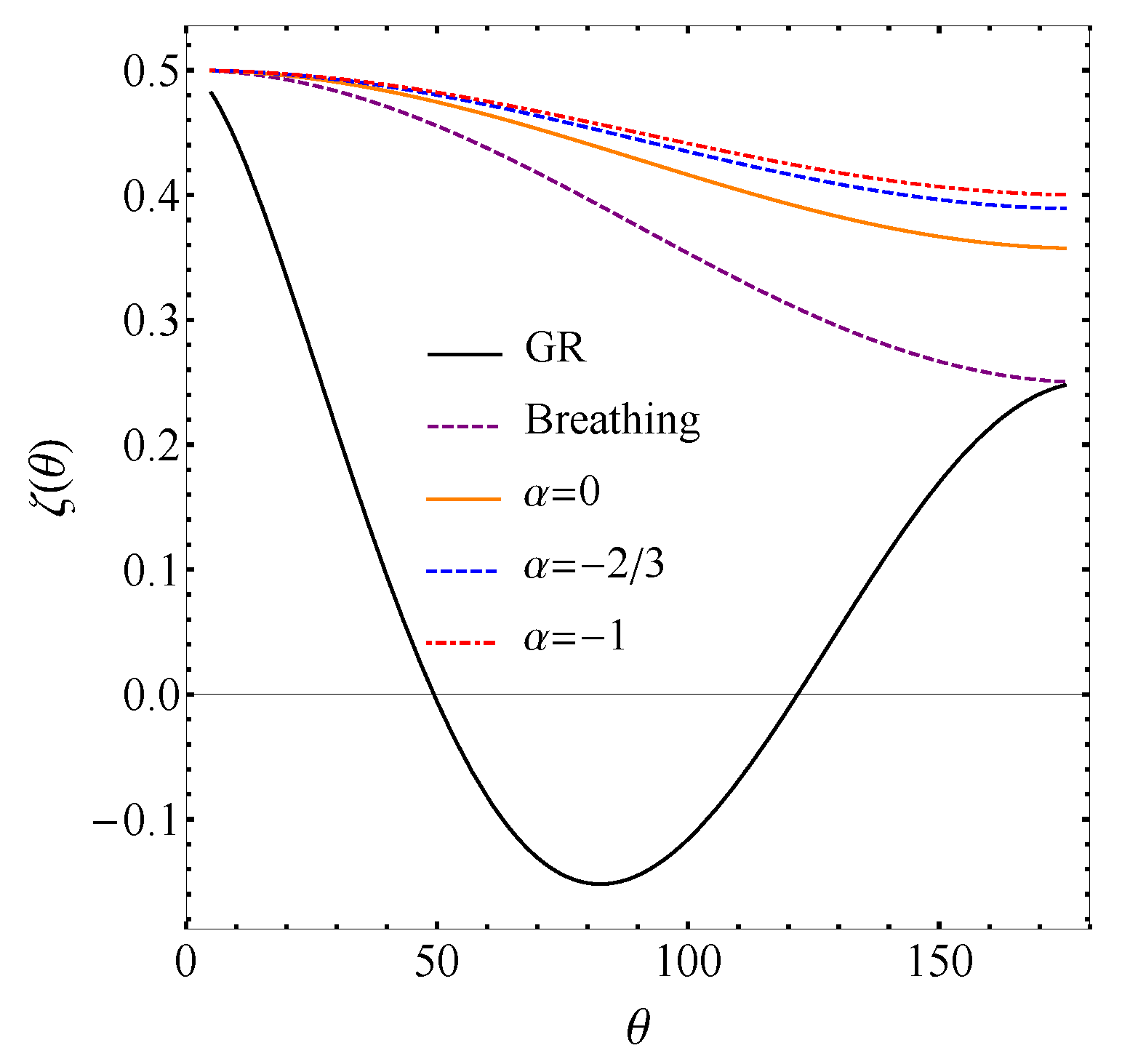
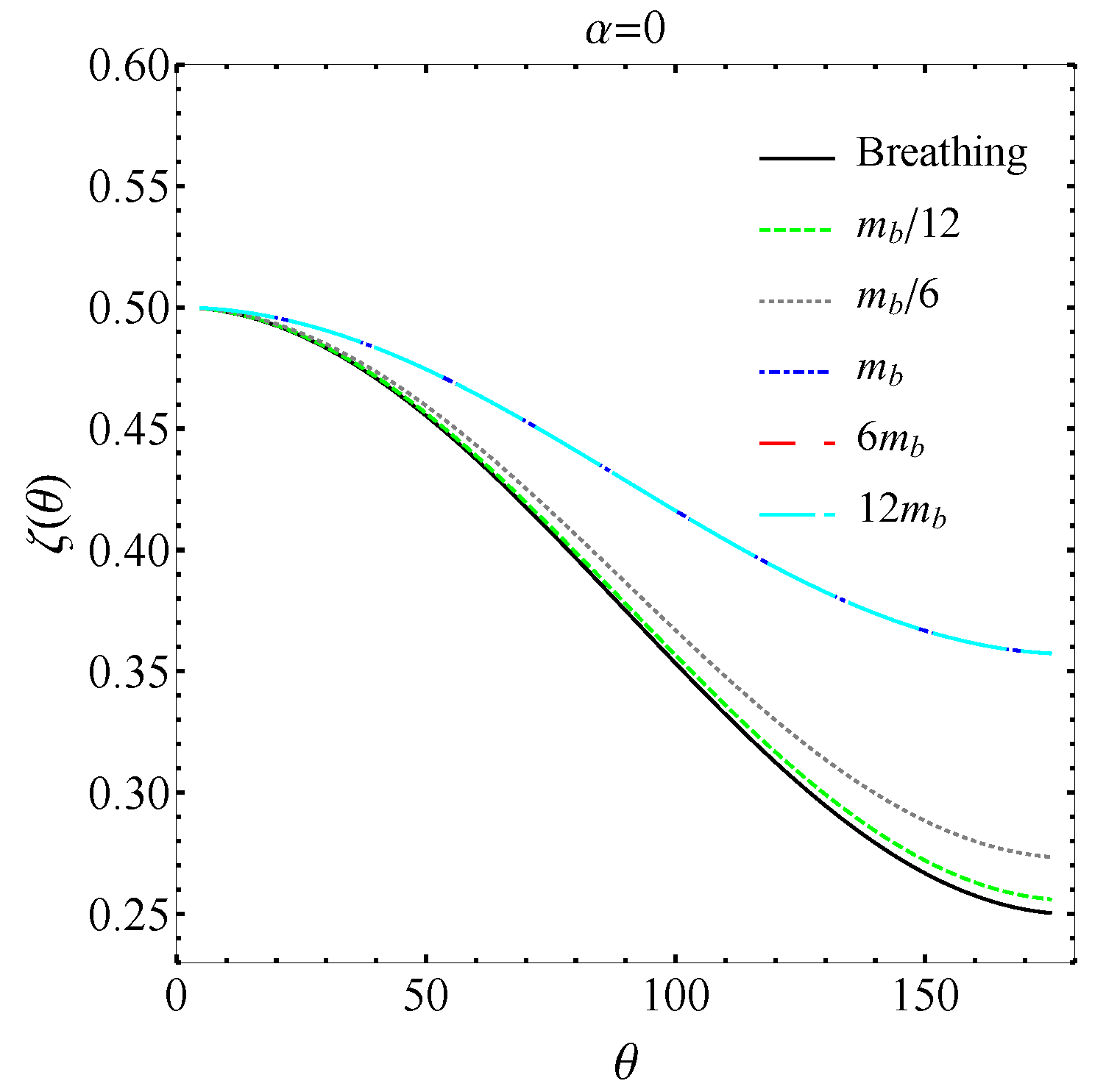
5. Gravitational Wave Polarizations in Einstein-æther Theory and Generalized TeVeS Theory
5.1. Einstein-æther Theory
5.2. Generalized TeVeS Theory
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Scientific, L.I.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Isi, M.; Weinstein, A.J.; Mead, C.; Pitkin, M. Detecting Beyond-Einstein Polarizations of Continuous Gravitational Waves. Phys. Rev. D 2015, 91, 082002. [Google Scholar] [CrossRef]
- Isi, M.; Pitkin, M.; Weinstein, A.J. Probing Dynamical Gravity with the Polarization of Continuous Gravitational Waves. Phys. Rev. D 2017, 96, 042001. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv, 2017; arXiv:1702.00786. [Google Scholar]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quant. Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Hobbs, G.; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N.D.; Burgay, M.; Burke-Spolaor, S.; Champion, D.; Cognard, I.; et al. The international pulsar timing array project: Using pulsars as a gravitational wave detector. Class. Quant. Gravity 2010, 27, 084013. [Google Scholar] [CrossRef]
- Kramer, M.; Champion, D.J. The European Pulsar Timing Array and the Large European Array for Pulsars. Class. Quant. Gravity 2013, 30, 224009. [Google Scholar] [CrossRef]
- Prasia, P.; Kuriakose, V.C. Detection of massive Gravitational Waves using spherical antenna. Int. J. Mod. Phys. D 2014, 23, 1450037. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First search for nontensorial gravitational waves from known pulsars. Phys. Rev. Lett. 2018, 120, 031104. [Google Scholar] [CrossRef] [PubMed]
- Newman, E.; Penrose, R. An Approach to Gravitational Radiation by a Method of Spin Coefficients. J. Math. Phys. 1962, 3, 566–578. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lee, D.L.; Lightman, A.P. Gravitational-wave observations as a tool for testing relativistic gravity. Phys. Rev. D 1973, 8, 3308–3321. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lee, D.L.; Lightman, A.P.; Wagoner, R.V.; Will, C.M. Gravitational-wave observations as a tool for testing relativistic gravity. Phys. Rev. Lett. 1973, 30, 884–886. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Hou, S.; Gong, Y.; Liu, Y. Polarizations of Gravitational Waves in Horndeski Theory. Eur. Phys. J. C 2018, 78, 378. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- O’Hanlon, J. Intermediate-Range Gravity: A Generally Covariant Model. Phys. Rev. Lett. 1972, 29, 137–138. [Google Scholar] [CrossRef]
- Teyssandier, P.; Tourrenc, P. The Cauchy problem for the R+R2 theories of gravity without torsion. J. Math. Phys. 1983, 24, 2793–2799. [Google Scholar] [CrossRef]
- Corda, C. The production of matter from curvature in a particular linearized high order theory of gravity and the longitudinal response function of interferometers. J. Cosmol. Astropart. Phys. 2007, 2007, 009. [Google Scholar] [CrossRef]
- Corda, C. Massive gravitational waves from the R**2 theory of gravity: Production and response of interferometers. Int. J. Mod. Phys. A 2008, 23, 1521–1535. [Google Scholar] [CrossRef]
- Capozziello, S.; Corda, C.; De Laurentis, M.F. Massive gravitational waves from f(R) theories of gravity: Potential detection with LISA. Phys. Lett. B 2008, 669, 255–259. [Google Scholar] [CrossRef]
- Liang, D.; Gong, Y.; Hou, S.; Liu, Y. Polarizations of gravitational waves in f(R) gravity. Phys. Rev. D 2017, 95, 104034. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Einstein-Aether waves. Phys. Rev. D 2004, 70, 024003. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the MOND paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Seifert, M.D. Stability of spherically symmetric solutions in modified theories of gravity. Phys. Rev. D 2007, 76, 064002. [Google Scholar] [CrossRef]
- Sagi, E. Propagation of gravitational waves in generalized TeVeS. Phys. Rev. D 2010, 81, 064031. [Google Scholar] [CrossRef]
- Gong, Y.; Hou, S.; Liang, D.; Papantonopoulos, E. Gravitational waves in Einstein-æther and generalized TeVeS theory after GW170817. Phys. Rev. D 2018, 97, 084040. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I. Testing f(R)-theories using the first time derivative of the orbital period of the binary pulsars. Mon. Not. R. Astron. Soc. 2014, 431, 741–748. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I. Probing the physical and mathematical structure of f(R)-gravity by PSR J0348 + 0432. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550040. [Google Scholar] [CrossRef]
- Dyadina, P.I.; Alexeyev, S.O.; Capozziello, S.; De Laurentis, M.; Rannu, K.A. Strong-field tests of f(R)-gravity in binary pulsars. Int. J. Mod. Phys. Conf. Ser. 2016, 41, 1660131. [Google Scholar] [CrossRef]
- Dyadina, P.; Alexeyev, S.; Capozziello, S.; De Laurentis, M. Verification of f(R)-gravity in binary pulsars. EPJ Web Conf. 2016, 125, 03005. [Google Scholar] [CrossRef]
- Dyadina, P.I.; Alexeyev, S.O.; Rannu, K.A.; Capozziello, S.; Laurentis, M.D. Tests of f(R)-gravity in binary pulsars. In Proceedings of the 14th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (MG14) (In 4 Volumes), Rome, Italy, 12–18 July 2015; Volume 2, pp. 1273–1278. [Google Scholar]
- Faulkner, T.; Tegmark, M.; Bunn, E.F.; Mao, Y. Constraining f(R) Gravity as a Scalar Tensor Theory. Phys. Rev. D 2007, 76, 063505. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, X.; Zhao, W. Constraining f(R) gravity in solar system, cosmology and binary pulsar systems. Phys. Lett. B 2018, 777, 286–293. [Google Scholar] [CrossRef]
- Arnowitt, R.L.; Deser, S.; Misner, C.W. The Dynamics of general relativity. Gen. Relativ. Gravit. 2008, 40, 1997–2027. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.L.; Diehl, R.; Domingo, A.; et al. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational-wave Event GW170817. Astrophys. J. 2017, 848, L15. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef] [PubMed]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- Sakstein, J.; Jain, B. Implications of the Neutron Star Merger GW170817 for Cosmological Scalar-Tensor Theories. Phys. Rev. Lett. 2017, 119, 251303. [Google Scholar] [CrossRef] [PubMed]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy after GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Gong, Y. Constraints on Horndeski Theory Using the Observations of Nordtvedt Effect, Shapiro Time Delay and Binary Pulsars. Eur. Phys. J. C 2018, 78, 247. [Google Scholar] [CrossRef]
- Gong, Y.; Papantonopoulos, E.; Yi, Z. Constraints on Scalar-Tensor Theory of Gravity by the Recent Observational Results on Gravitational Waves. arXiv, 2017; arXiv:gr-qc/1711.04102. [Google Scholar]
- Crisostomi, M.; Koyama, K. Vainshtein mechanism after GW170817. Phys. Rev. D 2018, 97, 021301. [Google Scholar] [CrossRef]
- Rakhmanov, M. Response of test masses to gravitational waves in the local Lorentz gauge. Phys. Rev. D 2005, 71, 084003. [Google Scholar] [CrossRef]
- Hellings, R.W.; Downs, G.S. Upper Limits on the Isotropic Gravitational Radiation Background from Pulsar Timing Analysis. Astrophys. J. 1983, 265, L39–L42. [Google Scholar] [CrossRef]
- Lee, K.J.; Jenet, F.A.; Price, R.H. Pulsar Timing as a Probe of Non-Einsteinian Polarizations of Gravitational Waves. Astrophys. J. 2008, 685, 1304–1319. [Google Scholar] [CrossRef]
- Lee, K.; Jenet, F.A.; Price, R.H.; Wex, N.; Kramer, M. Detecting massive gravitons using pulsar timing arrays. Astrophys. J. 2010, 722, 1589–1597. [Google Scholar] [CrossRef]
- Chamberlin, S.J.; Siemens, X. Stochastic backgrounds in alternative theories of gravity: Overlap reduction functions for pulsar timing arrays. Phys. Rev. D 2012, 85, 082001. [Google Scholar] [CrossRef]
- Lee, K.J. Pulsar timing arrays and gravity tests in the radiative regime. Class. Quant. Gravit. 2013, 30, 224016. [Google Scholar] [CrossRef]
- Gair, J.; Romano, J.D.; Taylor, S.; Mingarelli, C.M.F. Mapping gravitational-wave backgrounds using methods from CMB analysis: Application to pulsar timing arrays. Phys. Rev. D 2014, 90, 082001. [Google Scholar] [CrossRef]
- Gair, J.R.; Romano, J.D.; Taylor, S.R. Mapping gravitational-wave backgrounds of arbitrary polarisation using pulsar timing arrays. Phys. Rev. D 2015, 92, 102003. [Google Scholar] [CrossRef]
- Hou, S.; Gong, Y. Gravitational Waves in Einstein-æther Theory and Generalized TeVeS Theory after GW170817. Universe 2018, 4, 84. [Google Scholar] [CrossRef]
- Elliott, J.W.; Moore, G.D.; Stoica, H. Constraining the new Aether: Gravitational Cerenkov radiation. J. High Energy Phys. 2005, 2005, 066. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hughes, S.A. The Basics of gravitational wave theory. New J. Phys. 2005, 7, 204. [Google Scholar] [CrossRef]
- Gong, Y.; Hou, S. Gravitational Wave Polarizations in f(R) Gravity and Scalar-Tensor Theory. In Proceedings of the 13th International Conference on Gravitation, Astrophysics and Cosmology and 15th Italian-Korean Symposium on Relativistic Astrophysics (IK15), Seoul, Korea, 3–7 July 2017; Volume 168, p. 01003. [Google Scholar]
- Shao, L.; Wex, N. New tests of local Lorentz invariance of gravity with small-eccentricity binary pulsars. Class. Quant. Gravit. 2012, 29, 215018. [Google Scholar] [CrossRef]
- Shao, L.; Caballero, R.N.; Kramer, M.; Wex, N.; Champion, D.J.; Jessner, A. A new limit on local Lorentz invariance violation of gravity from solitary pulsars. Class. Quant. Gravit. 2013, 30, 165019. [Google Scholar] [CrossRef]
- Shapiro, I.I. A century of relativity. Rev. Mod. Phys. 1999, 71, S41–S53. [Google Scholar] [CrossRef]
- Jacobson, T. Einstein-aether gravity: A Status report. In Proceedings of the From Quantum to Emergent Gravity: Theory and Phenomenology, Trieste, Italy, 11–15 June 2007. [Google Scholar]
- Yagi, K.; Blas, D.; Yunes, N.; Barausse, E. Strong Binary Pulsar Constraints on Lorentz Violation in Gravity. Phys. Rev. Lett. 2014, 112, 161101. [Google Scholar] [CrossRef] [PubMed]
- Yagi, K.; Blas, D.; Barausse, E.; Yunes, N. Constraints on Einstein-Æther theory and Hoǎva gravity from binary pulsar observations. Phys. Rev. D 2014, 89, 084067. [Google Scholar] [CrossRef]
- Oost, J.; Mukohyama, S.; Wang, A. Constraints on Einstein-aether theory after GW170817. Phys. Rev. D 2018, 97, 124023. [Google Scholar] [CrossRef]
- Milgrom, M. A Modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A Modification of the Newtonian dynamics: Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
| 1. | The expressions for and are too complicated to be reproduced here. |
| 2. | The expressions for and in generalized TeVeS theory are even more complicated, so they are not presented here, either. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Hou, S. The Polarizations of Gravitational Waves. Universe 2018, 4, 85. https://doi.org/10.3390/universe4080085
Gong Y, Hou S. The Polarizations of Gravitational Waves. Universe. 2018; 4(8):85. https://doi.org/10.3390/universe4080085
Chicago/Turabian StyleGong, Yungui, and Shaoqi Hou. 2018. "The Polarizations of Gravitational Waves" Universe 4, no. 8: 85. https://doi.org/10.3390/universe4080085
APA StyleGong, Y., & Hou, S. (2018). The Polarizations of Gravitational Waves. Universe, 4(8), 85. https://doi.org/10.3390/universe4080085





