Abstract
The Bronnikov model of nonlinear electrodynamics is investigated in general relativity. The magnetic black hole is considered and we obtain a solution giving corrections to the Reissner-Nordström solution. In this model spacetime at becomes Minkowski’s spacetime. We calculate the magnetic mass of the black hole and the metric function. At some parameters of the model there can be one, two or no horizons. The Hawking temperature and the heat capacity of black holes are calculated. We show that a second-order phase transition takes place and black holes are thermodynamically stable at some range of parameters.
Keywords:
nonlinear electrodynamics; magnetic black holes; Reissner-Nordström solution; thermodynamics; phase transitions PACS:
04.70.Bw; 04.70.Dy; 97.60.Lf
1. Introduction
The black hole (BH) physics is similar to ordinary thermodynamics. This analogy can help in understanding the theory of quantum gravity. The semiclassical analysis of a BH radiation shows that the initial state information is hidden inside of the event horizon [1]. Some questions appeared on the information loss paradox and the unitary of the theory. To answer these questions a backreaction and quantum gravity effects should be taken into account. In addition, the semiclassical calculations do not work for light black holes. The effects of quantum gravity can correctly describe the short distance behavior. At the same time, to avoid the short distance singularity, one can consider regular black holes. A study of regular black holes without singularities allows us to treat the minimum size as the Planck length. Not to search for quantum gravity, we concentrate here on the regular BH thermodynamics. Regular black hole solutions may be obtained by coupling general relativity and nonlinear electrodynamics (NLED).
Bardeen, Carter and Hawking [2] (see also [3]) suggested that BH is a thermodynamic object which obeys four laws of black hole mechanics. Thus, we can study such thermodynamic properties of black holes as phase transitions, the thermal stability, the black hole evaporation and others. Originally Davies and Hut [4,5] investigated BH phase transitions. The BH thermodynamics phase transitions can be investigated with the aid of the heat capacity in the canonical ensemble. The BH is unstable if the heat capacity becomes negative. When the discontinuities of the heat capacity occur, the phase transitions take place.
The attractive feature of NLED is that an upper limit on the electric field at the origin of point-like particles takes place [6,7,8,9,10]. In some models of NLED [6,7,8,9,10,11,12] the self-energy of charges is finite when definite conditions for the Lagrangian are satisfied [13,14]. Quantum corrections to classical electrodynamics also lead to NLED [15,16,17]. In addition, general relativity with NLED explains the universe inflation [18,19,20,21,22,23,24,25,26]. In the early universe, the initial singularities can also be avoided in NLED models [22]. In this paper we investigate BH solutions in the framework of Bronnikov’s model of NLED [27]. The correspondence principle holds in this model because at the weak field limit NLED is transformed into Maxwell’s electrodynamics. It was shown in [27] that the model includes the existence of a regular magnetic BH and monopoles. The theorem proven by [27] allows us to have a nontrivial case when the electric charge equals zero and the magnetic charge so that the magnetic field is equal to and spacetime possesses a regular center. The entire mass of the BH has the electromagnetic origin.
The thermodynamics of black holes and phase transitions are studied in this paper. In [28,29] similar issues of the BH thermodynamics were discussed. Some aspects of black hole physics were studied in [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].
The paper is organized as follows. Field equations and energy-momentum tensor are described in Section 2. In Section 3 general relativity with NLED is studied. We obtain the asymptotic of the metric and mass functions at and . Corrections to the Reissner-Nordström (RN) solution are found. In Section 4 we calculate the Hawking temperature and the heat capacity of black holes. It was demonstrated that the second-order phase transition takes place in black holes. We find the range where black holes are stable. We made a conclusion in Section 5.
The metric signature is given by and we explore the units with , .
2. Field Equations of NLED
In this section we consider field equations in Minkowski’s spacetime. Let us study NLED, proposed in [27], with the Lagrangian density
where , the field tensor is defined as and the parameter has the dimension of (length). The modified model was proposed and investigated in [47]. At the weak field limit, , the Lagrangian density (1) becomes Maxwell’s Lagrangian density, , and as result, the correspondence principle holds. Field equations found from Equation (1), by the variation of the action corresponding to Lagrangian density (1) with respect to the 4-potential , are given by
where
With the help of Equation (1) one obtains the electric displacement field
We find the magnetic field from the relation ,
Making use of Equations (4) and (5) one can represent field Equation (2) as the Maxwell equations
From the identity , where is the dual tensor, we obtain the second pair of nonlinear Maxwell’s equations
The relation, followed from Equations (4) and (5), is
Because , according to the criterion of [49], the dual symmetry is broken. In classical electrodynamics and in Born-Infeld electrodynamics the dual symmetry occurs but in QED, due to quantum corrections, the dual symmetry is violated.
The symmetrical energy-momentum tensor can be found from the relation
From Equations (1), (3) and (9) one obtains the energy-momentum tensor trace
As , the scale invariance is broken. At NLED (1) becomes Maxwell’s electrodynamics, , and the scale invariance is recovered.
3. Magnetized Black Holes
The action of general relativity with NLED is given by
where , G is the Newton constant and is the reduced Planck mass. The stability of a black hole with action (11) was studied in [36]. We investigate the magnetically charged black hole, and therefore, , . The Einstein and the electromagnetic field equations follow from action (11),
We use the line element with the spherical symmetry
and the metric function is given by [27]
The mass function is defined as follows:
with being the magnetic energy density and is the magnetic mass of the black hole. From Equation (9) at E = 0 we find the magnetic energy density
where , and q is a magnetic charge. It is convenient to introduce the dimensionless parameter . Then using Equations (16) and (17) one obtains the mass function
The mass function presented by Equation (18) has the same form as the solution given in [27]. We calculate the magnetic mass of the black hole
Making use of Equations (15) and (18) one finds the metric function
with . With the help of Equation (20) we obtain the asymptotic of the metric function at
Equation (21) gives the corrections to the RN solution which are in the order of . At , , and the spacetime becomes flat. It is easy to verify that
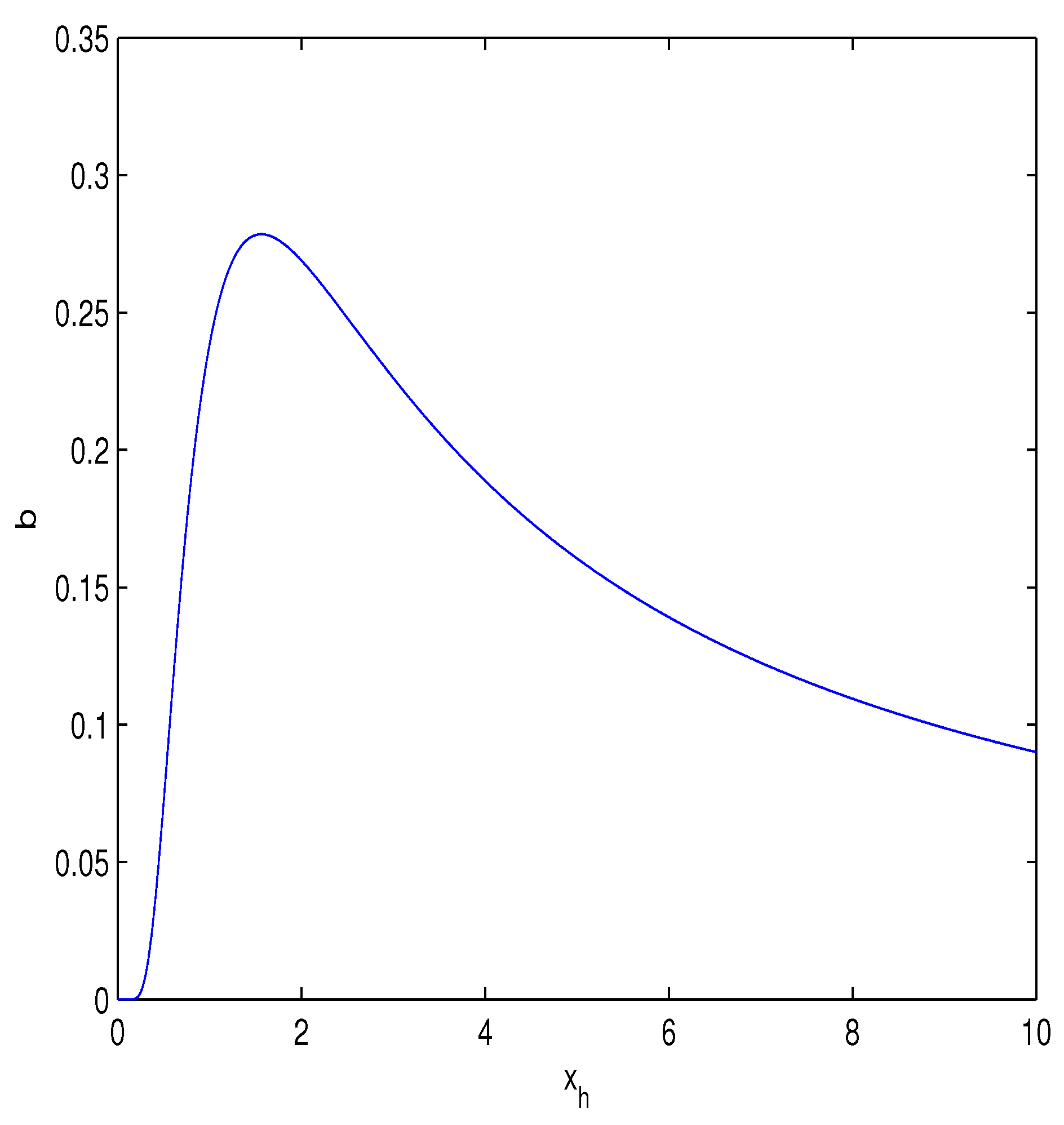
Equation (22) shows that the black hole is regular without conical singularity. The RN solution is recovered at . The plot of the function is represented in Figure 1 for different parameters .
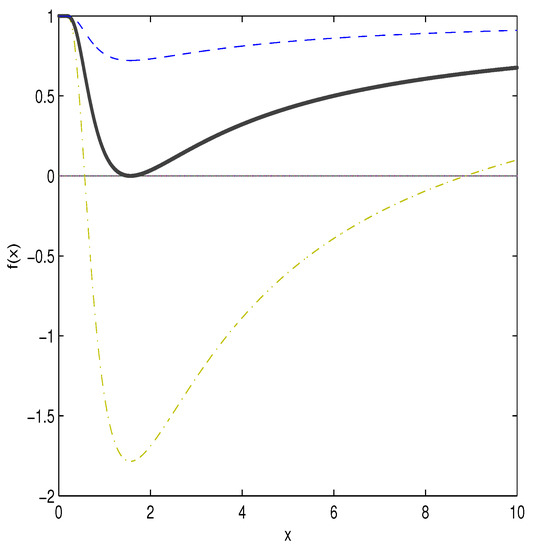
Figure 1.
The plot of the function . The dashed-dotted line corresponds to , the solid line corresponds to and the dashed line corresponds to .
According to Figure 1 at there are no horizons. There is one horizon at and the extreme singularity holds. When we have two horizons. The horizons are defined by the equation . Then from Equation (20) we come to the equation
The plot of the function is represented in Figure 2.
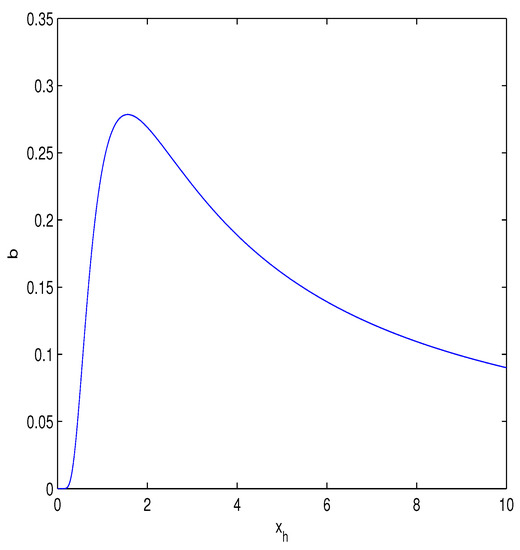
Figure 2.
The plot of the function .
From Equation (23) we obtain the inner and the outer horizons of the black hole which are given in Table 1.

Table 1.
The inner and outer horizons of the black hole.
It follows from Equations (10) at that at the energy-momentum trace becomes zero. As a result, in accordance with Equation (12) the Ricci scalar vanishes and spacetime becomes flat.
Let us discuss the equation of state of the BH inside the Cauchy horizon. From the expression for the pressure and Equation (17) we obtain the equation of state (for ) . This equation holds for any radius r. At , inside the Cauchy horizon, , , and . As a result, the equation of state for a de Sitter spacetime at is not the case for the BH described by the present model. However, regular black holes proposed by [30,37,48] possess a de Sitter center. Thus, the geometry of the BH at in Bronnikov’s model is different compared to other models of regular black holes.
4. Thermodynamics and Phase Transitions
We will study the possible phase transitions and thermal stability of magnetized black holes. Let us calculate the Hawking temperature which is given by
where is the surface gravity and is the horizon. Making use of Equations (15) and (16) we obtain the relations as follows:
It follows from Equation (20) that
Then one can verify that indeed this equation leads to (25) taking into account , , and Equations (17)–(19). With the help of Equations (17) and (23)–(25), we find the Hawking temperature
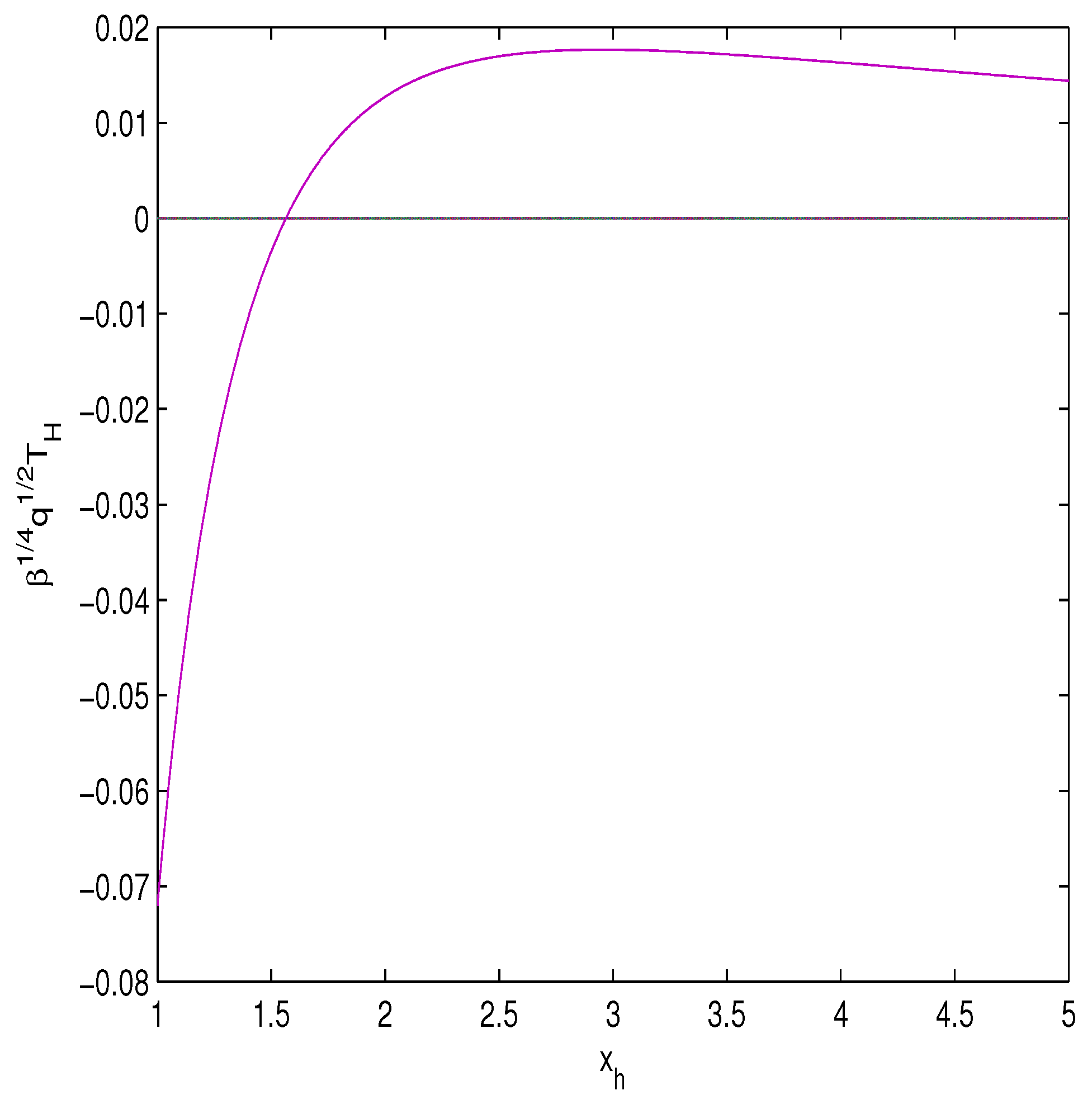
The plot of the function is given in Figure 3.
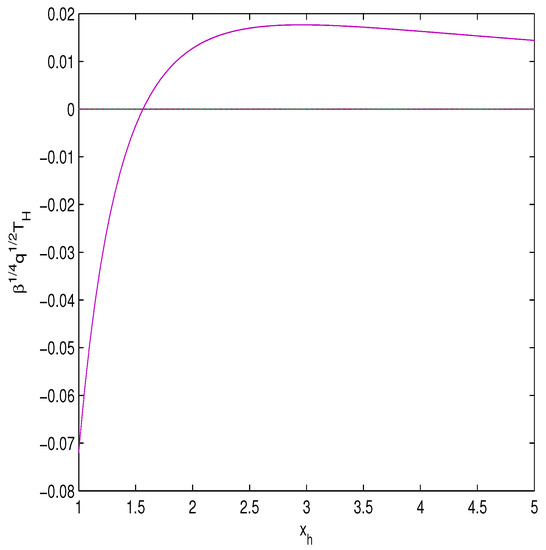
Figure 3.
The plot of the function vs. horizons .
The Hawking temperature becomes zero at () corresponding to the extreme case. At the Hawking temperature is positive and the black hole is stable. When the Hawking temperature becomes negative and the black hole is unstable. The maximum of the Hawking temperature holds at and the heat capacity is singular. At this point the second-order phase transition takes place. We calculate the heat capacity from the relation
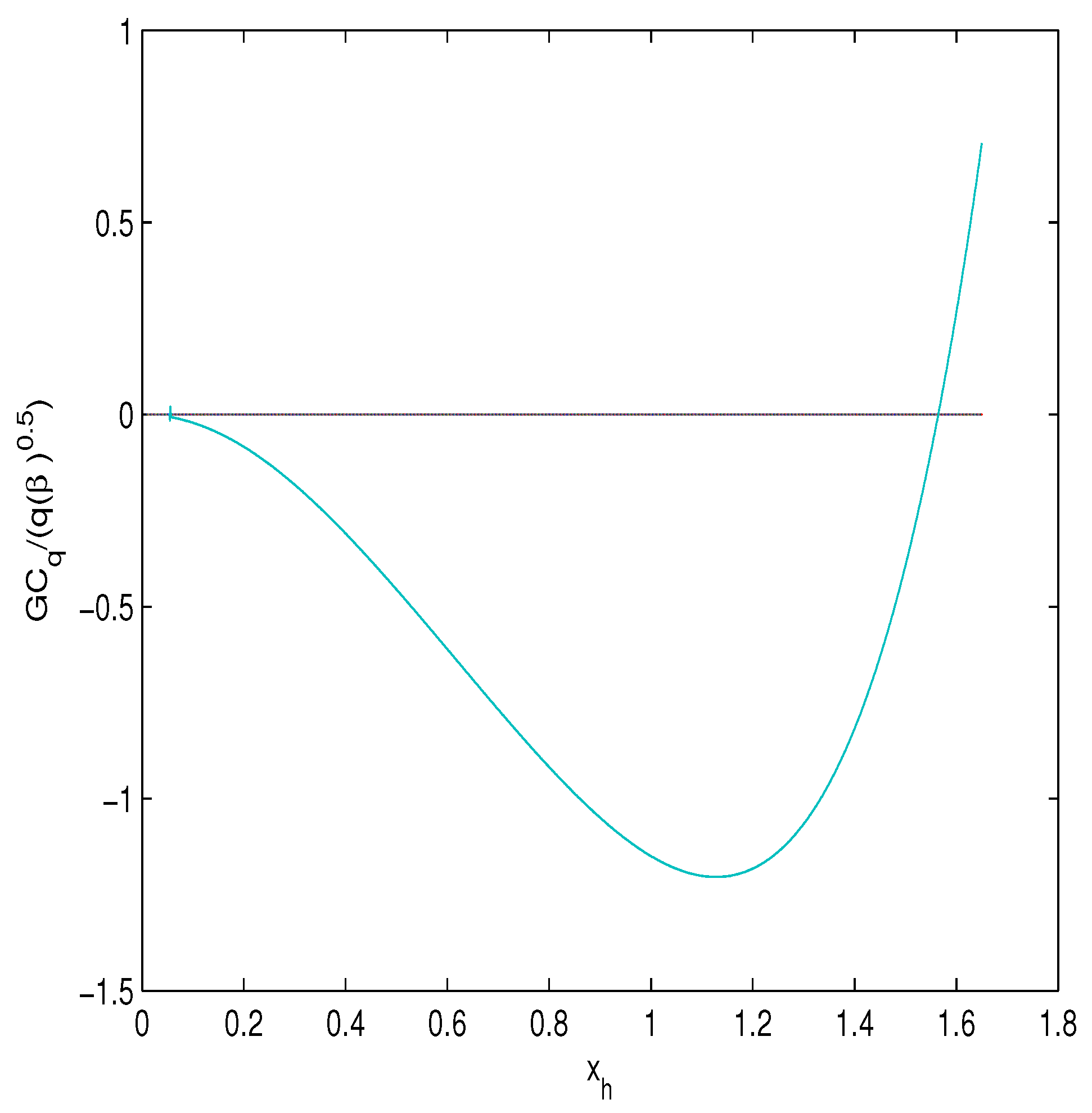
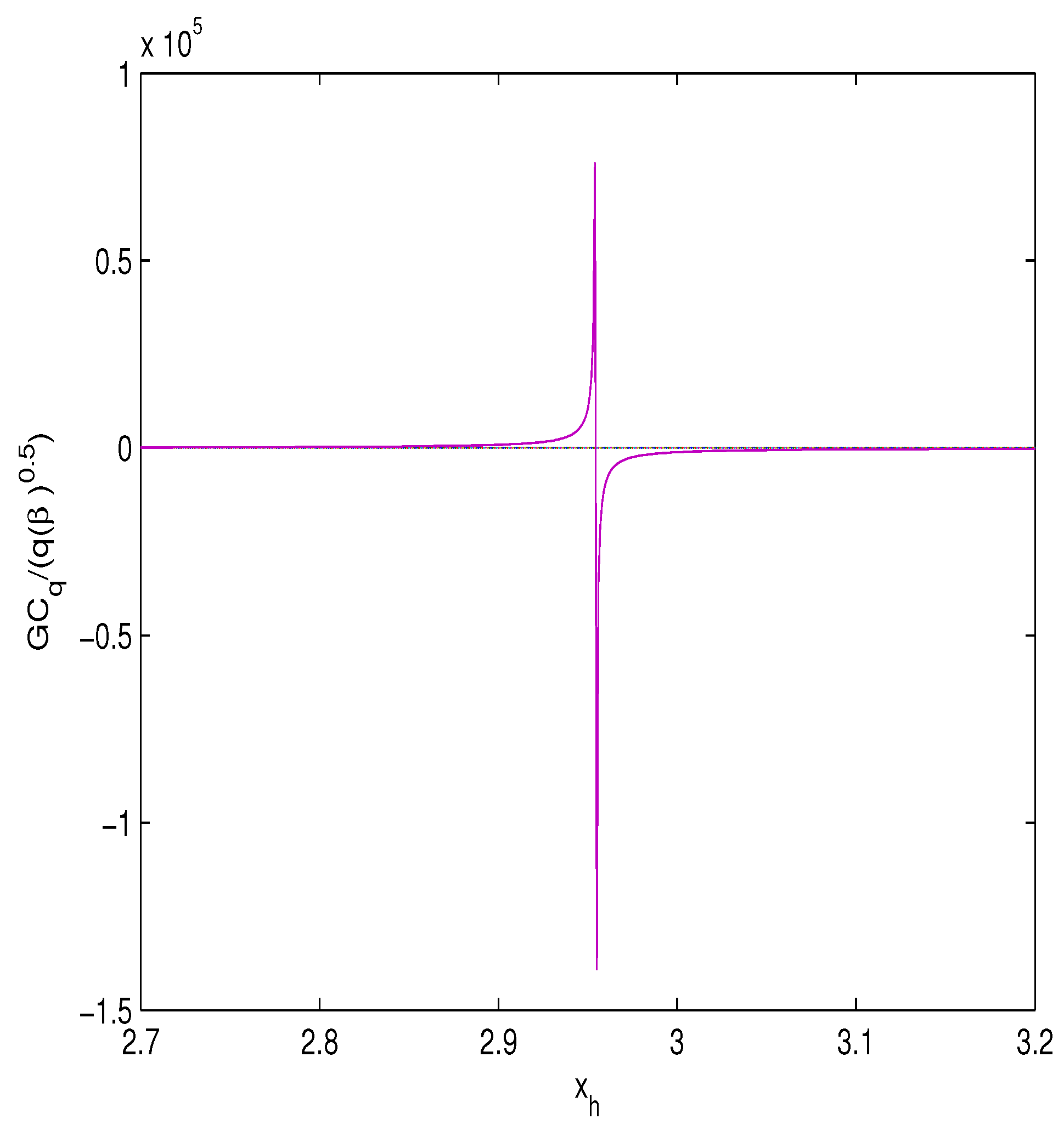
The entropy obeys the Hawking area low . In Figure 4 and Figure 5 one can find the plots of the function vs. the horizon for different values of .
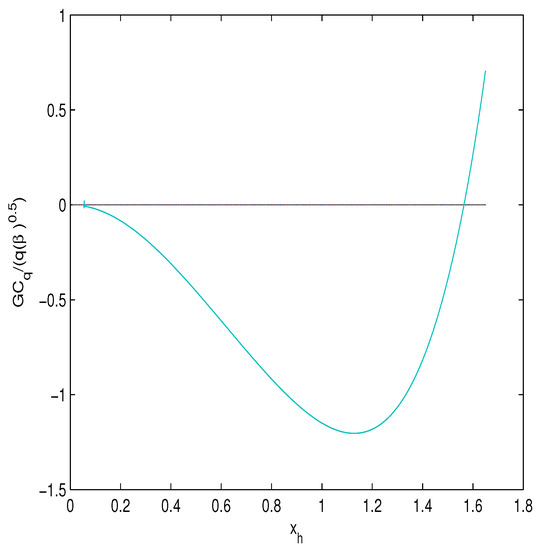
Figure 4.
The plot of the function vs. .
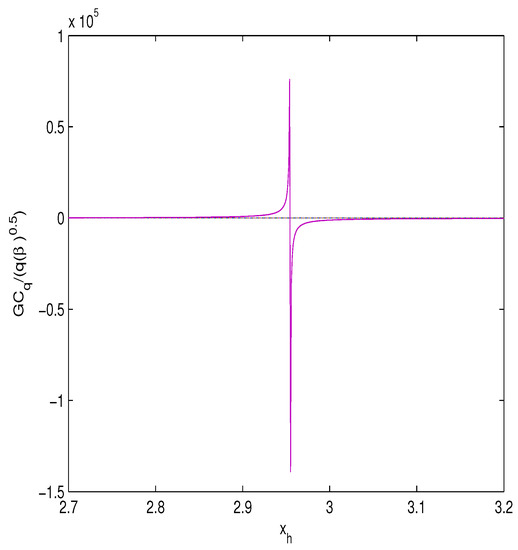
Figure 5.
The plot of the function vs. .
5. Conclusions
We have investigated the Bronnikov model of NLED which at the weak field limit becomes Maxwell’s electrodynamics and the correspondence principle holds. NLED coupled with the gravitational field was considered. The magnetized black holes were studied and we obtained the metric and the mass functions. At we obtained corrections to the RN solution that are in the order of . Physical values of the theory depend on the parameter of NLED . The Hawking temperature and the heat capacity of black holes were calculated and we demonstrated that second-order phase transitions take place in black holes for definite parameters . The thermodynamic stabilities of black holes were studied and it was shown that in the range the black holes are stable. In the framework of the non-commutative model with two horizons [50], similar phase transitions can happen. Phase transitions may appear also in alternative theories of gravity [51]. It should be mentioned that in models of black holes with two horizons the Hawking temperature is connected with each horizon. This leads in some models to the existence of a minimal and maximal temperature in the black body radiation [52]. The author of [53] found conditions in Massive Gravity for an observer to hold in the order to agree with the black-hole temperature. Within the Generalized Uncertainty Principle, authors of [54] have shown that there can exist a black hole remnant with a mass corresponding to a maximal temperature . There also exists a minimum length .
Funding
This research received no external funding.
Conflicts of Interest
The author declare no conflict of interest.
References
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Wald, R.M. The thermodynamics of black holes. Living Rev. Rel. 2001, 4, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.C.W. Thermodynamics of black holes. Rep. Prog. Phys. 1978, 41, 1313–1355. [Google Scholar] [CrossRef]
- Hut, P. Charged black holes and phase transitions. Mon. Not. R. Astr. Soc. 1977, 180, 379–389. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Proc. Royal Soc. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Gitman, D.M.; Shabad, A.E. A note on “Electron self-energy in logarithmic electrodynamics” by P. Gaete and J. Helayël-Neto. Eur. Phys. J. C 2014, 74, 3186–3187. [Google Scholar] [CrossRef]
- Kruglov, S.I. A model of nonlinear electrodynamics. Ann. Phys. 2015, 353, 299–306. [Google Scholar] [CrossRef]
- Kruglov, S.I. Nonlinear arcsin-electrodynamics. Ann. Phys. 2015, 527, 397–401. [Google Scholar] [CrossRef]
- Kruglov, S.I. Modified nonlinear model of arcsin-electrodynamics. Commun. Theor. Phys. 2016, 66, 59–65. [Google Scholar] [CrossRef]
- Costa, C.V.; Gitman, D.M.; Shabad, A.E. Finite field-energy of a point charge in QED. Phys. Scripta 2015, 90, 074012. [Google Scholar] [CrossRef]
- Kruglov, S.I. Remarks on Heisenberg–Euler-type electrodynamics. Mod. Phys. Lett. A 2017, 32, 1750092. [Google Scholar] [CrossRef]
- Gitman, D.M.; Shabad, A.E.; Shishmarev, A.A. Moving point charge as a soliton. arXiv 2016, arXiv:1509.06401[hep-th]. [Google Scholar]
- Adorno, T.C.; Gitman, D.M.; Shabad, A.E.; Shishmarev, A.A. Quantum Electromagnetic Nonlinearity Affecting Charges and Dipole Moments. Russ. Phys. J. 2017, 59, 177–1787. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der diracschen theorie des positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Adler, S.L. Photon splitting and photon dispersion in a strong magnetic field. Ann. Phys. 1971, 67, 599–647. [Google Scholar] [CrossRef]
- García-Salcedo, R.; Breton, N. Born-Infeld cosmologies. Int. J. Mod. Phys. A 2000, 15, 4341–4354. [Google Scholar] [CrossRef]
- Camara, C.S.; de Garcia Maia, M.R.; Carvalho, J.C.; Lima, J.A.S. Nonsingular FRW cosmology and nonlinear electrodynamics. Phys. Rev. D 2004, 69, 123504. [Google Scholar] [CrossRef]
- Elizalde, E.; Lidsey, J.E.; Nojiri, S.; Odintsov, S.D. Born-Infeld quantum condensate as dark energy in the universe. Phys. Lett. B 2003, 574, 1–7. [Google Scholar] [CrossRef]
- Novello, M.; Perez Bergliaffa, S.E.; Salim, J.M. Nonlinear electrodynamics and the acceleration of the universe. Phys. Rev. D 2004, 69, 127301. [Google Scholar] [CrossRef]
- Novello, M.; Goulart, E.; Salim, J.M.; Perez Bergliaffa, S.E. Cosmological effects of nonlinear electrodynamics. Class. Quant. Grav. 2007, 24, 3021–3036. [Google Scholar] [CrossRef]
- Vollick, D.N. Homogeneous and isotropic cosmologies with nonlinear electromagnetic radiation. Phys. Rev. D 2008, 78, 063524. [Google Scholar] [CrossRef]
- Kruglov, S.I. Universe acceleration and nonlinear electrodynamics. Phys. Rev. D 2015, 92, 123523. [Google Scholar] [CrossRef]
- Kruglov, S.I. Nonlinear electromagnetic fields as a source of universe acceleration. Int. J. Mod. Phys. A 2016, 31, 1650058. [Google Scholar] [CrossRef]
- Kruglov, S.I. Acceleration of Universe by Nonlinear Electromagnetic Fields. Int. J. Mod. Phys. D 2016, 25, 1640002. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.-W.; Park, Y.-J. Thermodynamics of regular black hole. Gen. Relativ. Grav. 2009, 41, 1051–1067. [Google Scholar] [CrossRef]
- Breton, N.; Bergliaffa, S.E.P. On the thermodynamical stability of black holes in nonlinear electrodynamics. Ann. Phys. 2015, 354, 440–454. [Google Scholar] [CrossRef]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the 5th International Conference on Gravitation and the Theory of Relativity, Tbilisi, Georgia, 9–13 September 1968. [Google Scholar]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rev. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Bousso, R.; Hawking, S.W. Pair creation of black holes during inflation. Phys. Rev. D 1996, 54, 6312–6322. [Google Scholar] [CrossRef]
- Bousso, R.; Hawking, S.W. (Anti-)Evaporation of Schwarzschild-de Sitter Black Holes. Phys. Rev. D 1998, 57, 2436–2442. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; Garćia, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Breton, N. Born-Infeld black hole in the isolated horizon framework. Phys. Rev. D 2003, 67, 124004. [Google Scholar] [CrossRef]
- Breton, N. Stability of nonlinear magnetic black holes. Phys. Rev. D 2005, 72, 044015. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Lemos, J.P.S.; Zanchin, V.T. Regular black holes: Electrically charged solutions, Reissner-Nordstróm outside a de Sitter core. Phys. Rev. D 2011, 83, 124005. [Google Scholar] [CrossRef]
- Flachi, A.; Lemos, J.P.S. Quasinormal modes of regular black holes. Phys. Rev. D 2013, 87, 024034. [Google Scholar] [CrossRef]
- Hendi, S.H. Asymptotic Reissner-Nordstroem black holes. Ann. Phys. 2013, 333, 282–289. [Google Scholar] [CrossRef]
- Balart, L.E.; Vagenas, C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef]
- Kruglov, S.I. Asymptotic Reissner-Nordström solution within nonlinear electrodynamics. Phys. Rev. D 2016, 94, 044026. [Google Scholar] [CrossRef]
- Kruglov, S.I. Corrections to Reissner-Nordström black hole solution due to exponential nonlinear electrodynamics. Europhys. Lett. 2016, 115, 60006. [Google Scholar] [CrossRef]
- Kruglov, S.I. Nonlinear arcsin-electrodynamics and asymptotic Reissner-Nordström black holes. Ann. Phys. 2016, 528, 588–596. [Google Scholar] [CrossRef]
- Kruglov, S.I. Black hole as a magnetic monopole within exponential nonlinear electrodynamics. Ann. Phys. 2017, 378, 59–70. [Google Scholar] [CrossRef]
- Kruglov, S.I. Born-Infeld-type electrodynamics and magnetic black holes. Ann. Phys. 2017, 383, 550–559. [Google Scholar] [CrossRef]
- Kruglov, S.I. Magnetically charged black hole in framework of nonlinear electrodynamics model. Int. J. Mod. Phys. A 2018, 33, 1850023. [Google Scholar] [CrossRef]
- Frolov, V.P. Notes on nonsingular models of black holes. Phys. Rev. D 2016, 94, 104056. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Rasheed, D. Electric-magnetic duality rotations in nonlinear electrodynamics. Nucl. Phys. B 1995, 454, 185–206. [Google Scholar] [CrossRef]
- Arraut, I.; Batic, D.; Nowakowski, M. Maximal extension of the Schwarzschild spacetime inspired by noncommutative geometry. J. Math. Phys. 2010, 51, 022503. [Google Scholar] [CrossRef]
- Arraut, I.; Chelabi, K. Non-linear massive gravity as a gravitational σ-model. Europhys. Lett. 2016, 115, 31001. [Google Scholar] [CrossRef]
- Nowakowski, M.; Arraut, I. The Minimum and Maximum Temperature of Black Body Radiation. Mod. Phys. Lett. A 2009, 24, 2133–2137. [Google Scholar] [CrossRef]
- Arraut, I. The Astrophysical Scales Set by the Cosmological Constant, Black-Hole Thermodynamics and Non-Linear Massive Gravity. Universe 2017, 3, 45. [Google Scholar] [CrossRef]
- Arraut, I.; Batic, D.; Nowakowski, M. Comparing two approaches to Hawking radiation of Schwarzschild-de Sitter black holes. Class. Quant. Grav. 2009, 26, 125006. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).