Primordial Power Spectra from an Emergent Universe: Basic Results and Clarifications
Abstract
1. Introduction
2. Primordial Tensor Power Spectra
2.1. The Mukhanov–Sasaki Equation for Tensor Perturbations
2.2. Initial Conditions
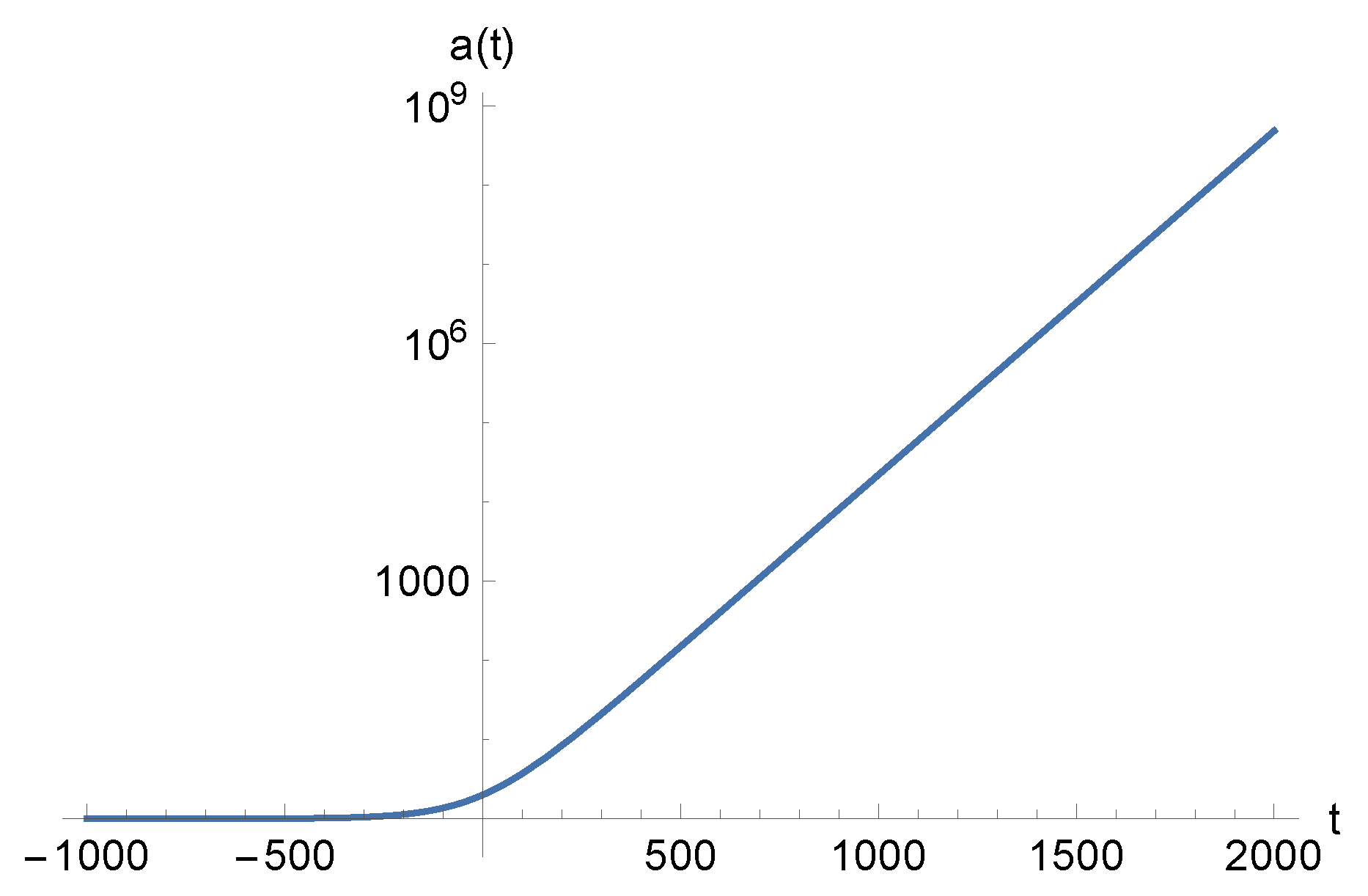
3. Purely Emergent Universe
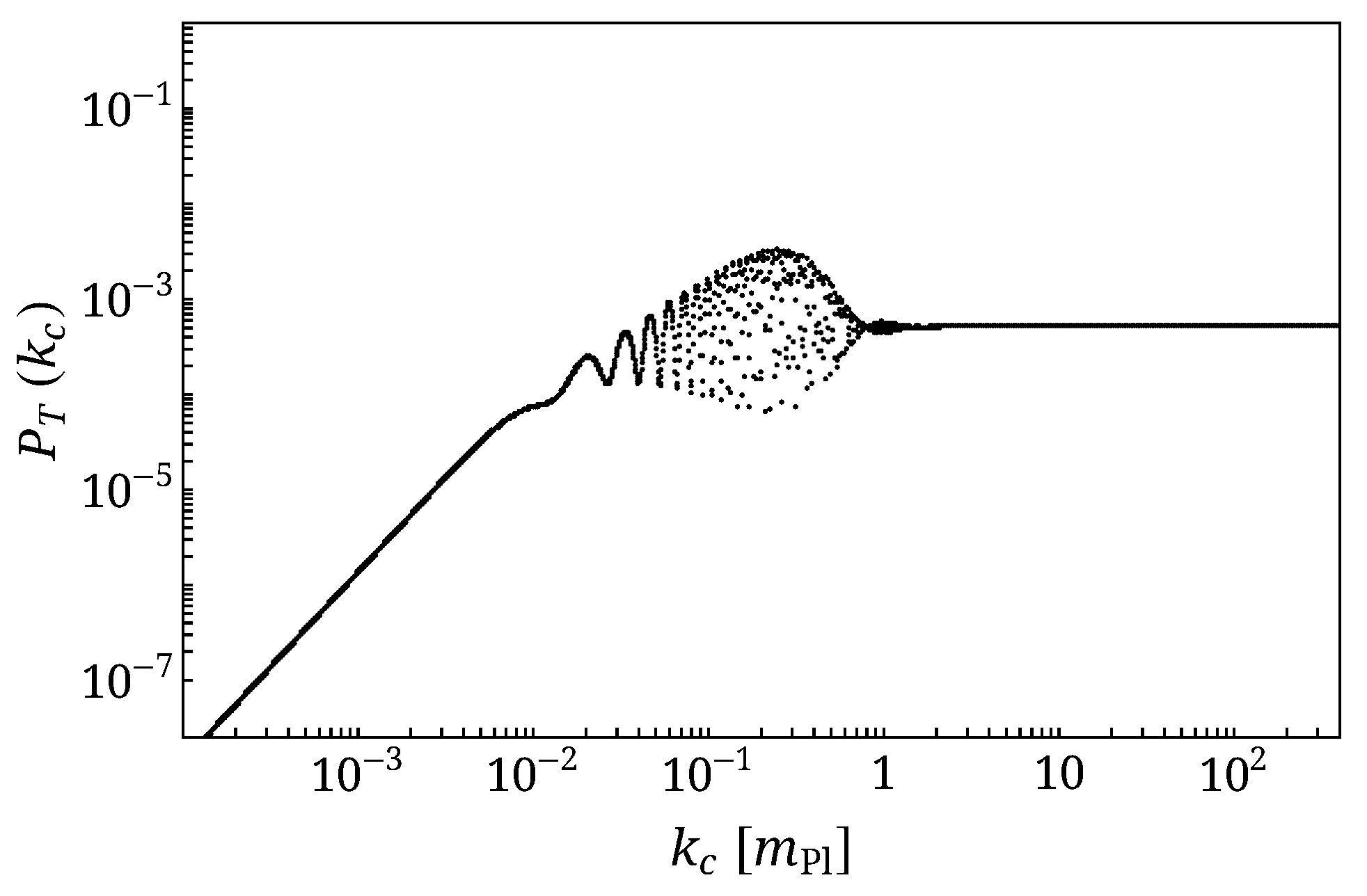
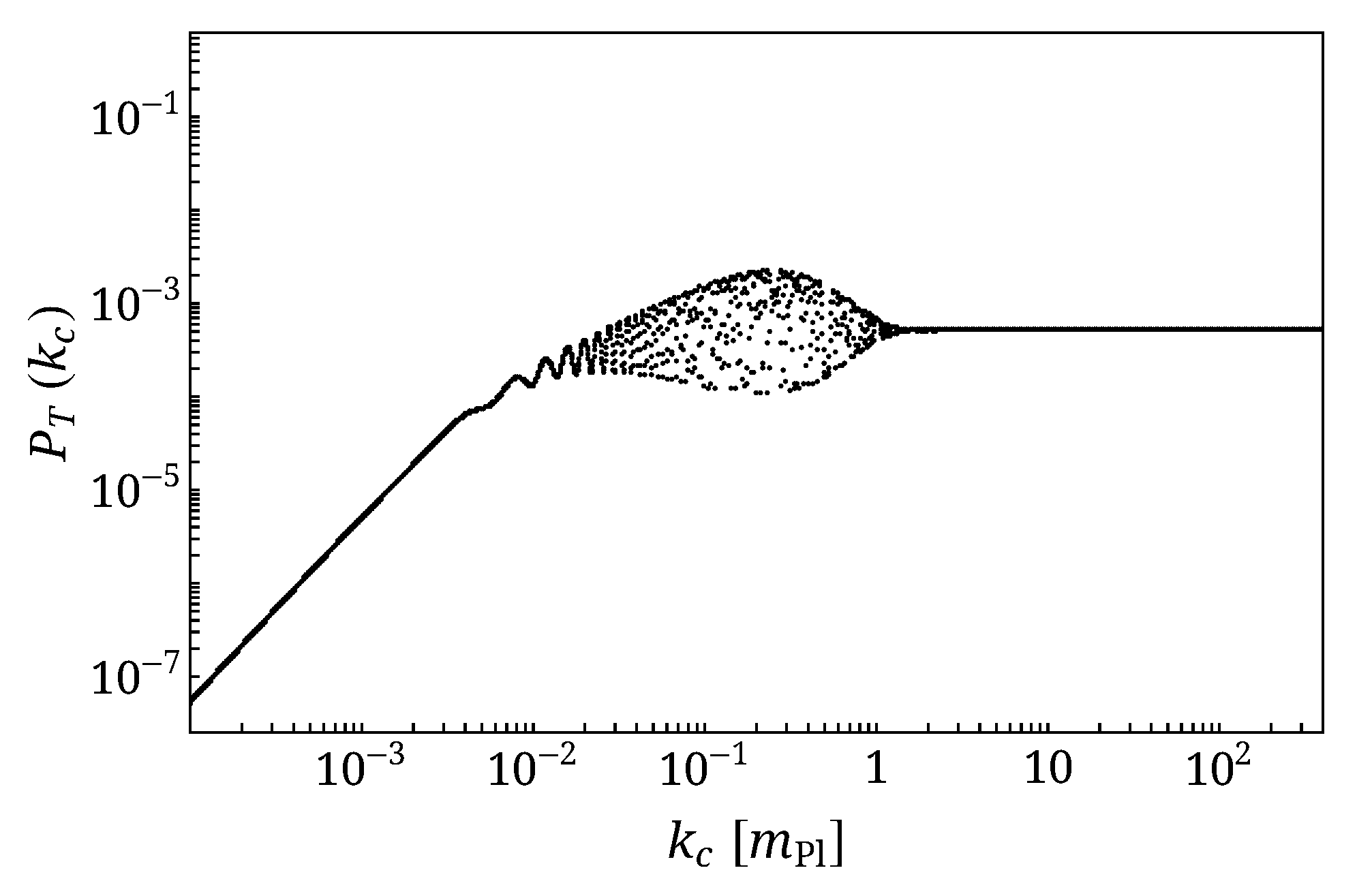
4. Emergent Universe with a Bounce
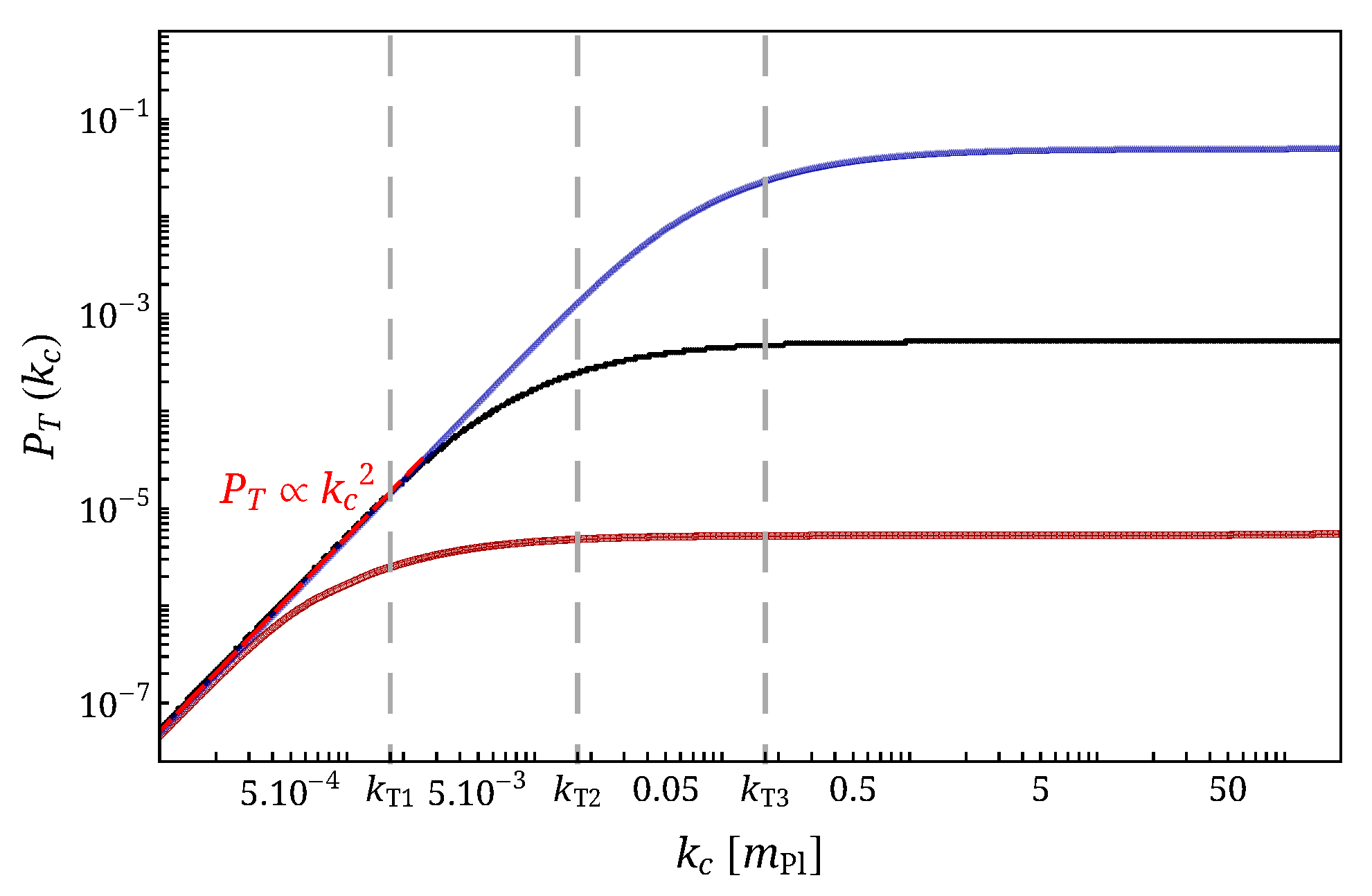
4.1. Impact of the Bounce Parameters on the Primordial Tensor Power Spectra
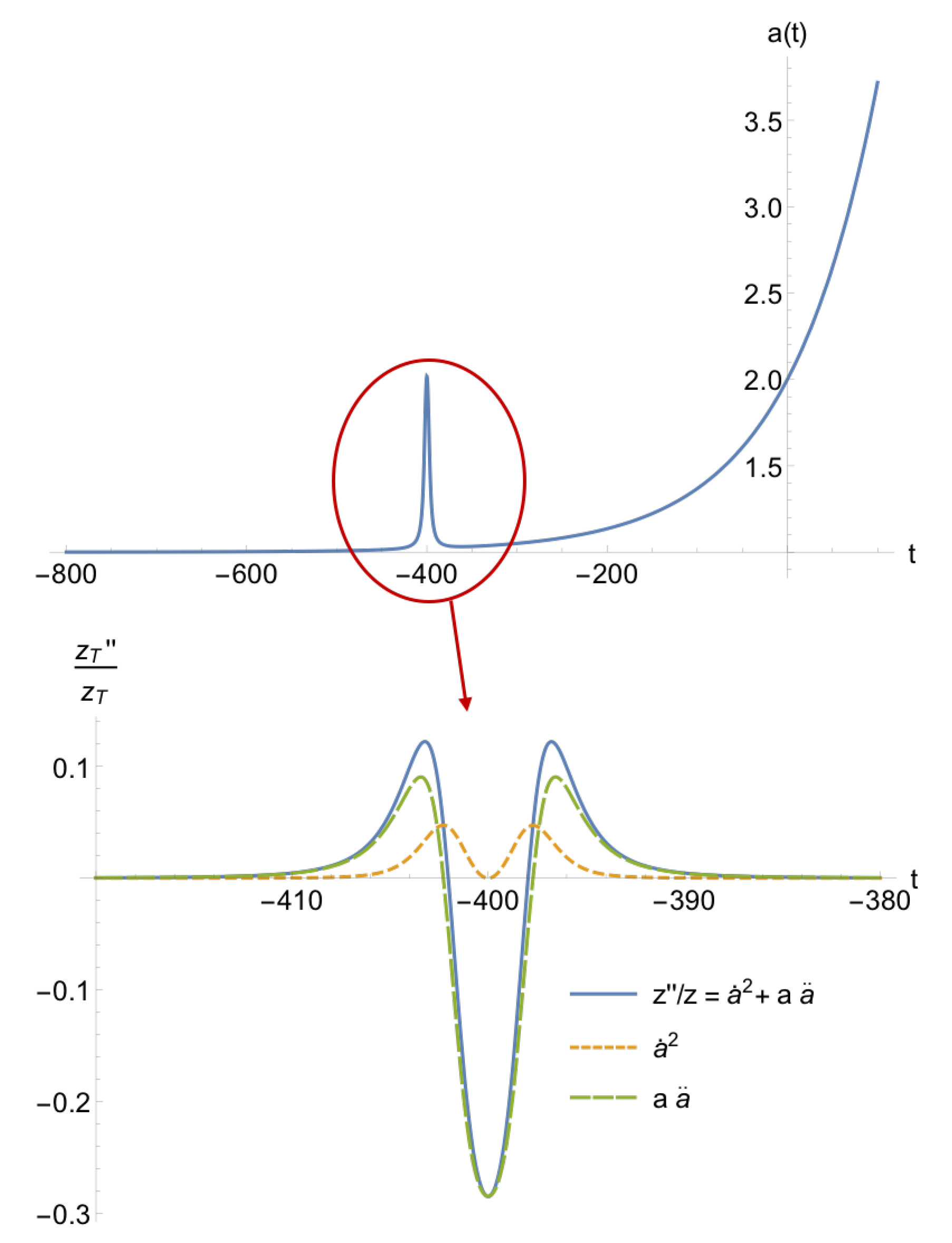
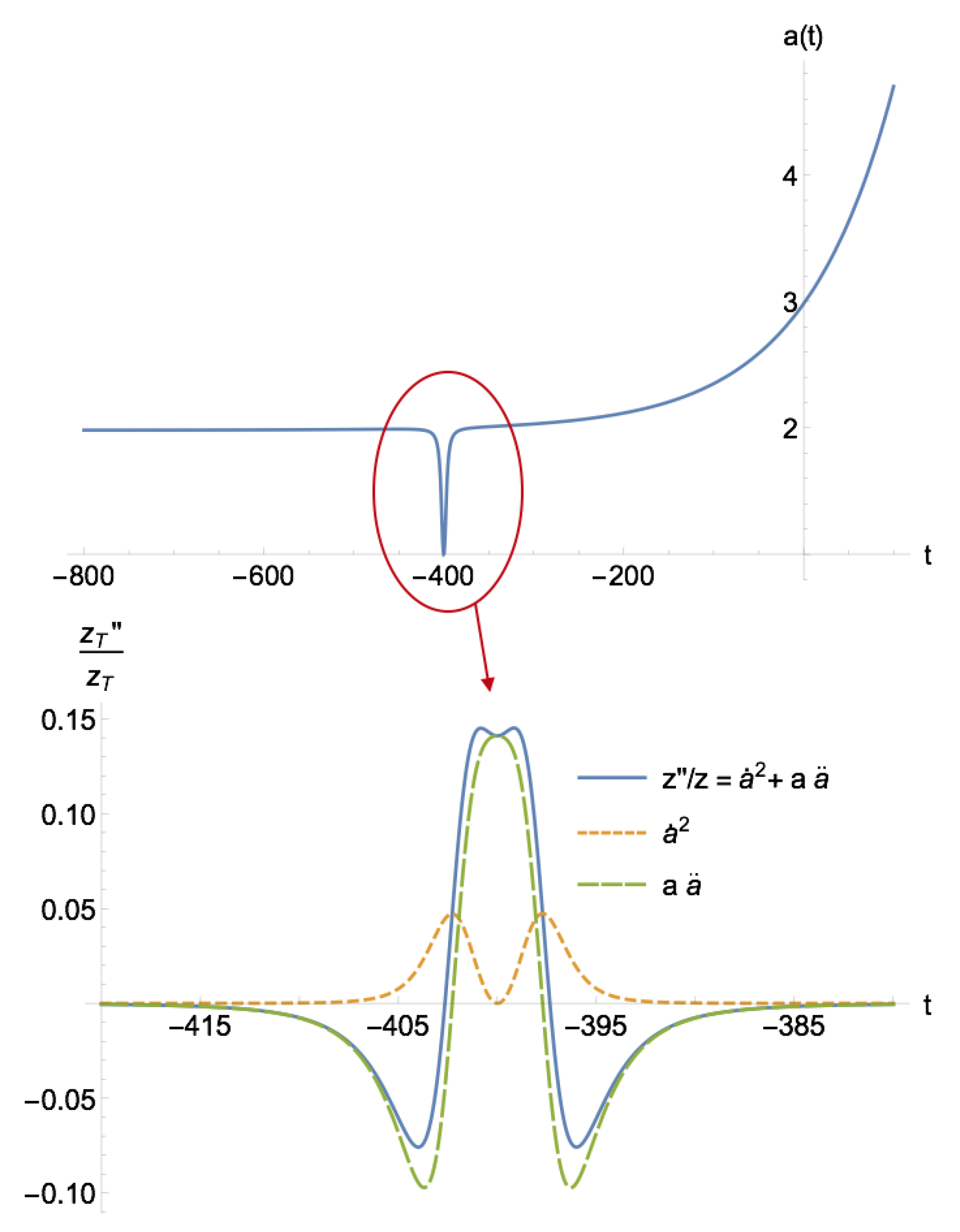
4.1.1. The Position of the Bounce
4.1.2. The Steepness of the Bounce B
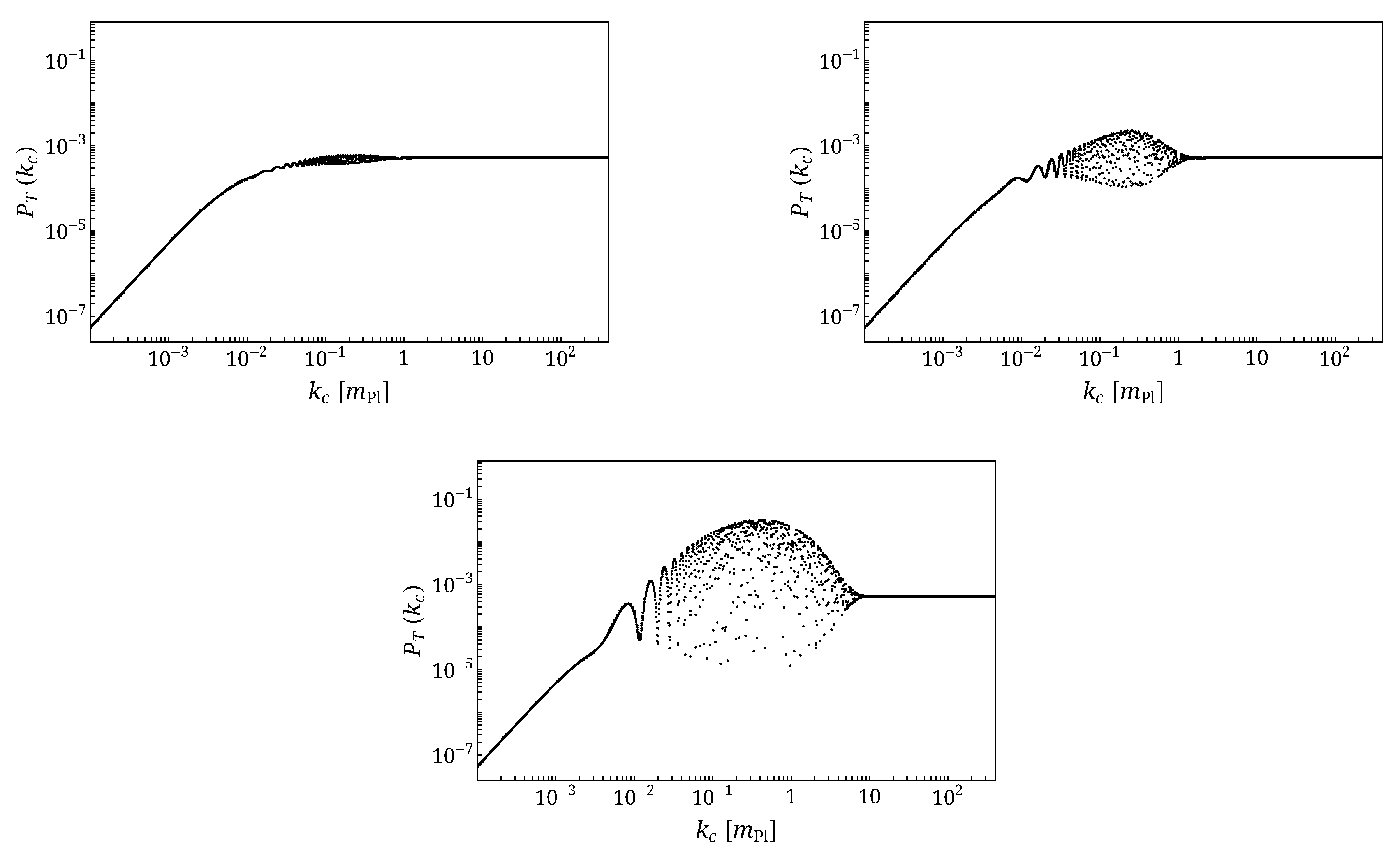
4.1.3. The Amplitude of the Bounce C
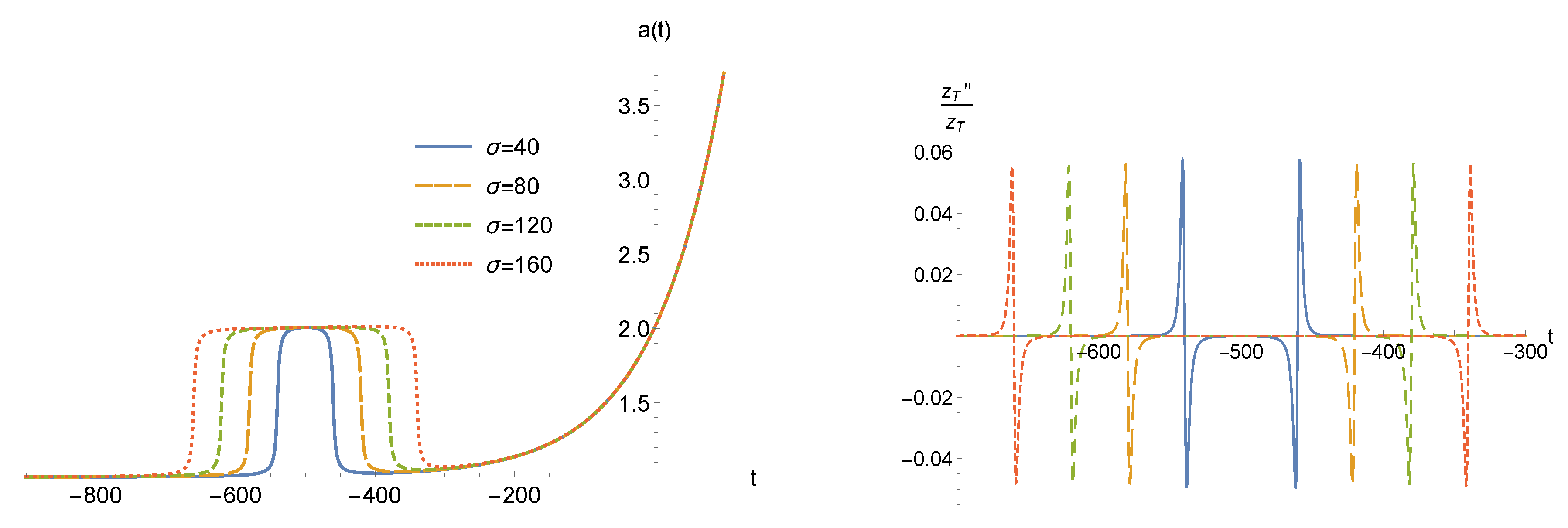
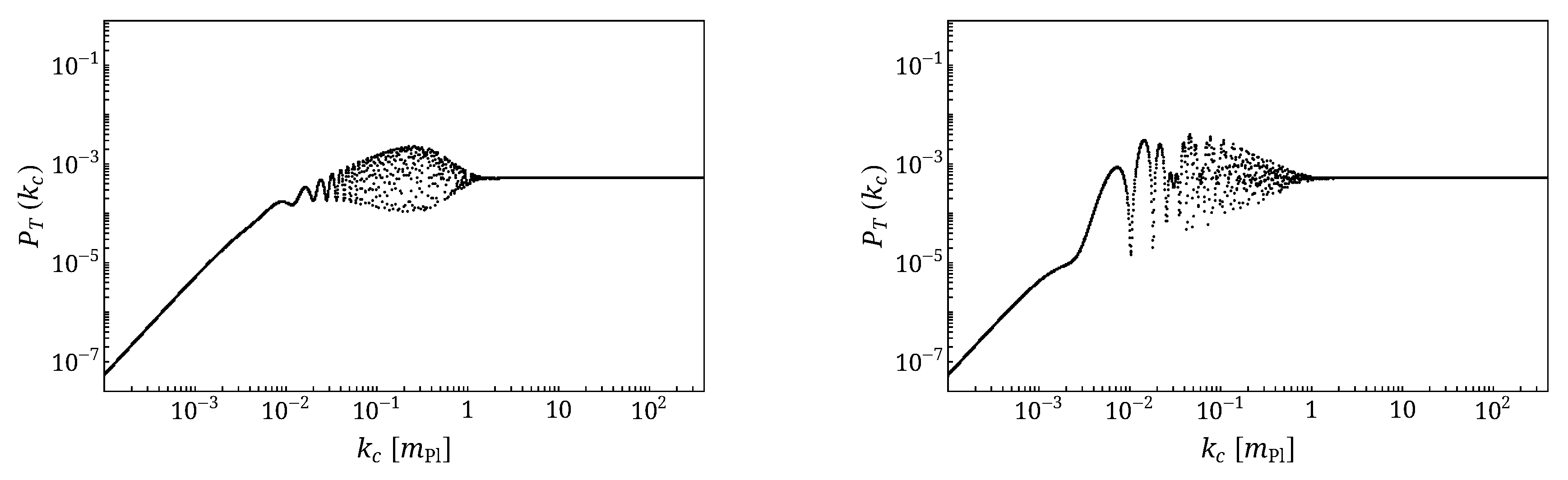
4.1.4. The Width of the Bounce
4.2. Impact of the Parameters Unrelated to the Bounce
4.2.1. The Hubble Parameter during Inflation
4.2.2. The Normalization of the Scale Factor
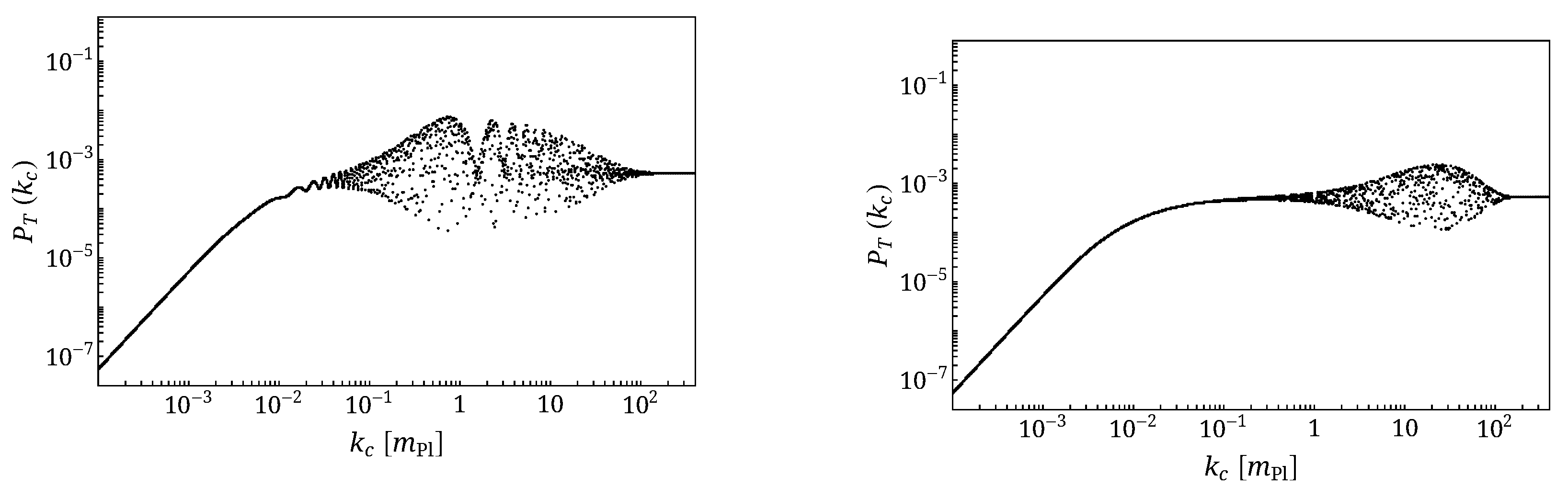
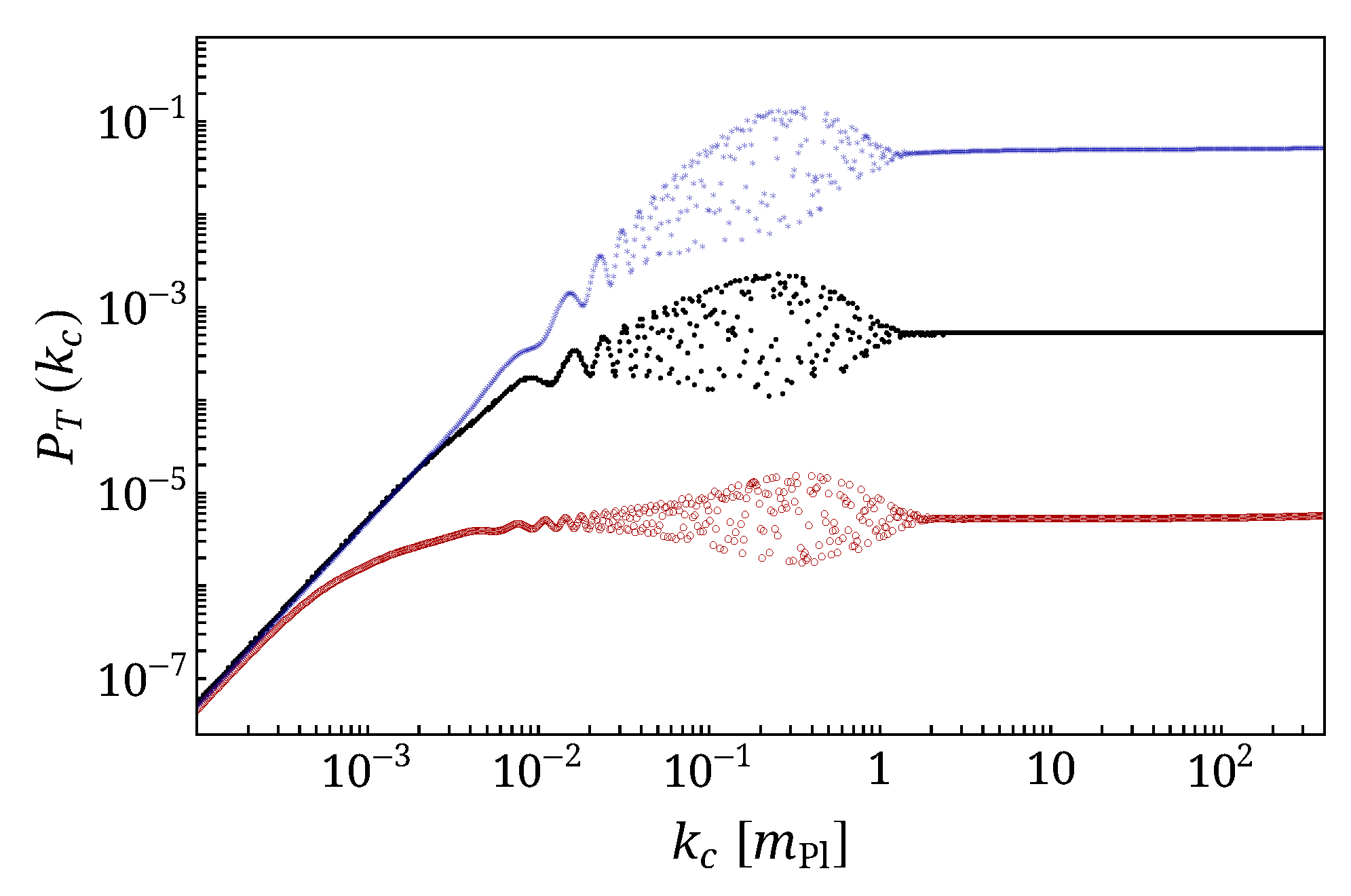
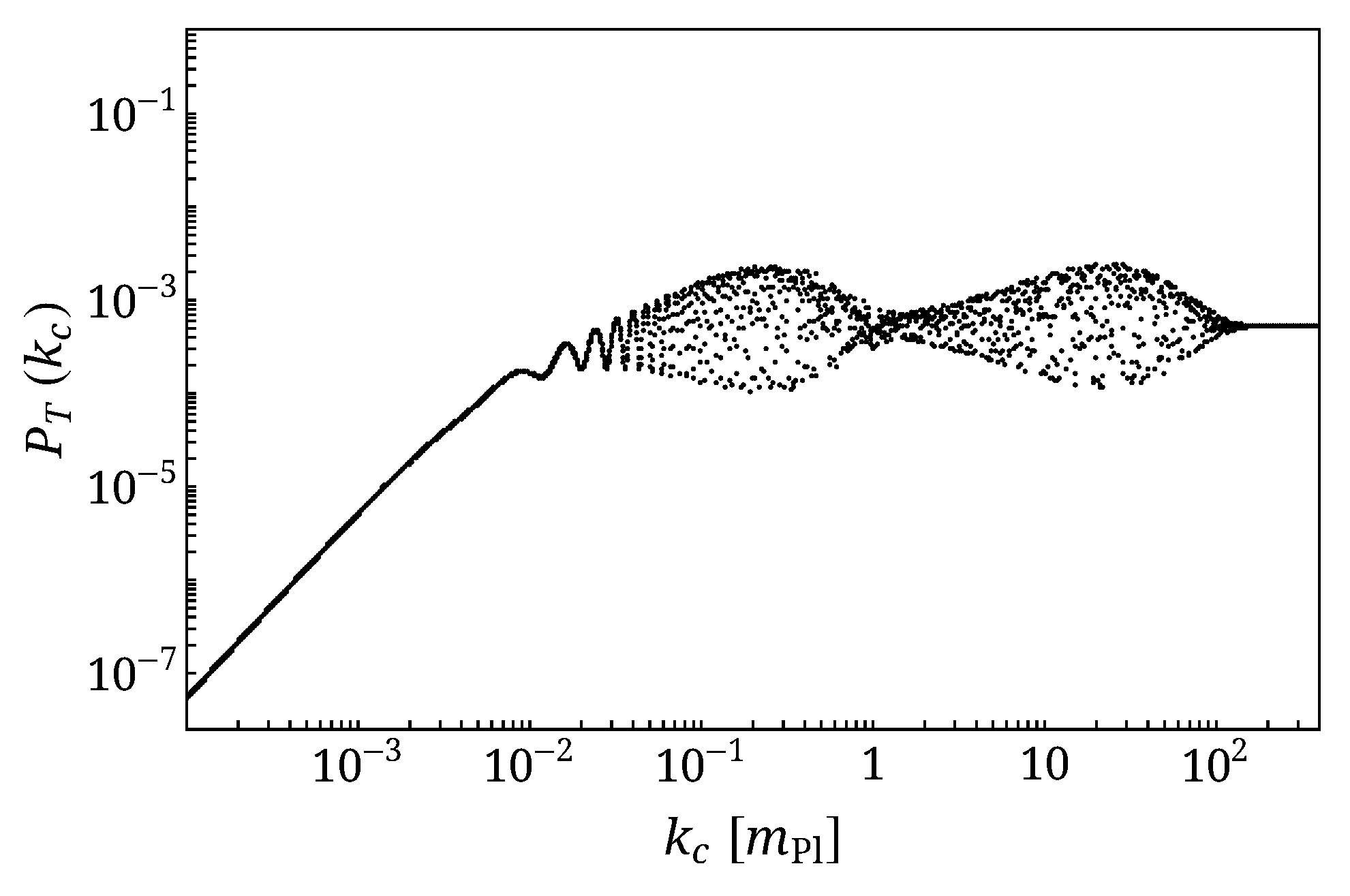
5. Multiple Bounces
6. Conclusions
- in and of itself, the existence of a static phase in the remote past of the Universe does not lead to a scale-invariant power spectrum.
- if the static phase is followed by a long enough stage of inflation, the spectrum might become flat in the observable range of wavenumbers.
- the consequences of the details of the evolution of the scale factor around the transition time, modeled as a mini-bounce (or anti-bounce), are not erased by inflation and appear as a “bullet” feature in the spectrum.
- the position of the mini-bounce has only a small influence on the shape of the “bullet”, but its steepness and amplitude control, respectively, the comobile position and the size of the bullet.
- multiple bounces can leave complex features in the spectrum. Bounces with different characteristics might leave distinguishable imprints in the tensor spectrum.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borde, A.; Vilenkin, A. Eternal inflation and the initial singularity. Phys. Rev. Lett. 1994, 72, 3305–3309. [Google Scholar] [CrossRef] [PubMed]
- Borde, A.; Vilenkin, A. Singularities in Inflationary Cosmology: A Review. Int. J. Mod. Phys. D 1996, 5, 813–824. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing cosmologies: Progress and problems. Found. Phys. 2017, 47, 797–850. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N. Has the Universe always expanded? Phys. Rev. D 2002, 65, 023513. [Google Scholar] [CrossRef]
- Falciano, F.T.; Lilley, M.; Peter, P. Primordial Black Holes from Inflaton Fragmentation into Oscillons. Phys. Rev. D 2008, 77, 083513. [Google Scholar] [CrossRef]
- Lin, C.; Brandenberger, R.H.; Perreault Levasseur, L. A Matter Bounce By Means of Ghost Condensation. J. Cosmol. Astropart. Phys. 2011, 2011, 19. [Google Scholar] [CrossRef]
- Qiu, T.; Evslin, J.; Cai, Y.-F.; Li, M.; Zhang, X. Bouncing Galileon Cosmologies. J. Cosmol. Astropart. Phys. 2011, 2011, 36. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H.; Toumbas, N. Thermal duality and non-singular cosmology in d-dimensional superstrings. Nucl. Phys. B 2012, 855, 280–307. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Qiu, T.; Piao, Y.-S.; Li, M.; Zhang, X. Bouncing Universe with Quintom Matter. J. High Energy Phys. 2007, 2007, 71. [Google Scholar] [CrossRef]
- Biswas, T.; Mazumdar, A.; Siegel, W. Bouncing Universes in String-inspired Gravity. J. Cosmol. Astropart. Phys. 2006, 2006, 9. [Google Scholar] [CrossRef]
- Biswas, T.; Brandenberger, R.; Mazumdar, A.; Siegel, W. Reconstruction of the Scalar-Tensor Lagrangian from a LCDM Background and Noether Symmetry. J. Cosmol. Astropart. Phys. 2007, 2007, 11. [Google Scholar] [CrossRef]
- Langlois, D.; Naruko, A. Bouncing cosmologies in massive gravity on de Sitter. Class. Quant. Grav. 2013, 30, 205012. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.-L.; Ovrut, B.A. A Cosmological Super-Bounce. Phys. Rev. D 2014, 90, 025005. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Barrau, A. Loop quantum cosmology: From pre-inflationary dynamics to observations. Class. Quant. Grav. 2015, 32, 234001. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The Ekpyrotic Universe: Colliding Branes and the Origin of the Hot Big Bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic Evolution in a Cyclic Universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Battefeld, T.; Watson, S. String Gas Cosmology. Rev. Mod. Phys. 2006, 78, 435. [Google Scholar] [CrossRef]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Gravitational echoes from macroscopic quantum gravity effects. J. High Energy Phys. 2017, 2017, 54. [Google Scholar] [CrossRef]
- Beesham, A.; Chervon, S.V.; Maharaj, S.D. An emergent universe supported by a nonlinear sigma model. Class. Quant. Grav. 2009, 26, 075017. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H.W. Emergent universe from the Horava-Lifshitz gravity. Phys. Rev. D 2010, 81, 103522. [Google Scholar] [CrossRef]
- Mukerji, S.; Chakraborty, S. Emergent universe in Horava gravity. Astrophys. Space Sci. 2011, 331, 665–671. [Google Scholar] [CrossRef]
- Mukerji, S.; Chakraborty, S. Emergent Universe in Einstein-Gauss-Bonnet Theory. Int. J. Theor. Phys. 2010, 49, 2446–2455. [Google Scholar] [CrossRef]
- Paul, B.C.; Ghose, S.; Thakur, P. Emergent Universe from A Composition of Matter, Exotic Matter and Dark Energy. Mon. Not. R. Astron. Soc. 2011, 413, 686–690. [Google Scholar] [CrossRef]
- Debnath, U.; Chakraborty, S. Emergent Universe with Exotic Matter in Brane World Scenario. Int. J. Theor. Phys. 2011, 50, 2892–2898. [Google Scholar] [CrossRef]
- Rudra, P. Emergent Universe with Exotic Matter in Loop Quantum Cosmology, DGP Brane World and Kaluza-Klein Cosmology. Mod. Phys. Lett. A 2012, 27, 1250189. [Google Scholar] [CrossRef]
- Chakraborty, S. Is Emergent Universe a Consequence of Particle Creation Process? Phys. Lett. B 2014, 732, 81–84. [Google Scholar] [CrossRef]
- Perez, A.; Sudarsky, D.; Bjorken, J.D. A microscopic model for an emergent cosmological constant. arXiv, 2018; arXiv:1804.07162. [Google Scholar] [CrossRef]
- Alesci, E.; Botta, G.; Cianfrani, F.; Liberati, S. Cosmological singularity resolution from quantum gravity: The emergent-bouncing universe. Phys. Rev. D 2017, 96, 046008. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Li, M.; Zhang, X. Emergent Universe Scenario via Quintom Matter. Phys. Lett. B 2012, 718, 248–254. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Wan, Y.; Zhang, X. Cosmology of the Spinor Emergent Universe and Scale-invariant Perturbations. Phys. Lett. B 2014, 731, 217–226. [Google Scholar] [CrossRef]
- Paul, B.C.; Thakur, P. Observational Constraints on EoS parameters of Emergent Universe. Astrophys. Space Sci. 2017, 362, 73. [Google Scholar] [CrossRef]
- Labraña, P. Emergent universe scenario and the low CMB multipoles. Phys. Rev. D 2015, 91, 083534. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, P.; Yu, H. Emergent universe in spatially flat cosmological model. J. Cosmol. Astropart. Phys. 2014, 2014, 48. [Google Scholar] [CrossRef]
- Ghose, S.; Thakur, P.; Paul, B.C. Observational Constraints on the Model Parameters of a Class of Emergent Universe. Mon. Not. R. Astron. Soc. 2012, 421, 20–24. [Google Scholar] [CrossRef]
- del Campo, S.; Guendelman, E.I.; Herrera, R.; Labrana, P. Emerging Universe from Scale Invariance. J. Cosmol. Astropart. Phys. 2010, 2010, 26. [Google Scholar] [CrossRef]
- Alesci, E.; Barrau, A.; Botta, G.; Martineau, K.; Stagno, G. Phenomenology of Quantum Reduced Loop Gravity in the isotropic cosmological sector. arXiv, 2018; arXiv:1808.10225. [Google Scholar] [CrossRef]
- Bolliet, B.; Barrau, A.; Martineau, K.; Moulin, F. Some Clarifications on the Duration of Inflation in Loop Quantum Cosmology. Class. Quant. Grav. 2017, 34, 145003. [Google Scholar] [CrossRef]
- Barrau, A.; Jamet, P.; Martineau, K.; Moulin, F. Scalar spectra of primordial perturbations in loop quantum cosmology. Phys. Rev. D 2018, 98, 086003. [Google Scholar] [CrossRef]
- Rovelli, C. Zakopane lectures on loop gravity. arXiv, 2011; arXiv:1102.3660. [Google Scholar]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Alesci, E.; Cianfrani, F. Loop Quantum Cosmology from Loop Quantum Gravity. Europhys. Lett. 2015, 111, 40002. [Google Scholar] [CrossRef]
- Ashtekar, A.; Wilson-Ewing, E. Loop quantum cosmology of Bianchi I models. Phys. Rev. D 2009, 79, 083535. [Google Scholar] [CrossRef]
- Bolliet, B.; Grain, J.; Stahl, C.; Linsefors, L.; Barrau, A. Comparison of primordial tensor power spectra from the deformed algebra and dressed metric approaches in loop quantum cosmology. Phys. Rev. D 2015, 91, 084035. [Google Scholar] [CrossRef]
- Barrau, A.; Bolliet, B. Some conceptual issues in loop quantum cosmology. arXiv, 2016; arXiv:1602.04452. [Google Scholar] [CrossRef]
- Martineau, K.; Barrau, A.; Grain, J. A first step towards the inflationary trans-Planckian problem treatment in Loop Quantum Cosmology. Int. J. Mod. Phys. D 2018, 27, 1850067. [Google Scholar] [CrossRef]
- Schander, S.; Barrau, A.; Bolliet, B.; Linsefors, L.; Mielczarek, J.; Grain, J. Primordial scalar power spectrum from the Euclidean Big Bounce. Phys. Rev. D 2016, 93, 023531. [Google Scholar] [CrossRef]
- Linsefors, L.; Barrau, A. Duration of inflation and conditions at the bounce as a prediction of effective isotropic loop quantum cosmolog. Phys. Rev. D 2013, 87, 123509. [Google Scholar] [CrossRef]
- Martineau, K.; Barrau, A.; Schander, S. Detailed investigation of the duration of inflation in loop quantum cosmology for a Bianchi-I universe with different inflaton potentials and initial conditions. Phys. Rev. D 2017, 95, 083507. [Google Scholar] [CrossRef]
- Barrau, A.; Bojowald, M.; Calcagni, G.; Grain, J.; Kagan, M. Anomaly-free cosmological perturbations in effective canonical quantum gravity. J. Cosmol. Astropart. Phys. 2015, 2015, 51. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rept. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef] [PubMed]

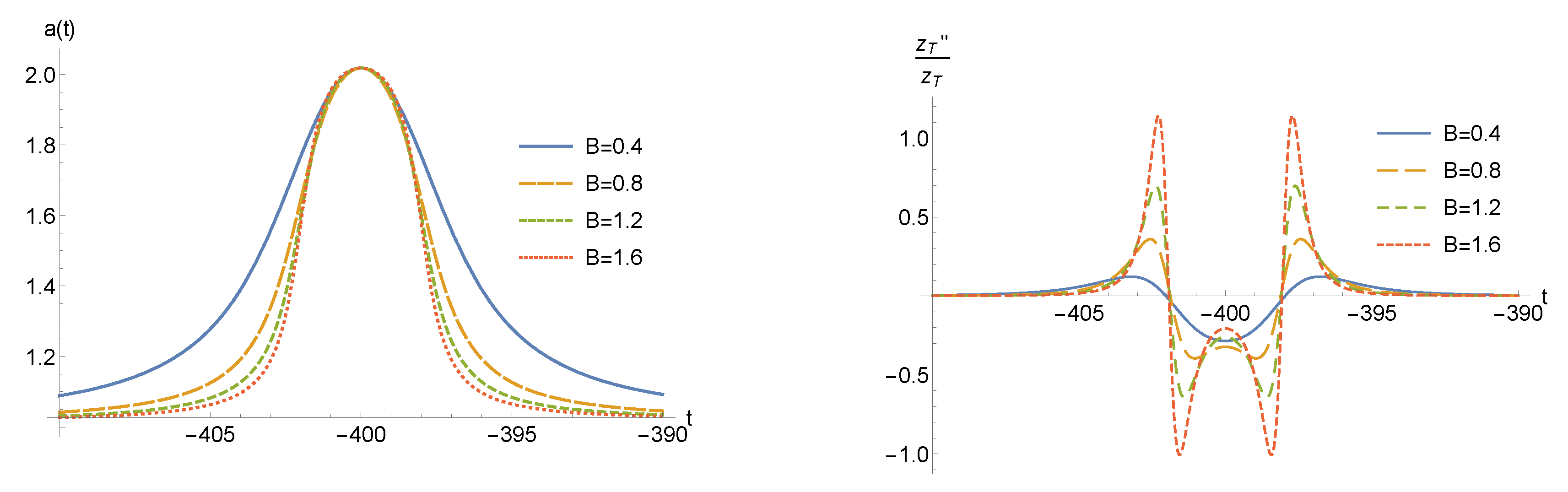
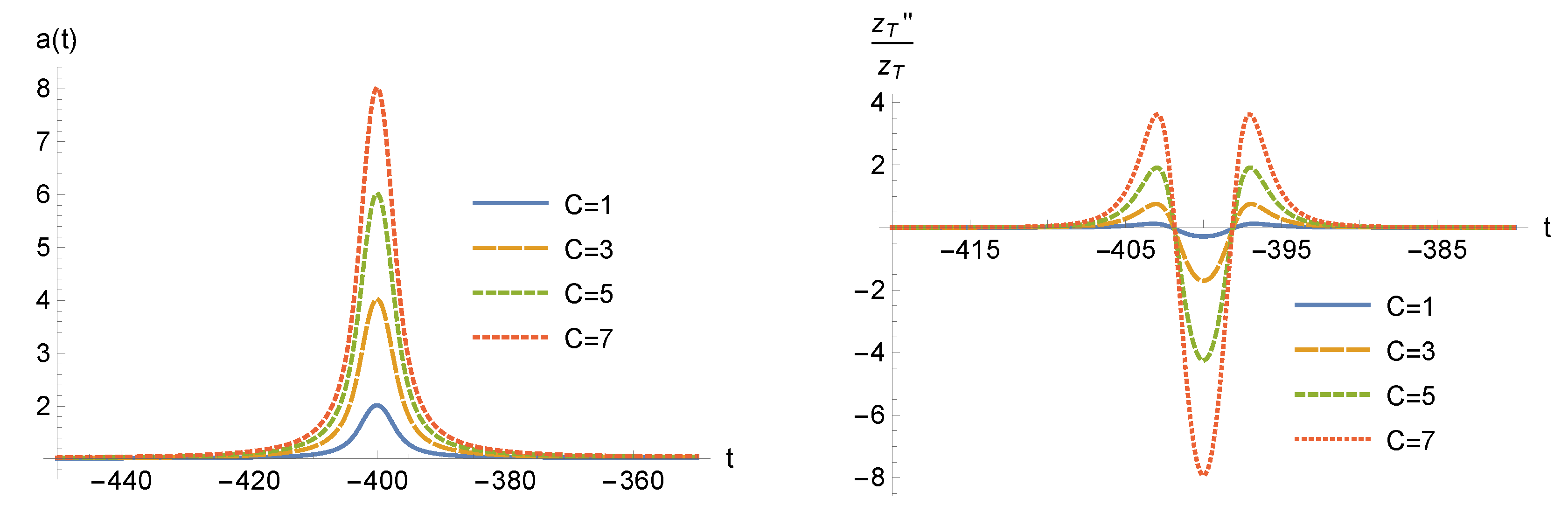

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martineau, K.; Barrau, A. Primordial Power Spectra from an Emergent Universe: Basic Results and Clarifications. Universe 2018, 4, 149. https://doi.org/10.3390/universe4120149
Martineau K, Barrau A. Primordial Power Spectra from an Emergent Universe: Basic Results and Clarifications. Universe. 2018; 4(12):149. https://doi.org/10.3390/universe4120149
Chicago/Turabian StyleMartineau, Killian, and Aurélien Barrau. 2018. "Primordial Power Spectra from an Emergent Universe: Basic Results and Clarifications" Universe 4, no. 12: 149. https://doi.org/10.3390/universe4120149
APA StyleMartineau, K., & Barrau, A. (2018). Primordial Power Spectra from an Emergent Universe: Basic Results and Clarifications. Universe, 4(12), 149. https://doi.org/10.3390/universe4120149





