Precision Determination of αs from Lattice QCD
Abstract
1. Introduction
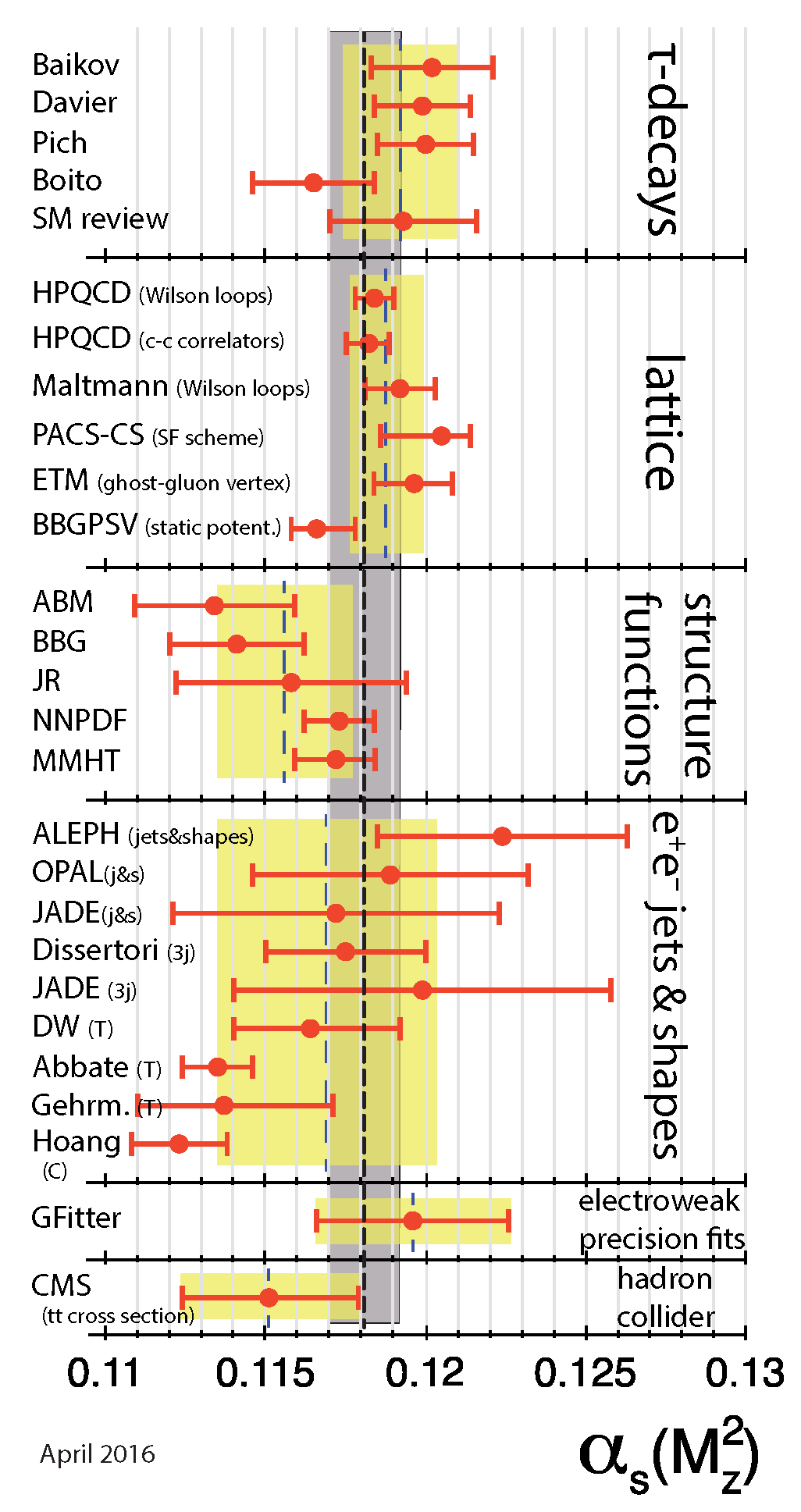
2. Determinations of : General Considerations
2.1. Phenomenological Determinations
2.2. Phenomenological Couplings and -Parameters
2.3. Lattice QCD Determinations
2.4. Finite-Volume Renormalization Schemes and Step-Scaling
3. The Schrödinger Functional and Finite-Volume Couplings
3.1. The SF Couplings
3.2. The GF Coupling
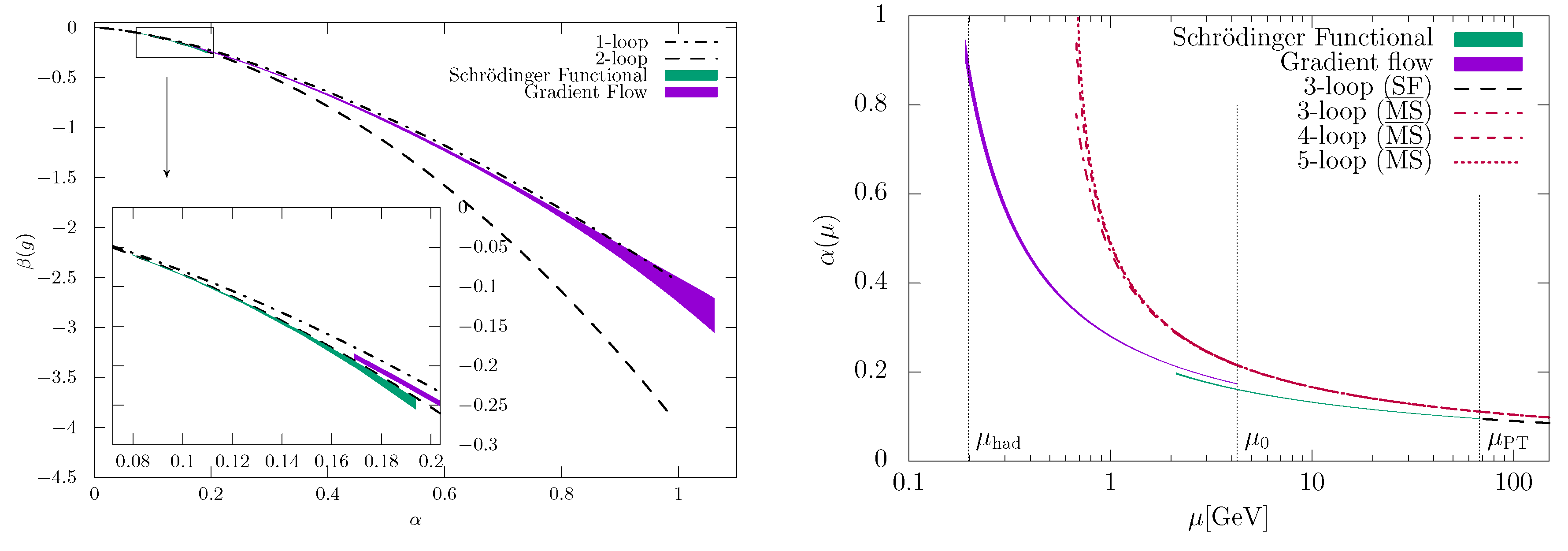
4. from the Femto-Universe
4.1. Determination of and the Accuracy of Perturbation Theory at High-Energy
4.2. Low-Energy Running and Determination of
4.3. Hadronic Matching and
4.4. Perturbative Decoupling and
5. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- Salam, G.P. The strong coupling: a theoretical perspective. In From My Vast Repertoire...: Guido Altarelli’s Legacy; Levy, A., Forte, S., Ridolfi, G., Eds.; World Scientific: Singapore, 2019; pp. 101–121. [Google Scholar]
- d’Enterria, D. αs status and perspectives (2018). In Proceedings of the 26th International Workshop on Deep Inelastic Scattering and Related Subjects (DIS 2018) Port Island, Kobe, Japan, 16–20 April 2018. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Dalla Brida, M.; Fritzsch, P.; Korzec, T.; Ramos, A.; Sint, S.; Sommer, R. Determination of the QCD Λ parameter and the accuracy of perturbation theory at high energies. Phys. Rev. Lett. 2016, 117, 182001. [Google Scholar] [CrossRef] [PubMed]
- Dalla Brida, M.; Fritzsch, P.; Korzec, T.; Ramos, A.; Sint, S.; Sommer, R. Slow running of the Gradient Flow coupling from 200 MeV to 4 GeV in Nf = 3 QCD. Phys. Rev. D 2017, 95, 014507. [Google Scholar] [CrossRef]
- Bruno, M.; Dalla Brida, M.; Fritzsch, P.; Korzec, T.; Ramos, A.; Schaefer, S.; Simma, H.; Sint, S.; Sommer, R. QCD Coupling from a Nonperturbative Determination of the Three-Flavor Λ Parameter. Phys. Rev. Lett. 2017, 119, 102001. [Google Scholar] [CrossRef] [PubMed]
- Dalla Brida, M.; Fritzsch, P.; Korzec, T.; Ramos, A.; Sint, S.; Sommer, R. A non-perturbative exploration of the high energy regime in Nf = 3 QCD. Eur. Phys. J. C 2018, 78, 372. [Google Scholar] [CrossRef]
- Sommer, R.; Wolff, U. Non-perturbative computation of the strong coupling constant on the lattice. Nucl. Part. Phys. Proc. 2015, 261–262, 155. [Google Scholar] [CrossRef]
- Weinberg, S. New approach to the renormalization group. Phys. Rev. D 1973, 8, 3497–3509. [Google Scholar] [CrossRef]
- Callan, C.G., Jr. Broken scale invariance in scalar field theory. Phys. Rev. D 1970, 2, 1541–1547. [Google Scholar] [CrossRef]
- Symanzik, K. Small distance behavior in field theory and power counting. Commun. Math. Phys. 1970, 18, 227–246. [Google Scholar] [CrossRef]
- Symanzik, K. Small distance behavior analysis and Wilson expansion. Commun. Math. Phys. 1971, 23, 49. [Google Scholar] [CrossRef]
- Montvay, I.; Munster, G. Quantum Fields on a Lattice; Cambridge Monographs on Mathematical Physics, Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Hernandez, M.P. Lattice field theory fundamentals. Modern perspectives in lattice QCD: Quantum field theory and high performance computing. In Proceedings of the International School, 93rd Session, Les Houches, France, 3–28 August 2009; pp. 1–91. [Google Scholar]
- Aoki, S. Review of lattice results concerning low-energy particle physics. Eur. Phys. J. C 2017, 77, 112. [Google Scholar] [CrossRef]
- Lüscher, M.; Weisz, P.; Wolff, U. A Numerical method to compute the running coupling in asymptotically free theories. Nucl. Phys. B 1991, 359, 221. [Google Scholar] [CrossRef]
- Lüscher, M.; Narayanan, R.; Weisz, P.; Wolff, U. The Schrödinger Functional: a renormalizable probe for non-abelian gauge theories. Nucl. Phys. B 1992, 384, 168. [Google Scholar] [CrossRef]
- Sint, S. On the Schrödinger functional in QCD. Nucl. Phys. B 1994, 421, 135. [Google Scholar] [CrossRef]
- Sint, S. One loop renormalization of the QCD Schrödinger functional. Nucl. Phys. B 1995, 451, 416–444. [Google Scholar] [CrossRef]
- Sint, S.; Sommer, R. The running coupling from the QCD Schrödinger functional: a one-loop analysis. Nucl. Phys. B 1996, 465, 71–98. [Google Scholar] [CrossRef]
- Narayanan, R.; Wolff, U. Two loop computation of a running coupling lattice Yang–Mills theory. Nucl. Phys. B 1995, 444, 425–446. [Google Scholar] [CrossRef]
- Bode, A.; Wolff, U.; Weisz, P. Two-loop computation of the Schrödinger functional in pure SU(3) lattice gauge theory. Nucl. Phys. B 1999, 540, 491–499. [Google Scholar] [CrossRef]
- Bode, A.; Weisz, P.; Wolff, U. Two-loop computation of the Schrödinger functional in lattice QCD. Nucl. Phys. B 2000, 576, 517–539. [Google Scholar] [CrossRef]
- Dalla Brida, M.; Hesse, D. Numerical Stochastic Perturbation Theory and the Gradient Flow. PoS 2014, Lattice2013, 326. [Google Scholar]
- Dalla Brida, M.; Lüscher, M. The gradient flow coupling from numerical stochastic perturbation theory. PoS 2016, LATTICE2016, 332. [Google Scholar]
- Dalla Brida, M.; Lüscher, M. SMD-based numerical stochastic perturbation theory. Eur. Phys. J. C 2017, 77, 308. [Google Scholar] [CrossRef]
- Lüscher, M.; Sommer, R.; Weisz, P.; Wolff, U. A precise determination of the running coupling in the SU(3) Yang–Mills theory. Nucl. Phys. B 1994, 413, 481–502. [Google Scholar] [CrossRef]
- de Divitiis, G.; Frezzotti, R.; Guagnelli, M.; Lüscher, M.; Petronzio, R.; Sommer, R.; Weisz, P.; Wolff, U. Universality and the approach to the continuum limit in lattice gauge theory. Nucl. Phys. 1995, B437, 447–470. [Google Scholar] [CrossRef]
- Narayanan, R.; Neuberger, H. Infinite N phase transitions in continuum Wilson loop operators. JHEP 2006, 03, 064. [Google Scholar] [CrossRef]
- Lüscher, M. Properties and uses of the Wilson flow in lattice QCD. J. High Energy Phys. 2010, 2010, 071. [Google Scholar] [CrossRef]
- Lüscher, M.; Weisz, P. Perturbative analysis of the gradient flow in non-abelian gauge theories. J. High Energy Phys. 2011, 2011, 51. [Google Scholar] [CrossRef]
- Fodor, Z.; Holland, K.; Kuti, J.; Nogradi, D.; Wong, C.H. The Yang–Mills gradient flow in finite volume. J. High Energy Phys. 2012, 2012, 7. [Google Scholar] [CrossRef]
- Fritzsch, P.; Ramos, A. The gradient flow coupling in the Schrödinger Functional. J. High Energy Phys. 2013, 2013, 8. [Google Scholar] [CrossRef]
- Ramos, A.; Sint, S. Symanzik improvement of the gradient flow in lattice gauge theories. Eur. Phys. J. 2016, C76, 15. [Google Scholar] [CrossRef]
- Fritzsch, P.; Dalla Brida, M.; Korzec, T.; Ramos, A.; Sint, S.; Sommer, R. Towards a new determination of the QCD Lambda parameter from running couplings in the three-flavour theory. PoS 2014, LATTICE2014, 291. [Google Scholar]
- Sommer, R. Scale setting in lattice QCD. PoS 2014, LATTICE2013, 015. [Google Scholar]
- Bruno, M.; Korzec, T.; Schaefer, S. Setting the scale for the CLS 2+1 flavor ensembles. Phys. Rev. 2017, D95, 74504. [Google Scholar] [CrossRef]
- Bruno, M.; Korzec, T.; Schaefer, S. Simulation of QCD with Nf = 2 + 1 flavors of non-perturbatively improved Wilson fermions. J. High Energy Phys. 2015, 2015, 43. [Google Scholar] [CrossRef]
- Dalla Brida, M.; Sint, S.; Vilaseca, P. The chirally rotated Schrödinger functional: theoretical expectations and perturbative tests. J. High Energy Phys. 2016, 2016, 102. [Google Scholar] [CrossRef]
- Dalla Brida, M.; Korzec, T.; Sint, S.; Vilaseca, P. High precision renormalization of the flavour non-singlet Noether currents in lattice QCD with Wilson quarks. arXiv, 2018; arXiv:1809.03383. [Google Scholar]
- Athenodorou, A.; Finkenrath, J.; Knechtli, F.; Korzec, T.; Leder, B.; Marinković, M.K.; Sommer, R. How perturbative are heavy sea quarks? arXiv, 2018; arXiv:1809.03383. [Google Scholar]
- Bruno, M.; Finkenrath, J.; Knechtli, F.; Leder, B.; Sommer, R. Effects of heavy sea quarks at low energies. Phys. Rev. Lett. 2015, 114, 102001. [Google Scholar] [CrossRef] [PubMed]
- Knechtli, F.; Korzec, T.; Leder, B.; Moir, G. Power corrections from decoupling of the charm quark. Phys. Lett. B 2017, 774, 649–655. [Google Scholar] [CrossRef]
| 1. | As is custom in phenomenology, when we generically refer to the strong coupling we actually refer to its value in the -scheme of dimensional regularization, evaluated at the Z-boson mass i.e., . |
| 2. | |
| 3. | We restrict our attention to mass-independent renormalization schemes which have simple renormalization group equations [9]. These are obtained by considering the observable for zero (renormalized) quark-masses. |
| 4. |


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalla Brida, M. Precision Determination of αs from Lattice QCD. Universe 2018, 4, 148. https://doi.org/10.3390/universe4120148
Dalla Brida M. Precision Determination of αs from Lattice QCD. Universe. 2018; 4(12):148. https://doi.org/10.3390/universe4120148
Chicago/Turabian StyleDalla Brida, Mattia. 2018. "Precision Determination of αs from Lattice QCD" Universe 4, no. 12: 148. https://doi.org/10.3390/universe4120148
APA StyleDalla Brida, M. (2018). Precision Determination of αs from Lattice QCD. Universe, 4(12), 148. https://doi.org/10.3390/universe4120148