Hybrid Detection of High Energy Showers in Urban Environments †
Abstract
1. Introduction
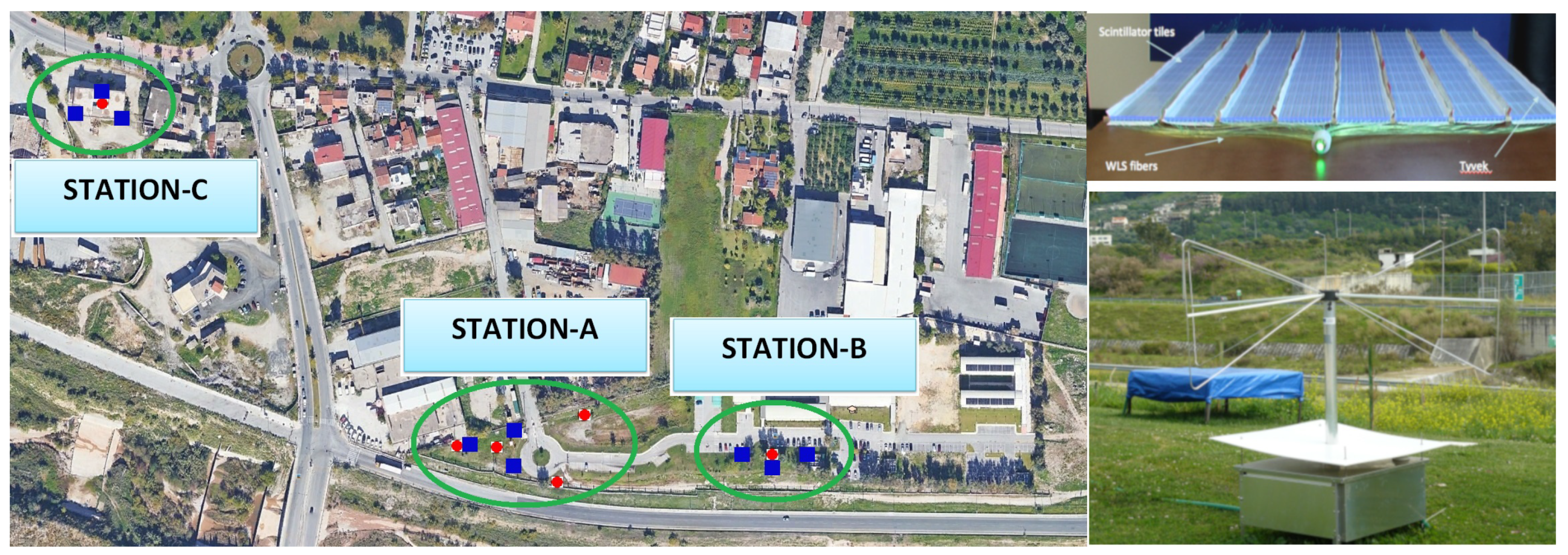
2. The Astroneu Array
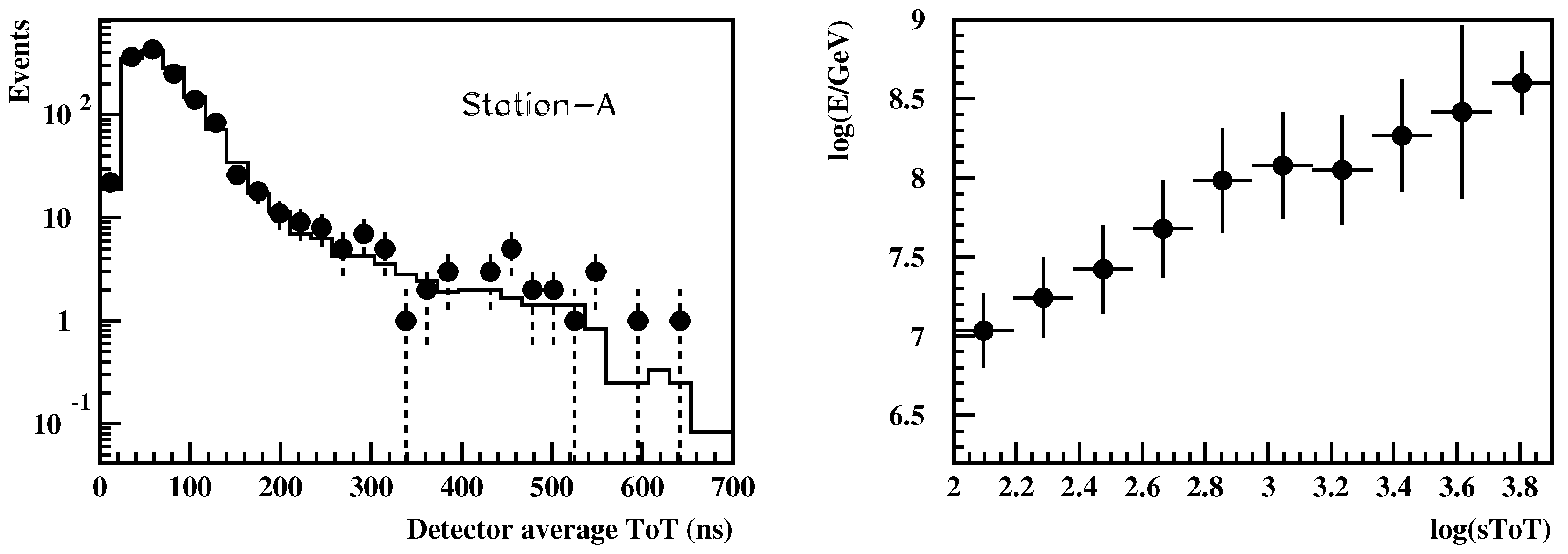
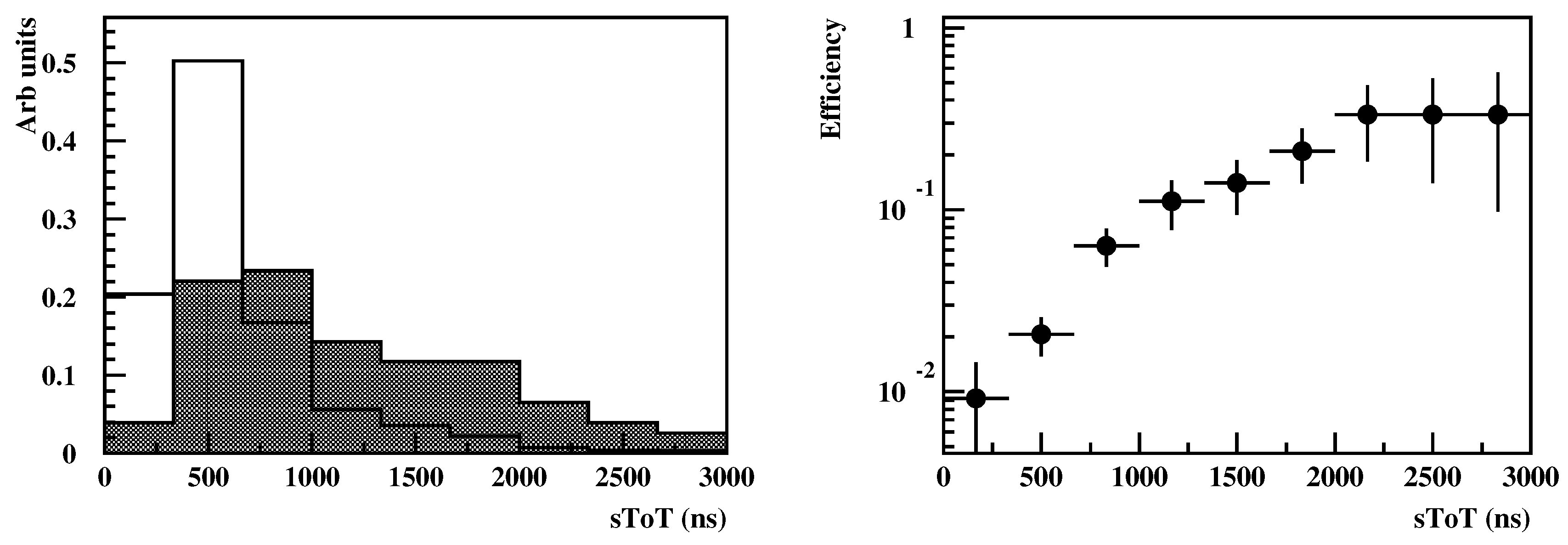
3. Selection of Very High Energy EAS
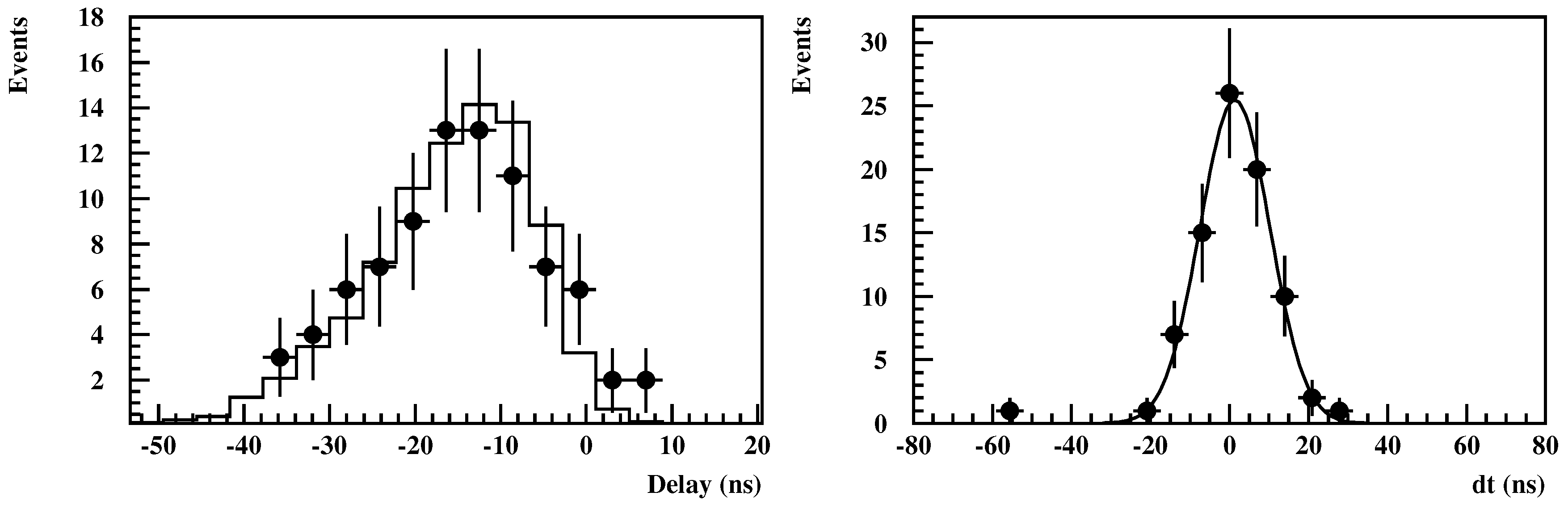
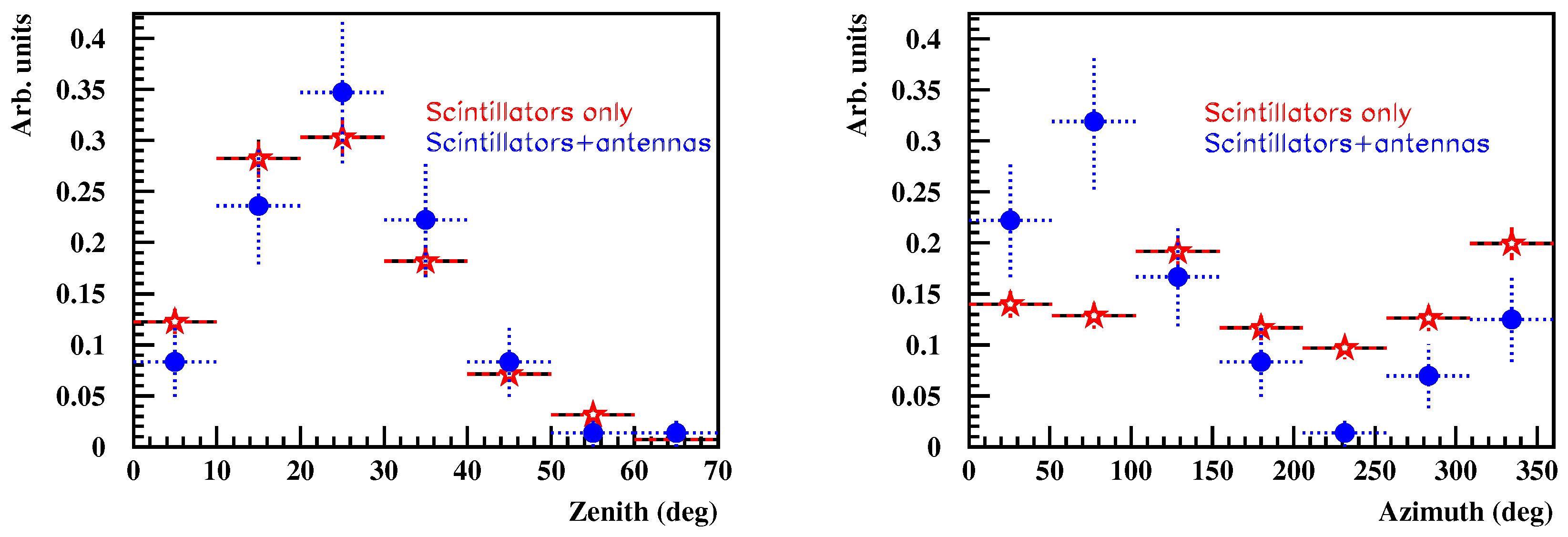
4. RF Signal Timing and Combined Angular Reconstruction
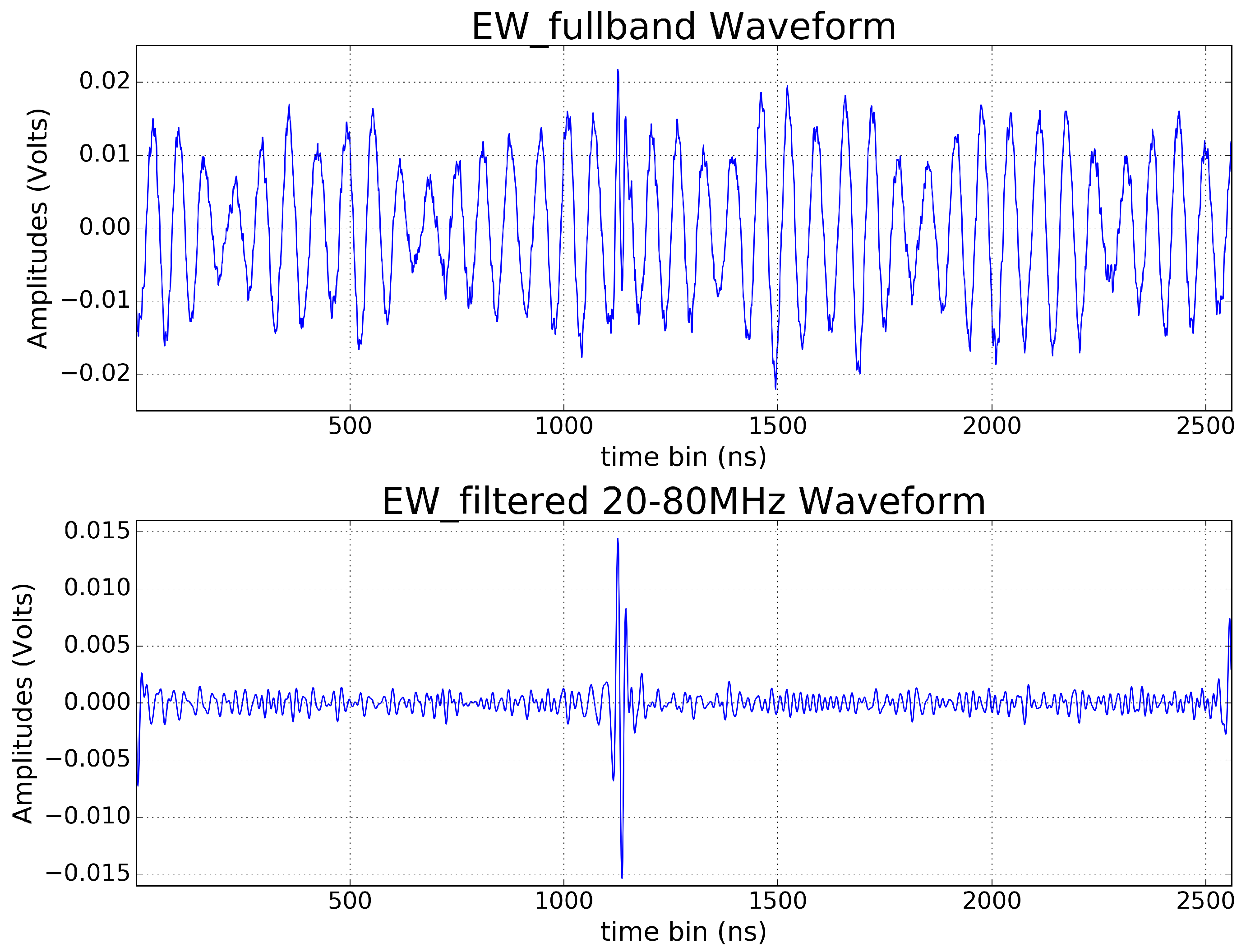
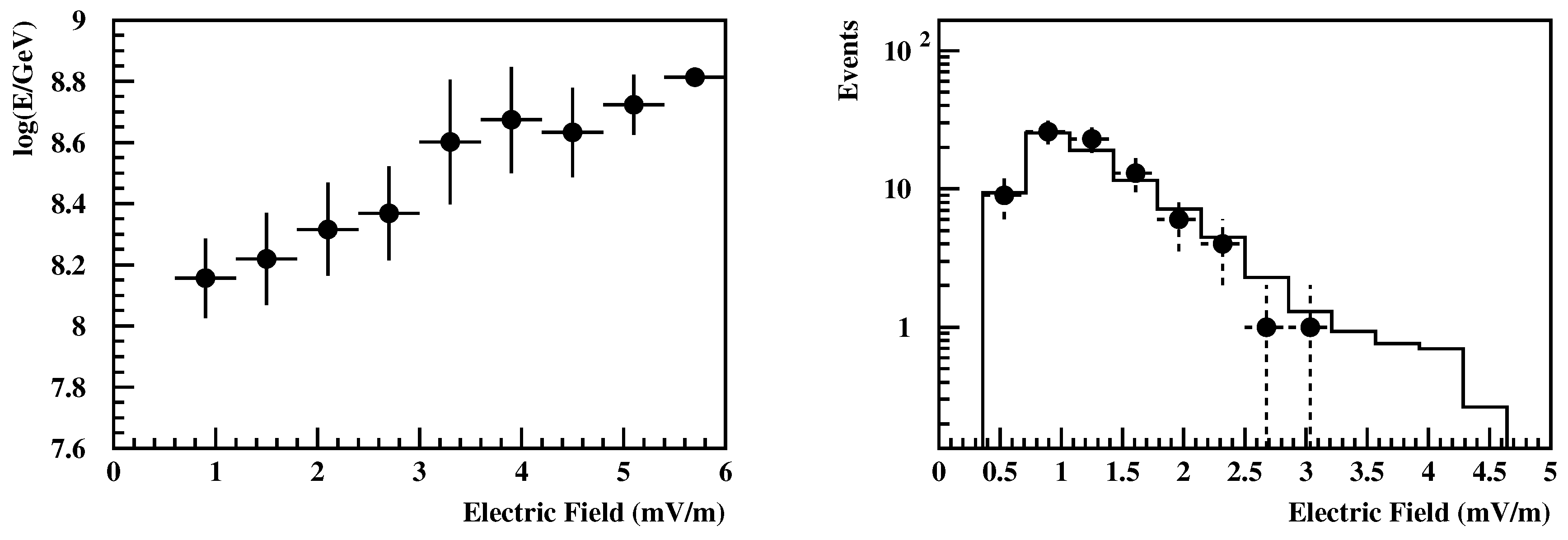
5. Electric Field Measurement
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schröder, F.G. Radio detection of cosmic-ray air showers and high-energy neutrinos. Prog. Part. Nucl. Phys. 2017, 93, 1–68. [Google Scholar] [CrossRef]
- Huege, T. Radio detection of cosmic ray air showers in the digital era. Phys. Rep. 2016, 620, 1–52. [Google Scholar] [CrossRef]
- Aab, A.; Almela, D.A.; Asorey, H.G.; Bertou, X.P.L.; Dasso, S.R.; Etchegoyen, A.; Figueira, J.M.; Filevich, A.; Freire, M.M.; Garcia, B.E.; et al. Energy estimation of cosmic rays with the Engineering Radio Array of the Pierre Auger Observatory. Phys. Rev. D 2016, 93, 122005. [Google Scholar] [CrossRef]
- Buitink, S.; Corstanje, A.; Falcke, H.; Hörandel, J.R.; Huege, T.; Nelles, A.; Rachen, J.P.; Rossetto, L.; Schellart, P.; Scholten, O.; et al. A large light-mass component of cosmic rays at 1017–1017.5 eV from radio observations. Nature 2016, 531, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bähren, L.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Chiavassa, A.; et al. Reconstructing energy and Xmax of cosmic ray air showers using the radio lateral distribution measured with LOPES. AIP Conf. Proc. 2013, 1535, 1–15. [Google Scholar]
- Falcke, H.; Apel, W.D.; Badea, A.F.; Bähren, L.; Bekk, K.; Bercuci, A.; Bertaina, M.; Biermann, P.L.; Blümer, J.; Bozdog, H.; et al. Detection and imaging of atmospheric radio flashes from cosmic ray air showers. Nature 2005, 435, 313. [Google Scholar] [CrossRef] [PubMed]
- Ardouin, D.; Bellétoile, A.; Charrier, D.; Dallier, R.; Denis, L.; Eschstruth, P.; Gousset, T.; Haddad, F.; Lamblin, J.; Lautridou, P.; et al. Radio-detection signature of high-energy cosmic rays by the CODALEMA experiment. Nucl. Instrum. Methods A 2005, 555, 148–163. [Google Scholar] [CrossRef]
- Avgitas, T.; Bourlis, G.; Fanourakis, G.K.; Gkialas, I.; Leisos, A.; Manthos, I.; Tsirigotis, A.; Tzamarias, S.E. Deployment and calibration procedures for accurate timing and directional reconstruction of EAS particle-fronts with Helycon stations. Unpublished. arXiv, 2017; arXiv:1702.04902. [Google Scholar]
- Avgitas, T.; Bourlis, G.; Fanourakis, G.K.; Gkialas, I.; Leisos, A.; Manthos, I.; Stamelakis, A.; Tsirigotis, A.; Tzamarias, S.E. Operation and performance of a pilot HELYCON cosmic ray telescope with 3 stations. Unpublished. arXiv, 2018; arXiv:1801.04768. [Google Scholar]
- Manthos, I.; Gkialas, I.; Bourlis, G.; Leisos, A.; Papaikonomou, A.; Tsirigotis, A.G.; Tzamarias, S.E. Cosmic Ray RF detection with the ASTRONEU array. Unpublished. arXiv, 2017; arXiv:1702.05794. [Google Scholar]
- Leisos, A.; Avgitas, T.; Bourlis, G.; Fanourakis, G.K.; Gkialas, I.; Manthos, I.; Stamelakis, A.; Tsirigotis, A.; Tzamarias, S.E. The Hellenic Open University Cosmic Ray Telescope: Research and Educational Activities. EPJ Web Conf. 2018, 182. [Google Scholar] [CrossRef]
- Charrier, D. Antenna development for astroparticle and radioastronomy experiments. Nucl. Instrum. Methods Phys. Res. Sect. A 2012, 662, S142–S145. [Google Scholar] [CrossRef]
- Hansen, S.; Jordan, T.; Kiper, T.; Claes, D.; Snow, G.; Berns, H.; Burnett, T.H.; Gran, R.; Wilkes, R.J. Low-cost data acquisition card for school-network cosmic ray detectors. IEEE Trans. Nucl. Sci. 2004, 51, 926–930. [Google Scholar] [CrossRef]
- Ardouin, D.; Belletoile, A.; Berat, C.; Breton, D.; Charrier, D.; Chauvin, J.; Chendeb, M.; Cordier, A.; Dagoret-Campagne, S.; Dallier, R.; et al. Geomagnetic origin of the radio emission from cosmic ray induced air showers observed by CODALEMA. Astropart. Phys. 2009, 31, 192–200. [Google Scholar] [CrossRef]
- Abreu, P.; Acounis, S.; Aglietta, M.; Ahlers, M.; Ahn, E.J.; Albuquerque, I.F.M.; Allen, J.; Allison, P.; Almela, A.; Castillo, J.A.; et al. Results of a self-triggered prototype system for radio-detection of extensive air showers at the Pierre Auger Observatory. J. Instrum. 2012, 7. [Google Scholar] [CrossRef]
- Heck, D.; Knapp, J.; Capdevielle, J.N.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers. Forschungszentrum Karlsruhe Report FZKA 6019. 1998. Available online: https://www.ikp.kit.edu/corsika/70.php (accessed on 30 November 2018).
- Tsirigotis, A.G.; Leisos, A.; Tzamarias, S.E. HOU Reconstruction & Simulation (HOURS): A complete simulation and reconstruction package for very large volume underwater neutrino telescopes. Nucl. Instrum. Methods A 2011, 626, S185–S187. [Google Scholar]
- Tsirigotis, A.G.; Leisos, A.; Tzamarias, S.E. Reconstruction efficiency and discovery potential of a Mediterranean neutrino telescope: A simulation study using the Hellenic Open University Reconstruction and Simulation (HOURS) package. Nucl. Instrum. Methods A 2013, 725, 68–71. [Google Scholar] [CrossRef]
- Marin, V.; Revenu, B. Simulation of radio emission from cosmic ray air shower with SELFAS2. Astropart. Phys. 2012, 35, 733. [Google Scholar] [CrossRef]
- Catalano, O.; D’Ali Staiti, G.; Gabriele, M.; La Fata, L. The longitudinal EAS profile at E > 1019 eV: A comparison between GIL analytical formula and the predictions of detailed Montecarlo simulations. In Proceedings of the 27th ICRC, Hamburg, Germany, 7–15 August 2001; p. 498. [Google Scholar]
- Burke, G.; Poggio, A. Numerical Electromagnetics Code (NEC) Method of Moments, Parts I, II, III; Tech. Rep.; NEC-l (1977); Lawrence Livermore National Laboratory: Livermore, CA, USA, 1977.
- Burke, G.; Poggio, A. Numerical Electromagnetics Code (NEC) Method of Moments, Parts I, II, III; Tech. Rep.; NEC-2 (1981); Lawrence Livermore National Laboratory: Livermore, CA, USA, 1981.
- Burke, G.; Poggio, A. Numerical Electromagnetics Code (NEC) Method of Moments, Parts I, II, III; Tech. Rep.; NEC-3 (1983); Lawrence Livermore National Laboratory: Livermore, CA, USA, 1983.
- Nonis, S. Studies for High Energy air shower identification using RF measurements with the ASTRONEU array. In Proceedings of the UHECR 2018, Paris, France, 8–12 October 2018. [Google Scholar]
| 1. | HELYCON (Hellenic Lyceum Cosmic Observatories Network) is a project aiming for the development of a network of extensive air shower detector stations, distributed in western Greece [11]. |
| 2. | In 2017 three more RF antennas were installed at station A. |
| 3. | The Quarknet board upon a trigger sends a NIM pulse (Quarknet-OUT trigger signal) to the station’s RFA external trigger input. |
| 4. | In subsequents steps of the analysis, a quality criterion is applied on the ToT value of each HDM rejecting small size pulses corresponding to less than 4 minimum ionizing particles. Consequently, the timing error of each HDM pulse is less than 3 ns [8]. |
| 5. | The collected charge in each HDM ( i.e., the particle density at the ground level) can be evaluated from the corresponding ToT value at any operating voltage threshold using charge parameterization curves established by calibration [8]. |
| 6. | Since the RF antenna is positioned inside the triangle defined by the positions of the HDMs, the expected time is negative. |
| 7. | The Quarknet-OUT trigger signal is produced with a jitter of 6.1 ns. |
| 8. | Even though in single station operation the effect is small due to the small inter-detector distance, the difference of the arrival time of the shower front between two stations deviates from the predicted value of the plane particle front approximation. |
| 9. | The electric field strength scales with the vector product , where v is the velocity of the shower and B the geomagnetic field. |
| 10. | The corresponding radius was 670 m and only high energy events were used (E > 10 eV), since low energy EAS is very unlikely to trigger both stations A and B. |
| 11. | From symmetry reasons the electric field distribution in each antenna is the same for station A and B. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leisos, A.; Nonis, S.; Tsirigotis, A.; Bourlis, G.; Papageorgiou, K.; Gkialas, I.; Manthos, I.; Tzamarias, S. Hybrid Detection of High Energy Showers in Urban Environments . Universe 2019, 5, 3. https://doi.org/10.3390/universe5010003
Leisos A, Nonis S, Tsirigotis A, Bourlis G, Papageorgiou K, Gkialas I, Manthos I, Tzamarias S. Hybrid Detection of High Energy Showers in Urban Environments . Universe. 2019; 5(1):3. https://doi.org/10.3390/universe5010003
Chicago/Turabian StyleLeisos, Antonios, Stavros Nonis, Apostolos Tsirigotis, George Bourlis, Kostas Papageorgiou, Ioannis Gkialas, Ioannis Manthos, and Spyros Tzamarias. 2019. "Hybrid Detection of High Energy Showers in Urban Environments " Universe 5, no. 1: 3. https://doi.org/10.3390/universe5010003
APA StyleLeisos, A., Nonis, S., Tsirigotis, A., Bourlis, G., Papageorgiou, K., Gkialas, I., Manthos, I., & Tzamarias, S. (2019). Hybrid Detection of High Energy Showers in Urban Environments . Universe, 5(1), 3. https://doi.org/10.3390/universe5010003





