Abstract
We cautiously review the treatment of pentaquark exotic baryons in chiral soliton models. We consider two examples and argue that any consistent and self-contained description must go beyond the mean field approximation that only considers the classical soliton and the canonical quantization of its (would-be) zero modes via collective coordinates.
1. Introduction
Exotic baryons carry quantum numbers that cannot be constructed as products of three quark states. In this discussion, which is based on Refs. [1,2,3], we will examine and review their description in the framework of chiral soliton models; see Ref. [4] for a recent review on these models. We distinguish between two types of exotic baryons: those with only the three light flavors (up, down, strange) and those that contain heavy flavors such as charm and bottom. Though their description in soliton models is fundamentally different, both require a three-flavor quantization of the soliton and considerations beyond the mean field approach.
It is important to stress that exotic baryons are actually resonances. Hence, they must be observed in scattering processes. To put this into the context of chiral soliton models we first investigate pentaquarks with light flavors and their role in the Skyrme model description of kaon nucleon scattering. By definition of solitons, no term linear in meson fluctuations, that eventually could be identified as a Yukawa interaction, should emerge. If it does, it is a mere short-coming of approximating the exact time-dependent soliton solution. Rather, in scattering the resonance content must be directly analyzed to obtain the widths of (collective) resonances. This implies that the decay width may not be estimated from axial current matrix elements of the collectively excited classical soliton. In turn, this suggests that mean field approaches as e.g., in Refs. [5,6,7,8] are not appropriate to describe resonance widths for hadronic decays. The full calculation indeed requires the introduction of both, collective and harmonic excitations of the classical soliton. The canonical formulation of these fluctuations also induces the constraints needed to avoid double counting errors. An alternative approach that approximates the collective fluctuations to be harmonic is known to be exact in the academic limit of infinitely many color degrees of freedom (). Since our approach may be applied to any (odd) value we compare and indeed find identical scattering data when .
The second example deals with pentaquarks that contain a single heavy quark (charm or bottom) or antiquark. The central element of heavy quark physics is the corresponding spin-flavor symmetry that predicts a degeneracy of heavy pseudoscalar and vector mesons [9,10,11,12,13]. A model with only chiral fields in a mean field formulation [14]1 will not be sufficient because it cannot combine these fields in a single multiplet. The model must be augmented accordingly with these additional fields and couple them to the chiral soliton. This advances the bound state approach to strangeness [16] and particularly shows that the heavy meson bound state selects the appropriate representation for the light flavor (up, down, strange) component of the baryon wave function which models the light diquark structure. Basic heavy baryons select the anti-triplet and the sextet. Pentaquarks with a heavy antiquark relate to the anti-sextet while those with a light antiquark have light flavors from the anti-decapentaplet.
2. Chiral Soliton Models
Chiral solition models are low-energy models for baryons. They are based on the conjecture, resulting from large considerations of QCD, that baryons are described as soliton solutions of a non-linear effective meson theory [17]. At low energies chiral symmetry is governing this effective theory. The most prominent such model is the Skyrme model [18,19], which was firstly applied to static baryon properties in Ref. [20]. This model only contains the pseudoscalar mesons and is too simple for a detailed description of baryon properties.2 Here we will nevertheless base our arguments on this model because it nicely illuminates the structure of chiral soliton models: in most aspects the generation of baryons states via canonical quantization of the soliton’s collective motion is the crucial ingredient while the microscopic details are of lesser relevance.
We are dealing with three light degrees of freedom so that the effective meson theory is a functional of the chiral field . Except for flavor symmetry breaking, the theory is invariant under global chiral transformations while symmetry breaking terms transform as the eighth component of an octet of the vector subgroup . The Skyrme soliton itself is a mapping from configuration space to . In the presence of flavor symmetry breaking it must be embedded in the isospin subgroup to minimize the classical energy. Then the static soliton assumes the hedgehog structure
The profile function (called chiral angle) is obtained from the variational principle to the classical energy, . The boundary condition and enforces unit topological charge, which is identified with the baryon number [22,23]. The classical energy only plays a minor role in the soliton picture of baryons because the soliton model is not renormalizable so that quantum corrections (the vacuum polarization energy) are difficult to control [24]. Hence, we focus on baryon mass differences in which both the classical and the vacuum polarization energies cancel.
In the next step towards generating baryon states, time-dependent solutions must be obtained. These are not known but there are two major approximations in three flavor models. One is based on the so-called bound state approach [16] that introduces harmonic fluctuations in strangeness direction. We will get back to this approach in the context of heavy baryons. The other approximation introduces time-dependent collective coordinates for the (approximate) vector symmetry [25]
thereby generalizing the two-flavor procedure of Ref. [20]. Integrating over space yields the collective coordinate Lagrangian (flavor symmetry breaking excluded, for the time being)
The moment of inertia tensor separates into non-strange () and strange () components due to the particular embedding, Equation (1). These are functionals of the soliton and the actual value depends on the particular model though they are always . The last term is only linear in the time derivative with a fixed coefficient. In purely mesonic theories it arises from the Wess-Zumino term [26] while in chiral quark soliton models it stems from the interaction of the chiral field with self-consistently constructed quark fields [27].
3. Collective Coordinate Quantization with Three Flavors
The generation of baryon states proceeds by canonically quantizing the angular degrees of freedom in . This introduces eight right generators
that are subject to the commutation relations . A Legendre transformation yields the Hamiltonian for the collective coordinates
where is the quadratic Casimir operator of . Again, flavor symmetry breaking terms have not been made explicit in . We diagonalize this Hamiltonian subject to the constraint . Since this can be directly imposed on the eigenstates. Without symmetry breaking these are elements of representations.
For we have and the representations with the lowest eigenvalues are the octet () and the decuplet () [25]. Their Young tableaux and particle content are shown in Figure 1.
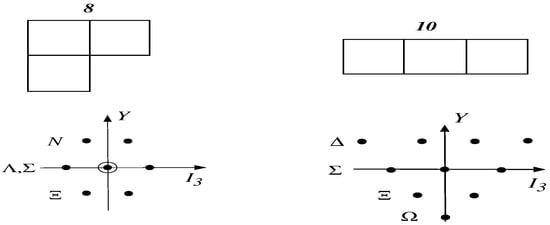
Figure 1.
Young tableaux and particle content of the low-lying representations.
In Young tableaux a single box represents a quark while the adjoint, stands for either two quarks or an antiquark, depending on the prescribed baryon number. Hence, for unit baryon number, the octet and decuplet represent three quark composites.
However, higher dimensional representations also solve the (flavor symmetric) eigenvalue problem. Examples are the anti-decuplet and the 27-plet that are shown in Figure 2.
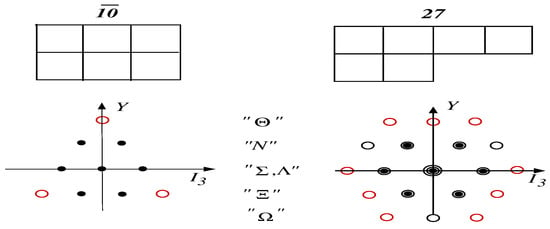
Figure 2.
(Color online) Young tableaux and particle content the anti-decuplet and the 27-plet representations. Red circles indicate exotic baryons that cannot be built from three quarks.
The Young tableaux interpretation immediately reveals that these higher dimensional representations contain baryons with additional quark antiquark pairs. Even more, some baryons in these representations have quantum numbers corresponding to exotic, non-three quark states3. The most prominent example is the pentaquark in the anti-decuplet whose valence quark content is . The eigenvalues of the octet and the anti-decuplet are 3 and 6, respectively. Hence, in a flavor symmetric world, the mass difference between the and the nucleon would be (for ).
These higher dimensional representations play another important role when including -flavor symmetry breaking that is reflected by the hadron masses varying with their strangeness content. The eigenstates of the collective coordinate Hamiltonian are no longer elements of a specific representation. Rather, baryon states with identical quantum numbers from different representations mix as the perturbative diagonalization of nicely reveals [29]. Even more, as pointed out by Yabu and Ando [30] this operator can indeed be diagonalized exactly (numerically) and higher order effects may be relevant in particular cases. We will get back to this in the context of heavy baryons.
4. Mass and Width
The essential question is: Do exotic elements of higher dimensional representations stand for sensible resonances, or are they merely artifacts of the collective coordinate quantization? This issue arises already in the simpler two-flavor version that predicts an exotic spin state well below [31].
To answer this question for soliton model calculations, it is imperative to recall the meaning of resonances in potential scattering. In the particular case of single channel potential scattering a resonance is signaled by the transition of the phase shift through with a positive slope [32]. To identify the potential, time-dependent harmonic fluctuations about the classical soliton, Equation (1) are introduced [33]. When augmenting the rotating hedgehog, Equation (2) by time-dependent fluctuations linear terms emerge that couple to the collective rotations. In early soliton model studies these terms were identified as Yukawa interactions and their transition matrix elements were used to estimate widths of -resonances [20]. An alternative to compute a width from a transition matrix element was to identify the pion field with axial current of the rotating soliton. This was justified as a generalized Goldberger-Treiman relation and was applied to the suggesting a surprisingly narrow resonance [5,6]. Yet this generalization is questionable since the soliton field equation is the same for and but the axial currents are not [2]. In fact, additional contributions to the axial current are not accounted for in PCAC. Neither does the soliton part of the chiral field correspond to an asymptotic meson state.
In any event, by pure definition of the soliton as a stationary point of the action there cannot exist a term linear in small amplitude fluctuations. If it nevertheless emerges, it just reflects that the background configuration is at best an approximation to the actual soliton. Thus, there is natural skepticism on plain Yukawa interactions in soliton models. This was definitely recognized early on as there have been numerous attempts [31,34,35,36,37,38,39,40,41,42,43,44] to improve on the -width estimate of Ref. [20].
When examining resonance scattering processes in soliton models there is no alternative to treating simultaneously the small amplitude fluctuations that correspond to asymptotic states and the collective rotations. At first sight this suggests double counting effects. However, Dirac constraints emerge that abandon Yukawa interactions, at least from the local and flavor symmetric part of the action. The Skyrme model description of this procedure is described in detail in Ref. [1] for the channel in kaon nucleon scattering. It combines rotations (collective motion) and vibrations (fluctuations) and is therefore called rotation-vibration-approach (RVA)4. The key features of this approach are:
- (1)
- The field equations are solved in two steps, first for the soliton and second for the (constraint) fluctuations. These are the two leading orders in the counting. Consequently, the above-mentioned inconsistency with PCAC is not an issue for the RVA.
- (2)
- The interaction between the collective models and the constrained fluctuations can be written as a separable potential that is similar to a resonance exchange. Reaction matrix theory can be applied to this potential to compute the exchange phase shift . The dependence originates from the matrix elements of the collective coordinate operators in the separable potential. As indicated after Equation (5) they need to be taken between elements of representations that vary with .
- (3)
- Up to a small (a few MeV) pole shift, passes through exactly at the momentum given by the mass difference between the and the nucleon predicted by the collective coordinate Hamiltonian, Equation (5). Modulo flavor symmetry breaking effects, this difference decreases by a factor of two when going from to .
- (4)
- The reaction matrix formalism also derives a width function from the separable potential. Up to flavor symmetry breaking this width function contains the matrix element of a single collective coordinate operator between the nucleon and the . It is, therefore, impossible that substantial cancellations between matrix elements of several operators occur as was argued in Ref. [5].
- (5)
- The BSA gives exact results in the limit. It is possible to modify the BSA such that the scattering fluctuations are orthogonal to the rotations described by the flavor rotations in Equation (2). For both BSA versions scattering phase shifts can be computed and their difference is the resonance phase shift .
The litmus test for the RVA is then whether or not . The left panel of Figure 3 impressively shows that this identity holds over the whole range of relevant kaon momenta.
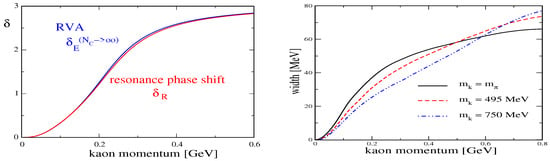
Figure 3.
(Color online) Skyrme model results for phase shifts and decay widths of kaon nucleon scattering in the channel.
There are two important conclusions from this analysis in the Skyrme model: First, the pentaquark resonance (state) is unavoidably predicted, it is not an artifact of the RRA. Second, the large predictions from this model calculation are based on the hedgehog structure of the soliton rather than on the particular model Lagrangian. Hence it is cogent that these predictions generalize to all chiral soliton models, thereby challenging results from the RRA reported in Refs. [5,6].
5. Heavy Baryons
When turning to heavy baryons, not only those with exotic quantum numbers, consistency with the heavy quark spin/flavor symmetry [9,10,11,12,13] is the major requirement to model building. Essentially it states that for hadrons containing heavy quarks, spin and flavor effects are suppressed by inverse powers of the heavy quark mass. In turn this implies for effective mesons theories that heavy pseudoscalar and vector mesons are on equal footing5. This particularly implies that baryons with a heavy quark cannot be constructed as solitons within models solely based on the (pseudoscalar) chiral field.
A suitable approach is to include vector () and pseudoscalar (P) fields with masses and M, respectively [46]. These fields represent mesons containing a single heavy quark and by themselves are three component vectors in flavor space that couple to the chiral field. When and M approach infinity, and P combine to a single multiplet whose dynamics is governed by the heavy quark spin/flavor symmetry. In the baryon sector the hedgehog configuration, Equation (1) induces an attractive potential for and P such that bound state solutions with energies emerge. Many approaches based on this picture have been reported earlier [45,47,48,49,50,51,52,53,54,55,56,57,58].
To leading order in the counting, these energies are the mass differences between baryons with a single heavy quark and the nucleon. More importantly, since the hedgehog dwells in the isospin subspace of the three-dimensional flavor space, so does the two-component bound state wave function of the heavy meson fields [46]:
As in Equation (2) collective coordinate quantization approximates the full field by the classical field rotating in flavor space: and . With
and similarly for , it is obvious that the Lagrangian contains contributions linear in . Appropriate normalization [59] of the bound state wave function, substitution into the Lagrange density, and integrating over space provides the collective coordinate part of the Lagrange function from the heavy fields [3]
Here is the Fourier amplitude of the bound state wave function. Upon quantization becomes the number operator for the bound state. Furthermore, is a functional of all profile functions and describes the hyperfine splitting among the heavy baryons (see Equation (8) below). To linear order the angular velocities do not contribute because the bound state wave function dwells in the isospin subspace.
The main result to be extracted from Equation (6) is its contribution to the constraint (assuming from now on) [3,55]
where when the bound state corresponds to a heavy quark () and when the bound state corresponds to a heavy antiquark (). Hence for a bound heavy quark the lowest lying representations are the anti-triplet and the sextet . Obviously, these representations describe the -diquark content of the heavy baryons. The particle content of the representations is displayed in Figure 4.
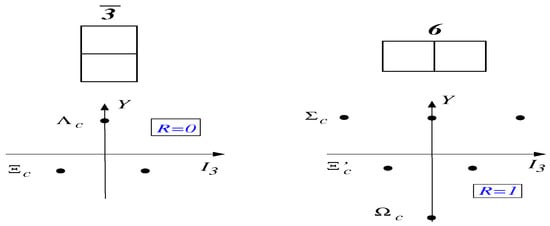
Figure 4.
representations for the diquark content of ordinary heavy baryons.
Of course, none-occupation () of the heavy meson bound state falls back to the ordinary baryons, as in Figure 1.
Quantizing the canonical momentum yields the intermediate spin quantum number R. The hedgehog structure causes R to equal the isospin of the zero-strangeness element in a given representation. That is, for the anti-triplet and for sextet. Adding the intrinsic spin of the heavy meson bound state gives the total baryon spin . In total the mass formula reads [3]
where is the eigenvalue obtained from diagonalizing flavor symmetry breaking: for prescribed I, R and [30]. Factorizing , with being a collective coordinate operator with a fixed coefficient which is determined from the profile functions, we consider a tunable parameter to eventually study non-linear effects of flavor symmetry breaking. Model results for the baryon spectrum computed from Equation (8) have been reported in Ref. [3] and there is no need to repeat them here. However, it is important to stress that, both the constraint on , that selects the relevant representation(s), and the form of the hyperfine splitting (last term in Equation (8)) inherently arise from the model calculation once compulsory extensions of the mean field treatment are implemented. This makes fully obsolete the adjustment of the classical action (using external specifications) to accommodate the heavy sector as in Ref. [14]. Such an accommodation causes the moments of inertia ( and ) to vary with and may even require to modify the leading order (in ) field equation. Stated otherwise, without an extension of the mean field approach the heavy and light sectors cannot be connected consistently.
Similar to the anti-decuplet () in the non-heavy sector the next to lowest representation, the anti-decapentaplet (), shown in Figure 5, plays a twofold role for the spectrum of heavy baryons.
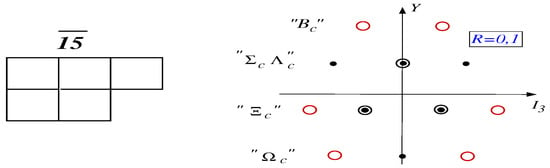
Figure 5.
(Color online) Young tableaux and particle content of the anti-decapentaplet (). Black circles denote ordinary diquarks whose quantum numbers relate to two quark states. Double circles indicate two states with different R quantum numbers. Red circles denote exotic states that cannot be built from two quarks.
First, the contains diquarks with the same (observable) quantum numbers as the members of the and/or . When diagonalizing flavor symmetry breaking these member states mix to build the eigenfunctions . Second, the contains exotic members (red circles in Figure 5) that represent composites of three quarks and an antiquark from the sector.
In Figure 6 we show the flavor symmetry breaking eigenvalue of these states as a function of the strength of the symmetry breaking. We actually observe that the order of the eigenvalues for and type states is reversed as the strength assumes its empirical value, . Also the eigenvalue for , the candidate for the lowest charmed exotic baryon, significantly deviates from a straight line. These findings doubt the truncation of the perturbation expansion at the first order [60] when describing the spectrum of these states. The fact that eigenvalues grow less than linear also leads to a lower prediction for the masses of the exotic heavy baryons. Using the parameters as determined in Ref. [3] predicts
for the mass differences of the charmed exotic baryons.
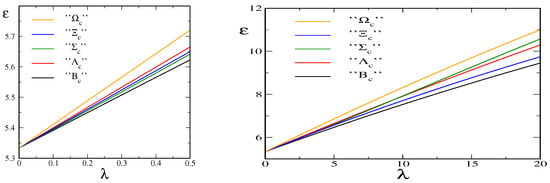
Figure 6.
(Color online) Flavor symmetry breaking eigenvalues for states that at are pure states, cf. Figure 5. The parameter measures the strength of symmetry breaking.
Finally, let us have a brief look at pentaquarks with a heavy antiquark. They are constructed from heavy meson bound states with negative energy eigenvalues. The resulting binding energy is significantly less than that of ordinary bound states and may even be unbound in the charm sector [46]. Since negative energy eigenvalues correspond to and , the lowest dimensional representation available is the anti-sextet () representing four (light) quarks as shown in Figure 7.
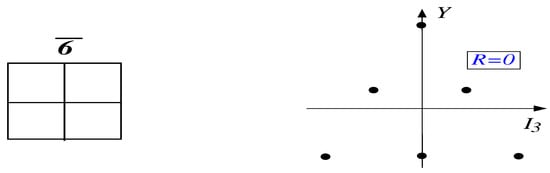
Figure 7.
Young tableaux and flavor content of the anti-sextet representation.
This representation has and thus the states must be compared to those from the anti-triplet. The collective coordinate quantization induces a mass difference ∼300 MeV which is much larger than the typical binding energy. Hence this model estimate suggests that such baryons most probably do not exist.
6. Summary
We have reviewed two examples for the description of exotic baryons in chiral soliton models. The main purpose of this endeavor has been to reflect on conceptual issues rather than any accurate reproduction of empirical data by tuning parameters. Though most of the results are based on the Skyrme model treatment of the chiral field, they generalize to any chiral model with a hedgehog soliton.
Exotic baryons naturally emerge in chiral soliton models as elements in higher dimensional representations when quantizing the three light flavor degrees of freedom. Then these baryons are flavor rotational excitations so that their excitation energy may be significantly lower than expected from the respective constituent quark masses. Of course, there is reason to assume this soliton model prediction could be a mere artifact of the collective coordinate approximation. However, a careful analysis of the pentaquark reveals that this is not the case and the indeed shows up as a resonance in the Skyrme model analysis of kaon nucleon scattering. As a by-product of this analysis we have seen that any estimate of the hadronic width of (exotic) baryon resonances must include the subtle interplay of collective and vibrational modes. Obviously, such estimates are more complicated than just generalizing the Goldberger-Treiman relation.
In the context of baryons with a heavy quark (or antiquark) we have seen that the heavy meson bound state wave function, when properly included in the collective coordinate approximation, automatically selects the pertinent light flavor representation. This concerns both types of exotic heavy baryons, those with a heavy antiquark as well as those with a light antiquark. The presented approach does not account for a back-reaction of the heavy meson bound state on the chiral field. Since the bound state couples at this will not affect the soliton itself because it obeys a field equation that arises from the part of the action.
The main conclusion is that the description of exotic baryons within chiral soliton models is not complete on the mean field level. It would require specifications from the outside which are not guaranteed to be consistent within the model itself. As examples thereof, we have argued against the fabrication of a Yukawa coupling and the adjustment of the constraint that selects the flavor representation. On the contrary, the proper incorporation of (harmonic) fluctuations, which goes beyond the mean field approach, produces these specifications in a self-contained manner. Hence such fluctuations are essential to understand the structure and properties of exotic baryons in chiral soliton models.
Funding
The project is supported in part by the National Research Foundation of South Africa (NRF) by grant number 109497.
Acknowledgments
Some of the results presented here were obtained in collaborations with J. Schechter, H. Walliser and J. P. Blanckenberg whose contributions are gratefully acknowledged. The author would also like to thank the organizers to make the International Conference on New Frontier in Physics a worthwhile event.
Conflicts of Interest
The author declares no conflict of interest.
References
- Walliser, H.; Weigel, H. Bound state versus collective coordinate approaches in chiral soliton models and the width of the Theta+ pentaquark. Eur. Phys. J. A 2005, 26, 361–382. [Google Scholar] [CrossRef]
- Weigel, H. Axial current matrix elements and pentaquark decay widths in chiral soliton models. Phys. Rev. D 2007, 75, 114018. [Google Scholar] [CrossRef]
- Blanckenberg, J.P.; Weigel, H. Heavy Baryons with Strangeness in a Soliton Model. Phys. Lett. B 2015, 750, 230. [Google Scholar] [CrossRef]
- Weigel, H. Chiral Soliton Models for Baryons; Lecture Notes in Physics; Springer-Verlag: Berlin/Heidelberg, Germany, 2008; Volume 743. [Google Scholar]
- Diakonov, D.; Petrov, V.; Polyakov, M.V. Exotic anti-decuplet of baryons: Prediction from chiral solitons. Z. Phys. A 1997, 359, 305. [Google Scholar] [CrossRef]
- Ellis, J.R.; Karliner, M.; Praszałowicz, M. Chiral soliton predictions for exotic baryons. JHEP 2004, 0405, 002. [Google Scholar] [CrossRef]
- Kim, H.C.; Polyakov, M.V.; Praszałowicz, M.; Yang, G.S. Strong decays of exotic and nonexotic heavy baryons in the chiral quark-soliton model. Phys. Rev. D 2017, 96, 094021. [Google Scholar] [CrossRef]
- Praszałowicz, M. Heavy baryon decay widths in the large Nc limit in chiral theory. Eur. Phys. J. C 2018, 78, 690. [Google Scholar] [CrossRef]
- Eichten, E.; Feinberg, F. Spin Dependent Forces in QCD. Phys. Rev. D 1981, 23, 2724. [Google Scholar] [CrossRef]
- Shifman, M.A.; Voloshin, M.B. On Annihilation of Mesons Built from Heavy and Light Quark and anti-B0 <—> B0 Oscillations. Sov. J. Nucl. Phys. 1987, 45, 292. [Google Scholar]
- Isgur, N.; Wise, M.B. Weak Transition Form-factors Between Heavy Mesons. Phys. Lett. B 1990, 237, 527. [Google Scholar] [CrossRef]
- Georgi, H. An Effective Field Theory for Heavy Quarks at Low-energies. Phys. Lett. B 1990, 240, 447. [Google Scholar] [CrossRef]
- Neubert, M. Heavy quark symmetry. Phys. Rep. 1994, 245, 259. [Google Scholar] [CrossRef]
- Yang, G.S.; Kim, H.C.; Polyakov, M.V.; Praszałowicz, M. Pion mean fields and heavy baryons. Phys. Rev. D 2016, 94, 071502. [Google Scholar] [CrossRef]
- Kim, H.C. Heavy baryons in a pion mean-field approach: A brief review. J. Korean Phys. Soc. 2018, 73, 165. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Klebanov, I.R. Bound State Approach to Strangeness in the Skyrme Model. Nucl. Phys. B 1985, 262, 365. [Google Scholar] [CrossRef]
- Witten, E. Baryons in the 1/n Expansion. Nucl. Phys. 1979, B160, 57. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A Nonlinear field theory. Proc. R. Soc. Lond. A 1961, 260, 127. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The Origins of Skyrmions. Int. J. Mod. Phys. A 1988, 3, 2745. [Google Scholar] [CrossRef]
- Adkins, G.S.; Nappi, C.R.; Witten, E. Static Properties of Nucleons in the Skyrme Model. Nucl. Phys. B 1983, 228, 552. [Google Scholar] [CrossRef]
- Jain, P.; Johnson, R.; Park, N.W.; Schechter, J.; Weigel, H. The Neutron—Proton Mass Splitting Puzzle in Skyrme and Chiral Quark Models. Phys. Rev. D 1989, 40, 855. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. B 1983, 223, 422. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1983, 223, 433. [Google Scholar] [CrossRef]
- Meier, F.; Walliser, H. Quantum corrections to baryon properties in chiral soliton models. Phys. Rep. 1997, 289, 383. [Google Scholar] [CrossRef]
- Guadagnini, E. Baryons as Solitons and Mass Formulae. Nucl. Phys. B 1984, 236, 35. [Google Scholar] [CrossRef]
- Jain, S.; Wadia, S.R. Large N Baryons: Collective Coordinates of the Topological Soliton in SU(3) Chiral Model. Nucl. Phys. B 1985, 258, 713. [Google Scholar] [CrossRef]
- Alkofer, R.; Reinhardt, H.; Weigel, H. Baryons as chiral solitons in the Nambu-Jona-Lasinio model. Phys. Rep. 1996, 265, 139. [Google Scholar] [CrossRef]
- Biedenharn, L.C.; Dothan, Y. Monopolar Harmonics in SU(3)f as Eigenstates of the Skyrme-Witten Model for Baryons. In From SU(3) To Gravity; Gotsman, E., Tauber, G., Eds.; Cambridge University Press: Cambridge, UK, 1985; p. 15. [Google Scholar]
- Park, N.W.; Schechter, J.; Weigel, H. Axial Current Matrix Elements of the Nucleon Based on an Exact Diagonalization of the SU(3) Skyrme Model Hamiltonian. Phys. Lett. B 1989, 228, 420. [Google Scholar] [CrossRef]
- Yabu, H.; Ando, K. A New Approach to the SU(3) Skyrme Model. Nucl. Phys. B 1988, 301, 601. [Google Scholar] [CrossRef]
- Dorey, N.; Hughes, J.; Mattis, M.P. Skyrmion quantization and the decay of the Delta. Phys. Rev. D 1994, 50, 5816. [Google Scholar] [CrossRef]
- Newton, R.G. Scattering Theory of Waves and Particles; Springer: New York, NY, USA, 1982; Chapter 11.2.2. [Google Scholar]
- Schwesinger, B.; Weigel, H.; Holzwarth, G.; Hayashi, A. The Skyrme Soliton in Pion, Vector and Scalar Meson Fields: πN Scattering and Photoproduction. Phys. Rep. 1989, 173, 173. [Google Scholar] [CrossRef]
- Uehara, M. Vanishing of the Yukawa Interaction From the Skyrmion—Pion Lagrangian. Prog. Theor. Phys. 1986, 75, 212–215. [Google Scholar] [CrossRef]
- Uehara, M. On the Surviving Pion—Skyrmion Yukawa Coupling. Prog. Theor. Phys. 1987, 78, 984. [Google Scholar] [CrossRef]
- Saito, S. The Yukawa Coupling Term in the Skyrme Model. Prog. Theor. Phys. 1987, 78, 746. [Google Scholar] [CrossRef]
- Holzwarth, G.; Hayashi, A.; Schwesinger, B. The Width of the Δ1232 Resonance in the Skyrme Model. Phys. Lett. B 1987, 191, 27. [Google Scholar] [CrossRef]
- Verschelde, H. Δ Decay in the Skyrme Model. Phys. Lett. B 1988, 209, 34. [Google Scholar] [CrossRef]
- Diakonov, D.; Petrov, V.Y.; Pobylitsa, P.V. Born Diagrams in the Pion - Skyrmion Scattering. Phys. Lett. B 1988, 205, 372. [Google Scholar] [CrossRef]
- Holzwarth, G. Elastic Pion Nucleon P Wave Scattering in Soliton Models. Phys. Lett. B 1990, 241, 165. [Google Scholar] [CrossRef]
- Holzwarth, G.; Pari, G.; Jennings, B.K. Low-energy pion - nucleon P wave scattering in the Skyrme model. Nucl. Phys. A 1990, 515, 665. [Google Scholar] [CrossRef]
- Hayashi, A.; Saito, S.; Uehara, M. Meson scattering off a moving soliton and a solution of the Yukawa coupling problem. Phys. Lett. B 1990, 246, 15. [Google Scholar] [CrossRef]
- Hayashi, A.; Saito, S.; Uehara, M. Pion-nucleon scattering in the Skyrme model and the P wave Born amplitudes. Phys. Rev. D 1991, 43, 1520. [Google Scholar] [CrossRef]
- Hayashi, A.; Saito, S.; Uehara, M. Pion-nucleon scattering in the soliton model. Prog. Theor. Phys. Suppl. 1992, 109, 45. [Google Scholar] [CrossRef]
- Schechter, J.; Subbaraman, A. Excited heavy baryons in the bound state picture. Phys. Rev. D 1995, 51, 2311. [Google Scholar] [CrossRef]
- Schechter, J.; Subbaraman, A.; Vaidya, S.; Weigel, H. Heavy quark solitons: Towards realistic masses. Nucl. Phys. A 1995, 590, 655–679. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V. Hyperfine splittings of baryons containing a heavy quark in the Skyrme model. Phys. Lett. B 1992, 294, 273. [Google Scholar] [CrossRef]
- Guralnik, Z.; Luke, M.E.; Manohar, A.V. Properties of baryons containing a heavy quark in the Skyrme model. Nucl. Phys. B 1993, 390, 474. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V.; Wise, M.B. The Baryon Isgur-Wise function in the large N(c) limit. Nucl. Phys. B 1993, 396, 38. [Google Scholar] [CrossRef]
- Min, D.P.; Oh, Y.s.; Park, B.Y.; Rho, M. Soliton structure of heavy baryons. arXiv, 1992; arXiv:hep-ph/9209275. [Google Scholar]
- Lee, H.K.; Nowak, M.A.; Rho, M.; Zahed, I. NonAbelian Berry phases in baryons. Ann. Phys. 1993, 227, 175. [Google Scholar] [CrossRef]
- Nowak, M.A.; Zahed, I.; Rho, M. Heavy solitonic baryons. Phys. Lett. B 1993, 303, 130. [Google Scholar] [CrossRef]
- Min, D.P.; Oh, Y.s.; Park, B.Y.; Rho, M. Heavy quark symmetry and skyrmions. Int. J. Mod. Phys. E 1995, 4, 47. [Google Scholar] [CrossRef]
- Gupta, K.S.; Momen, M.A.; Schechter, J.; Subbaraman, A. Heavy quark solitons. Phys. Rev. D 1993, 47, R4835. [Google Scholar] [CrossRef]
- Momen, A.; Schechter, J.; Subbaraman, A. Heavy quark solitons: Strangeness and symmetry breaking. Phys. Rev. D 1994, 49, 5970. [Google Scholar] [CrossRef]
- Oh, Y.S.; Park, B.Y.; Min, D.P. Heavy baryons as Skyrmion with 1/m(Q) corrections. Phys. Rev. D 1994, 49, 4649. [Google Scholar] [CrossRef]
- Oh, Y.S.; Park, B.Y.; Min, D.P. Heavy quark symmetry and the Skyrme model. Phys. Rev. D 1994, 50, 3350. [Google Scholar] [CrossRef]
- Oh, Y.S.; Park, B.Y. Energy levels of the soliton—Heavy meson bound states. Phys. Rev. D 1995, 51, 5016. [Google Scholar] [CrossRef]
- Harada, M.; Qamar, A.; Sannino, F.; Schechter, J.; Weigel, H. Hyperfine splitting of low lying heavy baryons. Nucl. Phys. A 1997, 625, 789. [Google Scholar] [CrossRef]
- Kim, H.C.; Polyakov, M.V.; Praszałowicz, M. Possibility of the existence of charmed exotica. Phys. Rev. D 2017, 96, 014009. [Google Scholar] [CrossRef]
| 1 | Listing the references on the mean field description for heavy baryons in soliton models can hardly be exhaustive. The interested reader my trace them from the review [15]. |
| 2 | For example, other meson fields are needed to reproduce the neutron-proton mass difference [21]. Consult the review [4] for further examples. |
| 3 | To the author’s knowledge the occurrence of these exotic baryons in the collective quantization scheme was first noticed by Biedenharn and Dothan [28]. |
| 4 | The omission of fluctuations, Equation (2) is called the rigid rotator approach (RRA) and finding the scattering data for the decoupled fluctuations goes by the label bound state approach (BSA) [16]. |
| 5 | For an infinitely heavy quark, they are elements of a single multiplet [45]. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).