Results from the OPERA Experiment in the CNGS Beam
Abstract
1. Introduction
2. Materials and Methods
2.1. The OPERA Experiment
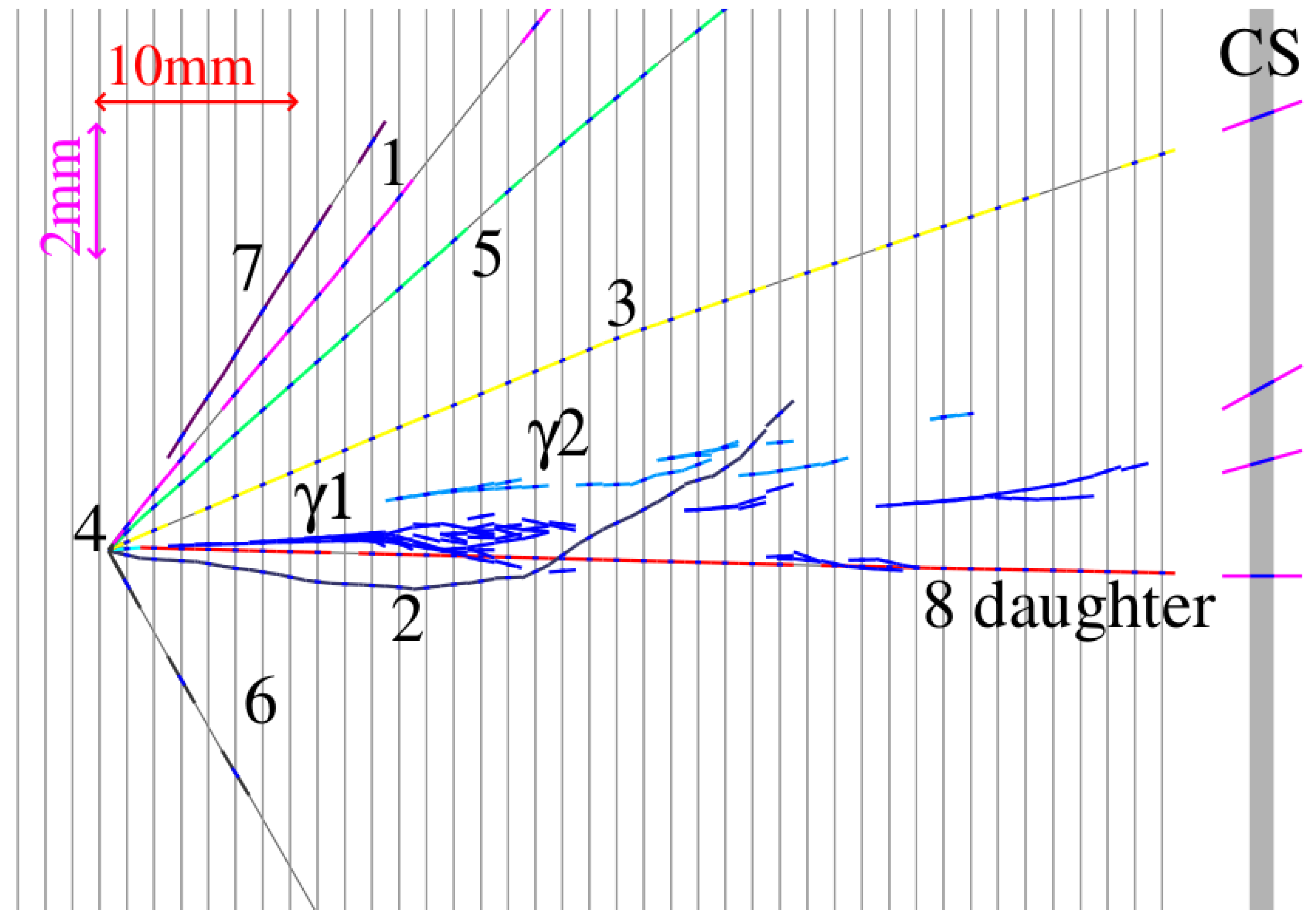
2.2. Events Classification and Scanning
3. Results
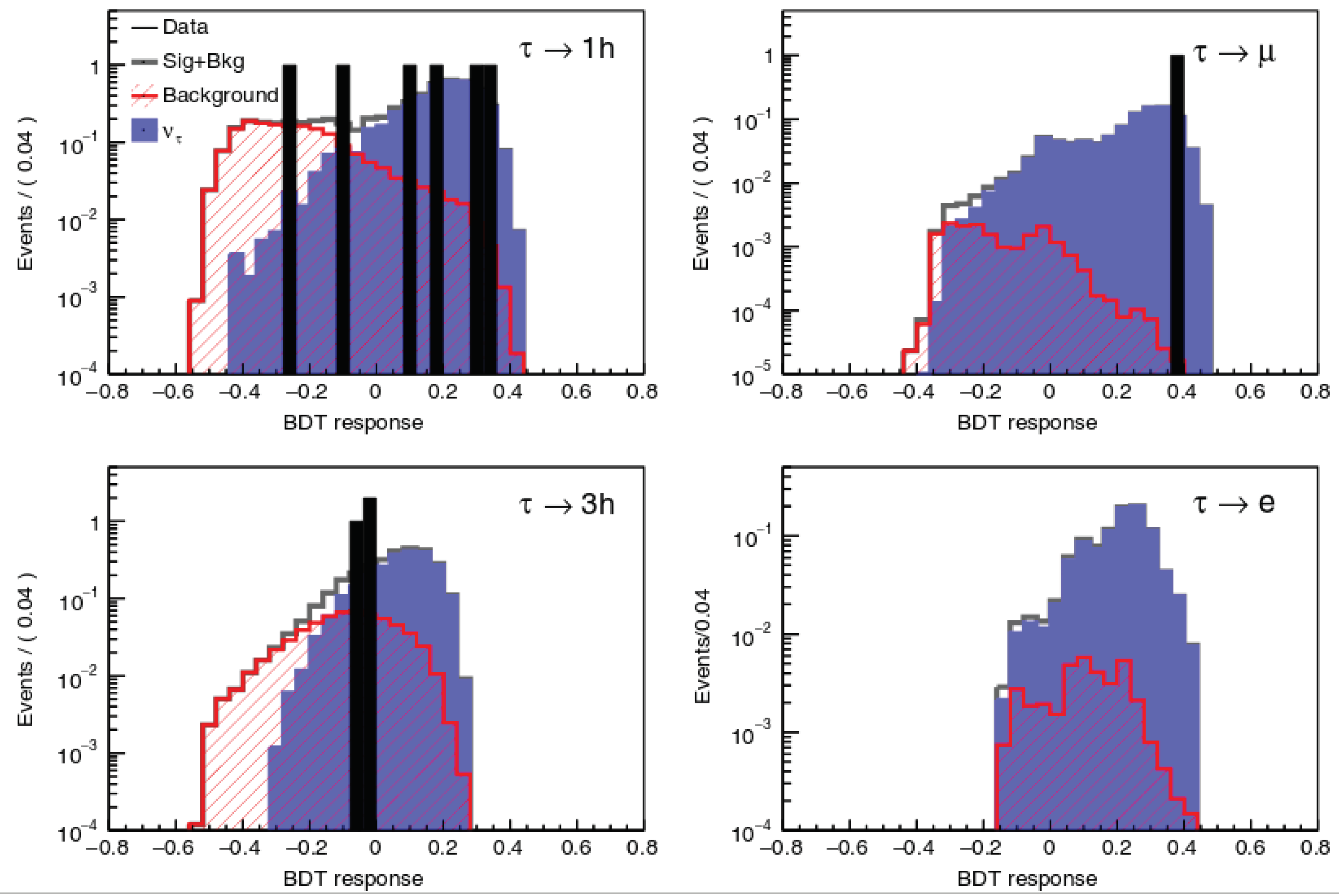
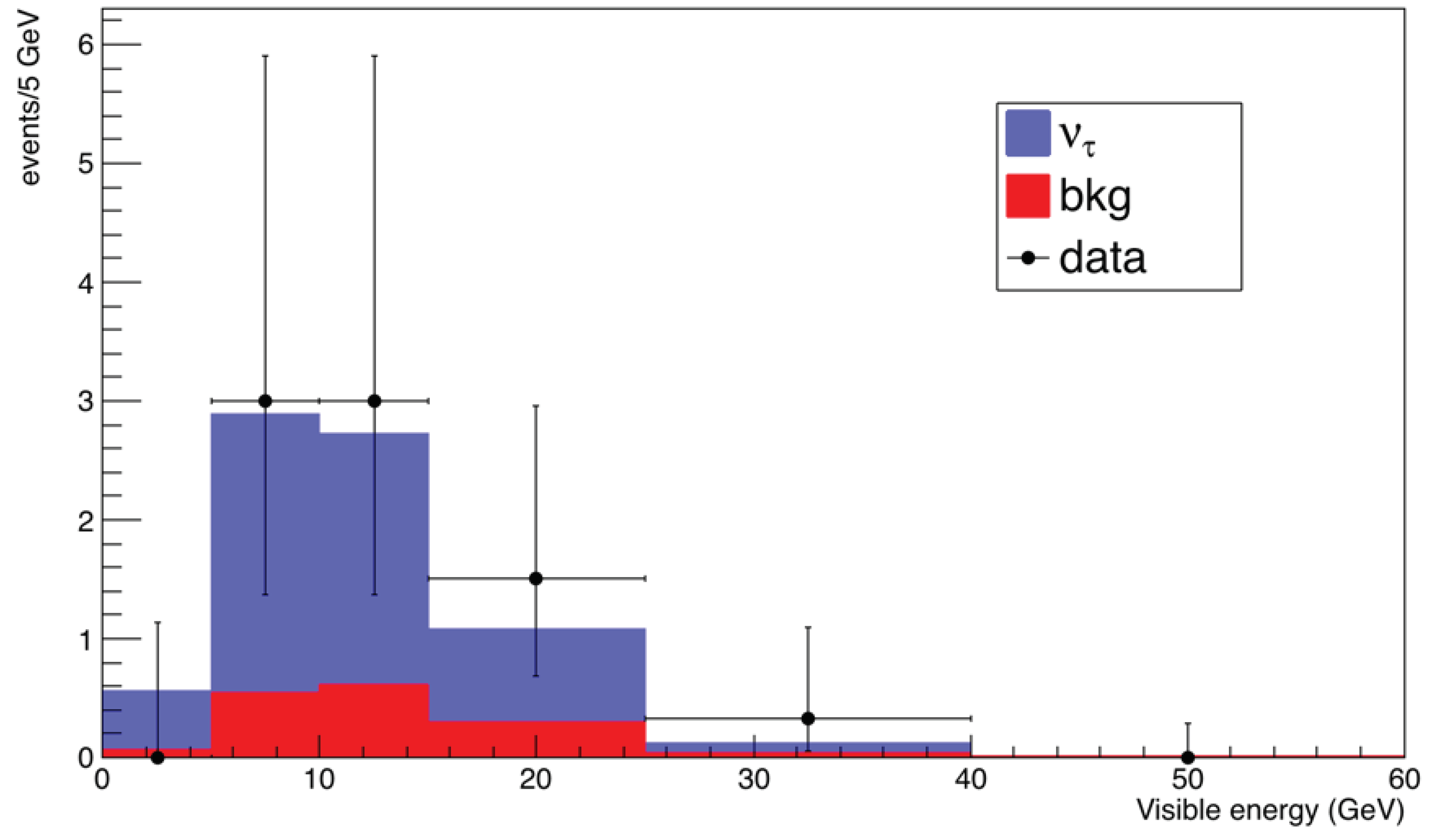
3.1. Oscillations
3.2. Oscillations
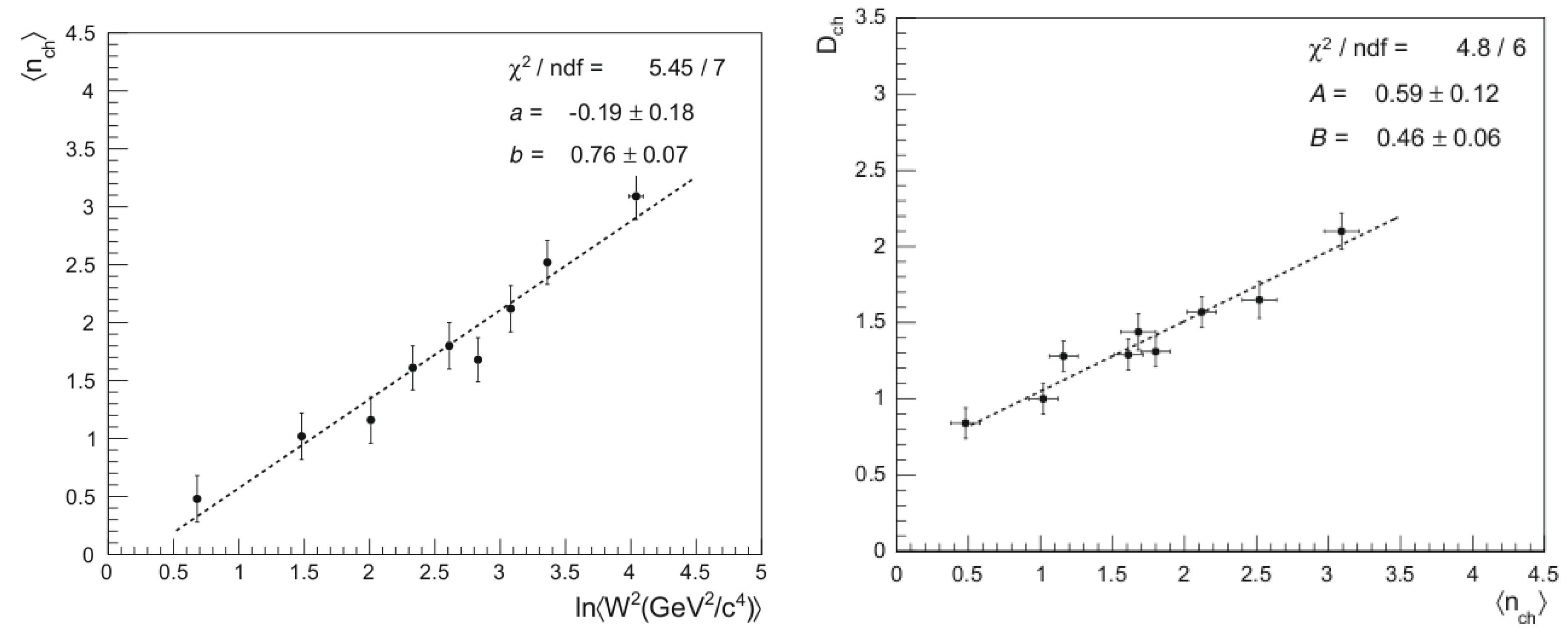
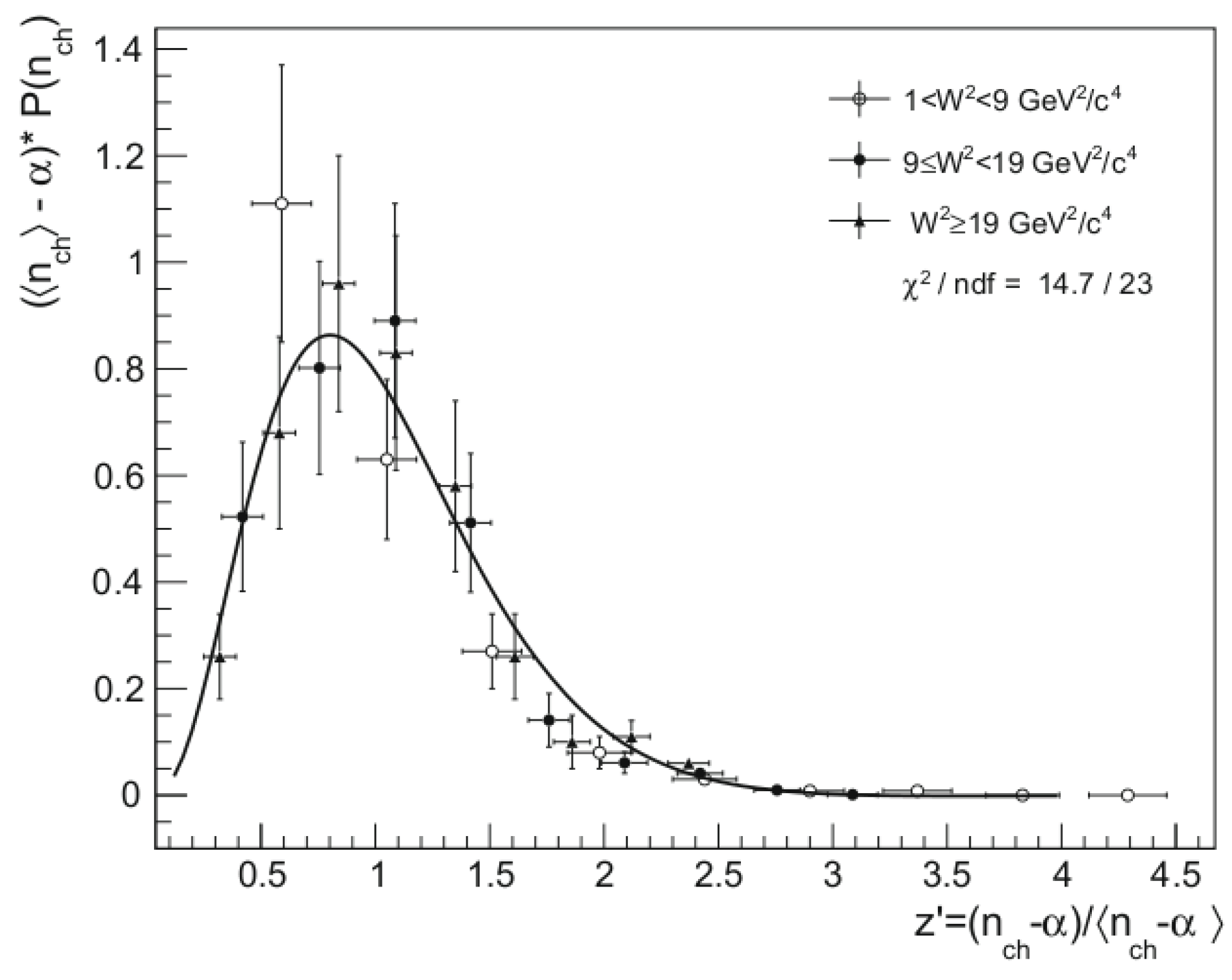
3.3. Charged Hadron Multiplicities in Charged-Current Neutrino–Lead Interactions
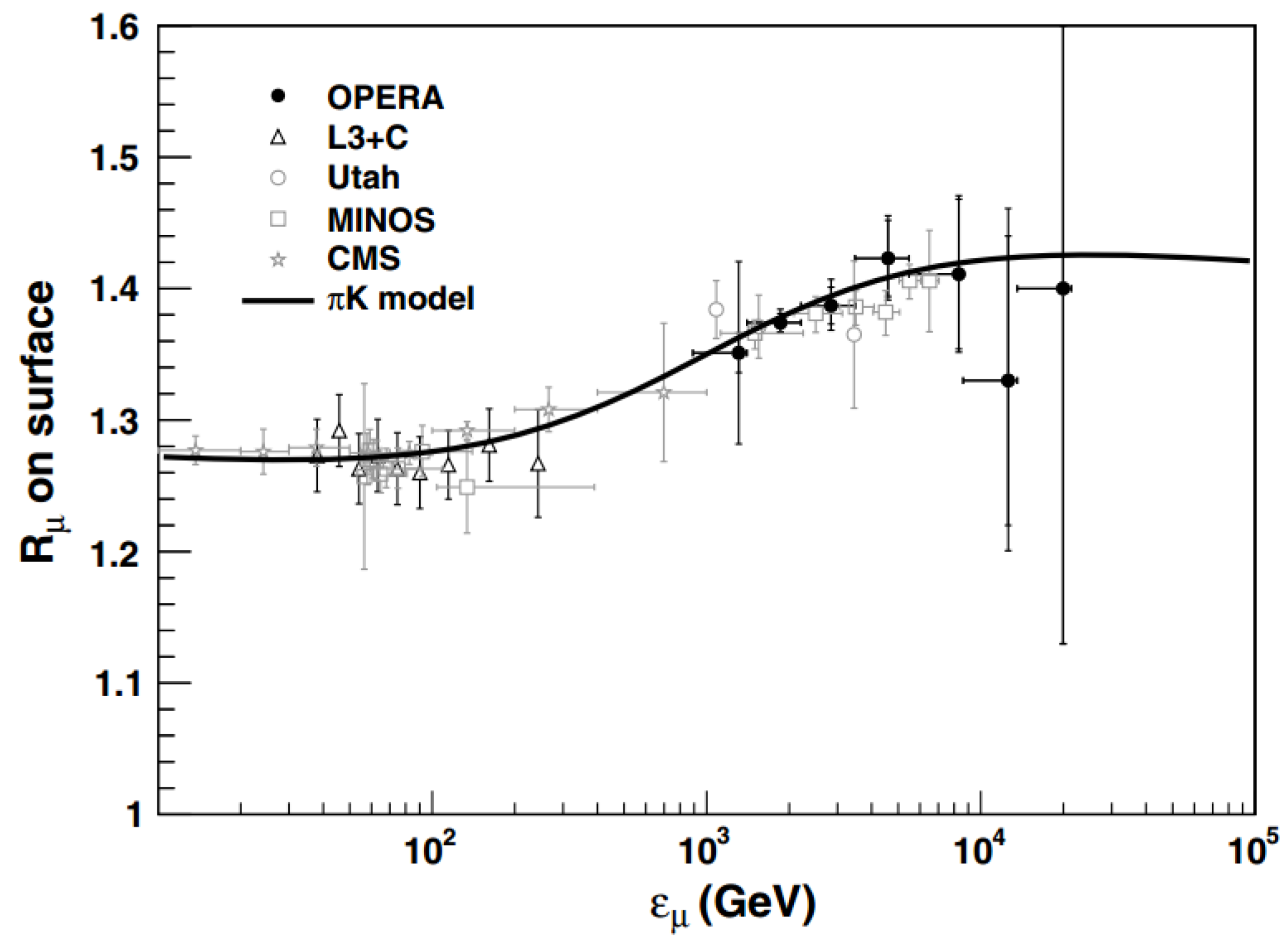
3.4. Cosmic Ray Physics
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamura, K.; Petkov, S.T. Neutrino Masses, Mixing, and Oscillations. Available online: pdg.lbl.gov/2018/reviews/rpp2018-rev-neutrino-mixing.pdf (accessed on 5 December 2019).
- The Super-Kamiokande Collaboration. Evidence for Oscillation of Atmospheric Neutrinos. Phys. Lett. B 1998, 81, 1562. [Google Scholar] [CrossRef]
- The OPERA Collaboration. The OPERA experiment in the CERN to Gran Sasso neutrino beam. J. Instrum. 2009, 4, P04018. [Google Scholar]
- The OPERA Collaboration. Procedure for short-lived particle detection in the OPERA experiment and its application to charm decays. Eur. Phys. J. C 2014, 74, 2986. [Google Scholar] [CrossRef]
- The OPERA Collaboration. New results on νμ→ντ appearance with the OPERA experiment in the CNGS beam. J. High Energy Phys. 2013, 2013, 036. [Google Scholar] [CrossRef]
- The OPERA Collaboration. Discovery of τ Neutrino Appearance in the CNGS Neutrino Beam with the OPERA Experiment. Phys. Rev. Lett. 2015, 115, 121802. [Google Scholar] [CrossRef] [PubMed]
- The OPERA Collaboration. Final Results of the OPERA Experiment on ντ Appearance in the CNGS Neutrino Beam. Phys. Rev. Lett. 2018, 120, 211801. [Google Scholar] [CrossRef] [PubMed]
- Longhin, A.; Paoloni, A.; Pupilli, F. Large-Angle Scattering of Multi-GeV Muons on Thin Lead Targets. IEEE Trans. Nucl. Sci. 2015, 62, 2216. [Google Scholar] [CrossRef]
- Andreopoulos, C.; Barry, C.; Dytman, S.; Gallagher, H.; Golan, T.; Hatcher, R.; Perdue, G.; Yarba, J. The GENIE Neutrino Monte Carlo Generator: Physics and User Manual. arxiv, 2015; arXiv:1510.05494. [Google Scholar]
- The OPERA Collaboration. Limits on muon-neutrino to tau-neutrino oscillations induced by a sterile neutrino state obtained by OPERA at the CNGS beam. J. High Energy Phys. 2015, 2015, 069. [Google Scholar] [CrossRef]
- The OPERA Collaboration. Final results of the search for νμ→νe oscillations with the OPERA detector in the CNGS beam. J. High Energy Phys. 2018, 2018, 151. [Google Scholar] [CrossRef]
- Huber, P.; Lindner, M.; Winter, W. Simulation of long-baseline neutrino oscillation experiments with GLoBES (General Long Baseline Experiment Simulator). Comput. Phys. Commun. 2005, 167, 195. [Google Scholar] [CrossRef]
- Huber, P.; Kopp, J.; Lindner, M.; Rolinec, M.; Winter, W. New features in the simulation of neutrino oscillation experiments with GLoBES 3.0: General Long Baseline Experiment Simulator. Comput. Phys. Commun. 2007, 177, 432. [Google Scholar] [CrossRef]
- The OPERA Collaboration. Study of charged hadron multiplicities in charged-current neutrino–lead interactions in the OPERA detector. Eur. Phys. J. C 2018, 78, 62. [Google Scholar] [CrossRef]
- Koba, F.; Nielsen, H.B.; Olesen, P. Scaling of multiplicity distributions in high-energy hadron collisions. Nucl. Phys. B 1972, 40, 317–334. [Google Scholar] [CrossRef]
- Buras, A.J.; Dias de Deus, J.; Moller, R. Multiplicity scaling at low energies, a generalized Wroblewski-formula and the leading particle effect. Phys. Lett. B 1973, 47, 251–254. [Google Scholar] [CrossRef]
- The OPERA Collaboration. Measurement of the TeV atmospheric muon charge ratio with the complete OPERA data set. Eur. Phys. J. C 2014, 74, 2933. [Google Scholar] [CrossRef]
- The OPERA Collaboration. Measurement of the cosmic ray muon flux seasonal variation with the OPERA detector. arxiv, 2018; arXiv:1810.10783. [Google Scholar]
- The Super-Kamiokande Collaboration. A Measurement of the Tau Neutrino Cross Section in Atmospheric Neutrino Oscillations with Super-Kamiokande. Phys. Rev. D 2018, 98, 052006. [Google Scholar] [CrossRef]
- Moriyama, S. et al. [Super-Kamiokande Collaboration] New atmospheric and solar results from Super-Kamiokande. J. Phys. Conf. Ser. 2017, 888, 012005. [Google Scholar] [CrossRef]
- The Minos Collaboration. Combined analysis of muon-neutrino disappearance and muon-neutrino to electron-neutrino appearance in MINOS using accelerator and atmospheric neutrinos. Phys. Rev. D 2014, 112, 191811. [Google Scholar]
- The T2K Collaboration. Measurement of neutrino and antineutrino oscillations by the T2K experiment including a new additional sample of νe interactions at the far detector. Phys. Rev. D 2017, 98, 019902. [Google Scholar]
- The NOνA Collaboration. New constraints on oscillation parameters from νe appearance and νμ disappearance in the NOν A experiment. Phys. Rev. D 2018, 98, 032012. [Google Scholar] [CrossRef]
- The Daya Bay Collaboration. Measurement of electron antineutrino oscillation with 1958 days of operation at Daya Bay. arxiv, 2018; arXiv:1809.02261. [Google Scholar]
- The RENO Collaboration. Measurement of neutrino mixing angle θ13 and mass difference from reactor antineutrino disappearance in the RENO experiment. Nucl. Phys. B 2016, 908, 94–115. [Google Scholar] [CrossRef]
- The Double Chooz Collaboration. Measurement of θ13 in Double Chooz using neutron captures on hydrogen with novel background rejection techniques. J. High Energy Phys. 2016, 2016, 163. [Google Scholar] [CrossRef]
- The MiniBooNE collaboration. Observation of a Significant Excess of Electron-Like Events in the MiniBooNE Short-Baseline Neutrino Experiment. arxiv, 2018; arXiv:1805.12028. [Google Scholar]
- The Minos and the Daya Bay Collaborations. Limits on Active to Sterile Neutrino Oscillations from Disappearance Searches in the MINOS, Daya Bay, and Bugey-3 Experiments. Phys. Rev. Lett. 2016, 117, 151801. [Google Scholar] [CrossRef]
- The DONuT Collaboration. Final tau-neutrino results from the DONuT experiment. Phys. Rev. D 2008, 78, 052002. [Google Scholar] [CrossRef]
- The SHiP Collaboration. A facility to Search for Hidden Particles (SHiP) at the CERN SPS. arxiv, 2015; arXiv:1504.04956. [Google Scholar]

| Variable | h | h | ||
|---|---|---|---|---|
| (mm) | <2.6 | <2.6 | <2.6 | <2.6 |
| (rad) | <0.02 | <0.02 | <0.02 | <0.02 |
| (GeV/c) | >1 | >1 | >1 | |
| (GeV/c) | >0.15 | >0.1 | >0.1 | |
| Negative | ||||
| or unknown |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paoloni, A.; , O.B.o.O.C. Results from the OPERA Experiment in the CNGS Beam. Universe 2018, 4, 143. https://doi.org/10.3390/universe4120143
Paoloni A, OBoOC. Results from the OPERA Experiment in the CNGS Beam. Universe. 2018; 4(12):143. https://doi.org/10.3390/universe4120143
Chicago/Turabian StylePaoloni, Alessandro, and On Behalf of OPERA Collaboration . 2018. "Results from the OPERA Experiment in the CNGS Beam" Universe 4, no. 12: 143. https://doi.org/10.3390/universe4120143
APA StylePaoloni, A., & , O. B. o. O. C. (2018). Results from the OPERA Experiment in the CNGS Beam. Universe, 4(12), 143. https://doi.org/10.3390/universe4120143





