Abstract
In the first part of this talk, we review some prerequisites for and essential arguments involved in the construction of the thermal-ground-state estimate underlying the deconfining phase in the thermodynamics of SU(2) Quantum Yang–Mills theory and how this structure supports its distinct excitations. The second part applies deconfining SU(2) Yang–Mills thermodynamics to the Cosmic Microwave Background in view of (i) a modified temperature-redshift relation with an interesting link to correlation-length criticality in the 3D Ising model, (ii) the implied minimal changes in the dark sector of the cosmological model, and (iii) best-fit parameter values of this model when confronted with the spectra of the angular two-point functions temperature-temperature (TT), temperature-E-mode-polarisation (TE), E-mode-polarisation-E-mode-polarisation (EE), excluding the low-l physics. The latter, which so far is treated in an incomplete way due to the omission of radiative effects, is addressed in passing.
1. Introduction
Based on perturbative asymptotic freedom at zero temperature [1,2,3], the predictions of thermodynamical potentials and plasma polarisation effects in four-dimensional Yang–Mills thermodynamics suggest themselves (naively as it turns out) to small-coupling expansions at high temperature, see, e.g., [4]. That such an approach does not lend itself to the usual, physically approximating, truncated asymptotic series in powers of a small fundamental coupling g was pointed out early in [5], however. In the talk by Thierry Grandou within this session [6], this is demonstrated exemplarily for the damping rate of a heavy fermion propagating through a hot gauge plasma [7], suggesting the existence of an infinite and thus hardly controllable tower of momentum scales, each implying a resummation within an associated class of loop diagrams. On the other hand, the approach of lattice gauge theory to the computation of thermodynamical quantities, albeit genuinely nonperturbative [8,9], is subject to infrared artefacts due to finite-size limitations [10], the imprecisely known nonperturbative beta function [8], and the prescription of seemingly unphysical boundary conditions in the so-called integral method [9].
All this has nurtured the suspicion that deconfining Yang–Mills thermodynamics actually is subject to highly nonperturbative physics, even at high temperatures. Talking of nonperturbative field configurations, the 1970s and early 1980s have seen tremendously fertile developments in constructing, in principle, all exact, (anti)selfdual solutions to the Euclidean Yang–Mills equation on [11,12] and on the four-torus [13,14,15]. Note that such (classical) configurations imply the weight in the partition function, where k refers to the topological charge, with the perturbative expansion point being an essential zero (coefficients of the expansion of such a weight into powers of the coupling g are identically zero to all orders). Therefore, (anti)selfdual field configurations are ignored in perturbation theory.
A genuine shortcoming of the perturbative treatment in Quantum Yang–Mills theory is the triviality of its a priori ground-state estimate, implying the need for renormalization: the mathematical meaningless situation, arising from unconstrained quantum fluctuations (Paul A. M. Dirac), is remedied by subtractions of infinities and re-definitions of the parameters in the defining action. A major accomplishment in the development of perturbatively accessed gauge theory as an essential pillar of the successful Standard Model of Particle Physics (SMPP) was to show that this renormalization programme does not spoil the predictivity of the theory in keeping untouched the set of parameters that characterises the defining Lagrangian [16,17,18]. Driven by the short-range nature of the weak interactions, gauge-symmetry breaking was introduced into the SMPP in the framework of the Glashow–Salam–Weinberg theory in terms of an SU(2) fundamentally charged scalar (Higgs) field subject to a renormalisable selfinteraction. Such a Higgs sector, however, only vaguely represents the phase structure and associated gauge-symmetry breaking patterns of the pure and nonperturbatively approached Yang–Mills theory [19]. The nonperturbative a priori estimate of each phase’s ground state in the latter case clearly links to its (gapped or ungapped) excitations, thereby ruling both classical and quantum radiative behaviour in distinct spectral domains [19].
Based on the classical Euclidean Yang–Mills action void of matter fields, the key to dynamical gauge-symmetry breaking in pure Quantum Yang–Mills theory is the construction of a useful thermal-ground-state estimate in the deconfining phase. Here, we only review the SU(2) case, the more involved situation of SU(3) is treated in [19,20]. In short, this construction represents spatially densely packed (anti)caloron centers with overlapping peripheries in terms of an inert, adjoint scalar field and an effective pure-gauge configuration , respectively, both arising upon spatial coarse-graining. The (anti)caloron field is an exact, nonpropagating solution to the (anti)selfduality or Bogomol’nyi-Prasad-Sommerfield (BPS) equation. As a consequence, a vacuum equation of state emerges subject to an energy density , T denoting temperature. Here, the mass scale represents a constant of integration in the potential being the solution of a first-order ordinary differential equation (ODE) in the field [21]. This ODE represents a consistency requirement for simultaneously solving the Euler–Lagrange and BPS equations associated with its effective action. Being charged under the adjoint representation of SU(2), is an element of the algebra1 su(2) and breaks SU(2) down to U(1). Thus, there are two massive quasi-particle modes and one massless one in the effective gauge field.
If the wavelength l associated with the propagation of the massless mode either falls below the length scale or even below the length , this disturbance either is forced into off-shellness by a violation of the Bianchi identity for the U(1) field strength tensor due to (anti)selfdual monopoles or it probes (anti)caloron centers, respectively. On the other hand, for , the massless mode represents undulating and propagating repolarisations of (anti)selfdual dipole densities, that is, it propagates on-shell as an electromagnetic wave [22]. Probing (anti)caloron centers indeterministically provokes fluctuations, each carrying quanta of energy and momentum , where [23]. (From now on, we set the speed of light c in vacuum and ℏ equal to unity: .) This is because the only physically continuable quantity from imaginary to real time, which can be provided by an (anti)caloron center, is its Euclidean action. Notice that this action, when interpreted as a winding number, is localized at the (anti)caloron’s inmost spacetime point and, in matching with the effective theory, must be interpreted as Planck’s quantum of action ℏ [24]. (In association with the physics of (anti)caloron centers, only static quantities have an interpretation in Minkowskian spacetime, the Euclidean time dependence of, e.g., the (anti)caloron field strength is void of meaning.) Massive modes always represent the quantum physics of (anti)caloron centers regardless of their wavelength and thus associate with quanta of energy and momentum k, respectively. Here, e denotes the coupling in the effective theory for the deconfining phase whose T dependence is governed by the Legendre transformation between pressure P and energy density on the one-loop level [20]. There is a singled-out, physical, and completely fixed gauge in the deconfining phase (unitary-Coulomb) in which the kinematic constraints, arising from the demand that radiative corrections and/or 4-vertices must not probe (anti)caloron centers (to allow for this would amount to a double counting of thermal quantum effects because these are already included in the propagators), enjoy a simple formulation. As a consequence, thermodynamical quantities are computable with 99%-accuracy in only considering the above sketched a priori estimate of the thermal ground state plus free (quasi-particle) fluctuations [20]. For an improvement of the ground-state’s a priori estimate, the mild violation of spatial isotropy and homogeneity introduced by peripheral overlaps and packing voids of (anti)caloron centers can be considered in terms of radiative corrections [25]. Potentially, these are subject to resummations to all loop orders (see [26] for the case of dihedral diagrams in the massive sector).
This talk is organised as follows. In Section 2, we discuss (anti)calorons with topological charge modulus one of trivial (Harrington–Shepard) and nontrivial holonomy (Lee–Lu–Kraan–van Baal)2, and we review essential arguments involved in the construction of the a priori estimate of the thermal ground state. Subsequently, the ensuing ground-state structure and the properties of excitations are elucidated, including kinematic constraints governing the radiative corrections. In addition, some arguments on why a physics model describing the so-far probed electromagnetic spectrum needs to invoke a degree-of-thermalisation dependent mixing of Cartan subalgebras in at least two SU(2) Yang–Mills theories are provided. In Section 3, we review the implications of deconfining SU(2) Yang–Mills thermodynamics once the postulate is made that any spatially sufficiently extended thermal photon gas, and, in particular, the Cosmic Microwave Background (CMB), are subjected to this gauge dynamics. In such a situation, to determine the Yang–Mills scale (or critical temperature of the deconfining-preconfining phase transition), the isotropic cosmic radio background (unexplained extragalactic emission) and associated low-frequency excesses in line temperatures over the CMB baseline temperature of K, see [27,28,29,30,31] and references therein, are taken as an indication for the onset of the Meissner effect due to condensed (electric) monopoles. (An electric-magnetically dual interpretation of U(1) charges in SU(2) Yang–Mills theory is implied by the fine-structure constant being dimensionless and [24].) This is because a Meissner massiveness implies the evanescence of conventionally equipartitioned electromagnetic waves in the deep Rayleigh–Jeans regime. Evanescent waves, however, do not propagate and thus can no longer be globally thermalised. This moves their spectral intensity away from that of classical thermal equipartitioning. Rather, a pile-up of low-frequency modes around frequency zero takes place now (the shortest-range fluctuations of lowest volume-integrated classical energy) whose spectral width essentially is given by the Meissner mass [32]. Since is small on the scale of and, since rises with infinite slope in lowering T through [20], one concludes that to a high precision. This prompts the name SU(2) for the Yang–Mills theory describing extended thermal photon gases. Once is fixed in terms of , the temperature-redshift (z) relation of SU(2) in an Friedmann-Lemaitre-Robertson-Walker (FLRW) universe can be computed from the demand of energy conservation for this fluid. The T-z relation for asymptotically high z can be stated exactly as a linear relation whose coefficient coincides to accuracy with the critical exponent for the correlation length of the magnetisation in the 3D Ising model. We argue that this is expected because both theories are in the same universality class and since a conformal map from a fictitious Yang–Mills temperature to the physical Ising temperature can be constructed in the critical regime. For the correlation length to diverge in the usual power-law fashion, one deduces its exponentially faster divergence compared to the spatial system size. This implies that critical behaviour is well discernible on a finite, spatially expanding system of fixed heat content. The remainder of Section 3 reviews the application of the T-z relation of SU(2) to the cosmological model. There are simple arguments which imply a modified dark sector. We provide recently obtained (and not yet published) results for fits to the Planck data of the TT, TE, and EE angular power spectra (using a modified version of CLASS and CAMEL) and discuss the values of some of the thus extracted cosmological parameters. In particular, the value of the Hubble constant almost perfectly coincides with the central value of a recent local-cosmology extraction from the distance-redshift curve of SNe Ia [33]—in contrast to the fits of the standard CDM model to the same CMB data. In addition, the new fits favour a low redshift of re-ionisation which agrees with pin-downs of the onset of the Gunn–Peterson trough in the spectra of high-z quasars (see, e.g., [34]). Finally, we provide an outlook on how the spectral overshoot in TT at low l, which is presently predicted by SU(2), can potentially be cured by taking screening effects into account at low z. In Section 4, we give a brief summary and discuss future research.
2. Thermal Ground State and (Quasi-Particle) Excitations
2.1. Charge-Modulus One (Anti)calorons
The Euclidean (second-order) Yang–Mills equations are satisfied by solutions to the first-order equations
where is the field-strength tensor, the totally antisymmetric symbol in 4D with , g the fundamental gauge coupling, () the set of SU(2) generators in the fundamental representation, normalised as tr , and denotes the gauge potential. In general, configurations, which obey Equation (1), associate with vanishing energy-momentum. Thus, they do not propagate and therefore qualify as ground-state inducers. Specifically, at finite temperature, one is led to consider periodic gauge-field configurations, , where . In the following, we set . Since the group manifold of SU(2) is the three-sphere , and since solutions to Equation (1) with finite action S on , whose boundary is —instantons—are stabilized by and classified according to, e.g., their topological charge . The case was discovered in [11], the associated gauge-field configuration exhibiting winding about at spacetime infinity. The construction of all instantons is subject to an algebraic constraint ((anti)selfduality on a point), representing data such as k, scale variables , locations of centers , and su(2) orientations thereof [12]. However, an important subset of configurations with can be obtained by virtue of the observation that a large gauge transformation SU(2) applied to the solution of [11] dewinds it at infinity at the price of introducing winding about the point of maximum action density. This re-casts the gauge-field configuration to the following form:
where is the anti-symmetric, anti-selfdual ’t Hooft symbol, arising from the projection of the pure-gauge configuration onto the generators . (The (anti)instanton solution is obtained by replacing by its selfdual counterpart .) The important fact about Equation (2) is that the prepotential of an (anti)instanton of ( denoting the spacetime point of maximum action density—the (anti)instanton center) can be promoted to an arbitrary integer topological charge by superposition of terms where and [35,36] are the associated sets of scale parameters and centers, respectively. In particular, setting and , for renders the prepotential periodic in . Without an essential restriction of generality, we may specialise to to obtain [37]
where . On the slice the configuration associated with Equations (2) and (3) possesses exactly one unit of topological charge localised at . Exhibiting a Polyakov loop at spatial infinity of value unity, this configuration—the Harrington–Shepard (HS) (anti)caloron—is said to be of trivial holonomy.
It is necessary for our discussion in Section 2.2 to analyse this solution as a function of distance to its center. This was done in [38] with the following result. For (), the prepotential takes the form , where , such that the solution represents an ordinary instanton with a rescaled scale parameter obeying . For , the configuration becomes static because then . Moreover, for , it represents a static, selfdual monopole, , and, for , one observes a static selfdual dipole, of dipole moment s where .
The solutions of nontrivial holonomy were constructed [39,40,41] based on Werner Nahm’s transformation between (anti)selfdual Yang–Mills fields on and the dual torus [13,14,15]. The dual torus to is such that selfdual data needs to be prescribed on a real interval only to construct the selfdual gauge field on via the Nahm transformation. Thus, instead of a 4D partial differential equation (PDE), only an ODE subject to certain jump conditions needs to be solved which reflect the demand for overall magnetic charge neutrality of a system of BPS monopole and its antimonopole (magnetic charge w.r.t. U(1)⊂SU(2) surviving the gauge-symmetry breaking imposed by ). The thus obtained nontrivial-holonomy configuration can be connected smoothly to the above-discussed trivial-holonomy (anti)caloron. Note that the trivial-holonomy limit transmutes a pair of localised magnetic BPS monopole and its antimonopole, separated by the scale s and both of finite mass, into a pair of a delocalised, massless monopole and its localised, massive antimonopole. The BPS monopole and its antimonopole can be considered static because the attraction mediated by the spatial components of their gauge fields (magnetic Coulomb force) is cancelled precisely by the repulsion exerted by the temporal components (Higgs force). In a heroic computation following the lines of [35], where the case of a (anti)instanton was investigated, Dmitri Diakonov and collaborators have computed the one-loop quantum weight of a nontrivial-holonomy (anti)caloron [42] for the limit . As it turns out, this limit is the relevant one in describing (anti)calorons of the thermal ground state estimate in the deconfining phase of SU(2) Yang–Mills thermodynamics because of the existence of a dimensionless critical temperature and the fact that the emergence of the field is strongly dominated by (anti)calorons of scale parameter . The result of [42] shows that such configurations are unstable under Gaussian quantum noise: large holonomy implies (anti)caloron dissociation into their constituent monopoles and antimonopoles, whereas small holonomy is driven back to trivial holonomy, identifying the latter to be a stable situation.
2.2. Thermal-Ground-State Estimate: (Anti)caloron Centers vs. Peripheries
Having identified trivial-holonomy (anti)calorons as viable and relevant field configurations for the a priori estimate of the thermal ground state, we now sketch the essential steps in deriving the field from a spatial coarse-graining involving the following set of dimensionless phases:
where
The Wilson lines in Equation (5) are calculated along the straight spatial line connecting the points and , and demands path-ordering. In Equation (4), the sum is over the HS caloron (C) and anticaloron (A), and signals a family of (dimensionless) phases of the field whose continuous parameters emerge partially by evaluation of the right-hand side and partially relate to temporal shift moduli. It is straightforward to argue [19] that Equation (4) is unique: adjointly transforming one-point functions as potential integrands vanish identically due to (anti)selfduality, higher n-point functions and higher topological charges are excluded by dimensional counting, the coincidence of the spatial (anti)caloron center with is demanded by spatial isotropy, and the straight-line evaluation of Wilson lines is dictated by the absence of any spatial scale on the classical (Euclidean) level. This allows for omitting the path-ordering prescription since is a spatial hedge-hog, centered at , which assigns to each direction in the same direction in su(2).
As a result of performing the integrations in Equation (4), one derives to be the kernel of the uniquely determined linear differential operator . By absorbing explicit dependence in into a potential , giving rise to ’s action density , and by demanding consistency between the BPS equations,
and the Euler–Lagrange equation
one derives the following first-order equation for V [19,21]
Equation (8) has the solution
Since the BPS equations for (square root of the potential V on its right-hand side) needs to be satisfied in addition to the Euler–Lagrange equation (first derivative of V on their right-hand sides), the usual additive shift symmetry of the potential due to the Euler–Lagrange equation is not an option: The result (with ) turns out to be a good a priori estimate of the thermal ground state’s energy density and pressure, respectively, and this result is unique once the integration constant has been fixed by experimental data.
It is important to note that the integration over the instanton scale parameter depends cubically on the upper integration limit and that the dependence on of this integral saturates very rapidly for into a harmonic one. Therefore, the kernel in Equation (4) of the differential operator is strongly dominated by a small band of values centred at the cutoff , and one can show that and therefore also that for all temperatures of the deconfining phase [19].
In discussing the implications of (anti)caloron structure for the physics of the massless mode, one neatly needs to distinguish the situation of a thermal ensemble and the consideration of an isolated excitation/disturbance. Let us start by considering an isolated plane wave of mean intensity I and wavelength l. For its propagation to be supported by undulating repolarisations of the (anti)selfdual dipole densities provided by trivial-holonomy (anti)caloron peripheries, the following inequality needs to be satisfied [22]
Relation (10) is derived from the demand that l needs to be larger than length scale s for the caloron periphery to appear like a static and (anti)selfdual dipole field,
and the fact that I for a plane wave is [22]
Moreover, one easily derives [19] that
and
From Equations (13) and (14), and from Figure 1, we conclude that the “dipole length scale” s (the dipole moment) falls below the “coarse-graining length scale” for sufficiently low temperatures and that then also falls below . Therefore, the derivation of , which assumes spatial isotropy and is based on a trivial analytic continuation in (staticity of (anti)caloron field strength for leading to saturation of the dependence of Equation (4) for both ) [43]), is not applicable for such low temperatures.
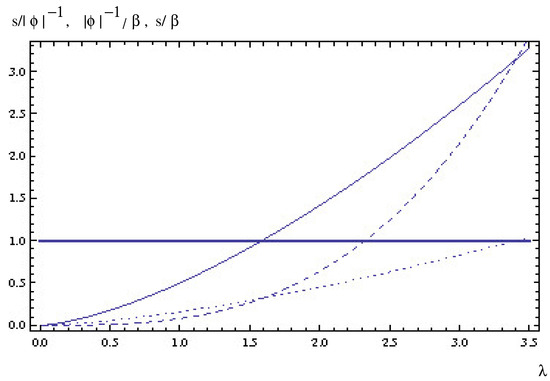
Figure 1.
Plot of the ratios (solid), (dashed), and (dotted) versus small values of .
However, relation (10) does not depend on , and therefore one should regard it as a unique continuation of the high- reasoning to the low- regime3, thus maintaining its validity there. For example, setting eV and eV (intensity of a 30 keV synchrotron beam of photons per second and square millimeter) the requirement on the wavelength l to be in agreement with (10) is
while for eV one would require ! The situation for a light bulb of intensity Wm requires and , respectively, for eV [44] and eV. Therefore, to be in agreement with the observation of wave-like propagation of electromagnetic disturbances up to the X-ray regime, at the same time acknowledging that the bulk of the blackbody spectrum certainly associates with photonic fluctuations4, one is led to consider a thermalisation dependent mixing of the Cartan subalgebras in two SU(2) Yang–Mills theories of disparate scales eV and eV [44]: propagating, directed electromagnetic disturbances are waves in SU(2), a thermal photon gas is described by SU(2) with the deep Rayleigh–Jeans regime being subject to wave-like excitations, and intermediates of these two extremes are associated with a nontrivial mixing angle.
3. SU(2) and the Cosmological Model
The postulate that any extended thermal photon gas is subject to SU(2) applies, in particular, to the CMB itself. In this section, we will explain how the scale eV is fixed by the radio excess in the CMB, what SU(2) implies towards the CMB temperature-redshift relation, what this, in turn, means for the dark sector of the cosmological model a high redshifts, and which values cosmological parameters assume in the accordingly modified cosmological model when confronted with temperature and polarisation data as provided in unprecedented signal-to-noise ratios and angular resolution by the Planck collaboration.
3.1. The Postulate of SU(2) Describing Thermal Photon Gases
As already mentioned in the introduction, the critical temperature of SU(2) is sharply determined by the present CMB temperature K [45], resting on the fact that, in cooling the CMB down by virtue of the Universe’s expansion, the onset of the preconfining phase transition critically generates a Meissner mass for the formerly massless mode. Frequencies with and then associate with evanescent waves whose spectral distribution no longer follows the Rayleigh–Jeans law because they do not thermalise anymore [32] and energetically (exponential spatial fall-off of intensity) are favoured to occur at zero frequency. In [32], we have, in accordance with the two conditions above, extracted MHz, which is very small compared to GHz, implying that , albeit below is extremely close to .
3.2. Temperature-Redshift Relation and 3D Ising Criticality
Reviewing the arguments in [46], let us now discuss one immediate implication of SU(2) with for the CMB temperature (T)—redshift (z) relation which is obtained as the solution to the equation for energy conservation in an FLRW universe
where , P, and a denote SU(2) energy density and pressure, respectively, and a refers to the cosmological scale factor, normalized such that today . Upon appeal to the Legendre transformation between P and and its T-differentiated version, one finds
where M denotes an arbitrary mass scale, and the entropy density s is given as
Note that s does not receive a direct contribution from the thermal ground state [19] because such a term cancels in the sum . The important feature of Equation (17) is that its right-hand side solely refers to the boundary values of the state variable s at and T. In this sense, the solution carries topological information if s at and at T is characterised by conformal physics only. This, indeed, is the case for and (conformal points: and ). Namely, for , where the Stefan–Boltzmann limit is well saturated [19], is proportional to . On the other hand, we know that at the excitations of the theory represent a free photon gas because the mass of vector modes diverges [19]. Therefore, is proportional to . As a consequence, the ratio in Equation (17) reads
where g refers to the number of relativistic degrees of freedom at the respective temperatures. We have (two photon polarizations plus three polarizations for each of the two vector modes) and (two photon polarizations). Substituting this into Equation (19) and inserting the result into Equation (17), we arrive at
In [47], we have used the value , which is a good approximation to
In [48], it was argued that the order parameter for deconfinement in 4D SU(2) Yang–Mills thermodynamics, the 3D Polyakov-loop variable , should obey long-range dynamics governed by (electric) center symmetry. This is the global symmetry of the 3D Ising model void of an external magnetic field. Being members of the same universality class, the critical exponents of the correlation lengths thus should coincide in both theories. The superb agreement between [49] and ,
is indicative of such a link between the two theories even though appears as a coefficient in a cosmological T-z relation and not as a critical exponent governing the divergence of the correlation length l. To explore this connection further, one may continue the asymptotic behavior of Equation (20) down to , where a diverges, positing that a strictly monotonic increasing function of the scale factor a describes the ratio of the Ising correlation length l to some reference length within the critical regime. Note that lowering the temperature through the critical regime at fixed energy content is facilitated by an increase of spatial system size (a), which implies a much more pronounced increase of the correlation length l as we shall see now. Namely, for the asymptotic, scale-invariant (conformal) solution in (20), continued to , one may link the fictitious Yang–Mills temperature ratio to the physical Ising-model temperature ratio , denoting the critical temperature of the Ising phase transition, as
Obviously, implies that . Substituting Equation (23) into Equation (20) and exponentiating, we arrive at
As , this yields the same critical behavior for , and the above-mentioned strictly monotonic function thus turns out to be the exponential map. This means that the onset of the divergence of can be well discerned at finite system sizes as .
3.3. Dark Matter at High Redshifts
In [47,50], it is explained why the asymptotic solution in Equation (20) implies a change of the dark sector in the Hubble parameter with
where is the baryonic density parameter, denotes the contribution of the SU(2) plasma, is the critical density , and refers to the neutrino density parameter. The dark-sector density parameter exhibits reduced dark matter at high z and interpolates to the conventional CDM model at low z:
where the subscripts edm and pdm refer to emergent and primordial dark matter, respectively, denotes the ratio to of the vacuum energy due to a cosmological constant, and is the redshift at which emergent dark matter is released instantaneously from a dark-energy like component as the Universe cools down. An important parameter in this SU(2) driven model of a spatially flat Universe is the fraction of primordial dark matter to today’s dark matter
3.4. Results on TT, TE, and EE
In [50], the model of Equation (25) was fitted to the angular power spectra associated with the temperature auto correlation TT, the temperature-E-mode-polarisation cross correlation TE, and the E-mode-polarisation auto correlation based on the 2015 Planck data (see Figure 2 for the case TT). We have used a modified CLASS code to compute the spectra and CAMEL to perform the likelihood maximisations using lowTEB, HiLLiPOP, and lensing [51]. Leaving out lowTEB does not influence the fit results in any essential way.
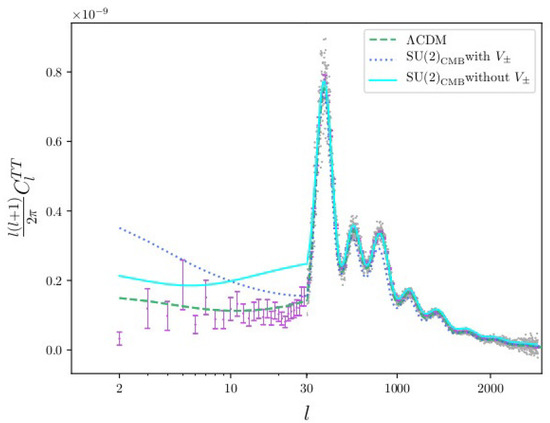
Figure 2.
The TT power spectra (blue error bars and grey dots are 2015 Planck data, dashed line is best-fit Lambda-Cold-Dark-Matter (CDM) model, dotted line SU(2), also taking into account in perturbation equations (+), and solid line SU(2), only taking massless mode into account in perturbation equations ().
Version , which is favoured by physical arguments on the propagation of temperature perturbations by the wave-like part of the massless mode’s spectrum deep in the Rayleigh–Jeans regime [50], fits the TT data best (for TE and EE + and SU(2) can hardly be distinguished) for . At low l, both versions exhibit excesses. This could be due to the omission of (anti)screening effects in the dispersion law of the massless mode [52,53,54], which imply a dynamical breaking of statistical isotropy at low z.
In Figure 3, the value of versus other key cosmological parameters is depicted for likelihood maximisations, which do not exceed , to characterise their scatter. Notably, we obtain a low value for the re-ionisation redshift , essentially in agreement with its extraction in detecting the Gunn–Peterson trough in high-redshift quasar spectra [34], a low value of the baryon density which deviates by about 30% from the Big-Bang-nucleosynthesis (BBN) deuterium concordance value but matches the value of typical baryon censuses [55] (see [56], however, for an apparent, alternative resolution of the missing-baryon problem, and a best-fit value of coincident with the most recent and most precise SNe Ia distance-redshift extraction that is based on a locally calibrated cosmological distance ladder (and not on the high-z calibration of an inverted distance ladder [33,57])). Notice the low value of , demanding a red-tilted spectrum of primordial, adiabatic curvature perturbations.
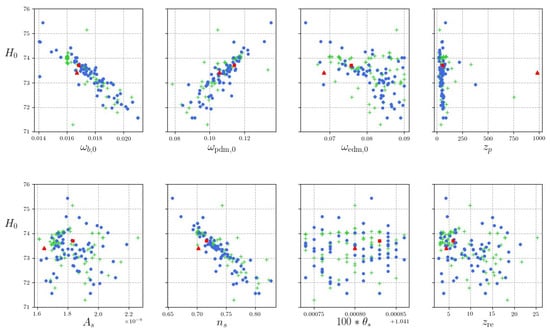
Figure 3.
Scatter plots of for fitted parameter values, requiring that (best-fit: for , for +). Crosses and dots refer to + and , whose best-fit parameter values are indicated by a solid triangle and a solid square, respectively.
4. Conclusions
In this talk, we have reviewed the construction of the thermal ground state in the deconfining phase of SU(2) Yang–Mills thermodynamics. The outcome of this construction imposes a strong contraint on the (anti)caloron scale parameter, , and therefore on the static configuration of the (anti)selfdual field outside the central region where spatial coarse-graining is performed. A relation between a classical plane wave’s intensity I, its frequency , and the Yang–Mills scale of the SU(2) theory is obtained by appeal to the condition that the wavelength l must be larger than the dipole scale . Because s and I do depend on , this relation does not exhibit any dependence on and therefore can be (trivially) continued to small values of , permitting very small wavelengths to classically propagate, provided that is sufficiently large. To cover Max Planck’s spectral intensity of a blackbody for all thermal photon gases and the propagation of isolated electromagnetic waves of so-far measured/observed intensity and frequency, at least two SU(2) Yang–Mills theories of disparate scales eV [32] and eV [44]—SU(2) and SU(2)—are thus required, subject to a thermalisation dependent mixing angle for their Cartan subalgebras. Subsequently, implications of SU(2) for the cosmological model were elucidated. In a first step, the T-z relation for the CMB, which exhibits curvature at low z and asymptotes into a modified linear behaviour at large z, was reviewed. The asymptotic coefficient in this relation is strongly conjectured to be linked to the critical exponent for the correlation length in the 3D Ising transition in the absence of an external magnetic field, and we have given arguments why such a link should exist. Finally, we have explored the implications of the new T-z relation for the dark-matter sector of the flat-space FLRW cosmological model. Fits to the 2015 Planck data on TT, TE, and EE have revealed values for directly measurable parameters (, , and ) that are in line with local cosmological observations but exhibit considerable tension with global fits to the standard cosmological model (including BBN and a high-z confidence in CDM).
An important target of future investigation is the effect of SU(2)-induced (anti)screening in the dispersion law of the massless mode [52,53,54]. Since this effect breaks statistical isotropy dynamically, one should simulate an ensemble of CMB skies, search for matches of angular power spectra, and consider appropriately designed statistics [58,59,60,61] to assess whether typical members are extremely unlikely in the standard CDM model.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gross, D.J.; Wilczek, F. Ultraviolet behavior of non-abelian gauge theories. Phys. Rev. Lett. 1973, 30, 1343. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable perturbative results for strong interactions? Phys. Rev. Lett. 1973, 30, 1346. [Google Scholar] [CrossRef]
- Khriplovich, I.B. Green’s functions in theories with non-abelian gauge group. Sov. J. Nucl. Phys. 1969, 10, 235–242. [Google Scholar]
- Braaten, E.; Pisarski, R.D. Soft amplitudes in hot gauge theories: A general analysis. Nucl. Phys. B 1990, 337, 559–634. [Google Scholar] [CrossRef]
- Linde, A.D. Infrared problem in the thermodynamics of the Yang-Mills gas. Phys. Lett. B 1980, 96, 289–292. [Google Scholar] [CrossRef]
- Bischer, I.; Grandou, T.; Hofmann, R. Perturbative peculiarities of quantum fields at non-zero temperature. Presented at the 7th International Conference on New Frontiers in Physics (ICNFP 2018), Kolymbari, Greece, 4–12 Jully 2018. [Google Scholar]
- Braaten, E.; Pisarski, R.D. Calculation of the quark damping rate in hot QCD. Phys. Rev. D 1992, 46, 1829. [Google Scholar] [CrossRef]
- Deng, Y. The energy and pressure in SU(3) lattice gauge theory at finite temperature. Nucl. Phys. B Proc. Suppl. 1988, 9, 334–338. [Google Scholar] [CrossRef]
- Engels, J.; Fingberg, J.; Karsch, F.; Miller, D.; Weber, M. Non-perturbative thermodynamics of SU (N) gauge theories. Phys. Lett. B 1990, 252, 625–630. [Google Scholar] [CrossRef]
- Engels, J.; Karsch, F.; Scheideler, T. Determination of anisotropy coefficients for SU(3) gauge actions from the integral and matching methods. Nucl. Phys. B 1999, 564, 303–324. [Google Scholar] [CrossRef]
- Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle solutions of the Yang-Mills equations. Phys. Lett. B 1975, 59, 85–87. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Atiyah, M.F.; Hitchin, N.J.; Drinfeld, V.G.; Manin, Y.I. Construction of instantons. Phys. Lett. A 1978, 65, 185–187. [Google Scholar] [CrossRef]
- Nahm, W. A simple formalism for the BPS monopole. Phys. Lett. B 1980, 90, 413–414. [Google Scholar] [CrossRef]
- Nahm, W. All Self-Dual Multimonopoles for Arbitrary Gauge Groups. In Structural Elements in Particle Physics and Statistical Mechanics, NATO Advanced Study Institutes Series (Series B: Physics); Honerkamp, J., Pohlmeyer, K., Römer, H., Eds.; Springer: Boston, MA, USA, 1981; Volume 82. [Google Scholar]
- Nahm, W. Self-dual monopoles and calorons. In Group Theoretical Methods in Physics. Lecture Notes in Physics; Denardo, G., Ghirardi, G., Weber, T., Eds.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 201. [Google Scholar]
- ’t Hooft, G. Renormalization of massless Yang-Mills fields. Nucl. Phys. B 1971, 33, 173–199. [Google Scholar]
- ’t Hooft, G.; Veltman, M. Regularization and renormalization of gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. Combinatorics of gauge fields. Nucl. Phys. B 1972, 50, 318–353. [Google Scholar] [CrossRef]
- Hofmann, R. The Thermodynamics of Quantum Yang–Mills Theory: Theory and Applications; World Scientific: Singapore, 2016. [Google Scholar]
- Hofmann, R. Nonperturbative approach to Yang–Mills thermodynamics. Int. J. Mod. Phys. A 2005, 20, 4123–4216, Erratum in 2006, 21, 6515. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R. Thermal ground state in deconfining Yang-Mills thermodynamics. Progr. Theor. Phys. 2007, 118, 759–767. [Google Scholar] [CrossRef]
- Grandou, T.; Hofmann, R. Thermal Ground State and Nonthermal Probes. Adv. Math. Phys. 2015, 2015, 197197. [Google Scholar] [CrossRef]
- Hofmann, R. SU(2) Yang–Mills Theory: Waves, Particles, and Quantum Thermodynamics. Entropy 2016, 18, 310. [Google Scholar] [CrossRef]
- Hofmann, R.; Kaviani, D. The quantum of action and finiteness of radiative corrections: Deconfining SU(2) Yang-Mills thermodynamics. Quantum Matter 2012, 1, 41–52. [Google Scholar] [CrossRef]
- Schwarz, M.; Hofmann, R.; Giacosa, F. Radiative corrections to the pressure and the one-loop polarization tensor of massless modes in SU(2) Yang-Mills thermodynamics. Int. J. Mod. Phys. A 2007, 22, 1213–1237. [Google Scholar] [CrossRef]
- Bischer, I.; Grandou, T.; Hofmann, R. Massive loops in thermal SU(2) Yang–Mills theory: Radiative corrections to the pressure beyond two loops. Int. J. Mod. Phys. A 2017, 32, 1750118. [Google Scholar] [CrossRef]
- Fixsen, D.J.; Kogut, A.; Levin, S.; Limon, M.; Lubin, P.; Mirel, P.; Seiffert, M.; Singal, J.; Wollack, E.; Villela, T.; et al. ARCADE 2 measurement of the absolute sky brightness at 3-90 GHz. Astrophys. J. 2011, 734, 5. [Google Scholar] [CrossRef]
- Reich, P.; Reich, W. A radio continuum survey of the northern sky at 1420 MHz. II. Astrophys. Suppl. Ser. 1986, 63, 205–288. [Google Scholar]
- Roger, R.S.; Costain, C.H.; Landecker, T.L.; Swerdlyk, C.M. The radio emission from the Galaxy at 22 MHz. Astron. Astrophys. Suppl. Ser. 1999, 137, 7–19. [Google Scholar] [CrossRef]
- Maeda, K.; Alvarez, H.; Aparici, J.; May, J.; Reich, P. A 45-MHz continuum survey of the northern hemisphere. Astron. Astrophys. Suppl. Ser. 1999, 140, 145–154. [Google Scholar] [CrossRef]
- Haslam, C.G.T.; Klein, U.; Salter, C.J.; Stoffel, H.; Wilson, W.E.; Cleary, M.N.; Cooke, D.J.; Thomasson, P. A 408 MHz all-sky continuum survey. Astron. Astrophys. 1981, 100, 209–219. [Google Scholar]
- Hofmann, R. Low-frequency line temperatures of the CMB (Cosmic Microwave Background). Annalen Phys. 2009, 18, 634–639. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New parallaxes of galactic cepheids from spatially scanning the hubble space telescope: Implications for the hubble constant. Astrophys. J. 2018, 855, 136. [Google Scholar] [CrossRef]
- Becker, R.H.; Fan, X.; White, R.L.; Strauss, M.A.; Narayanan, V.K.; Lupton, R.H.; Gunn, J.E.; Annis, J.; Bahcall, N.A.; Brinkmann, J. Evidence for Reionization at z∼6: Detection of a Gunn-Peterson Trough in a z = 6.28 Quasar. Astrophys. J. 2001, 122, 2850. [Google Scholar]
- ’t Hooft, G. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys. Rev. D 1976, 14, 3432, Erratum in 1978, 18, 2199. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Conformal properties of a Yang-Mills pseudoparticle. Phys. Rev. D 1976, 14, 517. [Google Scholar] [CrossRef]
- Harrington, B.J.; Shepard, H.K. Periodic Euclidean solutions and the finite-temperature Yang-Mills gas. Phys. Rev. D 1978, 17, 2122. [Google Scholar] [CrossRef]
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and instantons at finite temperature. Rev. Mod. Phys. 1981, 53, 43. [Google Scholar] [CrossRef]
- Kraan, T.C.; Van Baal, P. Exact T-duality between Calorons and Taub-NUT spaces. Phys. Lett. B 1998, 428, 268–276. [Google Scholar] [CrossRef]
- Kraan, T.C.; Van Baal, P. Periodic Instantons with non-trivial Holonomy. Nucl. Phys. B 1998, 533, 627–659. [Google Scholar] [CrossRef]
- Lee, K.; Lu, C. SU(2) calorons and magnetic monopoles. Phys. Rev. D 1998, 58, 025011. [Google Scholar] [CrossRef]
- Diakonov, D.; Gromov, N.; Petrov, V.; Slizovskiy, S. Quantum weights of dyons and of instantons with nontrivial holonomy. Phys. Rev. D 2004, 70, 036003. [Google Scholar] [CrossRef]
- Herbst, U.; Hofmann, R. Emergent Inert Adjoint Scalar Field in SU(2) Yang-Mills Thermodynamics due to Coarse-Grained Topological Fluctuations. ISRN High Energy Phys. 2012, 2012, 373121. [Google Scholar] [CrossRef]
- Hofmann, R. The Isolated Electron: De Broglie’s Hidden Thermodynamics, SU(2) Quantum Yang-Mills Theory, and a Strongly Perturbed BPS Monopole. Entropy 2017, 19, 575. [Google Scholar] [CrossRef]
- Mather, J.C.; Cheng, E.S.; Cottingham, D.A.; Eplee, R.E., Jr.; Fixsen, D.J.; Hewagama, T.; Isaacman, R.B.; Jensen, K.A.; Meyer, S.S.; Noerdlinger, P.D.; et al. Measurement of the cosmic microwave background spectrum by the COBE FIRAS instrument. Astrophys. J. 1994, 420, 439. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R. Exact determination of asymptotic CMB temperature-redshift relation. Mod. Phys. Lett. A 2018, 33, 1850029. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R. SU(2)CMB at high redshifts and the value of H0. Mon. Not. R. Astron. Soc. 2017, 469, 1233–1245. [Google Scholar] [CrossRef]
- Svetitsky, B.; Yaffe, L.G. Critical behavior at finite-temperature confinement transitions. Nucl. Phys. B 1982, 210, 423–447. [Google Scholar] [CrossRef]
- Kos, F.; Poland, D.; Simmons-Duffin, D.; Vichi, A. Precision islands in the Ising and O (N) models. J. High Energy Phys. 2016, 2016, 36. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R.; Kramer, D. SU(2)CMB and the cosmological model: Angular power spectra. Mon. Not. R. Astron. Soc. 2018, in press. [Google Scholar] [CrossRef]
- Aghanim, N.; et al. [Planck Collaboration] Planck 2015 results-XI. CMB power spectra, likelihoods, and robustness of parameters. Astron. Astrophys. 2016, 594, A11. [Google Scholar]
- Ludescher, J.; Hofmann, R. Thermal photon dispersion law and modified black-body spectra. Ann. Phys. 2009, 18, 271–280. [Google Scholar] [CrossRef]
- Falquez, C.; Hofmann, R.; Baumbach, T. Modification of black-body radiance at low temperatures and frequencies. Ann. Phys. 2010, 522, 904–911. [Google Scholar] [CrossRef]
- Hofmann, R. The fate of statistical isotropy. Nature Phys. 2013, 9, 686. [Google Scholar] [CrossRef]
- Shull, J.M.; Smith, B.D.; Danforth, C.W. The baryon census in a multiphase intergalactic medium: 30% of the baryons may still be missing. Astrophys. J. 2012, 759, 23. [Google Scholar] [CrossRef]
- Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C.W.; Elvis, M.; Fiore, F.; et al. Observations of the missing baryons in the warm–hot intergalactic medium. Nature 2018, 558, 406. [Google Scholar] [CrossRef] [PubMed]
- Macaulay, E.; Nichol, R.C.; Bacon, D.; Brout, D.; Davis, T.M.; Zhang, B.; Bassett, B.A.; Scolnic, D.; Möller, A.; D’Andrea, C.B. First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant. arXiv, 2018; arXiv:1811.02376. [Google Scholar]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. CMB anomalies after Planck. Class. Quant. Gravity 2016, 33, 184001. [Google Scholar]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large-scale alignments from WMAP and Planck. Mon. Not. R. Astron. Soc. 2015, 449, 3458–3470. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Lack of large-angle TT correlations persists in WMAP and Planck. Mon. Not. R. Astron. Soc. 2015, 451, 2978–2985. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large-Angle CMB Suppression and Polarization Predictions. Mon. Not. R. Astron. Soc. 2013, 434, 3590–3596. [Google Scholar] [CrossRef]
| 1. | We follow the convention to denote group G’s Lie algebra by g. |
| 2. | The holonomy of a gauge-field configuration at finite temperature relates to its Polyakov loop at spatial infinity: If this quantity coincides with an element of the center of the group SU(2) then one speaks of a trivial holonomy, if this is not the case then the configuration is said to be of nontrivial holonomy. |
| 3. | The existence of phase boundaries in the thermalised situation is irrelevant when a monochromatic plane wave is considered. |
| 4. | For the present CMB with K and eV condition (11), when converted into an upper bound on frequency , it reads MHz. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).