The ABC of Higher-Spin AdS/CFT
Abstract
1. Introduction
2. Review and Summary of Results
2.1. Higher Spin Partition Functions in Euclidean AdS Spaces
2.2. Variants of Higher Spin Theories and Key Results
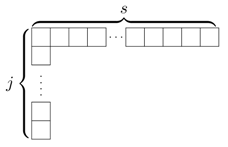
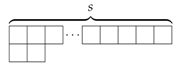
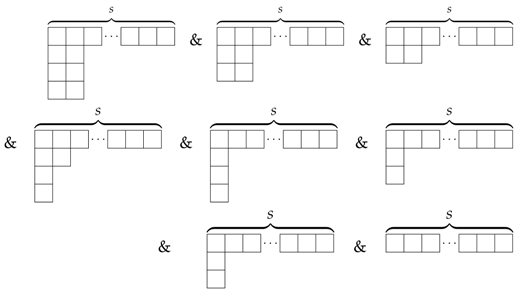
3. Matching the Sphere Free Energy
3.1. The AdS Spectral Zeta Function
3.1.1. The Spectral Density for Arbitrary Representation
3.2. Calculations in Even d
3.2.1. Type B Theories
Spectrum
Majorana–Weyl Projection
Sample Calculations
3.2.2. Fermionic Higher Spins in Type AB Theories
Spectrum
Sample Calculation: AdS
3.2.3. Type C Theories
Spectrum
3.3. Calculations in Odd d
3.3.1. Preliminaries
Alternate Regulators
Integrals
3.3.2. Calculational Method and Type A Example
Computing :
Computing :
3.3.3. Type B Theories
Non-Minimal Theory
Minimal Theories
3.3.4. Type AB Theories
Spectrum and Results
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. S 1 ×S d-1 Partition Functions and Casimir Energies
Type A Theories
Type B Theories
Type AB Theories
Type C Theories
| d | Non-Minimal | Self-Dual | Minimal | Self-dual |
|---|---|---|---|---|
| 4 | ||||
| 6 | 0 | |||
| 8 | ||||
| 10 | 0 | |||
| 12 | ||||
| 14 | 0 |
Appendix B. Some Technical Details on the One-Loop Calculations in Hyperbolic Space
Appendix B.1. Hurwitz Zeta Regularization
Appendix B.2. Identity for Odd d Free Energy Calculations
Appendix B.3. Evaluating
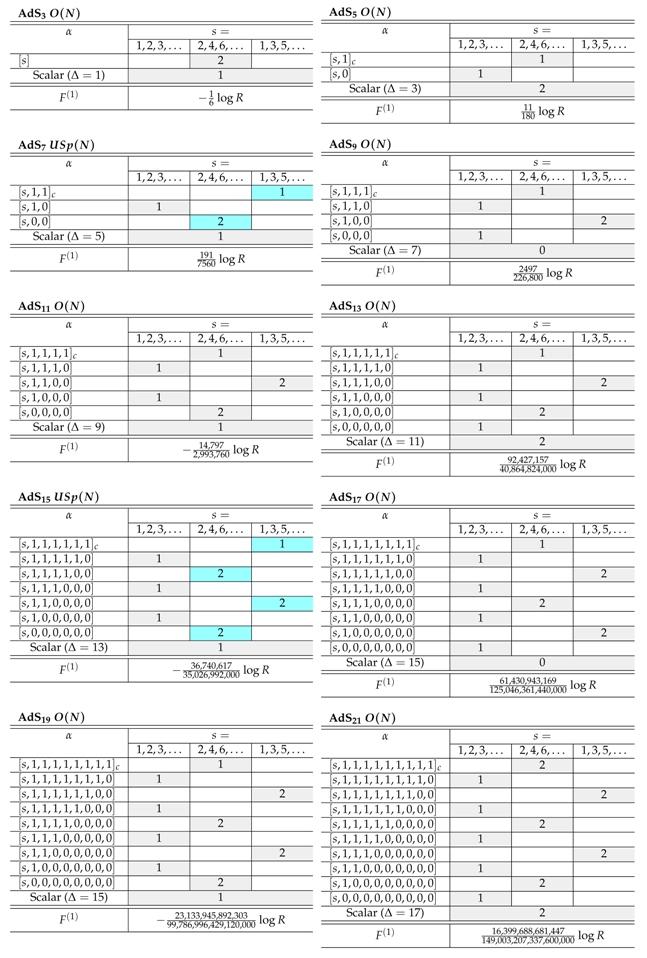
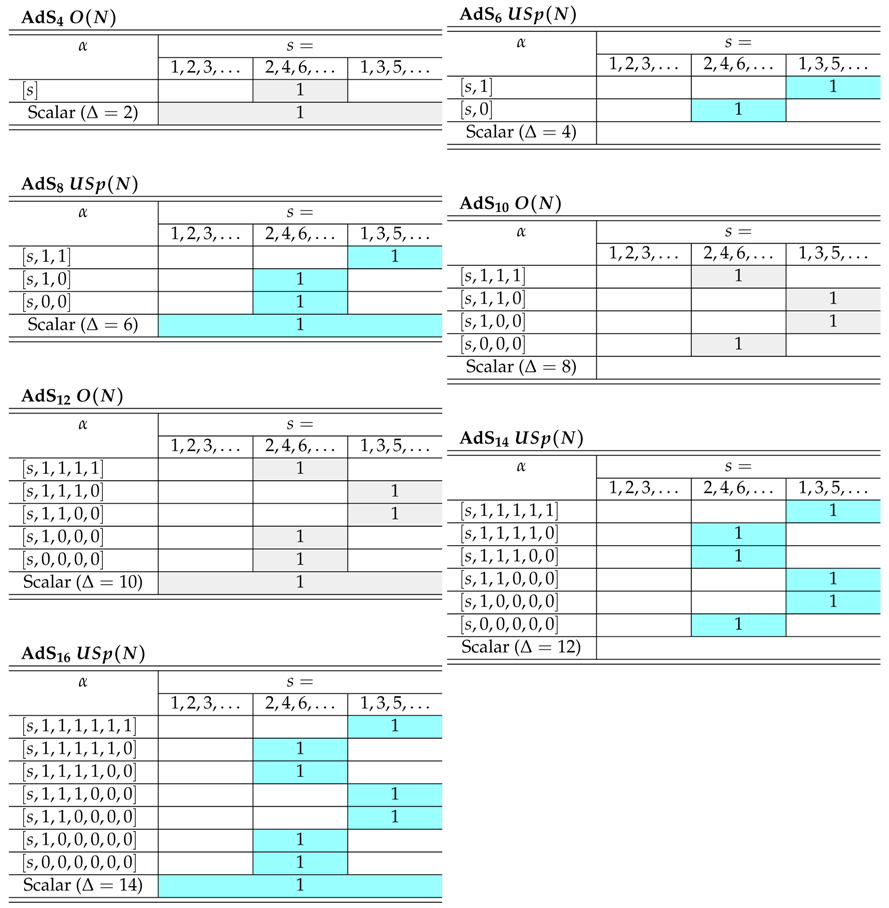
Appendix C. Spectra of Higher Spin Theories and Their Free Energy Contributions
Appendix C.1. Type B Theories
| AdS | ||||
|---|---|---|---|---|
| Towers of Spins | Contribution to F from One Tower Summed Over: | |||
| () | ||||
 | ||||
 | 0 | |||
| Scalar | Contribution to F by one scalar | |||
| AdS | ||||
|---|---|---|---|---|
| Towers of Spins | Contribution to F from One Tower Summed Over: | |||
| () | ||||
 | ||||
 | ||||
 | ||||
| Scalar | Contribution to F by one scalar | |||
| AdS | ||||
|---|---|---|---|---|
| Towers of Spins | Contribution to F from One Tower Summed Over: | |||
| () | ||||
 | ||||
 | ||||
 | ||||
 | ||||
| Scalar | Contribution to F by one scalar | |||
| AdS | ||||
|---|---|---|---|---|
| Towers of Spins | Contribution to F from One Tower Summed Over: | |||
| () | ||||
 | ||||
 | ||||
 | ||||
 | ||||
 | ||||
| Scalar | Contribution to F by one scalar | |||
Appendix C.2. Calculation of in Type AB Theories
Appendix C.2.1. AdS7
Appendix C.2.2. AdS9
Appendix C.3. Free Energy Values for Type C Theories in AdS9
| AdS Type C | ||||
|---|---|---|---|---|
| Towers of Spins | Contribution to F from One Tower Summed Over: | |||
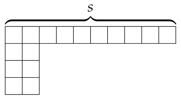 | ||||
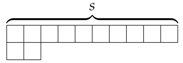 | ||||
 | ||||
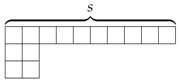 | ||||
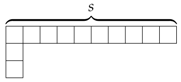 | ||||
 | ||||
| Other Particles | Contribution to F by one particle | |||
Appendix C.3.1. Spectra of Spins for Type C Theories
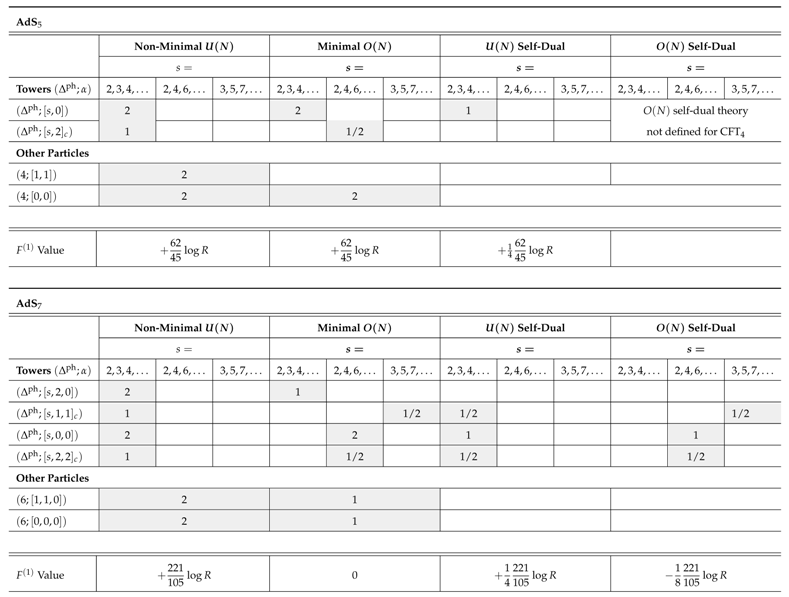
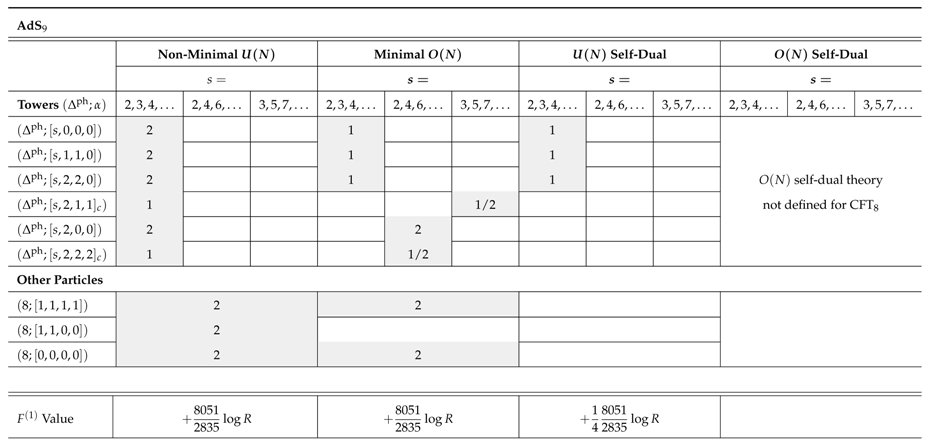
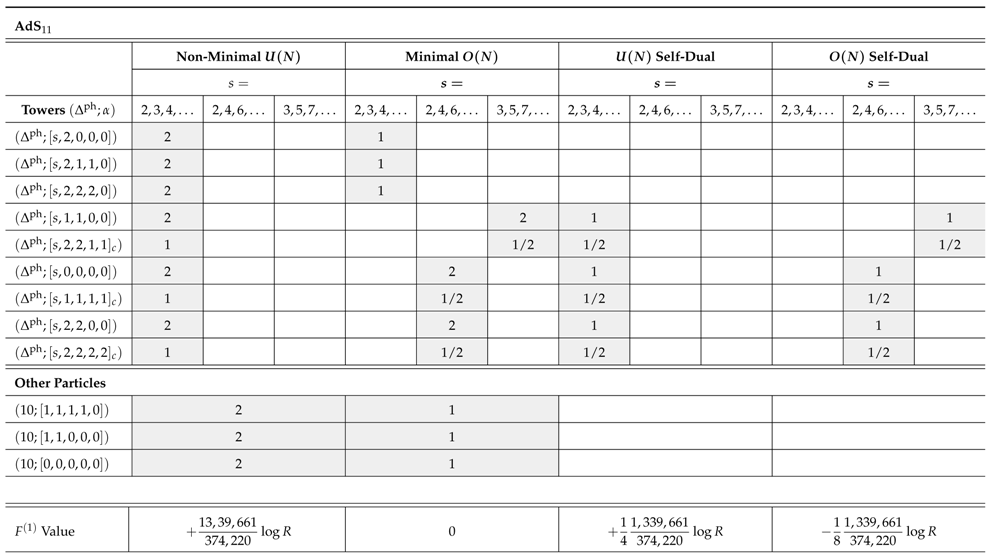
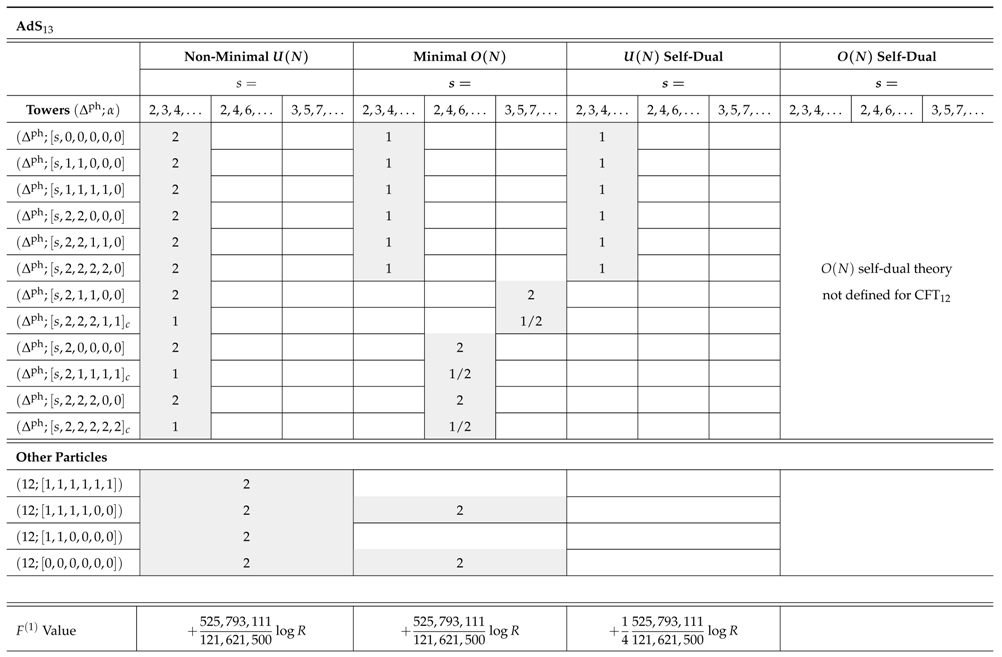
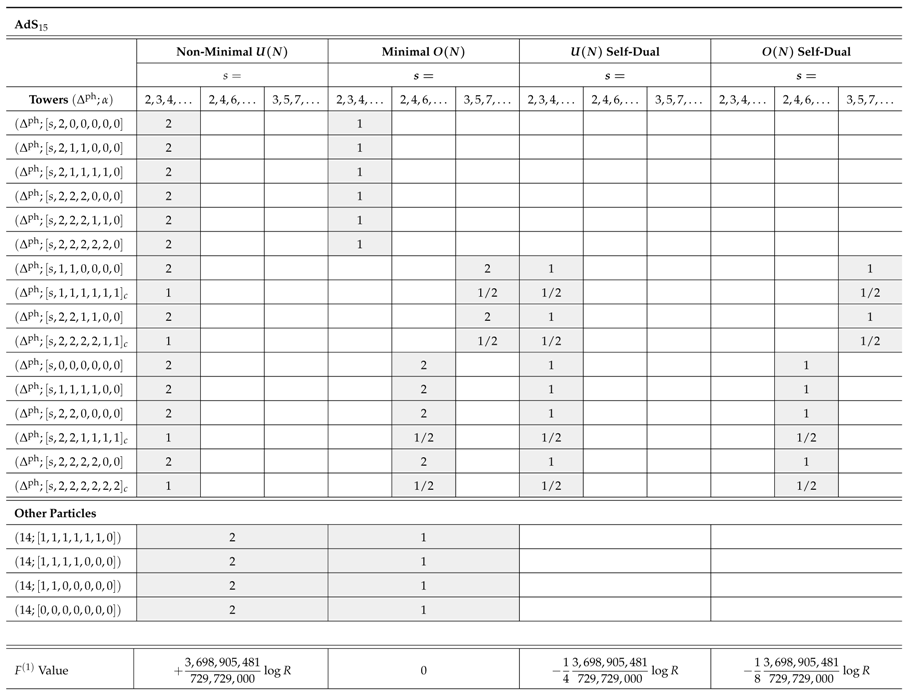
References
- Maldacena, J.M. The Large N Limit of Superconformal Field Theories and Supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge Theory Correlators from Non-Critical String Theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter Space and Holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Fradkin, E.; Vasiliev, M.A. On the Gravitational Interaction of Massless Higher Spin Fields. Phys. Lett. B 1987, 189, 89–95. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Consistent equation for interacting gauge fields of all spins in (3 + 1)-dimensions. Phys. Lett. B 1990, 243, 378–382. [Google Scholar] [CrossRef]
- Vasiliev, M.A. More on equations of motion for interacting massless fields of all spins in (3 + 1)-dimensions. Phys. Lett. B 1992, 285, 225–234. [Google Scholar] [CrossRef]
- Vasiliev, M. Nonlinear equations for symmetric massless higher spin fields in (A)dS(d). Phys. Lett. B 2003, 567, 139–151. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Higher spin superalgebras in any dimension and their representations. J. High Energy Phys. 2004, 2004, 046. [Google Scholar] [CrossRef]
- Giombi, S.; Yin, X. The Higher Spin/Vector Model Duality. J. Phys. A Math. Theor. 2013, 46, 214003. [Google Scholar] [CrossRef]
- Giombi, S. TASI Lectures on the Higher Spin-CFT Duality. In Proceedings of the 2015 Theoretical Advanced Study Institute in Elementary Particle Physics, Boulder, CO, USA, 1–26 June 2015; pp. 137–214. [Google Scholar]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213–219. [Google Scholar] [CrossRef]
- Sezgin, E.; Sundell, P. Holography in 4D (super) higher spin theories and a test via cubic scalar couplings. J. High Energy Phys. 2005, 2005, 044. [Google Scholar] [CrossRef]
- Leigh, R.G.; Petkou, A.C. Holography of the N = 1 higher-spin theory on AdS(4). J. High Energy Phys. 2003, 2003, 011. [Google Scholar] [CrossRef]
- Aharony, O.; Gur-Ari, G.; Yacoby, R. d = 3 Bosonic Vector Models Coupled to Chern-Simons Gauge Theories. J. High Energy Phys. 2012, 2012, 037. [Google Scholar] [CrossRef]
- Giombi, S.; Minwalla, S.; Prakash, S.; Trivedi, S.P.; Wadia, S.R.; Yin, X. Chern-Simons Theory with Vector Fermion Matter. Eur. Phys. J. C 2012, 72, 2112. [Google Scholar] [CrossRef]
- Beccaria, M.; Tseytlin, A.A. Higher spins in AdS5 at one loop: Vacuum energy, boundary conformal anomalies and AdS/CFT. J. High Energy Phys. 2014, 2014, 114. [Google Scholar] [CrossRef]
- Beccaria, M.; Tseytlin, A.A. Vectorial AdS5/CFT4 duality for spin-one boundary theory. J. Phys. A Math. Theor. 2014, 47, 492001. [Google Scholar] [CrossRef]
- Beccaria, M.; Macorini, G.; Tseytlin, A.A. Supergravity one-loop corrections on AdS7 and AdS3, higher spins and AdS/CFT. Nucl. Phys. B 2015, 892, 211–238. [Google Scholar] [CrossRef]
- Giombi, S.; Yin, X. Higher Spin Gauge Theory and Holography: The Three-Point Functions. J. High Energy Phys. 2010, 2010, 115. [Google Scholar] [CrossRef]
- Maldacena, J.; Zhiboedov, A. Constraining Conformal Field Theories with A Higher Spin Symmetry. J. Phys. A Math. Theor. 2013, 46, 214011. [Google Scholar] [CrossRef]
- Maldacena, J.; Zhiboedov, A. Constraining conformal field theories with a slightly broken higher spin symmetry. Class. Quantum Gravity 2013, 30, 104003. [Google Scholar] [CrossRef]
- Didenko, V.; Skvortsov, E. Towards higher-spin holography in ambient space of any dimension. J. Phys. A Math. Theor. 2013, 46, 214010. [Google Scholar] [CrossRef]
- Didenko, V.E.; Skvortsov, E.D. Exact higher-spin symmetry in CFT: All correlators in unbroken Vasiliev theory. J. High Energy Phys. 2013, 2013, 158. [Google Scholar] [CrossRef]
- Boulanger, N.; Kessel, P.; Skvortsov, E.D.; Taronna, M. Higher spin interactions in four-dimensions: Vasiliev versus Fronsdal. J. Phys. A Math. Theor. 2016, 49, 095402. [Google Scholar] [CrossRef]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Quartic AdS Interactions in Higher-Spin Gravity from Conformal Field Theory. J. High Energy Phys. 2015, 2015, 149. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R. One Loop Tests of Higher Spin AdS/CFT. J. High Energy Phys. 2013, 2013, 068. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Safdi, B.R. Higher Spin AdSd+1/CFTd at One Loop. Phys. Rev. D 2014, 89, 084004. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tseytlin, A.A. Partition Functions and Casimir Energies in Higher Spin AdSd+1/CFTd. Phys. Rev. D 2014, 90, 024048. [Google Scholar] [CrossRef]
- Jevicki, A.; Jin, K.; Yoon, J. 1/N and loop corrections in higher spin AdS4/CFT3 duality. Phys. Rev. D 2014, 89, 085039. [Google Scholar] [CrossRef]
- Zamolodchikov, A.B. Irreversibility of the Flux of the Renormalization Group in a 2D Field Theory. J. Exp. Theor. Phys. Lett. 1986, 43, 730–732. [Google Scholar]
- Cardy, J.L. Is There a c Theorem in Four-Dimensions? Phys. Lett. B 1988, 215, 749–752. [Google Scholar] [CrossRef]
- Komargodski, Z.; Schwimmer, A. On Renormalization Group Flows in Four Dimensions. J. High Energy Phys. 2011, 2011, 099. [Google Scholar] [CrossRef]
- Myers, R.C.; Sinha, A. Seeing a C-Theorem with Holography. Phys. Rev. D 2010, 82, 046006. [Google Scholar] [CrossRef]
- Jafferis, D.L.; Klebanov, I.R.; Pufu, S.S.; Safdi, B.R. Towards the F-Theorem: Field Theories on the Three-Sphere. J. High Energy Phys. 2011, 2011, 102. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Pufu, S.S.; Safdi, B.R. F-Theorem without Supersymmetry. J. High Energy Phys. 2011, 2011, 038. [Google Scholar] [CrossRef]
- Casini, H.; Huerta, M. On the RG running of the entanglement entropy of a circle. Phys. Rev. D 2012, 85, 125016. [Google Scholar] [CrossRef]
- Shenker, S.H.; Yin, X. Vector Models in the Singlet Sector at Finite Temperature. arXiv, 2011; arXiv:1109.3519. [Google Scholar]
- Sachdev, S.; Ye, J.-W. Gapless spin fluid ground state in a random, quantum Heisenberg magnet. Phys. Rev. Lett. 1993, 70, 3339. [Google Scholar] [CrossRef] [PubMed]
- Kitaev, A. A Simple Model of Quantum Holography. Available online: http://online.kitp.ucsb.edu/online/entangled15/kitaev/ and http://online.kitp.ucsb.edu/online/entangled15/kitaev2/ (accessed on 11 January 2018).
- Sachdev, S. Bekenstein-Hawking Entropy and Strange Metals. Phys. Rev. X 2015, 5, 041025. [Google Scholar] [CrossRef]
- Polchinski, J.; Rosenhaus, V. The Spectrum in the Sachdev-Ye-Kitaev Model. J. High Energy Phys. 2016, 2016, 1. [Google Scholar] [CrossRef]
- Jevicki, A.; Suzuki, K.; Yoon, J. Bi-Local Holography in the SYK Model. J. High Energy Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D.; Yang, Z. Conformal symmetry and its breaking in two dimensional Nearly Anti-de-Sitter space. Progr. Theor. Exp. Phys. 2016, 2016, 12C104. [Google Scholar] [CrossRef]
- Almheiri, A.; Polchinski, J. Models of AdS2 backreaction and holography. J. High Energy Phys. 2015, 2015, 014. [Google Scholar] [CrossRef]
- Fernando, S.; Gunaydin, M. Minimal unitary representation of 5d superconformal algebra F(4) and AdS6/CFT5 higher spin (super)-algebras. Nucl. Phys. B 2015, 890, 570–605. [Google Scholar] [CrossRef]
- Günaydin, M.; Skvortsov, E.D.; Tran, T. Exceptional F(4) higher-spin theory in AdS6 at one-loop and other tests of duality. J. High Energy Phys. 2016, 2016, 168. [Google Scholar] [CrossRef]
- Pang, Y.; Sezgin, E.; Zhu, Y. One Loop Tests of Supersymmetric Higher Spin AdS4/CFT3. Phys. Rev. D 2017, 95, 026008. [Google Scholar] [CrossRef]
- Camporesi, R. Zeta function regularization of one loop effective potentials in anti-de Sitter space-time. Phys. Rev. D 1991, 43, 3958–3965. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. Arbitrary spin effective potentials in anti-de Sitter space-time. Phys. Rev. D 1993, 47, 3339–3344. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. Spectral functions and zeta functions in hyperbolic spaces. J. Math. Phys. 1994, 35, 4217–4246. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. The Plancherel measure for p-forms in real hyperbolic spaces. J. Geom. Phys. 1994, 15, 57–94. [Google Scholar] [CrossRef]
- Flato, M.; Fronsdal, C. Quantum Field Theory of Singletons: The Rac. J. Math. Phys. 1981, 22, 1100. [Google Scholar] [CrossRef]
- Dolan, F. Character formulae and partition functions in higher dimensional conformal field theory. J. Math. Phys. 2006, 47, 062303. [Google Scholar] [CrossRef]
- Anselmi, D. Theory of higher spin tensor currents and central charges. Nucl. Phys. B 1999, 541, 323–368. [Google Scholar] [CrossRef]
- Anselmi, D. Higher spin current multiplets in operator product expansions. Class. Quantum Gravity 2000, 17, 1383–1400. [Google Scholar] [CrossRef]
- Alkalaev, K. Mixed-symmetry tensor conserved currents and AdS/CFT correspondence. J. Phys. A Math. Theor. 2013, 46, 214007. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R. Interpolating between a and F. J. High Energy Phys. 2015, 2015, 117. [Google Scholar] [CrossRef]
- Gaberdiel, M.R.; Gopakumar, R.; Saha, A. Quantum W-symmetry in AdS3. J. High Energy Phys. 2011, 2011, 1–22. [Google Scholar] [CrossRef]
- Gaberdiel, M.R.; Grumiller, D.; Vassilevich, D. Graviton 1-loop partition function for 3-dimensional massive gravity. J. High Energy Phys. 2010, 2010, 094. [Google Scholar] [CrossRef]
- Gupta, R.K.; Lal, S. Partition Functions for Higher-Spin theories in AdS. J. High Energy Phys. 2012, 2012, 071. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Pufu, S.S.; Safdi, B.R.; Tarnopolsky, G. AdS Description of Induced Higher-Spin Gauge Theory. J. High Energy Phys. 2013, 2013, 016. [Google Scholar] [CrossRef]
- Casini, H.; Huerta, M. Entanglement Entropy for the N-Sphere. Phys. Lett. B 2010, 694, 167–171. [Google Scholar] [CrossRef]
- Diaz, D.E.; Dorn, H. Partition functions and double-trace deformations in AdS/CFT. J. High Energy Phys. 2007, 2007, 046. [Google Scholar] [CrossRef]
- Casini, H.; Huerta, M.; Myers, R.C. Towards a Derivation of Holographic Entanglement Entropy. J. High Energy Phys. 2011, 2011, 036. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. Dictionary on Lie superalgebras. arXiv, 1996; arXiv:9607161. [Google Scholar]
- Van Proeyen, A. Tools for supersymmetry. Ann. Univer. Craiova Phys. 1999, 9, 1–48. [Google Scholar]
- Frappat, L.; Sciarrino, A.; Sorba, P. Dictionary on Lie Algebras and Superalgebras; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Cappelli, A.; D’Appollonio, G. On the trace anomaly as a measure of degrees of freedom. Phys. Lett. B 2000, 487, 87–95. [Google Scholar] [CrossRef]
| 1. | This theory may be coupled to the 5dChern–Simons gauge theory to impose the singlet constraint. |
| 2. | In the collective field approach to the bulk theory the action does exist, and the matching of free energies works by construction [29]. However, the precise connection of this formalism with the Vasiliev equations remains an open problem. |
| 3. | Let us note that one can also consider a “non-minimal” type-B model by starting with the free theory of N complex fermions (with N even), and imposing a singlet constraint on the spectrum (but not the symplectic Majorana condition on the fermions). This can be done in any d, and the resulting higher-spin theories are the fermionic analog of the symplectic type-A theories discussed in [26]. In AdS, one obtains this way a spectrum containing a parity odd scalar, one tower of higher-spin fields of all even spins , and three towers of odd-spin fields, as in the scalar case in [26]. One can analogously work out the spectra of such non-minimal type-B theories in higher dimensions, following similar steps as outlined in Section 3.2.1 for minimal theories. |
| 4. | The choice of the p-form is made to ensure that the current operators satisfy the unitary bound, as well as conformal invariance. |
| 5. | We choose the root above the unitarity bound. The alternate root corresponds to gauging the HS symmetry at the boundary [62]. |
| 6. | The heat-kernel is related to the spectral zeta-function by a Mellin transformation. |
| 7. | This can be thought as the representation that specifies the dual CFT operator. From AdS point of view, one may view as the little group for a massive particle in dimensions. |
| 8. | |
| 9. | As in the case of totally symmetric fields, the representation labeling the ghosts can be understood from CFT point of view from the structure of the character of the short representations of the conformal algebra and the corresponding null states, see [54]. |
| 10. | Note that, technically, for all Type B theories the field of spin in the tower of spins of representation is not a gauge field. However, for conciseness we still use the symbol for these fields; the corresponding ghost contribution is zero, so it does not make a practical difference. |
| 11. | To obtain this result, we note that in , complex conjugation flips the chirality of a Weyl spinor, while in the Weyl representation is self-conjugate. Therefore, in order to obtain invariant operators, we should use Equation (4.20) of [54] for , and Equation (4.23) of the same reference for . |
| 12. | As an example, consider the bilinear . If M is symmetric, this operator clearly vanishes. On the other hand, consider . In this case, if M is an antisymmetric matrix, then this is equal to . In turn, this means that , and so this operator is a total derivative and is not included in the spectrum of primaries. |
| 13. | Note that, had we tried to impose the standard Majorana condition, we would have retained the totally symmetric fields of all odd spins. Then, the spectrum would not include a graviton, i.e., the dual CFT would not have a stress tensor. |
| 14. | Similar shifts and scaling will be applied in the higher dimensional Type B cases, as well as the Type AB and C cases, and details of transformations to the Hurwitz-zeta function can be found in Appendix B.1. |
| 15. | With mass . |
| 16. | The factor of two in (76) just accounts for the fact that the representations are complex. |
| 17. | |
| 18. | For all Type C theories, the field of spin in the towers of spins of representation are not gauge fields, but we will still use the symbol for conciseness. See footnote 10 for similar remarks. |
| 19. | This corresponds to Equation (4.20) in [54]. This is because in complex conjugation maps self-dual to anti self-dual forms. |
| 20. | This corresponds to Equation (4.23) in [54]. |
| 21. | In that paper, an “averaged” regulator of was preferred for the Type A theory calculations, and it can be shown to give the same result as the regulators (97) and (98) that we will use in our calculations. In Type AB theories, however, it appears that “averaged” regulator does not work, and we will use the shifts defined in (97) and (98) in all theories consistently. |
| 22. | While not needed, the integral results for , can be identified with the Hurwitz-Lerch Phi function ,
|
| 23. | Alternatively, one could first write , evaluate the integral coming from the first term by analytic continuation in z, and the one coming from the second term directly at , since it converges. |
| 24. | |
| 25. | This is because of symmetry under . Any function symmetric under this exchange gives a zero contribution under the integral in (A2). |
| 26. | See Appendix D of [18] for a discussion of this. |
| 27. | This makes use of the identity,
|
| Type of Theory | Shift to | |
|---|---|---|
| Type A Theories | ||
| Non-Minimal : | No shift | |
| Minimal : | ||
| Type B Theories | ||
| Non-Minimal : | No shift | |
| Minimal | in (mod 8): | |
| in (mod 8): | ||
| Weyl Projection: | No shift | |
| Majorana–Weyl: | (mod 8): | |
| Type C Theories (p-Forms) | ||
| Non-minimal | : | |
| : | ||
| Minimal | : | |
| : | No shift | |
| Self-dual | : | |
| : | ||
| Self-dual | : | Not defined |
| : | ||
| Type of Theory | Shift to | |
|---|---|---|
| Type A Theories | ||
| Non-Minimal : | No shift | |
| Minimal : | ||
| Type B Theories | ||
| Non-Minimal : | Shifted by (14) | |
| Minimal | in (mod 8): | See Section 3.3.3 |
| in (mod 8): | See Section 3.3.3 | |

| d | (Minimal Type B) |
|---|---|
| 3 | |
| 5 | |
| 7 | |
| 9 | |
| 11 | |
| 13 | |
| 15 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giombi, S.; Klebanov, I.R.; Tan, Z.M. The ABC of Higher-Spin AdS/CFT. Universe 2018, 4, 18. https://doi.org/10.3390/universe4010018
Giombi S, Klebanov IR, Tan ZM. The ABC of Higher-Spin AdS/CFT. Universe. 2018; 4(1):18. https://doi.org/10.3390/universe4010018
Chicago/Turabian StyleGiombi, Simone, Igor R. Klebanov, and Zhong Ming Tan. 2018. "The ABC of Higher-Spin AdS/CFT" Universe 4, no. 1: 18. https://doi.org/10.3390/universe4010018
APA StyleGiombi, S., Klebanov, I. R., & Tan, Z. M. (2018). The ABC of Higher-Spin AdS/CFT. Universe, 4(1), 18. https://doi.org/10.3390/universe4010018




