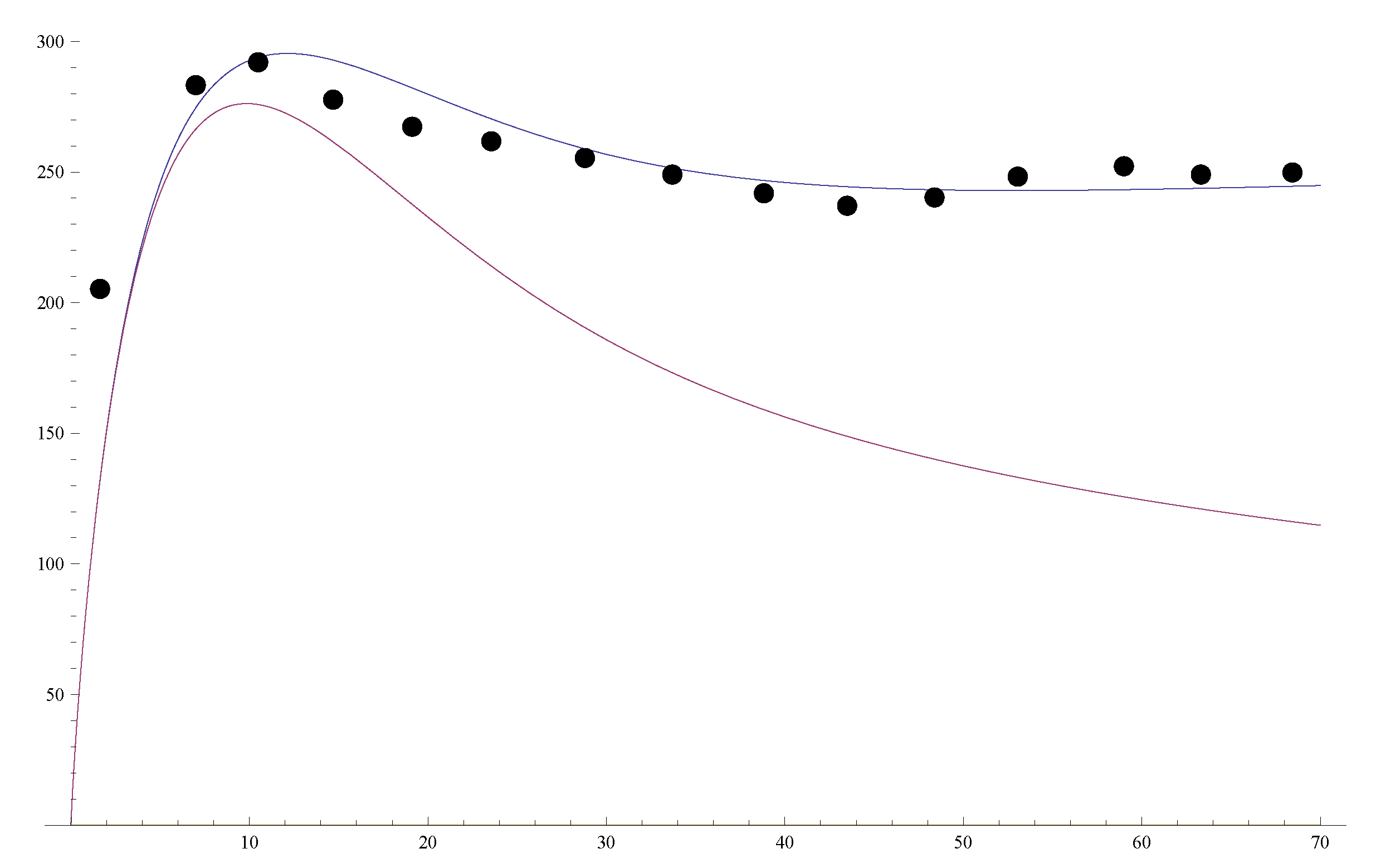1. Effective Three-Graviton Interaction
Regarding the well-known problems of dark matter and dark energy, numerous possibilities of modified gravity are considered (see, e.g., review [
1] and recent work [
2]). This approach assumes the existence of new effective interactions of the gravitational field in addition to the fundamental Einstein–Hilbert Lagrangian. In view of the extreme interest in the problem of modified gravity, we consider the possibility of the spontaneous generation of effective interactions in quantum gravity theory.
In the present talk
1, we discuss the possibility of an anomalous gravitational interaction in terms of non-perturbative effects of Einstein–Hilbert gravity. For this purpose, we rely on an approach induced by the N.N. Bogoliubov compensation principle [
4,
5]. In works [
6,
7,
8,
9,
10], this approach was applied to studies of the spontaneous generation of effective non-local interactions in renormalizable gauge theories. The approach is described in detail in a recent book [
11]. In particular, papers [
9,
10] deal with an application of the approach to the electroweak interaction and the possibility of the spontaneous generation of an effective anomalous three-boson interaction of the following form:
where
is the electroweak coupling. Here,
is a form-factor, which guarantees effective interaction (Equation (
1)) acting in a limited region of the momentum space. This form-factor is uniquely defined by the compensation equation of the Bogoliubov approach. We use an approximate scheme, the accuracy of which was estimated to be ≃
[
6]. Up to this precision, the approach gives unique results for physical parameters; thus we have no adjusting parameters in the scheme. The wouldbe existence of effective interaction (Equation (
1)) leads to important non-perturbative effects in the electroweak interaction. Its consequences were considered in works [
9,
10]. We note that the interaction by Equation (
1) was considered for a long period of time on phenomenological grounds [
12,
13].
We take the interaction by Equation (
1) as a leading hint for the choosing of an effective interaction in gravity theory. Considering links between vector non-abelian gauge theories and the theory of gravity, one can easily see that the gauge field
plays the same role as the Riemann curvature tensor
. Thus the anomalous interaction, which is strictly analogous to the interaction by Equation (
1), is the following:
Here,
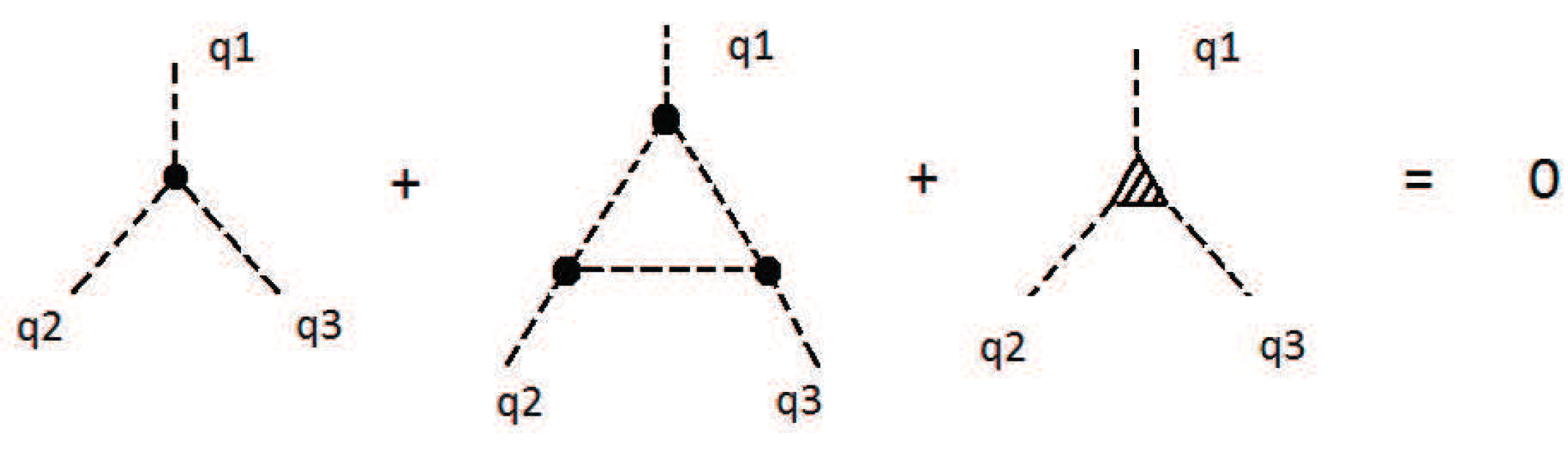
F is again some form-factor to be defined by a compensation equation. This equation corresponds to the diagrams of
Figure 1.
Performing calculations using FORM, we achieved the following integral equation with integrations in the Euclid momentum space:
where
is the inhomogeneous part of the equation, which in
Figure 1 is denoted by the striped triangle.
Assuming
, we obtain by successive differentiations of Equation (
3) a linear differential equation for
. Introducing the following new variable:
we have
the differential equation is equivalent to Equation (
3) with boundary conditions. Taking into account these conditions, we have the following solution (details can be found in work [
6]):
where
is a Meijer function [
14].
On the other hand, assuming
, we may calculate
from Equations (
6) and (
8), which gives
However, the form-factor
has to be unity at zero. Thus there is evidently an additional contribution to
, that is
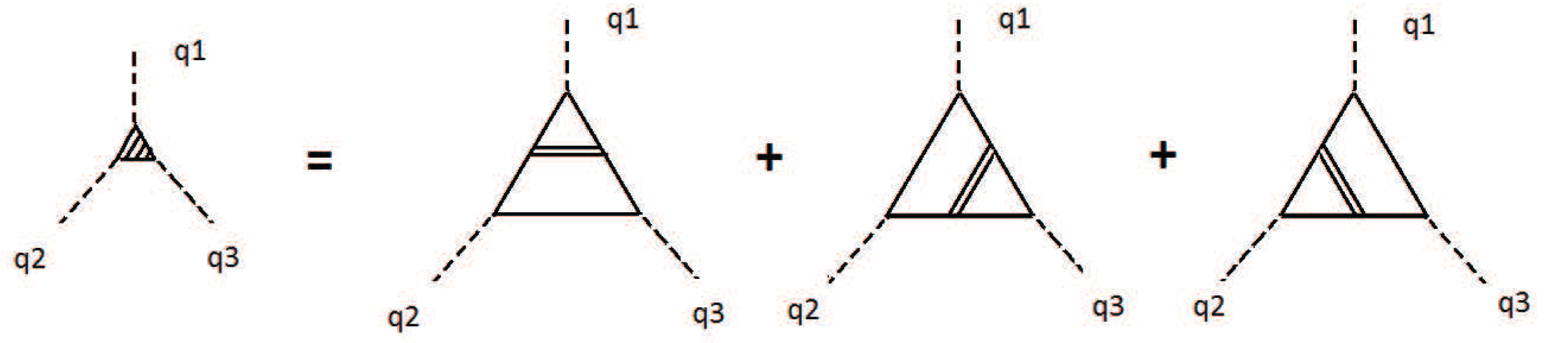
This contribution might be given by diagrams including matter fields, for example, by those being presented in
Figure 2. First of all, we draw attention to the presence of the
Z exchange in
Figure 2. The dominant contribution is provided by the lightest particles, namely, by neutrinos. The interaction of
Z with neutrinos contains the
matrix, and thus the Trace inevitably contains the antisymmetric tensor
, which is present in the interaction by Equation (
2). The vertex of a graviton interaction with a neutrino, as well as with any spinor field, is the following:
where
is connected with the Planck mass:
and
is the momentum of the incomingneutrino, while
is the momentum of the outgoing neutrino. We have an additional contribution to the electroweak interaction:
where according to the usual parametrization [
15], we have
We readily estimate that these diagrams give the following contribution to the inhomogeneous part of the equation:
where
is the usual gravitation coupling constant,
is the electroweak gauge constant, and
is a coefficient of the order of unity. From the main Equation (
3), we have the following condition:
Equation (
15) must be equal to
Then, on account of the number of neutrinos
and the previous relations (Equations (
3) and (
17)), we obtain the following estimate for the coupling constant of the effective interaction by Equation (
2)
G. In doing so, we have to bear in mind that the integral Equation (
3) is divided by a coupling constant
G as a result of the overall procedure of searching for non-trivial solutions of compensation equations. Thus we have
As a matter of fact, for the moment, we cannot substitute a reliable value for the average neutrino mass
into Equation (
18). We may safely assert that it is not zero because of the existence of the effect of neutrino oscillations. In any case, it may not be more than
eV (see data [
15]). In view of this, we have taken for the estimate just neutrinos as the particles having the smallest masses of all the particles giving a contribution to the coupling constant
G. It is evident that massless particles, namely photons and gluons, do not give a contribution because of the parity conservation of their interactions. To obtain a more definite connection between the two parameters
G and
, one needs perform difficult calculations, which will be done elsewhere. However our estimate (Equation (
18)) allows us to consider effects of the interaction by Equation (
2) and to conclude if it is advisable to continue studies in this direction.
With the physical mass of
Z and bearing in mind Equation (
12), where the Planck mass
1.22 × 10
GeV is very large, we understand that the possible value (Equation (
18)) is essentially larger than the seemingly natural value, which one can estimate under premise, so that only gravitational effects can define the quantity under study
The interaction by Equation (
2) due to a presence of the antisymmetric tensor
gives no contribution to spherically symmetric problems of gravitation (Schwartzschield solution, Friedmann solution, etc.). However, it could manifest itself in problems without spherical symmetry in a rotating system (e.g., a spiral galaxy). The considerable enhancement of the possible value of Equation (
18) in comparison to the natural value (Equation (
19)) by the following factor:
is quite remarkable and may lead to observable effects. Here we use also the estimation of the logarithm in Equation (
18).
The propagator of a graviton is the following [
16]:
It is important to note that the effective interaction by Equation (
2) is
P- and
T-non-invariant. This might be important for the consideration of baryon asymmetry of the universe, which inevitably needs a
T-odd interaction [
17].
2. A Model for a Running Gravity Coupling
We have considered the above wouldbe properties of quantum gravity. The theory itself contains a dimensional coupling constant:
In conventional quantum field theory, such a quantity corresponds to a running coupling, for example,
in QCD. Thus one should expect that the quantity of Equation (
22) is also the running coupling. However, quantum gravity theory is non-renormalizable. This means of course that perturbation theory does not work and we have no regular method to obtain an expression for the running coupling. Thus the application of a non-perturbative approach is necessary. As a matter of fact, in gauge theories of the Standard Model, contributions of a non-perturbative nature may also be present. We may refer just to the strong coupling
, in which the well-known non-physical Landau singularity appears in perturbative calculations. It is a general belief that non-perturbative contributions somehow eliminate this singularity. In particular, in work [
18], it is shown that the singularity is eliminated as a result of the spontaneous generation of an effective non-perturbative three-gluon interaction, which is analogous to Equation (
1). In any case, a discussion of possible running properties of gravity coupling (Equation (
22)) is worth attention. In this section, we consider a model for such running in view of obtaining an impression, if such searches are advisable.
Now, previous experience [
6,
7,
8,
9,
10,
11,
12,
13,
18,
19,
20,
21] has shown that solutions of compensation equations are usually expressed in terms of Meijer functions [
14]. Thus we use these useful functions in our attempts here. On the other hand, it is very important to have some hints as to the scale of the possible non-perturbative effects. Here, the example that is considered in the previous Section may be instructive. Namely, we see that in Equation (
18), both
and the neutrino mass
are present. That is the scale of the length dimension that, again with
eV, may be estimated as follows:
We see that this estimate gives a scale, which is appropriate to the size of a galaxy.
We now assume that the running Newton gravity coupling constant
, which is proportional to coupling
(Equation (
22)) depends on a distance in the following way:
where
is of the order of magnitude of
(Equation (
23)) and
is simply the well-known Newton constant. We use Meijer functions for representation of the effect, because in all cases of different problems, we encounter these functions in the momentum space. It is remarkable that the Fourier transform of a Meijer function is again a Meijer function. We choose the coefficients in Equation (
24) so that for
, and for
. The last asymptote corresponds to the accelerated expansion of the universe, which usually is prescribed to dark energy.
Now we apply Equation (
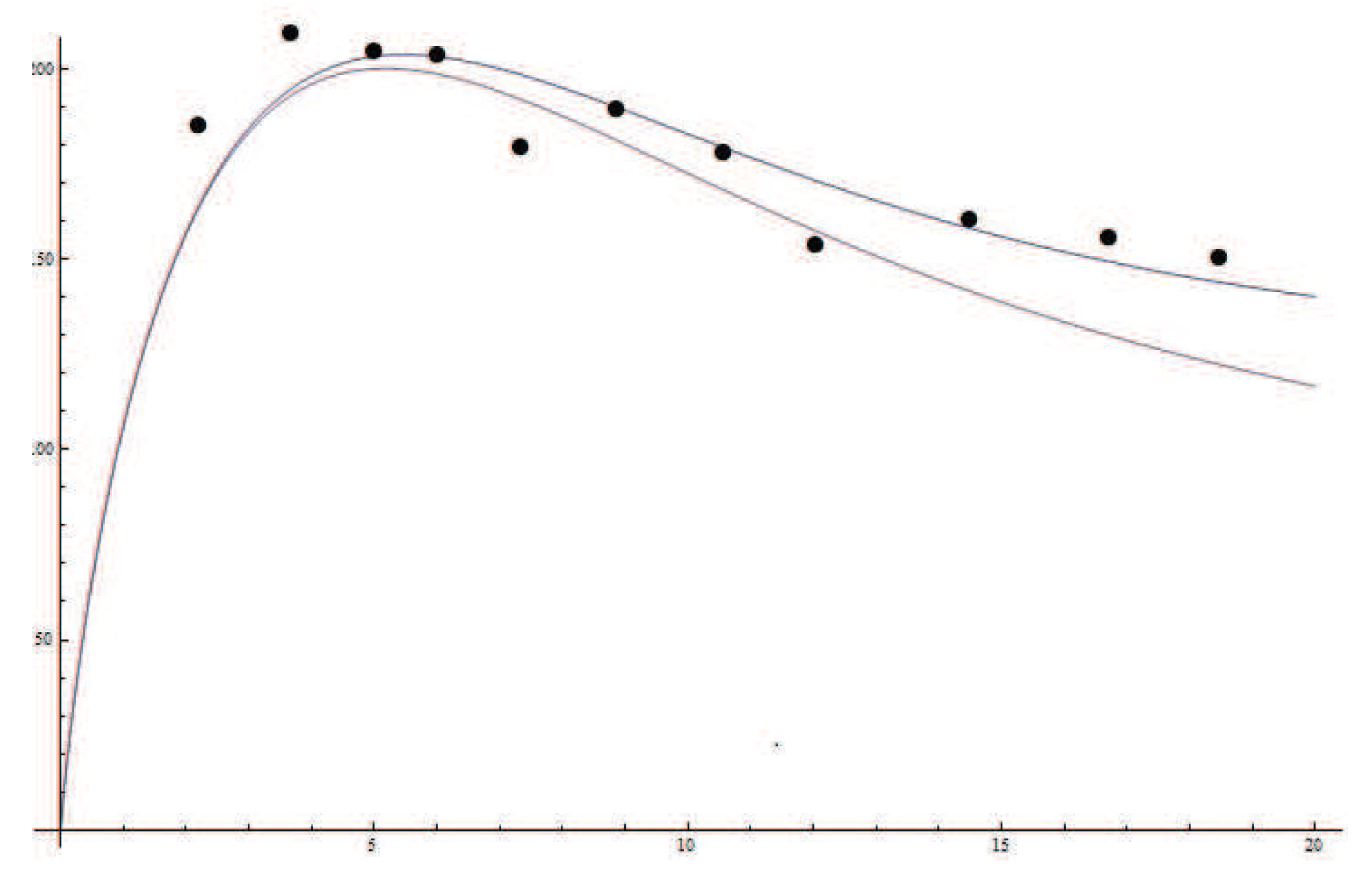
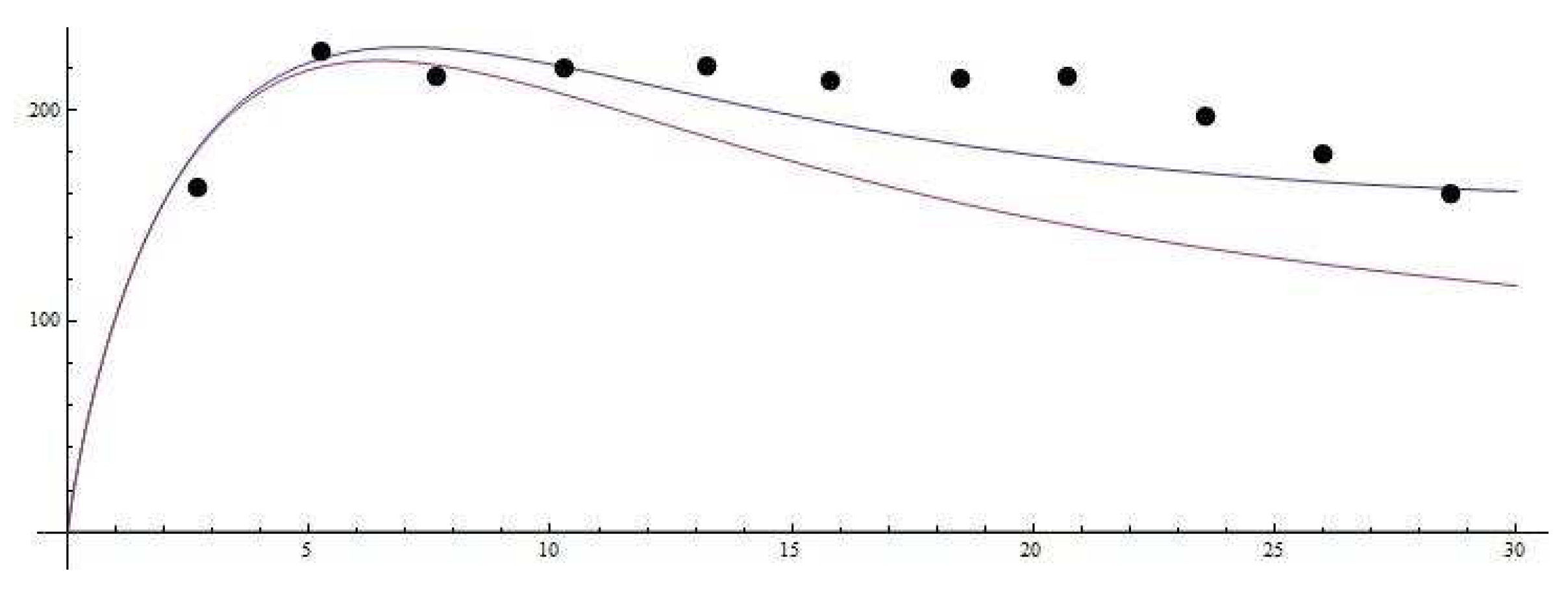
24) to the rotation curves of galaxies. We take
. We take for the rotation curve of a flat-disk galaxy the following expression:
where
is a galaxy mass in
,
is its radius in kpc, and
r is a distance in a rotation curve, also in kpc. Then we adjust the galaxy mass and radius to obtain a corresponding rotation curve. We have taken three galaxies as examples. The black spots in the figures denote observational data, taken from [
22]. The upper curves in the figures correspond to Equation (
25). The lower curves in the figures correspond to
(i.e., without our effect).
Galaxy NGC 6674,
;
Figure 3.
Galaxy NGC 3521,
;
Figure 4.
Galaxy NGC 2683,
;
Figure 5.