Abstract
We investigate the effect of intense magnetic fields on the -dimensional reduced- magnetohydrodynamical (MHD) expansion of hot and dense quark–gluon plasma (QGP) produced in = 200 GeV Au+Au collisions. For the sake of simplicity, we consider the case in which the magnetic field points in the direction perpendicular to the reaction plane. We also consider this field to be external, with energy density parametrized as a two-dimensional Gaussian. The width of the Gaussian along the directions orthogonal to the beam axis varies with the centrality of the collision. The dependence of the magnetic field on proper time () is parametrized for the case of zero and finite electrical conductivity of the QGP. We solve the equations of motion of ideal hydrodynamics for such an external magnetic field. For collisions with a non-zero impact parameter we observe a considerable increase in the elliptic-flow coefficient of in the presence of an external magnetic field, and the increment in is found to depend on the evolution and the initial magnitude of the magnetic field.
1. Introduction
Two positively charged heavy nuclei produce ultra-intense magnetic fields in collider experiments at the Relativistic Heavy Ion Collider (RHIC) and at the Large Hadron Collider (LHC); for example, for 200 GeV Au+Au collisions. The intensity of the magnetic field in the transverse plane grows approximately linearly with the center-of-mass energy () [1]. The corresponding electric field in the transverse plane also becomes very large, as it is enhanced by a Lorentz factor. Such intense electric and magnetic fields are believed to have a strong impact on the dynamics of high-energy heavy-ion collisions. For example, in the case of an imbalance in the number of left- versus right-handed fermions, a charge current is induced in the quark–gluon plasma (QGP), leading to the separation of electrical charges, which is known as the “chiral magnetic effect” (CME) [2].
Relativistic dissipative hydrodynamics has so far been successfully applied to explain the experimentally measured flow harmonics in heavy-ion collisions. The success of hydrodynamics implies that a QGP with small shear-viscosity-to-entropy-density ratio is formed in Au+Au collisions at top RHIC energies within a short time interval of ∼–. However, the possible effect of a magnetic field on the hydrodynamical evolution has so far not been studied extensively, except for some simplified cases, and most recently, using some approximate form of the equations of relativistic magnetohydrodynamics (MHD). Here, we study the -dimensional expansion of matter with vanishing magnetization in terms of the dynamics of a perfect fluid in the presence of an external magnetic field. We refer to this approach as “reduced MHD”, and we note that this is not a self-consistent solution of the full set of MHD equations, as we only use a parametrized form for the evolution of the magnetic field and do not solve Maxwell’s equations together with the conservation equations of energy and momentum. For the sake of simplicity, we also assume that the electrical conductivity is infinite (i.e., the ideal-MHD limit), as this allows us to eliminate the electric field in favour of the magnetic field. Assuming a perfectly conducting fluid under the influence of an external magnetic field still represents a reasonable first approximation, which, however, calls for a future improvement towards a self-consistent MHD solution. For some recent developments in the field of numerical and analytical study of relativistic MHD in high-energy heavy-ion collisions, see [3,4,5,6]. We also assume that the magnetic field only points into the y-direction. The goal of our study is to clarify how large the external magnetic field has to be and how slowly it has to decay in order to make a sizeable impact on the momentum anisotropy of charged particles. We use natural units , where and are the electric permittivity and magnetic permeability in vacuum, respectively, and the electric charge , where is the fine-structure constant. In these units, the quantity has dimension . Throughout the paper, the components of four-tensors are indicated with Greek indices, whereas three-vectors are denoted as boldface symbols. The metric tensor in flat spacetime is ().
2. Mathematical Setup and Results
In order to obtain the fluid evolution in the transverse plane, we assume a Bjorken-scaling expansion in the longitudinal direction so that, on account of boost invariance, we may restrict the discussion to the plane, where for reasons of symmetry, . In this case, it is advantageous to use Milne coordinates , where , and the metric tensor is given by . The energy–momentum conservation equations then take the following form:
where , , , and .
with . It is also worthwhile to note that the magnetic induction field is orthogonal to , where , and it is a space-like vector, .
The total energy–momentum tensor is given as ; here, and are fluid energy density, pressure, and four-velocity, respectively. From Equation (3), it is clear that a magnetic field along the y-direction decreases the total pressure. However, because driving the evolution of the fluid are the pressure gradients, a constant magnetic field does not lead to a change in the fluid acceleration. We note that for our case, the spatial distribution of the magnetic field (which is a very good approximation of the true magnetic field configuration of heavy-ion collisions) is such that the pressure gradients are enhanced (reduced) along the x (y)-axis, respectively. Ultimately, this will result in an increase in the momentum-space anisotropy of the fluid and consequently a larger elliptic flow.
We solve the energy–momentum conservation Equations (1)–(3) by using a modified version of the publicly available -dimensional perfect fluid dynamics code “AZHYDRO” [7]. In order to solve the system of coupled partial differential equations, a set of initial conditions needs to be specified. In particular, at the initial time of the hydrodynamical evolution, which we choose as , we set , while the initial energy density in the transverse plane is obtained from the Glauber model via the popular two-component form. We use the Equation of State (EoS) indicated as “s95p-PCE165-v0” in [8], which is constructed from lattice-QCD data at a high temperature and a partially chemically equilibrated hadron resonance gas at a low temperature. The kinetic freeze-out temperature is set to 130 MeV.
In a QGP with nonzero electrical conductivity, we parametrize the evolution of the magnetic field as in [9]:
Data from [9] are fitted by setting and adjusting the constants, giving , , and .
Figure 1 shows the temporal evolution of the magnetic field for various values of and , which gives a different initial value of the magnetic field and a different time evolution, respectively. The space variation of the magnetic field is taken as a two- dimensional Gaussian; for details see [10]. Figure 2 shows the elliptic-flow coefficient of as a function of the transverse momentum for non-central collisions with . The solid red line corresponds to the result for zero magnetic field; the dashed blue, dash-dotted magenta, and dotted black lines correspond to results with an external magnetic field for , and , respectively. It is clear from Figure 2 that changes in are noticeable when the magnetic field decay is substantially delayed. For the largest initial value of the magnetic field considered here, that is, for , we notice a considerable enhancement of the elliptic-flow coefficient, which can become as large as for (cf. dotted black line in Figure 2). A more realistic magnetic field evolution with initial leads to a smaller increase in the elliptic-flow coefficient (blue dashed line), thus highlighting that fairly realistic values of the magnetic field can have a considerable impact on the ellipticity of the flow of particles. Overall, these results and their implications for the understanding of the physics of ultra-relativistic heavy-ion collisions clearly call for the extension of this study towards a fully self-consistent MHD treatment of the evolution of hot and dense strongly interacting matter created in heavy-ion collisions.
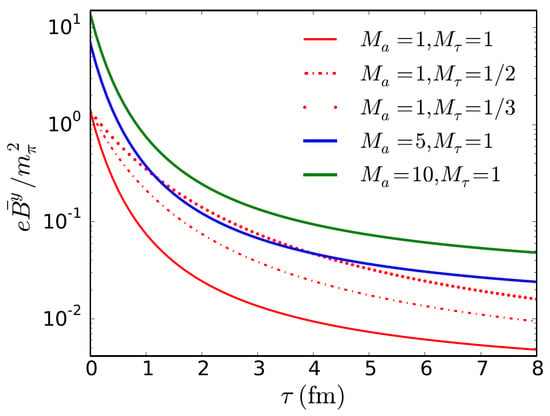
Figure 1.
Time evolution of in medium with a finite conductivity for collisions; the red solid line is a fit of data given in [9]. Other lines correspond to various values of fit parameter.
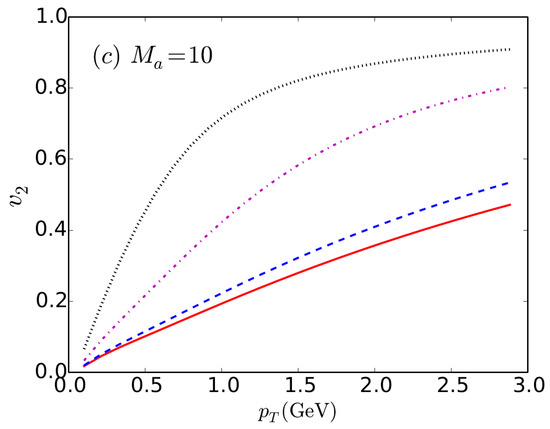
Figure 2.
The elliptic-flow coefficient for as a function of transverse momentum for collisions. The solid red line corresponds to the result for zero magnetic field; the dashed blue, dash-dotted magenta, and dotted black lines correspond to results for an external magnetic field with , and , respectively.
3. Discussion
We have investigated the effect of a strong external magnetic field on the evolution of matter created in Au+Au collisions within a -dimensional reduced-MHD description. In particular, we have assumed that the external magnetic field has only a non-vanishing component transverse to the reaction plane, and we have employed the spacetime variation suggested in [1,9].
A substantial change in the fluid velocity and, consequently, in the elliptic-flow coefficient of is observed when the magnetic field is sufficiently large, that is, for , or when a nonzero electrical conductivity of the QGP is accounted for such that it decays slowly, that is, for . Under these conditions, the elliptic-flow coefficient can become as large as for (all of the values reported refer to an initial magnetic field strength of ).
Our results were obtained under some simplifying assumptions: (1) We have used an analytic prescription for the magnetic-field evolution, but the latter should really be the result of a self-consistent solution of the full set of ideal-MHD equations. (2) We have considered event-averaged values for the initial energy density and the magnetic field, but both of these fluctuate event-to-event in reality. Indeed, a previous study [11] has shown that because of the event-by-event fluctuations of both the magnetic energy density and the fluid energy density, in some cases, the ratio of these two quantities can be ∼1. In such cases, the magnetic field will have a larger effect than considered here. (3) We have neglected the x component of the magnetic field, as we expect that in the present geometrical setup. Although this is a good approximation for peripheral collisions, in central collisions, is of the same order as when initial state fluctuation is considered. (4) We have considered a decay of the magnetic field pertaining to a constant electrical conductivity [9]. However, one should use the appropriate temperature-dependent electrical conductivity of the QGP. (5) We have considered here only perfect fluids [12], but it is important to also take into account dissipative corrections to the fluid evolution. We believe a nonzero magnetic field will have an impact on the value of the shear viscosity-to-entropy density ratio extracted from a comparison to experimental data. (6) We also note that the -dimensional hydrodynamics solution assumes the Bjorken-Hwa scaling solution along the longitudinal direction, which is a good approximation only at mid-rapidity and high-energy collisions, but a -dimensional calculation shows that a more realistic longitudinal-flow profile gives a different elliptic flow [13], and hence it is also important that one uses a proper longitudinal initial condition when studying the effect of the magnetic field at finite rapidities.
It will be interesting to study in a future work the corrections to the final particle spectra due to the magnetic field at and after freeze-out, as well as the investigation of smaller collision energies, for which the decay of the magnetic field is slower, and thus its impact on the fluid evolution is expected to be more pronounced.
Acknowledgments
V.R. is supported by the DST-INSPIRE faculty research grant, India.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Deng, W.T.; Huang, X.-G. Event-by-event generation of electromagnetic fields in heavy-ion collisions. Phys. Rev. C 2012, 85, 044907. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy ion collisions: “Event by event P and CP violation”. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef]
- Pang, L.G.; Endrödi, G.; Petersen, H. Magnetic-field-induced squeezing effect at energies available at the BNL Relativistic Heavy Ion Collider and at the CERN Large Hadron Collider. Phys. Rev. C 2016, 93, 044919. [Google Scholar] [CrossRef]
- Das, A.; Dave, S.S.; Saumia, P.S.; Srivastava, A.M. Effects of magnetic field on the plasma evolution in relativistic heavy-ion collisions. Phys. Rev. C 2017, 96, 034902. [Google Scholar] [CrossRef]
- Pu, S.; Yang, D.L. Transverse flow induced by inhomogeneous magnetic fields in the Bjorken expansion. Phys. Rev. D 2016, 93, 054042. [Google Scholar] [CrossRef]
- Inghirami, G.; Del Zanna, L.; Beraudo, A.; Moghaddam, M.H.; Becattini, F.; Bleicher, M. Numerical magneto-hydrodynamics for relativistic nuclear collisions. Eur. Phys. J. C 2016, 76, 659. [Google Scholar] [CrossRef]
- Kolb, P.F.; Sollfrank, J.; Heinz, U.W. Anisotropic flow from AGS to LHC energies. Phys. Lett. B 1999, 459, 667–673. [Google Scholar] [CrossRef]
- Huovinen, P.; Petreczky, P. QCD Equation of State and Hadron Resonance Gas. Nucl. Phys. A 2010, 837, 26–53. [Google Scholar] [CrossRef]
- Tuchin, K. Time and space dependence of the electromagnetic field in relativistic heavy-ion collisions. Phys. Rev. C 2013, 88, 024911. [Google Scholar] [CrossRef]
- Roy, V.; Pu, S.; Rezzolla, L.; Rischke, D.H. Effect of intense magnetic fields on reduced-MHD evolution in = 200 GeV Au + Au collisions. Arxiv, 2017; arXiv:1706.05326. [Google Scholar]
- Roy, V.; Pu, S. Event-by-event distribution of magnetic field energy over initial fluid energy density in = 200 GeV Au-Au collisions. Phys. Rev. C 2015, 92, 064902. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Pang, L.; Wang, Q.; Wang, X.N. Effects of initial flow velocity fluctuation in event-by-event (3+1)D hydrodynamics. Phys. Rev. C 2012, 86, 024911. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).