The Relation between Fundamental Constants and Particle Physics Parameters
Abstract
:1. Introduction
2. Observational Constraints
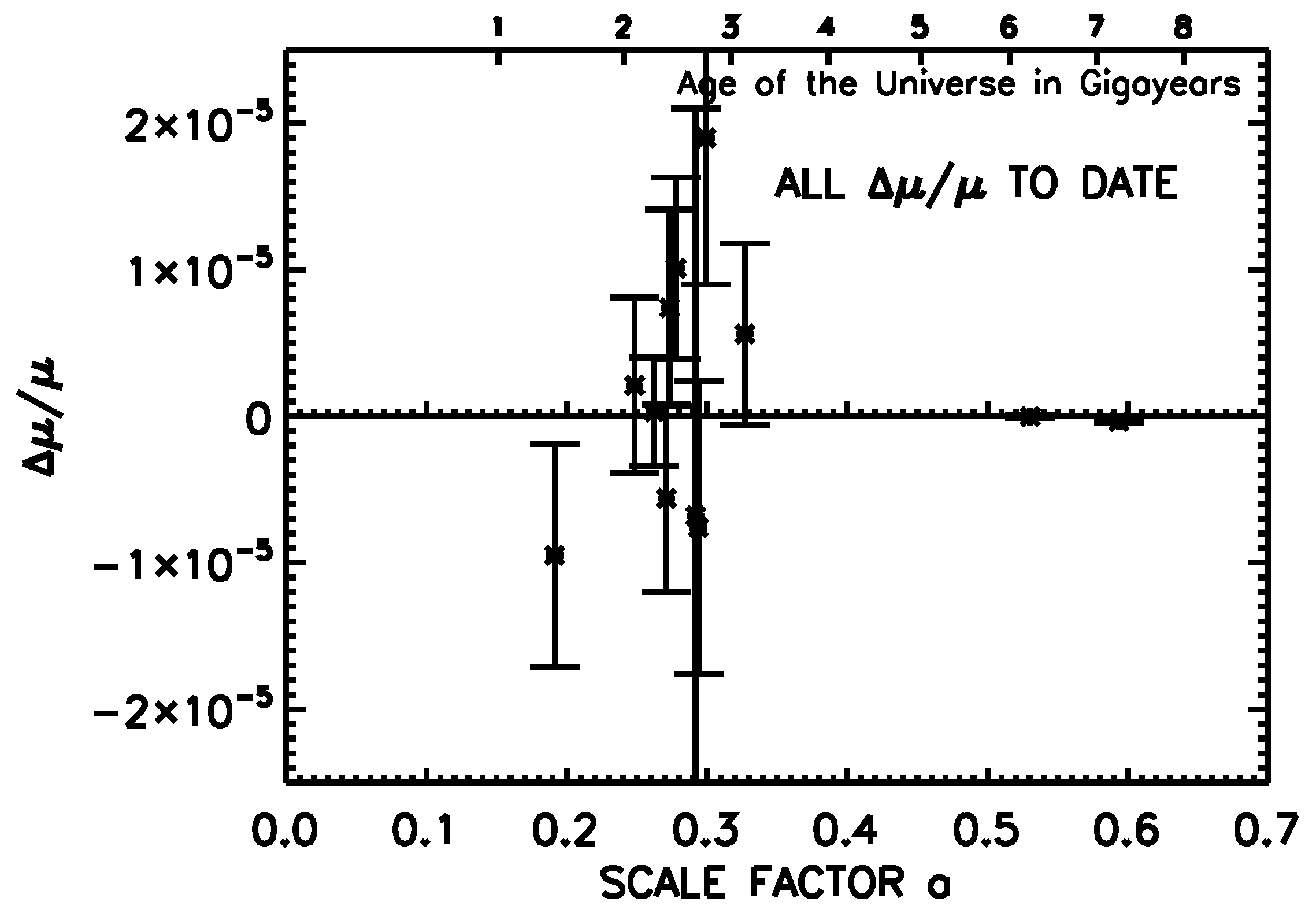
2.1. Constraints
2.2. α Constraints
3. The Dependence of Fundamental Constants on the Physics Parameters
3.1. The Proton to Electron Mass Ratio
3.2. The Fine Structure Constant
The Physics of R
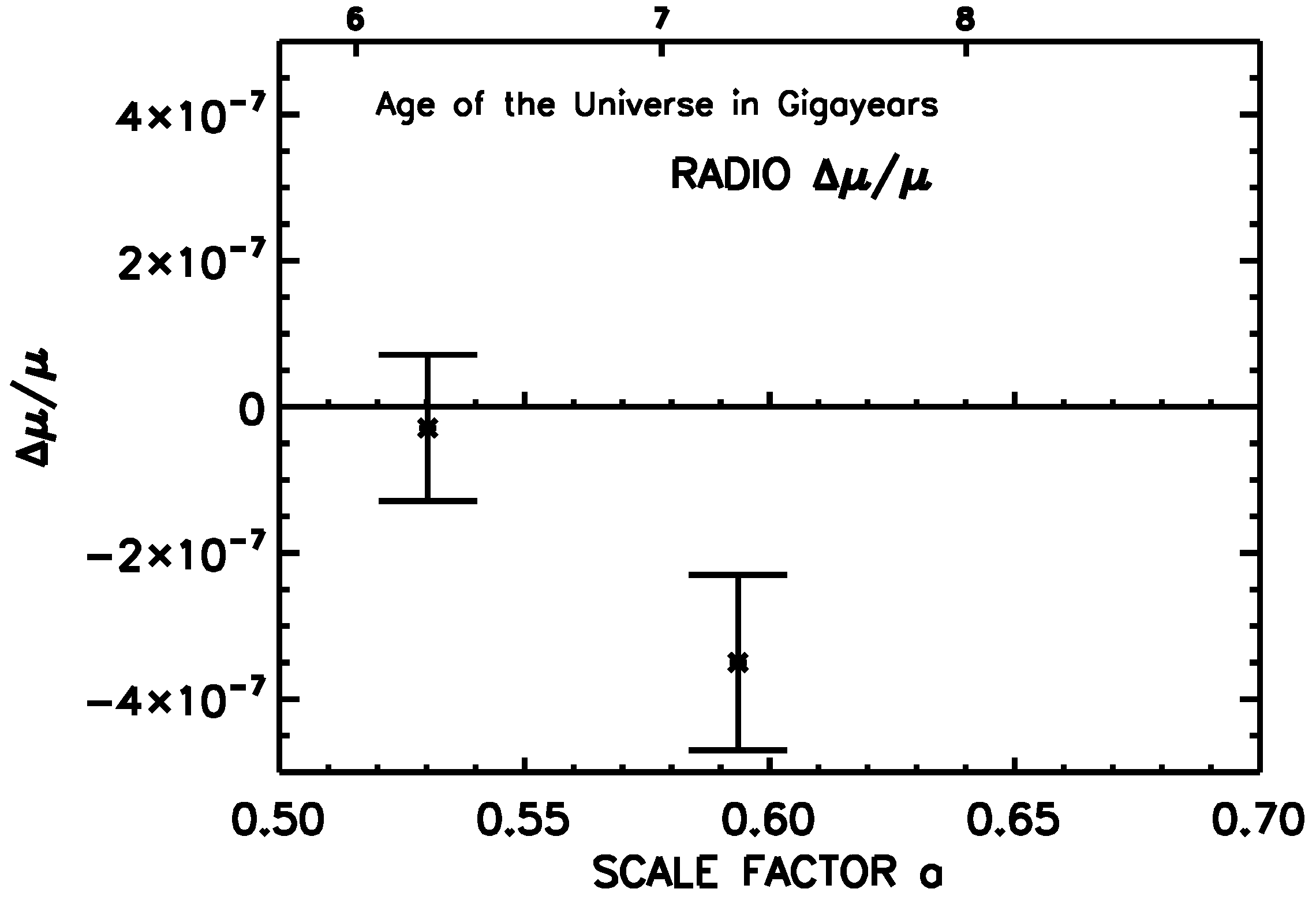
4. Observational Constraints on
Individual Constraints on and
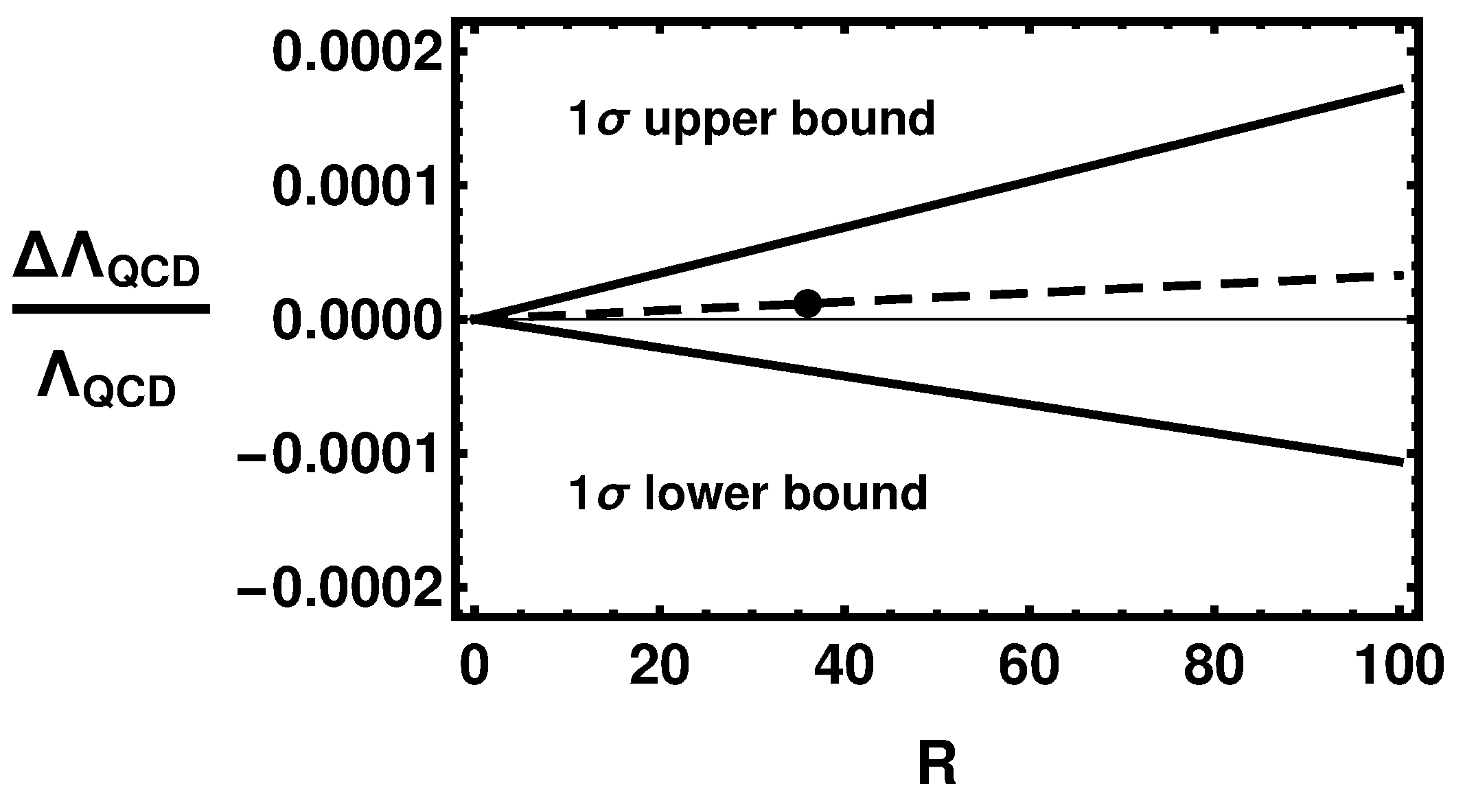
5. Constraints from a Given Model
6. A Model Dependent Limit on
7. Conclusions
Conflicts of Interest
References
- Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Dzuba, V.A.; Barrow, J.D.; Churchill, C.W.; Prochaska, J.X.; Wolfe, A.M. Further Evidence for Cosmological Evolution of the Fine Structure Constant. Phys. Rev. Lett. 2001, 87, 091301. [Google Scholar] [CrossRef] [PubMed]
- Calmet, X.; Fritzsch, H. Symmetry Breaking and Time Variation of Gauge Couplings. Phys. Lett. B 2002, 540, 173–178. [Google Scholar] [CrossRef]
- Campbell, B.A.; Olive, K.A. Nucleosynthesis and the time dependence of fundamental couplings. Phys. Lett. B 1995, 345, 429–434. [Google Scholar] [CrossRef]
- Chamoun, N.; Landou, S.J.; Mosquera, M.E.; Vucetich, H. Helium and deuterium abundances as a test for the time variation of the fine structure constant and the Higgs vacuum expectation value. J. Phys. G Nucl. Part. Phys. 2007, 34, 163–176. [Google Scholar] [CrossRef]
- Coc, A.; Nunes, N.J.; Olive, K.A.; Uzan, J.-P.; Vangioni, E. Coupled variations of fundamental couplings and primordial nucleosynthesis. Phys. Rev. D 2007, 76, 023511. [Google Scholar] [CrossRef]
- Dent, T. Fundamental constants and their variability in theories of High Energy Physics. Eur. Phys. J. Spec. Top. 2008, 163, 297–313. [Google Scholar] [CrossRef]
- Dine, M.; Nir, Y.; Raz, G.; Volansky, T. Time variations in the scale of grand unification. Phys. Rev. D 2003, 67, 015009. [Google Scholar] [CrossRef]
- Langacker, P.; Segre, G.; Strassler, M.J. Implications of gauge unification for time variation of the fine structure constant. Phys. Lett. B 2002, 528, 121–128. [Google Scholar] [CrossRef]
- Langacker, P. Time Variation of Fundamental Constants as a Probe of New Physics. Int. J. Mod. Phys. A 2004, 19, 157–165. [Google Scholar] [CrossRef]
- Uzan, J.-P. Varying constants, Gravitation and Cosmology. Living Rev. Relativ. 2011, 14, 2. [Google Scholar] [CrossRef]
- Thompson, R.I. The Determination of the Electron to Proton Inertial Mass Ratio via Molecular Transitions. Astrophys. Lett. 1975, 15, 3–4. [Google Scholar]
- Kanekar, N.; Ubachs, W.; Menten, K.M.; Bagdonaite, J.; Brunthaler, A.; Henkel, C.; Muller, S.; Bethlem, H.L.; Dapra, M. Constraints on changes in the proton-electron mass ratio using methanol lines. Mon. Not. R. Astron. Soc. 2015, 448, L104–L108. [Google Scholar] [CrossRef]
- Bagdonaite, J.; Ubachs, W.; Murphy, M.T.; Whitmore, J.B. Constraint on a Varying Proton-Electron Mass Ratio 1.5 Billion Years after the Big Bang. Phys. Rev. Lett. 2015, 114, 071301. [Google Scholar] [CrossRef] [PubMed]
- Wendt, M.; Reimers, D. Variability of the proton-to-electron mass ratio on cosmological scales. Eur. Phys. J. Spec. Top. 2008, 163, 197–206. [Google Scholar] [CrossRef]
- King, J.A.; Murphy, M.T.; Ubachs, W.; Webb, J.K. New constraint on cosmological variation of the proton-to-electron mass ratio from Q0528-250. Mon. Not. R. Astron. Soc. 2011, 417, 3010–3024. [Google Scholar] [CrossRef] [Green Version]
- Vasquez, F.A.; Rahamani, H.; Noterdaeme, N.; Petitjean, P.; Srianand, R.; Ledoux, C. Molecular hydrogen in the zabs = 2:66 damped Lyman-alpha absorber towards Q J 0643-5041. Astron. Astrophys. 2014, 562, A88. [Google Scholar]
- King, J.A.; Webb, J.K.; Murphy, M.T.; Carswell, R.F. Stringent Null Constraint on Cosmological Evolution of the Proton-to-Electron Mass Ratio. Phys. Rev. Lett. 2008, 101, 251304. [Google Scholar] [CrossRef] [PubMed]
- Bagdonaite, J.; Murphy, M.T.; Kaper, L.; Ubachs, W. Constraint on a variation of the proton-to-electron mass ratio from H2 absorption towards quasar Q2348-011. Mon. Not. R. Astron. Soc. 2012, 421, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, H.; Wendt, M.; Srianand, R.; Noterdaeme, P.; Petitjean, P.; Molaro, P.; Whitmore, J.B.; Murphy, M.T.; Centurion, M.; Fathivavsari, H.; et al. The UVES large program for testing fundamental physics—II. Constraints on a change in μ towards quasar HE 0027-1836. Mon. Not. R. Astron. Soc. 2013, 435, 861–878. [Google Scholar] [CrossRef]
- Dapra, M.; van der Laan, M.; Murphy, M.T.; Ubachs, W. Constraint on a varying proton-to-electron mass ratio from H2 and HD absorption at zabs = 2.34. arXiv, 2016; arXiv:1611.05191v2. [Google Scholar]
- Malec, A.L.; Buning, R.; Murphy, M.T.; Milutinovic, N.; Ellison, S.L.; Prochaska, J.X.; Kaper, L.; Tumlinson, J.; Carswell, R.F.; Ubachs, W. Keck telescope constraint on cosmological variation of the proton-to-electron mass ratio. Mon. Not. R. Astron. Soc. 2010, 403, 1541–1555. [Google Scholar] [CrossRef]
- Kanekar, N. Constraining Changes in the Proton–Electron Mass Ratio with Inversiona and Rotational Lines. Astrophys. J. Lett. 2011, 728, L12. [Google Scholar] [CrossRef]
- Webb, J.K.; King, J.A.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B. Indications of a spatial variation of the fine structure constant. Phys. Rev. Lett. 2011, 107, 191101. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.T.; Malec, A.; Prochaska, J.X. Precise limits on cosmological variability of the fine-structure constant with zinc and chromium quasar absorption lines. Mon. Not. R. Astron. Soc. 2016, 461, 2461–2479. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thompson, R.I. The Relation between Fundamental Constants and Particle Physics Parameters. Universe 2017, 3, 6. https://doi.org/10.3390/universe3010006
Thompson RI. The Relation between Fundamental Constants and Particle Physics Parameters. Universe. 2017; 3(1):6. https://doi.org/10.3390/universe3010006
Chicago/Turabian StyleThompson, Rodger I. 2017. "The Relation between Fundamental Constants and Particle Physics Parameters" Universe 3, no. 1: 6. https://doi.org/10.3390/universe3010006
APA StyleThompson, R. I. (2017). The Relation between Fundamental Constants and Particle Physics Parameters. Universe, 3(1), 6. https://doi.org/10.3390/universe3010006





