Cosmological Perturbations in Phantom Dark Energy Models
Abstract
:1. Introduction
- i
- ii
- iii
2. Background Models
- i
- ii
- The LR abrupt event model: an event of the type LR [11,12,13] can be caused by a perfect fluid whose EoS and energy density can be written as [12]where . In order to fix the free parameters of this model, we use the results obtained in [12], where the authors use the data given by the Supernova Cosmology Project [25,26] to constrain the parameters: , , and .
- iii
- The LSBR abrupt event model: the event denominated as LSBR can be induced by a perfect fluid whose EoS deviates from that of a cosmological constant by adding a constant parameter [14]. Therefore, the corresponding EoS and energy density in terms of the scale factor can be written asNote that plays the role of a cosmological constant. In this case, we have chosen the numerical value taken in [14]: , while for and , we have used the same values as in the case for the BR.
3. Perturbed Equations
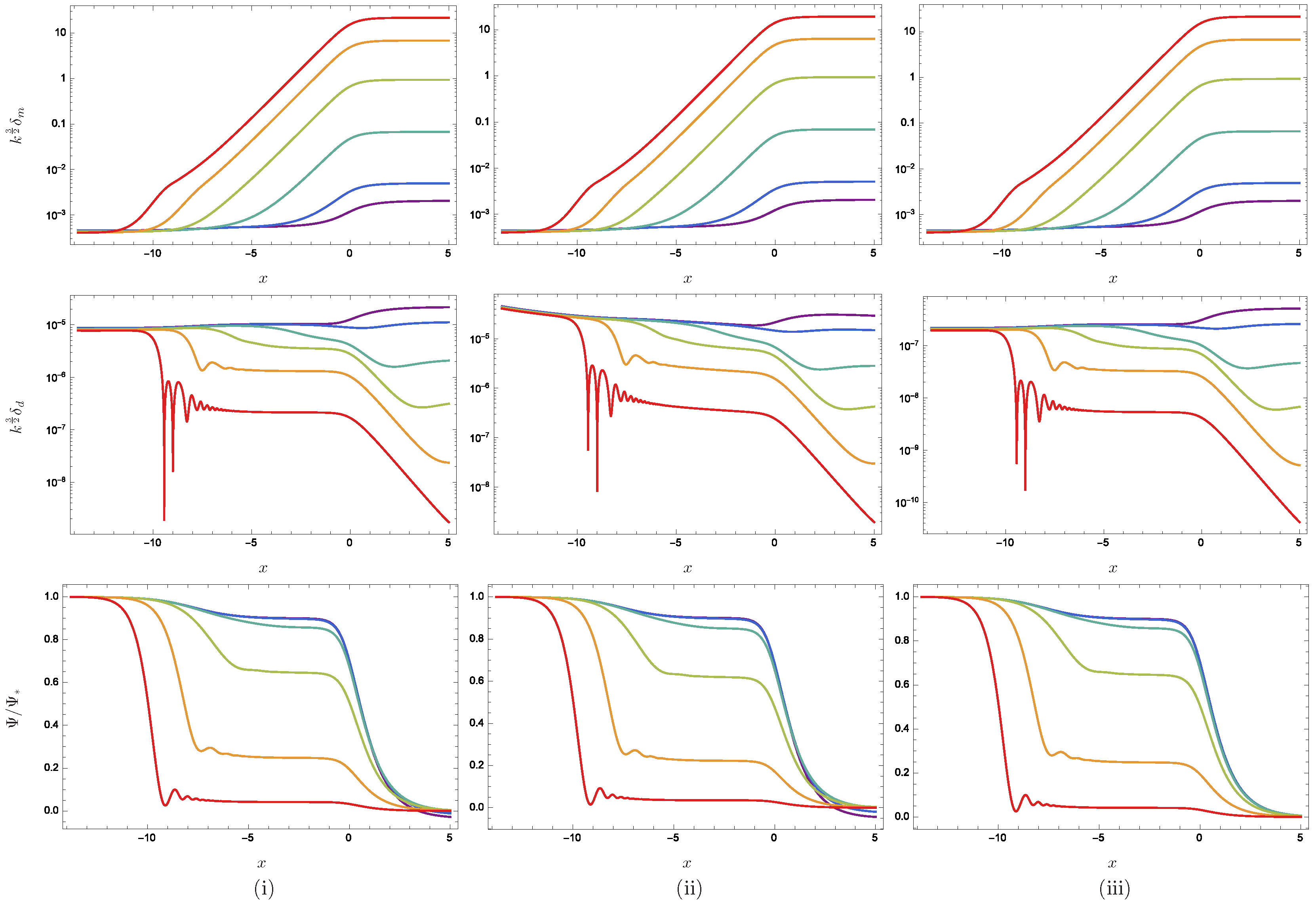
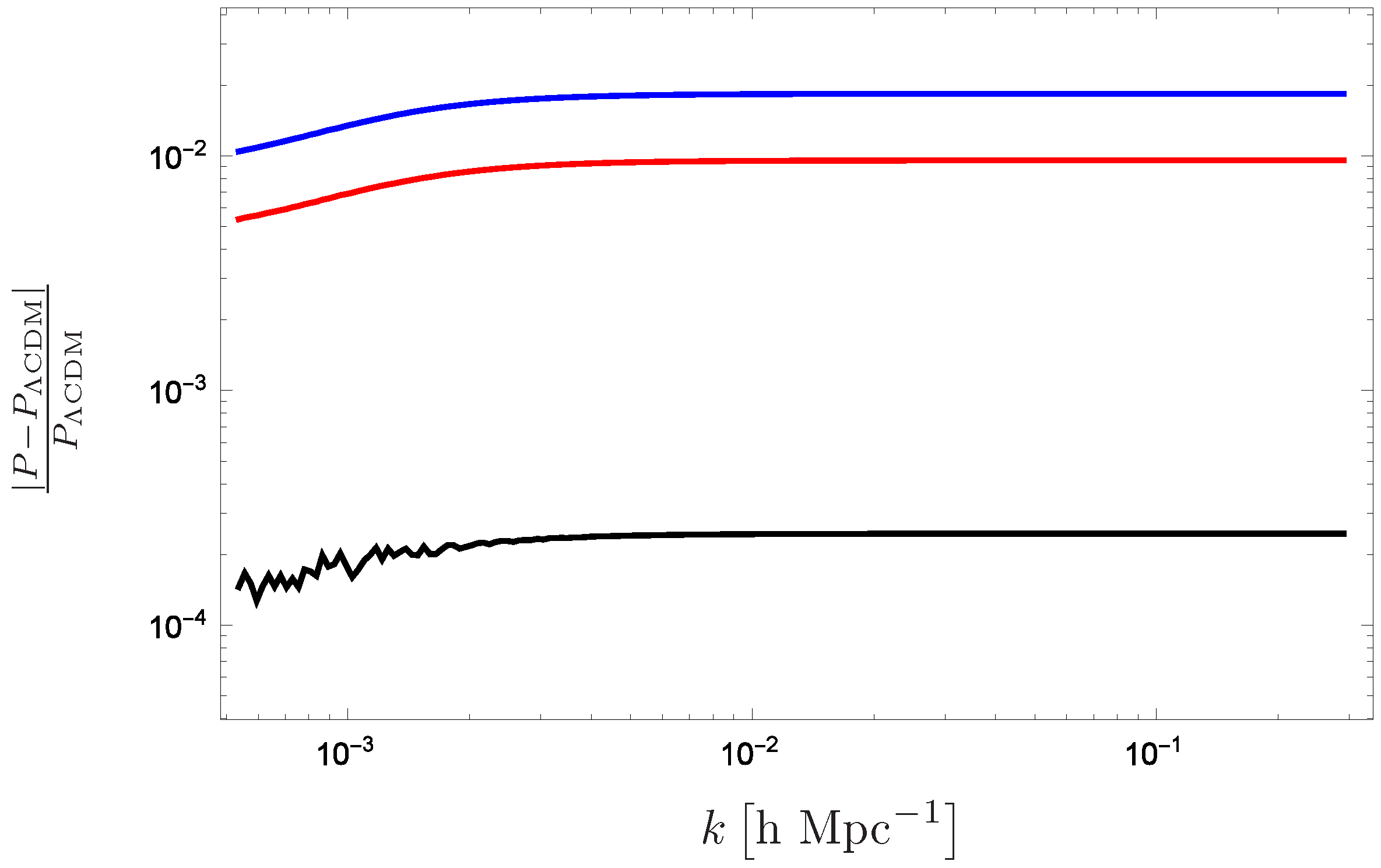
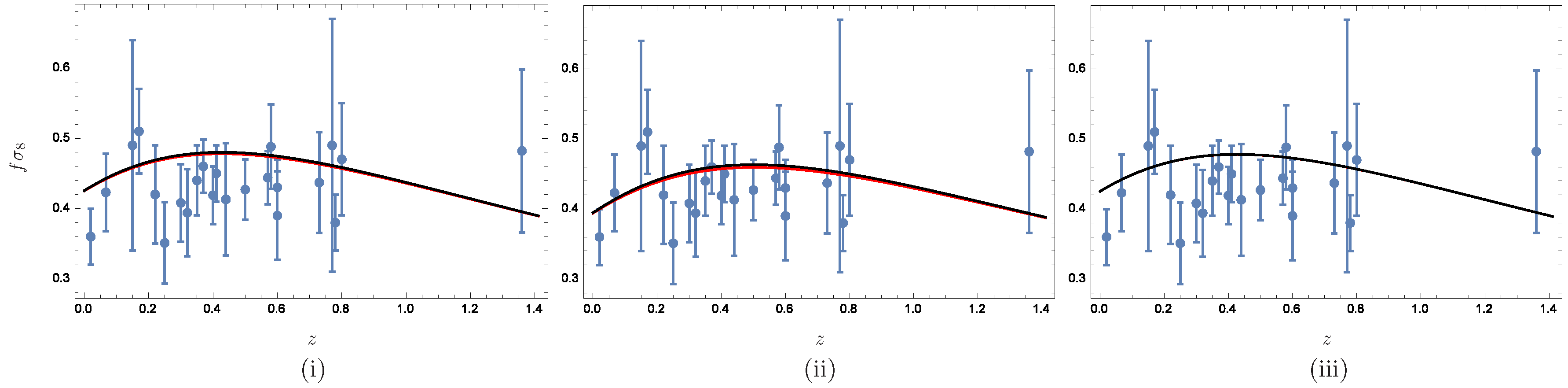
4. Results
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S. Supernova Cosmology Project Collaboration. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2015, 594, A13. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.I.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer Science & Business Media: New York, NY, USA, 2011; Volume 170. [Google Scholar]
- Morais, J.; Bouhmadi-López, M.; Capozziello, S. Can f (R) gravity contribute to (dark) radiation? J. Cosmol. Astropart. Phys. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Future and origin of our universe: Modern view. Grav. Cosmol. 2000, 6, 157–163. [Google Scholar]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than -1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]
- González-Díaz, P.F. K-essential phantom energy: Doomsday around the corner? Phys. Lett. B 2003, 586, 1–4. [Google Scholar] [CrossRef]
- Ruzmaikina, T.; Ruzmaikin, A.A. Quadratic corrections to the Lagrangian density of the gravitational field and the singularity. Sov. Phys. JETP 1970, 30, 372. [Google Scholar]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. The Little Rip. Phys. Rev. D 2011, 84, 063003. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J.; Nojiri, S.; Odintsov, S.D.; Scherrer, R.J. Models for Little Rip Dark Energy. Phys. Lett. B 2012, 708, 204–211. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Errahmani, A.; Martín-Moruno, P.; Ouali, T.; Tavakoli, Y. The little sibling of the big rip singularity. Int. J. Mod. Phys. D 2015, 24, 1550078. [Google Scholar] [CrossRef]
- Morais, J.; Bouhmadi-López, M.; Sravan Kumar, K.; Marto, J.; Tavakoli, Y. Interacting 3-form dark energy models: Distinguishing interactions and avoiding the Little Sibling of the Big Rip. Phys. Dark Universe 2017, 15, 7–30. [Google Scholar] [CrossRef]
- Da̧browski, M.P.; Kiefer, C.; Sandhöfer, B. Quantum phantom cosmology. Phys. Rev. D 2006, 74, 044022. [Google Scholar] [CrossRef]
- Albarran, I.; Bouhmadi-López, M. Quantisation of the holographic Ricci dark energy model. J. Cosmol. Astropart. Phys. 2015, 2015, 51. [Google Scholar] [CrossRef]
- Albarran, I.; Bouhmadi-López, M.; Cabral, F.; Martín-Moruno, P. The quantum realm of the “Little Sibling” of the Big Rip singularity. J. Cosmol. Astropart. Phys. 2015, 2015, 44. [Google Scholar] [CrossRef]
- Albarran, I.; Bouhmadi-López, M.; Kiefer, C.; Marto, J.; Vargas Moniz, P. Classical and quantum cosmology of the little rip abrupt event. Phys. Rev. D 2016, 94, 063536. [Google Scholar] [CrossRef]
- Balcerzak, A.; Denkiewicz, T. Density preturbations in a finite scale factor singularity universe. Phys. Rev. D 2012, 86, 023522. [Google Scholar] [CrossRef]
- Denkiewicz, T. Dark energy and dark matter perturbations in singular universes. J. Cosmol. Astropart. Phys. 2015, 2015, 37. [Google Scholar] [CrossRef]
- Denkiewicz, T. Dynamical dark energy models with singularities in the view of the forthcoming results of the growth observations. arXiv 2015. [Google Scholar]
- Astashenok, A.V.; Odintsov, S.D. Confronting dark energy models mimicking ΛCDM epoch with observational constraints: Future cosmological perturbations decay or future Rip? Phys. Lett. B 2013, 718, 1194–1202. [Google Scholar] [CrossRef]
- Planck 2015 Results: Cosmological Parameter Tables. Available online: https://wiki.cosmos.esa.int/planckpla2015/images/0/07/Params_table_2015_limit95.pdf (accessed on 28 February 2017).
- WMAP Cosmological Parameters. Available online: http://lambda.gsfc.nasa.gov/product/map/dr4/params/lcdm_sz_lens_wmap7_bao_h0.cfm (accessed on 28 February 2017).
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and Light Curves of Six Type Ia Supernovae at 0.511 < z < 1.12 and the Union2 Compilation (The Supernova Cosmology Project). Astrophys. J. 2010, 716, 712–738. [Google Scholar]
- Kurki-Suonio, H. Cosmological Perturbation Theory; Lecture Notes; University of Helsinki: Helsinki, Finland, 2003. [Google Scholar]
- Bardeen, J.M. Gauge-invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882. [Google Scholar] [CrossRef]
- Bean, R.; Dore, O. Probing dark energy perturbations: The Dark energy equation of state and speed of sound as measured by WMAP. Phys. Rev. D 2004, 69, 083503. [Google Scholar] [CrossRef]
- Väliviita, J.; Majerotto, E.; Maartens, R. Large-scale instability in interacting dark energy and dark matter fluids. J. Cosmol. Astropart. Phys. 2008, 2008, 20. [Google Scholar] [CrossRef]
- Ballesteros, G.; Lesgourgues, J. Dark energy with non-adiabatic sound speed: Initial conditions and detectability. J. Cosmol. Astropart. Phys. 2010, 2010, 14. [Google Scholar] [CrossRef]
- Wang, Y.; Percival, W.; Cimatti, A.; Mukherjee, P.; Guzzo, L.; Baugh, C.M.; Carbone, C.; Franzetti, P.; Garilli, B.; Geach, J.E.; et al. Designing a space-based galaxy redshift survey to probe dark energy. Mon. Not. R. Astron. Soc. 2010, 409, 737–749. [Google Scholar] [CrossRef]
- Albarran, I.; Bouhmadi-López, M.; Morais, J. Cosmological perturbations in an effective and genuinely phantom dark energy Universe. arXiv 2016. [Google Scholar]
- 1.In this work we disregard any anisotropy at the linear level of the scalar perturbations, therefore, from this point onward we will set [27].
- 2.From now on, all perturbed quantities referred to in the manuscript represent the Fourier transform action of such perturbations, even though no specific notation is used, e.g., , where k is the wave-number.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albarran, I.; Bouhmadi-López, M.; Morais, J. Cosmological Perturbations in Phantom Dark Energy Models. Universe 2017, 3, 22. https://doi.org/10.3390/universe3010022
Albarran I, Bouhmadi-López M, Morais J. Cosmological Perturbations in Phantom Dark Energy Models. Universe. 2017; 3(1):22. https://doi.org/10.3390/universe3010022
Chicago/Turabian StyleAlbarran, Imanol, Mariam Bouhmadi-López, and João Morais. 2017. "Cosmological Perturbations in Phantom Dark Energy Models" Universe 3, no. 1: 22. https://doi.org/10.3390/universe3010022
APA StyleAlbarran, I., Bouhmadi-López, M., & Morais, J. (2017). Cosmological Perturbations in Phantom Dark Energy Models. Universe, 3(1), 22. https://doi.org/10.3390/universe3010022




