Abstract
We review the concept of ‘noncommutative spacetime’ approached from an operational stand-point and explain how to endow it with suitable geometrical structures. The latter involves i.a. the causal structure, which we illustrate with a simple—‘almost-commutative’—example. Furthermore, we trace the footprints of noncommutive geometry in the foundations of quantum field theory.
1. Introduction
The idea that spacetime may be quantised was first pondered by Werner Heisenberg in the 1930s (see [1] for a historical review). His proposal was motivated by the urgency of providing a suitable regularisation for quantum electrodynamics. The first concrete model of a quantum spacetime, based on a noncommutative algebra of ‘coordinates’, was constructed by Hartland Snyder in 1949 [2] and extended by Chen-Ning Yang shortly afterwards [3]. With the development of the renormalisation theory, the concept of quantum spacetime became, however, less popular.
The revival of Heisenberg’s idea came in the late 1990s with the development of noncommutative geometry [4,5,6]. The latter is an advanced mathematical theory sinking its roots in functional analysis and differential geometry. It permits one to equip noncommutative algebras with differential calculi, compatible with their inherent topology [7,8,9].
Meanwhile, on the physical side, it became clear that the concept of a point-like event is an idealisation—untenable in the presence of quantum fields. This is because particles can never be strictly localised [10,11,12] and, more generally, quantum states cannot be distinguished by means of observables in a very small region of spacetime (cf. [13], p. 131).
Nowadays, there exists a plethora of models of noncommutative (i.e., quantum) spacetimes. Most of them are connected with some quantum gravity theory and founded on the postulate that there exists a fundamental length-scale in Nature, which is of the order of Planck length m (see, for instance, [14] for a comprehensive review).
The ‘hypothesis of noncommutative spacetime’ is, however, plagued with serious conceptual problems (cf. for instance, [15]). Firstly, one needs to adjust the very notions of space and time. This is not only a philosophical problem, but also a practical one: we need a reasonable physical quantity to parametrise the observed evolution of various phenomena. Secondly, the classical spacetime has an inherent Lorentzian geometry, which determines, in particular, the causal relations between the events. This raises the question: Are noncommutative spacetimes also geometric in any suitable mathematical sense? This riddle not only affects the expected quantum gravity theory, but in fact any quantum field theory, as the latter are deeply rooted in the principles of locality and causality.
In this short review we advocate a somewhat different approach to noncommutative spacetime (cf. [16,17]), based on an operational viewpoint. We argue that the latter provides a conceptually transparent framework, although this comes at the price of involving rather abstract mathematical structures. In the next section we introduce the language of -algebras and provide a short survey of the operational viewpoint on noncommutative spacetime. Subsequently, we briefly sketch the rudiments of noncommutative geometry à la Connes [4]. Next, we discuss the notion of causality suitable in this context, summarising the outcome of our recent works [18,19,20,21,22,23,24,25,26]. Finally, we explain how the presumed noncommutative structure of spacetime extorts a modification of the axioms of quantum field theory and thus might yield empirical consequences.
2. Noncommutative Spacetime—An Operational Approach
The operational viewpoint on physics is founded on the Heisenberg cut (cf. for instance, [13, p. 3]), which divides the world into the system and an observer capable of making measurements. Any physicist longing to model a given physical phenomenon should have at his disposal a suitable set of observables, i.e., measurable quantities. These need not, in general, have definite numerical values, but could be associated with measurements, the outcomes of which are probabilistic—as indeed happens in quantum mechanics. The system, on the other hand, can find itself in different states. The statistical results of measurements of a given observable will depend on the state of the system. Note that the outcomes of any reasonable measurement in any state should be finite, hence the observables should be bounded in an appropriate sense.
The natural mathematical structure of the set of observables is that of a -algebra [13,27,28] (see, e.g., [29,30] for mathematical details). The latter is a (complex) vector space closed under multiplication and involution operations. In addition to the algebraic structure, -algebras are equipped with a suitable topology, which we shall shortly describe.
A state of the modelled system should attribute to a given observable a real number, which corresponds to the statistical outcome of a certain experiment. In terms of mathematics, it means that a state ρ of the system should be a positive linear functional on . The number is then the expectation value of the observable in the state ρ. Since such a quantity should be finite, ρ needs to be normalised, what is conveniently implemented by demanding that , where is the unit element of 1. The set of all states on , i.e., positive linear functionals normalised to 1, will be denoted by .
Let us now turn to the topological structures of the sets of observables and states. Since the expectation values are finite, one can define a natural norm on : . This norm, on top of its usual algebraic features, possesses an additional property: for any , . completed in such a norm constitutes a -algebra of observables. The norm can then be carried over to equipping it with an induced (weak-) topology.
Note that once we have identified the complete algebra of observables modelling a given system, its states are determined by the algebraic structure of . Indeed, for all must imply , i.e., “the observables separate the states” (cf. [27, Section 1.3]). Furthermore, is a convex set and, by the Krein–Milman theorem, it has extreme points called the pure states. In other words, any state in can be written as a convex combination of the elements of —the set of pure states on .
The -algebraic incarnation of the operational paradigm provides a rigorous unified framework to study both classical physics and quantum mechanics [27,28] and, with a bit more effort, general quantum field theory [13]. If classical objects are being modelled, the corresponding -algebra of observables is commutative, what reflects the fact that all possible measurements are mutually compatible. This is no longer true in the quantum realm, ergo a suitable must be noncommutative.
A pivotal concept in functional analysis is the Gelfand representation, which shows that every commutative -algebra is isomorphic to the algebra of continuous complex-valued functions (vanishing at infinity) on some locally compact topological space X. Moreover, is homeomorphic to X itself and comprises all (Radon) probability measures on X. This mathematical feature corresponds to the fact that all uncertainties in classical physics come from our subjective lack of knowledge, which forces us to effectively model the system in terms of mixed, rather than pure states. In principle, we could however make sharper and sharper measurements of an observable , in such a way that the uncertainty
would become arbitrarily small. In fact, for , for any pure state δ.
In quantum systems, the multiplication of different observables will not, in general, be commutative. This means that, on top of the inevitable experimental inaccuracies, there exist some objective uncertainties. For instance, if is the -algebra composed of bounded functions of the position and momentum operators (cf. [31]), then there is no state in , for which both and vanish [27, Section 3.6]. Nevertheless, the uncertainties of the observables and independently can be made arbitrarily small.
The idea that the measurements of a particle’s position and momentum are incompatible was postulated by Heisenberg on the basis of theoretical considerations [32] and verified experimentally some four decades later [33]. Hence, the empirical fact that some operations are mutually incompatible leads to the conclusion that physical systems ought to be modelled by noncommutative algebras of observables.
In the same spirit, Sergio Doplicher, Klaus Fredenhagen and John E. Roberts argued [16,17] that the measurements of spacetime localisation of any phenomenon are in fact mutually incompatible. This is because any attempts of acute localisation would cause extreme energy condensation in a small volume of space, which in turn would lead to black hole formation, so that the desired information would become irreversibly trapped under the event horizon. This argumentation leads to the following heuristic uncertainties
which can indeed be derived from (an algebra of operators affiliated with) a -algebra. It is important to stress that the argument of Doplicher, Fredenhagen and Roberts is not based on any new physical principle, but solely on the gravitational collapse described by classical General Relativity.
Adopting the operational viewpoint on physics, one is thus lead to the conclusion that a spacetime should be modelled by a noncommutative -algebra , rather than the commutative one—. But what becomes of the spacetime itself? On the strength of Gelfand duality, one can recover as the space of pure states of the algebra . It is therefore natural to regard the ‘noncommutative spacetime’ as the space of pure states of the noncommutative algebra (cf. [17, p. 188]). But, the classical spacetime we experience in macroscopic phenomena is more than just a topological space—it has an inherent geometry.
3. Noncommutative Geometry à la Connes
As advertised in the Introduction, the programme of extending the classical differential geometry to an abstract algebraic setting flowered in the 1990s. One of its most prominent avenues is the noncommutative geometry à la Connes [4]. It emerged from recognising the pivotal role played by the Dirac operators in modern geometry [34]. The archetype of a Dirac operator is the differential operator acting on spinors, encountered in the celebrated Dirac equation. It turns out that operators of such type appear naturally in a much more general framework involving interactions modelled by connections on vector bundles over curved manifolds. Moreover, the (generalised) Dirac operators carry a surprising amount of information about the geometry of the underlying space [34,35]. This interplay between the geometry and the algebra of operators inspired the following abstract notion, which is the cornerstone of Connes’ noncommutative geometry:
Definition 1.
A (unital) spectral triple consists of
- —a dense -subalgebra of a -algebra ;
- —a separable Hilbert space with a faithful representation via bounded operators;
- —an unbounded self-adjoint operator on with a compact resolvent.
These three elements are tied together with the requirement that the operator extends to a bounded operator on for all .
The demand that should be a dense subalgebra of reflects the fact comprises ‘smooth’ elements of , which do not form a -algebra on their own. It guarantees, in particular, that the notion of a state on is sound and . On the other hand, the existence of a faithful representation of is guaranteed by the Gelfand–Naimark–Segal construction. It is standard to omit the symbol π once the representation has been fixed.
The key element of Connes’ approach is the operator , which provides the actual geometry. It has to play along with the algebra , so the demand ought to be regarded as a compatibility condition between and , with serving as a common ground for the two of them. Intuitively, can be regarded as a differential of an element (more precisely, a one-form [4]).
Example 1.
Let be a compact Riemannian manifold with a spin structure. Then
- —the algebra of smooth functions on ,
- —the space of square summable sections of the spinor bundle S over ,
- —the (curved) Dirac operator associated with S,
If is even-dimensional, then the spinors over are chiral and the Hilbert space decomposes as via the chirality operator , i.e., , for .
The above example illustrates a commutative spectral triple, i.e., based on a commutative algebra . A strong motivation behind the structure encapsulated in Definition 1 is provided by the celebrated Connes’ Reconstruction Theorem [36]. It states that, under some additional technical assumptions, every commutative spectral triple emerges from a spin Riemannian manifold. This can be seen as a far-reaching generalisation of the Gelfand representation, allowing one to recover the entire differential and metric structure of a topological space from purely algebraic data.
The point of noncommutative geometry is, however, to venture beyond the commutative world. An easy noncommutative example is provided by matrix algebras:
Example 2.
Let for some and let be any selfadjoint element of . Then, and , together with , constitute a spectral triple.
More generally, any finite (complex) -algebra, (which, by the Wedderburn Theorem, can always be written as ) admits a number of compatible Dirac operators, which can be classified [37] (see also [38, Section 2.5]). This example is, in an appropriate sense, 0-dimensional, as the Hilbert space is finite dimensional.
The two above examples can be put together to yield an almost-commutative geometry:
Example 3.
Let and be as in Examples 1 and 2 respectively and let be even dimensional. Then = , , is a spectral triple.
Almost commutative geometries are the primary terrain for the application of Connes’ noncommutative geometry in particle physics [38,39] and cosmology [40,41]. However, the landscape of Connes noncommutative geometry is much broader. It includes various classical ‘pathological’ spaces, such as fractals [42], isospectral deformations [43] (in particular the celebrated noncommutative torus [7,44]) or quantum groups [45] and their homogeneous spaces [46].
When it comes to the physical applications, the Reader might be worried about the adjectives “compact” and “Riemannian” lurking in Example 1, as spacetimes are typically only locally compact and possess an indefinite metric. Indeed, although all three constituents: , and can be equally well defined on a locally compact Lorentzian manifold , the operator would seldom have a compact resolvent. Whereas the problem of non-compactness is mild and can be circumvented [47], the issue of signature is more serious. Nevertheless, the programme of pseudo-Riemannian noncommutative geometry is being developed by several authors [18,48,49,50,51,52,53,54,55,56,57,58,59,60]. At the level of technical details, this venture is far from being complete, but on the conceptual side it is sharp. The vital difference with the standard approach is the commitment of a Krein space [61], which is a Hilbert space equipped additionally with an indefinite inner product.
Commutative Lorentzian spectral triples can be constructed from globally hyperbolic spacetimes, as in Example 1. In this context, is a Krein space [62] with the Hermitian inner product and the natural, Lorentz invariant, indefinite inner product , with denoting the Hermitian first flat gamma matrix.
The concept of almost-commutative geometry naturally carries over to the Lorentzian setting [19,57] and the noncommutative examples include the Moyal–Minkowski spectral triple [53,63].
4. Causality in Noncommutative Spacetimes
The noncommutative geometry presented in the previous section was planted on the algebra of observables. It can thus be seen as a ‘Heisenberg picture of geometry’. To obtain the usual—‘Schrödinger’—picture, we need to transfer the geometry onto the space of (pure) states on :
Definition 2.
A noncommutative spacetime is the space of pure states on a noncommutative -algebra , the geometry of which is governed by a Lorentzian spectal triple .
How does this come about in practice? In the framework of Riemannian spectral triples, the operator defines a (pseudo)distance on the space of states [4,64]:
For a commutative spectral triple with and , Formula (1) yields precisely the geodesic distance on (see [52] for a pedagogical derivation), i.e.,
The distance function on Lorentzian manifolds has much more cumbersome analytical properties than its Riemannian counterpart (for instance, it can be infinite or discontinuous [65]). In [18] we proposed an analogue of Formula (1), but its equality to the classical Lorentzian distance function is proven only for Minkowski spacetime. Moreover, whereas in the Riemannian case the distance function uniquely determines the metric on globally (on the strength of the Myers–Steenrod Theorem), in the Lorentzian context such a reconstruction is, in general, only available locally—in convex normal neighbourhoods (cf. [65, Chapter 4]).
On the other hand, Lorentzian manifolds admit a causal structure, which determines the metric up to a conformal factor and provides an unique insight into the global structure of the spacetime at hand. In [18] we have shown that the causal structure of a given spacetime can be recovered from the purely algebraic data of the associated Lorentzian spectral triple and generalised to the noncommutative realm.
Definition 3.
Let be a Lorentzian spectral triple. For two states we define
If is constructed from a globally hyperbolic spacetime , then [18, Theorem 7] shows that on the relation defined by (2) is indeed exactly the causal relation determined by the Lorentzian metric2. Moreover, Definition 3 designates a well-defined partial order in full generality of noncommutative spacetimes, whenever there are enough elements in satisfying the condition on the RHS of (2) to separate the states in (cf. [18, Proposition 6]).
We shall now illustrate the implications of Definition 3 on a simple almost-commutative spacetime. Let be a globally hyperbolic spacetime and the associated Lorentzian spectral triple. We form an almost-commutative spectral triple as follows (see [22] for the full story):
for some free parameter .
Note that is actually a commutative algebra and , thus the noncommutative spacetime at hand can be seen as two disjoint copies (‘sheets’) of the classical spacetime . However, although the spacetime geometry on each copy is classical, the off-diagonal part of the operator allows one to ‘jump’ between the sheets. This peculiarity is attested by the following result [22, Theorem 9] and illustrated on Figure 1.
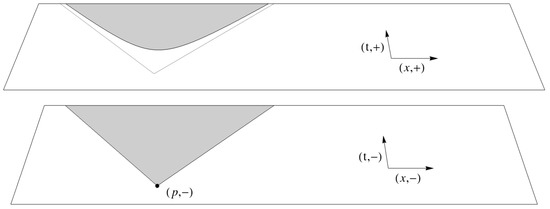
Figure 1.
The causal structure of a two-sheeted 2-dim Minkowski spacetime. The shaded region illustrates the causal future of the event .
Theorem 1.
Let be the proper time along a causal curve in M. Two states are causally related with if and only if
Observe that the boundary of the cone on the upper sheet has the same shape as a mass hyperboloid . This fact has recently been related to the dispersion relation of massive fermions [68]. Even more curiously, the numerical value , which becomes once the physical dimensions are (unambiguously) restored, is precisely the half-period of Zitterbewegung [69,70]—the trembling motion of a massive Dirac fermion. This remarkable concurrence, along with its physical implications, has been explored in [26].
5. The Foundations of Quantum Field Theory Revisited
In this report we have reviewed the concept of a noncommutative spacetime approached from an operational angle. We showed that such conceived noncommutative spacetime has an inherent—noncommutative—geometry. The latter, although capable of inducing counter-intuitive effects (as illustrated on the example of the two-sheeted spacetime), is rigid, i.e., not subject to typically quantum properties. In particular, the question of the causal inference of ‘events’ (i.e., pure states on ) is still a yes/no question. On the other hand, the ‘events’ themselves are afflicted with an objective uncertainty resulting from the noncommutativity of the algebra of observables3. It delineates a panorama of Planck scale physics more in the spirit of the Penrose’ twistor theory (cf. [71], Figure 33.7), which is radically different than the one painted by the Lorentz-invariance-violating theories (cf. [72]) or the ‘quantum causality’ concept [73].
On the empirical side, we have evidence neither of quantum spacetime, nor of quantum gravity in any frame. Moreover, there exist various competing models of noncommutative spacetimes, differing from the presented one both on the conceptual and the mathematical side (cf. for instance [5,58,59,74,75,76,77,78,79]). However, the operational approach enhanced by noncommutative geometry à la Connes offers a unique testing ground to hunt for specific physical effects via the almost-commutative models.
An almost-commutative spacetime (cf. Example 3) is simply a Cartesian product of a spacetime and an internal space [19,21], as all of the pure states on the algebra are separable [30, Theorem 11.3.7]. In other words, there is no entanglement between spacetime and the internal space of an almost-commutative model. On the other hand, the (noncommutative) geometry does mix the degrees of freedom. In particular, the causal structure not only forbids a superluminal motion in , but imposes explicit bounds on the speed of change in the models’ internal space. This effect was visible in the example presented in the previous section, where the internal space consisted of just two points, and it would manifest itself in any almost-commutative spacetime (see e.g., [19]).
One of the cornerstones of quantum field theory is the micro-causality axiom, which demands that the local observables related to the spacelike separated regions of spacetime commute. However, the lesson from almost-commutative geometry is that when fields have additional degrees of freedom, the QFT should be established on , rather than on itself. Consequently, the causal structure of needs to be taken into account when constructing the field operators.
Let us briefly sketch this idea on the example of the two-sheeted spacetime: the almost-commutative spacetime at hand models a single massive Dirac fermion (cf. [26]). One can thus construct the standard quantum theory based on two fields , satisfying the standard anticommutation relations. However, at the classical level, the theory is equivalent to the one involving two massless (Weyl) spinors with the mass term interpreted as the interaction between the two4. Consequently, one could construct an interacting quantum field theory involving four fields , , , . Now, the standard approach assumes that the fields are initially free, i.e., for all and one takes into account the interaction by the standard perturbative techniques. The almost-commutative viewpoint, on the other hand, suggests that one should include the interaction by demanding that only if , where d is the Lorentzian distance function.
In the example presented above it is likely that the resulting quantum field theories would be equivalent, i.e., they would lead to the same S-matrix. However, the almost-commutative framework allows one to repeat the construction on a curved spacetime, where the intuitions from the flat case generally fail (cf. [80]). What is more, the above-sketched procedure generalises in a straightforward way to the case of other, non-gravitational, interactions (cf. [22,26]). The causal structure of almost-commutative spacetimes might thus open a new avenue towards the construction of a nonperturbative algebra of quantum fields. The upshot of the operational viewpoint is that the same paradigm of rigidity of the causal structure could serve to build quantum fields over noncommutative spacetimes (following the pioneering work [17]), challenging the standard conclusions about the inevitable breakdown of the Lorentz symmetry [81,82,83].
Acknowledgments
M.E. was supported by the Foundation for Polish Science under the programme START 2016. M.E. acknowledges the support of the Marian Smoluchowski Kraków Research Consortium “Matter–Energy–Future” within the programme KNOW.
Conflicts of Interest
The author declares no conflict of interest.
References
- Akofor, E.; Balachandran, A.P.; Joseph, A. Quantum fields on the Groenewold–Moyal plane. Int. J. Mod. Phys. A 2008, 23, 1637–1677. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized Space-Time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Yang, C.N. On Quantized Space-Time. Phys. Rev. 1947, 72, 874. [Google Scholar] [CrossRef]
- Connes, A. Noncommutative Geometry; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Madore, J. An Introduction to Noncommutative Differential Geometry and its Physical Applications; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1999; Volume 257. [Google Scholar]
- Majid, S. Foundations of Quantum Group Theory; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Connes, A. C*-algèbres et géométrie différentielle. C. R. Acad. Sci. Paris Sér. 1980, 290, A599–A604. [Google Scholar]
- Woronowicz, S.L. Differential calculus on compact matrix pseudogroups (quantum groups). Commun. Math. Phys. 1989, 122, 125–170. [Google Scholar] [CrossRef]
- Dubois-Violette, M.; Kerner, R.; Madore, J. Noncommutative differential geometry of matrix algebras. J. Math. Phys. 1990, 31, 316–322. [Google Scholar] [CrossRef]
- Malament, D. In defense of dogma: Why there cannot be a relativistic quantum mechanical theory of (localizable) particles. In Perspectives on Quantum Reality; Clifton, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 1–10. [Google Scholar]
- Reeh, H.; Schlieder, S. Bemerkungen zur Unitäräquivalenz von Lorentzinvarianten Feldern. Il Nuovo Cimento 1961, 22, 1051–1068. [Google Scholar] [CrossRef]
- Yngvason, J. Localization and entanglement in relativistic quantum physics. In The Message of Quantum Science: Attempts Towards a Synthesis; Blanchard, P., Fröhlich, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 325–348. [Google Scholar]
- Haag, R. Local Quantum Physics: Fields, Particles, Algebras; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Relat. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Garay, L.J. Quantum graivty and minimum length. Int. J. Mod. Phys. A 1995, 10, 145–165. [Google Scholar] [CrossRef]
- Doplicher, S.; Fredenhagen, K.; Roberts, J.E. Spacetime quantization induced by classical gravity. Phys. Lett. B 1994, 331, 39–44. [Google Scholar] [CrossRef]
- Doplicher, S.; Fredenhagen, K.; Roberts, J.E. The quantum structure of spacetime at the Planck scale and quantum fields. Commun. Math. Phys. 1995, 172, 187–220. [Google Scholar] [CrossRef]
- Franco, N.; Eckstein, M. An algebraic formulation of causality for noncommutative geometry. Class. Quantum Gravity 2013, 30, 135007. [Google Scholar] [CrossRef]
- Franco, N.; Eckstein, M. Exploring the causal structures of almost commutative geometries. Symmetry Integr. Geom. Methods Appl. 2014, 10, 010. [Google Scholar] [CrossRef]
- Franco, N.; Eckstein, M. Noncommutative geometry, Lorentzian structures and causality. In Mathematical Structures of the Universe; Eckstein, M., Heller, M., Szybka, S., Eds.; Copernicus Center Press: Kraków, Poland, 2014; pp. 315–340. [Google Scholar]
- Eckstein, M.; Franco, N. Causal structure for noncommutative geometry. In Proceedings of the Frontiers of Fundamental Physics 14, Marseille, France, 15–18 July 2014.
- Franco, N.; Eckstein, M. Causality in noncommutative two-sheeted space-times. J. Geom. Phys. 2015, 96, 42–58. [Google Scholar] [CrossRef]
- Eckstein, M.; Miller, T. Causality for nonlocal phenomena. Ann. Henri Poincaré 2017, 1–48. [Google Scholar] [CrossRef]
- Eckstein, M.; Miller, T. Causal evolution of wave packets. Phys. Rev. A 2017, 95, 032106. [Google Scholar] [CrossRef]
- Miller, T. Polish spaces of causal curves. J. Geom. Phys. 2017, 116, 295–315. [Google Scholar] [CrossRef]
- Eckstein, M.; Franco, N.; Miller, T. Noncommutative geometry of Zitterbewegung. Phys. Rev. D 2017, in press. [Google Scholar]
- Strocchi, F. An Introduction to the Mathematical Structure of Quantum Mechanics; World Scientific: Singapore, 2008. [Google Scholar]
- Keyl, M. Fundamentals of quantum information theory. Phys. Rep. 2002, 369, 431–548. [Google Scholar] [CrossRef]
- Dixmier, J. C*-Algebras; North-Holland Publishing Company: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Kadison, R.V.; Ringrose, J.R. Fundamentals of the Theory of Operator Algebras; Academic Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Petz, D. An Invitation to the Algebra of Canonical Commutation Relations; Leuven University Press: Leuven, Belgium, 1990. [Google Scholar]
- Heisenberg, W. The Physical Principles of the Quantum Theory; Courier Corporation: North Chelmsford, MA, USA, 1930. [Google Scholar]
- Shull, C.G. Single-slit diffraction of neutrons. Phys. Rev. 1969, 179, 752–754. [Google Scholar] [CrossRef]
- Friedrich, T.; Nestke, A. Dirac Operators in Riemannian Geometry. In Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2000; Volume 25. [Google Scholar]
- Várilly, J. Dirac Operators and Spectral Geometry. Lecture Notes. 2006. Available online: www.impan.pl/swiat-matematyki/notatki-z-wyklado~/varilly_dosg.pdf (accessed on 14 March 2017).
- Connes, A. On the spectral characterization of manifolds. J. Noncommut. Geom. 2013, 7, 1–82. [Google Scholar] [CrossRef]
- Krajewski, T. Classification of finite spectral triples. J. Geom. Phys. 1998, 28, 1–30. [Google Scholar] [CrossRef]
- van Suijlekom, W.D. Noncommutative Geometry and Particle Physics; Springer: Berlin, Germany, 2015. [Google Scholar]
- Chamseddine, A.H.; Connes, A.; Marcolli, M. Gravity and the standard model with neutrino mixing. Adv. Theor. Math. Phys. 2007, 11, 991–1089. [Google Scholar] [CrossRef]
- Marcolli, M. Building cosmological models via noncommutative geometry. Int. J. Geom. Methods Mod. Phys. 2011, 8, 1131–1168. [Google Scholar] [CrossRef]
- Sakellariadou, M. Cosmological consequences of the noncommutative spectral geometry as an approach to unification. J. Phys. Conf. Ser. 2011, 283, 012031. [Google Scholar] [CrossRef]
- Christensen, E.; Ivan, C.; Schrohe, E. Spectral triples and the geometry of fractals. J. Noncommut. Geom. 2012, 6, 249–274. [Google Scholar] [CrossRef]
- Connes, A.; Landi, G. Noncommutative manifolds, the instanton algebra and isospectral deformations. Commun. Math. Phys. 2001, 221, 141–159. [Google Scholar] [CrossRef]
- Rieffel, M.A. C*-algebras associated with irrational rotations. Pac. J. Math. 1981, 93, 415–429. [Google Scholar] [CrossRef]
- Chakraborty, P.S.; Pal, A. Equivariant spectral triples on the quantum SUq(2) group. K-Theory 2003, 28, 107–126. [Google Scholar] [CrossRef]
- Dąbrowski, L.; Sitarz, A. Dirac operator on the standard Podleś quantum sphere. Banach Center Publ. 2003, 61, 49–58. [Google Scholar]
- Gayral, V.; Iochum, B. The spectral action for Moyal planes. J. Math. Phys. 2005, 46, 043503. [Google Scholar] [CrossRef]
- Strohmaier, A. On noncommutative and pseudo-Riemannian geometry. J. Math. Phys. 2006, 56, 175–195. [Google Scholar] [CrossRef]
- van Suijlekom, W.D. The noncommutative Lorentzian cylinder as an isospectral deformation. J. Math. Phys. 2004, 45, 537–556. [Google Scholar] [CrossRef]
- Paschke, M.; Sitarz, A. Equivariant Lorentzian spectral triples. arXiv, 2006; arXiv:math-ph/0611029. [Google Scholar]
- Barrett, J. Lorentzian version of the noncommutative geometry of the standard model of particle physics. J. Math. Phys. 2007, 48, 012303. [Google Scholar] [CrossRef]
- Franco, N. Lorentzian Approach to Noncommutative Geometry. Ph.D. Thesis, University of Namur, Namur, Belgium, 2011. [Google Scholar]
- Verch, R. Quantum Dirac field on Moyal–Minkowski spacetime—Illustrating quantum field theory over Lorentzian spectral geometry. Acta Phys. Pol. B Suppl. 2011, 4, 507–530. [Google Scholar] [CrossRef]
- van den Dungen, K.; Paschke, M.; Rennie, A. Pseudo-Riemannian spectral triples and the harmonic oscillator. J. Math. Phys. 2013, 73, 37–55. [Google Scholar] [CrossRef]
- Franco, N. Temporal Lorentzian spectral triples. Rev. Math. Phys. 2014, 26, 1430007. [Google Scholar] [CrossRef]
- van den Dungen, K.; Rennie, A. Indefinite Kasparov modules and pseudo-Riemannian manifolds. Ann. Henri Poincaré 2016, 17, 3255–3286. [Google Scholar] [CrossRef]
- van den Dungen, K. Krein spectral triples and the fermionic action. Math. Phys. Anal. Geom. 2016, 19, 4. [Google Scholar] [CrossRef]
- Besnard, F.; Bizi, N. On the definition of spacetimes in noncommutative geometry, Part I. arXiv, 2016; arXiv:1611.07830. [Google Scholar]
- Besnard, F. On the definition of spacetimes in noncommutative geometry, Part II. arXiv, 2016; arXiv:1611.07842. [Google Scholar]
- Bizi, N.; Brouder, C.; Besnard, F. Space and time dimensions of algebras with applications to Lorentzian noncommutative geometry and the standard model. arXiv, 2016; arXiv:1611.07062. [Google Scholar]
- Bognár, J. Indefinite Inner Product Spaces; Springer: Berlin, Germany, 1974. [Google Scholar]
- Baum, H. Spin-Strukturen und Dirac-Operatoren über Pseudoriemannschen Mannigfaltigkeiten; Teubner-Texte zur Mathematik; Leipzig: Teubner, Germany, 1981; Volume 41. [Google Scholar]
- Franco, N.; Wallet, J.C. Metrics and causality on Moyal planes. In Noncommutative Geometry and Optimal Transport; Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 2016; Volume 676, pp. 147–173. [Google Scholar]
- Rieffel, M.A. Metrics on state spaces. Doc. Math. 1999, 4, 559–600. [Google Scholar]
- Beem, J.; Ehrlich, P.; Easley, K. Global Lorentzian Geometry; Monographs and Textbooks in Pure and Applied Mathematics; CRC Press: Boca Raton, FL, USA, 1996; Volume 202. [Google Scholar]
- Minguzzi, E. Time functions as utilities. Commun. Math. Phys. 2010, 298, 855–868. [Google Scholar] [CrossRef]
- Miller, T. On the causality and K-causality between measures. Universe 2017, in press. [Google Scholar]
- Watcharangkool, A.; Sakellariadou, M. Noncommutative geometrical origin of the energy-momentum dispersion relation. Phys. Rev. D 2017, 95, 025027. [Google Scholar] [CrossRef]
- Schrödinger, E. Über die kräftefreie Bewegung in der relativistischen Quantenmechanik. Sitzungber. Preuss. Akad. Wiss. Phys. Math. Kl. 1930, 24, 418–428. [Google Scholar]
- Hestenes, D. The zitterbewegung interpretation of quantum mechanics. Found. Phys. 1990, 20, 1213–1232. [Google Scholar] [CrossRef]
- Penrose, R. The Road to Reality: A Complete Guide to the Laws of the Universe; Jonathan Cape: London, UK, 2004. [Google Scholar]
- Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Relat. 2005, 8, 2003. [Google Scholar] [CrossRef] [PubMed]
- Brukner, Č. Quantum causality. Nat. Phys. 2014, 10, 259–263. [Google Scholar] [CrossRef]
- Besnard, F.; Bizi, N. The disappearance of causality at small scale in almost-commutative manifolds. arXiv, 2014; arXiv:1411.0878. [Google Scholar]
- Besnard, F. Two roads to noncommutative causality. J. Phys. Conf. Ser. 2015, 634, 012009. [Google Scholar] [CrossRef]
- Sitarz, A. Pointless Geometry. In Mathematical Structures of the Universe; Eckstein, M., Heller, M., Szybka, S., Eds.; Copernicus Center Press: Kraków, Poland, 2014; pp. 301–314. [Google Scholar]
- Majid, S. Quantum groups and noncommutative geometry. J. Math. Phys. 2000, 41, 3892–3942. [Google Scholar] [CrossRef]
- Heller, M.; Sasin, W.; Lambert, D. Groupoid approach to noncommutative quantization of gravity. J. Math. Phys. 1997, 38, 5840–5853. [Google Scholar] [CrossRef]
- Heller, M.; Pysiak, L.; Sasin, W. Conceptual Unification of Gravity and Quanta. Int. J. Theor. Phys. 2007, 46, 2494–2512. [Google Scholar] [CrossRef]
- Kobakhidze, A.; Manning, A.; Tureanu, A. Observable Zitterbewegung in curved spacetimes. Phys. Lett. B 2016, 757, 84–91. [Google Scholar] [CrossRef]
- Greenberg, O.W. Failure of microcausality in quantum field theory on noncommutative spacetime. Phys. Rev. D 2006, 73, 045014. [Google Scholar] [CrossRef]
- Soloviev, M.A. Failure of microcausality in noncommutative field theories. Phys. Rev. D 2008, 77, 125013. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Joseph, A.; Padmanabhan, P. Causality and statistics on the Groenewold–Moyal plane. Found. Phys. 2010, 40, 692–702. [Google Scholar] [CrossRef]
- 1.In general, does not need to contain a unit. However, it always contains an approximate unit, which can be utilised to rigorously express the normalisation requirement [29].
- 2.In fact, one can extend this result (cf. [66,67]) to stably causal spacetimes, in which case one recovers the Sorkin–Woolgar relation—the smallest closed partial order containing the causal order.
- 3.A concrete model of a noncommutative spacetime with nonlocal events, but a rigid causal structure was developed in [63].
- 4.Such a viewpoint leads to the so-called ‘zigzag picture of the electron’ [71, Section 25.2].
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).