Abstract
The Petrov classification of stress-energy tensors provides a model-independent definition of a vacuum by the algebraic structure of its stress-energy tensor and implies the existence of vacua whose symmetry is reduced as compared with the maximally symmetric de Sitter vacuum associated with the Einstein cosmological term. This allows to describe a vacuum in general setting by dynamical vacuum dark fluid, presented by a variable cosmological term with the reduced symmetry which makes vacuum fluid essentially anisotropic and allows it to be evolving and clustering. The relevant solutions to the Einstein equations describe regular cosmological models with time-evolving and spatially inhomogeneous vacuum dark energy, and compact vacuum objects generically related to a dark energy: regular black holes, their remnants and self-gravitating vacuum solitons with de Sitter vacuum interiors—which can be responsible for observational effects typically related to a dark matter. The mass of objects with de Sitter interior is generically related to vacuum dark energy and to breaking of space-time symmetry. In the cosmological context spacetime symmetry provides a mechanism for relaxing cosmological constant to a needed non-zero value.
1. Introduction
Dark Energy is described by the equation of state with responsible for accelerated expansion . The best fit, at 68% CL [1], corresponds to the cosmological constant λ related to the vacuum density by .
In the Einstein equations with the cosmological constant the cosmological term corresponds to the de Sitter vacuum (false vacuum in the Standard Model)
which is able also to support the inflationary dynamics in the very early Universe. The problem is that the first inflation needs the value at the GUT level g·cm, the QFT estimates the value of by g·cm which by many orders of magnitude exceeds the observational value g·cm, and the Einstein equations require .
Alternative models typically impose for some reason (still unknown) and introduce a dark energy of a non-vacuum origin which mimics λ when necessary (for a review [2,3,4]).
In this paper we present the time-dependent and spatially inhomogeneous vacuum dark energy which is intrinsically related to the spacetime symmetry and can be evolving and clustering.
2. Vacuum Dark Energy
2.1. Vacuum Dark Fluid
QFT does not contain an appropriate symmetry to zero out , or to reduce it to a certain non-zero value. A relevant symmetry does however exist in General Relativity. It follows from the Petrov classification for the algebraic structure of stress-energy tensors, , as intrinsically related to it (via the Einstein equations) the spacetime symmetry.
Eigenvectors of form a comoving reference frame with a time-like eigenvector representing a velocity. In the Petrov classification the maximally symmetric de Sitter vacuum (1) is denoted by [(IIII)]—all eigenvalues equal. As a result it has an infinite set of comoving reference frames which makes impossible to fix a velocity with respect to it which is the most general intrinsic property of a vacuum. with [(IIII)] generates the maximally symmetric de Sitter spacetime for any underlying particular model of . The isotropic medium is denoted by [I(III)] and anisotropic media by [IIII].
A maximal symmetry [(IIII)] can be reduced to [5,6]
which represents a vacuum dark fluid invariant under the Lorentz boosts in the α-direction(s) which still makes impossible to single out a preferred comoving reference frame and thus to fix the velocity with respect to a medium specified by (2), but makes density and pressures time- and spatially-dependent. The Petrov classification suggests the following types of vacuum dark fluid [7]: [(IIII)]—isotropic vacuum dark fluid (de Sitter vacuum); [(II)II], [(III)I], [(II)(II)]—anisotropic vacuum dark fluids, associated with variable cosmological term [6]
It generates spacetimes which contain regions of the de Sitter vacuum with the restored maximal symmetry; transitions to regions with the reduced vacuum symmetry involve breaking of spacetime symmetry from the de Sitter group.
2.2. Spherically Symmetric Vacuum Dark Energy
A spherically symmetric vacuum dark fluid, defined by () [5], generates spacetimes with the obligatory de Sitter center [8,9]. Regular spacetimes with the de Sitter center are described by the metric [6,8,9]
The number of the spacetime horizons is related to the number of the de Sitter vacuum scales, [10].
For the case of two vacuum scales a stress-energy tensor for vacuum dark energy connects two de Sitter vacua, at the center and at infinity,
and the metric evolves between two de Sitter asymptotics with . Spacetime can have at most 3 horizons and describes five possible configurations shown in Figure 1: regular cosmological black hole within the mass range , between the event horizon and the internal Cauchy horizon in the universe with the cosmological horizon (Figure 1a); two double-horizon states, and , and two one-horizon states (Figure 1b) [11].
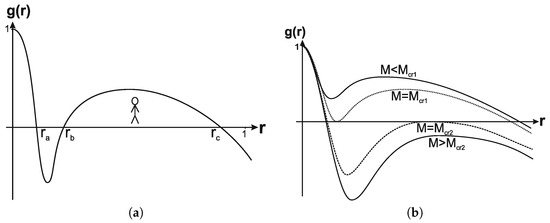
Figure 1.
Typical behavior of the metric function for the case of two vacuum scales.
Dependently on the coordinate mapping, solutions to the Einstein equations with the source term (5) describe cosmological models or compact objects with the de Sitter vacuum interiors.
3. Regular Cosmological Models
Lemaître class cosmological models are described by the metric ([10] and references therein)
Coordinates are the Lagrange (comoving) coordinates. For Lemaître observers, shown in Figure 2 for the case of the one-horizon spacetime with the same global structure as for the de Sitter spacetime (Figure 2 right), for spatially flat models with evolution starts with the non-singular non-simultaneous de Sitter bang at from the regular timelike surface . It is followed by the anisotropic stage at which the expansion in the transversal direction with is accompanied by shrinking in the radial direction where until [10,12].
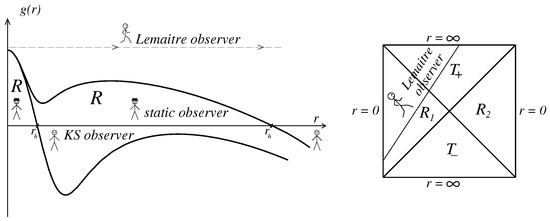
Figure 2.
One-horizon spacetimes with vacuum dark fluid.
Regular models of the Kantowski-Sachs type are described by the metric . These are homogeneous anisotropic T-models. Evolution starts with a null bang from the Killing horizon ( in Figure 2), and pre-bang information from a regular asymptotically de Sitter region behind the horizon is available for KS observers (shown in Figure 2 left) [12].
More general class of regular homogeneous anisotropic T-models is described by the t-dependent metric
Characteristic features of this class models are (i) existence of a Killing horizon; (ii) a null bang from horizon; (iii) pre-bang information available; (iv) creation of matter from anisotropic vacuum [13].
4. Spacetime Singled Out By the Holographic Principle
The partition function calculated as the path integral for a canonical ensemble of metrics from the class (4), which satisfy and are generated by source terms with , reads [15]
The specific heat of a horizon is given by [16]
The Holographic Principle states that the number of quantum degrees of freedom in a spatial volume is bounded from above by its surface area [17]. It is also formulated as the Conjecture: A physical system can be completely specified by data stored on its boundary [18].
Quantum evaporation proceeds with decreasing mass M [16]. In the case of one-horizon spacetime with the de Sitter global structure and two vacuum scales (initial and final) the process directed towards diminishing M starts in the state (Figure 3a). Evaporation results in the state (the Nariai solution) with the negative specific heat according to (10), which is thermodynamically unstable. There exists, however, another possibility presented by the class of one-horizon solutions with the inflection point instead of extrema (Figure 3b). In this case quantum evaporation of the cosmological horizon starts in the state and goes towards the triple-horizon spacetime determined by , which define uniquely the final mass , the horizon raius and the key parameter () [19].
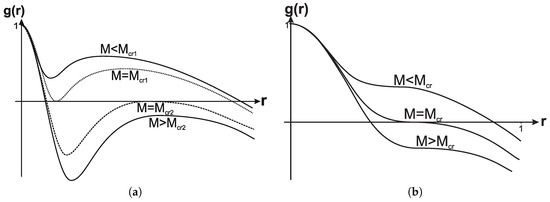
Figure 3.
Two options for quantum evaporation of one-horizon spacetimes.
The triple-horizon spacetime is distinguished by quantum dynamics of the cosmological horizon as the only thermodynamically stable final product of its evaporation: Evaporation stops when and . What is most important—evaporation stops with the finite non-zero value of the cosmological constant given by the finite value of , so that the spacetime symmetry acts as the symmetry which provides, via the Holographic Principle, the mechanism of relaxing of the cosmological constant to a certain tightly fixed non-zero value.
Choosing a density profile one can calculate the final value of and compare it with that given by observations. We apply the density profile [5]
It describes vacuum polarization effects, which contribute all together to vacuum polarization in the gravitational field [5], in the simple semiclassical model , where the gravitational (tidal) force , and the critical (de Sitter) force [8,20].
Estimate with and GeV, gives cm, g, and . Observational value g·cm corresponds to .
5. Regular Compact Objects with de Sitter Vacuum Interiors
5.1. Regular Black Holes and Vacuum Gravitational Solitons G-Lumps
The early proposals of replacing a singularity with the de Sitter vacuum were based on the hypotheses of self-regulation of geometry by vacuum polarization effects [21], of the existence of the limiting curvature [22], and of the symmetry restoration at the GUT scale in the course of the gravitational collapse [5,23]. The first solution describing regular black hole with the de Sitter interior [5] was obtained with the density profile (11). A loop quantum gravity provides arguments in favor of a regular black hole with the de Sitter interior [24,25,26,27].
During evaporation a regular black hole with three horizons (shown in Figure 1a) evolves to its extreme state with the double horizon (the curve in Figure 1b). Behavior of temperature of the event horizon shown in Figure 4a, is generic for black holes with the de Sitter center [16,20]. In the maximum of temperature, the specific heat (shown in Figure 4b) is broken and changes sign, i.e., the second order phase transition occurs which is followed by the quantum cooling [16,20,28]. At the double horizon temperature vanishes while specific heat becomes positive, in accordance with (10).
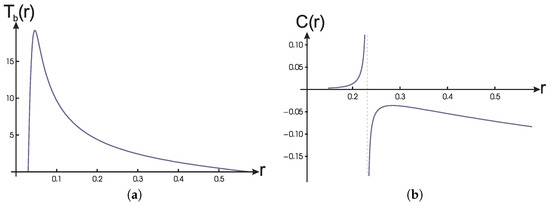
Figure 4.
Temperature (a) and specific heat (b) of the black hole horizon.
Maximal temperature at the phase transition is given by . For the density profile (11) with and GeV, temperature at the phase transition [20].
Spacetime without the event horizon (the upper curve, , at the Figure 1b) represents a vacuum gravitational soliton G-lump [8,20], a non-singular non-dissipative particle-like structure taking itself together by its own gravitational self-interaction. Energy of G-lump calculated in the minisuperspace model is , where is the transversal pressure (normalized to ) at the minimum of the G-lump potential [8].
Regular black holes, their remnants and self-gravitating vacuum solitons G-lumps with de Sitter vacuum interiors can be responsible for observational effects typically related to a dark matter [29].
5.2. Regular Black Hole Remnants
BH remnants are considered as a reliable source of dark matter for more than three decades [30,31,32]. Singular black hole remnants are plagued by the existential problem: No evident symmetry or quantum number exists which would prevent complete evaporation [18,33]. On the other hand, complete evaporation would involve a fundamental change in the spacetime structure in the transition from a spacetime with the distinguished center (distinguished by the singularity), the Schwarzschild-de Sitter spacetime (the curve 3 in Figure 5a), to the globally regular maximally symmetric de Sitter spacetime (Figure 5b) and actually would require to find an answer to the question—How to evaporate a singularity? [34].
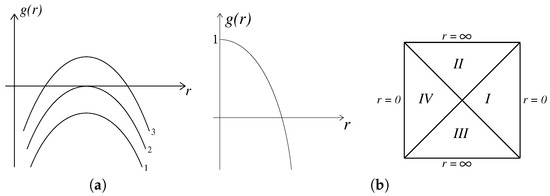
Figure 5.
Evolution of the Schwarzschild-de Sitter black hole in the case of complete evaporation. (a) Schwarzschild-de Sitter metric function; (b) De Sitter metric function and global structure.
A regular black hole leaves behind a thermodynamically stable double-horizon remnant generically related to vacuum dark energy through its interior de Sitter vacuum ([16,35] and references therein). Mass of the remnant is given by . For the density profile (11) with and GeV, the mass [20].
5.3. Graviatoms with the de Sitter Interiors
Regular primordial black holes, their remnants and G-lumps can arise during first and second (100–200 MeV [36]) inflationary stages in a quantum collapse of primordial fluctuations. Probability of tunnelling in a collapse is given by [37]
where is the scale of the inflationary vacuum. At the first inflation, , regular objects with the interior de Sitter vacuum can arise with masses g. For any mass is possible, as well as for regular objects arising at the second inflationary stage, .
Regular primordial black holes, their remnants and G-lumps can capture available particles and form graviatoms ([37] and references therein) - gravitationally bound () quantum systems with charged particles. Conditions of the existence of graviatoms [37] constrain the masses of captured particles by GeV for . They can be (i) GUT particles captured at the first inflation; and (ii) leptoquarks survived in galactic haloes [38].
Observational signatures of graviatoms as heavy dark matter candidates provide additional signatures for inhomogeneity of the early Universe [39]. Most promising is the oscillatory electromagnetic radiation of graviatom whose characteristic frequency depends on the scale of the interior de Sitter vacuum [37]. For the density profile (11) . Detection of cosmic photons is possible up to GeV [40]. In graviatoms with the GUT scale interiors, where baryon and lepton numbers are not conserved, a remnant component of graviatom can induce proton decay, which could in principle serve as an additional observational signature of graviatom for heavy dark matter searches at the IceCUBE experiment [39].
5.4. Mass and Spacetime Symmetry
Masses of objects with the de Sitter vacuum interiors are generically related to the de Sitter vacuum and to breaking of spacetime symmetry from the de Sitter group in the origin [8].
In the Standard Model de Sitter vacuum appears as the false vacuum of the Higgs field responsible for particle mass. Calculation of mass in the gravito-electroweak vortex by the Casimir formula in de Sitter space provides explanation for the observational effect known as negative mass-square difference for neutrinos [41,42]. This can also explain appearance of the minimal length scale cm at the energy scale TeV in the annihilation reaction [43]. QED hypotheses applied in the -test predict increasing of the total cross section. Contrary to these expectations, the fit displays a minimum with the negative fit parameter with a significance about . The scale cm fits inside the internal de Sitter region where gravity is repulsive. The minimal length scale can be thus understood as a distance at which electromagnetic attraction is balanced by the gravitational repulsion of the interior de Sitter vacuum [43].
6. Summary and Discussion
Algebraic classification of stress-energy tensors and related (via the Einstein equations) spacetime symmetry implies the possibility to introduce in general setting dynamical vacuum dark energy which can be evolving and clustering. It is presented by the class of regular spherical solutions to the Einstein equations specified by which generate the metrics .
These metrics belong to the Kerr-Schild class and can be presented as , where is the Minkowski metric and are principal null congruences. This is the special class of algebraically degenerated solutions to the Einstein equations. In the algebraically special Kerr-Shild geometry the Einstein equations take the linear form, , and pseudotensor of gravitational energy [44]. They admit decomposition into free-falling (2 + 1)-dimensional shells with the associated conserved stress-energy tensors, each of shells can be treated as a closed system and described by a (2 + 1) Hamiltonian [45].
Regular spherical solutions of the class have obligatory de Sitter center, represent dynamical vacuum dark energy on the basis of spacetime symmetry, and describe, dependently on a mapping (reference frame), regular cosmological dark energy models and regular compact objects with the de Sitter vacuum interiors (black holes, their remnants and gravitational solitons).
In the case of two vacuum scales (e.g., for initial inflation and the present accelerated expansion) the Holographic Principle singles out the triple-horizon spacetime as the only thermodynamically stable product of quantum evaporation of the cosmological horizon. What is most important—the spacetime symmetry appears to be that (lacking in QFT) symmetry which provides, via the Holographic Principle, the mechanism of relaxing cosmological constant to a certain non-zero value, tightly fixed by quantum dynamics of quantum evaporation of the cosmological horizon. Choice of the density profile related to vacuum polarization effects and of the GUT scale for the first inflation gives the non-zero final value of the vacuum density in remarkable agreement with its observational value.
Regular compact objects generically related to vacuum dark energy through their de Sitter vacuum interiors, include regular black holes, their remnants and vacuum gravitational solitons G-lumps, which can be responsible for observational effects typically related to a dark matter.
Mass of objects is generically related to breaking of spacetime symmetry from the de Sitter group in the origin which is confirmed by explanation of observational effects in high energy physics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Joyce, A.; Lombriser, L.; Schmidt, F. Dark Energy Versus Modified Gravity. Ann. Rev. Nucl. Part. Sci. 2016, 66, 95–122. [Google Scholar] [CrossRef]
- Rivera, A.B.; Farieta, J.G. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. arXiv, 2016; arXiv:1605.01984. [Google Scholar]
- Colepand, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Relativ. Gravit. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quantum Gravity 2002, 19, 725–740. [Google Scholar] [CrossRef]
- Dymnikova, I. Spherically symmetric space-time with the regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dymnikova, I.; Galaktionov, E. Multihorizon spherically symmetric spacetimes with several scales of vacuum energy. Class. Quantum Gravity 2012, 29, 095025–095047. [Google Scholar] [CrossRef]
- Dymnikova, I.; Soltysek, B. Spherically symmetric space-time with two cosmological constants. Gen. Relativ. Gravit. 1998, 30, 1775–1793. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dobosz, A.; Dymnikova, I. Nonsingular vacuum cosmologies with a variable cosmological term. Class. Quantum Gravity 2003, 20, 3797–3814. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dymnikova, I. Regular homogeneous T-models with vacuum dark fluid. Class. Quantum Gravity 2007, 24, 5803–5816. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Padmanabhan, T. Classical and quantum thermodynamics of horizons in spherically symmetric spacetimes. Class. Quantum Gravity 2002, 19, 5387–5408. [Google Scholar] [CrossRef]
- Dymnikova, I.; Korpusik, M. Regular black hole remnants in de Sitter space. Phys. Lett. B 2010, 685, 12–18. [Google Scholar] [CrossRef]
- ’t Hooft, G. Dimensional reduction in quantum gravity. arXiv, 1999; arXiv:9310026. [Google Scholar]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Dymnikova, I. Triple-horizon spherically symmetric spacetime and holographic principle. Int. J. Mod. Phys. D 2012, 21, 1242007. [Google Scholar] [CrossRef]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quantum Gravity 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black holes as possible sources of closed and semiclosed worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Dymnikova, I. Internal structure of nonsingular spherical black holes. In Internal Sructure of Black Holes and Spacetime Singularities; Burko, M., Ori, A., Eds.; Institute of Physics Publishing: Bristol, UK, 1997; Volume 13, pp. 422–440. [Google Scholar]
- Perez, A. Spin foam models for quantum gravity. Class. Quantum Gravity 2003, 20, R43–R104. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005–083017. [Google Scholar] [CrossRef]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. A 2009, 24, 1229–1308. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.W.; Park, Y.J. Black hole thermodynamics with generalized uncertainty principle. Phys. Lett. B 2007, 645, 393–397. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Dark ingredients in one drop. Cent. Eur. J. Phys. 2011, 9, 644–653. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Khlopov, M.Y. Cosmology, primordial black holes, and supermassive particles. Sov. Phys. Uspekhi 1985, 28, 213–232. [Google Scholar] [CrossRef]
- MacGibbon, J.H. Can Planck-mass relics of evaporating black holes close the Universe? Nature 1987, 329, 308–309. [Google Scholar] [CrossRef]
- Carr, B.J.; Gilbert, J.H.; Lidsey, J.E. Black hole relics and inflation: Limits on blue perturbation spectra. Phys. Rev. D 1994, 50, 4853–4867. [Google Scholar] [CrossRef]
- Ellis, G.F.R. Astrophysical black holes may radiate, but they do not evaporate. arXiv, 2013; arXiv:1310.4771. [Google Scholar]
- Dymnikova, I. Regular black hole remnants. In Proceedings of the International Conference on Invisible Universe, Paris, France, 29 June–3 July 2009.
- Dymnikova, I.; Korpusik, M. Thermodynamics of Regular Cosmological Black Holes with the de Sitter Interior. Entropy 2011, 13, 1967–1991. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J.; Schwarz, D.J. Phase transitions in the early and present universe. Ann. Rev. Nucl. Part. Sci. 2006, 56, 441–500. [Google Scholar] [CrossRef]
- Dymnikova, I.; Fil’chenkov, M. Graviatoms with de Sitter interior. Adv. High Energy Phys. 2013, 2013, 746894. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Yu.V. Do active galactic nuclei convert dark matter unto visible particles? Mod. Phys. Lett. A 2008, 23, 1151–1159. [Google Scholar] [CrossRef]
- Dymnikova, I.; Khlopov, M. Regular black hole remnants and graviatoms with de Sitter interior as heavy dark matter candidates probing inhomogeneity of the early universe. Int. J. Mod. Phys. D 2015, 24, 1545002. [Google Scholar] [CrossRef]
- Kalashev, O.E.; Rubtsov, G.I.; Troitsky, S.V. Sensitivity of cosmic-ray experiments to ultrahigh-energy photons: reconstruction of the spectrum and limits on the superheavy dark matter. Phys. Rev. D 2009, 80, 103006. [Google Scholar] [CrossRef]
- Ahluwalia, D.V.; Dymnikova, I. A theoretical case for negative mass-square for sub-eV particles. Int. J. Mod. Phys. D 2003, 12, 1787–1794. [Google Scholar] [CrossRef]
- Dymnikova, I. Space-time symmetry and mass of a lepton. J. Phys. A: Math. Theor. 2008, 41, 304033–304053. [Google Scholar] [CrossRef]
- Dymnikova, I.; Sakharov, A.; Ulbricht, J. Appearance of a minimal length in e+ e- annihilation. Adv. High Energy Phys. 2014, 2014, 707812. [Google Scholar] [CrossRef]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment ofthe Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385–2396. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Rabinowitz, A.I. Linearity Non Self-Interacting Spherically Symmetric Gravitational Fields, the “Sphereland Equivalence Principle” and Hamiltonian Bubbles. Gen. Relativ. Gravit. 1996, 28, 117–128. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).