Constraining the Primordial Black Hole Mass Function by the Lensing Events of Fast Radio Bursts

Abstract

Light from fast radio bursts (FRBs) can be deflected by the gravitational lensing effect of primordial black holes (PBHs), if they are distributed along the path from the FRBs to the observer. Consequently, the PBH mass function can be constrained by the lensing events of FRBs. In this work, four different PBH mass functions are investigated (i.e., the monochromatic, log-normal, skew log-normal, and power-law distributions), and the constraints on the model parameters are obtained, if the PBH abundance $f_{\mathrm{PBH}}$ and the event rate of lensed FRBs $\overline{\mathit{\tau }}$ are given. We find that, if $\overline{\mathit{\tau }}<{10}^{-4}$ in future FRB experiments, $f_{\mathrm{PBH}}$ will be less than ${10}^{-2.5}$ in most of the PBH mass range from 1–$100M_{\odot }$ for the monochromatic mass function. Moreover, for the three extended mass functions, $\overline{\mathit{\tau }}$ increases when the PBH mass distributions spread to larger masses, setting more stringent constraints on $f_{\mathrm{PBH}}$.

1. Introduction

Thanks to various accurate cosmological observations in the last decades (e.g., from the supernovae and the cosmic microwave background), we have gradually come to the conclusion that our Universe is composed of $71\%$ dark energy, $24\%$ dark matter (DM), and only $5\%$ baryonic matter [1]. DM, which does not interact with electromagnetic waves, reveals its existence only via gravitational effects. Hence, the basic composition of DM remains an important unsolved mystery in cosmology. So far, many particle candidates for DM have been suggested in the literature, such as axions [2], axion-like particles [3], heavy sterile neutrinos [4], and weakly interacting massive particles [5], with their masses ranging from ${10}^{-22}\mathrm{eV}/{\mathrm{c}}^2$ to $100\mathrm{TeV}/{\mathrm{c}}^2$ [6]. Meanwhile, there is another potential non-particle candidate for DM: primordial black holes (PBHs) [7,8,9,10].

Different from astrophysical black holes formed as the remnants of stars, PBHs can form directly from the gravitational collapse of overdense regions in the very early Universe (before the Big Bang nucleosynthesis). Therefore, the PBH mass range can span dozens of orders of magnitude, from the Planck mass (${10}^{-5}$ g) to supermassive order (${10}^{10}{M}_{\odot }$, with $M_{\odot }=1.989\times {10}^{33}$ g being the solar mass), without the lower Oppenheimer limit at around $3M_{\odot }$ [11,12] or the mass gap at around 50–130 $M_{\odot }$ due to supernova pair-instability [13,14,15,16,17,18]. For more detailed investigations on the PBH formation mechanisms (e.g., the relation of the PBH mass spectrum and the physics in the early Universe), see Ref. [19]. Currently, as direct [20,21,22,23] and indirect [24,25,26] DM particle detections are both facing obstacles, PBH is becoming a natural and compelling research area, arousing increasing research interest, see Ref. [27] and the references therein.

To describe the physical properties of PBHs, the most important quantity is the PBH abundance $f_{\mathrm{PBH}}$, which is defined as its proportion in DM mass density at the present time. The observational constraints on PBHs refer to the upper bounds of $f_{\mathrm{PBH}}$ in different mass ranges. If $f_{\mathrm{PBH}}\sim 0.1$, PBHs can be considered as an effective candidate for DM. While, if $f_{\mathrm{PBH}}$ is much less than unity (e.g., $f_{\mathrm{PBH}}\ll {10}^{-3}$), its possibility as DM can be safely excluded in the relevant mass range. Till now, by means of evaporation, lensing, dynamics, accretion, and gravitational-wave constraints, $f_{\mathrm{PBH}}$ has been limited to below $1\%$ in most of its mass range. Another important factor that may influence $f_{\mathrm{PBH}}$ is the clustering of PBHs. Different from the simple case of uniformly distributed PBHs, such clustering can alleviate or even avoid the existing constraints on $f_{\mathrm{PBH}}$, especially in the microlensing constraints [28,29,30,31,32,33,34]. With all these ingredients considered, there still remains a completely open mass window at ${10}^{17}$–${10}^{22}$ g (the asteroid mass range), where PBHs can compose all DM [35,36,37,38].

Amongst various observational methods to constrain the PBH abundance, gravitational lensing (GL) is one of the most effective ways, especially suitable for the PBHs with masses around ${10}^{-10}$–${10}^3{M}_{\odot }$ [39,40,41,42,43]. GL phenomenon occurs when light from a remote source is deflected as it travels near a massive object, such as a star, black hole, galaxy, or even galaxy cluster, whose gravitational pull causes the path of light to curve [44,45,46,47,48,49]. GL can be primarily categorized into strong and weak forms according to its strength. Strong GL is caused by a massive object with strong gravitational field, manifesting as magnification, distortion, and distinct multiple images of the source, with the Einstein ring as a particular example. While, weak GL occurs when the mass of the lensing object is not substantial enough to produce the pronounced effects in strong GL. Instead, it merely causes minute deflection of light, without multiple images or the Einstein ring.

Today, GL serves not only as a fundamental test of our understanding of gravity [50,51,52,53], but also as a powerful tool for studying distant astronomical events [54,55,56]. GL is an indirect method to explore DM by observing the deflection of light from the violent phenomena occurring in the distant Universe, like supernova explosions, gamma ray bursts, and fast radio bursts (FRBs). Using two important GL effects (the magnification and the time delay effects), we are able to obtain the information of the signal sources, such as the relative positions of the source, lens, and observer, as well as the mass and distribution of intermediate DM (including PBHs) that plays the role of the lensing object [57,58,59].

Currently, FRB is a hot research topic in astronomy and cosmology. FRBs are millisecond-duration flashes of radio waves [60,61,62,63,64,65,66,67,68], and can be used in measuring the Hubble constant [69,70,71,72], determining the equation of state of dark energy [73], searching for the missing baryons in the Universe [74,75], and exploring the history of cosmic reionization [76]. The first FRB was accidentally discovered by Lorimer’s team when analyzing the archival data from the Parkes Telescope in Australia [77]. At present, many telescopes are dedicated to observing FRBs, with the notable ones as the Canadian Hydrogen Intensity Mapping Experiment (CHIME) [78,79,80,81,82], the Five-hundred-meter Aperture Spherical radio Telescope in China [83], and the Australian Square Kilometer Array Pathfinder [84,85]. To date, more than 1000 FRBs have been detected, including both non-repeating bursts, which are the pulses that occur only once, and repeating bursts, which are the signals that have been observed to recur [86].

Unfortunately, the physical origin of FRBs remains unknown. Although there have been various theories attempting to explain the mechanisms of FRBs, most of them are still largely theoretical [87,88,89,90,91,92,93]. Meanwhile, locating the sources of FRBs also poses significant challenges, with only a dozen of them having been traced back to their host galaxies [94,95,96]. More accurate localization of FRBs can construct a more precise relation between the redshift and dispersion measure [97,98,99], which not only enables further constraints on cosmological parameters, but also helps clarify the distribution of baryonic matter and DM in the Universe [100,101].

Among all the unsolved mysteries of FRBs, the redshift distribution possesses essential importance, as it is closely related to our understanding of the origin of FRBs. Various sources of FRBs may lead to different redshift distributions, which is a rather complicated issue, depending on many influential astrophysical factors, such as the progenitors and the cosmic environment [102,103]. For example, the Galactic FRB 20200428, associated with the young magnetar SGR 1935 + 2154 [104,105], initially supported the hypothesis that FRBs trace the star formation history (SFH) in the Universe. However, the FRB 20200120E, discovered in a globular cluster of M81 [106,107], challenged this viewpoint, indicating that some FRBs are actually related to ancient star populations. Moreover, FRBs seem to be deeply related to neutron stars [108]. In Ref. [109], the interaction of light fermionic DM particles with the nuclear medium in neutron stars and the relevant emissions were investigated. Also, many authors have studied the accretion of PBHs by neutron stars, leading to various high-energy astrophysical scenarios, including FRBs with the incidence rate consistent with observational data [110,111,112,113]. In addition, non-repeating and repeating FRBs are usually considered to have different origins. For instance, the former may be induced by the violent merger of compact binaries, and the redshift distribution thus follows the evolution of stellar mass density in the Universe. Altogether, at present, the limited sample of localized FRBs has been obtained solely by identifying their host galaxies [114,115], so we still lack an empirical redshift distribution for FRBs [116]. Nevertheless, the rapid growth of the FRB events will enable us to understand the relation between the redshift distribution and the sources of FRBs via their statistical characteristics [117]. In this work, we will choose a two-segment redshift distribution (TSRD) for FRBs, and the reason will be explained in detail in Section 4.1.

This work is a comprehensive study on PBHs, GL, and FRBs. Our aim is to constrain the PBH mass function via the GL effect of FRBs. In general, telling the difference between lensed and unlensed FRBs is a very challenging topic, relying on a set of key observational signatures. The most decisive signature comes from the strong GL effect, in which two or more images of the same FRB can be observed, but with different arriving times. These multiple images should have identical waveforms, with the same spectral structure and consistent polarization. Especially, for repeating lensed FRBs, the time delay between the multiple images should be constant for every burst and the same at all radio frequencies, whereas unlensed repeating FRBs typically show more random behaviors in morphology, timing, and brightness. Albeit no lensed FRBs have been confirmed in the known 1000 events, they are generally expected to be detectable in the coming years. Therefore, our work will predict the upper bound of $f_{\mathrm{PBH}}$ with current observational data, and by assuming the event rate of lensed FRBs, we are able to obtain the allowed ranges of the model parameters in the PBH mass functions, which can be tested in the future FRB experiments. In previous literature, for simplicity, PBHs are often assumed to have a uniform mass, that is, they follow a monochromatic mass function. However, in reality, PBHs may have a certain mass range and distribution, so they can have an extended mass function. Such an extension is a double-edged sword. It can relax the abundance constraint in some mass range, but may also induce more serious tension in other mass range simultaneously. Therefore, in this work, we will perform a thorough investigation of the PBH mass functions, with both monochromatic and extended forms taken into account.

This paper is organized as follows. In Section 2, Section 3 and Section 4, we review the physical fundamentals of PBHs, GL, and FRBs, respectively. The monochromatic and three extended PBH mass functions are introduced, three different redshift distributions of FRBs are compared, and the lensing optical depth is calculated, which allows the prediction of the event rate of lensed FRBs. Then, in Section 5, by assuming the values of this rate, the PBH mass functions can be constrained. We conclude in Section 6.

2. PBHs

In this section, we first explain the PBH abundance $f_{\mathrm{PBH}}$ and the mass function $\mathit{\psi }\left(M\right)$, and then introduce the monochromatic and three frequently-used extended mass functions.

The PBH abundance $f_{\mathrm{PBH}}$ is defined as its proportion in DM mass density today,

$$\begin{array}{c}\hfill f_{\mathrm{PBH}}\equiv {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{PBH}}}{{\mathit{\rho }}_{\mathrm{DM}}}},\end{array}$$

where ${\mathit{\rho }}_{\mathrm{PBH}}$ and ${\mathit{\rho }}_{\mathrm{DM}}$ are the mass densities of PBH and DM, respectively, and

$$\begin{array}{c}\hfill {\mathit{\rho }}_{\mathrm{PBH}}=\int M\mathrm{d}n=\int M{\displaystyle \frac{\mathrm{d}n}{\mathrm{d}M}}\mathrm{d}M=\int {\displaystyle \frac{\mathrm{d}n}{\mathrm{d}\ln M}}\mathrm{d}M,\end{array}$$

with M and n being the PBH mass and number density.

Next, the PBH mass function $\mathit{\psi }\left(M\right)$ is defined as

$$\begin{array}{c}\hfill \mathit{\psi }\left(M\right)\equiv {\displaystyle \frac{1}{{\mathit{\rho }}_{\mathrm{DM}}}}{\displaystyle \frac{\mathrm{d}n}{\mathrm{d}\ln M}}.\end{array}$$

Hence, $\mathit{\psi }\left(M\right)$ possesses the dimension of ${\left[M\right]}^{-1}$, and its relation to the PBH abundance is

$$\begin{array}{c}\hfill f_{\mathrm{PBH}}=\int \mathit{\psi }\left(M\right)\mathrm{d}M.\end{array}$$

(1)

Below, we introduce four different kinds of PBH mass functions.

• Monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$
  The simplest PBH mass function has the monochromatic form; in other words, all PBHs have the same mass $M_{\mathrm{c}}$, so we have

  $$\begin{array}{c}\hfill {\mathit{\psi }}_{\mathrm{mon}}\left(M\right)=f_{\mathrm{PBH}}\mathit{\delta }(M-M_{\mathrm{c}}).\end{array}$$

  (2)
  This monochromatic mass function is usually used as a toy model in PBH physics, serving as a first step in more realistic models. In such models, PBHs with different masses may have extended mass functions, and ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$ can be regarded as the limit of these extended mass functions, if the PBH masses are nearly equal.
• Log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$
  The most frequently-used extended mass function is the log-normal one [118], in which the probability distribution function (PDF) of PBH mass is the normal distribution on the logarithmic mass axis. Hence, the PBH mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ is

  $$\begin{array}{c}\hfill {\mathit{\psi }}_{\mathrm{LN}}\left(M\right)={\displaystyle \frac{f_{\mathrm{PBH}}}{\sqrt{2\mathit{\pi }}\mathit{\sigma }M}}exp\left[-{\displaystyle \frac{{\ln }^2(M/M_{\mathrm{c}})}{2{\mathit{\sigma }}^2}}\right],\end{array}$$

  (3)

  where $M_{\mathrm{c}}$ is the characteristic mass of PBHs, and $\mathit{\sigma }$ is the width of the mass distribution (i.e., the PBH mass spread). Thus, ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ satisfies the PBH abundance in Equation (1).
• Skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$
  Furthermore, we may consider a more complex skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$, which allows a deviation from the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ [119],

  $$\begin{array}{c}\hfill {\mathit{\psi }}_{\mathrm{SL}}\left(M\right)={\mathit{\psi }}_{\mathrm{LN}}\left(M\right)\left\{1+\mathrm{erf}\left[A{\displaystyle \frac{\ln (M/M_{\mathrm{c}})}{\sqrt{2}\mathit{\sigma }}}\right]\right\},\end{array}$$

  (4)

  where $\mathrm{erf}\left(x\right)={\displaystyle \frac{2}{\sqrt{\mathit{\pi }}}}{\int }_0^x{e}^{-t^2}\mathrm{d}t$ is the error function, and a new parameter A indicates the skewness from the log-normal mass distribution.
• Power-law mass function ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$
  Another typical extended mass function has a truncated power-law form [120],

  $$\begin{array}{c}\hfill {\mathit{\psi }}_{\mathrm{PL}}\left(M\right)\propto M^{\mathit{\gamma }-1}(M_{\min }<M<M_{\max }),\end{array}$$

  (5)

  where $M_{\min }$ and $M_{\max }$ are the lower and upper bounds of PBH masses. From the relation in Equation (1), the coefficient of proportionality in Equation (5) is $\mathit{\gamma }{f}_{\mathrm{PBH}}/(M_{\max }^{\mathit{\gamma }}-M_{\min }^{\mathit{\gamma }})$ when $\mathit{\gamma }\ne 0$ or $f_{\mathrm{PBH}}/\ln (M_{\max }/M_{\min })$ when $\mathit{\gamma }=0$. Therefore, the power-law mass function is still a two-parameter model essentially.
  To compare with the log-normal mass function, we may define an effective characteristic mass $M_{\mathrm{c}}$ and its variance ${\mathit{\sigma }}^2$ for the power-law mass function [120],

  $$\begin{array}{c}\hfill \ln M_{\mathrm{c}}\equiv {⟨\ln M⟩}_{\mathit{\psi }},{\mathit{\sigma }}^2\equiv {⟨{\ln }^{2}M⟩}_{\mathit{\psi }}-{⟨\ln M⟩}_{\mathit{\psi }}^2,\end{array}$$

  (6)

  where the average of a quantity X is defined as

  $$\begin{array}{c}\hfill {⟨X⟩}_{\mathit{\psi }}\equiv {\displaystyle \frac{1}{f_{\mathrm{PBH}}}}\int \mathrm{d}M\mathit{\psi }\left(M\right)X\left(M\right).\end{array}$$
  By this means, for the power-law mass function, we obtain $M_{\mathrm{c}}=M_{\mathrm{cut}}{e}^{-1/\mathit{\gamma }}$ and $\mathit{\sigma }=1/|\mathit{\gamma }|$, where $M_{\mathrm{cut}}$ stands for $M_{\max }$ when $\mathit{\gamma }>0$ or $\max (M_{\min },M_{\ast })$ when $\mathit{\gamma }<0$, since the PBH mass should necessarily be larger than $M_{\ast }\sim {10}^{15}\mathrm{g}$ (i.e., the mass of the PBHs evaporating at the present epoch) [120].

Altogether, we have listed four different PBH mass functions, as shown in Figure 1. The monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$ is a one-parameter model, the log-normal and power-law mass functions ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ and ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ are two-parameter models, and the skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ is a three-parameter model, respectively. We will explore their effects in constraining the PBHs in Section 5 in order.

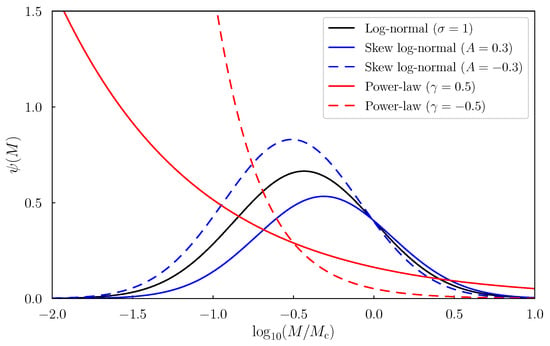
Figure 1. Different PBH mass functions. The black line is the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, with $\mathit{\sigma }=1$; the solid and dashed blue lines represent the skew log-normal mass functions ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$, with the same $\mathit{\sigma }$ and $A=0.3$ and $-0.3$; the solid and dashed red lines correspond to the power-law mass functions ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$, with $\mathit{\gamma }=0.5$ and $-0.5$ (for simplicity, we do not show the lower and upper bounds $M_{\min }$ and $M_{\max }$ on the mass axis).

3. GL

In this section, we first introduce the time delay function from the lens equation, and then derive the lensing optical depth, which will be used to calculate the event rate of lensed FRBs in the next section.

3.1. Lens Equation and Time Delay Function

In GL phenomenon, lights emitted from a distant source are deflected by the gravitational field of a massive lensing object, leading to a distorted (magnified or sheared) image or multiple images to the observer, along with a time delay in their arrivals.

The lens equation for the GL effect relates the angular position of the source $\mathit{\beta }$, the angular position of the image $\mathit{\theta }$, and the deflection angle $\hat{\mathit{\alpha }}$ [44,121], as shown in Figure 2,

$$\begin{array}{c}\hfill \mathit{\beta }=\mathit{\theta }-{\displaystyle \frac{D_{\mathrm{LS}}}{D_{\mathrm{S}}}}\hat{\mathit{\alpha }}.\end{array}$$

In particular, when the source is aligned with the lens and the observer (i.e., $\mathit{\beta }=\mathbf{0}$), we obtain the angular position of the image as the Einstein radius ${\mathit{\theta }}_{\mathrm{E}}$ for a point lens [66,122],

$$\begin{array}{c}\hfill {\mathit{\theta }}_{\mathrm{E}}=\sqrt{{\displaystyle \frac{4GM}{c^2}}{\displaystyle \frac{D_{\mathrm{LS}}}{D_{\mathrm{L}}{D}_{\mathrm{S}}}}},\end{array}$$

(7)

where G is gravitational constant, c is the speed of light, M is the mass of the lens, and $D_{\mathrm{LS}}$, $D_{\mathrm{L}}$, and $D_{\mathrm{S}}$ are the angular diameter distances from the source to the lens, from the lens to the observer, and from the source to the observer, respectively.

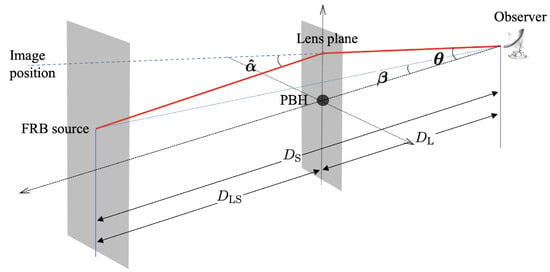
Figure 2. A diagram of GL effect, with a FRB as the source and a PBH as the lensing object. The diagram illustrates the geometric relation of the angular position of the source $\mathit{\beta }$, the angular position of the image $\mathit{\theta }$, and the deflection angle $\hat{\mathit{\alpha }}$. Meanwhile, the diagram shows the angular diameter distances from the source to the lens $D_{\mathrm{LS}}$, from the lens to the observer $D_{\mathrm{L}}$, and from the source and to observer $D_{\mathrm{S}}$, respectively.

Here, we should emphasize that the applicability of the lens equation is based on geometrical optics. However, if the mass M of the lens is tiny, the relevant physical Einstein radius $R_{\mathrm{E}}$ would be too small, even comparable to the wavelengths $\mathit{\lambda }$ of FRBs. Under this circumstance, wave optics is indispensable, especially in the microlensing observations [123].

From Equation (7), we have

$$\begin{array}{c}\hfill R_{\mathrm{E}}={\mathit{\theta }}_{\mathrm{E}}{D}_{\mathrm{L}}=\sqrt{{\displaystyle \frac{4GM}{c^2}}{\displaystyle \frac{D_{\mathrm{LS}}{D}_{\mathrm{L}}}{D_{\mathrm{S}}}}}\approx \sqrt{{\displaystyle \frac{4GM{D}_{\mathrm{L}}}{c^2}}},\end{array}$$

where we have used the approximation $D_{\mathrm{LS}}\approx D_{\mathrm{S}}\gg D_L$. The relevant Fresnel number is $F=R_{\mathrm{E}}^2/(\mathit{\lambda }{D}_{\mathrm{L}})$ [124]. Then, we take F to be unity as the criterion and obtain $M=\mathit{\lambda }{c}^2/\left(4G\right)$. As the typical values of $\mathit{\lambda }$ are around 0.2 m, we have $M\sim {10}^{-5}{M}_{\odot }$. Since it is much smaller than the lower bound of $1M_{\odot }$ as we will consider in this work, there is no necessity of wave optics, and geometrical optics is already sufficient.

In GL effect, lights from different paths will reach the observer at different times. Considering the cosmic expansion, the time delay between the arrivals of two images reads [66,122,125]

$$\begin{array}{c}\hfill \Delta t(M,z_{\mathrm{L}},y)={\displaystyle \frac{4GM}{c^3}}(1+z_{\mathrm{L}})\left[{\displaystyle \frac{y}{2}}\sqrt{y^2+4}+\ln \left({\displaystyle \frac{\sqrt{y^2+4}+y}{\sqrt{y^2+4}-y}}\right)\right],\end{array}$$

(8)

where $z_{\mathrm{L}}$ is the redshift of the lens, and $y\equiv \mathit{\beta }/{\mathit{\theta }}_{\mathrm{E}}$ is the dimensionless impact parameter, indicating the relative position of the source in the lens plane.

Next, we discuss the range of y. On the one hand, if two images of different sizes are produced in GL effect, we usually measure them by the magnification $\mathit{\mu }$. The ratio $R_{\mathrm{f}}$ of the magnifications of the two images ${\mathit{\mu }}_{+}$ and ${\mathit{\mu }}_{-}$ can be obtained as [125]

$$\begin{array}{c}\hfill R_{\mathrm{f}}=\left|{\displaystyle \frac{{\mathit{\mu }}_{+}}{{\mathit{\mu }}_{-}}}\right|={\displaystyle \frac{y^2+2+y\sqrt{y^2+4}}{y^2+2-y\sqrt{y^2+4}}}>1.\end{array}$$

Typically, the threshold of $R_{\mathrm{f}}$ is selected as $\overline{R_{\mathrm{f}}}=5$ [122], meaning that the ratio of the magnifications of the two images cannot be too large, otherwise the dimmer image will be too small to be detected. This threshold serves as a constraint on the maximum time delay, corresponding to the maximum impact parameter as $y_{\max }\left(\overline{R_{\mathrm{f}}}\right)={[(1+{\overline{R}}_{\mathrm{f}})/\sqrt{{\overline{R}}_{\mathrm{f}}}-2]}^{1/2}$. On the other hand, the observed time delay $\Delta t$ must be larger than certain reference time $\overline{\Delta t}$, so that the lensed images can be resolved by a telescope. This will lead to the minimum impact parameter $y_{\min }(M,z_{\mathrm{L}},\overline{\Delta t})$, which can be obtained from Equation (8) numerically. In general, for the lensing systems with the PBH masses in the range of 1–$100M_{\odot }$, the time delay between multiple images is $\overline{\Delta t}\sim 0.1\mathrm{ms}$ [126,127].

3.2. Lensing Optical Depth

Now, we turn to the lensing optical depth. First, for simplicity, we assume that all PBHs as lensing objects have the same mass M (i.e., the PBH mass function is monochromatic). Thus, the comoving number density $n_{\mathrm{L}}$ of the PBHs is

$$\begin{array}{c}\hfill n_{\mathrm{L}}\left(f_{\mathrm{PBH}}\right)={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{PBH}}}{M}}={\displaystyle \frac{f_{\mathrm{PBH}}{\mathit{\rho }}_{\mathrm{DM}}}{M}}={\displaystyle \frac{f_{\mathrm{PBH}}{\Omega }_{\mathrm{DM}}{\mathit{\rho }}_{\mathrm{cr}}}{M}}={\displaystyle \frac{f_{\mathrm{PBH}}{\Omega }_{\mathrm{DM}}}{M}}{\displaystyle \frac{3H_0^2}{8\mathit{\pi }G}},\end{array}$$

(9)

where ${\Omega }_{\mathrm{DM}}\equiv {\mathit{\rho }}_{\mathrm{DM}}/{\mathit{\rho }}_{\mathrm{cr}}=0.24$ is the DM density fraction, and ${\mathit{\rho }}_{\mathrm{cr}}\equiv 3H_0^2/(8\mathit{\pi }G)$ is the present critical density of the Universe, with $H_0=67.4\pm 0.5\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ being the Hubble constant [1]. Second, the lensing cross section ${\mathit{\sigma }}_{\mathrm{L}}$, which encodes the ability to deflect light by PBHs, can be obtained as [122,125,126],

$$\begin{array}{c}\hfill {\mathit{\sigma }}_{\mathrm{L}}(M,z_{\mathrm{L}},z_{\mathrm{S}},\overline{\Delta t})={\displaystyle \frac{4\mathit{\pi }GM}{c^2}}{\displaystyle \frac{D_{\mathrm{LS}}{D}_{\mathrm{L}}}{D_{\mathrm{S}}}}\left[y_{\max }^2\left({\overline{R}}_{\mathrm{f}}\right)-y_{\min }^2(M,z_{\mathrm{L}},\overline{\Delta t})\right],\end{array}$$

(10)

where $z_{\mathrm{S}}$ is the redshift of the source.

In Section 4, when computing the lensing probability of FRBs by the PBHs, we need to study the opacity of the Universe, which is characterized as the lensing optical depth $\mathit{\tau }$ [122],

$$\begin{array}{c}\hfill \mathit{\tau }(M,f_{\mathrm{PBH}},z_{\mathrm{S}},\overline{\Delta t})={\int }_0^{z_{\mathrm{S}}}\mathrm{d}\mathit{\chi }\left(z_{\mathrm{L}}\right)n_{\mathrm{L}}\left(f_{\mathrm{PBH}}\right){(1+z_{\mathrm{L}})}^2{\mathit{\sigma }}_{\mathrm{L}}(M,z_{\mathrm{L}},z_{\mathrm{S}},\overline{\Delta t}),\end{array}$$

(11)

where $\mathit{\chi }\left(z_{\mathrm{L}}\right)$ denotes the comoving distance of the lens,

$$\begin{array}{c}\hfill \mathit{\chi }\left(z_{\mathrm{L}}\right)=c{\int }_0^{z_{\mathrm{L}}}{\displaystyle \frac{\mathrm{d}{z}^{\prime }}{H\left(z^{\prime }\right)}},\end{array}$$

(12)

with $H\left(z\right)$ being the Hubble expansion rate in terms of the redshift z. From Equation (11), it is easy to see that the lensing optical depth $\mathit{\tau }$ is dimensionless.

Then, substituting $n_{\mathrm{L}}$ in Equation (9), ${\mathit{\sigma }}_{\mathrm{L}}$ in Equation (10), and $\mathit{\chi }$ in Equation (12) into Equation (11), we obtain the lensing optical depth $\mathit{\tau }$ for the monochromatic PBH mass function as

$$\begin{array}{cc}\hfill \mathit{\tau }(M,f_{\mathrm{PBH}},z_{\mathrm{S}},\overline{\Delta t})& ={\displaystyle \frac{3}{2}}{\Omega }_{\mathrm{DM}}{f}_{\mathrm{PBH}}{\int }_0^{z_{\mathrm{S}}}\mathrm{d}{z}_{\mathrm{L}}{\displaystyle \frac{H_0^2}{cH\left(z_{\mathrm{L}}\right)}}{\displaystyle \frac{D_{\mathrm{LS}}{D}_{\mathrm{L}}}{D_{\mathrm{S}}}}{(1+z_{\mathrm{L}})}^2\hfill \\ \hfill & \times \left[y_{\max }^2\left({\overline{R}}_{\mathrm{f}}\right)-y_{\min }^2(M,z_{\mathrm{L}},\overline{\Delta t})\right].\hfill \end{array}$$

(13)

Naturally, if the PBH mass function is not monochromatic, the lensing optical depth can be generalized by replacing the constant PBH abundance $f_{\mathrm{PBH}}$ in Equation (13) to an integral of the PBH extended mass function $\int \mathrm{d}M\mathit{\psi }\left(M\right)$ [126],

$$\begin{array}{cc}\hfill \mathit{\tau }(\mathit{\psi }\left(M\right),z_{\mathrm{S}},\overline{\Delta t})& ={\displaystyle \frac{3}{2}}{\Omega }_{\mathrm{DM}}\int \mathrm{d}M\mathit{\psi }\left(M\right){\int }_0^{{\mathrm{z}}_{\mathrm{S}}}\mathrm{d}{z}_{\mathrm{L}}{\displaystyle \frac{H_0^2}{cH\left(z_{\mathrm{L}}\right)}}{\displaystyle \frac{D_{\mathrm{LS}}{D}_{\mathrm{L}}}{D_{\mathrm{S}}}}{(1+z_{\mathrm{L}})}^2\hfill \\ \hfill & \times \left[y_{\max }^2\left({\overline{R}}_{\mathrm{f}}\right)-y_{\min }^2(M,z_{\mathrm{L}},\overline{\Delta t})\right].\hfill \end{array}$$

(14)

4. FRBs

In this section, we first explain the redshift PDF of FRBs in detail, and then provide the most important quantity in our work, the event rate of lensed FRBs.

4.1. Redshift PDF of FRBs

In general, the number of FRBs $\mathrm{d}N$ is proportional to their redshift interval $\mathrm{d}{z}_{\mathrm{S}}$ and the observation time $\mathrm{d}{t}_{\mathrm{obs}}$. Their ratio is encoded in the redshift PDF of FRBs $N\left(z_{\mathrm{S}}\right)$ [128],

$$\begin{array}{c}\hfill N\left(z_{\mathrm{S}}\right)\propto {\displaystyle \frac{\mathrm{d}N}{\mathrm{d}{t}_{\mathrm{obs}}\mathrm{d}{z}_{\mathrm{S}}}}={\displaystyle \frac{\mathrm{d}t}{\mathrm{d}{t}_{\mathrm{obs}}}}{\displaystyle \frac{\mathrm{d}V}{\mathrm{d}{z}_{\mathrm{S}}}}{\displaystyle \frac{\mathrm{d}N}{\mathrm{d}t\mathrm{d}V}},\end{array}$$

(15)

where $N\left(z_{\mathrm{S}}\right)$ is decomposed as a product of three factors: the first one $\mathrm{d}t/\mathrm{d}{t}_{\mathrm{obs}}=1/(1+z_{\mathrm{S}})$ is due to the cosmic time dilation, the second one is the comoving volume per unit redshift $\mathrm{d}V/\mathrm{d}{z}_{\mathrm{S}}=4\mathit{\pi }{\mathit{\chi }}^2\left(z_{\mathrm{S}}\right)c/H\left(z_{\mathrm{S}}\right)$, and the third one $\mathrm{d}N/\left(\mathrm{d}t\mathrm{d}V\right)$ is the intrinsic event rate density of FRBs (also as a function of $z_{\mathrm{S}}$). The coefficient of proportionality in Equation (15) will ensure the normalization condition as $\int \mathrm{d}{z}_{\mathrm{S}}N\left(z_{\mathrm{S}}\right)=1$.

Furthermore, $\mathrm{d}N/\left(\mathrm{d}t\mathrm{d}V\right)$ can be shown to be proportional to the variation rate ${\dot{\mathit{\rho }}}_{\ast }$ of the comoving mass density of stars, which includes both long-lived stars and stellar remnants, such as white dwarfs, neutron stars, and black holes [129,130,131,132,133]. According to the specific forms of ${\dot{\mathit{\rho }}}_{\ast }$, the redshift PDF of FRBs $N\left(z_{\mathrm{S}}\right)$ can be classified into different types. Below, we list three frequently-used ones.

• In the simplest case with ${\dot{\mathit{\rho }}}_{\ast }=\mathrm{const}.$, the redshift PDF of FRBs $N_{\mathrm{const}}\left(z_{\mathrm{S}}\right)$ is [126,134]

  $$\begin{array}{c}\hfill N_{\mathrm{const}}\left(z_{\mathrm{S}}\right)={\mathcal{N}}_{\mathrm{const}}{\displaystyle \frac{{\mathit{\chi }}^2\left(z_{\mathrm{S}}\right)}{H\left(z_{\mathrm{S}}\right)(1+z_{\mathrm{S}})}}exp\left[-{\displaystyle \frac{d_{\mathrm{L}}^2\left(z_{\mathrm{S}}\right)}{2d_{\mathrm{L}}^2\left(z_{\mathrm{cut}}\right)}}\right].\end{array}$$

  (16)
  Above, a Gaussian cutoff factor is introduced to reflect the threshold of the instrumental signal-to-noise ratio, where $d_{\mathrm{L}}\left(z_{\mathrm{S}}\right)=(1+z_{\mathrm{S}})\mathit{\chi }\left(z_{\mathrm{S}}\right)$ is the luminosity distance, and $z_{\mathrm{cut}}$ is the cutoff redshift. When choosing $z_{\mathrm{cut}}=0.5$, $N_{\mathrm{const}}\left(z_{\mathrm{S}}\right)$ can be fitted to the current FRB catalog [122]. Moreover, the coefficient of proportionality in Equation (15) is now absorbed in the normalization factor ${\mathcal{N}}_{\mathrm{const}}$.
• In more realistic models, FRBs are believed to originate from the evolutionary process of stars. In other words, the variation rate ${\dot{\mathit{\rho }}}_{\ast }$ also depends on redshift $z_{\mathrm{S}}$, following the SFH in the Universe [99,135],

  $$\begin{array}{c}\hfill {\dot{\mathit{\rho }}}_{\ast \mathrm{SFH}}\left(z_{\mathrm{S}}\right)\propto {\displaystyle \frac{{(1+z_{\mathrm{S}})}^{2.6}}{1+{[(1+z_{\mathrm{S}})/3.2]}^{6.2}}}.\end{array}$$
  Hence, the redshift PDF of FRBs can be generalized to

  $$\begin{array}{c}\hfill N_{\mathrm{SFH}}\left(z_{\mathrm{S}}\right)={\mathcal{N}}_{\mathrm{SFH}}{\displaystyle \frac{{\dot{\mathit{\rho }}}_{\ast \mathrm{SFH}}\left(z_{\mathrm{S}}\right){\mathit{\chi }}^2\left(z_{\mathrm{S}}\right)}{H\left(z_{\mathrm{S}}\right)(1+z_{\mathrm{S}})}}exp\left[-{\displaystyle \frac{d_{\mathrm{L}}^2\left(z_{\mathrm{S}}\right)}{2d_{\mathrm{L}}^2\left(z_{\mathrm{cut}}\right)}}\right],\end{array}$$

  (17)

  where ${\mathcal{N}}_{\mathrm{SFH}}$ is the normalization factor.
• Besides, Ref. [128] also provided several different redshift distribution models based on the corrected SFH. After the Kolmogorov–Smirnov test, a TSRD model was found to best fit the data, which predicts more (or fewer) FRBs at smaller (or larger) redshifts compared with the SFH model, and is parameterized as

  $$\begin{array}{c}\hfill {\dot{\mathit{\rho }}}_{\ast \mathrm{TSRD}}\left(z_{\mathrm{S}}\right)\propto {\displaystyle \frac{{(1+z_{\mathrm{S}})}^a}{1+{[(1+z_{\mathrm{S}})/C]}^{a+b}}},\end{array}$$

  with the model parameters as $a=1.3$, $b=5.8$, and $C=4.2$ [128]. Thus, the redshift PDF of FRBs in the TSRD model reads

  $$\begin{array}{c}\hfill N_{\mathrm{TSRD}}\left(z_{\mathrm{S}}\right)={\mathcal{N}}_{\mathrm{TSRD}}{\displaystyle \frac{{\dot{\mathit{\rho }}}_{\ast \mathrm{TSRD}}\left(z_{\mathrm{S}}\right){\mathit{\chi }}^2\left(z_{\mathrm{S}}\right)}{H\left(z_{\mathrm{S}}\right)(1+z_{\mathrm{S}})}}exp\left[-{\displaystyle \frac{d_{\mathrm{L}}^2\left(z_{\mathrm{S}}\right)}{2d_{\mathrm{L}}^2\left(z_{\mathrm{cut}}\right)}}\right],\end{array}$$

  (18)

  where ${\mathcal{N}}_{\mathrm{TSRD}}$ is the normalization factor.

The redshift PDFs of FRBs in the above three models are shown in Figure 3. We observe that the constant ${\dot{\mathit{\rho }}}_{\ast }$ and SFH models (the dashed and dotted lines) predict more FRBs at lower and higher redshifts, and the TSRD model (the solid line) is located between them.

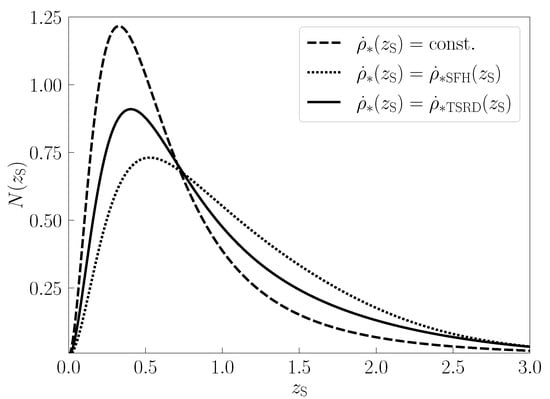
Figure 3. The redshift PDFs of FRBs in the constant ${\dot{\mathit{\rho }}}_{\ast }$ model (the dashed line), SFH model (the dotted line), and the TSRD model (the solid line). The redshift PDF in TSRD model lies between the other two models. Moreover, all three redshift PDFs become tiny when the redshift $z_{\mathrm{S}}$ is beyond 3.

4.2. Event Rate of Lensed FRBs

Finally, we explore the event rate of lensed FRBs, by which the PBH mass function will be constrained in the next section.

First, the integral lensing optical depth $\overline{\mathit{\tau }}$ can be obtained via an integral of the lensing optical depth $\mathit{\tau }$ in Equation (14), multiplied with the redshift PDF of FRBs $N\left(z_{\mathrm{S}}\right)$ in Equation (15) [122],

$$\begin{array}{c}\hfill \overline{\mathit{\tau }}(\mathit{\psi }\left(M\right),f_{\mathrm{PBH}},\overline{\Delta t})=\int \mathrm{d}{z}_{\mathrm{S}}\mathit{\tau }(\mathit{\psi }\left(M\right),f_{\mathrm{PBH}},z_{\mathrm{S}},\overline{\Delta t})N\left(z_{\mathrm{S}}\right).\end{array}$$

(19)

From Figure 3, we see that all the three redshift PDFs become negligible when $z_{\mathrm{S}}>3$, so for the calculations in Section 5, the integral interval in Equation (19) can be safely set from 0 to 4, in order to include as many FRBs as possible across different redshifts. Moreover, since both $\mathit{\tau }$ and $N\left(z_{\mathrm{S}}\right)$ are dimensionless quantities, $\overline{\mathit{\tau }}$ is also dimensionless.

When lensed FRBs events occur, we denote their number as $N_{\mathrm{FRB}}^{\mathrm{lensed}}$, and its ratio to the total number of FRB events $N_{\mathrm{FRB}}$ is the event rate of lensed FRBs (i.e., the lensing probability). Usually, we consider that the PBHs as the lensing objects are in an optically thin regime, which is primarily defined by demanding the lensing optical depth $\mathit{\tau }\ll 1$. In this case, we believe that the radiation passing through this medium merely experiences very little attenuation, and most of the radiation can penetrate without being significantly absorbed or scattered. Therefore, the lensing probability P can be expressed as [122,126,136]

$$\begin{array}{c}\hfill P=1-e^{-\overline{\mathit{\tau }}}\approx \overline{\mathit{\tau }}.\end{array}$$

Thus, the event rate of lensed FRBs is

$$\begin{array}{c}\hfill {\displaystyle \frac{N_{\mathrm{FRB}}^{\mathrm{lensed}}}{N_{\mathrm{FRB}}}}\approx \overline{\mathit{\tau }},\end{array}$$

which is just the integral lensing optical depth $\overline{\mathit{\tau }}$ in Equation (19).

5. Constraints on the PBH Mass Functions

With all the preparations above, in this section, we will constrain the four different PBH mass functions $\mathit{\psi }\left(M\right)$ introduced in Section 2 via the event rate of lensed FRBs $\overline{\mathit{\tau }}$. Here, we should first make clear the physical meaning of our constraints. Although the current average annual observation from CHIME is approximately 1000 FRBs [78,79,80,81,82], no lensed FRB events have been detected so far [137,138]. Consequently, we are unable to constrain $\mathit{\psi }\left(M\right)$ directly from real observational data. However, if the PBH abundance $f_{\mathrm{PBH}}$ is given, $\overline{\mathit{\tau }}$ can be obtained from the integral of the lensing optical depth $\mathit{\tau }$. Conversely, by giving the values of $\overline{\mathit{\tau }}$, we can determine $f_{\mathrm{PBH}}$ the allowed parameter ranges in $\mathit{\psi }\left(M\right)$. This is what we mean by “constraints”. Below, we focus on the PBHs with the abundance $f_{\mathrm{PBH}}=0.01$ and their characteristic masses from 1 to $100M_{\odot }$. The basic reasons for choosing this mass range are twofold. First, if the PBH mass is too small, its GL effect will be tiny. (For example, the Schwarzschild radius of an asteroid with the mass of ${10}^{20}$ g is merely the size of an atom.) Therefore, the GL constraints on $f_{\mathrm{PBH}}$ are usually suitable for the PBHs with masses over $1M_{\odot }$. Second, for even larger PBHs (e.g., with the mass around $1000M_{\odot }$), the gravitational-wave constraints on $f_{\mathrm{PBH}}$ is more stringent. In this mass range, PBHs have been ruled out as a candidate of DM. Nevertheless, the GL constraints can still be considered as a complementary method. Altogether, the GL constraints on $f_{\mathrm{PBH}}$ are most effective in the mass range from 1 to $100M_{\odot }$.

5.1. Monochromatic Mass Function

Due to the simplicity of the monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$ in Equation (2), it is often used as the starting point to constrain the PBH abundance. Substituting Equation (2) into Equations (13) and (19) and considering the three different redshift PDFs of FRBs in Equations (16)–(18), we obtain the mass dependence of the event rate of lensed FRBs $\overline{\mathit{\tau }}$ in Figure 4, with the dashed line for the constant ${\dot{\mathit{\rho }}}_{\ast }$ model, the dotted line for the SFH model, and the solid line for the TSRD model, respectively.

Figure 4. The event rate of lensed FRBs (i.e., the integral lensing optical depth) $\overline{\mathit{\tau }}$ as a function of the PBH mass $M_{\mathrm{c}}$ for the monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$, with three different redshift PDFs of FRBs: the constant ${\dot{\mathit{\rho }}}_{\ast }$ model (the dashed line), the SFH model (the dotted line), and the TSRD model (the solid line), respectively. Here, we consider the PBH mass range in 1–$100M_{\odot }$ and set the PBH abundance as $f_{\mathrm{PBH}}=0.01$. The TSRD model predicts a moderate $\overline{\mathit{\tau }}$ between the results from the constant ${\dot{\mathit{\rho }}}_{\ast }$ and the SFH models.

From Figure 4, we find that $\overline{\mathit{\tau }}$ first increases monotonically as expected, and then approaches a constant when the PBH mass is large enough. It is because once we fix $\Delta t$ in Equation (8), the minimum of the impact parameter $y_{\min }$ gradually tends to a very low constant as M increases. This further results in the lensing optical depth $\mathit{\tau }$ in Equation (13) and the integral lensing optical depth $\overline{\mathit{\tau }}$ in Equation (19) being almost constant at large masses. For example, $\overline{\mathit{\tau }}$ is around $6.5\times {10}^{-4}$ in the TSRD model when the PBH mass is larger than $10M_{\odot }$, meaning that if 10,000 FRBs are observed in future, no more than 7 lensed events will be detected. Moreover, the constant ${\dot{\mathit{\rho }}}_{\ast }$ and the SFH models predict the lowest and highest $\overline{\mathit{\tau }}$, with the result from the TSRD model between them, consistent with their redshift PDFs in Figure 3. Hence, the TSRD model not only best fits the experimental data in the Kolmogorov–Smirnov test, but also sets a moderate constraint on the PBH abundance for the monochromatic mass function, so in the following subsections, we will only consider the redshift PDF of FRBs in this model.

Furthermore, we can equivalently transform Figure 4 to the constraints on the PBH abundance $f_{\mathrm{PBH}}$. Now, in the TSRD model, we fix the event rate of lensed FRBs $\overline{\mathit{\tau }}$ to different values and show $f_{\mathrm{PBH}}$ as a function of the PBH mass $M_{\mathrm{c}}$ in Figure 5. We observe that $f_{\mathrm{PBH}}$ is a monotonically decreasing function of $M_{\mathrm{c}}$, and when $M_{\mathrm{c}}\gtrsim 10M_{\odot }$, $f_{\mathrm{PBH}}$ approaches a constant. Such constraints on $f_{\mathrm{PBH}}$ are consistent with the previous analysis in Ref. [136]. For instance, if we assume $\overline{\mathit{\tau }}<{10}^{-4}$, we will have $f_{\mathrm{PBH}}<{10}^{-2.5}$ in most of the PBH mass range from 1 to $100M_{\odot }$. While, if future observations detect more than one lensed event among 10,000 FRBs, the constraint on $f_{\mathrm{PBH}}$ in the relevant mass range will be relaxed accordingly.

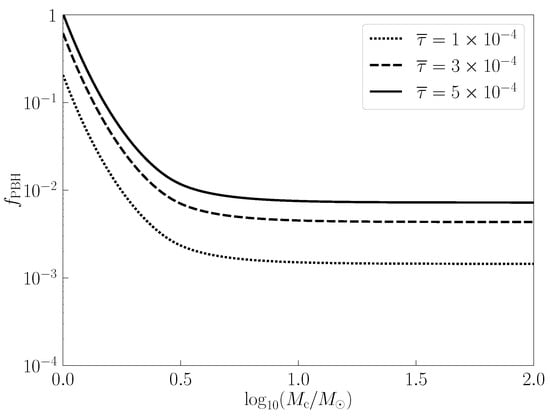
Figure 5. The PBH abundance $f_{\mathrm{PBH}}$ as a function of the PBH mass $M_{\mathrm{c}}$ for the monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$ in the TSRD model, with the event rate of lensed FRBs $\overline{\mathit{\tau }}$ fixed to different values of ${10}^{-4}$, $3\times {10}^{-4}$, and $5\times {10}^{-4}$, respectively. We observe that $f_{\mathrm{PBH}}$ monotonically decreases with $M_{\mathrm{c}}$ and approaches a constant when $M_{\mathrm{c}}\gtrsim 10M_{\odot }$, consistent with the almost constant $\overline{\mathit{\tau }}$ at large masses in Figure 4.

5.2. Log-Normal Mass Function

Now, we turn to the more realistic log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ in Equation (3). This is a two-parameter model (i.e., the characteristic mass $M_{\mathrm{c}}$ and the width of the mass distribution $\mathit{\sigma }$), so when referring to the constraints on ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, we mean to determine the allowed parameter space of $M_{\mathrm{c}}$ and $\mathit{\sigma }$, if the event rate of lensed FRBs $\overline{\mathit{\tau }}$ is given. Same as before, from Equations (3), (14) and (19), we first show the dependence of $\overline{\mathit{\tau }}$ on $M_{\mathrm{c}}$ in Figure 6. This is an extension of Figure 4, but with different values of $\mathit{\sigma }$. Obviously, the solid line with $\mathit{\sigma }=0$ is just the solid line obtained from the TSRD model for the monochromatic mass function in Figure 4. Also, with $\mathit{\sigma }$ increasing, $\overline{\mathit{\tau }}$ increases more slowly.

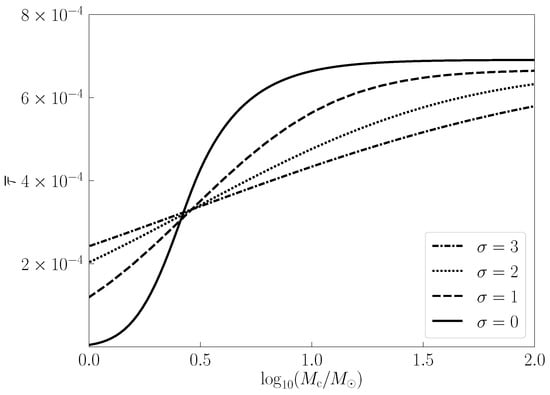
Figure 6. Same as Figure 4, but for the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, with different width of mass distribution $\mathit{\sigma }=0$, 1, 2, and 3, respectively. When $\mathit{\sigma }=0$, the solid line is the same as the solid line in Figure 4, as the log-normal mass function reduces to the monochromatic one. With $\mathit{\sigma }$ increasing, $\overline{\mathit{\tau }}$ increases more slowly.

Furthermore, we can show our results in a two-dimensional $M_{\mathrm{c}}$–$\mathit{\sigma }$ plane in Figure 7. The colors illustrate $\overline{\mathit{\tau }}$ from ${10}^{-4}$ to $7\times {10}^{-4}$, and the four curves correspond to four different values of $\overline{\mathit{\tau }}$ as $1/5000$, $1/4000$, $1/3000$, and $1/2000$, respectively. In other words, once the specific value of $\overline{\mathit{\tau }}$ is given, the allowed parameter ranges of $M_{\mathrm{c}}$ and $\mathit{\sigma }$ can be read from the relevant curve. From Figure 7, first, irrespective of the values of $\mathit{\sigma }$, $\overline{\mathit{\tau }}$ increases with $M_{\mathrm{c}}$ in all cases. This is expected, as larger PBHs always increase the lensing optical depth. At the lower right corner, where $M_{\mathrm{c}}$ is around $100M_{\odot }$ and $\mathit{\sigma }$ tends to 0 (i.e., the log-normal mass function reduces to be monochromatic), we have $\overline{\mathit{\tau }}\sim 6.5\times {10}^{-4}$, consistent with the result in Figure 4. Second but more interestingly, $\overline{\mathit{\tau }}$ is not a monotonic function of $\mathit{\sigma }$, as can be easily seen from the slopes of the four curves. When ${log}_{10}(M_{\mathrm{c}}/M_{\odot })\lesssim {10}^{0.5}$ (i.e., $M_{\mathrm{c}}\lesssim 3M_{\odot }$), the slopes are negative (the curves with $\overline{\mathit{\tau }}=1/5000$ and $1/4000$), so $\overline{\mathit{\tau }}$ increases with $\mathit{\sigma }$; on the contrary, when ${log}_{10}(M_{\mathrm{c}}/M_{\odot })\gtrsim {10}^{0.5}$ (i.e., $M_{\mathrm{c}}\gtrsim 3M_{\odot }$), the slopes are positive (the curves with $\overline{\mathit{\tau }}=1/2000$), so $\overline{\mathit{\tau }}$ decreases with $\mathit{\sigma }$. Such difference can also be seen in Figure 6 and is understandable. If the characteristic mass $M_{\mathrm{c}}$ is small, when the mass width $\mathit{\sigma }$ increases, the mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ broadens and spreads over a wider mass range. The influence from the even smaller PBHs is negligible, and the appearance of the larger PBHs has a greater impact, naturally enhancing the event rate of lensed FRBs $\overline{\mathit{\tau }}$. In contrast, if $M_{\mathrm{c}}$ is large, when $\mathit{\sigma }$ increases, $\overline{\mathit{\tau }}$ decreases. This is mainly because the log-normal form of the mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ extends more towards lower mass when $M_{\mathrm{c}}$ is large, so the smaller PBHs dominate the mass distribution, resulting in a decrease of $\overline{\mathit{\tau }}$. Altogether, the above two different trends explain the fan-shaped distribution of colors in Figure 7. In addition, when ${log}_{10}(M_{\mathrm{c}}/M_{\odot })\sim {10}^{0.5}$ (i.e., $M_{\mathrm{c}}\sim 3M_{\odot }$), a curve with $\overline{\mathit{\tau }}\sim 1/3000\sim 3\times {10}^{-4}$ is approximately perpendicular to the mass axis, explaining the coincidence of the four curves around the point $(0.5,3\times {10}^{-4})$ in Figure 6.

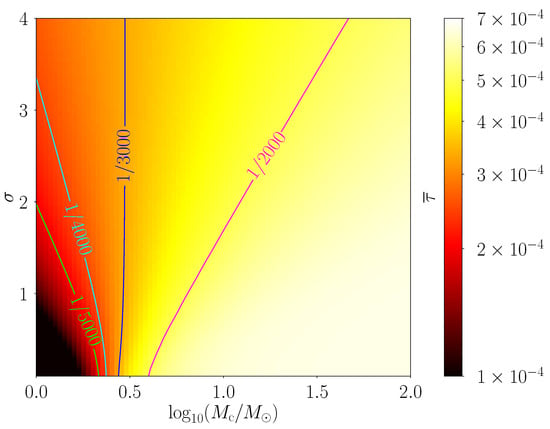
Figure 7. The event rate of lensed FRBs $\overline{\mathit{\tau }}$ in the two-dimensional parameter plane (i.e., the characteristic mass $M_{\mathrm{c}}$ and the width of the mass distribution $\mathit{\sigma }$) for the log-normal PBH mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$. The different colors illustrate $\overline{\mathit{\tau }}$ from ${10}^{-4}$ to $7\times {10}^{-4}$, with four curves corresponding to $\overline{\mathit{\tau }}=1/5000$, $1/4000$, $1/3000$, and $1/2000$, respectively. First, $\overline{\mathit{\tau }}$ monotonically increases with $M_{\mathrm{c}}$, as larger PBHs always enhance the lensing optical depth. Second, $\overline{\mathit{\tau }}$ increases with $\mathit{\sigma }$ when $M_{\mathrm{c}}$ is small, but decreases with $\mathit{\sigma }$ when $M_{\mathrm{c}}$ is large. Such discrepancy is due to the different distribution behaviors of ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ at small and large $M_{\mathrm{c}}$.

5.3. Skew Log-Normal Mass Function

Next, we continue to investigate the skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ in Equation (4), which is a three-parameter model, with $M_{\mathrm{c}}$ and $\mathit{\sigma }$ as those in the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ and a new parameter A characterizing the deviation from ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$. Therefore, we will focus on A and explore its impact on the event rate of lensed FRBs $\overline{\mathit{\tau }}$. Below, we set $A=0.3$ and $-0.3$, and our results are shown in Figure 8a and Figure 8b, respectively.

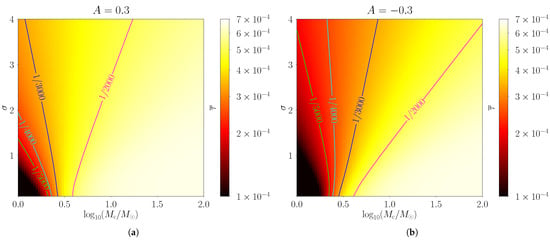
Figure 8. Same as Figure 7, but for the skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$, with the skew parameter $A=0.3$ and $-0.3$ in left and right panels, respectively. (a) When $A>0$, ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ is skewed rightwards compared with the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, and more PBHs are distributed at larger masses, resulting in a larger $\overline{\mathit{\tau }}$. Hence, the bright area in Figure 8a is larger than that in Figure 7, and all the curves rotate to the left. (b) When $A<0$, the situation is exactly the opposite.

From Figure 8a,b, we find that the influences on $\overline{\mathit{\tau }}$ from $M_{\mathrm{c}}$ and $\mathit{\sigma }$ are similar to those in the log-normal case in Section 5.2 as expected. Moreover, compared with Figure 7, the bright area in Figure 8a is larger, and all the curves clearly rotate to the left, indicating that $\overline{\mathit{\tau }}$ increases with the skew parameter A. This behavior can also be understood from the solid blue line in Figure 1. We see that, compared with the log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ with $A=0$ (the black line in Figure 1), when $A>0$, the skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ significantly shifts rightwards. Therefore, more PBHs are distributed at larger masses, resulting in a larger $\overline{\mathit{\tau }}$. In contrast, when $A<0$, ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ is skewed leftwards, and more PBHs are distributed at smaller masses, which in turn decreases $\overline{\mathit{\tau }}$, darkens the colors in Figure 8b, and rotates the curves to the right.

5.4. Power-Law Mass Function

Last, we consider the power-law mass function ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ in Equation (5), with our results plotted in Figure 9a with the power $\mathit{\gamma }>0$ and in Figure 9b with the power $\mathit{\gamma }<0$. Essentially, ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ is also a two-parameter model, and the effective characteristic mass $M_{\mathrm{c}}$ and the width of the mass distribution $\mathit{\sigma }$ can be obtained via Equation (6). Attention, in Figure 9a,b, we can merely determine the sign of $\mathit{\gamma }$, as its specific value varies with $M_{\mathrm{c}}$ and $\mathit{\sigma }$.

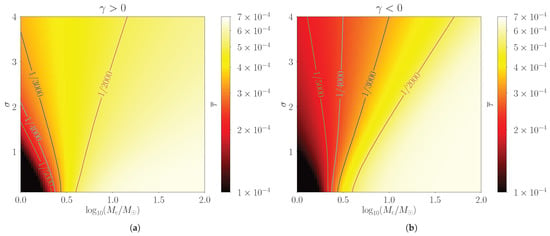
Figure 9. Same as Figure 8, but for the power-law mass function ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$. (a) When the power $\mathit{\gamma }>0$, Figure 9a looks quite like Figure 8a, because a positive power also shifts the PBH mass distribution to large mass region, and thus increases the event rate of lensed FRBs $\overline{\mathit{\tau }}$. (b) When $\mathit{\gamma }<0$, the situation is exactly the opposite.

Generally speaking, the distributions of the event rate of lensed FRBs $\overline{\mathit{\tau }}$ for the power-law mass function ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ are qualitatively analogous to those for the skew log-normal mass function ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$, since they both deviate from the log-normal one ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$ in the similar way. When $\mathit{\gamma }>0$, more PBHs are concentrated in the large mass region, as can be seen from the solid red line in Figure 1, so $\overline{\mathit{\tau }}$ can be enhanced accordingly. Therefore, Figure 9a quite resembles Figure 8a, with larger bright area compared with Figure 7 and the curves rotated to the left. Nevertheless, When $\mathit{\gamma }<0$, more PBHs have lower masses, as shown in the dashed red line in Figure 1, so $\overline{\mathit{\tau }}$ becomes smaller. Hence, Figure 9b is similar to Figure 8b, with darker colors and the curves rotated to the right.

6. Conclusions

In modern cosmology, PBHs and FRBs are receiving increasing interests due to the rapid developments in gravitational-wave physics and radio astronomy, and GL effect is an effective method to relate these two research areas, in which FRBs behave as the source, and PBHs play the role of lens. Consequently, the event rate of lensed FRBs (i.e., the integral lensing optical depth) $\overline{\mathit{\tau }}$ can be used as an efficient way to constrain the PBH abundance $f_{\mathrm{PBH}}$ and mass function $\mathit{\psi }\left(M\right)$.

On the one hand, due to the lack of the knowledge in the origin of FRBs, their redshift PDF $N\left(z_{\mathrm{S}}\right)$ is also unclear. Therefore, in this work, we investigate three different models for $N\left(z_{\mathrm{S}}\right)$: the constant ${\dot{\mathit{\rho }}}_{\ast }$ model, the SFH model, and the TSRD model. On the other hand, since PBHs have not been experimentally confirmed till now, we explore four different PBH mass functions: the monochromatic distribution ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$, the log-normal distribution ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, the skew log-normal distribution ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$, and the power-law distribution ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$, respectively. In these mass functions, the model parameters include the characteristic mass $M_{\mathrm{c}}$, the mass width $\mathit{\sigma }$, the skew parameter A, the power $\mathit{\gamma }$, etc. By “constraining the PBH mass functions”, we mean to determine the allowed ranges for the model parameters mentioned above, if the event rate of lensed FRBs $\overline{\mathit{\tau }}$ is given. By this means, we wish to provide a full picture and thorough understanding of the PBH abundance and mass distribution.

Our basic conclusions can be drawn as follows.

• For the simplest monochromatic mass function ${\mathit{\psi }}_{\mathrm{mon}}\left(M\right)$, we find that, if $f_{\mathrm{PBH}}$ is given, $\overline{\mathit{\tau }}$ increases with $M_{\mathrm{c}}$ and approaches a constant when $M_{\mathrm{c}}\gtrsim 10M_{\odot }$, as shown in Figure 4. Moreover, the TSRD model predicts a moderate $\overline{\mathit{\tau }}$, as its redshift PDF $N_{\mathrm{TSRD}}\left(z_{\mathrm{S}}\right)$ lies between those from the constant ${\dot{\mathit{\rho }}}_{\ast }$ and the SFH models, as shown in Figure 3. Equivalently, we also show the dependence of $f_{\mathrm{PBH}}$ on $M_{\mathrm{c}}$ in Figure 5, with $\overline{\mathit{\tau }}$ fixed. We observe that $f_{\mathrm{PBH}}$ decreases with $M_{\mathrm{c}}$ and approaches a constant when $M_{\mathrm{c}}\gtrsim 10M_{\odot }$.
• For the more realistic log-normal mass function ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, $\overline{\mathit{\tau }}$ can be obtained in the two-dimensional $M_{\mathrm{c}}$–$\mathit{\sigma }$ plane in Figure 7, with four curves corresponding to different values of $\overline{\mathit{\tau }}$. The allowed ranges of $M_{\mathrm{c}}$ and $\mathit{\sigma }$ can be obtained, once the specific value of $\overline{\mathit{\tau }}$ is given. When $M_{\mathrm{c}}\lesssim 3M_{\odot }$, the slopes of the curves are negative, meaning that $\overline{\mathit{\tau }}$ increases with $\mathit{\sigma }$, but when $M_{\mathrm{c}}\gtrsim 3M_{\odot }$, the situation is exactly the opposite. These different behaviors can be understood from the special log-normal form of ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$. Moreover, when $\mathit{\sigma }\to 0$, the result naturally reduces to the monochromatic case.
• The skew log-normal and power-law mass functions ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ and ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ can both be regarded as the extension of ${\mathit{\psi }}_{\mathrm{LN}}\left(M\right)$, and their results are similar. For positive A and $\mathit{\gamma }$, the mass distributions in ${\mathit{\psi }}_{\mathrm{SL}}\left(M\right)$ and ${\mathit{\psi }}_{\mathrm{PL}}\left(M\right)$ shift to larger masses, enhancing $\overline{\mathit{\tau }}$ accordingly. As a result, the colors in Figure 8a and Figure 9a are brighter than Figure 7, and the curves with fixed $\overline{\mathit{\tau }}$ rotate to the left. In contrast, for negative A and $\mathit{\gamma }$, the results are the opposite, as shown in Figure 8b and Figure 9b.

Altogether, in this work, we obtain the event rate of lensed FRBs $\overline{\mathit{\tau }}$ by integrating the lensing optical depth and redshift PDF of FRBs. The model parameters for different PBH mass functions can be read from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, if the PBH abundance $f_{\mathrm{PBH}}$ is given. Conversely, if $\overline{\mathit{\tau }}$ is fixed, $f_{\mathrm{PBH}}$ can also be constrained, as shown in Figure 5. Nonetheless, since no lensed FRB event has been detected by now, there is no reliable information of $\overline{\mathit{\tau }}$, and we merely know that its upper bound is less than ${10}^{-3}$. Therefore, finding such events is crucial in future FRB experiments, and if the lensed FRB events are confirmed, the constraints on $f_{\mathrm{PBH}}$ would be relatively relaxed. Here, we briefly give some experimental prospects [139]. Besides the CHIME, the European Very Long Baseline Interferometry Network (EVN) can also be applied to observe FRBs [140]. The EVN has very high angular resolution, allowing FRBs to be localized with milli-arcsecond precision. Consequently, once the CHIME detects an FRB, the EVN can perform rapid follow-up observations, particularly beneficial for studying repeating FRBs, and can be used for pinpointing the exact positions of FRBs. In addition, new facilities, including the Deep Synoptic Array-2000 [141], the Canadian Hydrogen Observatory and Radio transient Detector [142], and the Bustling Universe Radio Survey Telescope in Taiwan (BURSTT) [143] will jointly boost the annual FRB yield by orders of magnitude in the coming years. For instance, the BURSTT-2048 is expected to detect 24 lensed FRBs out of 1700 FRBs per year if $f_{\mathrm{PBH}}\sim 1$, and can thus constrain the PBH abundance with its mass even down to ${10}^{-4}{M}_{\odot }$.