Birth of an Isotropic and Homogeneous Universe with a Running Cosmological Constant
Abstract
1. Introduction
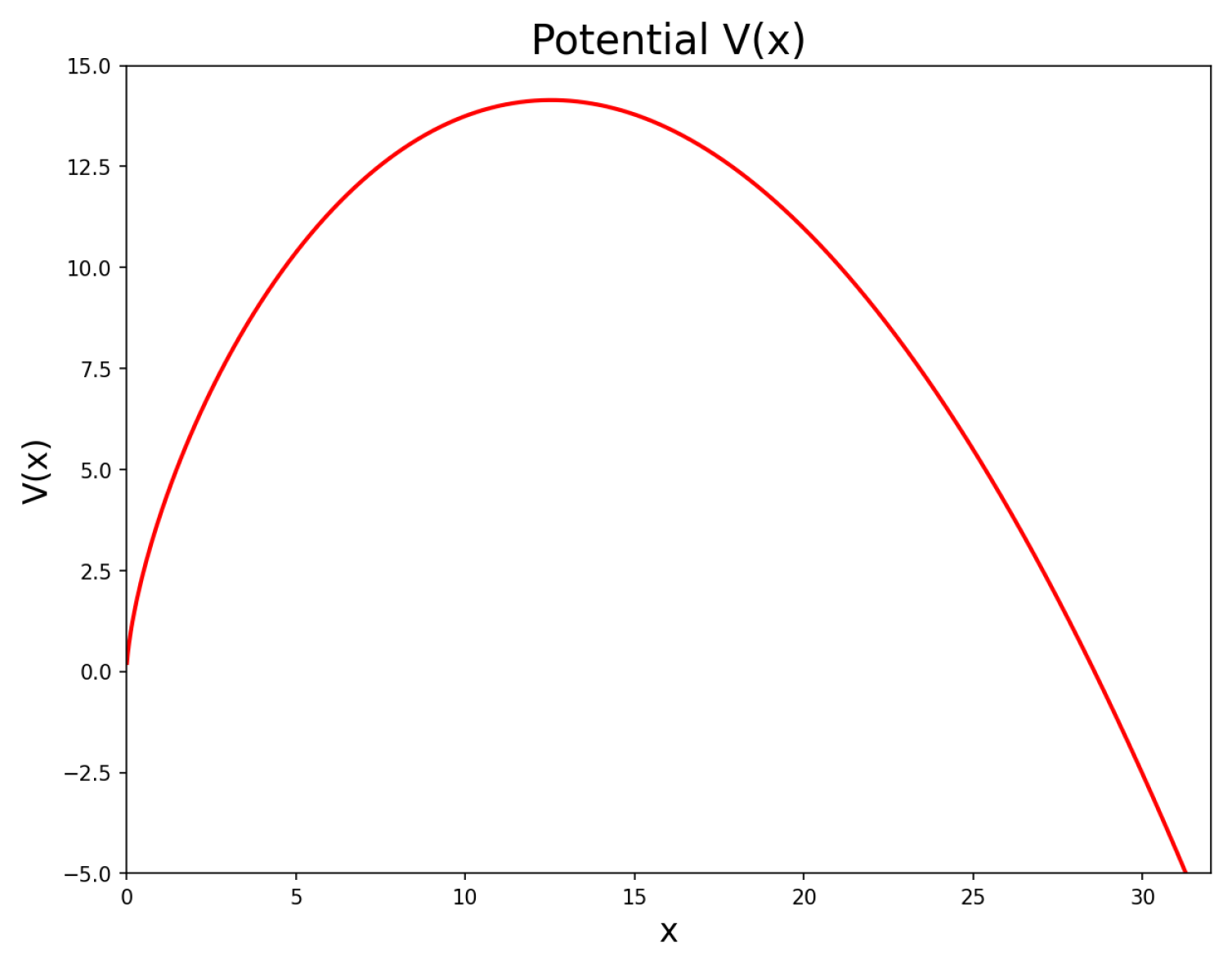
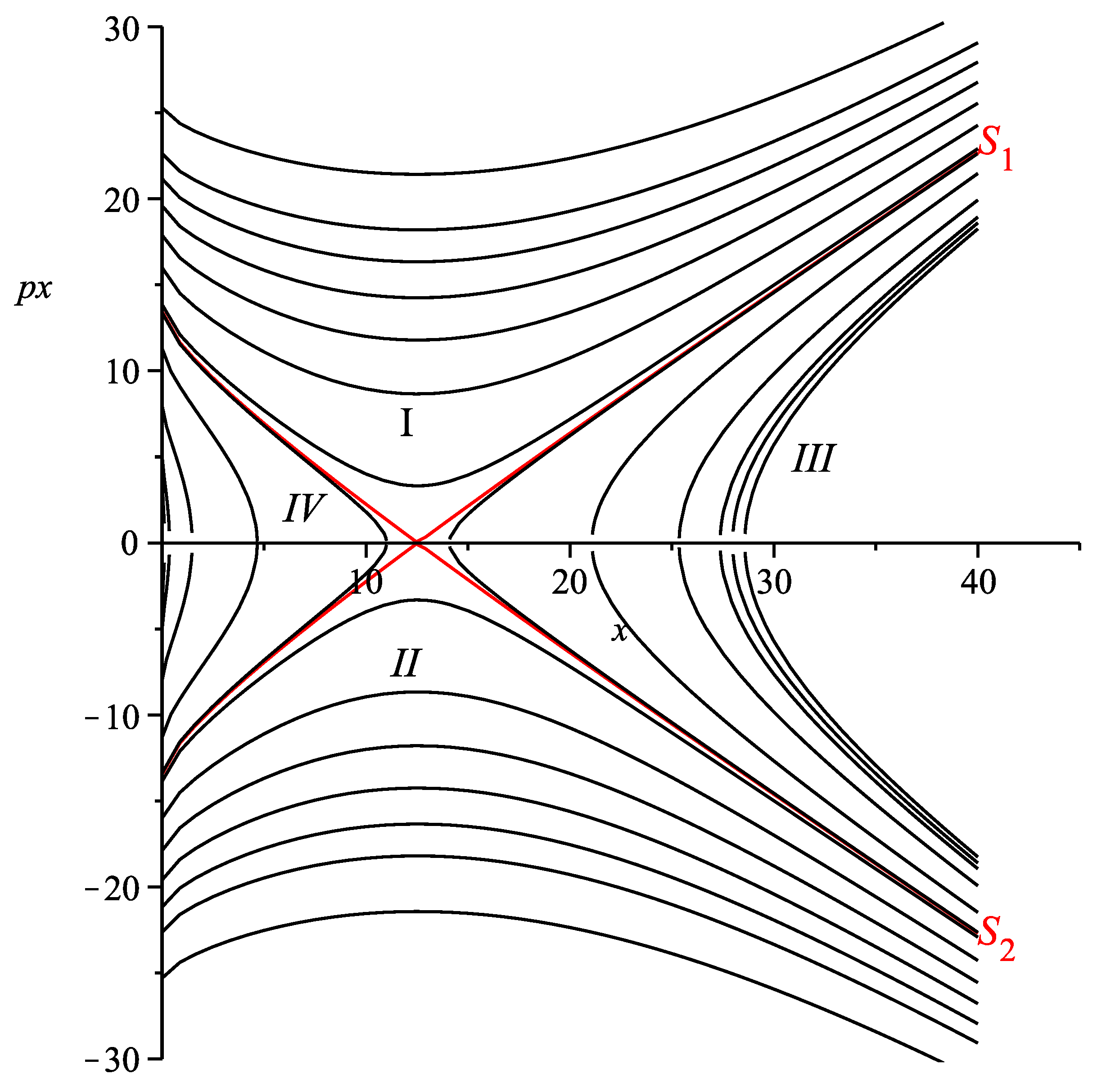
2. The Classical Model
3. Canonical Quantization
3.1. WKB Tunneling Probability
3.2. Integrated Tunneling Probability
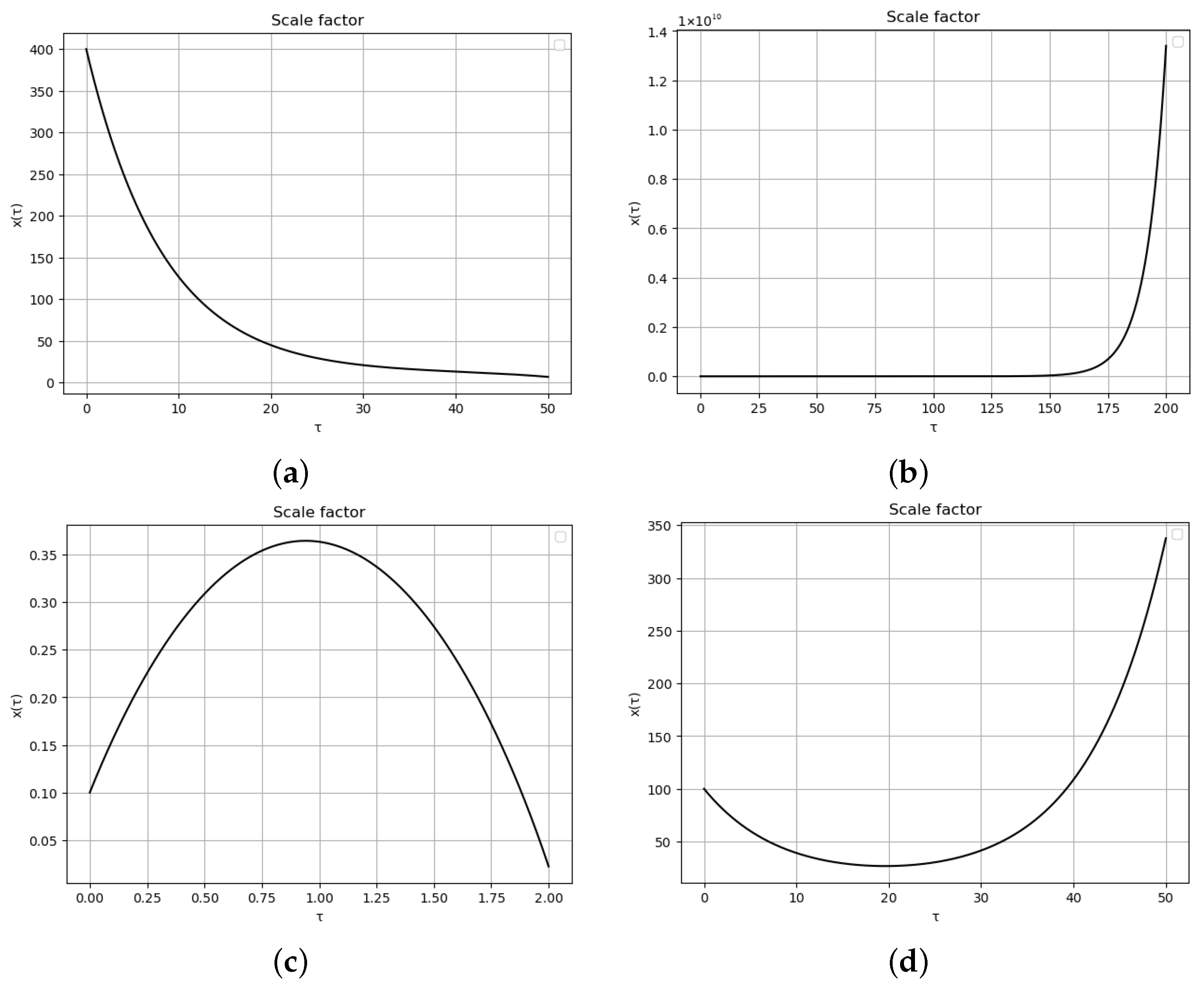
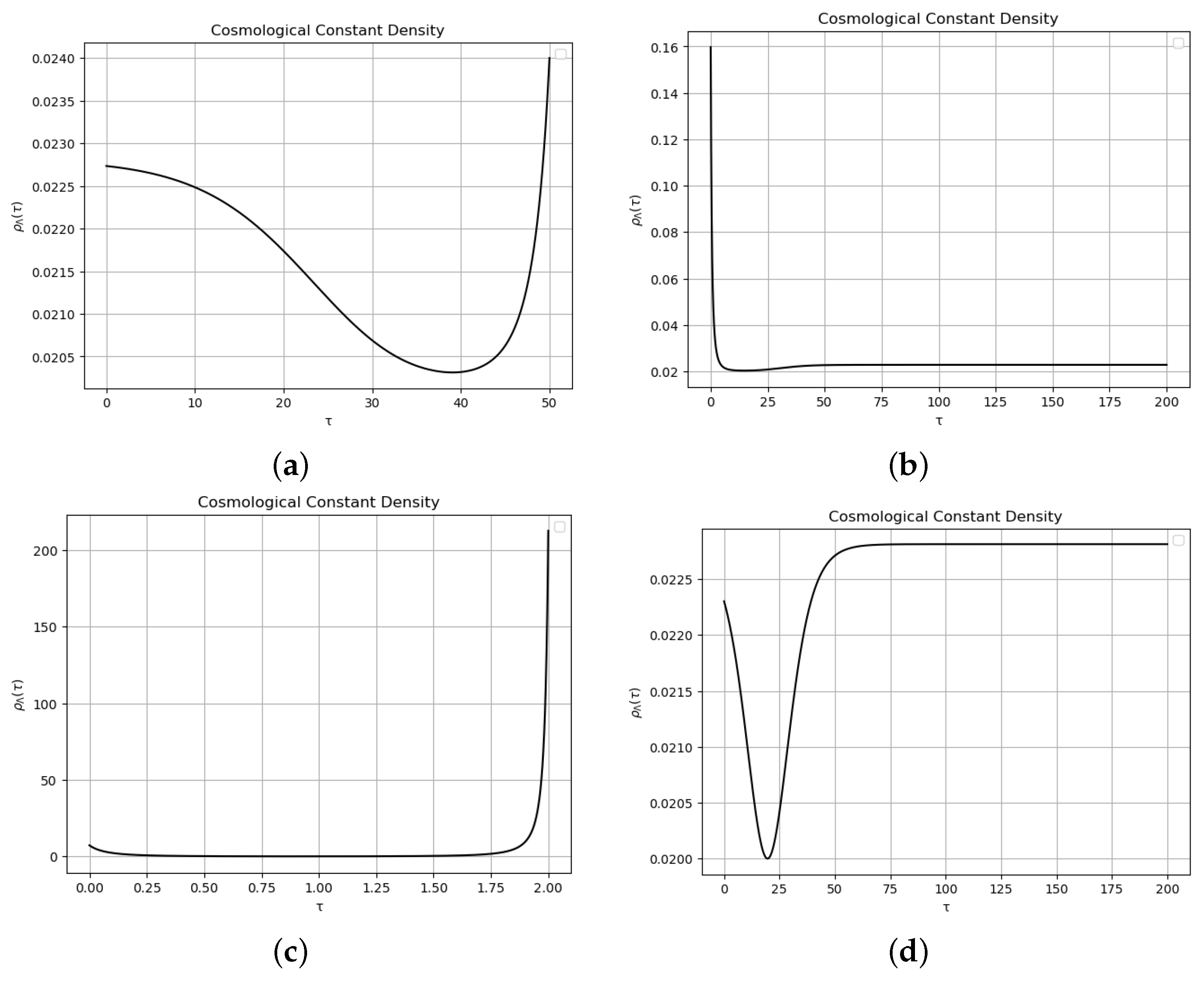
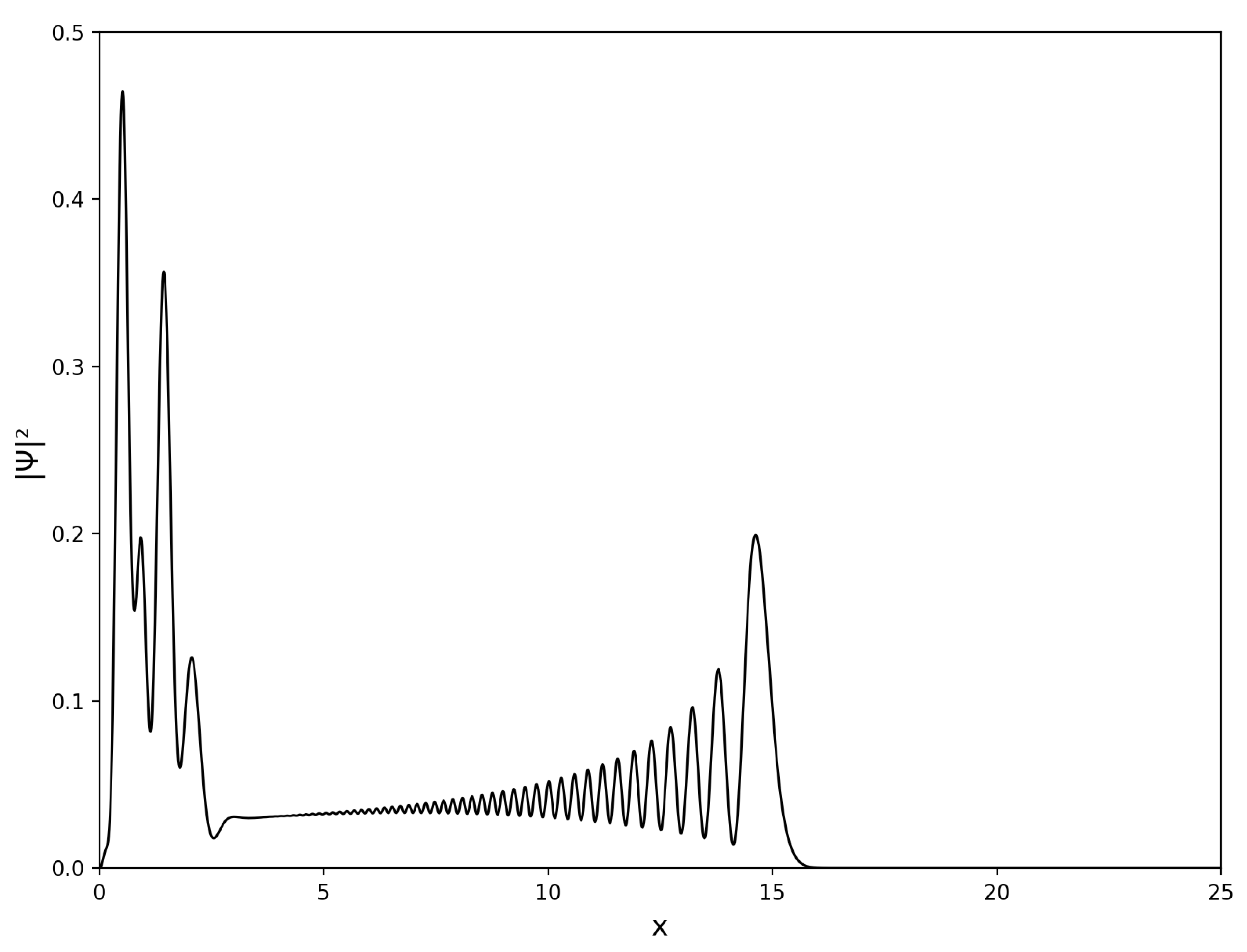
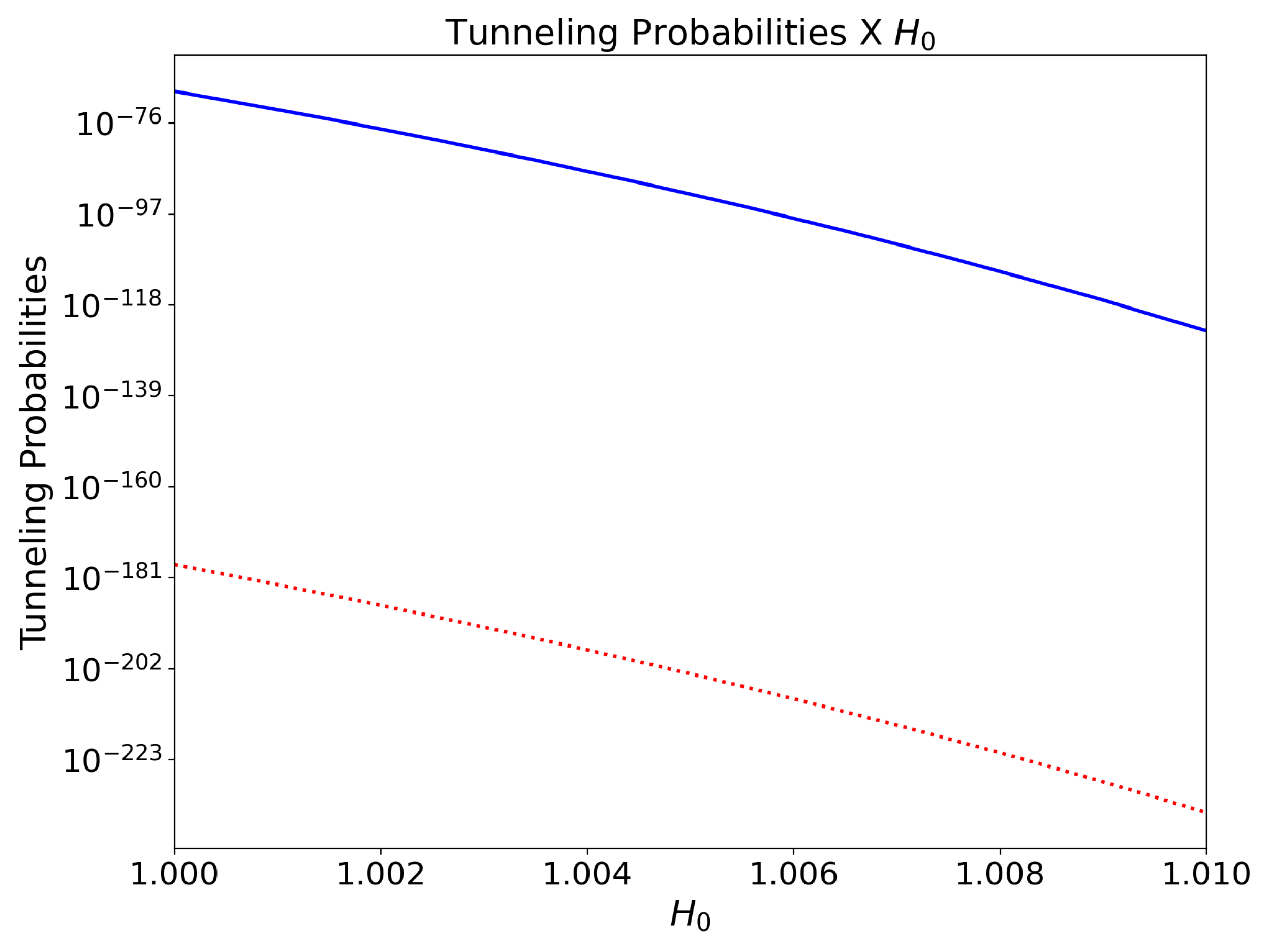
4. Results
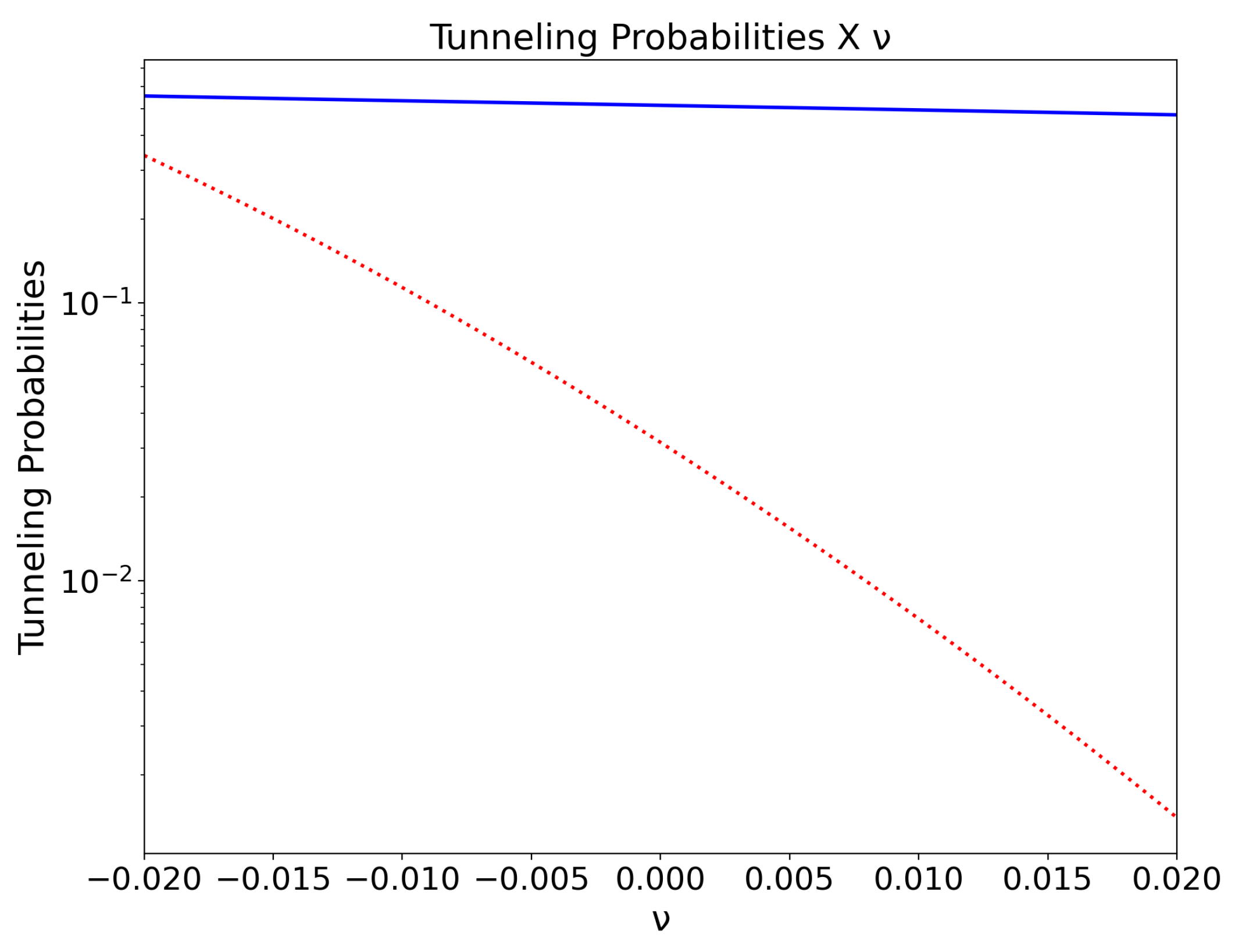
4.1. The Phenomenological Parameter
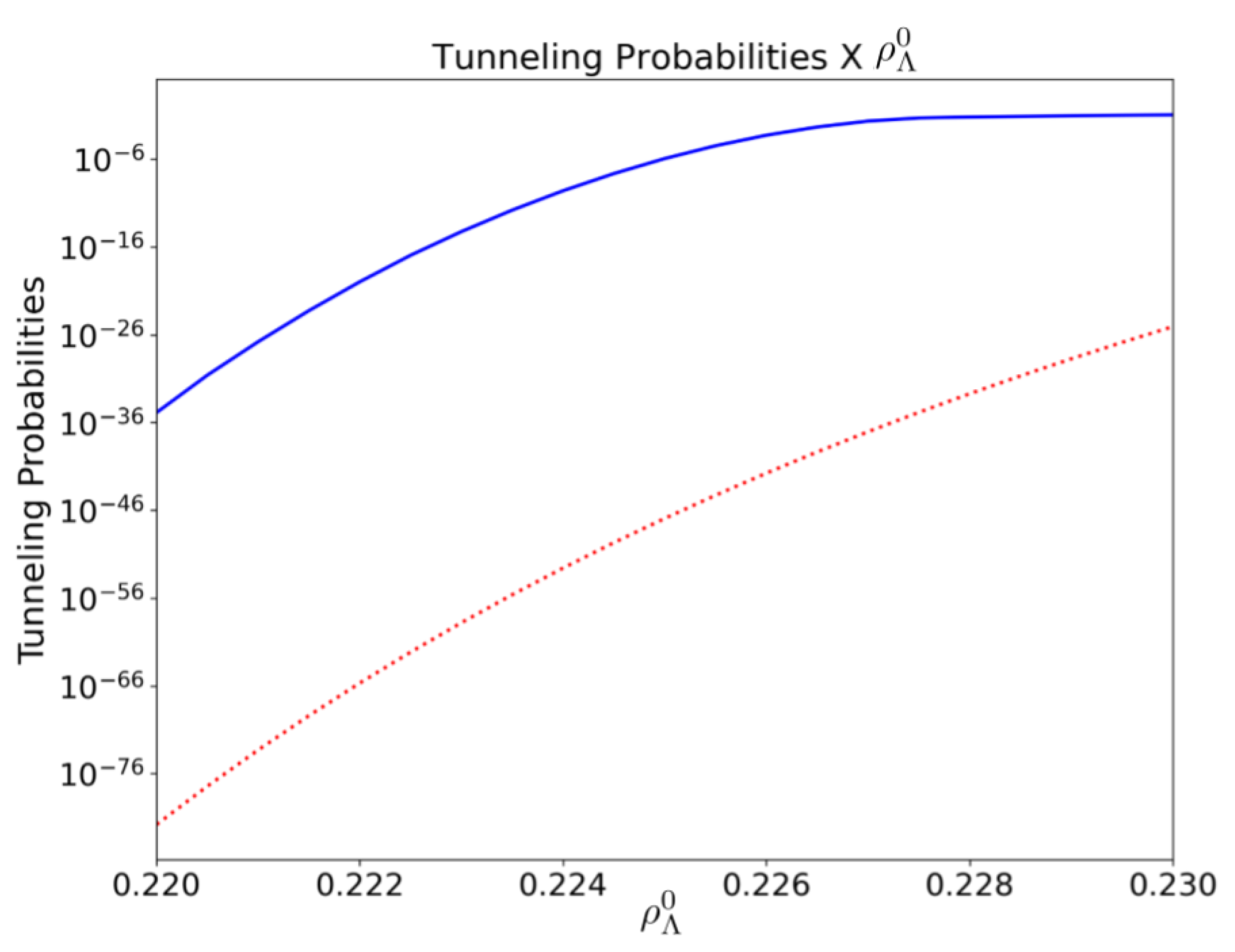
4.2. The Cosmological Constant Energy Density
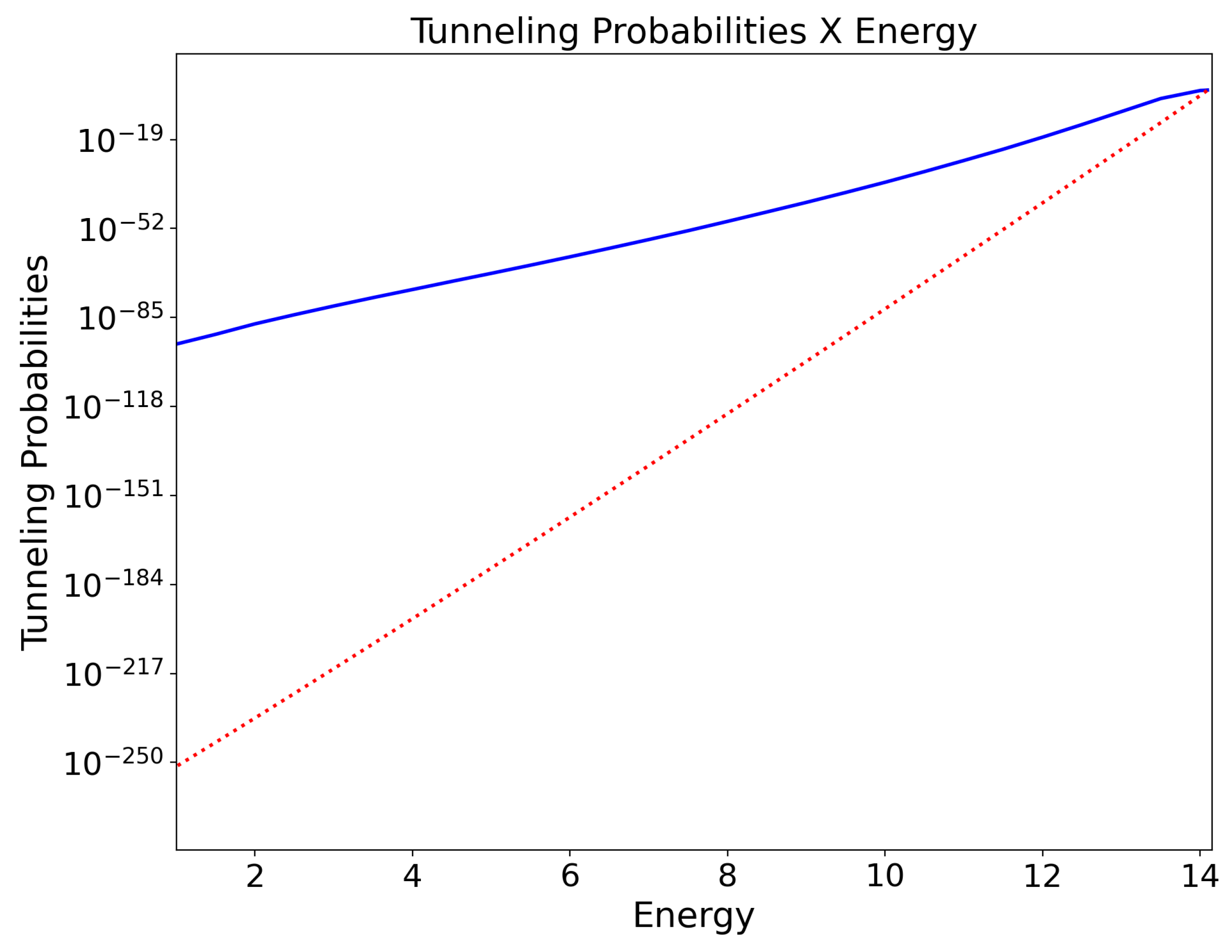
4.3. Energy E
4.4.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Schutz Formalism
References
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Wheeler, J.A. Superspace and the nature of quantum geometrodynamics. In Battelle Rencontres; Benjamin, Inc.: Tokyo, Japan, 1968; pp. 242–307. Available online: https://www.osti.gov/biblio/4124259 (accessed on 8 September 2025).
- Moniz, P.V. Quantum Cosmology—The Supersymmetric Perspective—Vol. 1: Fundamentals. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 803. [Google Scholar]
- Grishchuk, L.P.; Zeldovich, Y.B. Quantum Structure of Space and Time; Duff, M., Isham, C., Eds.; Cambridge University Press: Cambridge, UK, 1982; ISBN 9781107404588. [Google Scholar]
- Vilenkin, A. Creation of Universes from Nothing. Phys. Lett. B 1982, 117, 25. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Creation of Universes. Phys. Rev. D 1984, 30, 509. [Google Scholar] [CrossRef]
- Vilenkin, A. Boundary Conditions in Quantum Cosmology. Phys. Rev. D 1986, 33, 3560. [Google Scholar] [CrossRef] [PubMed]
- Hartle, J.B.; Hawking, S.W. Wave Function of the Universe. Phys. Rev. D 1983, 28, 2960. [Google Scholar] [CrossRef]
- Linde, A.D. Quantum Creation of the Inflationary Universe. Lett. Nuovo C 1984, 39, 401. [Google Scholar] [CrossRef]
- Rubakov, V.A. Quantum Mechanics in the Tunneling Universe. Phys. Lett. B 1984, 148, 280. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Cosmology and Eternal Inflation; Gibbons, G.W., Shellard, E.P.S., Rankin, S.J., Eds.; Cambridge University Press: Cambridge, UK, 2003; pp. 649–666. [Google Scholar] [CrossRef]
- Bouhmadi-Lopez, M.; Moniz, P.V. FRW quantum cosmology with a generalized Chaplygin gas. Phys. Rev. D 2005, 71, 063521. [Google Scholar] [CrossRef]
- de Barros, J.A.; Silva, E.V.C.; Monerat, G.A.; Oliveira-Neto, G.; Filho, L.G.F.; Romildo, P., Jr. Tunneling probability for the birth of an asymptotically DeSitter universe. Phys. Rev. D 2007, 75, 104004. [Google Scholar] [CrossRef]
- Monerat, G.A.; Oliveira-Neto, G.; Silva, E.V.C.; Filho, L.G.F.; Romildo, P., Jr.; Fabris, J.C.; Fracalossi, R.; Gonçalves, S.V.B.; Alvarenga, F.G. The dynamics of the early universe and the initial conditions for inflation in a model with radiation and a Chaplygin gas. Phys. Rev. D 2007, 76, 024017. [Google Scholar] [CrossRef]
- Monerat, G.A.; Santos, C.G.M.; Oliveira-Neto, G.; Silva, E.V.C.; Filho, L.G.F. The dynamics of the early universe in a model with radiation and a generalized Chaplygin gas. Eur. Phys. J. Plus 2021, 136, 34. [Google Scholar] [CrossRef]
- Monerat, G.A.; Alvarenga, F.G.; Gonçalves, S.V.B.; Oliveira-Neto, G.; Santos, C.G.M.; Silva, E.V.C. The effects of dark energy on the early Universe with radiation and an ad hoc potential. Eur. Phys. J. Plus 2022, 137, 117. [Google Scholar] [CrossRef]
- da Rocha, N.M.N.; Monerat, G.A.; Alvarenga, F.G.; Gonçalves, S.V.B.; Oliveira-Neto, G.; Silva, E.V.C.; Santos, C.G.M. Early universe with dust and Chaplygin gas. Eur. Phys. J. Plus 2022, 137, 1103. [Google Scholar] [CrossRef]
- Oliveira-Neto, G.; Canedo, D.L.; Monerat, G.A. Tunneling probabilities for the birth of universes with radiation, cosmological constant and an ad hoc potential. Eur. Phys. J. Plus 2023, 138, 400. [Google Scholar] [CrossRef]
- Junior, A.O.C.; Oliveira-Neto, G.; Monerat, G.A. Primordial dust universe in the Hořava-Lifshitz theory. Mod. Phys. Lett. A 2024, 39, 2450112. [Google Scholar] [CrossRef]
- Junior, A.O.C.; Oliveira-Neto, G.; Monerat, G.A. The initial moments of a Hořava-Lifshitz cosmological model. Gen. Relativ. Gravit. 2024, 56, 125. [Google Scholar] [CrossRef]
- Monerat, G.A.; Brumatto, H.J.; Oliveira-Neto, G.; Alvarenga, F.G.; Silva, E.V.C.; Ribeiro, A.L.B. Non-singular birth of the universe: High-performance numerical solutions of the Wheeler-DeWitt equation. Phys. Lett. B 2025, 868, 139623. [Google Scholar] [CrossRef]
- Bojowald, M.; Halnon, T. Time in quantum cosmology. Phys. Rev. D 2018, 98, 066001. [Google Scholar] [CrossRef]
- Robles-Pérez, S.J. Quantum cosmology in the light of quantum mechanics. Galaxies 2019, 7, 50. [Google Scholar] [CrossRef]
- Muniz, C.R.; Cunha, M.S.; Bezerra, V.B.; Vieira, H.S. A cosmologia quântica de wheeler-dewitt e o universo despedaçado. Conex.-Ciênc. Tecnol.-Centen. Eclipse Sobral 2019, 13, 70–76. [Google Scholar] [CrossRef]
- Moniz, P.V.; Jalalzadeh, S. From fractional quantum mechanics to quantum cosmology: An overture. Mathematics 2020, 8, 313. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Jalalzadeh, S.; Moniz, P.V. Broadening quantum cosmology with a fractional whirl. Mod. Phys. Lett. A 2021, 36, 2140005. [Google Scholar] [CrossRef]
- Canedo, D.L.; Moniz, P.; Oliveira-Neto, G. Quantum Creation of a Friedmann-Robertson-Walker Universe: Riesz Fractional Derivative Applied. Fractal Fract. 2025, 9, 349. [Google Scholar] [CrossRef]
- Pinto-Neto, N. The de Broglie-Bohm quantum theory and its application to quantum cosmology. Universe 2021, 7, 134. [Google Scholar] [CrossRef]
- Kiefer, C.; Peter, P. Time in quantum cosmology. Universe 2022, 8, 36. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Costa, E.W.O.; Moniz, P.V. de Sitter fractional quantum cosmology. Phys. Rev. D 2022, 105, L121901. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Mohammadi, A.; Demir, D. A quantum cosmology approach to cosmic coincidence and inflation. Phys. Dark Univ. 2023, 40, 101227. [Google Scholar] [CrossRef]
- Wang, C.C.E.; Wu, J.H.P. Quantum Cosmology on Quantum Computer. arXiv 2024, arXiv:2410.22485. Available online: https://arxiv.org/abs/2410.22485 (accessed on 8 September 2025). [CrossRef]
- Anninos, D.; Baracco, C.; Mühlmann, B. Remarks on 2D quantum cosmology. J. Cosmol. Astropart. Phys. 2024, 2024, 031. [Google Scholar] [CrossRef]
- Piazza, F.; Vareilles, S. Cosmological perturbations meet Wheeler DeWitt. arXiv 2024, arXiv:2412.19782. [Google Scholar] [CrossRef]
- Gielen, S. Quantum Cosmology. In Encyclopedia of Mathematical Physics; Elsevier: Amsterdam, The Netherlands, 2025; pp. 520–530. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Cosmological Constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Cortes, M.; Liddle, A.R. Interpreting DESI’s evidence for evolving dark energy. J. Cosmol. Astropart. Phys. 2024, 12, 007. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. Cosmology with a time-variable cosmological ‘constant’. Astrophys. J. Part 2-Lett. Ed. 1988, 325, L17–L20. [Google Scholar]
- Chen, W.; Wu, Y.S. Implications of a cosmological constant varying as R−2. Phys. Rev. D 1990, 41, 695. [Google Scholar] [CrossRef]
- Carvalho, J.C.; Lima, J.A.S.; Waga, I. Cosmological consequences of a time-dependent Λ term. Phys. Rev. D 1992, 46, 2404. [Google Scholar] [CrossRef]
- Ratra, B.; Quillen, A. Gravitational lensing effects in a time-variable cosmological “constant” cosmology. Mon. Not. R. Astron. Soc. 1992, 259, 738–742. [Google Scholar] [CrossRef]
- Starobinsky, A.A. How to determine an effective potential for a variable cosmological term. J. Exp. Theor. Phys. Lett. 1998, 68, 757–763. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. Scaling behavior of the cosmological constant and the possible existence of new forces and new light degrees of freedom. Phys. Lett. B 2000, 475, 236–246. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant and the weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Singh, C.P.; Kumar, S. Bianchi Type-I Space-Time with Variable Cosmological Constant. Int. J. Theor. Phys. 2008, 47, 3171–3179. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. The scaling evolution of the cosmological constant. J. High Energy Phys. 2002, 2002, JHEP02. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J.; España-Bonet, C.; Ruiz-Lapuente, P. Variable cosmological constant as a Planck scale effect. Phys. Lett. B 2003, 574, 149–155. [Google Scholar] [CrossRef]
- España-Bonet, C.; Ruiz-Lapuente, P.; Shapiro, I.L.; Sola, J. Testing the running of the cosmological constant with type Ia supernovae at high z. J. Cosmol. Astropart. Phys. 2004, 2, 006. [Google Scholar] [CrossRef]
- Fabris, J.C.; Shapiro, I.L.; Sola, J. On the cosmological constant and the Einstein field equations. J. Cosmol. Astropart. Phys. 2007, 2, 016. [Google Scholar] [CrossRef]
- Oliveira, V.G.; Oliveira-Neto, G.; Shapiro, I.L. Kantowski-Sachs Model with a Running Cosmological Constant and Radiation. Universe 2024, 10, 83. [Google Scholar] [CrossRef]
- Agudelo Ruiz, J.A.; Fabris, J.C.; Velasquez-Toribio, A.M.; Shapiro, I.L. Constraints from Observational Data for a Running Cosmological Constant and Warm Dark Matter with Curvature. Gravit. Cosmol. 2020, 26, 316–325. [Google Scholar] [CrossRef]
- Ruiz, J.A.A.; Netto, T.d.; Fabris, J.C.; Shapiro, I.L. Primordial universe with the running cosmological constant. Eur. Phys. J. C 2020, 80, 851. [Google Scholar] [CrossRef]
- Hamber, H.W.; Toriumi, R. Inconsistencies from a running cosmological constant. Int. J. Mod. Phys. D 2013, 22, 1330023. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. Can the cosmological “constant” run?—It may run. arXiv 2008, arXiv:0808.0315. [Google Scholar]
- Shapiro, I.L.; Solà, J. On the possible running of the cosmological “constant”. Phys. Lett. B 2009, 682, 105–113. [Google Scholar] [CrossRef]
- AGuth, H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Ashoorioon, A. Exit from inflation with a first-order phase transition and a gravitational wave blast. Phys. Lett. B 2015, 747, 446–453. [Google Scholar] [CrossRef]
- D’Inverno, R.; Vickers, J. Introducing Einstein’s Relativity; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Arnowitt, R.; Deser, S.; Misner, C.W. The Dynamics of General Relativity in Gravitation: An Introduction to Current Research; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman and Company: New York, NY, USA, 1973. [Google Scholar]
- Schutz, B.F. Perfect Fluids in General Relativity: Velocity Potentials and a Variational Principle. Phys. Rev. D 1970, 2, 2762. [Google Scholar] [CrossRef]
- Gotay, M.J.; Demaret, J. Quantum cosmological singularities. Phys. Rev. D 1983, 28, 2402. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
- Dirac, P.A.M. Generalized Hamiltonian Dynamics. Can. J. Math. 1950, 2, 129–148. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Monographs Series; Belfer Graduate School of Science: Kent, UK, 1964. [Google Scholar]
- Merzbacher, E. Quantum Mechanics; Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Lemos, N.A. Radiation dominated quantum Friedmann models. J. Math. Phys. 1996, 37, 1449–1460. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P.J. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. In Proceedings of the Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1947; Volume 43, pp. 50–67. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]

| Energy | ||||
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro Júnior, A.O.; Diniz, A.C.; Oliveira-Neto, G.; Monerat, G.A. Birth of an Isotropic and Homogeneous Universe with a Running Cosmological Constant. Universe 2025, 11, 310. https://doi.org/10.3390/universe11090310
Castro Júnior AO, Diniz AC, Oliveira-Neto G, Monerat GA. Birth of an Isotropic and Homogeneous Universe with a Running Cosmological Constant. Universe. 2025; 11(9):310. https://doi.org/10.3390/universe11090310
Chicago/Turabian StyleCastro Júnior, A. Oliveira, A. Corrêa Diniz, G. Oliveira-Neto, and G. A. Monerat. 2025. "Birth of an Isotropic and Homogeneous Universe with a Running Cosmological Constant" Universe 11, no. 9: 310. https://doi.org/10.3390/universe11090310
APA StyleCastro Júnior, A. O., Diniz, A. C., Oliveira-Neto, G., & Monerat, G. A. (2025). Birth of an Isotropic and Homogeneous Universe with a Running Cosmological Constant. Universe, 11(9), 310. https://doi.org/10.3390/universe11090310






