Exploring the Impact of Self-Excited Alfvén Waves on Transonic Winds: Applications in Galactic Outflows
Abstract
1. Introduction
2. Four-Fluid Cosmic Ray Plasma Model
3. Results
3.1. Cosmic Rays and Waves in the Coupled Stage
3.2. Cosmic Rays and Waves in the De-Coupled Stage
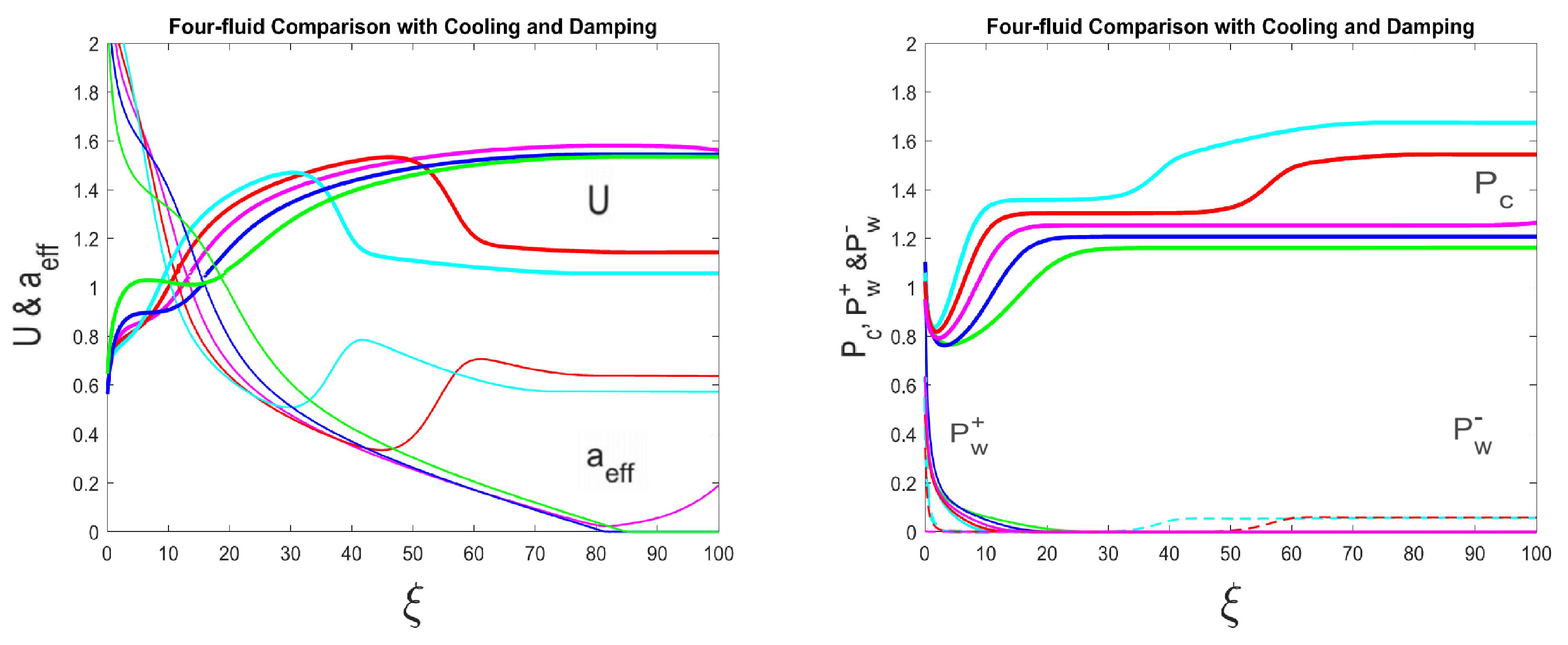
3.3. Cosmic Rays and Waves in the Re-Coupled Stage
4. Implications in Galactic Outflows
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cox, D. The Three-Phase Interstellar Medium Revisited. Annu. Rev. Astron. Astrophys. 2005, 43, 337–385. [Google Scholar] [CrossRef]
- Ferrière, K.M. The interstellar environment of our galaxy. Rev. Mod. Phys. 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Chin, Y.-C.; Wentzel, D.G. Nonlinear dissipation of Alfvén waves. Astrophys. Space Sci. 1972, 16, 465–477. [Google Scholar] [CrossRef]
- Lerche, I. Unstable Magnetosonic Waves in a Relativistic Plasma. Astrophys. J. 1967, 147, 689–696. [Google Scholar] [CrossRef]
- Skilling, J. Cosmic ray streaming—I. Effect of Alfvén waves on particles. Mon. Not. R. Astron. Soc. 1975, 172, 557–566. [Google Scholar] [CrossRef]
- Skilling, J. Cosmic ray streaming—II. Effect of particles on Alfvén waves. Mon. Not. R. Astron. Soc. 1975, 172, 245–254. [Google Scholar] [CrossRef]
- Skilling, J. Cosmic ray streaming—III. Self-consistent solutions. Mon. Not. R. Astron. Soc. 1975, 172, 255–269. [Google Scholar] [CrossRef]
- Wentzel, G. Hydromagnetic Waves Excited by Slowly Streaming Cosmic Rays. Astrophys. J. 1968, 152, 987–996. [Google Scholar] [CrossRef]
- Wentzel, G. Cosmic-ray propagation in the Galaxy: Collective effects. Annu. Rev. Astron. Astrophys. 1974, 12, 71–96. [Google Scholar] [CrossRef]
- Parker, E.N. The Dynamical State of the Interstellar Gas and Field. Astrophys. J. 1966, 145, 811–833. [Google Scholar] [CrossRef]
- Parker, E.N. Theoretical Studies of the Solar Wind Phenomenon. Space Sci. Rev. 1969, 9, 325–360. [Google Scholar] [CrossRef]
- Hanasz, M.; Lesch, H. Cosmic-Ray Evolution in Parker-unstable Galactic Magnetic Fields. Astrophys. J. 2000, 543, 235–244. [Google Scholar] [CrossRef]
- Hanasz, M. Incorporation of cosmic ray transport into the ZEUS MHD code. Astron. Astrophys. 2003, 412, 331–339. [Google Scholar] [CrossRef]
- Kuwabara, T.; Nakamura, K.; Ko, C.M. Nonlinear Parker Instability with the Effect of Cosmic-Ray Diffusion. Astrophys. J. 2004, 607, 828–839. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ko, C.M. Parker-Jeans Instability of Gaseous Disks Including the Effect of Cosmic Rays. Astrophys. J. 2006, 636, 290–302. [Google Scholar] [CrossRef]
- Ko, C.M.; Lo, Y.Y. Stability of a cosmic-ray Magentohydrodynamical system. Astrophys. J. 2009, 691, 1587–1594. [Google Scholar] [CrossRef]
- Lo, Y.Y.; Ko, C.M. 3D Magneto-hydrodynamic simulations of Parker instability with cosmic rays. Comput. Phys. Commun. 2011, 182, 177–179. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ko, C.M. Analysis of Magnetorotational Instability with the effect of Cosmic-Ray diffusion. Astrophys. J. 2006, 798, 79. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Hallman, E.; Jones, T.W. Cosmological Shock Waves and Their Role in the Large-Scale Structure of the Universe. Astrophys. J. 2003, 593, 599–610. [Google Scholar] [CrossRef]
- Weinberg, S. Eikonal Method in Magnetohydrodynamics. Phys. Rev. 1962, 126, 1899–1909. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamical theory of the solar wind. Space Sci. Rev. 1965, 4, 666–708. [Google Scholar] [CrossRef]
- Alazraki, G.; Couturier, P. Solar Wind Acceleration Caused by the Gradient of Alfvén Wave Pressure. Astron. Astrophys. 1971, 13, 380–389. [Google Scholar]
- Belcher, J.W. Alfvénic Wave Pressures and the Solar Wind. Astrophys. J. 1971, 168, 509–524. [Google Scholar] [CrossRef]
- Belcher, J.W.; Davis, L., Jr. Large-amplitude Alfvén waves in the interplanetary medium, 2. J. Geophys. Res. 1971, 76, 3534–3563. [Google Scholar] [CrossRef]
- Hollweg, J.V. Alfvén Waves in a Two-Fluid Model of the Solar Wind. Astrophys. J. 1973, 181, 547–566. [Google Scholar] [CrossRef]
- Hollweg, J.V. Some physical processes in the solar wind. Rev. Geophys. Space Phys. 1978, 16, 689–720. [Google Scholar] [CrossRef]
- Webb, G.M.; Anco, S.C.; Meleshko, S.V.; Kaptsov, E.I. Noether’s theorems and conservation laws in magnetohydrodynamics and Chew–Goldberger–Low plasmas. Rev. Mod. Plasma Phys. 2024, 8, 1–92. [Google Scholar] [CrossRef]
- Hollweg, J.V. On WKB expansions for Alfvén waves in the solar wind. J. Geophys. Res. 1990, 95, 14873–14879. [Google Scholar] [CrossRef]
- Hollweg, J.V. Non-WKB Alfvén waves in the solar wind: Propagation and reflection of pulses. AIP Conf. Proc. 1996, 382, 327–330. [Google Scholar]
- McKenzie, J.F.; Völk, H.J. Non-linear theory of cosmic ray shocks including self-generated Alfvén waves. Astron. Astrophys. 1982, 116, 191–200. [Google Scholar]
- McKenzie, J.F. Interaction between Alfvén waves and a multicomponent plasma with differential ion streaming. J. Geophys. Res. Space Phys. 1994, 99, 4193–4200. [Google Scholar] [CrossRef]
- Heinemann, M.; Olbert, S. Non-WKB Alfvén waves in the solar wind. J. Geophys. Res. Space Phys. 2003, 85, 1311–1327. [Google Scholar] [CrossRef]
- Marsch, E.; Tu, C.Y. Dynamics of correlation functions with Elsässer variables for inhomogeneous MHD turbulence. J. Plasma Phys. 1989, 41, 479–491. [Google Scholar] [CrossRef]
- Zhou, Y.; Matthaeus, W.H. Transport and Turbulence Modeling of Solar Wind Fluctuations. J. Geophys. Res. Space Phys. 1990, 95, 10291–10311. [Google Scholar] [CrossRef]
- Zhou, Y.; Matthaeus, W.H. Remarks on transport theories of interplanetary fluctuations. J. Geophys. Res. Space Phys. 1990, 95, 14863–14871. [Google Scholar] [CrossRef]
- Li, B.; Li, X. Propagation of Non-Wentzel-Kramers-Brillouin Alfvén Waves in a Multicomponent Solar Wind with Differential Ion Flow. Astrophys. J. 2007, 661, 1222–1233. [Google Scholar] [CrossRef]
- Velli, M. On the propagation of ideal, linear Alfven waves in radially stratified stellar atmospheres and winds. Astron. Astrophys. 1993, 270, 304–314. [Google Scholar]
- Ipavich, F.M. Galactic winds Driven by Cosmic Rays. Astrophys. J. 1975, 196, 107–120. [Google Scholar] [CrossRef]
- Breitschwerdt, D.; McKenzie, J.F.; Völk, H.J. Galactic winds. I. Cosmic ray and wave-driven winds from the galaxy. Astron. Astrophys. 1991, 245, 79–98. [Google Scholar]
- Breitschwerdt, D.; McKenzie, J.F.; Völk, H.J. Galactic winds. II—Role of the disk-halo interface in cosmic ray driven galactic winds. Astron. Astrophys. 1993, 269, 54–66. [Google Scholar]
- Zirakashvili, V.N.; Breitschwerdt, D.; Ptuskin, V.S.; Völk, H.J. Magnetohydrodynamic wind driven by cosmic rays in a rotating galaxy. Astron. Astrophys. 1996, 311, 113–126. [Google Scholar]
- Dogiel, V.A.; Ko, C.M. Sources and Radiations of the Fermi Bubbles. Universe 2024, 10, 424. [Google Scholar] [CrossRef]
- Dorfi, E.A.; Breitschwerdt, D. Time-dependent galactic winds. I. Structure and evolution of galactic outflows accompanied by cosmic ray acceleration. Astron. Astrophys. 2012, 540, A77. [Google Scholar] [CrossRef]
- Dorfi, E.A.; Steiner, D.; Ragossnig, F.; Breitschwerdt, D. Time-dependent galactic winds. II. Effects of boundary variations in the disc and galactic halo. Astron. Astrophys. 2019, 630, A107. [Google Scholar] [CrossRef]
- Everett, J.E.; Zweibel, E.G.; Benjamin, R.A.; McCammon, D.; Rocks, L.; Gallagher, J.S., III. The Milky Way’s Kiloparsec-Scale Wind: A Hybrid Cosmic-Ray and Thermally Driven Outflow. Astrophys. J. 2008, 674, 258–270. [Google Scholar] [CrossRef]
- Farber, R.; Ruszkowski, M.; Yang, H.-Y.K.; Zweibel, E.G. Impact of Cosmic-Ray Transport on Galactic Winds. Astrophys. J. 2018, 856, 112. [Google Scholar] [CrossRef]
- Girichidis, P.; Thorsten, N.; Walch, S.; Hanasz, M.; Mac Low, M.M.; Ostriker, P.J.; Gatto, A.; Peters, T.; Wünsch, R.; Glover, S.C.O.; et al. Launching cosmic-ray-driven outflows from the magnetized interstellar medium. Astrophys. J. 2016, 816, L19. [Google Scholar] [CrossRef]
- Heintz, E.; Zweibel, E.G. The Parker Instability with Cosmic-Ray Streaming. Astrophys. J. 2003, 860, 97. [Google Scholar] [CrossRef]
- Heintz, E.; Bustard, C.; Zweibel, E.G. The Role of the Parker Instability in Structuring the Interstellar Medium. Astrophys. J. 2020, 891, 157. [Google Scholar] [CrossRef]
- Holguin, F.; Ruszkowski, M.; Lazarian, A.; Farber, R.; Yang, H.-Y.K. Role of cosmic-ray streaming and turbulent damping in driving galactic winds. Mon. Not. R. Astron. Soc. 2019, 490, 1271–1282. [Google Scholar] [CrossRef]
- Irshad, K.; Ramzan, B.; Qazi, S.N.A.; Areeb, F.; Rasheed, A.; Jamil, M. Continuous solutions of cosmic-rays and waves in astrophysical environments. Sci. Rep. 2023, 13, 22850. [Google Scholar] [CrossRef]
- Ko, C.M.; Dougherty, M.K.; McKenzie, J.F. Structure and stability of a static galactic halo including cosmic ray and Alfven wave effects. Astron. Astrophys. 1991, 242, 62–68. [Google Scholar]
- Ko, C.M. A three-fluid static galactic halo model in flux-tube formulation. Astron. Astrophys. 1991, 242, 85–92. [Google Scholar]
- Ko, C.M.; Ramzan, B.; Chernyshov, D.O. Outflows in the Presence of Cosmic Rays and Waves with Cooling. Astron. Astrophys. 2021, 654, A63. [Google Scholar] [CrossRef]
- Majeed, U.; Ramzan, B. Galactic outflows in different geometries. Adv. Space Res. 2024, 75, 1378–1389. [Google Scholar] [CrossRef]
- Mao, S.A.; Ostriker, E.C. Galactic Disk Winds Driven by Cosmic Ray Pressure. Astrophys. J. 2018, 854, 89. [Google Scholar] [CrossRef]
- Ramzan, B.; Ko, C.M.; Chernyshov, D.O. Outflows in the Presence of Cosmic Rays and Waves. Astrophys. J. 2020, 905, 1–14. [Google Scholar] [CrossRef]
- Ramzan, B.; Qazi, S.N.A.; Salarzai, I.; Tahir, M.; Mirza, A.M.; Rasheed, A.; Jamil, M. A fluid approach to cosmic-ray modified shocks. Adv. Space Res. 2024, 74, 4250–4263. [Google Scholar] [CrossRef]
- Recchia, S.; Blasi, P.; Morlino, G. On the radial distribution of Galactic cosmic rays. Mon. Not. R. Astron. Soc. 2016, 462, L88–L92. [Google Scholar] [CrossRef]
- Recchia, S. Cosmic ray driven Galactic winds. Int. J. Mod. Phys. D 2020, 29, 2030006-50. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Yang, H.-Y.K.; Zweibel, E. Global Simulations of Galactic Winds Including Cosmic-Ray Streaming. Astrophys. J. 2017, 834, 208. [Google Scholar] [CrossRef]
- Wiener, J.; Peng, O.S.; Zweibel, G.E. Interaction of cosmic rays with cold clouds in galactic haloes. Mon. Not. R. Astron. Soc. 2017, 467, 646–660. [Google Scholar]
- Yang, H.-Y.K.; Ruszkowski, M.; Ricker, P.M.; Zweibel, E.; Lee, D. The Fermi Bubbles: Supersonic Active Galactic Nucleus Jets with Anisotropic Cosmic-Ray Diffusion. Astrophys. J. 2012, 761, 1–19. [Google Scholar] [CrossRef]
- Yu, B.P.; Owen, E.R.; Wu, K.; Ferreras, I. A hydrodynamical study of outflows in starburst galaxies with different driving mechanisms. Astron. Astrophys. 2020, 492, 3179–3193. [Google Scholar] [CrossRef]
- Zhang, D. A Review of the Theory of Galactic Winds Driven by Stellar Feedback. Universe 2018, 6, 114. [Google Scholar] [CrossRef]
- Ko, C.M. A note on the hydrodynamical description of cosmic ray propagation. Astron. Astrophys. 1992, 259, 377–381. [Google Scholar]
- Ko, C.M. Continuous solutions of the hydrodynamic approach to cosmic-ray propagation. J. Plasma Phys. 2001, 65, 305–317. [Google Scholar] [CrossRef]
- Frieman, E.; Rotenburg, M. On Hydromagnetic Stability of Stationary Equilibria. Rev. Mod. Phys. 1960, 32, 898–902. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Pfrommer, C. Cosmic ray feedback in galaxies and galaxy clusters. Astron. Astrophys. Rev. 2023, 31, 4. [Google Scholar] [CrossRef]
- Thomas, T.; Pfrommer, C.; Pakmor, R. Why are thermally and cosmic ray-driven galactic winds fundamentally different? Astron. Astrophys. 2025, 698, A104. [Google Scholar] [CrossRef]
- Ko, C.M.; Breitschwerdt, D.; Chernyshov, D.O.; Cheng, H.; Dai, L.; Dogiel, V.A. Analytical and Numerical Studies of Central Galactic Outflows Powered by Tidal Disruption Events: A Model for the Fermi Bubbles? Astrophys. J. 2020, 904, 46. [Google Scholar] [CrossRef]
- Bustard, C.; Zweibel, E.G.; D’Onghia, E. A Versatile Family of Galactic Winds. Astrophys. J. 2016, 819, 29. [Google Scholar]
- Brüggen, M.; Scannapieco, E. The Launching of Cold Clouds by Galaxy Outflows. IV. Cosmic-Ray-driven Acceleration. Astrophys. J. 2020, 905, 15. [Google Scholar] [CrossRef]
- Ramzan, B.; Mir, Z.; Rasheed, A.; Jamil, M. Transonic plasma winds with cosmic-rays and waves. Phys. Scr. 2023, 98, 125005. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramzan, B.; Qazi, S.N.A.; Ko, C.-M. Exploring the Impact of Self-Excited Alfvén Waves on Transonic Winds: Applications in Galactic Outflows. Universe 2025, 11, 290. https://doi.org/10.3390/universe11090290
Ramzan B, Qazi SNA, Ko C-M. Exploring the Impact of Self-Excited Alfvén Waves on Transonic Winds: Applications in Galactic Outflows. Universe. 2025; 11(9):290. https://doi.org/10.3390/universe11090290
Chicago/Turabian StyleRamzan, Bilal, Syed Nasrullah Ali Qazi, and Chung-Ming Ko. 2025. "Exploring the Impact of Self-Excited Alfvén Waves on Transonic Winds: Applications in Galactic Outflows" Universe 11, no. 9: 290. https://doi.org/10.3390/universe11090290
APA StyleRamzan, B., Qazi, S. N. A., & Ko, C.-M. (2025). Exploring the Impact of Self-Excited Alfvén Waves on Transonic Winds: Applications in Galactic Outflows. Universe, 11(9), 290. https://doi.org/10.3390/universe11090290





