From Gamma Rays to Cosmic Rays: Lepto-Hadronic Modeling of Blazar Sources as Candidates for Ultra-High-Energy Cosmic Rays
Abstract
1. Introduction
2. Blazar Sample Overview: AP Librae, 1H 1914–194, and PKS 0735+178
2.1. AP Librae
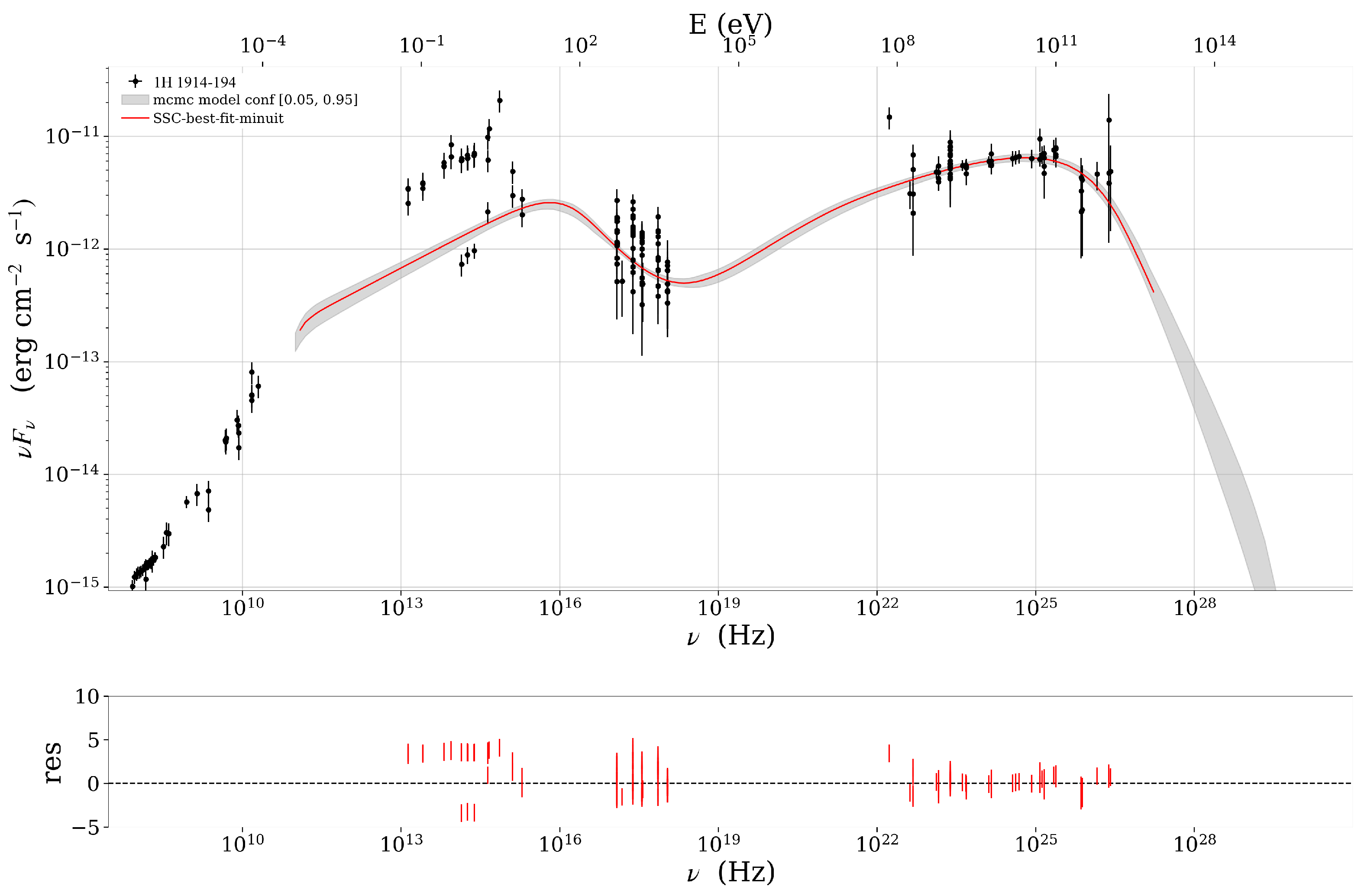
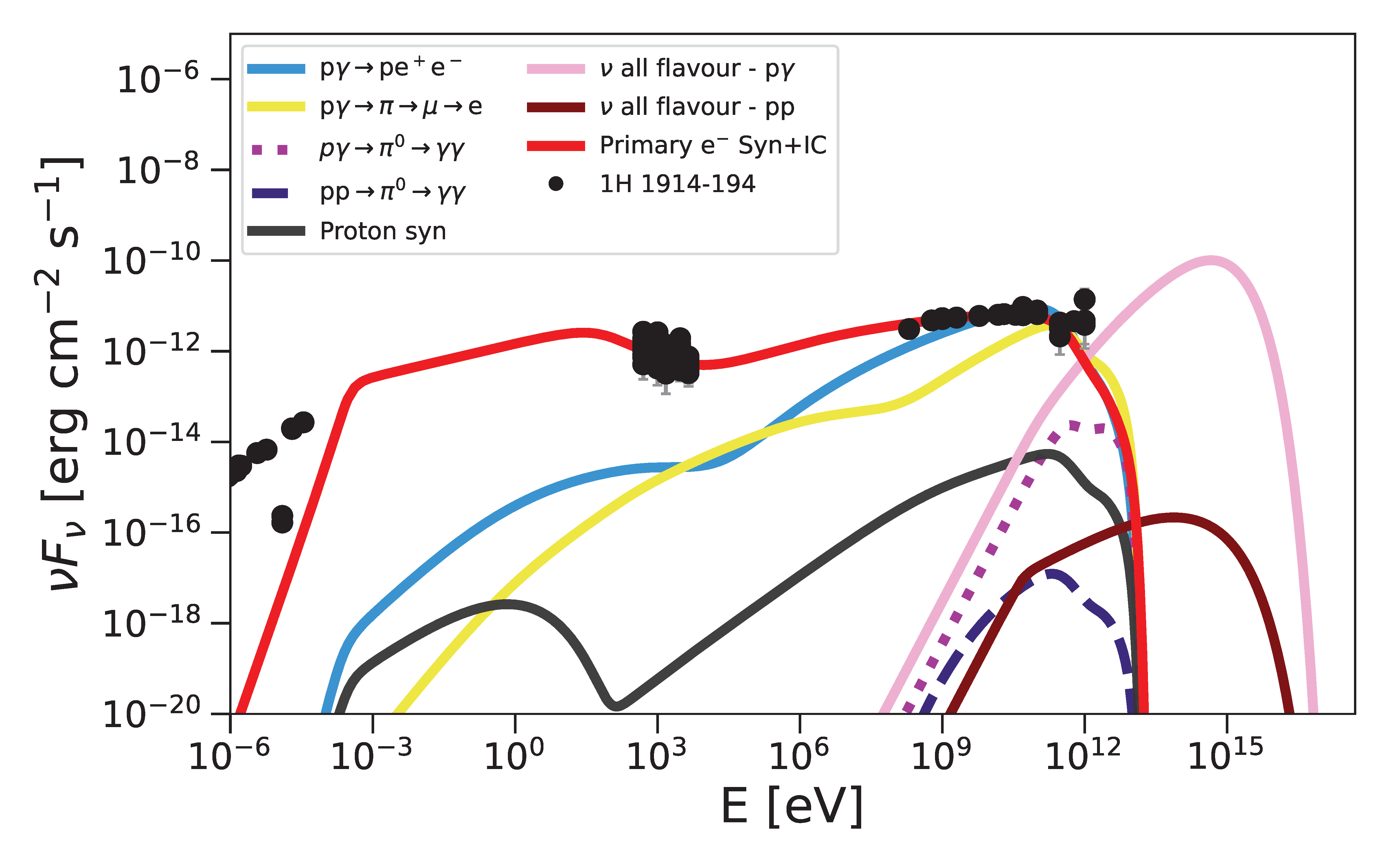
2.2. 1H 1914–194
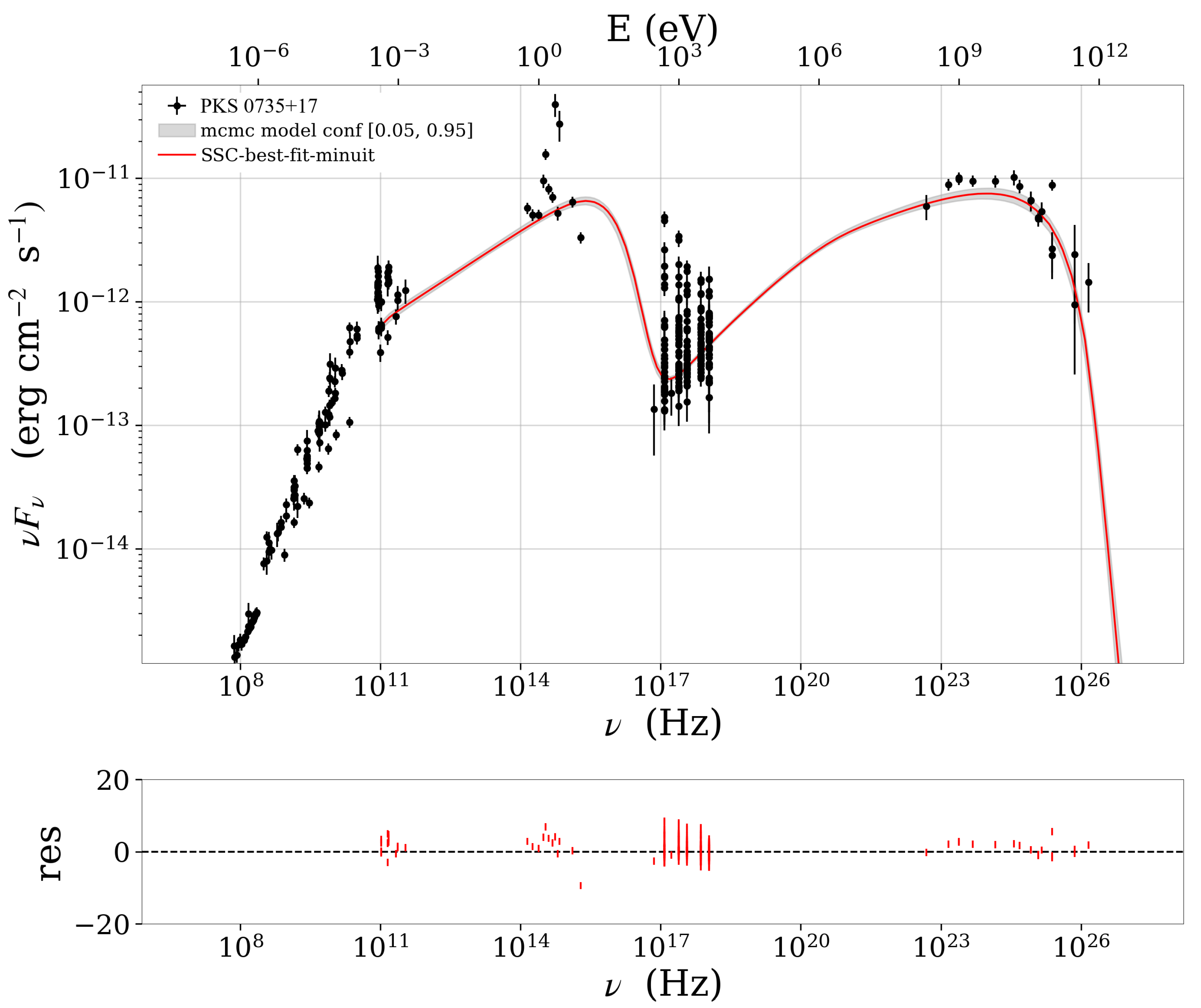
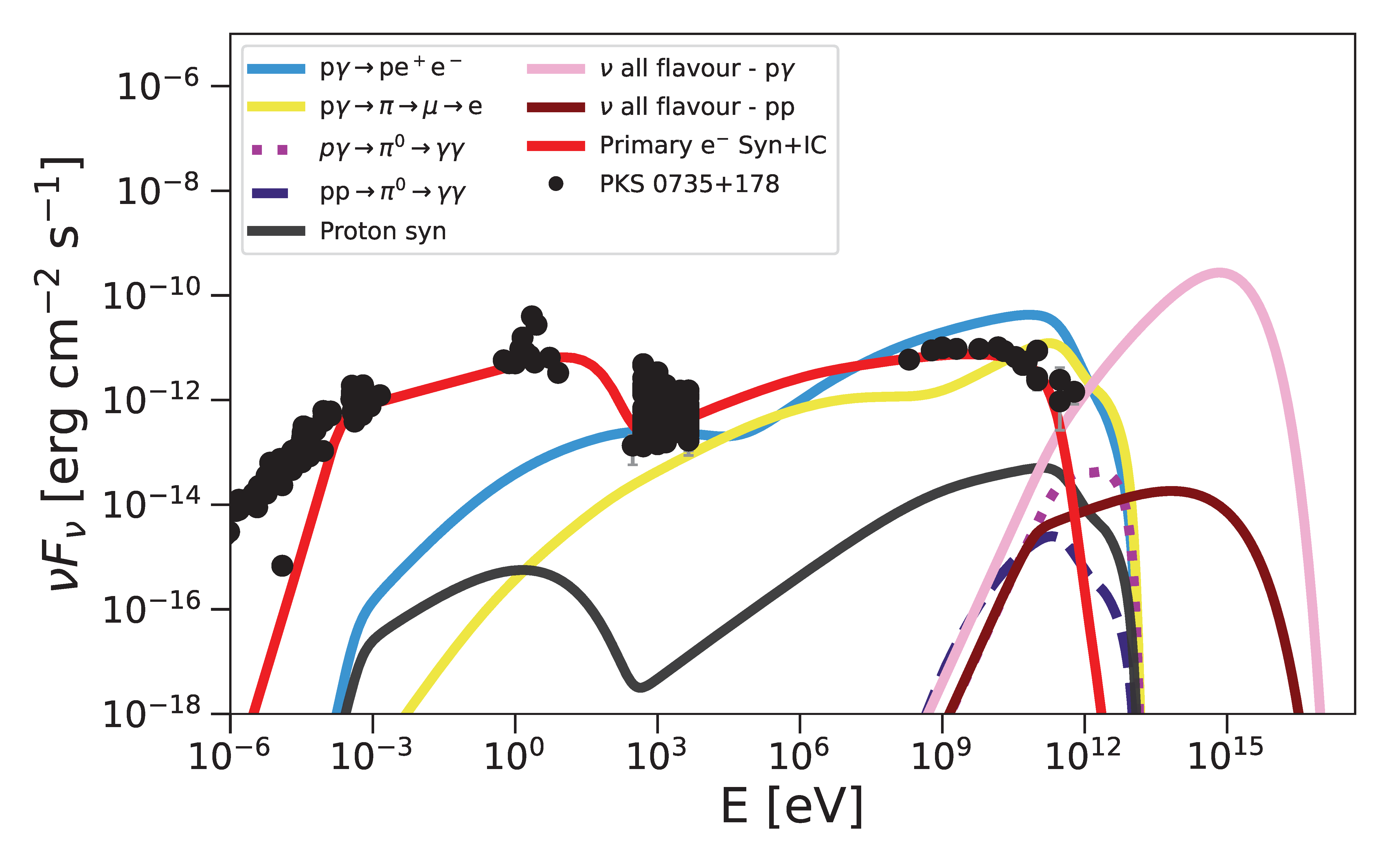
2.3. PKS 0735+178
3. Multi-Wavelength SED Modeling of BL Lacs
3.1. Leptonic SED Fitting
3.2. Lepto-Hadronic SED Modeling
4. Results and Discussion
4.1. Synchrotron Self-Compton (SSC) Modeling
4.2. Lepto-Hadronic Spectral Energy Distribution Modeling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGN | Active Galactic Nucleus |
| BL Lac | BL Lacertae object |
| BLR | Broad-Line Region |
| CMB | Cosmic Microwave Background |
| DT | Dusty Torus |
| EBL | Extragalactic Background Light |
| EC | External Compton |
| HBL | High-Synchrotron-Peaked BL Lac |
| HE | High Energy |
| HSP | High-Synchrotron-Peaked BL Lac (synonym of HBL) |
| IBL | Intermediate-Synchrotron-Peaked BL Lac |
| ISP | Intermediate-Synchrotron-Peaked BL Lac |
| LEdd | Eddington Luminosity |
| LBL | Low-Synchrotron-Peaked BL Lac |
| MCMC | Markov Chain Monte Carlo |
| SSC | Synchrotron Self-Compton |
| SED | Spectral Energy Distribution |
| UHECR | Ultra-High-Energy Cosmic Ray |
| VHE | Very High Energy |
| CDM | Lambda Cold Dark Matter cosmological model |
| 1 | https://firmamento.hosting.nyu.edu/home, accessed on 1 April 2025 |
| 2 | https://fallingstar-data.com/forcedphot/, accessed on 10 July 2025. |
References
- Aab, A.; Abreu, P.; Aglietta, M.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Castillo, J.A.; Alvarez-Muñiz, J.; Anastasi, G.A.; Anchordoqui, L.; et al. An Indication of Anisotropy in Arrival Directions of Ultra-high-energy Cosmic Rays through Comparison to the Flux Pattern of Extragalactic Gamma-Ray Sources*. Astrophys. J. Lett. 2018, 853, L29. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Pereira, J.P.; Coimbra-Araújo, C.H.; dos Anjos, R.C.; Coelho, J.G. Binary Coalescences as Sources of Ultrahigh-Energy Cosmic Rays. Phys. Rev. Lett. 2024, 132, 091401. [Google Scholar] [CrossRef]
- Murase, K.; Dermer, C.D.; Takami, H.; Migliori, G. Blazars as Ultra-High-Energy Cosmic-Ray Sources: Implications for TeV Gamma-Ray Observations. Astrophys. J. 2012, 749, 63. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, X.; Cao, Z. TeV Blazars as the Sources of Ultra High Energy Cosmic Rays. Int. J. Astron. Astrophys. 2014, 4, 499–509. [Google Scholar] [CrossRef]
- Giommi, P.; Padovani, P. Astrophysical Neutrinos and Blazars. Universe 2021, 7, 492. [Google Scholar] [CrossRef]
- MAGIC Collaboration; MWL Collaborators. The variability patterns of the TeV blazar PG 1553 + 113 from a decade of MAGIC and multiband observations. Mon. Not. R. Astron. Soc. 2024, 529, 3894–3911. [Google Scholar] [CrossRef]
- Murase, K.; Stecker, F.W. High-Energy Neutrinos from Active Galactic Nuclei. In The Encyclopedia of Cosmology. Set 2: Frontiers in Cosmology. Volume 2: Neutrino Physics and Astrophysics; Stecker, F.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 483–540. [Google Scholar]
- Mannheim, K.; Stanev, T.; Biermann, P.L. Neutrinos from flat-spectrum radio quasars. Astron. Astrophys. 1992, 260, L1–L3. [Google Scholar]
- Aartsen, M.; Ackermann, M.; Adams, J.; Aguilar, J.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. The IceCube Neutrino Observatory: Instrumentation and online systems. J. Instrum. 2017, 12, P03012. [Google Scholar] [CrossRef]
- Sahayanathan, S.; Godambe, S. Modelling the very high energy flare of 3C 279 using one-zone leptonic model. Mon. Not. R. Astron. Soc. 2011, 419, 1660–1666. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Strittmatter, P.A.; Serkowski, K.; Carswell, R.; Stein, W.A.; Merrill, K.M.; Burbidge, E.M. Compact extragalactic nonthermal sources. Astrophys. J. 1972, 175, L7–L13. [Google Scholar] [CrossRef]
- Disney, M.J.; Peterson, B.A.; Rodgers, A.W. The Redshift and Composite Nature of AP Librae (pks 1514-24). Astrophys. J. Lett. 1974, 194, L79. [Google Scholar] [CrossRef]
- Jones, D.H.; Read, M.A.; Saunders, W.; Colless, M.; Jarrett, T.; Parker, Q.A.; Fairall, A.P.; Mauch, T.; Sadler, E.M.; Watson, F.G.; et al. The 6dF Galaxy Survey: Final redshift release (DR3) and southern large-scale structures. Mon. Not. R. Astron. Soc. 2009, 399, 683–698. [Google Scholar] [CrossRef]
- Bolton, J.G.; Gardner, F.F.; Mackey, M.B. The Parkes catalogue of radio sources, declination zone −20° to −60°. Aust. J. Phys. 1964, 17, 340. [Google Scholar] [CrossRef]
- Bond, H.E. The Optically Variable Radio Source PKS 1514-24 = AP Librae. Astrophys. J. Lett. 1971, 167, L79. [Google Scholar] [CrossRef]
- Biraud, F. Rapid Optical Variability of the Source PKS 1514-24. Nature 1971, 232, 178–179. [Google Scholar] [CrossRef]
- Woo, J.H.; Urry, C.M.; van der Marel, R.P.; Lira, P.; Maza, J. Black Hole Masses and Host Galaxy Evolution of Radio-Loud Active Galactic Nuclei. Astrophys. J. 2005, 631, 762. [Google Scholar] [CrossRef]
- Schwartz, D.A.; Ku, W.H.M. Studies of BL Lac objects with the Einstein X-ray Observatory: The absolute volume density. Astrophys. J. 1983, 266, 459–465. [Google Scholar] [CrossRef]
- Hartman, R.C.; Bertsch, D.L.; Bloom, S.D.; Chen, A.W.; Deines-Jones, P.; Esposito, J.A.; Fichtel, C.E.; Friedlander, D.P.; Hunter, S.D.; McDonald, L.M.; et al. The Third EGRET Catalog of High-Energy Gamma-Ray Sources. Astrophys. J. 1999, 123, 79–202. [Google Scholar] [CrossRef]
- Armstrong, P.; Chadwick, P.M.; Cottle, P.J.; Dickinson, J.E.; Dickinson, M.R.; Dipper, N.A.; Hilton, S.E.; Hogg, W.; Holder, J.; Kendall, T.R.; et al. The University of Durham Mark 6 Gamma Ray Telescope. Exp. Astron. 1999, 9, 51–80. [Google Scholar] [CrossRef]
- Chadwick, P.M.; Lyons, K.; McComb, T.J.L.; Orford, K.J.; Osborne, J.L.; Rayner, S.M.; Shaw, S.E.; Turver, K.E. A Search for Very High Energy Gamma Rays from Active Galactic Nuclei Visible from the Southern Hemisphere. Astrophys. J. 1999, 521, 547–551. [Google Scholar] [CrossRef][Green Version]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Baughman, B.M.; et al. Bright Active Galactic Nuclei Source List from the First Three Months of the Fermi Large Area Telescope All-Sky Survey. Astrophys. J. 2009, 700, 597–622. [Google Scholar] [CrossRef]
- Hofmann, W. Very High Energy gamma-ray emission from AP Lib detected by H.E.S.S. Astron. Telegr. 2010, 2743, 1. [Google Scholar]
- Fortin, P.; Fegan, S.; Horan, D.; Sanchez, D.; Fermi LAT Collaboration; Gielbels, B.; Becherini, Y.; Dubus, G.; de Naurois, M.; Punch, M.; et al. Gamma-ray emission from AP Librae (PKS1514-241). In Proceedings of the 25th Texas Symposium on Relativistic Astrophysics, Heidelberg, Germany, 6–10 December 2010; p. 199. [Google Scholar] [CrossRef]
- Kaufmann, S. Extended X-ray jet and TeV emission in a low frequency peaked BL Lac object Extra-galactic sources II (Gamma-ray bursts). In Proceedings of the International Cosmic Ray Conference, Beijing, China, 11–18 August 2011; Volume 8, p. 201. [Google Scholar] [CrossRef]
- H. E. S. S. Collaboration; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Angüner, E.; Anton, G.; Backes, M.; Balenderan, S.; Balzer, A.; et al. The high-energy γ-ray emission of AP Librae. Astron. Astrophys. 2015, 573, A31. [Google Scholar] [CrossRef]
- Kaufmann, S.; Wagner, S.J.; Tibolla, O. Discovery of an Extended X-Ray Jet in AP Librae. Astrophys. J. 2013, 776, 68. [Google Scholar] [CrossRef]
- Basumallick, P.P.; Gupta, N. Constraints on Proton Synchrotron Origin of Very High Energy Gamma Rays from the Extended Jet of AP Librae. Astrophys. J. 2017, 844, 58. [Google Scholar] [CrossRef]
- Carangelo, N.; Falomo, R.; Kotilainen, J.; Treves, A.; Ulrich, M.H. Optical spectroscopy of BL Lac objects: New redshifts and mis-identified sources. Astron. Astrophys. 2003, 412, 651–655. [Google Scholar] [CrossRef][Green Version]
- Kollgaard, R.I.; Palma, C.; Laurent-Muehleisen, S.A.; Feigelson, E.D. Radio Constraints on Relativistic Beaming Models of BL Lacertae Objects. Astrophys. J. 1996, 465, 115. [Google Scholar] [CrossRef]
- Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. 3FHL: The Third Catalog of Hard Fermi-LAT Sources. Astrophys. J. Suppl. Ser. 2017, 232, 18. [Google Scholar] [CrossRef]
- Petropoulou, M.; Dimitrakoudis, S.; Padovani, P.; Mastichiadis, A.; Resconi, E. Photohadronic origin of γ-ray BL Lac emission: Implications for IceCube neutrinos. Mon. Not. R. Astron. Soc. 2015, 448, 2412–2429. [Google Scholar] [CrossRef]
- Righi, C.; Tavecchio, F.; Guetta, D. High-energy emitting BL Lacs and high-energy neutrinos. Prospects for the direct association with IceCube and KM3NeT. Astron. Astrophys. 2017, 598, A36. [Google Scholar] [CrossRef]
- Padovani, P.; Resconi, E.; Giommi, P.; Arsioli, B.; Chang, Y.L. Extreme blazars as counterparts of IceCube astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2016, 457, 3582–3592. [Google Scholar] [CrossRef]
- Fallah Ramazani, V.; Lindfors, E.; Nilsson, K. Empirical multi-wavelength prediction method for very high energy gamma-ray emitting BL Lacertae objects. Astron. Astrophys. 2017, 608, A68. [Google Scholar] [CrossRef]
- Resconi, E.; Coenders, S.; Padovani, P.; Giommi, P.; Caccianiga, L. Connecting blazars with ultrahigh-energy cosmic rays and astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2017, 468, 597–606. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. Astron. J. 1998, 115, 1693. [Google Scholar] [CrossRef]
- Massaro, E.; Maselli, A.; Leto, C.; Perri, M.; Giommi, P.; Piranomonte, S. The 5th edition of the Roma-BZCAT. A short presentation. Astrophys. Space Sci. 2015, 357, 75. [Google Scholar] [CrossRef]
- Britzen, S.; Witzel, A.; Gong, B.P.; Zhang, J.W.; Gopal-Krishna; Goyal, A.; Aller, M.F.; Aller, H.D.; Zensus, J.A. Understanding BL Lacertae objects. Structural and kinematic mode changes in the BL Lac object PKS 0735+178. Astron. Astrophys. 2010, 515, A105. [Google Scholar] [CrossRef]
- Lott, B.; Gasparrini, D.; Ciprini, S. The Fourth Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope—Data Release 2. arXiv 2020, arXiv:2010.08406. [Google Scholar] [CrossRef]
- Carswell, R.F.; Strittmatter, P.A.; Williams, R.E.; Kinman, T.D.; Serkowski, K. Optical Observations of the Radio Source 0735+178. Astrophys. J. Letters 1974, 190, L101. [Google Scholar] [CrossRef]
- Falomo, R.; Ulrich, M.H. Optical imaging and spectroscopy of BL Lac objects. Astron. Astrophys. 2000, 357, 91–100. [Google Scholar] [CrossRef]
- Rector, T.A.; Stocke, J.T. The Properties of the Radio-Selected 1 Jy Sample of BL Lacertae Objects*. Astron. J. 2001, 122, 565. [Google Scholar] [CrossRef]
- Nilsson, K.; Pursimo, T.; Villforth, C.; Lindfors, E.; Takalo, L.O.; Sillanpää, A. Redshift constraints for RGB 0136+391 and PKS 0735+178 from deep optical imaging. Astron. Astrophys. 2012, 547, A1. [Google Scholar] [CrossRef]
- Falomo, R.; Treves, A.; Paiano, S. Optical view of neutrino emitter candidate PKS 0735 +178. Astron. Telegr. 2021, 15132. [Google Scholar]
- IceCube Collaboration. IceCube-211208A—IceCube observation of a high-energy neutrino candidate track-like event. GRB Coord. Netw. 2021, 31191, 1. [Google Scholar]
- Dzhilkibaev, Z.A.; Suvorova, O.; Baikal-GVD Collaboration. Baikal-GVD observation of a high-energy neutrino candidate event from the blazar PKS 0735+17 at the day of the IceCube-211208A neutrino alert from the same direction. Astron. Telegr. 2021, 15112, 1. [Google Scholar]
- Petkov, V.B.; Novoseltsev, Y.F.; Novoseltseva, R.V.; Baksan Underground Scintillation Telescope Group. Baksan Underground Scintillation Telescope observation of a GeV neutrino candidate event at the time of a gamma-ray flare of the blazar PKS 0735+17, a possible source of coinciding IceCube and Baikal high-energy neutrinos. Astron. Telegr. 2021, 15143, 1. [Google Scholar]
- Filippini, F.; Illuminati, G.; Heijboer, A.; Gatius, C.; Muller, R.; Dornic, D.; Huang, F.; Le Stum, S.; Palacios González, J.; Celli, S.; et al. Search for neutrino counterpart to the blazar PKS0735+178 potentially associated with IceCube-211208A and Baikal-GVD-211208A with the KM3NeT neutrino detectors. Astron. Telegr. 2022, 15290, 1. [Google Scholar]
- Prince, R.; Das, S.; Gupta, N.; Majumdar, P.; Czerny, B. Dissecting the broad-band emission from γ-ray blazar PKS 0735+178 in search of neutrinos. Mon. Not. R. Astron. Soc. 2023, 527, 8746–8754. [Google Scholar] [CrossRef]
- Tramacere, A.; Giommi, P.; Perri, M.; Verrecchia, F.; Tosti, G. Swift observations of the very intense flaring activity of Mrk 421 during 2006. I. Phenomenological picture of electron acceleration and predictions for MeV/GeV emission. Astron. Astrophys. 2009, 501, 879–898. [Google Scholar] [CrossRef]
- Tramacere, A.; Massaro, E.; Taylor, A.M. Stochastic Acceleration and the Evolution of Spectral Distributions in Synchro-Self-Compton Sources: A Self-consistent Modeling of Blazars’ Flares. Astrophys. J. 2011, 739, 66. [Google Scholar] [CrossRef]
- Tramacere, A. JetSeT: Numerical modeling and SED fitting tool for relativistic jets. Astrophysics Source Code Library, record ascl:2009.001, 2020. Available online: https://ui.adsabs.harvard.edu/abs/2020ascl.soft09001T/abstract (accessed on 10 July 2025).
- Dominguez, A.; Primack, J.R.; Rosario, D.J.; Prada, F.; Gilmore, R.C.; Faber, S.M.; Koo, D.C.; Somerville, R.S.; Pérez-Torres, M.A.; Pérez-González, P.; et al. Extragalactic Background Light Inferred from AEGIS Galaxy SED-type Fractions. Mon. Not. Roy. Astron. Soc. 2011, 410, 2556. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. The extragalactic optical-infrared background radiations, their time evolution and the cosmic photon-photon opacity. Astron. Astrophys. 2008, 487, 837. [Google Scholar] [CrossRef]
- Finke, J.D.; Razzaque, S.; Dermer, C.D. Modeling the Extragalactic Background Light from Stars and Dust. Astrophys. J. 2010, 712, 238–249. [Google Scholar] [CrossRef]
- Fan, J.H.; Yang, J.H.; Liu, Y.; Zhang, J.Y. The gamma-ray Doppler factor determinations for a Fermi blazar sample. Res. Astron. Astrophys. 2013, 13, 259. [Google Scholar] [CrossRef]
- Nalewajko, K. The brightest gamma-ray flares of blazars. Mon. Not. R. Astron. Soc. 2013, 430, 1324–1333. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Maraschi, L.; Celotti, A.; Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 2014, 515, 376. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G.; Ghirlanda, G.; Foschini, L.; Maraschi, L. TeV BL Lac objects at the dawn of the Fermi era. Mon. Not. R. Astron. Soc. 2010, 401, 1570–1586. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, E.W.; Zhang, S.N.; Bai, J.M. Radiation Mechanisms and Physical Properties of GeV–TeV BL Lac Objects. Astrophys. J. 2012, 752, 157. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Yang, H.Y.; Zheng, Y.G.; Kang, S.J. The Energy Budget in the Jet of High-frequency Peaked BL Lacertae Objects. Astrophys. J. 2024, 967, 104. [Google Scholar] [CrossRef]
- Dembinski, H.; Ongmongkolkul, P.; Deil, C.; Schreiner, H.; Feickert, M.; Burr, C.; Watson, J.; Rost, F.; Pearce, A.; Geiger, L.; et al. Scikit-Hep/Iminuit. 2024. Available online: https://zenodo.org/records/13923658 (accessed on 15 June 2025).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Ghisellini, G. Electron–positron pairs in blazar jets and γ-ray loud radio galaxies. Mon. Not. R. Astron. Soc. Lett. 2012, 424, L26–L30. [Google Scholar] [CrossRef]
- Klinger, M.; Rudolph, A.; Rodrigues, X.; Yuan, C.; de Clairfontaine, G.F.; Fedynitch, A.; Winter, W.; Pohl, M.; Gao, S. AM3: An Open-source Tool for Time-dependent Lepto-hadronic Modeling of Astrophysical Sources. Astrophys. J. Suppl. 2024, 275, 4. [Google Scholar] [CrossRef]
- Hümmer, S.; Rüger, M.; Spanier, F.; Winter, W. Simplified Models for Photohadronic Interactions in Cosmic Accelerators. Astrophys. J. 2010, 721, 630. [Google Scholar] [CrossRef]
- Aliu, E.; Archambault, S.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Boettcher, M.; Bouvier, A.; Bugaev, V.; Cannon, A.; et al. Multiwavelength observations of the AGN 1ES 0414+ 009 with VERITAS, Fermi-LAT, Swift-XRT, and MDM. Astrophys. J. 2012, 755, 118. [Google Scholar] [CrossRef]
- Acciari, M.C.V.; Ansoldi, S.; Antonelli, L.; Arbet Engels, A.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.; Becerra González, J.; Bednarek, W.; et al. An intermittent extreme BL Lac: MWL study of 1ES 2344+ 514 in an enhanced state. Mon. Not. R. Astron. Soc. 2020, 496, 3912–3928. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Long, G.B.; Yang, C.Y.; Bai, J.M. Verification of the diffusive shock acceleration in Mrk 501. Mon. Not. R. Astron. Soc. 2018, 478, 3855–3861. [Google Scholar] [CrossRef]
- Zacharias, M.; Wagner, S.J. The extended jet of AP Librae: Origin of the very high-energy γ-ray emission? Astron. Astrophys. 2016, 588, A110. [Google Scholar] [CrossRef]
- Plotkin, R.M.; Markoff, S.; Trager, S.C.; Anderson, S.F. Dynamical black hole masses of BL Lac objects from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2011, 413, 805–812. [Google Scholar] [CrossRef][Green Version]
- Acharyya, A.; Adams, C.B.; Archer, A.; Bangale, P.; Bartkoske, J.T.; Batista, P.; Benbow, W.; Brill, A.; Buckley, J.H.; Christiansen, J.L.; et al. Multiwavelength Observations of the Blazar PKS 0735+178 in Spatial and Temporal Coincidence with an Astrophysical Neutrino Candidate IceCube-211208A. Astrophys. J. 2023, 954, 70. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, X.; Paliya, V.S.; Garrappa, S.; Omeliukh, A.; Franckowiak, A.; Winter, W. Leptohadronic multi-messenger modeling of 324 gamma-ray blazars. Astron. Astrophys. 2024, 681, A119. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Ellison, D.C.; Double, G.P. Diffusive shock acceleration in unmodified relativistic, oblique shocks. Astropart. Phys. 2004, 22, 323–338. [Google Scholar] [CrossRef]


| Symbol | Description | AP Librae | 1H 1914–194 | PKS 0735+17 |
|---|---|---|---|---|
| Minimum electron Lorentz factor | ||||
| Break electron Lorentz factor | ||||
| Maximum electron Lorentz factor | ||||
| B [G] | Magnetic field strength | |||
| R [cm] | Radius of the emitting region (blob) | |||
| [deg] | Viewing angle | |||
| N [cm−3] | Particle number density | |||
| Spectral index below | ||||
| Spectral index above | ||||
| Bulk Lorentz factor |
| Parameter | Description | AP Librae | 1H 1914–194 | PKS 0735+17 |
|---|---|---|---|---|
| [erg cm−3] | Electron energy density | |||
| [erg cm−3] | Cold proton energy density | |||
| [erg cm−3] | Magnetic energy density | |||
| [erg cm−3] | Synchrotron photon energy density | |||
| [erg s−1] | Synchrotron radiative power | |||
| [erg s−1] | SSC radiative power | |||
| [erg s−1] | Total radiated power | |||
| [erg s−1] | Jet kinetic power | |||
| [erg s−1] | Jet electron power | |||
| [erg s−1] | Jet magnetic power | |||
| [erg s−1] | Jet cold proton power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuani Pereira, L.A.; Bernardo da Silva, S.V. From Gamma Rays to Cosmic Rays: Lepto-Hadronic Modeling of Blazar Sources as Candidates for Ultra-High-Energy Cosmic Rays. Universe 2025, 11, 266. https://doi.org/10.3390/universe11080266
Stuani Pereira LA, Bernardo da Silva SV. From Gamma Rays to Cosmic Rays: Lepto-Hadronic Modeling of Blazar Sources as Candidates for Ultra-High-Energy Cosmic Rays. Universe. 2025; 11(8):266. https://doi.org/10.3390/universe11080266
Chicago/Turabian StyleStuani Pereira, Luiz Augusto, and Samuel Victor Bernardo da Silva. 2025. "From Gamma Rays to Cosmic Rays: Lepto-Hadronic Modeling of Blazar Sources as Candidates for Ultra-High-Energy Cosmic Rays" Universe 11, no. 8: 266. https://doi.org/10.3390/universe11080266
APA StyleStuani Pereira, L. A., & Bernardo da Silva, S. V. (2025). From Gamma Rays to Cosmic Rays: Lepto-Hadronic Modeling of Blazar Sources as Candidates for Ultra-High-Energy Cosmic Rays. Universe, 11(8), 266. https://doi.org/10.3390/universe11080266






