A Tailored Deep Learning Network with Embedded Space Physical Knowledge for Auroral Substorm Recognition: Validation Through Special Case Studies
Abstract
1. Introduction
- 1.
- We developed a novel space knowledge embedding module called the Visual–Physical Interaction (VPI) module, which simultaneously incorporates eye movement patterns and scientific knowledge. The core of this module is the MLT-MLAT embedding, inspired by the physical characteristics and unique data attributes of auroral substorms. This method is based on the Altitude Adjusted Corrected Geomagnetic Coordinates (AACGM) system. The MLT-MLAT embedding approach closely aligns with space physics knowledge, offering an enhanced representation of auroral substorm features.
- 2.
- The eye movement patterns are considered a type of empirical knowledge in this work. As a result, an auroral substorm eye movement dataset is established by collecting eye movement data from space physicists. Auroral substorm events used in this study are comprehensive, including various types of auroral substorm sequences. We analyze these eye movement data and generate the eye movement patterns for various auroral substorms. In addition, we generate visual maps using an Eye Movement Pattern Prediction (EMPP) module, which learns from the eye movement patterns of experts.
- 3.
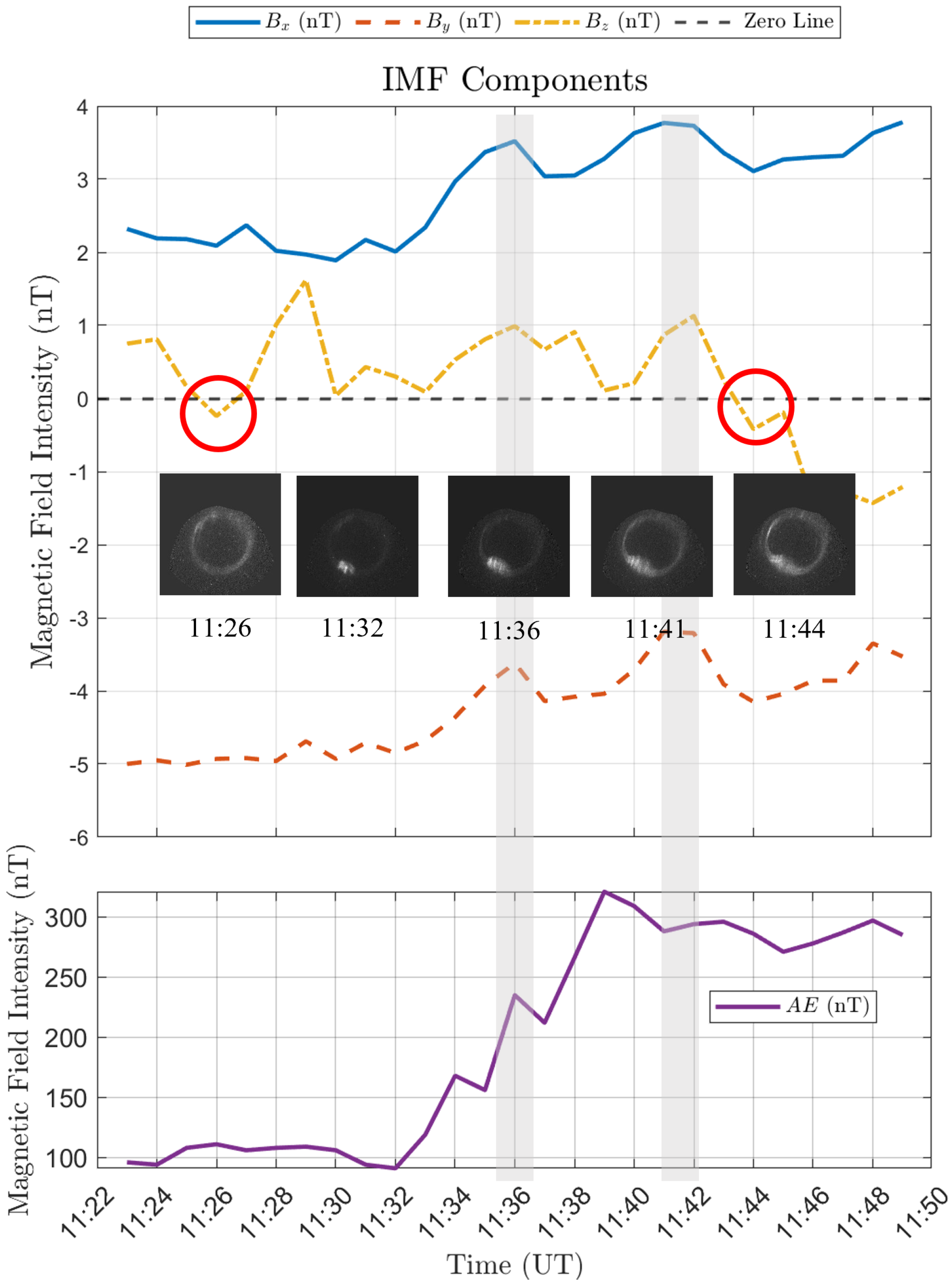
- We thoroughly analyze and compare the variation patterns of the Interplanetary Magnetic Field (IMF) and the AE index observed between auroral substorms that were correctly identified (easy samples) and those that were misclassified (difficult samples). By identifying these differences, we gain a deeper understanding of the inherent challenges and complex factors in auroral substorm recognition.
2. Data Collection and Process
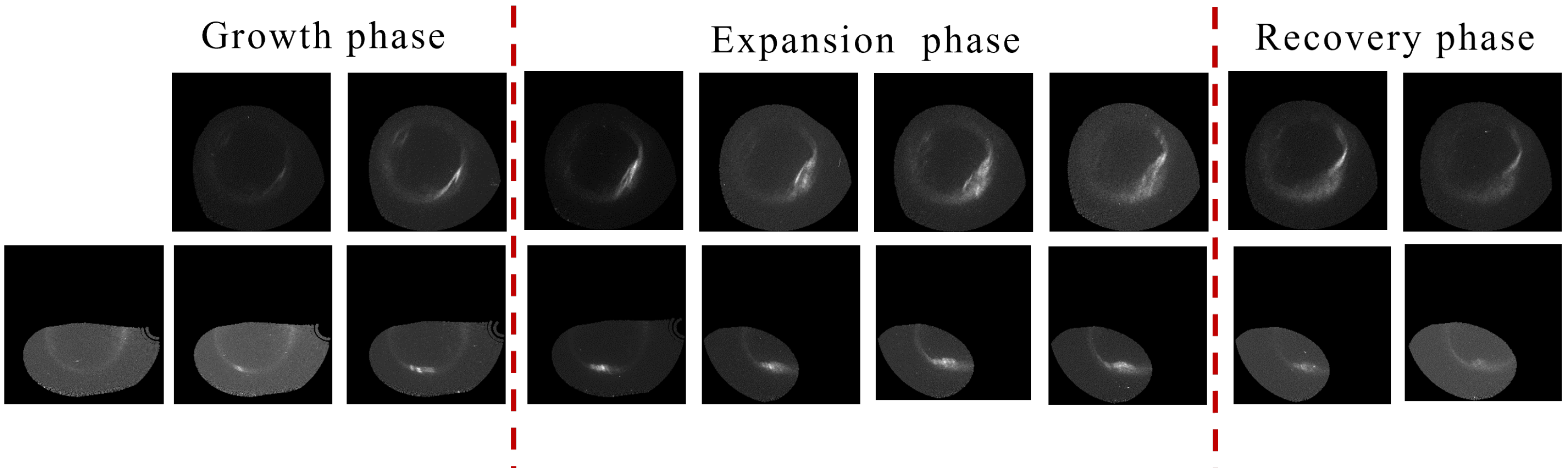
2.1. Auroral Substorm Data
- 1.
- The UVI images in the growth phase are within 10–20 min before the onset.
- 2.
- The UVI images of the expansion phase and the recovery phase are within 30–90 min after the onset.
- 3.
- The auroral substorm sequences are discontinuous due to occasional observation gaps. As a result, some UVI frames in a sequence may appear completely dark and were excluded. Only those sequences exhibiting clear auroral evolution consistent with the above criteria were retained.
- 4.
- Each sequence must include images within the onset and expansion phase. Consequently, the processed substorm sequences contain 5 to 26 qualified images.
2.2. Auroral Substorms Eye Movement Data
2.3. Data Preprocessing
3. Method
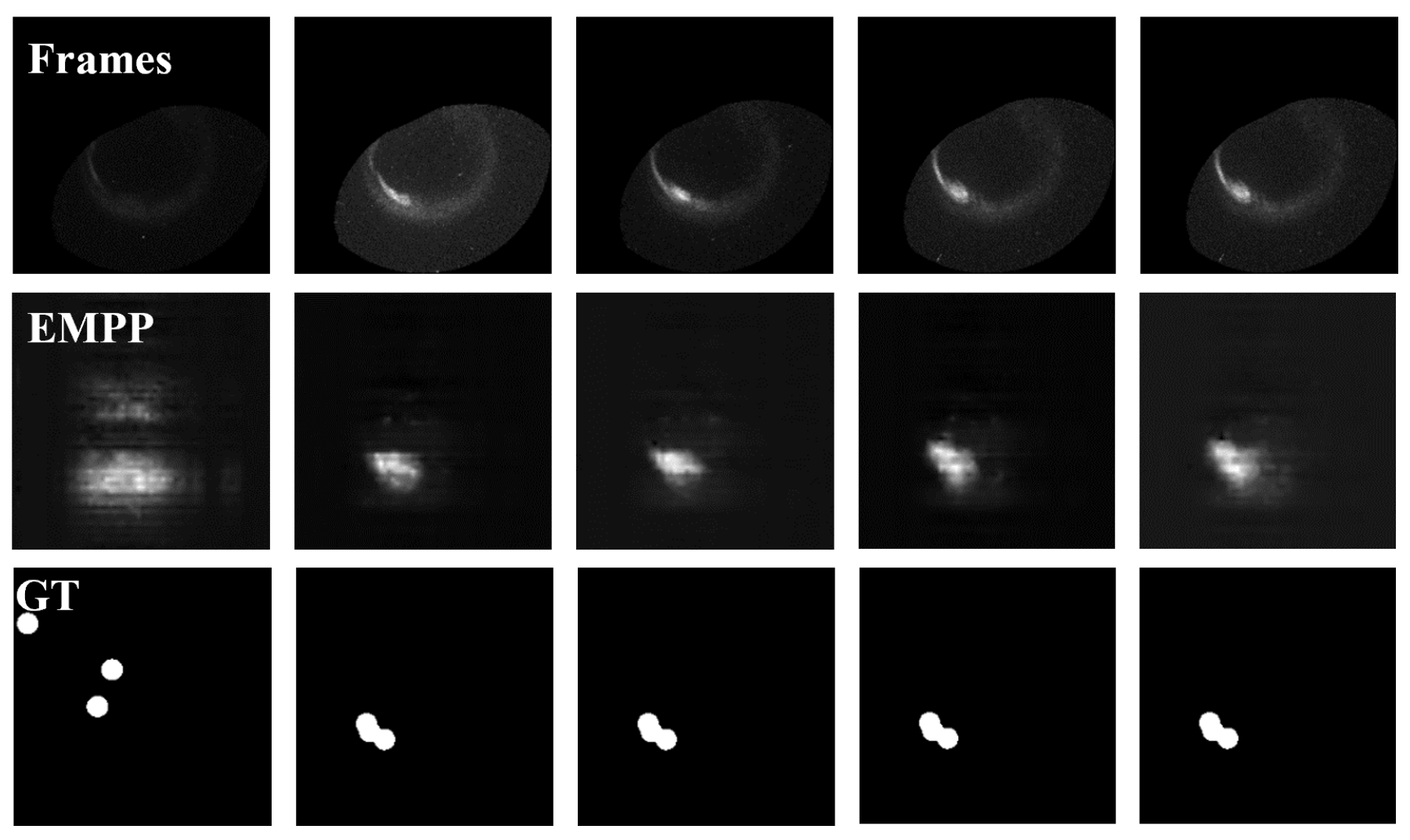
3.1. Eye Movement Pattern Prediction (EMPP) Module
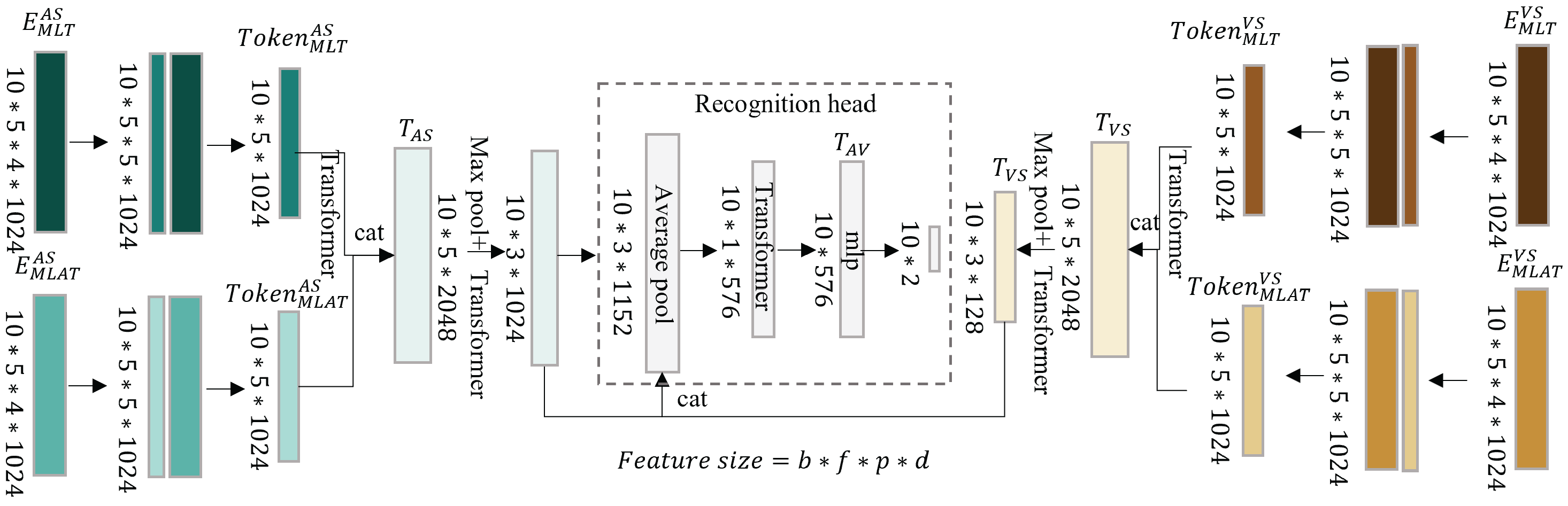
3.2. Visual–Physical Interaction (VPI) Module
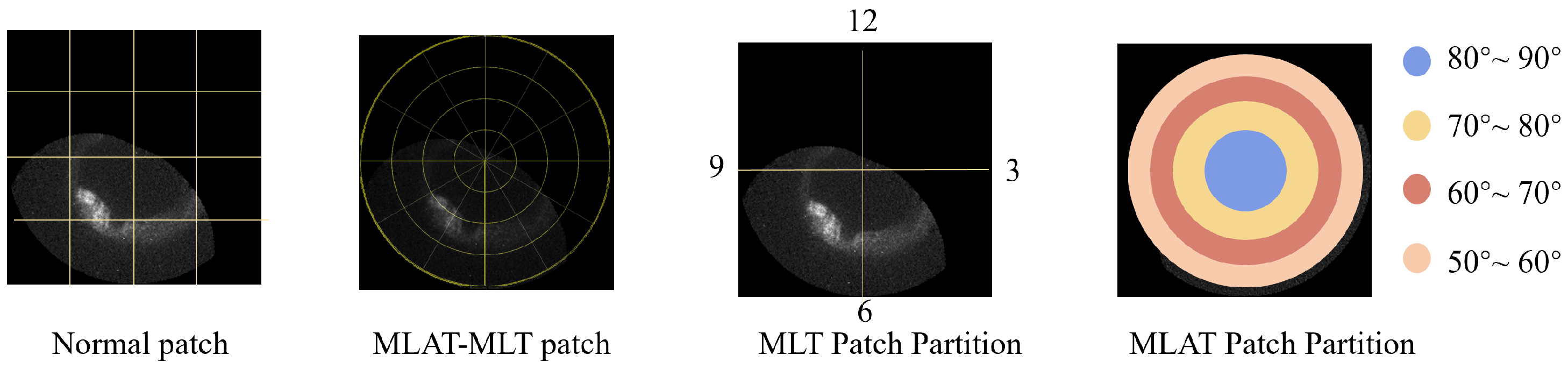
3.2.1. MLT-MLAT Embedding
3.2.2. Architecture of the VPI Module
4. Experimental Results
4.1. EMPP Results
4.2. VPI Results
- Accuracy: The proportion of correct predictions relative to total predictions, reflecting overall classification correctness.
- Precision: The ratio of true positive predictions to all positive classifications, quantifying prediction reliability with higher values indicating fewer false alarms.
- Recall (Sensitivity): The percentage of actual positive cases correctly identified, measuring detection completeness where higher values correspond to fewer missed events.
- F1-score: The harmonic mean balancing precision and recall, particularly critical for evaluating performance on imbalanced datasets where strict precision-recall tradeoffs exist.
4.2.1. Ablation Experiments
4.2.2. Comparative Experiments
5. Discussion
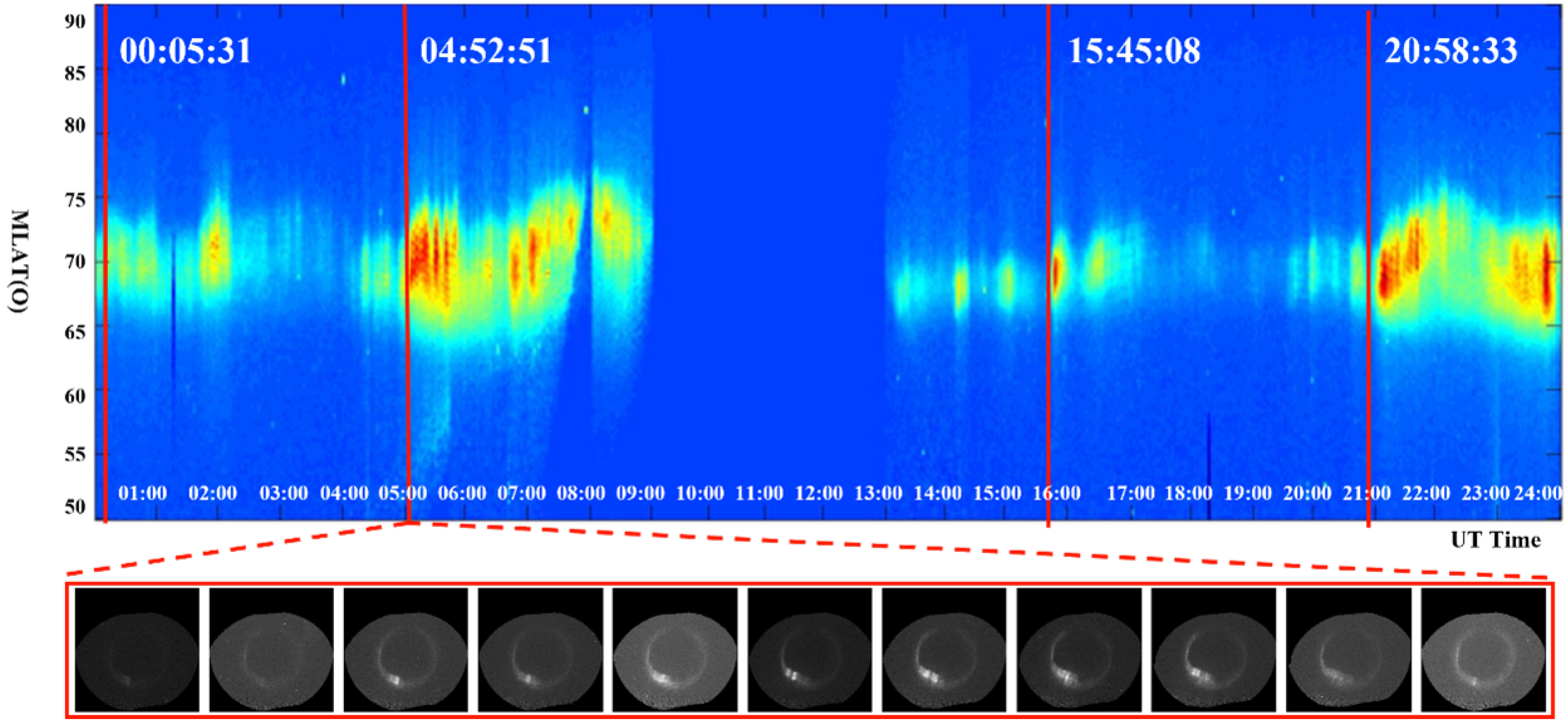
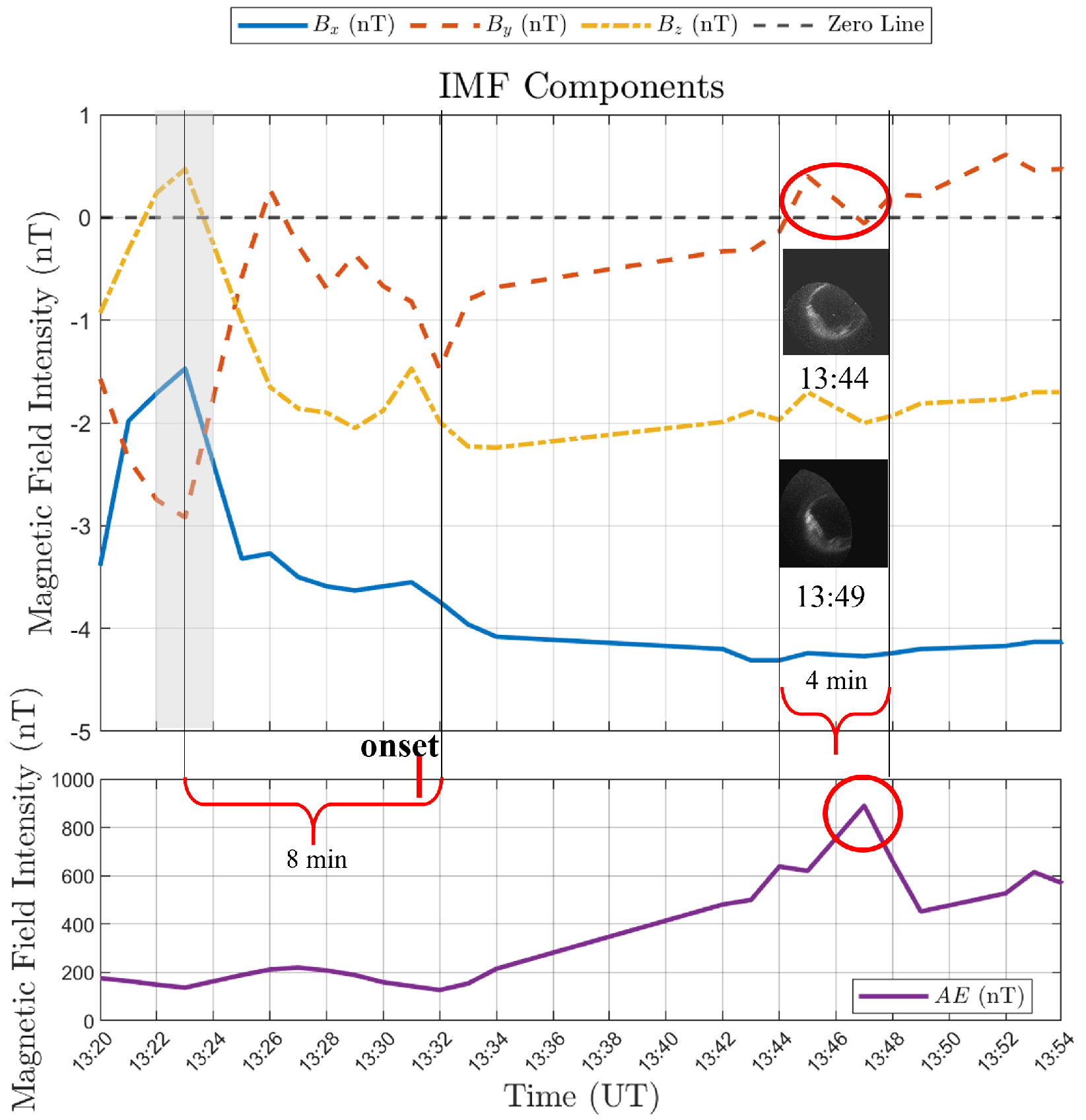
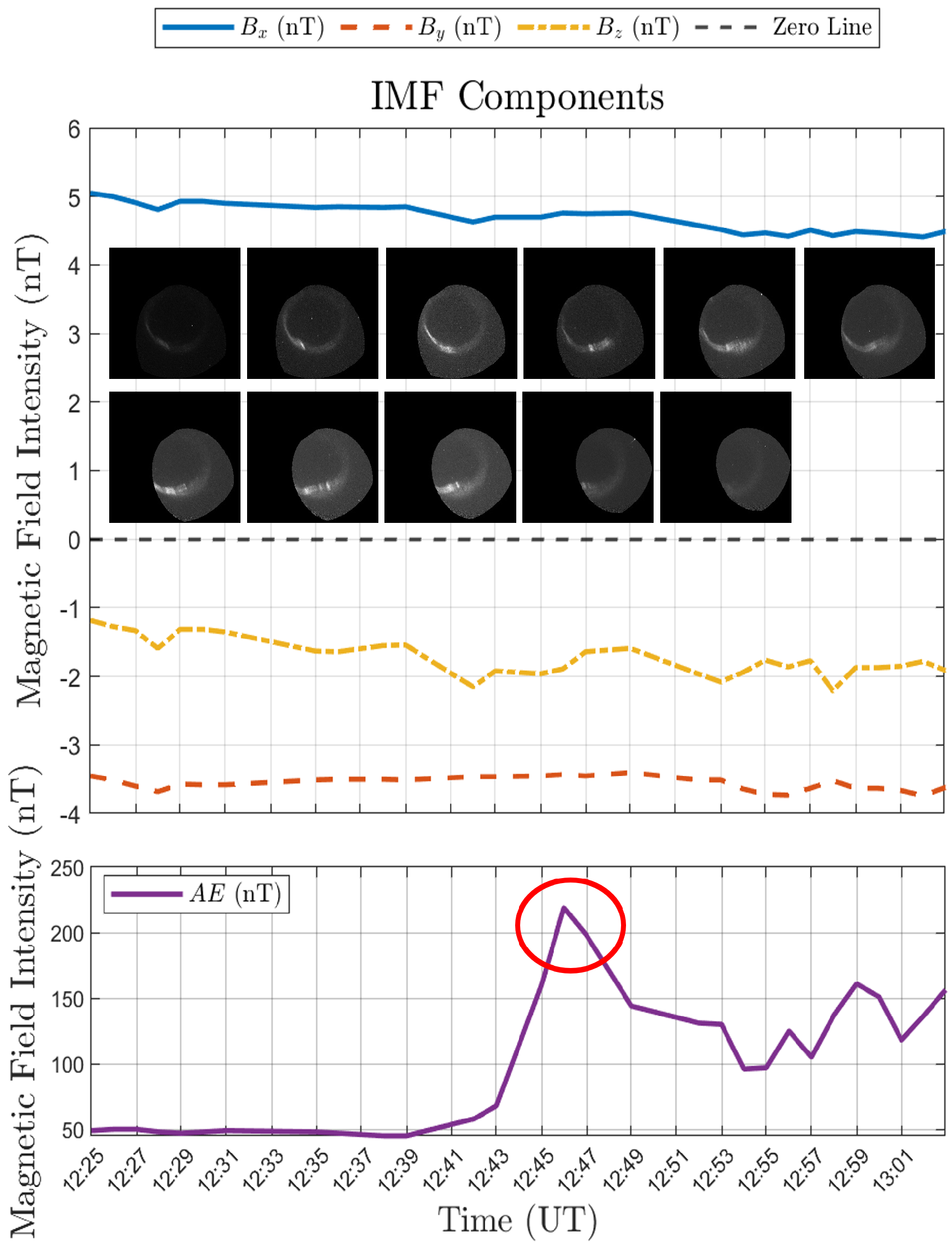
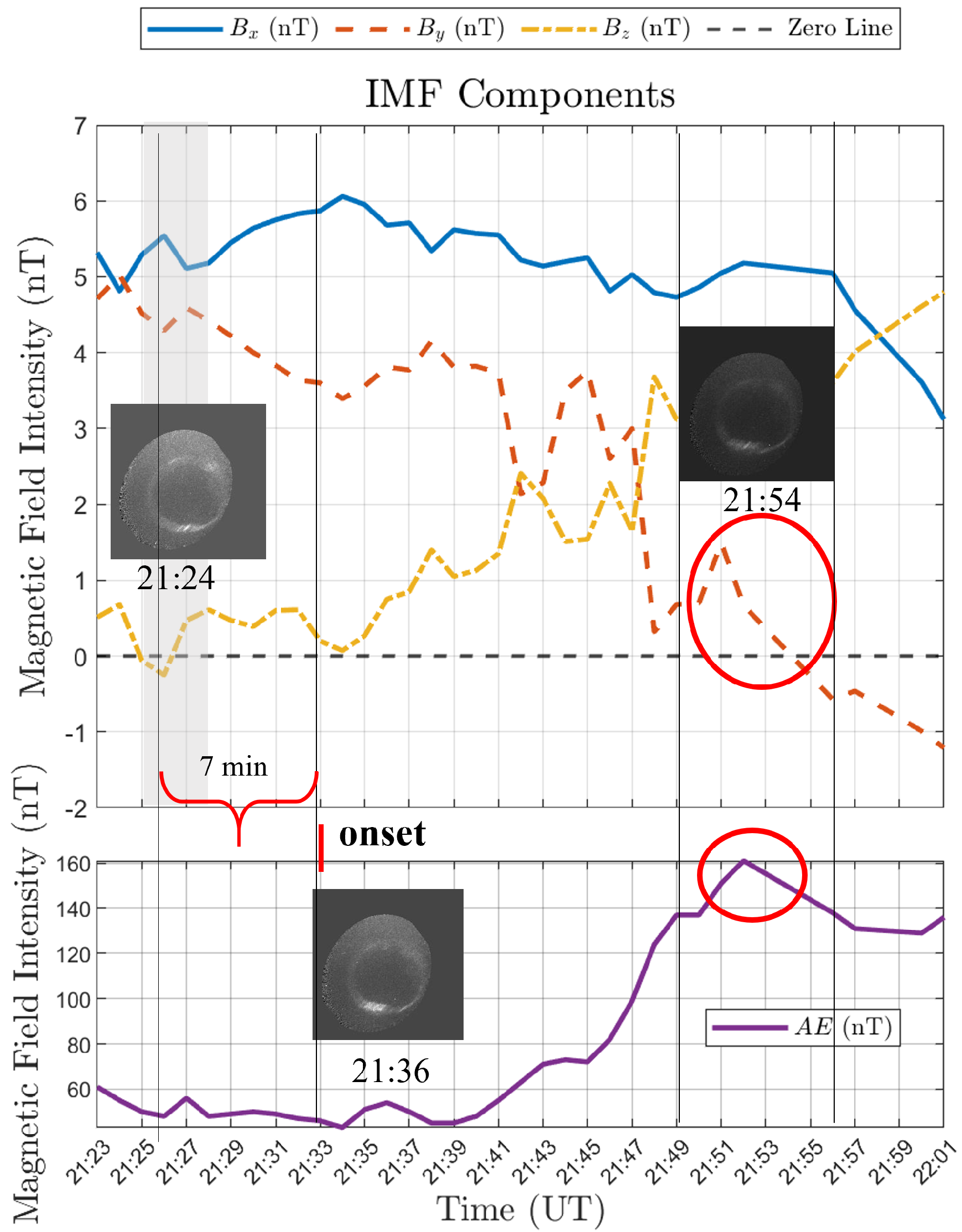
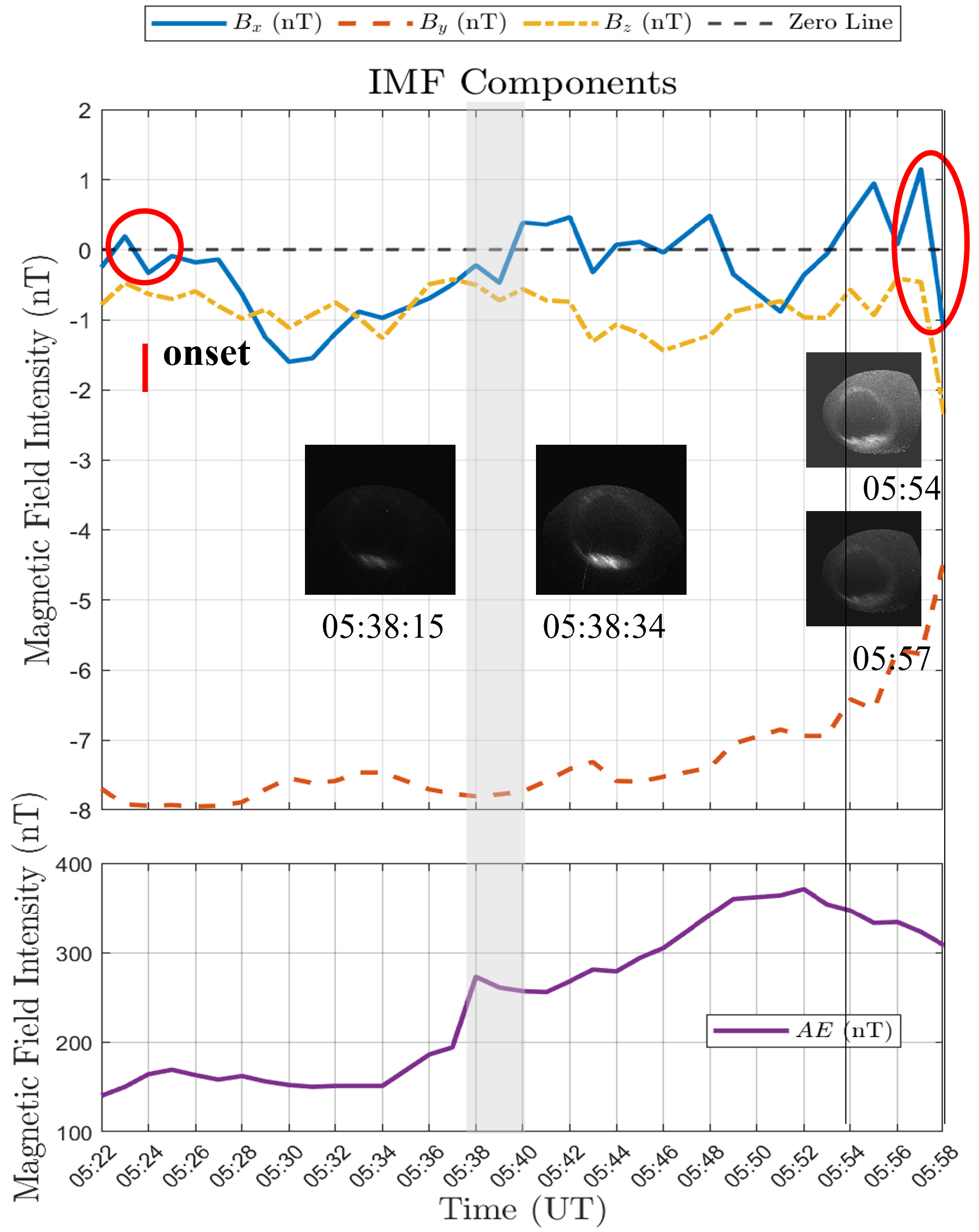
5.1. Case Example: Successful Cases
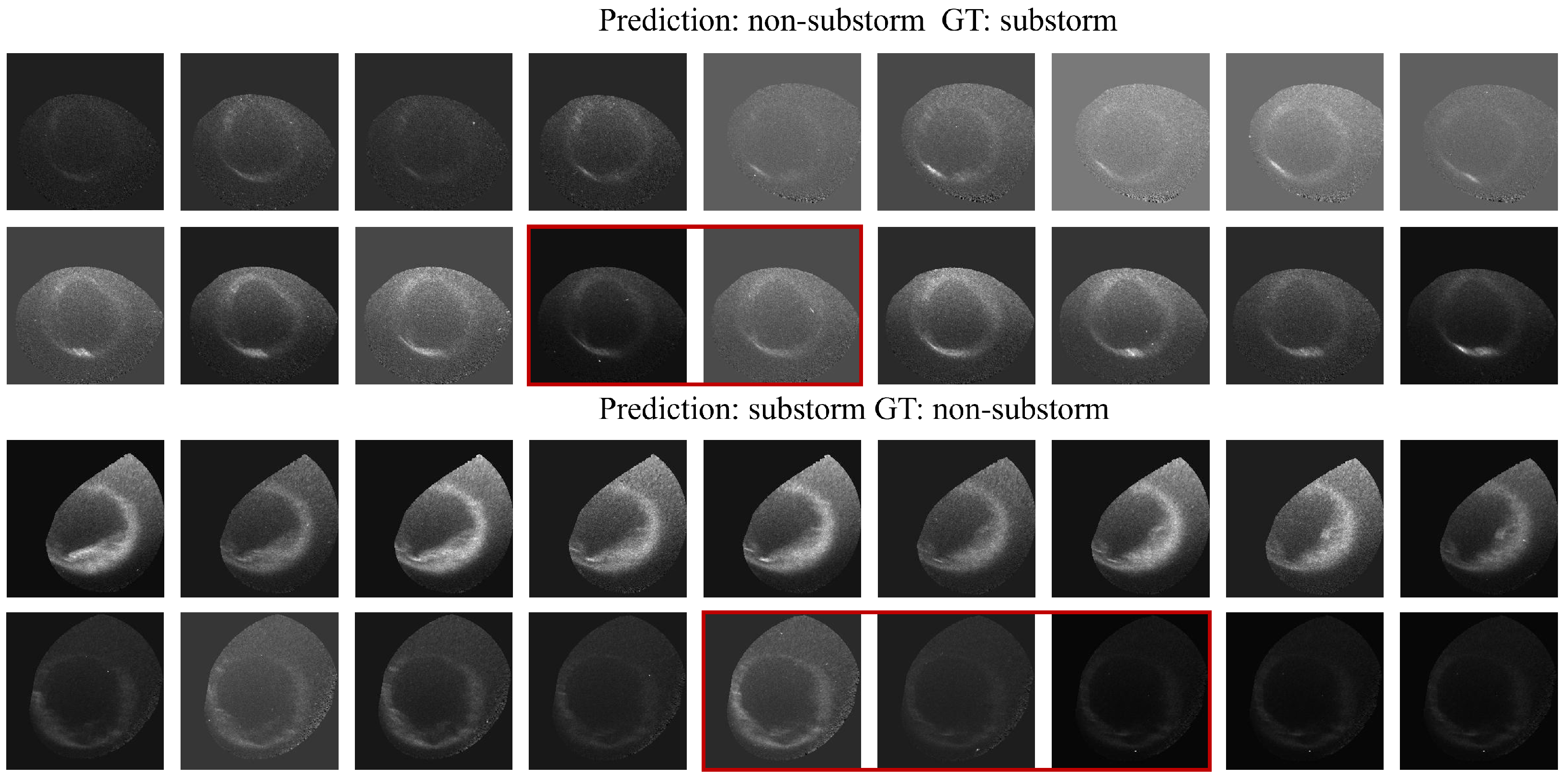
5.2. Case Example: Failure Cases
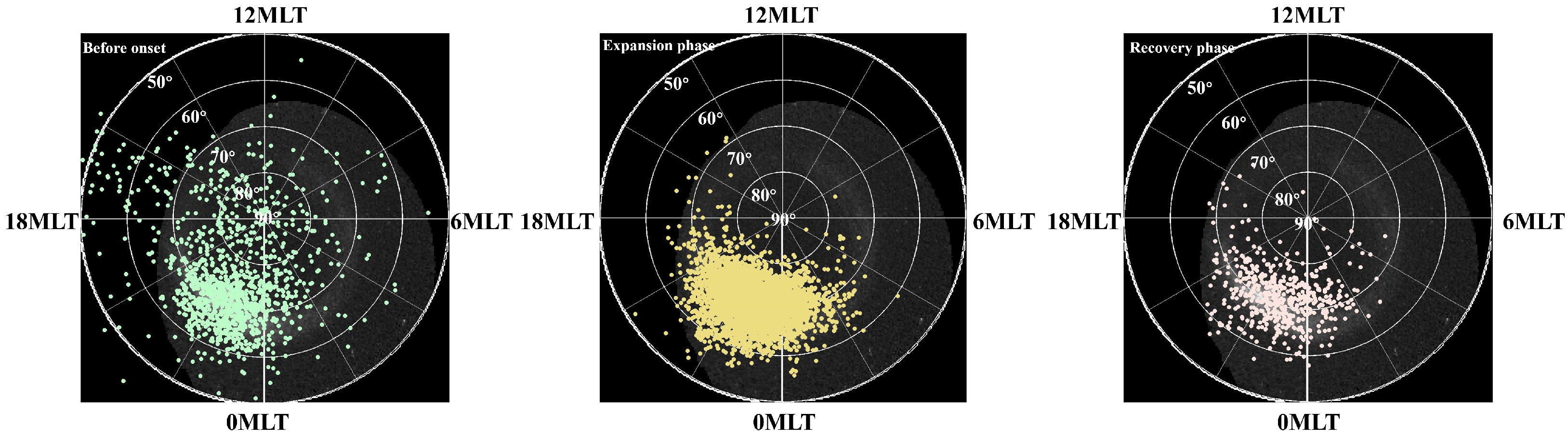
5.3. Comparative Analysis of Success and Failure Cases
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akasofu, S.I. The development of the auroral substorm. Planet. Space Sci. 1964, 12, 273–282. [Google Scholar] [CrossRef]
- Li, L.Y.; Cao, J.B.; Zhou, G.C.; Li, X. Statistical roles of storms and substorms in changing the entire outer zone relativistic electron population. J. Geophys. Res. Space Phys. 2009, 114, A12214. [Google Scholar] [CrossRef]
- Lui, A.T.Y. Tutorial on geomagnetic storms and substorms. IEEE Trans. Plasma Sci. 2000, 28, 1854–1866. [Google Scholar] [CrossRef]
- Lyons, L.R. A new theory for magnetospheric substorms. J. Geophys. Res. 1995, 100, 19069–19081. [Google Scholar] [CrossRef]
- McPherron, R.L. Magnetospheric substorms. Rev. Geophys. 1979, 17, 657–681. [Google Scholar] [CrossRef]
- Newell, P.; Gjerloev, J.W. Substorm and magnetosphere characteristic scales inferred from the supermag auroral electrojet indices. J. Geophys. Res. 2011, 116, A12232. [Google Scholar] [CrossRef]
- Newell, P.; Liou, K.; Gjerloev, J.; Sotirelis, T.; Wing, S.; Mitchell, E. Substorm probabilities are best predicted from solar wind speed. J. Atmos. Sol.-Terr. Phys. 2016, 146, 28–37. [Google Scholar] [CrossRef]
- Pudovkin, M. Physics of Magnetospheric Substorms: A Review. In Magnetospheric Substorms; Kan, J.R., Potemra, T.A., Eds.; American Geophysical Union: San Francisco, CA, USA, 2013; pp. 28–37. [Google Scholar]
- Liu, Z.Y.; Zong, W.G.; Zong, Q.G.; Wang, J.S.; Yu, X.Q.; Wang, Y.F.; Zou, H.; Fu, S.Y.; Yue, C.; Hu, Z.J.; et al. The Response of Auroral-Oval Waves to CIR-Driven Recurrent Storms: FY-3E/ACMag Observations. Universe 2023, 9, 213. [Google Scholar] [CrossRef]
- Brittnacher, M.; Spann, J.; Parks, G. Auroral observations by the polar Ultraviolet Imager (UVI). Adv. Space Res. 1997, 20, 1037–1042. [Google Scholar] [CrossRef]
- Frey, H.U.; Mende, S.B. Substorm onsets as observed by IMAGE-FUV. J. Geophys. Res. Space Phys. 2004, 104, A10304. [Google Scholar]
- Liou, K. Polar Ultraviolet Imager observation of auroral breakup. J. Geophys. Res. Space Phys. 2010, 115, A12219. [Google Scholar] [CrossRef]
- Akasofu, S.I. The roles of the north-south component of the interplanetary magnetic field on large-scale auroral dynamics observed by the DMSP satellite. Planet. Space Sci. 1975, 23, 1349–1354. [Google Scholar] [CrossRef]
- Caan, M.N.; McPherron, R.L.; Russell, C.T. Characteristics of the association between the interplanetary magnetic field and substorms. J. Geophys. Res. 1977, 82, 4837–4842. [Google Scholar] [CrossRef]
- Freeman, M.P.; Morley, S.K. A minimal substorm model that explains the observed statistical distribution of times between substorms. Geophys. Res. Lett. 2004, 31, L12807. [Google Scholar] [CrossRef]
- Henderson, M.G.; Reeves, G.D.; Belian, R.D.; Murphree, J.S. Observations of magnetospheric substorms occurring with no apparent solar wind/IMF trigger. J. Geophys. Res. 1996, 101, 10773–10791. [Google Scholar] [CrossRef]
- Vennerstrom, S.; Friis-Christensen, E.; Troshichev, O.A.; Andersen, V.G. Comparison between the polar cap index, PC, and the auroral electrojet indices AE, AL, and AU. J. Geophys. Res. Space Phys. 1991, 96, 101–113. [Google Scholar] [CrossRef]
- Alberti, T.; Faranda, D.; Consolini, G.; De Michelis, P.; Donner, R.V.; Carbone, V. Concurrent Effects between Geomagnetic Storms and Magnetospheric Substorms. Universe 2022, 8, 226. [Google Scholar] [CrossRef]
- Sutcliffe, P.R. Substorm onset identification using neural networks and Pi2 pulsations. Ann. Geophys. 1997, 15, 1257–1264. [Google Scholar] [CrossRef]
- Wang, H.; Lühr, H. Effects of solar illumination and substorms on auroral electrojets based on CHAMP observations. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028905. [Google Scholar] [CrossRef]
- Murphy, K.R.; Miles, D.M.; Watt, C.E.J.; Rae, I.J.; Mann, I.R.; Frey, H.U. Automated Determination of Auroral Breakup during the Substorm Expansion Phase Using All-Sky Imager Data. J. Geophys. Res. Space Phys. 2014, 119, 1414–1427. [Google Scholar] [CrossRef]
- Yang, X.; Gao, X.B.; Tao, D.C.; Li, X. Improving level set method for fast auroral oval segmentation. IEEE Trans. Image Process. 2014, 23, 2854–2865. [Google Scholar] [CrossRef]
- Fu, R.; Gao, X.B.; Jian, Y.J. Patchy Aurora Image Segmentation Based on ALBP and Block Threshold. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3380–3383. [Google Scholar]
- Niu, C.; Zhang, J.; Wang, Q.; Liang, J. Weakly Supervised Semantic Segmentation for Joint Key Local Structure Localization and Classification of Aurora Image. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7133–7146. [Google Scholar] [CrossRef]
- Yang, Q.J.; Liang, J.M. A method for automatic identification of substorm expansion phase onset from UVI images. Chin. J. Geophys. 2013, 56, 1435–1447. [Google Scholar]
- Syrjäsuo, M.; Donovan, E. Analysis of auroral images: Detection and tracking. Geophysica 2002, 38, 3–14. [Google Scholar]
- Li, Y.; Jiang, N. An Aurora Image Classification Method based on Compressive Sensing and Distributed WKNN. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; pp. 347–354. [Google Scholar]
- Zhong, Y.; Huang, R.; Zhao, J.; Zhao, B.; Liu, T. Aurora Image Classification Based on Multi-Feature Latent Dirichlet Allocation. Remote Sens. 2018, 10, 233. [Google Scholar] [CrossRef]
- Yang, X.; Gao, X.B.; Tao, D.C.; Li, X.; Han, B.; Li, J. Shape-constrained sparse and low-rank decomposition for auroral substorm detection. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 32–46. [Google Scholar] [CrossRef]
- Yang, Q.; Liang, J.; Hu, Z.; Zhao, H. Auroral Sequence Representation and Classification Using Hidden Markov Models. IEEE Trans. Geosci. Remote Sens. 2012, 50, 5049–5060. [Google Scholar] [CrossRef]
- Sado, T.; Kataoka, R.; Tanaka, Y. Substorm Onset Prediction from Auroral Image Sequences Using Deep Learning; ESSOAr: Online, 2022. [Google Scholar]
- Hu, Z.J.; Lian, H.F.; Zhao, B.R.; Han, B.; Zhang, Y.S. Automatic Identification of Auroral Substorms Based on Ultraviolet Spectrographic Imager Aboard Defense Meteorological Satellite Program (DMSP) Satellite. Universe 2023, 9, 412. [Google Scholar] [CrossRef]
- Syrjäsuo, M.; Donovan, E.; Qin, X.; Jackel, B.; Liang, J.; Voronkov, I.; Connors, M.; Spanswick, E.; Milling, D.; Frey, H. Automatic Classification of Auroral Images in Substorm Studies. In Proceedings of the 8th International Conference on Substorms (ICS-8), University of Calgary, Banff, AB, Canada, 27–31 March 2006; pp. 309–313. [Google Scholar]
- Han, B.; Gao, X.B.; Liu, H. Auroral Oval Boundary Modeling Based on Deep Learning Method. In 2015 International Conference on Intelligent Science and Big Data Engineering; Springer: Berlin, Germany, 2015; pp. 96–106. [Google Scholar]
- Hu, Z.J.; Han, B.; Lian, H.F. Modeling of ultraviolet auroral oval boundaries based on neural network technology. Sci. Sin. Technol. 2019, 49, 531–542. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, H.; Li, B. Automatic Identification of Aurora Fold Structure in All-Sky Images. Universe 2023, 9, 79. [Google Scholar] [CrossRef]
- Shang, Z.; Yao, Z.; Liu, J.; Xu, L.; Xu, Y.; Zhang, B.; Guo, R.; Wei, Y. Automated Classification of Auroral Images with Deep Neural Networks. Universe 2023, 9, 96. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Q.J. Classification of auroral images based on convolutional neural network. Chin. J. Polar Res. 2018, 30, 123–131. [Google Scholar]
- Clausen, L.B.N.; Nickisch, H. Automatic classification of auroral images from the Oslo Auroral THEMIS (OATH) data set using machine learning. J. Geophys. Res. Space Phys. 2018, 123, 5640–5647. [Google Scholar] [CrossRef]
- Sado, P.; Clausen, L.B.N.; Miloch, W.J.; Nickisch, H. Transfer learning aurora image classification and magnetic disturbance evaluation. J. Geophys. Res. Space Phys. 2022, 127, e2021JA029683. [Google Scholar] [CrossRef] [PubMed]
- Endo, T.; Matsumoto, M. Aurora Image Classification with Deep Metric Learning. Sensors 2022, 22, 6666. [Google Scholar] [CrossRef]
- Gu, G.H.; Huo, W.H.; Su, M.Y.; Fu, H. Asymmetric Supervised Deep Discrete Hashing Based Image Retrieval. J. Electron. Inf. Technol. 2021, 43, 3530–3537. [Google Scholar]
- Yang, X.; Wang, N.; Song, B.; Gao, X. Aurora Image Search with a Saliency-Weighted Region Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 12630–12643. [Google Scholar] [CrossRef]
- Hu, Z.J.; Han, B.; Zhang, Y.; Lian, H.; Wang, P.; Li, G.; Li, B.; Chen, X.C.; Liu, J.J. Modeling of ultraviolet aurora intensity associated with interplanetary and geomagnetic parameters based on neural networks. Space Weather 2021, 19, e2021SW002751. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, T.; Moen, J.I.; Wang, H. Aurora evolution prediction using ConvLSTM. Earth Space Sci. 2023, 10, e2022EA002721. [Google Scholar] [CrossRef]
- Lian, J.; Liu, T.; Zhou, Y. Aurora Classification in All-Sky Images via CNN–Transformer. Universe 2023, 9, 230. [Google Scholar] [CrossRef]
- Zhong, Y.; Yi, J.; Ye, R.; Zhang, L. Cross-Station Continual Aurora Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–12. [Google Scholar] [CrossRef]
- Partamies, N.; Dol, B.; Teissier, V.; Juusola, L.; Syrjäsuo, M.; Mulders, H. Auroral breakup detection in all-sky images by unsupervised learning. Ann. Geophys. 2024, 42, 103–115. [Google Scholar] [CrossRef]
- Ding, W.Z.; Cao, J.B.; Aimin, D. Statistical analysis of substorm onsets determined by geomagnetic indices. Chin. J. Space Sci. 2010, 30, 17–22. [Google Scholar] [CrossRef]
- Kullen, A.; Ohtani, S.; Karlsson, T. Geomagnetic signatures of auroral substorms preceded by pseudobreakups. J. Geophys. Res. 2019, 114, A04201. [Google Scholar] [CrossRef]
- McPherron, R.L.; Russell, C.T.; Aubry, M.P. Satellite studies of magnetospheric substorms on August 15, 1968: 9. Phenomenological model for substorms. J. Geophys. Res. 1973, 78, 3131–3149. [Google Scholar] [CrossRef]
- Maimaiti, M.; Kunduri, B.; Ruohoniemi, J.M.; Baker, J.B.H.; House, L.L. A Deep Learning-Based Approach to Forecast the Onset of Magnetic Substorms. Space Weather 2019, 17, 1534–1552. [Google Scholar] [CrossRef]
- Gromova, L.I.; Forster, M.; Feldstein, Y.I.; Ritter, P. Characteristics of the electrojet during intense magnetic disturbances. Ann. Geophys. 2018, 36, 1361–1391. [Google Scholar] [CrossRef]
- Huang, T.; Luhr, H.; Wang, H. Global characteristics of auroral Hall currents derived from the Swarm constellation: Dependencies on season and IMF orientation. J. Geophys. Res. 2017, 122, 378–392. [Google Scholar] [CrossRef]
- Huang, T.; Luhr, H.; Wang, H.; Xiong, C. The relationship of high-latitude thermospheric wind with ionospheric horizontal current, as observed by CHAMP satellite. Ann. Geophys. 2017, 35, 1249–1268. [Google Scholar] [CrossRef]
- Pulkkinen, T.I.; Tanskanen, E.L.; Viljanen, A.; Partamies, N.; Kauristie, K. Auroral electrojets during deep solar minimum at the end of solar cycle 23. J. Geophys. Res. 2011, 116, A04207. [Google Scholar] [CrossRef]
- Shue, J.H.; Kamide, K. Effects of solar wind density on auroral electrojets. Geophys. Res. Lett. 2001, 28, 2181–2184. [Google Scholar] [CrossRef]
- Singh, A.K.; Rawat, R.; Pathan, B.M. On the UT and seasonal variations of the standard and SuperMAG auroral electrojet indices. J. Geophys. Res. 2013, 118, 5059–5067. [Google Scholar] [CrossRef]
- Vennerstrom, S.; Moretto, T. Monitoring auroral electrojet with satellite data. Space Weather 2013, 11, 509–519. [Google Scholar] [CrossRef]
- Wang, H.; Luhr, H.; Ridley, A.; Ritter, P.; Yu, Y. Storm time dynamics of auroral electrojets: CHAMP observation and the space weather modeling framework comparison. Ann. Geophys. 2008, 26, 555–570. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Houlsby, N. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bylinskii, Z.; Judd, T.; Oliva, A.; Torralba, A.; Durand, F. What do different evaluation metrics tell us about saliency models? IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 740–757. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Liu, Z.; Ning, J.; Cao, Y.; Wei, Y.; Zhang, Z.; Lin, S.; Hu, H. Video Swin Transformer. arXiv 2021, arXiv:2106.13230. [Google Scholar] [CrossRef]
- Wasim, S.T.; Khattak, M.U.; Naseer, M.; Khan, S.; Shah, M.; Khan, F.S. Video-FocalNets: Spatio-Temporal Focal Modulation for Video Action Recognition. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 2–6 October 2023. [Google Scholar]
- Liang, Y.; Zhou, P.; Zimmermann, R.; Yan, S. DualFormer: Local-Global Stratified Transformer for Efficient Video Recognition. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 2–6 October 2023. [Google Scholar]
- Sado, P.; Clausen, L.B.N.; Miloch, W.J.; Nickisch, H. Substorm onset prediction using machine learning classified auroral images. Space Weather 2023, 21, e2022SW003300. [Google Scholar] [CrossRef]
- Wild, J.A.; Woodfield, E.E.; Morley, S.K. On the triggering of auroral substorms by northward turnings of the interplanetary magnetic field. Ann. Geophys. 2009, 27, 3559–3570. [Google Scholar] [CrossRef]
- Troshichev, O.A.; Kotikov, A.L.; Bolotinskaya, B.D.; Andrezen, V.G. Influence of the IMF azimuthal component on magnetospheric substorm dynamics. J. Geomagn. Geoelectr. 1986, 38, 1075–1088. [Google Scholar] [CrossRef]
- Liou, K.; Newell, P.T.; Sibeck, D.G.; Meng, C.I.; Brittnacher, M.; Parks, G. Observation of IMF and seasonal effects in the location of auroral substorm onset. J. Geophys. Res. Space Phys. 2001, 106, 5799–5810. [Google Scholar] [CrossRef]
- Sandholt, P.E.; Farrugia, C.J.; Moen, J.; Cowley, S.W.H. Dayside auroral configurations: Responses to southward and northward rotations of the interplanetary magnetic field. J. Geophys. Res. 1998, 103, 20279–20295. [Google Scholar] [CrossRef]
- Ohma, A.; Laundal, K.M.; Reistad, J.P.; Qstgaard, N. Evolution of IMF By induced asymmetries during substorms: Superposed epoch analysis at geosynchronous orbit. Front. Astron. Space Sci. 2022, 9, 958749. [Google Scholar] [CrossRef]
- Wing, S.; Newell, P.T.; Sibeck, D.G.; Baker, K.B. A large statistical study of the entry of interplanetary magnetic field Y component into the magnetosphere. Geophys. Res. Lett. 1995, 22, 2083–2086. [Google Scholar] [CrossRef]
- Lee, D.Y.; Choi, K.C.; Ohtani, S.; Lee, J.; Kim, K.C.; Park, K.S.; Kim, K.H. Can intense substorms occur under northward IMF conditions. J. Geophys. Res. 2010, 115, A00KA04. [Google Scholar] [CrossRef]
- Kamide, Y.; Akasofu, S.I. The auroral electrojet and global auroral features. J. Geophys. Res. 1975, 80, 3585–3602. [Google Scholar] [CrossRef]
- Petrukovich, A.A.; Baumjohann, W.; Nakamura, R.; Mukai, T.; Troshichev, O.A. Small substorms: Solar wind input and magnetotail dynamics. J. Geophys. Res. 2000, 105, 21109–21121. [Google Scholar] [CrossRef]
- Liou, K.; Meng, C.I.; Lui, A.T.Y.; Newell, P.T.; Wing, S. Magnetic dipolarization with substorm expansion onset. J. Geophys. Res. Space Phys. 2002, 107, SMP 23-1–SMP 23-12. [Google Scholar] [CrossRef]
- Han, Y.; Han, B. Eyemovement visual dataset and auroral substorm recognition model. Zenodo 2024. [Google Scholar] [CrossRef]




| Date | December 1996–February 1997 | March 1997–May 1997 | December 1997 |
|---|---|---|---|
| Substorm | 290 | 73 | 27 |
| Non-Substorm | 120 | 130 | - |
| Training dataset | test dataset | ||
| Date | December 1996–February 1997 | March 1997–May 1997 | December 1997 |
|---|---|---|---|
| Fixation maps | 336 | generate | 58 |
| Visual maps | 336 | generate | 58 |
| Subjects | 15 | ||
| Embedding Methods | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| MLAT-MLT | 0.9177 | 0.8584 | 0.97 | 0.9108 |
| MLAT | 0.9087 | 0.8349 | 0.94 | 0.8843 |
| MLT | 0.8918 | 0.8151 | 0.97 | 0.8858 |
| Model Inputs | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| Visual+MLAT-MLT | 0.8918 | 0.9310 | 0.81 | 0.8663 |
| Substorm+ MLAT-MLT | 0.9177 | 0.8584 | 0.97 | 0.9108 |
| Visual+Substorm +MLAT-MLT | 0.9264 | 0.9192 | 0.91 | 0.9146 |
| Models | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| Vit-3d’2021 | 0.9134 | 0.8846 | 0.92 | 0.9020 |
| Video-Swin-tiny’2021 | 0.8304 | 0.8 | 0.81 | 0.8050 |
| Video-Swin-small’2021 | 0.6391 | 0.5702 | 0.75 | 0.6479 |
| Video-FocalNet’2023 | 0.9091 | 0.8692 | 0.93 | 0.8986 |
| DualFormer-tiny’2023 | 0.8609 | 0.8384 | 0.83 | 0.8342 |
| Yang’s’2013 | - | 0.4928 | 0.9198 | 0.6417 |
| DCSD- C3D’2022 | - | 0.5701 | 0.9771 | 0.7201 |
| DCSD-R3D’2022 | - | 0.5573 | 0.9733 | 0.7088 |
| DCSD-R2Plus1D’2022 | - | 0.5788 | 0.9733 | 0.7259 |
| EMSF-R2Plus1D’2023 | 0.8826 | 0.8462 | 0.88 | 0.8627 |
| EMSF-C3D’2023 | 0.9087 | 0.8911 | 0.9 | 0.8955 |
| Ours | 0.9264 | 0.9029 | 0.93 | 0.9163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Han, B.; Hu, Z. A Tailored Deep Learning Network with Embedded Space Physical Knowledge for Auroral Substorm Recognition: Validation Through Special Case Studies. Universe 2025, 11, 265. https://doi.org/10.3390/universe11080265
Han Y, Han B, Hu Z. A Tailored Deep Learning Network with Embedded Space Physical Knowledge for Auroral Substorm Recognition: Validation Through Special Case Studies. Universe. 2025; 11(8):265. https://doi.org/10.3390/universe11080265
Chicago/Turabian StyleHan, Yiyuan, Bing Han, and Zejun Hu. 2025. "A Tailored Deep Learning Network with Embedded Space Physical Knowledge for Auroral Substorm Recognition: Validation Through Special Case Studies" Universe 11, no. 8: 265. https://doi.org/10.3390/universe11080265
APA StyleHan, Y., Han, B., & Hu, Z. (2025). A Tailored Deep Learning Network with Embedded Space Physical Knowledge for Auroral Substorm Recognition: Validation Through Special Case Studies. Universe, 11(8), 265. https://doi.org/10.3390/universe11080265







