Locally Generated Whistler-Mode Waves Before Dipolarization Fronts
Abstract
1. Introduction
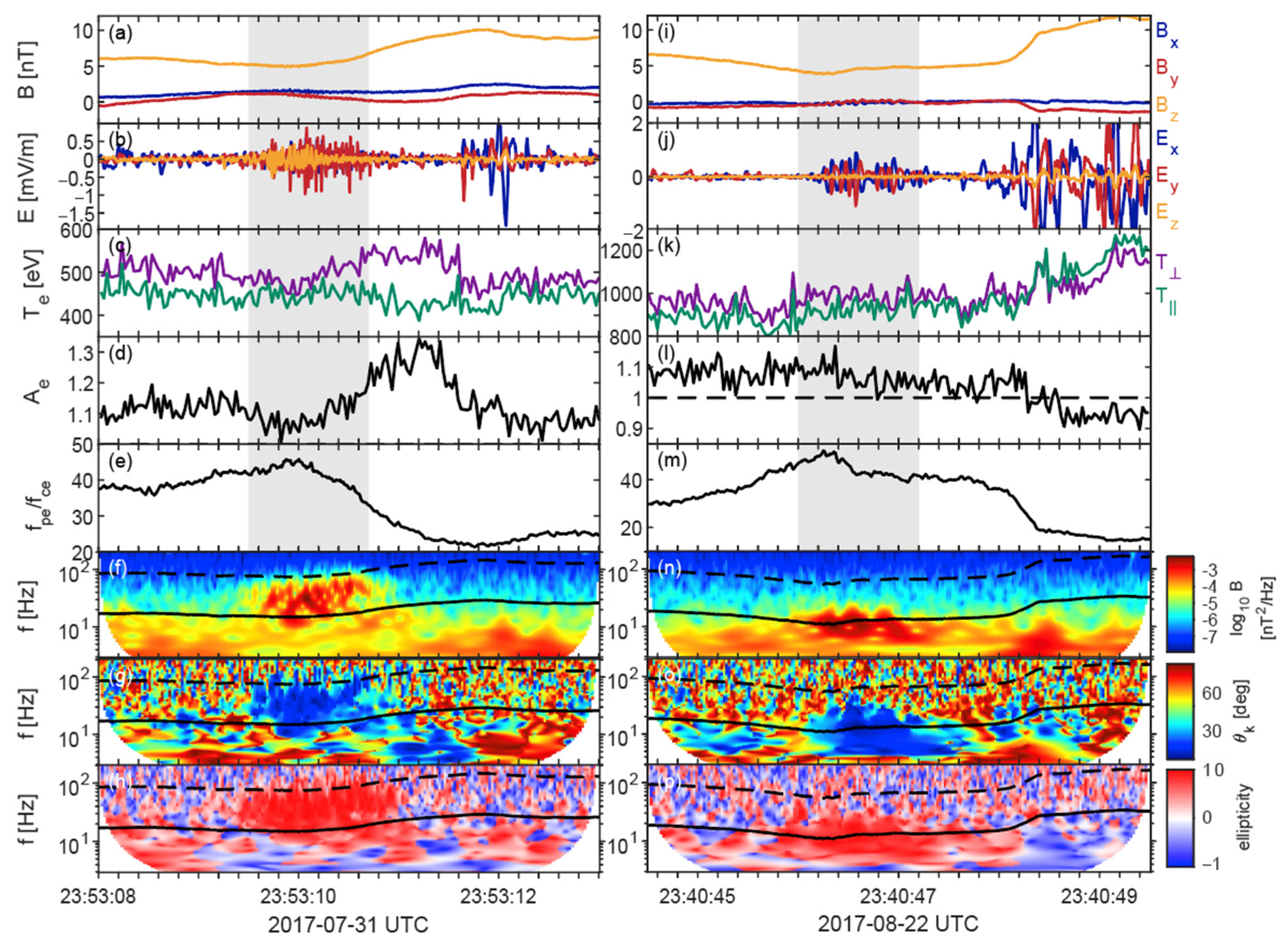
2. Observations
3. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Runov, A.; Angelopoulos, V.; Sitnov, M.I.; Sergeev, V.A.; Bonnell, J.; McFadden, J.P.; Larson, D.; Glassmeier, K.-H.; Auster, U. THEMIS observations of an earthward-propagating dipolarization front. Geophys. Res. Lett. 2009, 36, L14106. [Google Scholar] [CrossRef]
- Sergeev, V.; Angelopoulos, V.; Apatenkov, S.; Bonnell, J.; Ergun, R.; Nakamura, R.; McFadden, J.; Larson, D.; Runov, A. Kinetic structure of the sharp injection/dipolarization front in the flow-braking region. Geophys. Res. Lett. 2009, 36, L21105. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Runov, A.; Zhou, X.-Z.; Turner, D.L.; Kiehas, S.A.; Li, S.-S.; Shinohara, I. Electromagnetic Energy Conversion at Reconnection Fronts. Science 2013, 341, 1478–1482. [Google Scholar] [CrossRef] [PubMed]
- Schmid, D.; Nakamura, R.; Plaschke, F.; Volwerk, M.; Baumjohann, W. Two states of magnetotail dipolarization fronts: A statistical study. J. Geophys. Res. Space Phys. 2015, 120, 1096–1108. [Google Scholar] [CrossRef]
- Cao, J.-B.; Ren, G.; Ma, Y. Kinetic Analysis of the Energy Transport of Two-Flow Components in the Plasma Sheet. J. Geophys. Res. Space Phys. 2019, 124, 6730–6739. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Baumjohann, W.; Kennel, C.F.; Coroniti, F.V.; Kivelson, M.G.; Pellat, R.; Walker, R.J.; Lühr, H.; Paschmann, G. Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. Space Phys. 1992, 97, 4027–4039. [Google Scholar] [CrossRef]
- Cao, J.-B.; Ma, Y.D.; Parks, G.; Reme, H.; Dandouras, I.; Nakamura, R.; Zhang, T.L.; Zong, Q.; Lucek, E.; Carr, C.M.; et al. Joint observations by Cluster satellites of bursty bulk flows in the magnetotail. J. Geophys. Res. 2006, 111, A04206. [Google Scholar] [CrossRef]
- Fu, H.S.; Khotyaintsev, Y.V.; Vaivads, A.; André, M.; Huang, S.Y. Occurrence rate of earthward-propagating dipolarization fronts. Geophys. Res. Lett. 2012, 39, L10101. [Google Scholar] [CrossRef]
- Schmid, D.; Volwerk, M.; Plaschke, F.; Nakamura, R.; Baumjohann, W.; Wang, G.Q.; Wu, M.Y.; Zhang, T.L. A Statistical Study on the Properties of Dips Ahead of Dipolarization Fronts Observed by MMS. J. Geophys. Res. Space Phys. 2019, 124, 139–150. [Google Scholar] [CrossRef]
- Yao, Z.; Sun, W.J.; Fu, S.Y.; Pu, Z.Y.; Liu, J.; Angelopoulos, V.; Zhang, X.-J.; Chu, X.N.; Shi, Q.Q.; Guo, R.L.; et al. Current structures associated with dipolarization fronts. J. Geophys. Res. Space Phys. 2013, 118, 6980–6985. [Google Scholar] [CrossRef]
- Zhao, B.N.; Liu, C.M.; Cao, J.B.; Liu, Y.Y.; Xing, X.N. Energy Conversion in the Dip Region Preceding Dipolarization Front. Geophys. Res. Lett. 2024, 51, e2024GL109860. [Google Scholar] [CrossRef]
- Hamrin, M.; Norqvist, P.; Karlsson, T.; Nilsson, H.; Fu, H.S.; Buchert, S.; André, M.; Marghitu, O.; Pitkänen, T.; Klecker, B.; et al. The evolution of flux pileup regions in the plasma sheet: Cluster observations. J. Geophys. Res. Space Phys. 2013, 118, 6279–6290. [Google Scholar] [CrossRef]
- Khotyaintsev, Y.V.; Cully, C.M.; Vaivads, A.; André, M.; Owen, C.J. Plasma Jet Braking: Energy Dissipation and Nonadiabatic Electrons. Phys. Rev. Lett. 2011, 106, 165001. [Google Scholar] [CrossRef]
- Liu, C.M.; Cao, J.B.; Wang, T.Y.; Xing, X.N. Energy Transfer and Electron Heating in Turbulent Flux Pileup Region. Geophys. Res. Lett. 2022, 49, e2022GL101415. [Google Scholar] [CrossRef]
- Vaivads, A.; Retinò, A.; Khotyaintsev, Y.V.; André, M. Suprathermal electron acceleration during reconnection onset in the magnetotail. Ann. Geophys. 2011, 29, 1917–1925. [Google Scholar] [CrossRef]
- Birn, J.; Hesse, M.; Nakamura, R.; Zaharia, S. Particle acceleration in dipolarization events. J. Geophys. Res. Space Phys. 2013, 118, 1960–1971. [Google Scholar] [CrossRef]
- Birn, J.; Runov, A.; Hesse, M. Energetic ions in dipolarization events. J. Geophys. Res. Space Phys. 2015, 120, 7698–7717. [Google Scholar] [CrossRef]
- Lu, S.; Angelopoulos, V.; Fu, H. Suprathermal particle energization in dipolarization fronts: Particle-in-cell simulations. J. Geophys. Res. Space Phys. 2016, 121, 9483–9500. [Google Scholar] [CrossRef]
- Xing, X.N.; Liu, C.M.; Cao, J.B. Electron Rolling-Pin Distributions Preceding Dipolarization Fronts. Geophys. Res. Lett. 2023, 50, e2023GL105337. [Google Scholar] [CrossRef]
- Hwang, K.-J.; Goldstein, M.L.; F.-Viñas, A.; Schriver, D.; Ashour-Abdalla, M. Wave-particle interactions during a dipolarization front event. J. Geophys. Res. Space Phys. 2014, 119, 2484–2493. [Google Scholar] [CrossRef]
- Liu, C.M.; Fu, H.S.; Liu, Y.Y.; Xu, Y. Kinetics of Magnetic Hole Behind Dipolarization Front. Geophys. Res. Lett. 2021, 48, e2021GL093174. [Google Scholar] [CrossRef]
- Divin, A.; Khotyaintsev, Y.V.; Vaivads, A.; André, M.; Markidis, S.; Lapenta, G. Evolution of the lower hybrid drift instability at reconnection jet front. J. Geophys. Res. Space Phys. 2015, 120, 2675–2690. [Google Scholar] [CrossRef]
- Liu, C.M.; Xing, X.N.; Cao, J.B. Successive Energy Conversion at a Stepwise Dipolarization Front. APJ 2023, 954, 166. [Google Scholar] [CrossRef]
- Deng, X.; Ashour-Abdalla, M.; Zhou, M.; Walker, R.; El-Alaoui, M.; Angelopoulos, V.; Ergun, R.E.; Schriver, D. Wave and particle characteristics of earthward electron injections associated with dipolarization fronts. J. Geophys. Res. Space Phys. 2010, 115, A09225. [Google Scholar] [CrossRef]
- Liu, C.M.; Vaivads, A.; Graham, D.B.; Khotyaintsev, Y.V.; Fu, H.S.; Johlander, A.; André, M.; Giles, B.L. Ion-Beam-Driven Intense Electrostatic Solitary Waves in Reconnection Jet. Geophys. Res. Lett. 2019, 46, 12702–12710. [Google Scholar] [CrossRef]
- Zhang, X.; Angelopoulos, V. On the relationship of electrostatic cyclotron harmonic emissions with electron injections and dipolarization fronts. J. Geophys. Res. Space Phys. 2014, 119, 2536–2549. [Google Scholar] [CrossRef]
- Zhou, M.; Ashour-Abdalla, M.; Deng, X.; Schriver, D.; El-Alaoui, M.; Pang, Y. THEMIS observation of multiple dipolarization fronts and associated wave characteristics in the near-Earth magnetotail. Geophys. Res. Lett. 2009, 36, L20107. [Google Scholar] [CrossRef]
- Zhou, M.; Ni, B.; Huang, S.; Deng, X.; Ashour-Abdalla, M.; Nishimura, Y.; Yuan, Z.; Pang, Y.; Li, H. Observation of large-amplitude magnetosonic waves at dipolarization fronts. J. Geophys. Res. Space Phys. 2014, 119, 4335–4347. [Google Scholar] [CrossRef]
- Artemyev, A.V.; Neishtadt, A.I.; Angelopoulos, V. On the Role of Whistler-Mode Waves in Electron Interaction With Dipolarizing Flux Bundles. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030265. [Google Scholar] [CrossRef]
- Kasahara, S.; Miyoshi, Y.; Yokota, S.; Mitani, T.; Kasahara, Y.; Matsuda, S.; Kumamoto, A.; Matsuoka, A.; Kazama, Y.; Frey, H.U.; et al. Pulsating aurora from electron scattering by chorus waves. Nature 2018, 554, 337–340. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhao, B.N.; Cao, J.B.; Pollock, C.J.; Russell, C.T.; Liu, Y.Y.; Xing, X.N.; Linqvist, P.A.; Burch, J.L. Field–particle energy transfer during chorus emissions in space. Nature 2025, 637, 813–820. [Google Scholar] [CrossRef]
- Ozaki, M.; Miyoshi, Y.; Shiokawa, K.; Hosokawa, K.; Oyama, S.; Kataoka, R.; Ebihara, Y.; Ogawa, Y.; Kasahara, Y.; Yagitani, S.; et al. Visualization of rapid electron precipitation via chorus element wave–particle interactions. Nat. Commun. 2019, 10, 257. [Google Scholar] [CrossRef] [PubMed]
- Thorne, R.M.; Ni, B.; Tao, X.; Horne, R.B.; Meredith, N.P. Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 2010, 467, 943–946. [Google Scholar] [CrossRef]
- Thorne, R.M.; Li, W.; Ni, B.; Ma, Q.; Bortnik, J.; Chen, L.; Baker, D.N.; Spence, H.E.; Reeves, G.D.; Henderson, M.G.; et al. Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 2013, 504, 411–414. [Google Scholar] [CrossRef]
- Zhang, X.; Angelopoulos, V.; Artemyev, A.V.; Liu, J. Whistler and Electron Firehose Instability Control of Electron Distributions in and Around Dipolarizing Flux Bundles. Geophys. Res. Lett. 2018, 45, 9380–9389. [Google Scholar] [CrossRef]
- Viberg, H.; Khotyaintsev, Y.V.; Vaivads, A.; André, M.; Fu, H.S.; Cornilleau-Wehrlin, N. Whistler mode waves at magnetotail dipolarization fronts. J. Geophys. Res. Space Phys. 2014, 119, 2605–2611. [Google Scholar] [CrossRef]
- Li, H.; Zhou, M.; Deng, X.; Yuan, Z.; Guo, L.; Yu, X.; Pang, Y.; Huang, S. A statistical study on the whistler waves behind dipolarization fronts. J. Geophys. Res. Space Phys. 2015, 120, 1086–1095. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhou, M.; Deng, X.H.; Yuan, Z.G.; Pang, Y.; Wei, Q.; Su, W.; Li, H.M.; Wang, Q.Q. Kinetic structure and wave properties associated with sharp dipolarization front observed by Cluster. Ann. Geophys. 2012, 30, 97–107. [Google Scholar] [CrossRef]
- Le Contel, O.; Roux, A.; Jacquey, C.; Robert, P.; Berthomier, M.; Chust, T.; Grison, B.; Angelopoulos, V.; Sibeck, D.; Chaston, C.C.; et al. Quasi-parallel whistler mode waves observed by THEMIS during near-earth dipolarizations. Ann. Geophys. 2009, 27, 2259–2275. [Google Scholar] [CrossRef]
- Russell, C.T.; Anderson, B.J.; Baumjohann, W.; Bromund, K.R.; Dearborn, D.; Fischer, D.; Le, G.; Leinweber, H.K.; Leneman, D.; Magnes, W.; et al. The Magnetospheric Multiscale Magnetometers. Space Sci. Rev. 2016, 199, 189–256. [Google Scholar] [CrossRef]
- Le Contel, O.; Leroy, P.; Roux, A.; Coillot, C.; Alison, D.; Bouabdellah, A.; Mirioni, L.; Meslier, L.; Galic, A.; Vassal, M.C.; et al. The Search-Coil Magnetometer for MMS. Space Sci. Rev. 2016, 199, 257–282. [Google Scholar] [CrossRef]
- Burch, J.L.; Moore, T.E.; Torbert, R.B.; Giles, B.L. Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Ergun, R.E.; Tucker, S.; Westfall, J.; Goodrich, K.A.; Malaspina, D.M.; Summers, D.; Wallace, J.; Karlsson, M.; Mack, J.; Brennan, N.; et al. The Axial Double Probe and Fields Signal Processing for the MMS Mission. Space Sci. Rev. 2016, 199, 167–188. [Google Scholar] [CrossRef]
- Lindqvist, P.-A.; Olsson, G.; Torbert, R.B.; King, B.; Granoff, M.; Rau, D.; Needell, G.; Turco, S.; Dors, I.; Beckman, P.; et al. The Spin-Plane Double Probe Electric Field Instrument for MMS. Space Sci. Rev. 2016, 199, 137–165. [Google Scholar] [CrossRef]
- Pollock, C.; Moore, T.; Jacques, A.; Burch, J.; Gliese, U.; Saito, Y.; Omoto, T.; Avanov, L.; Barrie, A.; Coffey, V.; et al. Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 2016, 199, 331–406. [Google Scholar] [CrossRef]
- Liu, C.M.; Cao, J.B.; Xing, X.N.; Chen, Z.Z. Turbulent Energy Transfer at Dipolarization Fronts. Geophys. Res. Lett. 2023, 50, e2023GL104185. [Google Scholar] [CrossRef]
- Grigorenko, E.E.; Malykhin, A.Y.; Shklyar, D.R.; Fadanelli, S.; Lavraud, B.; Panov, E.V.; Avanov, L.; Giles, B.; Le Contel, O. Investigation of Electron Distribution Functions Associated With Whistler Waves at Dipolarization Fronts in the Earth’s Magnetotail: MMS Observations. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028268. [Google Scholar] [CrossRef]
- Zhang, X.; Angelopoulos, V.; Artemyev, A.V.; Liu, J. Energy Transport by Whistler Waves Around Dipolarizing Flux Bundles. Geophys. Res. Lett. 2019, 46, 11718–11727. [Google Scholar] [CrossRef]
- Santolík, O.; Parrot, M.; Lefeuvre, F. Singular value decomposition methods for wave propagation analysis. Radio Sci. 2003, 38, 1010. [Google Scholar] [CrossRef]
- Breuillard, H.; Le Contel, O.; Retino, A.; Chasapis, A.; Chust, T.; Mirioni, L.; Graham, D.B.; Wilder, F.D.; Cohen, I.; Vaivads, A.; et al. Multispacecraft analysis of dipolarization fronts and associated whistler wave emissions using MMS data. Geophys. Res. Lett. 2016, 43, 7279–7286. [Google Scholar] [CrossRef]
- Zhima, Z.; Cao, J.; Fu, H.; Liu, W.; Chen, L.; Dunlop, M.; Zhang, X.M.; Shen, X.H. Whistler mode wave generation at the edges of a magnetic dip. J. Geophys. Res. Space Phys. 2015, 120, 2469–2476. [Google Scholar] [CrossRef]
- Bellan, P.M. Revised single-spacecraft method for determining wave vector k and resolving space-time ambiguity. JGR Space Phys. 2016, 121, 8589–8599. [Google Scholar] [CrossRef]
- Xie, H. BO: A unified tool for plasma waves and instabilities analysis. Comput. Phys. Commun. 2019, 244, 343–371. [Google Scholar] [CrossRef]
- Sitnov, M.I.; Swisdak, M.; Divin, A.V. Dipolarization fronts as a signature of transient reconnection in the magnetotail. J. Geophys. Res. Space Phys. 2009, 114, A04202. [Google Scholar] [CrossRef]
- Divin, A.V.; Sitnov, M.I.; Swisdak, M.; Drake, J.F. Reconnection onset in the magnetotail: Particle simulations with open boundary conditions. Geophys. Res. Lett. 2007, 34, L09109. [Google Scholar] [CrossRef]
- Schindler, K. A theory of the substorm mechanism. J. Geophys. Res. 1974, 79, 2803–2810. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Liu, C.; Cao, J.; Liu, Y.; Xing, X. Locally Generated Whistler-Mode Waves Before Dipolarization Fronts. Universe 2025, 11, 249. https://doi.org/10.3390/universe11080249
Zhao B, Liu C, Cao J, Liu Y, Xing X. Locally Generated Whistler-Mode Waves Before Dipolarization Fronts. Universe. 2025; 11(8):249. https://doi.org/10.3390/universe11080249
Chicago/Turabian StyleZhao, Boning, Chengming Liu, Jinbin Cao, Yangyang Liu, and Xining Xing. 2025. "Locally Generated Whistler-Mode Waves Before Dipolarization Fronts" Universe 11, no. 8: 249. https://doi.org/10.3390/universe11080249
APA StyleZhao, B., Liu, C., Cao, J., Liu, Y., & Xing, X. (2025). Locally Generated Whistler-Mode Waves Before Dipolarization Fronts. Universe, 11(8), 249. https://doi.org/10.3390/universe11080249





