Spectral Dimensionality of Spacetime Around a Radiating Schwarzschild Black-Hole
Abstract
1. Introduction and Motivation
2. Relativistic Quantum Geometry
2.1. Quantum Geometric Description of Gravity
2.2. Background Einstein Equations with Geometric Quantum Gravitational Corrections Included
3. Quantum Geometric Fluctuations of Spacetime Around the SBH
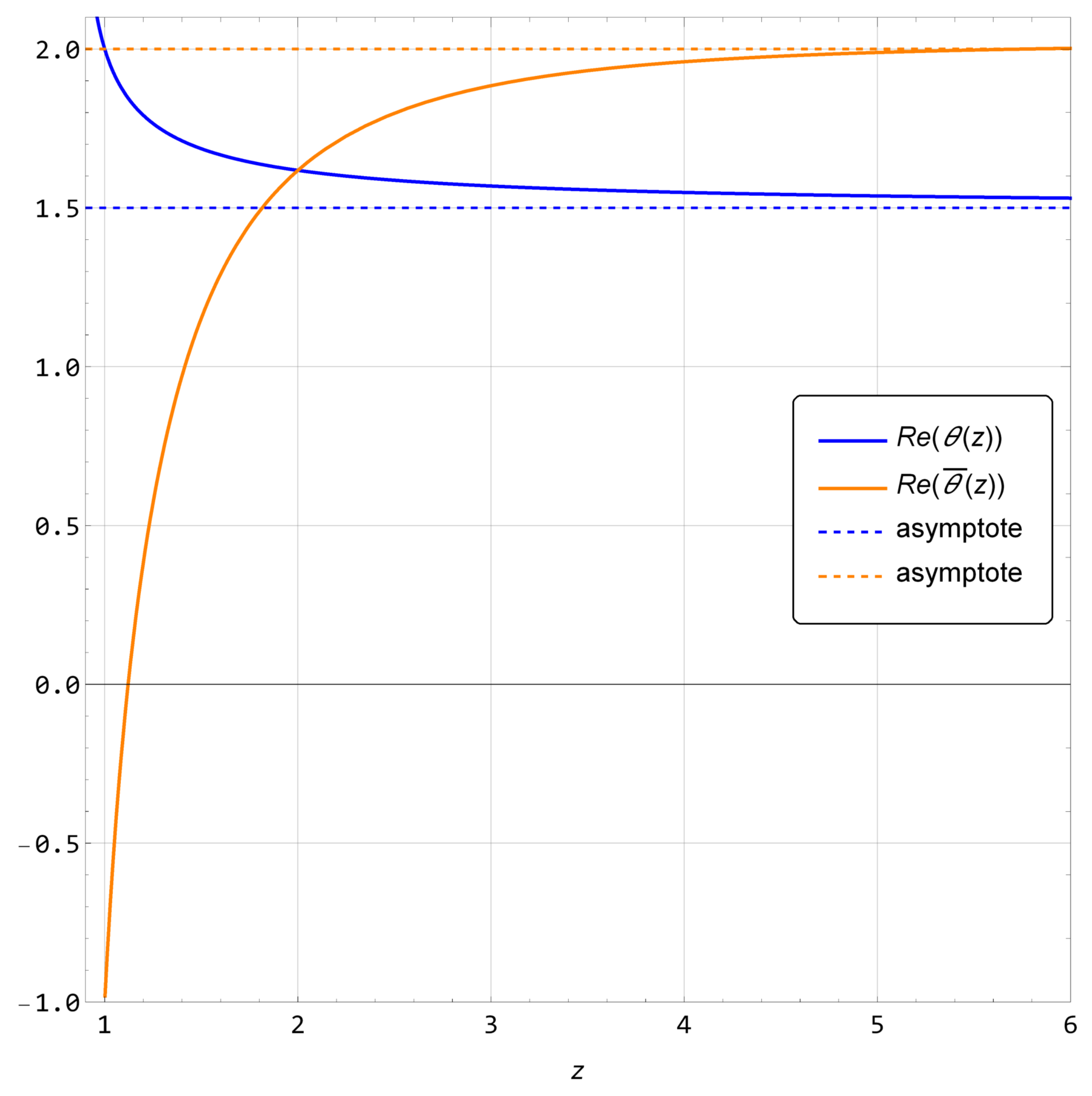
3.1. Calculation of Around the SBH
3.1.1. Solution for
3.1.2. Solution for
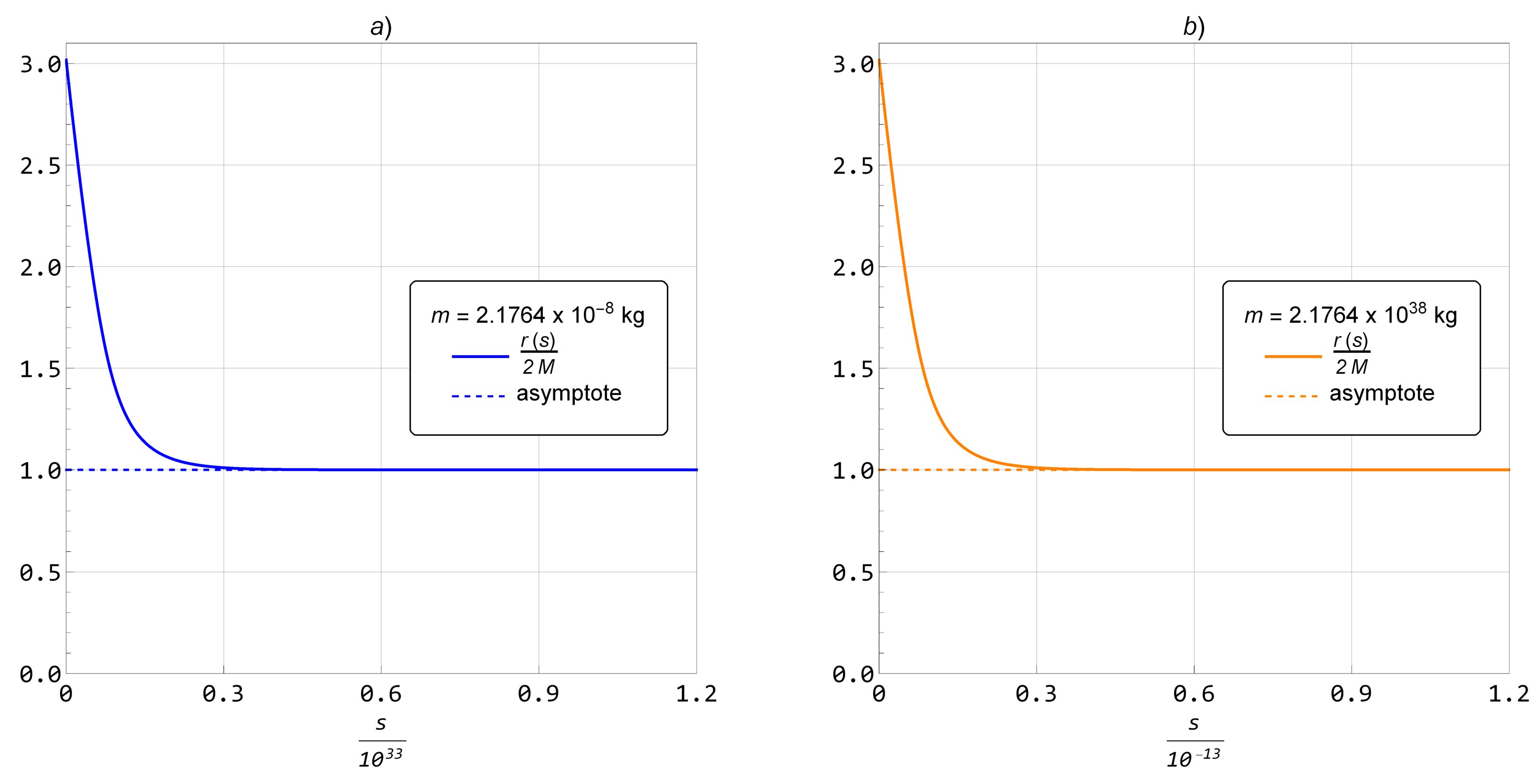
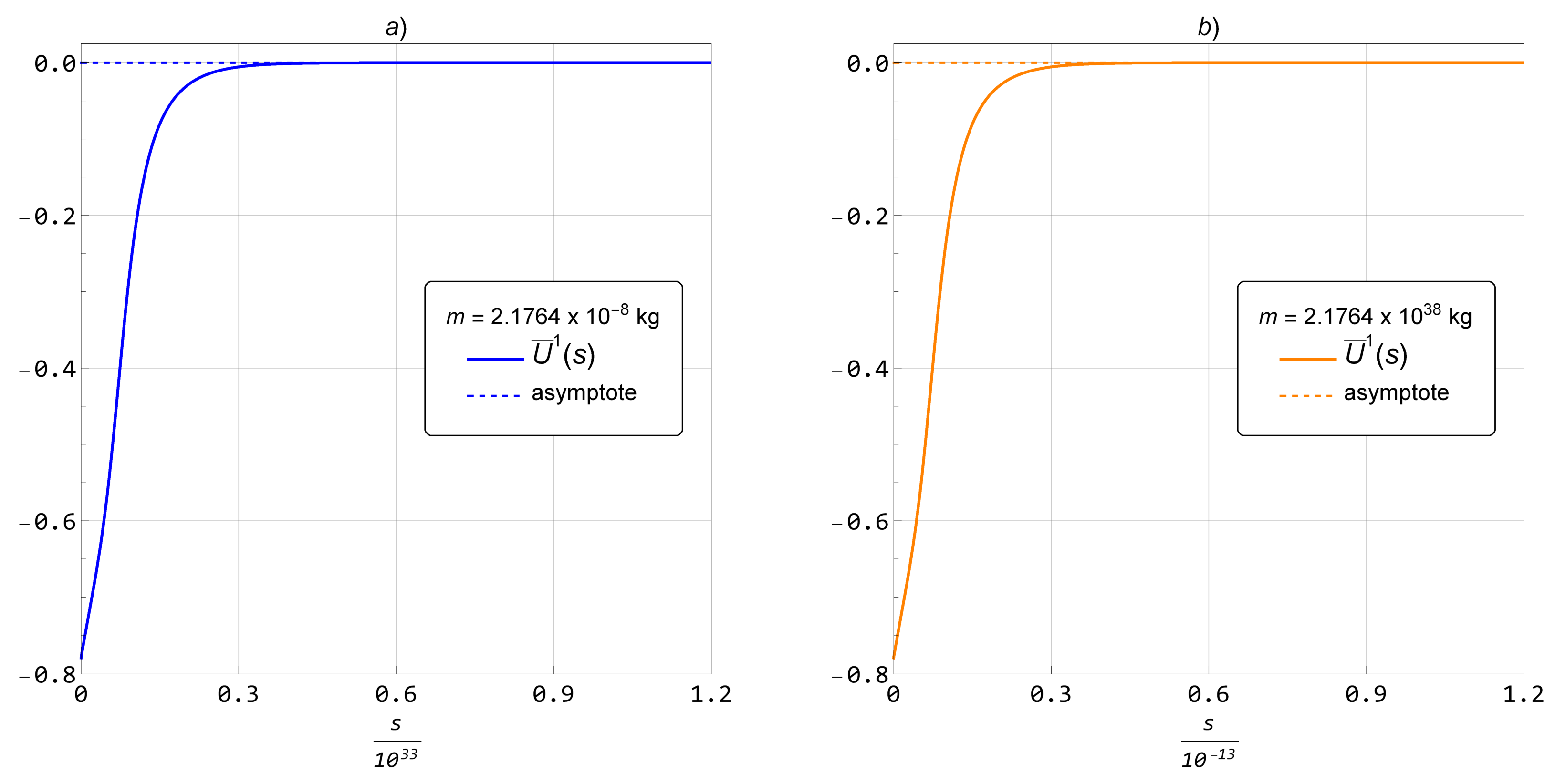
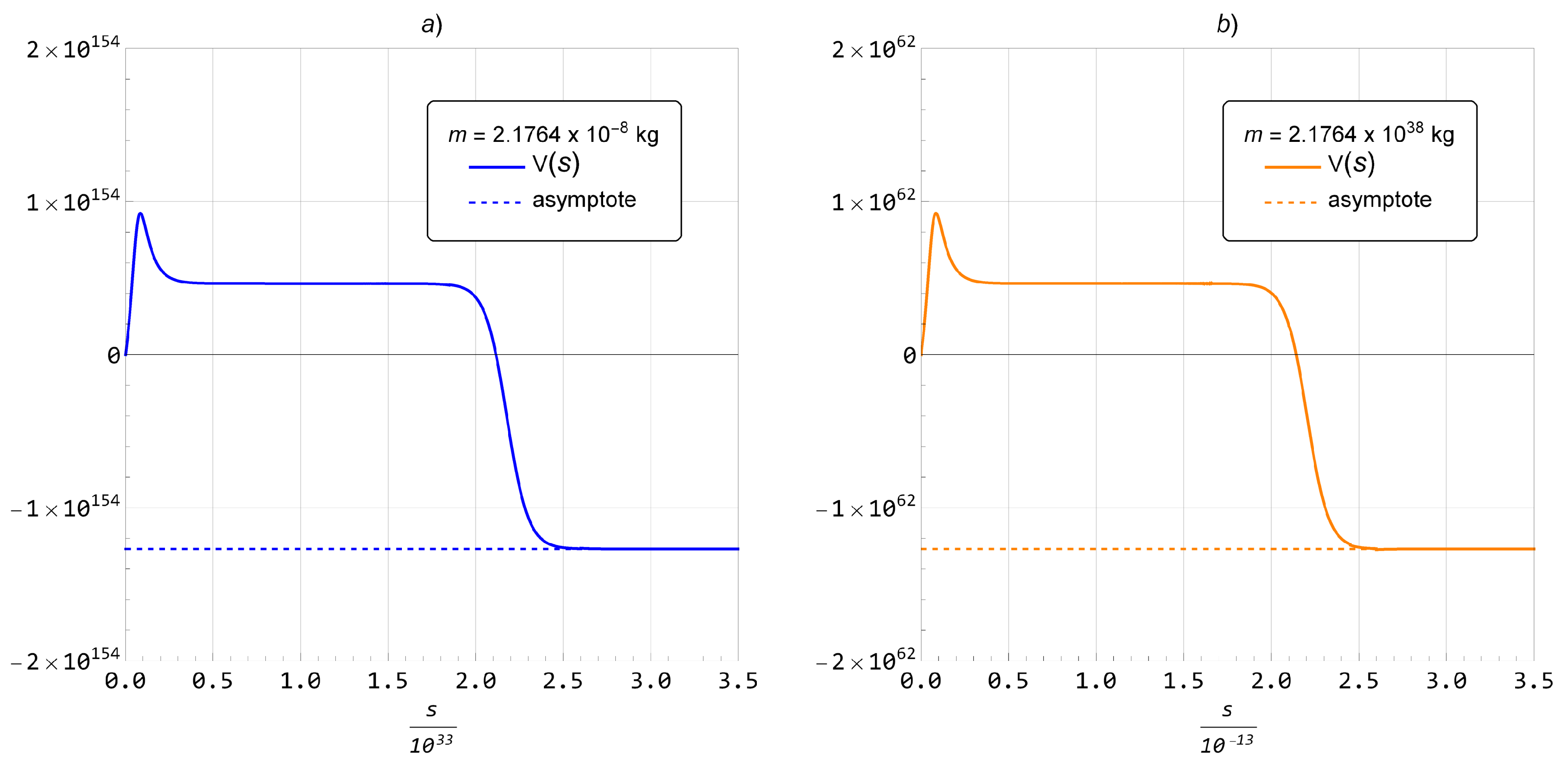
3.2. Effective Gravitational Potential and Mass Density with Geometric Quantum Gravitational Corrections Included
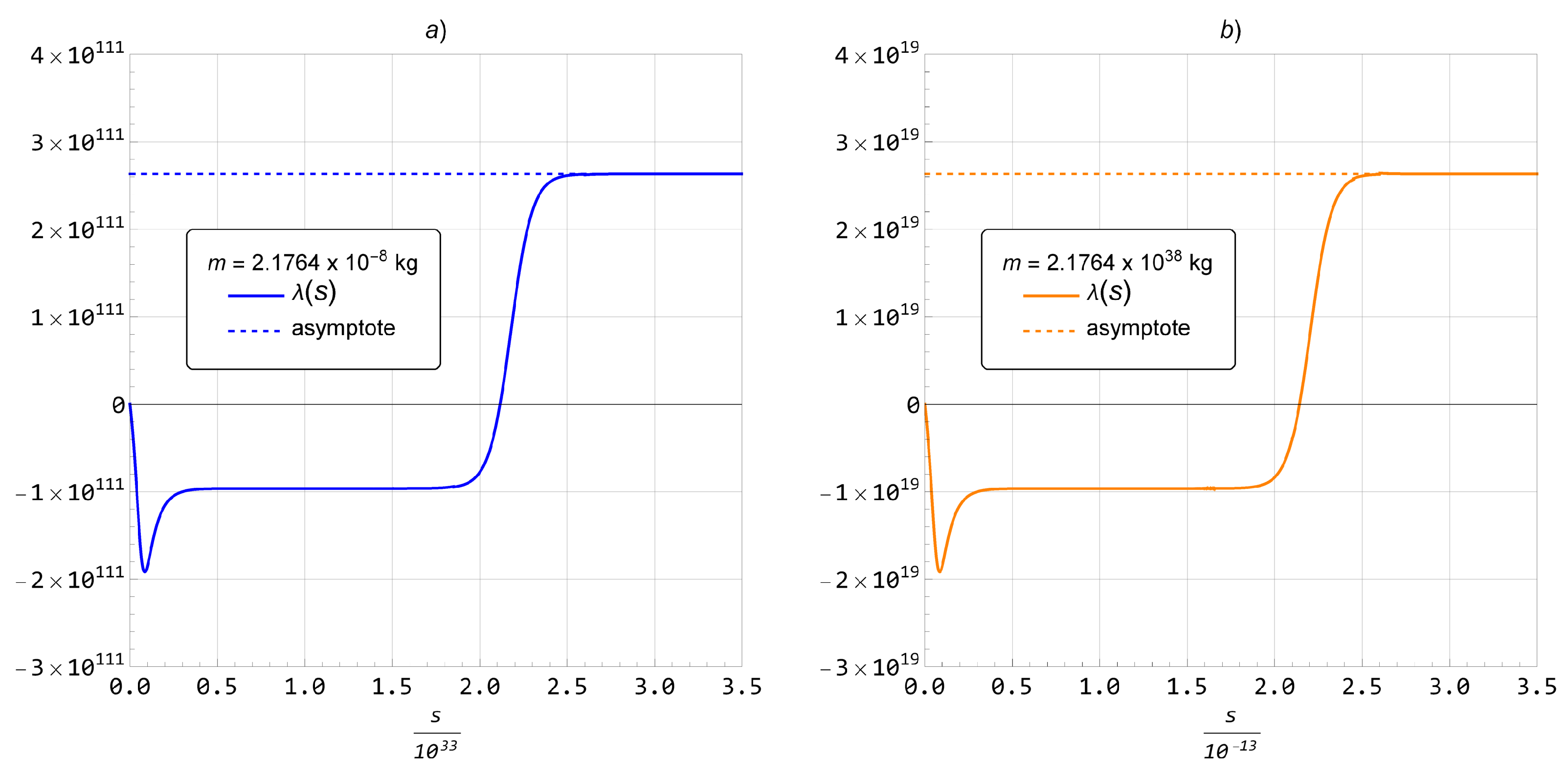
3.3. Spectral Dimensionality and Metric Tensor with Geometric Quantum Gravitational Corrections Included
4. Final Comments
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EH | Einstein–Hilbert |
| RQG | Relativistic Quantum Geometry |
| SBH | Schwarzschild black-hole |
| 1 | The covariant derivative of a -times contravariant and -times covariant mixture tensor field , on the extended manifold, is given by the -range quantum tensor: |
| 2 | Notar que . |
References
- Carlip, S. Quantum Gravity: A Progress Report. Rept. Prog. Phys. 2001, 64, 885. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.-L.; Bahamonde, S.; Bajardi, F. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. Prog. Part. Nucl. Phys. 2022, 125, 103948. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Relativ. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Belenchia, A.; Wald, R.M.; Giacomini, F.; Castro-Ruiz, R.; Brukner, Č.; Aspelmeyer, M. Quantum superposition of massive objects and the quantization of gravity. Phys. Rev. D 2018, 98, 126009. [Google Scholar] [CrossRef]
- Smolin, L. On the nature of quantum fluctuations and their relation to gravitation and the principle of inertia. Class. Quant. Grav. 1986, 3, 347–359. [Google Scholar] [CrossRef]
- Banks, T.; Fischler, W.; Shenker, S.H.; Susskind, L.M. Theory As A Matrix Model: A Conjecture. Phys. Rev. D 1997, 55, 5112. [Google Scholar] [CrossRef]
- Konechny, A.; Schwarz, A.S. Introduction to M(atrix) theory and noncommutative geometry. Phys. Rept. 2002, 360, 353–465. [Google Scholar] [CrossRef]
- Perez, A. Spin Foam Models for Quantum Gravity. Class. Quant. Grav. 2003, 20, R43. [Google Scholar] [CrossRef]
- Rovelli, C. Loop Quantum Gravity. Living Rev. Relativ. 1998, 1, 1. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Smolin, L. Spin networks and quantum gravity. Phys. Rev. D 1995, 52, 5743. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, A. On the nature of quantum geometrodynamics. Ann. Phys. 1957, 2, 604. [Google Scholar] [CrossRef]
- Ridao, L.S.; Bellini, M. Towards relativistic quantum geometry. Phys. Lett. B 2015, 751, 565. [Google Scholar] [CrossRef]
- Bellini, M.; Musmarra, J.I.; Magos Cortes, D. Geometric Hawking radiation of Schwarzschild Black Hole with novel quantum algebra. Astropart. Phys. 2024, 163, 103010. [Google Scholar] [CrossRef]
- Bellini, M.; Musmarra, J.I.; Anabitarte, M.; Sánchez, P.A. Early universe: Gravitational waves and tensor metric fluctuations. Phys. Dark Univ. 2023, 42, 101359. [Google Scholar] [CrossRef]
- Dong, R.; Kinney, W.H.; Stojkovic, D. Gravitational wave production by Hawking radiation from rotating primordial black holes. J. Cosmol. Astropart. Phys. 2016, 10, 34. [Google Scholar] [CrossRef]
- Carlip, S. Dimension and Dimensional Reduction in Quantum Gravity. Class. Quant. Grav. 2017, 34, 193001. [Google Scholar] [CrossRef]
- Abajian, J.; Carlip, S. Dimensional reduction in manifoldlike causal sets. Phys. Rev. D 2018, 97, 066007. [Google Scholar] [CrossRef]
- Carlip, S. Dimension and Dimensional Reduction in Quantum Gravity. Universe 2019, 5, 83. [Google Scholar] [CrossRef]
- Saueressig, F.; Khosravi, A. Black hole remnants from dynamical dimensional reduction? Phys. Rev. D 2022, 105, 066015. [Google Scholar] [CrossRef]
- Calcagni, G. Quantum gravity and gravitational-wave astronomy. Phys. Rev. D 2017, 96, 046001. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S.; Marsat, S.; Sakellariadou, M.; Tamanini, N.; Tasinato, G. Gravitational-wave luminosity distance in quantum gravity. J. Cosmol. Astropart. Phys. 2019, 10, 12. [Google Scholar] [CrossRef]
- Carlip, S.; Grumiller, D. Lower bound on the spectral dimension near a black hole. Phys. Rev. D 2011, 84, 084029. [Google Scholar] [CrossRef]
- Calcagni, G.; Rodríguez Fernández, D.; Ronco, M. Black holes in multi-fractional and Lorentz-violating models. Eur. Phys. J. C 2017, 77, 335. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bellini, M. Effective dimensionality of space-time in f(R)-general relativity with quantum boundary terms included. Eur. Phys. J. C 2024, 84, 1270. [Google Scholar] [CrossRef]
- Bellini, M. Preinflation: Quantum nature of space-time to explain dark energy and the cosmological parameter. Ann. Phys. 2025, 476, 169973. [Google Scholar] [CrossRef]
- Magos Cortes, D.; Bellini, M. Seminal electromagnetic fields from preinflation. Astrop. Phys. 2024, 163, 103006. [Google Scholar] [CrossRef]
- Palatini, A. Deduzione invariantiva delle equazioni gravitazionali dal principio di Hamilton. Rend. Circ. Mat. Palermo 1919, 43, 203. [Google Scholar] [CrossRef]
- Rumpf, M. Stochastic quantization of Einstein gravity. Phys. Rev. D 1986, 33, 942. [Google Scholar] [CrossRef] [PubMed]
- Bellini, M. Ricci flow in general relativity: Dynamics of gluon fields on an arbitrary curved background from unified spinor fields. Phys. Scripta 2021, 96, 065301. [Google Scholar] [CrossRef]
- Velten, H.; Caramês, T.R.P. To conserve, or not to conserve: A review of nonconservative theories of gravity. Universe 2021, 7, 38. [Google Scholar] [CrossRef]
- Bonder, Y.; Herrera, J.E.; Rubiol, A.M. Energy nonconservation and relativistic trajectories: Unimodular gravity and beyond. Phys. Rev. D 2023, 107, 084032. [Google Scholar] [CrossRef]
- Carballo-Rubio, R.; Garay, L.J.; García-Moreno, G. Unimodular gravity vs general relativity: A status report. Class. Quant. Grav. 2022, 39, 243001. [Google Scholar] [CrossRef]
- Landau, S.J.; Benetti, M.; Perez, A.; Sudarsky, D. Cosmological constraints on unimodular gravity models with diffusion. Phys. Rev. D 2023, 108, 043524. [Google Scholar] [CrossRef]
- Fabris, J.C.; Daouda, M.H.; Velten, H. Spherically Symmetric Configurations in Unimodular Gravity. Universe 2023, 9, 515. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Eiroa, E.F.; Figueroa-Aguirre, G. Charged thin shells in unimodular gravity. Eur. Phys. J. C 2024, 85, 623. [Google Scholar] [CrossRef]
- Salvio, A. Unimodular quadratic gravity and the cosmological constant. Phys. Lett. B 2024, 856, 138920. [Google Scholar] [CrossRef]
- Stojkovic, D. Vanishing dimensions: A review. Mod. Phys. Lett. A 2013, 72, 1330034. [Google Scholar] [CrossRef]
- Afshordi, N.; Stojkovic, D. Emergent Spacetime in Stochastically Evolving Dimensions. Phys. Lett. B 2014, 739, 117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellini, M.; Musmarra, J.I.; Sánchez, P.A.; Morales, A.S. Spectral Dimensionality of Spacetime Around a Radiating Schwarzschild Black-Hole. Universe 2025, 11, 243. https://doi.org/10.3390/universe11080243
Bellini M, Musmarra JI, Sánchez PA, Morales AS. Spectral Dimensionality of Spacetime Around a Radiating Schwarzschild Black-Hole. Universe. 2025; 11(8):243. https://doi.org/10.3390/universe11080243
Chicago/Turabian StyleBellini, Mauricio, Juan Ignacio Musmarra, Pablo Alejandro Sánchez, and Alan Sebastián Morales. 2025. "Spectral Dimensionality of Spacetime Around a Radiating Schwarzschild Black-Hole" Universe 11, no. 8: 243. https://doi.org/10.3390/universe11080243
APA StyleBellini, M., Musmarra, J. I., Sánchez, P. A., & Morales, A. S. (2025). Spectral Dimensionality of Spacetime Around a Radiating Schwarzschild Black-Hole. Universe, 11(8), 243. https://doi.org/10.3390/universe11080243






